1. Introduction
Network traffic modeling and analysis is a crucial issue to ensure the proper performance of the ICT system (Information and Communication Technologies), including the IoT (Internet of Things) and Industry 4.0. This concept defines the connection of many physical objects with each other and with internet resources via an extensive computer network. The IoT approach covers not only communication devices but also computers, telephones, tablets, and sensors used in the industry, transportation, etc. Changes in network development concepts and paradigms are a vital process in the current telecommunications arena. There is a transition from the Next Generation Network concept (NGN) to the Internet of Things (IoT), Ubiquitous Sensor Network (USN), Machine to Machine (M2M), and other proposals. The main reason for the change is the broad application of wireless sensor nodes and RFID (Radio-Frequency IDentification). According to forecasts, by 2020, it is expected that more than seven trillion wireless devices will be connected to the network [
1].
The IoT has gained considerable popularity in recent years. The idea behind the IoT is to extend everyday activities with computing power and internet connections and to enable them to detect, calculate, communicate, and control the surrounding environment. Existing IoT communication is dependent not only on modern cellular networks but also on home networks, usually connected to fiber-optic networks. Current networks sufficiently meet the requirements of existing IoT equipment. However, the projected future massive increase in IoT data traffic may be too much for existing mobile communication systems (3G, 4G, etc.) to handle, so it is necessary to implement 5G technology as soon as possible. IoT traffic is usually different from regular traffic, such as video conversations or file transfers. IoT data are mainly generated by a large number of IoT devices in the form of small packets and are mainly based on narrowband applications. User-generated regular data traffic appear from a small number of mobile devices in the shape of large packets [
2].
Network traffic monitoring and analysis (NTMA) is a critical element of network management, primarily to ensure the proper functioning of large IoT networks. As the complexity of internet services and the volume of traffic continue to increase, it becomes challenging to design scalable NTMA applications. Appropriate performance models require accurate traffic models that can capture the statistical characteristics of actual activity. This article shows that estimating the value of Hurst’s exponent allows for the analysis of current traffic patterns for the prediction of the future trend of data behavior, both of which can help in ensuring security and detecting attacks or other anomalies in network operations. By correctly estimating the Hurst parameter and creating appropriate patterns, it is possible to prepare for disturbing situations and to react to changes in the trends. Sudden deviations in the value of the exponent that concern the obtained base results probably signify problems and testify to the unusual behavior of the network, which is possibly related to cybercrime or network failure. Such traffic analysis methods can be ideal to protect critical data and maintain the continuity of offered internet services [
1,
2,
3,
4,
5].
The characteristics of individual samples, investigated during long-term and multifractal analyses, differ depending on the character of the network traffic. In cases when there are data sets that are storing records of traffic flowing through the tested communication network, it is possible to detect the nature of the traffic by analyzing samples from different periods of the network operation. In this way, by using long-term and multifractal analyses, it is possible to detect the anomalies of network traffic. The results of regular network operation analyses should be consistent with the results contained in the database. In the case of detecting anomalies or performing an attack on a given network, the analysis of samples of the infected network traffic should differ from the analysis of properly flowing traffic. Since the objects in the IoT are directly connected to the unsafe internet, the attacker can easily access the device’s limiting resources. Such public access to the internet makes things susceptible to hacking.
Our article aims to propose a comprehensive and practical introduction to the application of multifractal analysis in the study of traffic in the IoT network. The theoretical basis is defined, and the problems and traps related to the choice of scaling range, minimal regularity, spectrum approximation, and parameter estimation are discussed. It is shown that multifractal analysis is related to the other standard features of network traffic variability. This multifractal analysis aims to provide a global analysis of data variability [
6]. Because geometric structures are inherited from the evolution of data over time, multifractal analysis globally measures the local dynamics (or variability) of the analyzed bounded function. This measure is based on the Eh Hausdorf dimension and is referred to as a multifractal spectrum. The multifractal analysis provides powerful tools to understand the complex non-linear nature of time series in different fields [
7].
2. Literature Review
Network traffic can be stored both as an increasing number and as a sequence of intervals between adjacent events. The oldest model of the stream is the Poisson process. As a result of research on real network traffic, an internal correlation in streams was observed. The model based on the Poisson process did not take into account this feature of the generated traffic. Thus, subsequent models were developed that more accurately reflected the real character of the traffic flow in the network. However, many of them are characterized by autocorrelation, which disappears very quickly (exponentially). These are the so-called processes of short memory. The Poisson process has been used to model incoming connections in telecommunication networks due to its analytical simplicity. However, it is unsuitable for new types of network traffic that have emerged from basic internet protocols such as Transmission Control Protocol (TCP) and applications such as TELNET and FTP (File Transfer Protocol). New applications, such as video streaming, bring with them new traffic models that are necessary for traffic engineering. A detailed study of the different traffic characteristics in the IoT network is still not available, so in our work, we deal with this problem. The studies presented in [
4] showed that models using Poisson’s decomposition are not able to accurately reflect the explosiveness of TCP/IP traffic. Only the use of models of self-similar traffic enables the realistic rendering of TCP/IP traffic. Self-similarity is a phenomenon that retains the statistical properties of the model despite changes in the applied time scale. The most visible feature in the characteristics of network traffic that indicate the occurrence of self-similarity is the occurrence of densities and dilutions at intervals between events and the lack of blurring of this feature despite the use of several different time scales (e.g., seconds, minutes, and hours) [
5,
8]. Meanwhile, the development of new network services has caused traffic to change its characteristics. Currently, network traffic, especially in IoT infrastructure, is characterized by a much stronger, long-distance correlation.
Nowadays, the internet is based on the Internet Protocol (IP), which is managed by the Internet Engineering Task Force (IETF). The use of IP addresses to identify connected devices and traffic has become entirely natural. Therefore, one might think that a similar analogy could also be used in IoT for compliance purposes, but this is not so obvious. The industry has developed many other wireless communication technologies and networks to meet the needs of IoT applications, leading to numerous interoperability problems. Many providers have started without support for IPv6 but are slowly integrating it, which will allow us to apply our traffic analysis methods. Network traffic in the IoT contains a sequence of packets with incremented timestamps that represent a time series. Time series data represent a set of values obtained from sequential measurements in time. The traffic time series can also be used to monitor security. An analysis of anomalies in network traffic patterns can be used to detect the irregular behavior of intelligent devices caused by failures or security breaches. Currently, the IoT ecosystem offers many devices with a low-security level, which poses a high threat to the IoT system and enables distributed denial of service attacks (DDoS). Monitoring network activity from these devices to centralized hosts (or any other destination) is significant in ensuring the early detection of intrusions [
9]. Network traffic contains much useful information about the type of devices, users and applications used. Therefore, an analysis of this traffic is useful not only in detecting intrusions but also in identifying applications, classifying the use of services in applications, etc. [
10].
The idea of describing natural phenomena through the study of statistical scaling laws is not new. The authors in [
11] presented many studies that have been conducted on this subject, including those by Bachelier (1900), Frish (1995), Kolmogorov (1941), and Mandelbrot (1963). The main feature of fractal geometry is its ability to describe the irregular or fragmented shape of natural features and as other complex objects which traditional Euclidean geometry cannot analyze. This phenomenon is often expressed by the spatial or temporal laws of statistical scaling and is characterized by the maintenance of the power-law of real physical systems. This concept allows for simple, geometric interpretation and is often found in various fields such as geophysics, biology and fluid mechanics. Fractal geometry is widely used in general problems with image analysis, especially in medicine. It is applied in different ways with different results [
11].
In recent years, the analysis of long-term temporal relationships has become more critical. The topics of self-similarity and long-range dependence (LRD) in time series have become trendy fields of research [
12]. The most commonly used measure of self-similarity is the value of Hurst coefficient, H, introduced by hydrologist H.E. Hurst based on the observation of Nile level fluctuation. The closer the H value is to 1, the more clearly the phenomenon shows a self-similar character [
3].
A recent analysis of the traffic measurements from different communication networks showed that traffic is long-range dependent or fractal (self-similar). These developments revolutionized the understanding of network traffic by explaining the difference between theoretical performance estimates and performance measured in practice. In network traffic, long-range dependence corresponds to the slow decaying autocorrelation function and the heavy-tailed behavior of the probability density function.
There are various statistical techniques for estimating the Hurst parameter. By definition, the LRD phenomenon is related to the maintenance of the power-law of some second-order statistics (variance, covariance, etc.) of the process concerning the duration of observation. Many Hurst estimators are therefore based on the idea of measuring the slope of the linear adjustment on a log–log graph. Estimators of Hurst parameters can be divided into two categories: those operating in the time domain and those operating in the frequency domain. However, traditional estimators can be seriously biased. The rescaled range (R/S) estimator has poor statistical performance, with a high deviation and suboptimal variance. The estimator of discrete discomfort is only asymptotically impartial. An asymptotic set-up is not sufficient for a good estimator, which must be impartial, robust, and efficient [
9]. Our article aims to emphasize the superiority of the Hurst parameter estimator based on a multifractal spectrum.
Therefore, Hurst’s exponent can be considered a quantitative method of describing, e.g., traffic in computer networks or the IoT, determining its characteristics that describe overloads or states deviating from the accepted standards. In other words, changes in the intensity and characteristics of the traffic are significant for each other.
In [
13], a systematic literature review (SLR) of the Intrusion Detection Systems (IDS) in the IoT environment has been presented. Then detailed categorizations of the IDSs in the IoT—anomaly-based, signature-based, specification-based, and hybrid; centralized, distributed, and hybrid; simulation and theoretical; and denial of service attack, Sybil attack, replay attack, selective forwarding attack, wormhole attack, black hole attack, sinkhole attack, jamming attack, and false data attack—were also provided by using standard features. The authors discussed the advantages and disadvantages of the selected mechanisms, and directions for future trends were also provided.
LRD is a relatively new statistical concept in time series analysis and has been empirically shown to exist in many fields such as engineering, astronomy, finance, statistics, and hydrology. The analysis of real data is a challenge for both engineers and researchers. Therefore, LRD has been increasingly used in data analysis, including traffic.
In order to increase efficiency, the authors of [
8] used Multifractal Detrended Fluctuation Analysis (MDFA) for the multifractal analysis of discharge signals. Spectral studies of q-order Hurst, mass exponents and multifractals revealed differences between different voltage values applied to different types of signals (electrical and acoustic). The simulated HFD (Higuchi Fractal Dimension) and MDFA algorithms have proven to be useful in the real-time detection and analysis of pressure plate failures where early warning can prevent insulation system malfunctions. Additionally, the simultaneous analysis of electrical and acoustic signals using a synergy of these methods enhances the efficiency of the proposed system.
The authors in [
7] showed that the multifractal analysis of financial data for one and multidimensional time series arouses great interest in the community of ecophysics, mainly due to the invention of new methods and easier access to a massive amount of financial data. Many new methods of multifractal analysis are still being proposed, most of which are variants of existing classical methods. This paper presents some examples of multifractal analysis used in quantifying market inefficiencies, supporting risk management, and others.
The critical task in the empirical multifractal analysis is to determine the appropriate scaling range based on which scaling exponents are estimated. Usually, a small change in the scaling range results in significant changes in the estimated exponents. Very short time series can give “wrong” estimates because the estimated multifractal properties usually deviate more from shorter time series, as confirmed by the log–Poisson binomial. In addition, the estimated generalized Hurst exponents may significantly differ from the expected values, especially in the case of short time series. Therefore, statistical tests are necessary for empirical multifractal analysis. It is often the case that scaling exponents and multifractal spectrum derived from empirical time series are problematic, especially when there are linear or non-linear trends in the time series. The result is an erroneous estimation of the degree and nature of the multifractal, which has harmful effects on the understanding of network traffic behavior. The choice of scaling range is most important and challenging for short-term series [
7,
14,
15].
The authors in [
1] stipulated that models in networks with a large number of sensors and RFID should be well researched. The authors also analyzed USN motion models, and the test results showed that the traffic flows for fixed and mixed fixed/moving sensor nodes are self-similar with an average level of similarity in both cases. The motion flow for reconfiguration and signaling was found to be self-similar with a high level of self-similarity.
The area of anomaly detection in networks has attracted much attention in recent years, especially with the development of interconnected devices and social networks. The detection of anomalies covers a wide range of applications, from the detection of terrorist cells in anti-terrorist operations to the identification of unexpected mutations during the transcription of ribonucleic acid. Accordingly, many algorithmic anomaly detection techniques have been implemented. In the paper of [
16], a statistical evaluation of a set of popular spectral methods for the detection of anomalies in networks was carried out. The presented studies revealed several essential and critical shortcomings. The authors evaluated the performance of these algorithms by using simulated networks and extended the methods from binary to count networks.
Applications such as traffic classification and police control require a scalable approach in real-time. Anomaly detection and security mechanisms require the rapid identification and response of unforeseen events in the processing of millions of different events. The system must collect, store and process enormous collections of historical data in a post-mortem analysis. The authors in [
17], based on questionnaires, developed guidelines for future work on anomaly detection, conclusions, and research directions.
According to the authors of [
18], the manual (human-based) handling of anomalies in complex systems is not recommended, and automatic and intelligent handling is the right approach. In the article, the authors presented many case studies, challenges, and possible solutions for the implementation of computerized anomaly detection systems.
There are many approaches to the problem of anomaly detection. The authors of [
19] presented a method for detecting network anomalies based on a fuzzy cluster. The proposed method consisted of three stages: preprocessing, function selection, and clustering. The performance indicators used were cluster correctness, accuracy, and a false–positive ratio. According to the authors, the proposed method achieved better results in comparison to other methods.
The most known models of long-range dependent processes are the fractional motion of Brown (fBm) and fractional autoregressive integrated moving average (FARIMA) [
10]. In the context of Ethernet traffic, it should be noted that data are not stationary due to hidden periods, daily cycles, failures, various anomalies, etc. However, it is reasonable to expect that data will be stationary for smaller timescales when network conditions are relatively stable. Thus, Ethernet traffic is stationary at some scales and not stationary at other scales. Random data entry can be a general trend. These trends are the source of the transient state for a random input process. Estimating the Hurst parameter is necessary to detect the presence of LRD in a time series [
12].
Internet traffic monitoring is a crucial task for network security. To detect anomalies, the authors of [
20] proposed a multidimensional, self-similar model called the fractional operator BrownianMotion (OfBm) for a conventional similarity analysis in bytes and packets. A non-linear regression procedure based on the original branching and boundary solving procedure were developed in order to fully identify the two-dimensional OfBm. The proposed procedure for detecting anomalies of internet traffic used the Hurst exponent vector underlying the modeling of internet data based on OfBm.
Cyber-attack technologies are constantly being developed, and the number of new threats is steadily growing. In the article [
21], an innovative method of anomaly detection based on the estimation of self-similarity of systems and networks was proposed. As in our article, self-similarity properties, which are characterized by the Hurst parameter, were also used. By using the proposed method, the status of the network and system anomalies was determined through the calculation of the change of similarity value. The effectiveness and efficiency of this approach were developed based on the Defense Advanced Research Projects Agency (DARPA) Intrusion Detection Evaluation dataset created in 1999.
A different approach to the detection of anomalies was proposed in [
22]. The authors assumed that the time series of traffic flows should be considered a Poisson’s non-stationary process related to superstatistical theory. According to the superstatistical theory, a complex dynamic system can have a significant fluctuation of intense magnitude at large time scales, which causes the system to behave as non-stationary and non-linear, which are also features of network traffic flows. This idea provides a new way of dividing transient traffic time series into small stationary segments that can be modeled using Poisson’s distribution in sub-second time scales. To distinguish between normal traffic and anomalous traffic, the Hurst parameter was calculated and compared.
4. The Methodology of Network Traffic Anomaly Detection Study
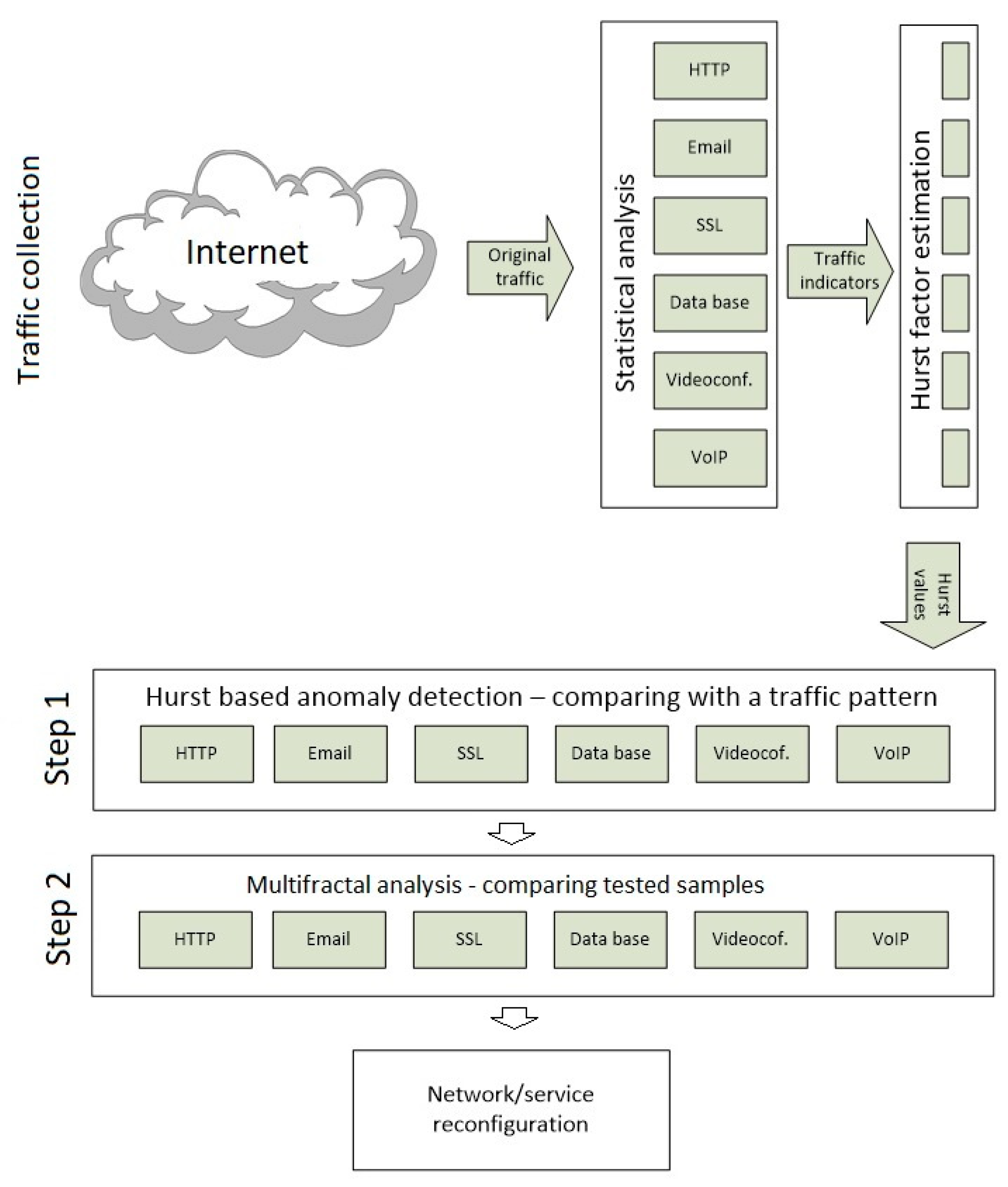
The network traffic pattern for each IoT device differs according to the type of protocol or communication technology used by the manufacturer. Nevertheless, the observation of traffic shows similarities. In order to achieve a precise analysis, it is therefore essential to find common traffic patterns for devices in a given category and to exclude similarities between devices in different categories. Our proposed approach allows us to analyze this problem and identify the device by making full use of hidden correlations and unchanging patterns from the flows of the underlying IoT network. When connected to a network, IoT devices generate traffic (incoming and outgoing) depending on some configuration features and application services. While different devices in a network can use different protocols and transfer data for different purposes, the vast majority of this traffic uses TCP/IP protocols. These packets include network configuration traffic (e.g., Network Time Protocol (NTP) and Domain Name System (DNS)) and routine communication between the device and the server. Therefore, our research was based on TCP/IP traffic analysis. Due to the wide implementation of security protocols such as the Secure Sockets Layer (SSL), Transport Layer Security (TLS), and Privacy Policy, only the packet header can be used to classify traffic. From traffic volume, packet length, network protocols, and traffic direction, i.e., incoming and outgoing, it is possible to separate user packets and control packets. User packets include user data and server–device communication packets (TCP, UDP - User Datagram Protocol, HTTP - Hypertext Transfer Protocol or other multi-layer protocols). Control packets support mainly functional protocol packets such as ICMP (Internet Control Message Protocol), ARP (Address Resolution Protocol), DNS, and NTP packets. The scheme of network traffic anomaly detection based on self-similarity consisted of a few modules: traffic collection, statistical analysis, statistical estimation and anomaly detection (
Figure 1).
To reduce the impact on normal network usage, when collecting local area network (LAN) traffic, the traffic on the router is reflected on the traffic collection server. Packets received from the router are processed. One can extract some traffic parameters, such as the number of packets and the total length of the packet. The purpose of the study was to observe traffic on the network and determine whether there were long-term dependencies throughout the network operation time and overtime intervals. In order to perform the work of all intercepted packets, we extracted those that had the most significant impact on the network. They were divided into main groups in terms of services and protocols: HTTP, HTTPS (HTTP Secure), Unknown, IP Security (IPsec), DNS, Secure Shel (SSH), and others.
The following statistical values of the selected traffic indicators were then calculated. The first step is to check if the traffic is stationary (h > 0.5). If so, a spectral analysis is performed to compare the current traffic patterns with the adopted safe working model. The values can be used to detect traffic anomalies. The calculated Hurst value is compared with the normal traffic model. If the value of the H parameter differs from the base value in the regular traffic model, the current traffic is considered to be anomalous. It is assumed that the Hurst parameter remains relatively stable.
A crucial task in assessing the security of the IoT system is to find the right features of the observed network traffic (directly measurable features) and/or the combination of these features (derivative features). These features should be linked to anomalies. This information can be useful to identify what is happening in the system and how to prevent it. As a rule, such devices can fulfill their function as mechanisms of initial traffic analysis for manual log analysis, but they are entirely useless for an automatic reaction.
To work with automatic response systems, the anomaly analysis system must be able to provide necessary information to the rules governing reactions. Information about the detection of an anomaly should go to the appropriate agent systems, which should take appropriate action. It can be concluded that each parameter identified and tested by the anomaly recognition system should be associated with an object that is identifiable in network traffic by other security measures, mainly by remotely managed network filters. Network filters operate in different layers of the ISO/OSI model (International Organization for Standardization/Open System Interconnection Reference Model). For each layer, network communication protocols, which uniquely define the form and format of the transmitted information units, are assigned. Based on experience and historical data, the parameters describing the behavior of network traffic can be related to weekdays, seasons, or working hours, as well as the use of characteristic phrases in the content of the transmitted information indicating the so-called “data leakage.” When using the Hurst parameter and spectral spectra, or, more precisely their deviations from the standard values, one could consider them as symptoms of unauthorized actions. The proposed method is based on the identification of anomalies in the current time window based on correct samples in the standard profile. For each interval, the value of the exponent was estimated in the first stage in order to determine the character of the motion and to determine the trend. If the similarity was confirmed, in the next step, the tested motion samples were checked for multifractal dependencies.
The article used data from the Internet Data Analysis Centre (CAIDA) [
30]. The obtained data encompass a set of passive network traffic tracked on a commercial backbone network. The institution mentioned above started collecting data in 2008 and has continued to do so day. Until 2014, data collection took place at the Chicago and San Jose nodes. In the years 2015–2016, traffic was recorded only at the Chicago nodes, but it was moved to New York in 2018. CAIDA analyzes, among other things, types of protocols, and it maintains daily statistics that are available on the organization’s website.
Figure 2 shows an example of generated statistics that show the number of transmitted packets per second, depending on the type of application.
The latest available downloadable data sets were selected for analysis. The first set consisted of measurements made in 2016. The packets were captured at the Equinix data center in Chicago. The measurements were taken over several days of sessions from January to April. The second set of data came from the Equinix data center in New York. The recording of intercepted traffic also took place on several-day sessions from March to May 2018. To ensure a meaningful comparison of the network traffic dependencies, different time periods were analyzed, and two sets of data were selected for each month. Dataset A (sample A) was related to data transmission at the Seattle–Chicago node for 2016 and the Sao Paulo–New York node for 2018. Dataset B (sample B) refers to data transmission in opposite directions at these nodes.
Table 1 contains the specific properties of all traffic samples extracted from the downloaded datasets.
5. Results
The determination of the Hurst coefficient for samples that store fragments of network traffic were done with the OriginPro 2017 software. This application was used to analyze various types of data. It also allowed us to generate graphs based on the data. To estimate the value of Hurst, the Hurst Exponent tool was used along with the rescaled range (R/S) method.
For the fractal analysis of data, the Matlab R2014a software and Fraclab 2.1 tool, specializing in processing images and signals utilizing fractal and multifractal analysis, were used. Thanks to a large number of implemented procedures, it was possible to calculate various fractal quantities, such as fractal dimension, Hӧlder exponents, and multifractal spectra.
5.1. Network Traffic Stationery and Spectrum Analysis—General Information
The proposed process of anomaly detection by comparing multifractal spectra following the presented concept must be preceded by the verification of the character of the traffic, i.e., its stationary character. The values of standard deviations differ depending on the sample and the average length of the data packets of the sets. In the case of the 2016 samples, the changes in the deviations were small. This means that for the data in sample B for 2016 with the higher average packet lengths, the standard deviation (defining the scattering of values around the mean) was lower compared to those in sample A. On the other hand, the standard deviations of the 2018 data samples was proportionally varied to the average size of the data packet.
Minor differences could be observed, especially for data samples A and B of 2018. For these sets, the discrepancy between the compared results was significant. In the case of variance, the values for each sample were distributed in a similar way to the results of the standard deviations.
The analysis of network traffic samples from 2016 and 2018 consisted of determining the estimated values of Hurst’s exponent and setting different intervals dividing the data into sub-series. The size of these intervals was selected within the range of multiples of number 2 from 21 to 211. Based on the results of estimates using the OriginPro 2017 tool, a graph of the Hurst’s exponent distribution was generated for each tested network traffic sample. The estimation of Hurst’s exponent value for network traffic samples consisted of the 30 thousand records allowed for the evaluation of the characteristics of the given traffic sample.
On the strength of the data, an upward trend in the calculated exponent values could be observed. The phenomenon presented above may have been caused by the characteristics of network traffic changes over time. The development of the IoT caused an increase in the number of new devices generating network traffic, which had an impact on the changing characteristics of packet flow in the network. Only one average estimated value reached a level below 0.7. The difference between the extreme values was approximately 0.09. This means that the probability of a given trend continued to differ by less than 10%. The average for all data in sample A for 2016 and 2018 was 0.735 (Figure 5). In the case of direction B, a difference between the samples from 2016 and the 2018 packet sets was visible. These discrepancies may have been the result of the influence of different nodes on which the packet transmissions took place. The balanced measurements of Hurst’s exponent for the first set of samples were much higher and exceeded 0.7. The average for these samples was 0.747. The average for 2018’s data set B was 0.611. The difference between the extreme values for all samples was 0.196. The average was estimated at 0.689, so the traffic was persistent and showed long-term dependencies despite the observed differences.
For the traffic flow recorded in 2016 between the Seattle and Chicago nodes, the calculated Hurst exponent value was the same for samples A and B. Much higher discrepancies could be seen between the Sao Paulo and New York nodes. The average for all tested samples was 0.712. Based on the definition of Hurst’s R/S estimation, it could be confirmed that network traffic in the tested backbone network had long-term properties.
Table 2 presents a summary of the mean values of Hurst’s exponent for all tested network traffic samples.
In order to see whether there were no disturbances (anomalies) in the network, the samples were subjected to spectral analysis. All samples were analyzed using three methods. Then, the results of spectrum-generating functions were compared with each other in order to determine the multifractal dependencies.
The first method of analysis was a function of determining the Legendre spectrum. It was a more natural way of analysis, but it is associated with the loss of information. Unlike, for example, finite element methods, spectral methods, the spectral accuracy cannot accurately handle an arbitrary, locally refined grid. The locally refined grid cannot be smoothly mapped to the standard spectral grid. In the general setting, the use of spectrum analysis implies a loss of some information because the Legendre spectrum is always a concave function. It is necessary to use this type of analysis along with the significant deviation approach to make its estimation easier and robust.
The second method is the function of estimating the spectrum of significant deviation, which carries more information by forming the determined values and the spectrum itself. To quickly evaluate the Legendre spectra, the third option of determining the spectrum measure was used, a method that allowed for the fastest estimation of the value in comparison with the Legendre spectrum function.
Each of the methods of multifractal spectrum analysis presented a different profile of the behavior of the tested network traffic sample. The values generated by the Legendre spectrum for all tested samples were arranged into a standard scheme that characterized the traffic data. This also applied to the broad deviation spectrum. In order to compare all the spectra, they were divided according to the type of spectrum and the node from which they originated.
5.2. Case of Normal Traffic State
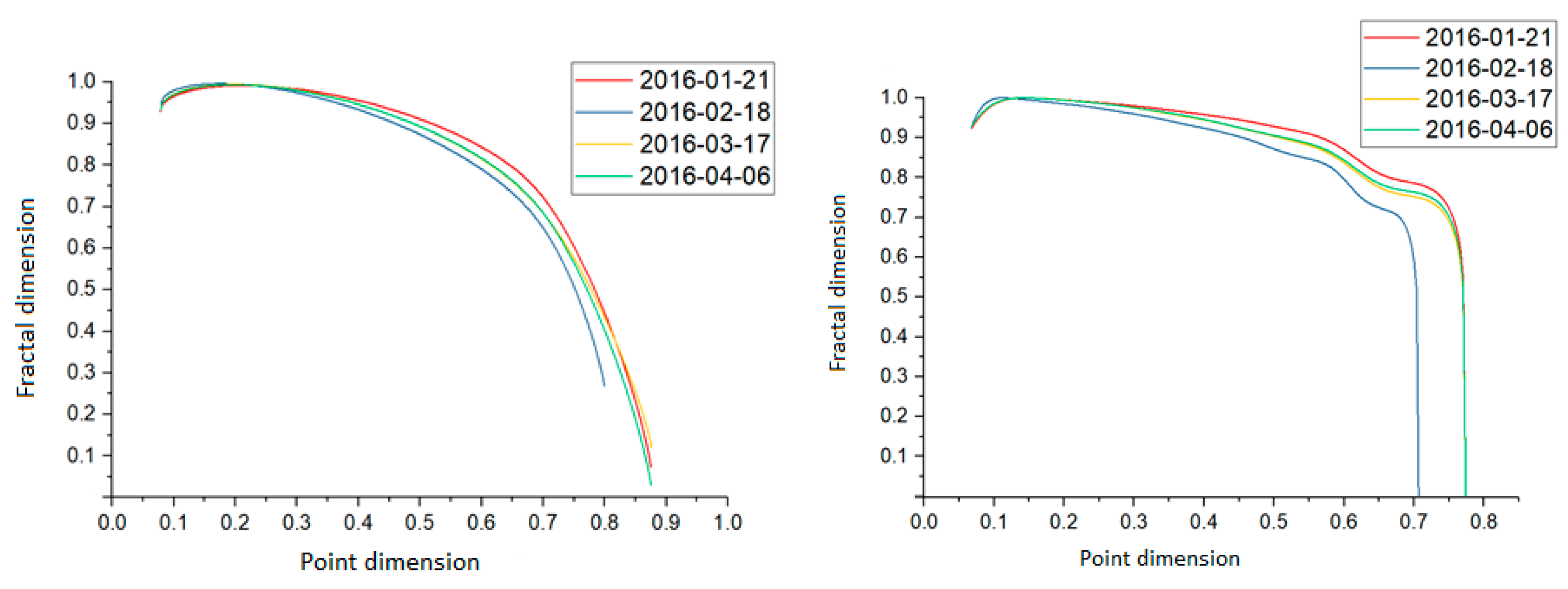
The analysis of data transmitted at the Chicago–Seattle node in 2016 (direction B) is shown in
Figure 3 and Figure 6. The distribution of Legendre’s spectra and the spectra of significant deviation are shown in the left and right graphs of
Figure 3, respectively.
The spectra generated for these packet sets had very similar characteristics. Both the first and the middle phase of the spectra were the same for all types of samples. Differences occurred only at the level of the final values of the fractal dimension. Therefore, these spectra confirmed the self-similar nature of the network traffic, as shown in the form of a time course of the length of packets flowing through the network.
The analysis of the spectra determined by the lines did not show any aberration, contrary to the analyzed sample A. All the spectra of significant deviation showed an entirely similar feature, which indicated the similarity of the flowing traffic. Possible anomalies occurring at the node could be immediately detected by a data sample that was strongly distant from the spectra visible on the graph.
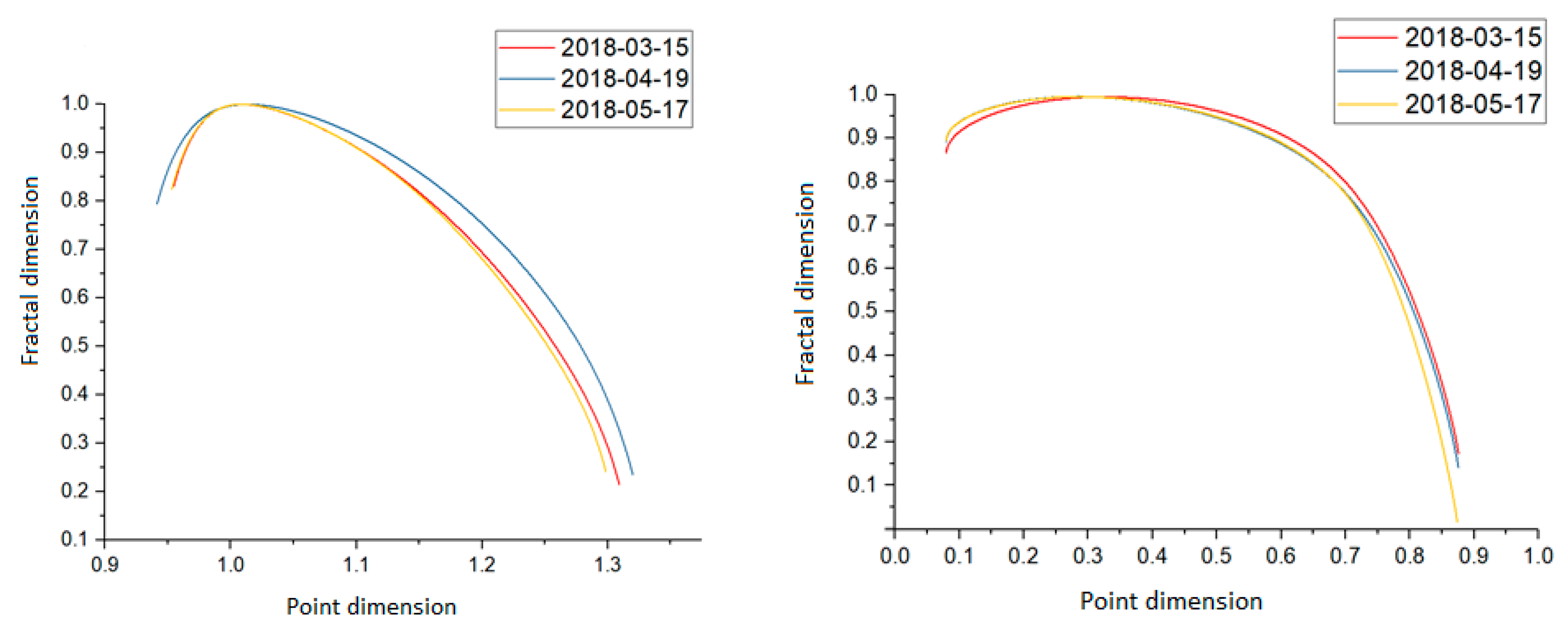
A detailed analysis of subsequent samples of the 2018 data is presented in
Figure 4. In detail,
Figure 4 presents the Legendre spectra and the distribution of the significant deviation spectra for the three tested sample A in the left and right graphs, respectively.
The Legendre’s spectra for these sample sets also had similar estimations. One could see a clear trace of the creation of a path of spectral value values for this data set. By analyzing new samples from other packet tracking series for this node in the future, one will be able to compare new results with those already obtained. If they overlap or the waveform is similar, the database of the nature of the movement will be enlarged. In the case of a sample containing an unusual movement associated with a network attack, the estimation of this spectrum should significantly differ from the path determined by the standard data flow, which will allow the detection of anomalies or threats.
Each of the spectra obtained had similar fractal dimension values. They did not show any deviation from the norm, as determined by the resulting path of the significant deviation spectra. The final phase overlapped for all spectra. Slight deviations occurred in the first and middle phases of the waveforms, but all of them were very close to each other.
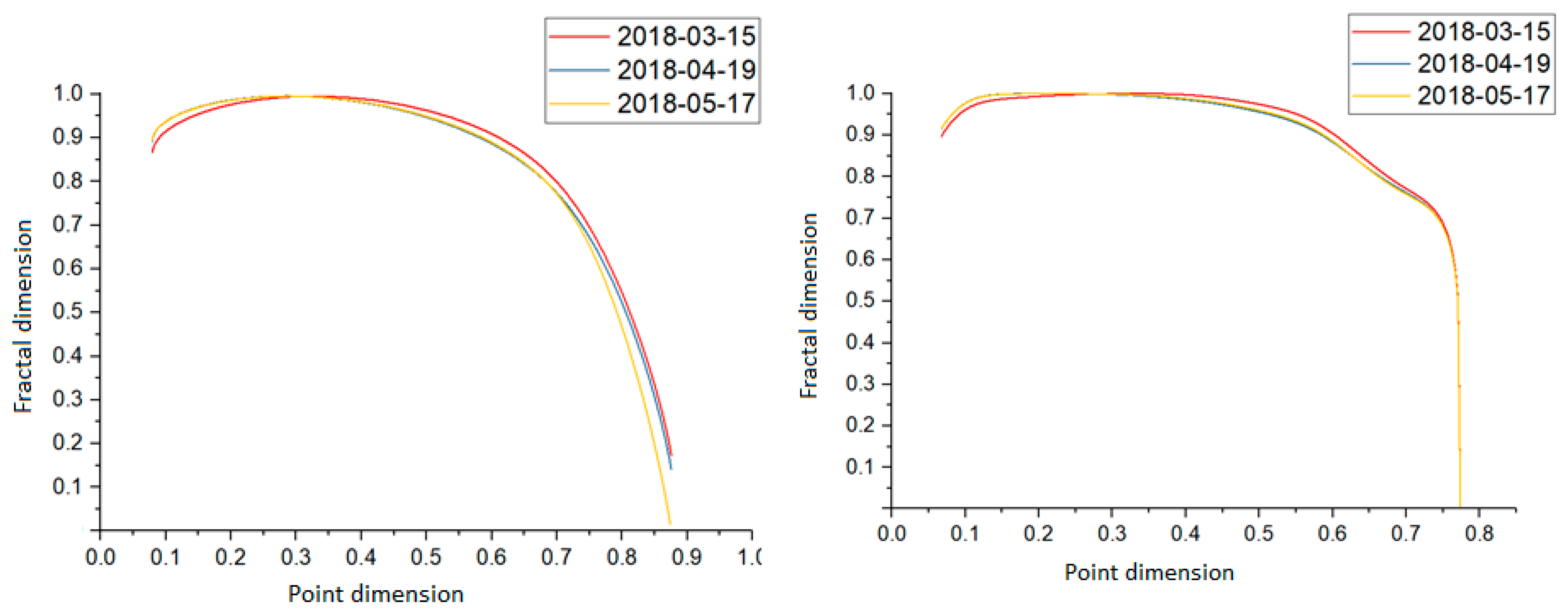
Figure 5 shows the Legendre spectra for the 2018 sample A generated by a faster measurement method and the distribution of the Legendre spectra for the 2018 sample B in the left and right graphs, respectively.
Despite the analysis of the data generated at another node, the results showed that the traffic flow was very similar to the set of sample B from 2016. The range of the point dimension, in which all the values of the fractal dimension fell, was also very similar. The characteristics of these spectra did not show any characteristic features. They did not show any significant deviation from each other, which may suggest that the sample data indicated a typical traffic path in which there were no symptoms associated with a network attack or suspicious packet flow. The significant deviation spectra for sample B taken from the New York–Sao Paulo node are shown in
Figure 6 (left graph).
The first phases of the spectra began in a similar value area. The subsequent phases of estimation ran in a very similar way, aiming at almost a typical end of the fractal and point dimension. There were no significant deviations in the results, which may suggest a similar conclusion to the Legendre spectra generated for this data set.
Figure 6 (right graph) shows a set of the Legendre spectra analyzed with a measure of value.
The interval of the point dimension, which contained the determined fractal values of the spectra, shifted towards slightly lower values than in the case of all the previously analyzed network traffic samples. The beginnings of all the spectra for the 2018 dataset B had different areas of the fractal dimension value concerning the point dimension. The subsequent phases overlapped or were very close to each other, which revealed a very similar nature of the estimation of the spectra of these samples.
5.3. Case of Anomaly Detection
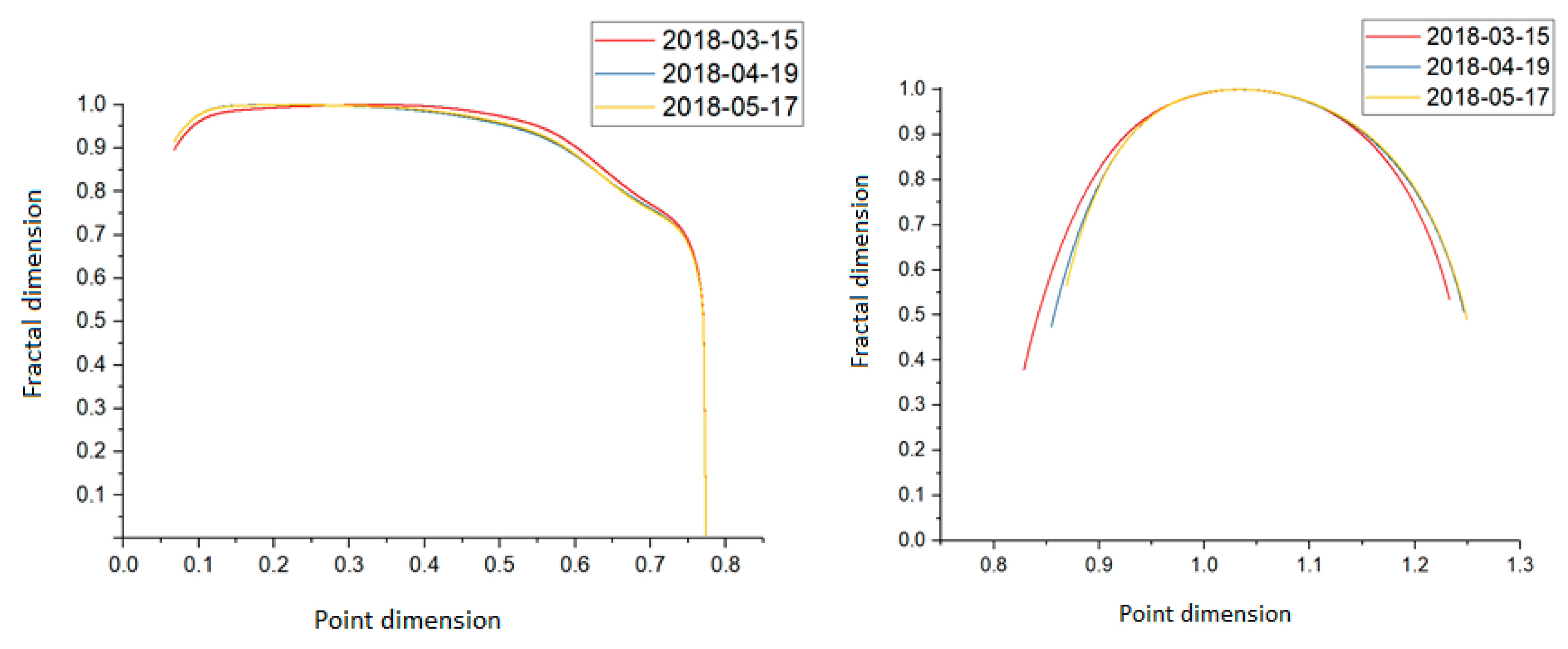
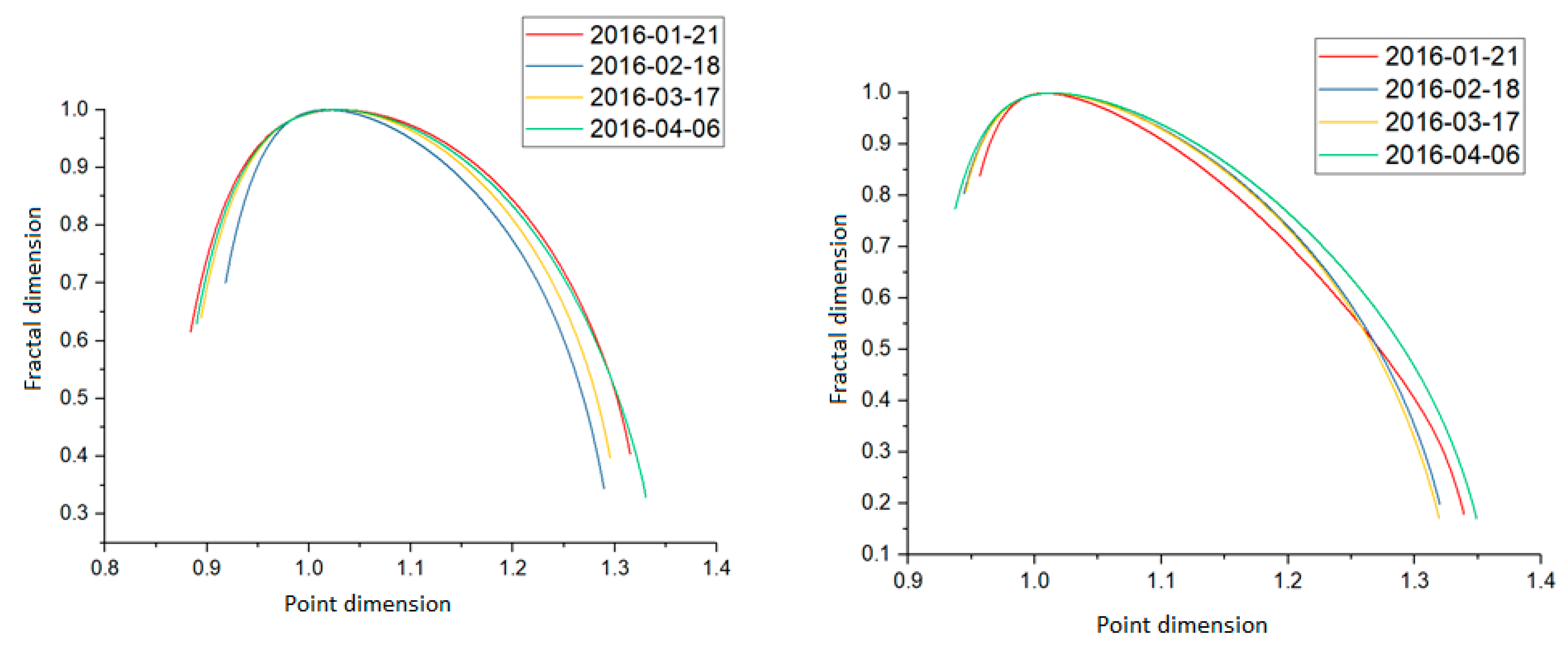
Figure 7 shows the evaluation of Legendre’s spectra for the 2016 sample A extracted from the data collected and the significant deviation for the same data set in the left and right graphs, respectively.
When analyzing the graphs, we can see that data transmission in the form of packets showed standard features for this method of generating spectra. All estimates overlapped and slightly differed in values, which was related to the dynamic structure of network traffic. However, the general character of this traffic was typical. The discrepancy between the tested samples concerns the series A of February 18, 2016. In this case, the final results of the fractal dimension generated higher values in comparison with the other samples.
Nevertheless, all series remained convergent. In the case of a substantial deviation spectrum, some discrepancies could be seen. For the three traffic samples taken in January, March, and April 2016, the traffic flow characteristics were similar. The initial and the final phase of the spectrum had very close values that came down to a characteristic waveform, but these values were not identical, as the difference was only visible in the thousandths or even ten-thousandths of the estimated results. Slight deviations were visible in the middle phase but did not change the nature of the sample. The data recorded on 18 February 2016 showed a deviation from the other values. The beginning and middle course of the spectrum propagation were very similar. In the final phase, there was a faster disappearance of the values concerning the point dimension. The fractal dimension showed very similar estimates concerning the rest of the generated spectra. The difference between the ends of the point dimension of the deviated sample and the others was 0.067. Due to the small deviation, this sample could not be considered an anomaly that would describe this movement as suspicious or infected. Perhaps the sudden change in packet flow characteristics may have been due to other reasons that were not relevant to the stability of the network. For the faster Legendre spectrum measure, the results of the analysis were collected and are presented in
Figure 8.
The estimates had higher values of the fractal dimension in relation to the analyses performed with the use of functions. All spectra showed similar characteristics concerning each other. The initial and final phases differed depending on the data set, but all had one common space for the maximum values of the fractal dimension, in which the spectra almost overlapped. For the sample of 18 February 2016, the initial phase was slightly different from the others, a difference which may have been the reason for the slightly different characteristics of the recorded motion. In the case of sample B, the spectra had a very similar distribution for all the tested samples. The samples from February and March 2016 were a particular case. They had almost the same waveform, clearly differing only in the final phases. The remaining samples did not stand out significantly, falling within a kind of path of the value that was determined by the spectrum. Compared to sample A of this year, the parabolic distribution of the obtained results was less developed. Additionally, in this case, the point dimension shifted to higher values and had a different course in comparison with the Legendre dimensions, as determined by the default function of the determination of the spectra.
We aimed to automatically compare spectra and identify anomalies. The presented analysis showed anomalies in traffic patterns on February 18th. Due to the nature of the traffic and the availability of data selected by CAIDA, it was not possible to determine the exact cause of the anomalies observed. The paper aimed to present a two-stage approach to the detection of anomalies using the H parameter and the multifractal spectrum.
6. Conclusions
The monitoring of data flows in the interconnected communication of IoT networks as wide-area computer networks is an essential issue in the context of network reliability and information security. The ability to detect anomalies in network traffic can significantly improve the management of network infrastructure and security. This paper presents the possibility of using the Hurst coefficient to determine the level of self-similarity of the traffic, which affects the ability to determine the typical operating states as well as the detection of certain anomalies such as an attack, refusal of access, overload and post-failure state. Additionally, this article presents the results of an analysis of traffic in the communication network using a statistical coefficient of similarity and multifracture spectrum. The presented results of the measurements and research confirmed that the analyzed traffic was self-similar and amounted to 0.5–1. The value of the H parameter increased with the increase in the level of network utilization. Therefore, network efficiency was determined by the self-similar properties of network traffic. Some of the most important physical phenomena can significantly increase the LRD in terms of user behavior, data generation, organization and search, traffic aggregation, network control, network control, etc. The results of analytical considerations and experiments showed that the similarity factor could be successfully applied in the analysis of traffic in computer networks and the communication infrastructure of IoT systems.
In order to compare the self-similar and multifractal statistical characteristics of the proposed model to those of the real traffic, some statistical data tests were conducted, such as the autocorrelation function and the multifractal spectrum. The values of Hurst’s exponent presented in the paper showed that network traffic is characterized by long-term dependencies. The analyzed cases showed that the appropriate network throughput was maintained, which emphasized the general characteristics and character of the traffic generated in nodes. The measured values of Hurst’s exponent allowed for an in-depth analysis of the current state of the network, as well as a forecast of the future trend of data behavior. Such use of this methodology enables a user to prepare for the maintenance or change of the trend in a timely manner. Sudden deviations of the exponent value with the obtained results are likely a sign of problems, which, for network traffic, indicates an unusual behavior of the network, possibly related to a cybercrime attack.
The solutions studied may be ideal for analyzing traffic in backbone networks for security and the detection of attacks. The tested methods—multifractal analysis, in particular—are sensitive to any deviation of traffic characteristics due to anomalies. Such traffic analysis methods can be ideal for protecting critical data and maintaining the continuity of internet services, including the IoT communication infrastructure.
In the proposed approach, the direct time series extraction from the network packet stream can be done quickly enough and for a sufficiently large set of classes to be able to cope with the expected scenarios for IoT network development. Evidence of the existence of multifractal behavior of traffic flows in computer networks has contributed to deeper traffic understanding and modeling. Through multifractal interpretation, an explanation of traffic behavior in timescales that are smaller than some hundreds of milliseconds is possible.