Study on Bubble Cavitation in Liquids for Bubbles Arranged in a Columnar Bubble Group
Abstract
Featured Application
Abstract
1. Introduction
2. Theoretical Model
3. Study of Resonance Frequency of Bubbles in a Bubble Group
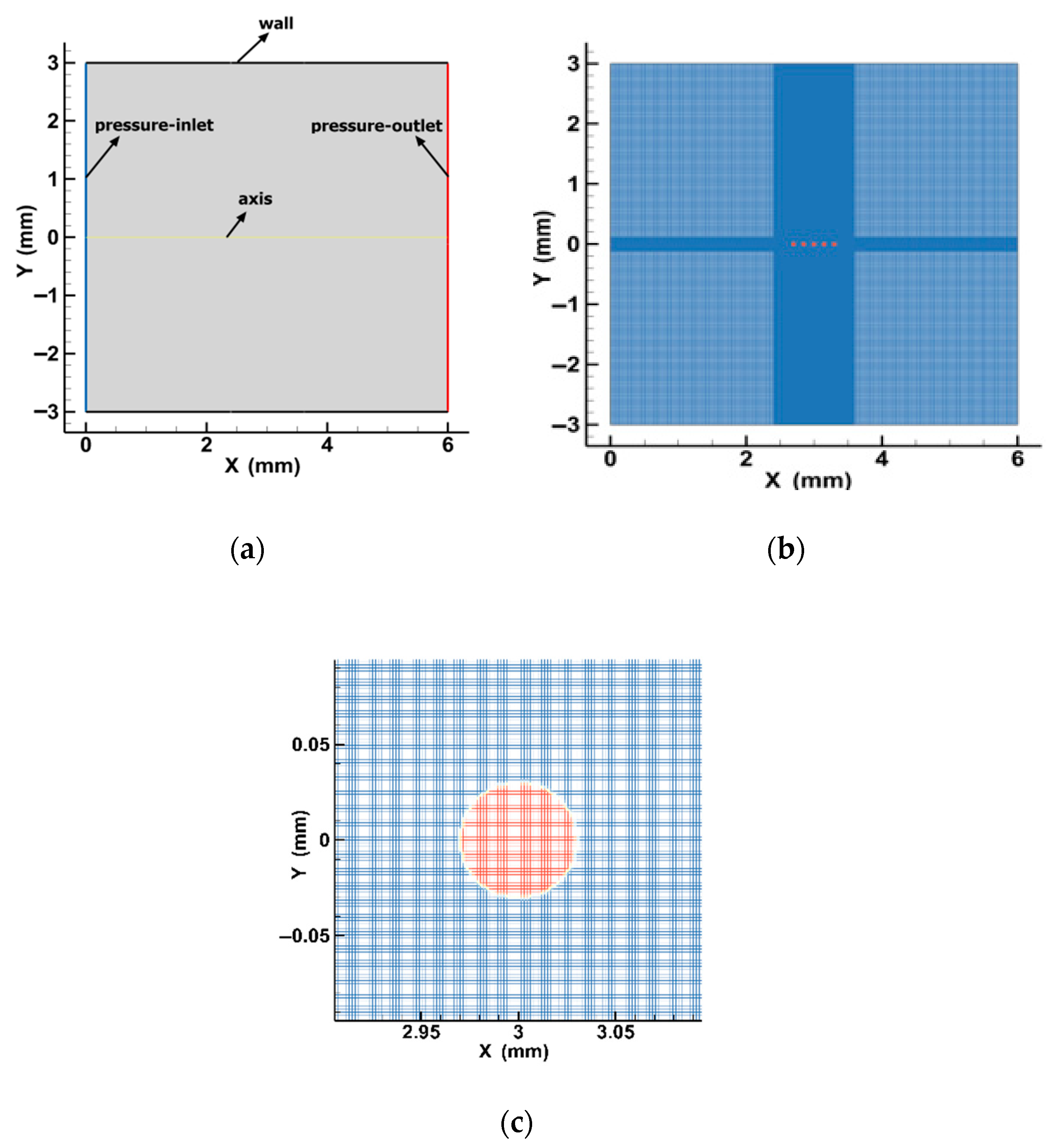
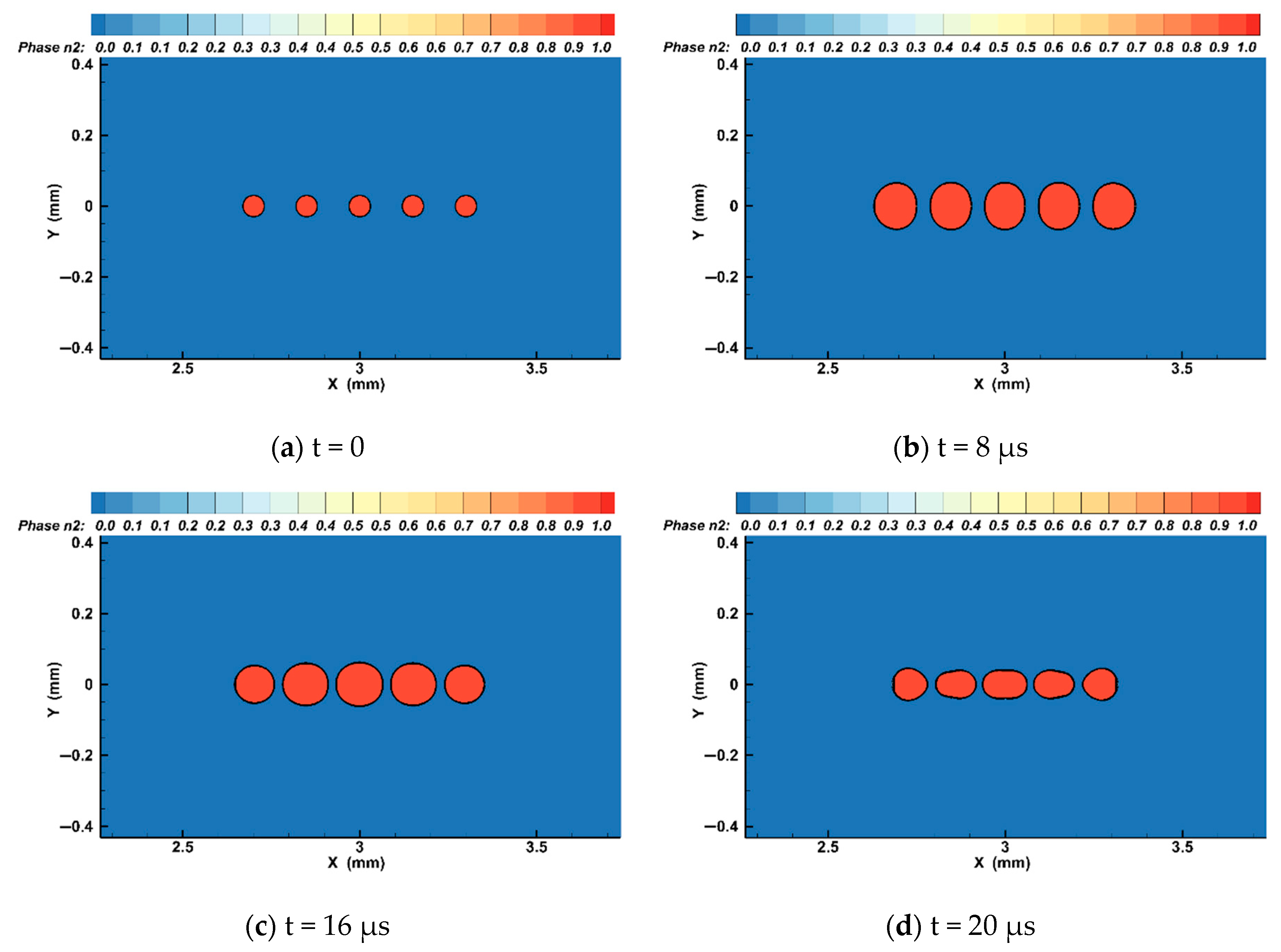
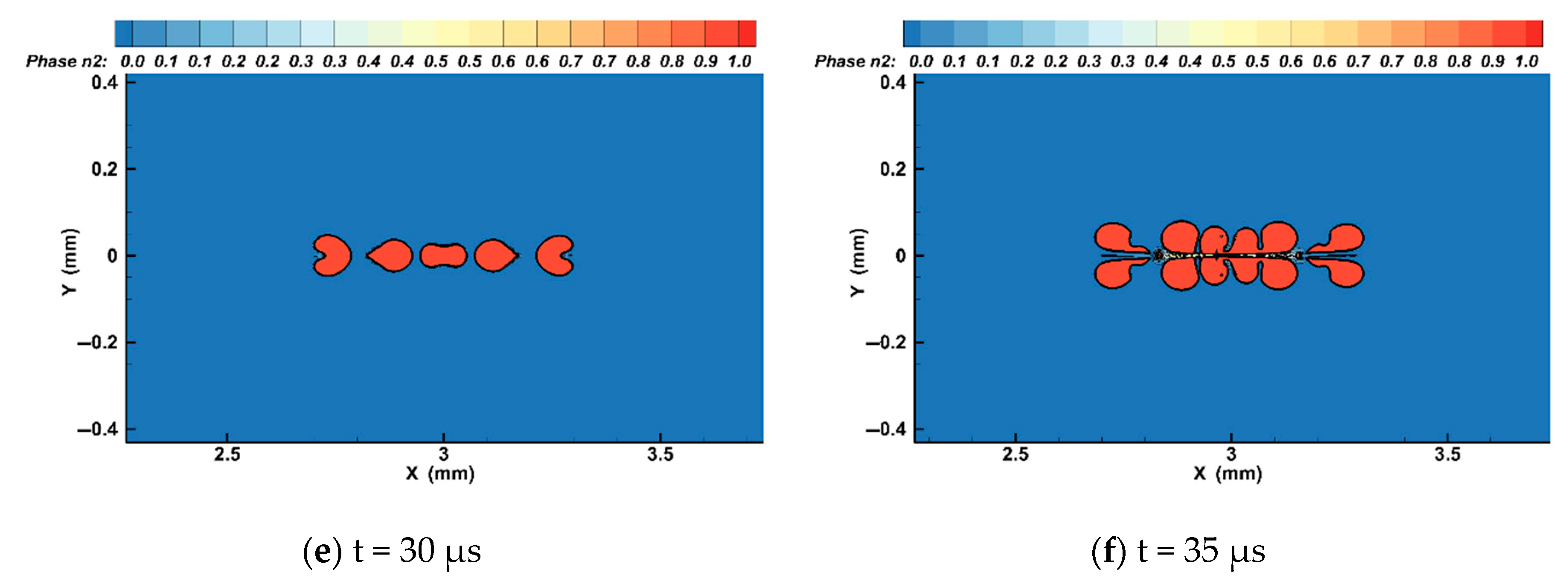
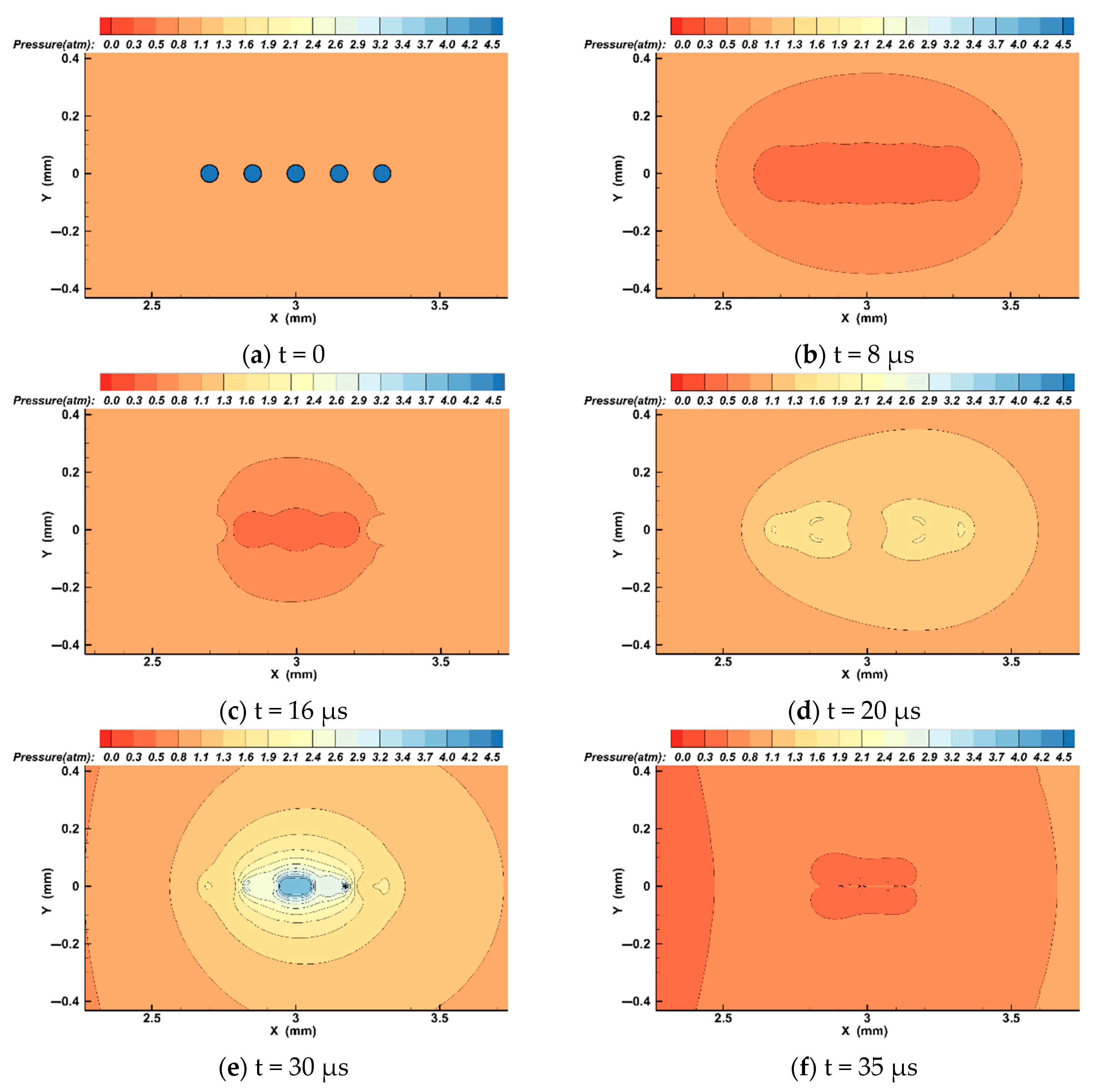
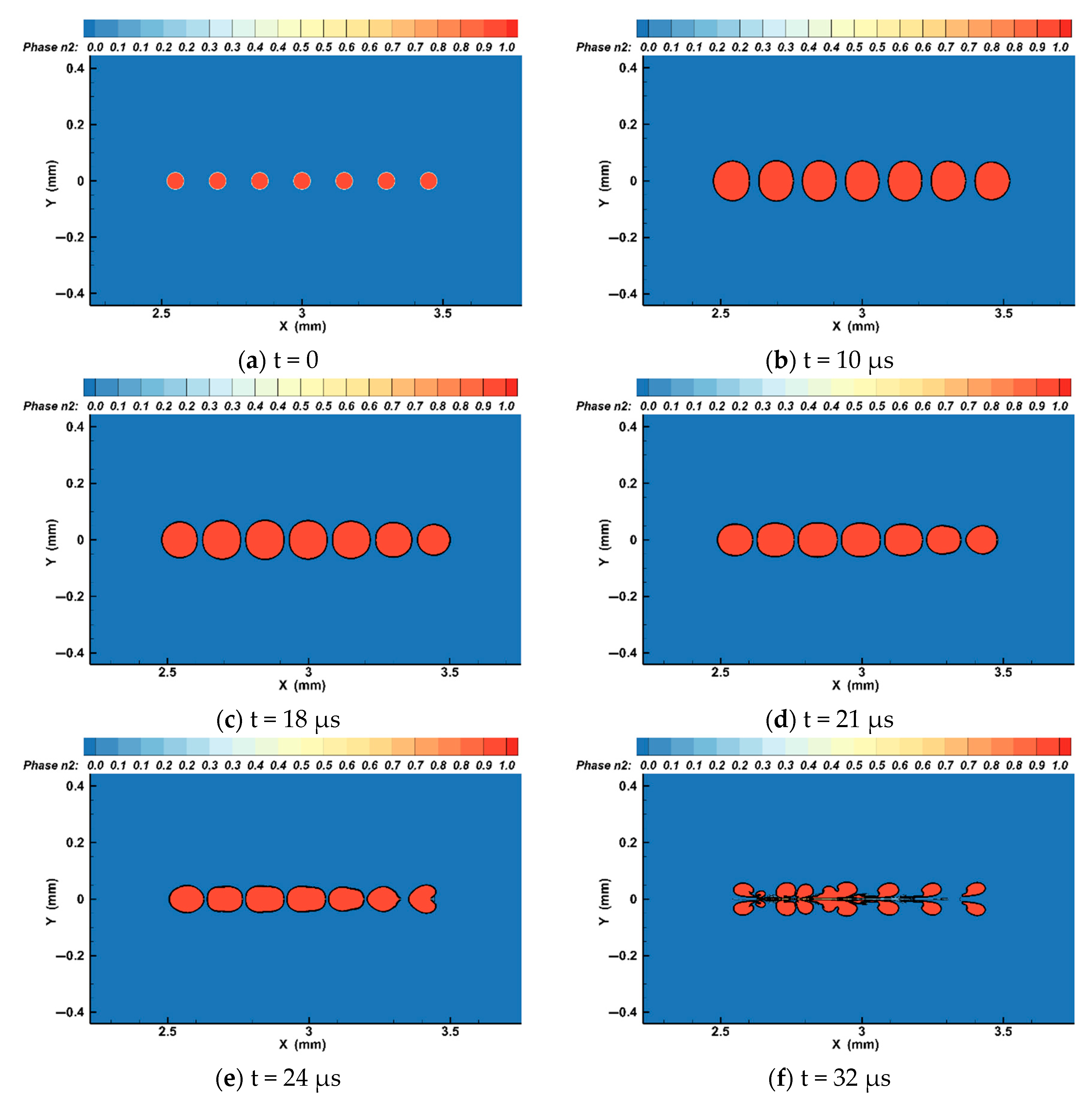
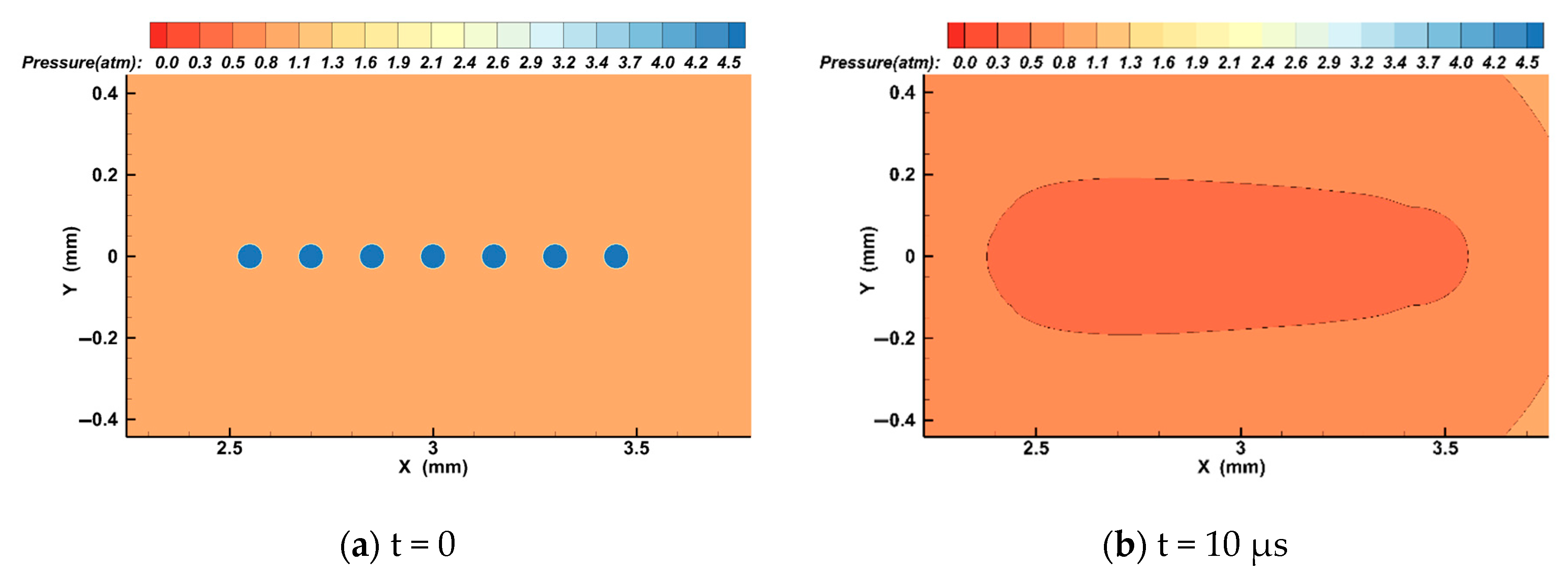
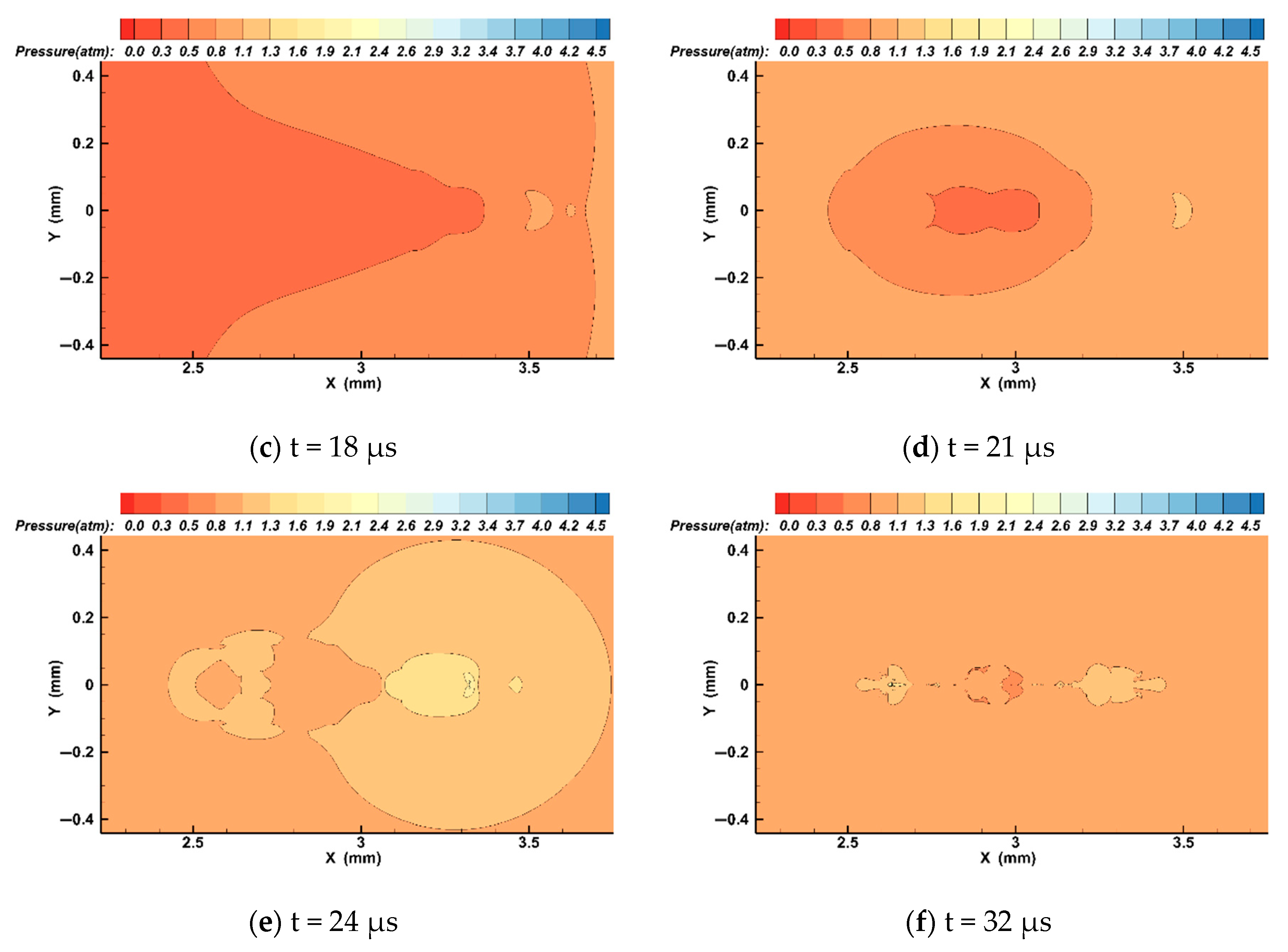
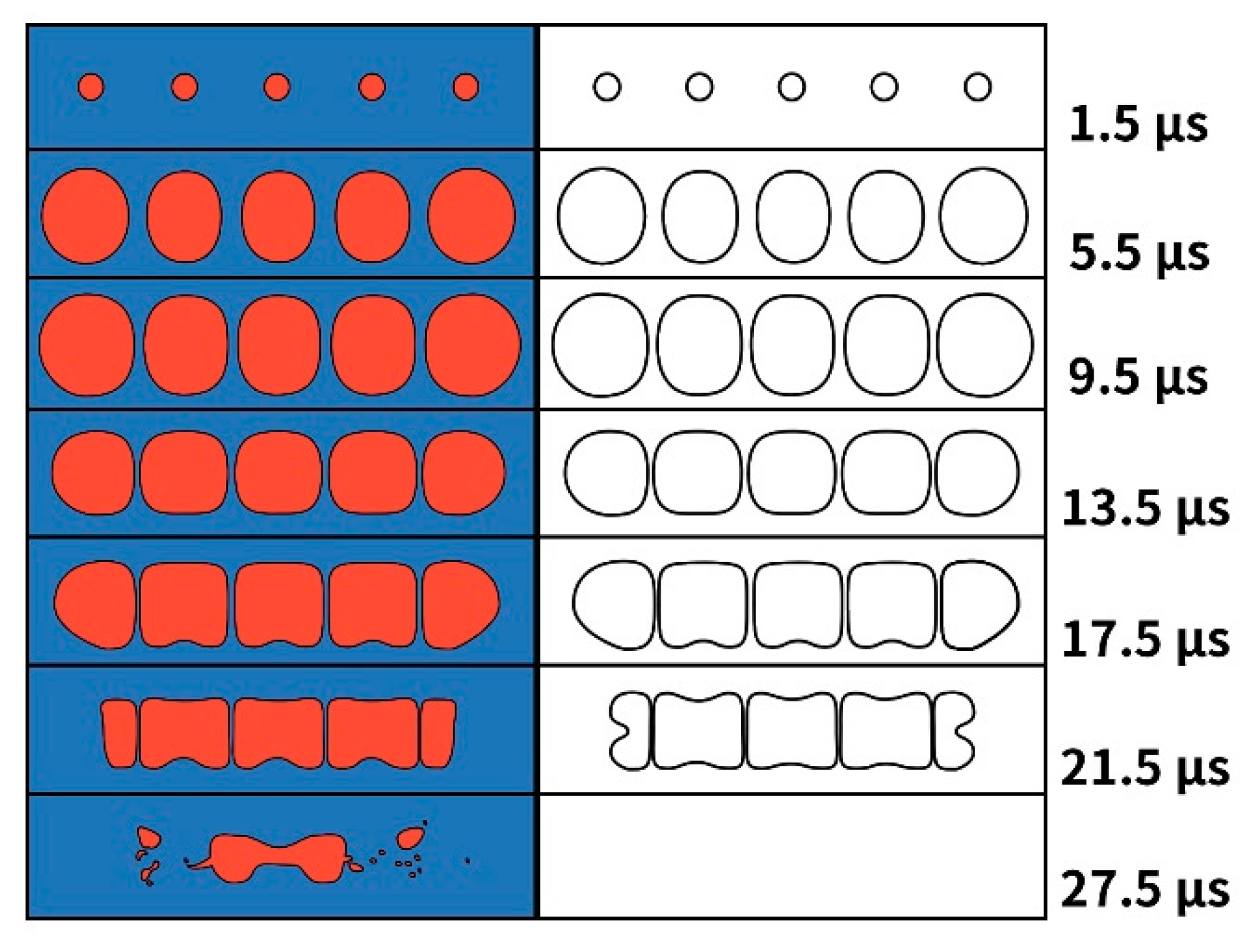
4. Fluent Analysis
5. Conclusions and Discussion
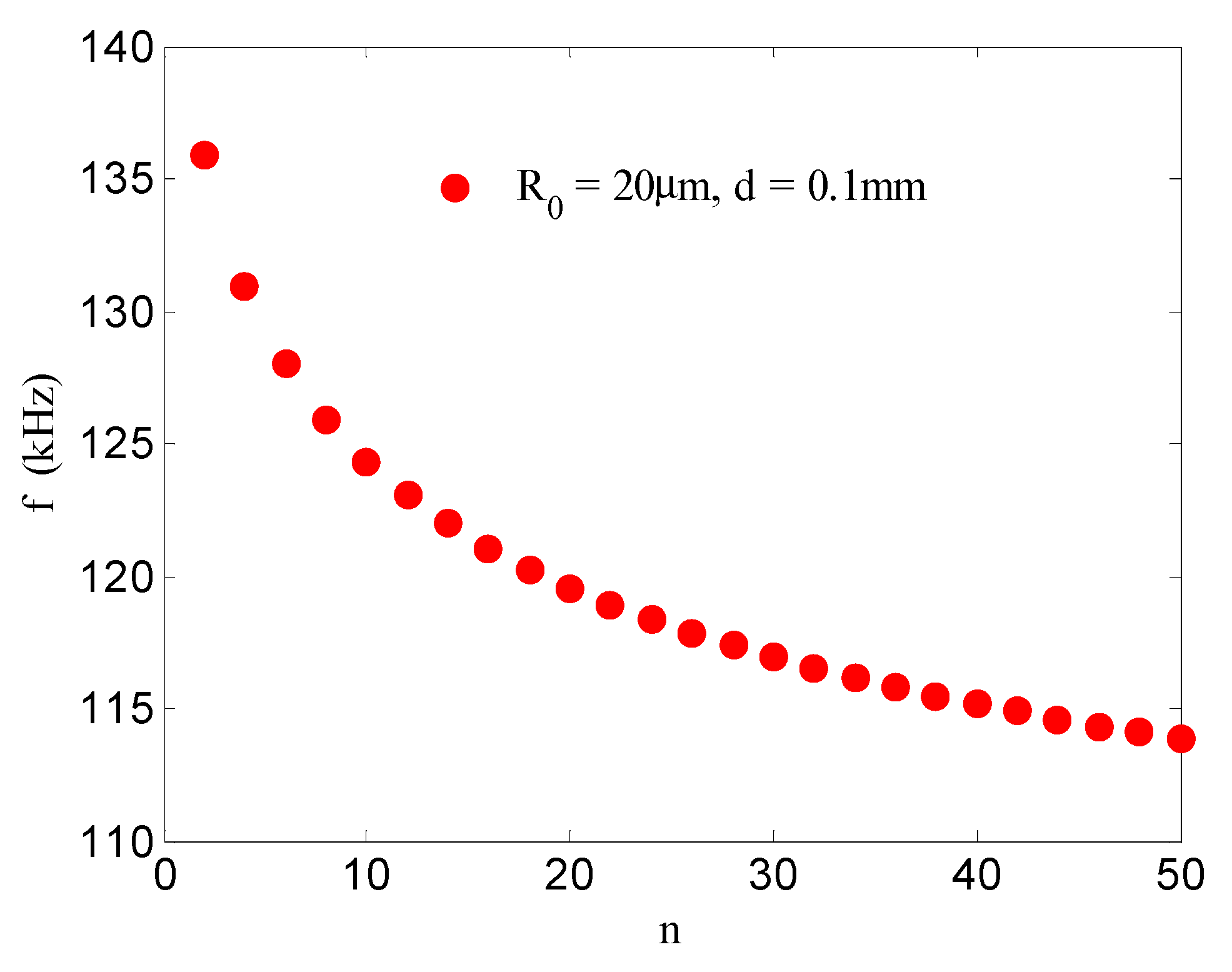
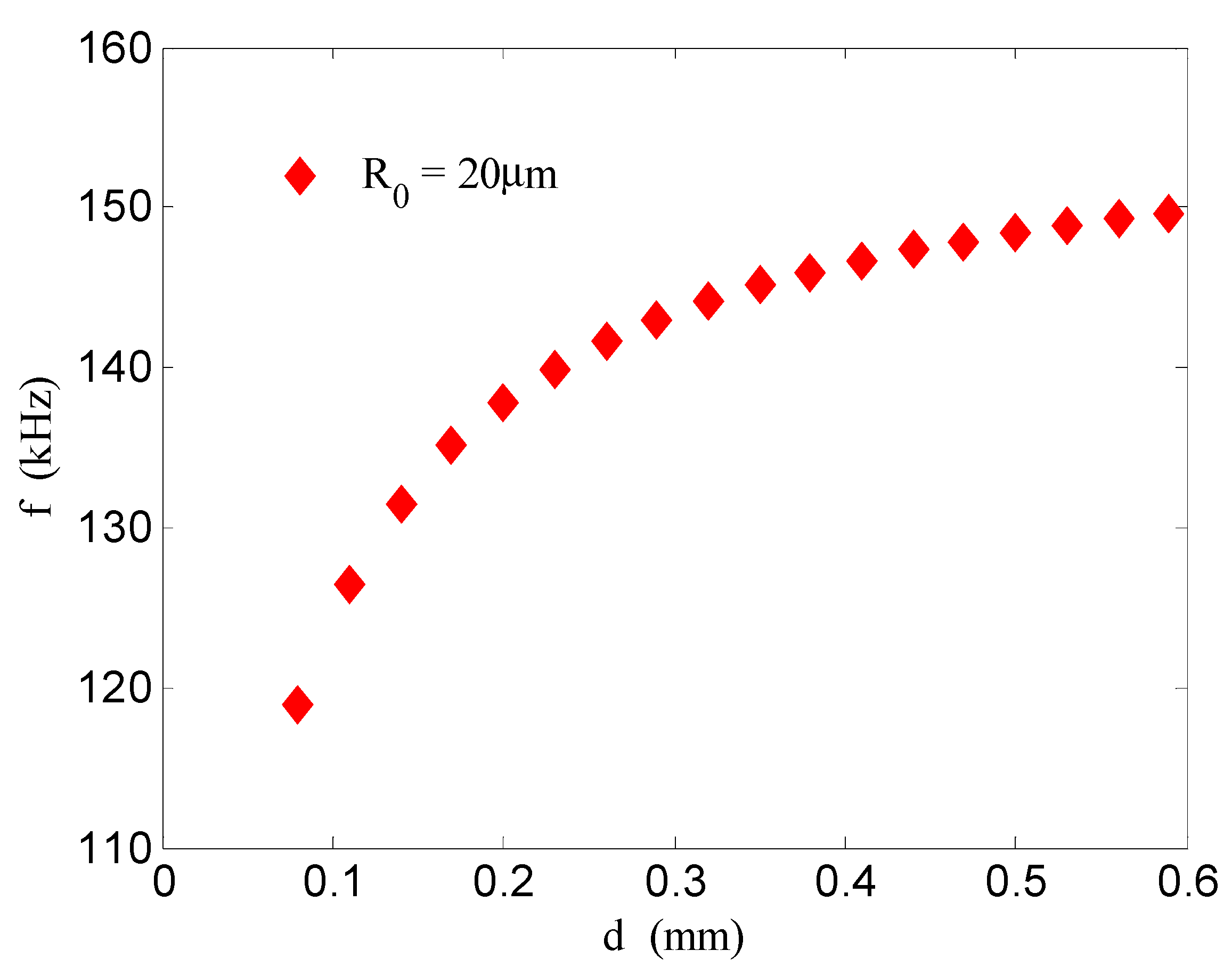
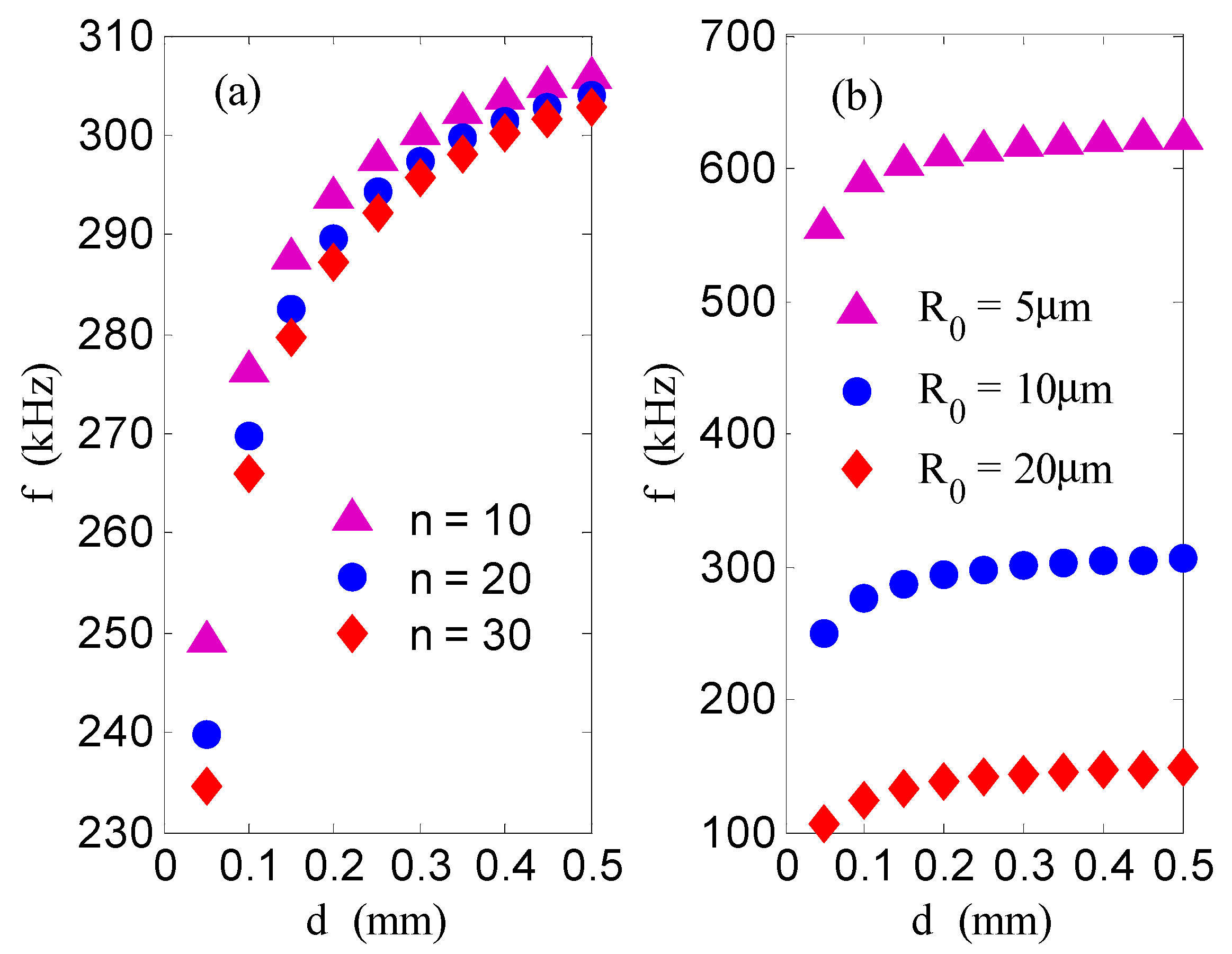
- There is a weak coupling interaction between bubbles in the bubble group which can change the resonance frequency of the bubbles. The resonance frequency of bubbles is affected by many factors such as the initial radius of the bubbles, the number of bubbles in a bubble group, and the distance between bubbles. With regard to these parameters, the initial radius of the bubbles and the distance between bubbles have the most significant effects on the resonance frequency of the bubbles. For the same number of bubbles, when the distance between the bubbles is larger, the interaction between the bubbles becomes weaker. When the distance between the bubbles increases to 20 times the initial radius of the bubbles, the resonance frequency of the bubbles returns to that of a single bubble. In this case, the interactions between bubbles can be ignored.
- The first bubble is affected by other bubbles behind it, and the resonance frequency reduces. The larger the number of bubbles, the stronger the interaction force between them, and the smaller the resonance frequency of the bubbles. However, when the number of bubbles increases to twenty and then continues to increase, the number of bubbles and the resonance frequency of the bubbles tends towards a fixed value.
- Through Fluent simulation results it was found that due to the mutual restriction between bubbles in the expansion process, the energy ratio of the two bubbles at the edge reaches its maximum volume first in the expansion process. Later, the bubbles begin to contract. Through contracting, the bubbles slowly become, and remain, ellipsoid in nature. After this, the two bubbles begin to collapse, forming a micro jet which points to the back of the bubble and along the axis of the center of the linear bubble group, breaking the bubble until it is completely torn apart.
- The maximum volume and collapse times of bubbles driven by sound parameters are different. The larger the driving frequency and the sound pressure are, the larger the maximum volume of the bubbles.
Author Contributions
Funding
Conflicts of Interest
References
- Ryl, J.; Wysocka, J.; Slepski, P.; Darowicki, K. Instantaneous impedance monitoring of synergistic effect between cavitation erosion and corrosion processes. Electrochim. Acta 2016, 203, 388–395. [Google Scholar] [CrossRef]
- Mason, T.J.; Lorimer, J.P. Applied Sonochemistry: Uses of Power Ultrasound in Chemistry and Processing; Wiley: Hoboken, NJ, USA, 2002. [Google Scholar]
- Bai, L.; Wu, P.; Liu, H.; Yan, J.; Su, C.; Li, C. Rod-shaped cavitation bubble structure in ultrasonic field. Ultrason. Sonochem. 2018, 44, 184–195. [Google Scholar] [CrossRef] [PubMed]
- Cui, P.; Zhang, A.M.; Wang, S.P.; Khoo, B.C. Ice breaking by a collapsing bubble. J. Fluid Mech. 2018, 841, 287–309. [Google Scholar] [CrossRef]
- Mo, R.Y.; Wang, C.H. Nonlinear acoustic response of two bubble oscillators. Acta Phys. Sin. 2019, 68, 144302. [Google Scholar]
- Jiang, L.; Liu, F.; Chen, H.; Wang, J.; Chen, D. Frequency spectrum of the noise emitted by two interacting cavitation bubbles in strong acoustic fields. Phys. Rev. E 2012, 85, 036312. [Google Scholar] [CrossRef] [PubMed]
- Mao, Y.; Peng, Y.; Zhang, J. Study of Cavitation Bubble Collapse near a Wall by the Modified Lattice Boltzmann Method. Water 2018, 10, 1439. [Google Scholar] [CrossRef]
- Teran, L.A.; Rodriguez, S.A.; Laín, S.; Jung, S. Interaction of particles with a cavitation bubble near a solid wall. Phys. Fluids 2018, 30, 123304. [Google Scholar] [CrossRef]
- Jang, N.W.; Gracewski, S.M.; Abrahamsen, B.; Buttaccio, T.; Halm, R.; Dalecki, D. Natural frequency of a gas bubble in a tube: Experimental and simulation results. J. Acoust. Soc. Am. 2009, 126, EL34–EL40. [Google Scholar] [CrossRef]
- Sassaroli, E.; Hynynen, K. Forced linear oscillations of micro-bubbles in blood capillaries. J. Acoust. Soc. Am. 2004, 115, 3235–3243. [Google Scholar] [CrossRef]
- Wang, C.H.; Lin, S.Y. The nonlinear standing wave inside the space of liquid. Sci. China Phys. Mech. Astron. 2010, 53, 496–503. [Google Scholar] [CrossRef]
- Luo, J.; Niu, Z. Jet and Shock Wave from Collapse of Two Cavitation Bubbles. Sci. Rep. 2019, 9, 1352. [Google Scholar] [CrossRef] [PubMed]
- Bremond, N.; Arora, M.; Ohl, C.D.; Lohse, D. Controlled Multibubble Surface Cavitation. Phys. Rev. Lett. 2006, 96, 224501. [Google Scholar] [CrossRef] [PubMed]
- Cui, P.; Wang, Q.X.; Wang, S.P.; Zhang, A.M. Experimental study on interaction and coalescence of synchronized multiple bubbles. Phys. Fluids 2016, 28, 012103. [Google Scholar] [CrossRef]
- An, Y. Formulation of multibubble cavitation. Phys. Rev. E 2011, 83, 066313. [Google Scholar] [CrossRef]
- Ohl, C.D.; Ikink, R. Shock-wave-induced jetting of micron-size bubbles. Phys. Rev. Lett. 2003, 90, 214502. [Google Scholar] [CrossRef]
- Tomita, Y.; Shima, A.; Ohno, T. Collapse of multiple gas bubbles by a shock wave and induced impulsive pressure. J. Appl. Phys. 1984, 56, 125. [Google Scholar] [CrossRef]
- Han, B.; Köhler, K.; Jungnickel, K.; Mettin, R.; Lauterborn, W.; Vogel, A. Dynamics of laser-induced bubble pairs. J. Fluid Mech. 2015, 771, 706–742. [Google Scholar] [CrossRef]
- Futakawa, M. Direct observation and theoretical study of cavitation bubbles in liquid. Phys. Rev. E 2007, 75, 046304. [Google Scholar]
- Doinikov, A.A.; Zavtrak, S.T. On the ‘‘bubble grapes’’ induced by a sound field. J. Acoust. Soc. Am. 1998, 99, 3849–3850. [Google Scholar] [CrossRef]
- Watanabe, R.; Yanagisawa, K.; Yamagata, T.; Fujisawa, N. Simultaneous shadowgraph imaging and acceleration pulse measurement of cavitating jet. Wear 2016, 358, 72–79. [Google Scholar] [CrossRef]
- Moussatov, A.; Granger, C.; Dubus, B. Cone-like bubble formation in ultrasonic cavitation field. Ultrason. Sonochem. 2007, 10, 191–195. [Google Scholar] [CrossRef]
- Mettin, R.; Luther, S.; Ohl, C.D.; Lauterborn, W. Acoustic cavitation structures and simulations by a particle model. Ultrason. Sonochem. 1999, 6, 25–29. [Google Scholar] [CrossRef]
- Peng-Li, Z.; Shu-Yu, L.; Hua-Ze, Z.; Tao, Z. Coupled resonance of bubbles in spherical cavitation clouds. Acta Phys. Sin. 2019, 68, 134301. [Google Scholar]
- Cannon, H.G. On the nature of the centrosomal force. J. Genet. 1923, 13, 47–78. [Google Scholar] [CrossRef]
- Ma, Y.; Lin, S.; Xu, J.; Tang, Y. Influnece of nonspherical effects on the secondary Bjerknes force in a strong acoustic field. Acta Phys. Sin. 2017, 66, 014302. [Google Scholar]
- König, W.; Ruprecht, E. Effects of convective clouds on the large-scale vorticity budge. Meteorol. Atmos. Phys. 1989, 41, 213–229. [Google Scholar] [CrossRef]
- Wang, C.; Hu, J.; Cao, H.; Lin, S.; An, S. Nonlinear resonance of bubble cluster driven by ultrasound. Sci. Sin. Phys. Mech. Astron. 2015, 45, 064301. [Google Scholar]
- Spratt, K.S.; Lee, K.M.; Wilson, P. Champagne acoustics. Phys. Today 2018, 71, 66. [Google Scholar] [CrossRef]
- Ida, M. Bubble-bubble interaction: A potential source of cavitation noise. Phys. Rev. E 2009, 79, 016307. [Google Scholar] [CrossRef]
- Ida, M.; Naoe, T.; Futakawa, M. Suppression of cavitation inception by gas bubble injection: A numerical study focusing on bubble-bubble interaction. Phys. Rev. E 2007, 76, 046309. [Google Scholar] [CrossRef]
- An, Y. Nonlinear bubble dynamics of cavitation. Phys. Rev. E 2012, 85, 016305. [Google Scholar] [CrossRef] [PubMed]
- Löfstedt, R.; Barber, B.P.; Putterman, S.J. Toward a Hydrodynamic Theory of Sonoluminescence. Phys. Fluids A Fluid Dyn. 1993, 5, 2911–2928. [Google Scholar] [CrossRef]
- Barnes, C.W. Euler’s Constant and e. Am. Math. Mon. 1984, 91, 428–430. [Google Scholar] [CrossRef]
- Guanjun, C. Harmonic series and Euler constant. J. Math. Technol. 1990, 6, 119–121. [Google Scholar]
- Bremond, N.; Arora, M.; Dammer, S.M.; Lohse, D. Dammer, Interaction of cavitation bubbles on a wall. Phys. Fluids 2006, 18, 121505. [Google Scholar] [CrossRef]
- Abbassi, W.; Besbes, S.; Elhajem, M.; Aissia, H.B.; Champagne, J.Y. Numerical simulation of free ascension and coaxial coalescence of air bubbles using the volume of fluid method (VOF). Comput. Fluids 2018, 161, 47–59. [Google Scholar] [CrossRef]


© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, P.-l.; Lin, S.-y. Study on Bubble Cavitation in Liquids for Bubbles Arranged in a Columnar Bubble Group. Appl. Sci. 2019, 9, 5292. https://doi.org/10.3390/app9245292
Zhang P-l, Lin S-y. Study on Bubble Cavitation in Liquids for Bubbles Arranged in a Columnar Bubble Group. Applied Sciences. 2019; 9(24):5292. https://doi.org/10.3390/app9245292
Chicago/Turabian StyleZhang, Peng-li, and Shu-yu Lin. 2019. "Study on Bubble Cavitation in Liquids for Bubbles Arranged in a Columnar Bubble Group" Applied Sciences 9, no. 24: 5292. https://doi.org/10.3390/app9245292
APA StyleZhang, P.-l., & Lin, S.-y. (2019). Study on Bubble Cavitation in Liquids for Bubbles Arranged in a Columnar Bubble Group. Applied Sciences, 9(24), 5292. https://doi.org/10.3390/app9245292



