The Generalized Coefficients of Earth Pressure: A Unified Approach
Abstract
1. Introduction
2. Cauchy’s First Law of Motion
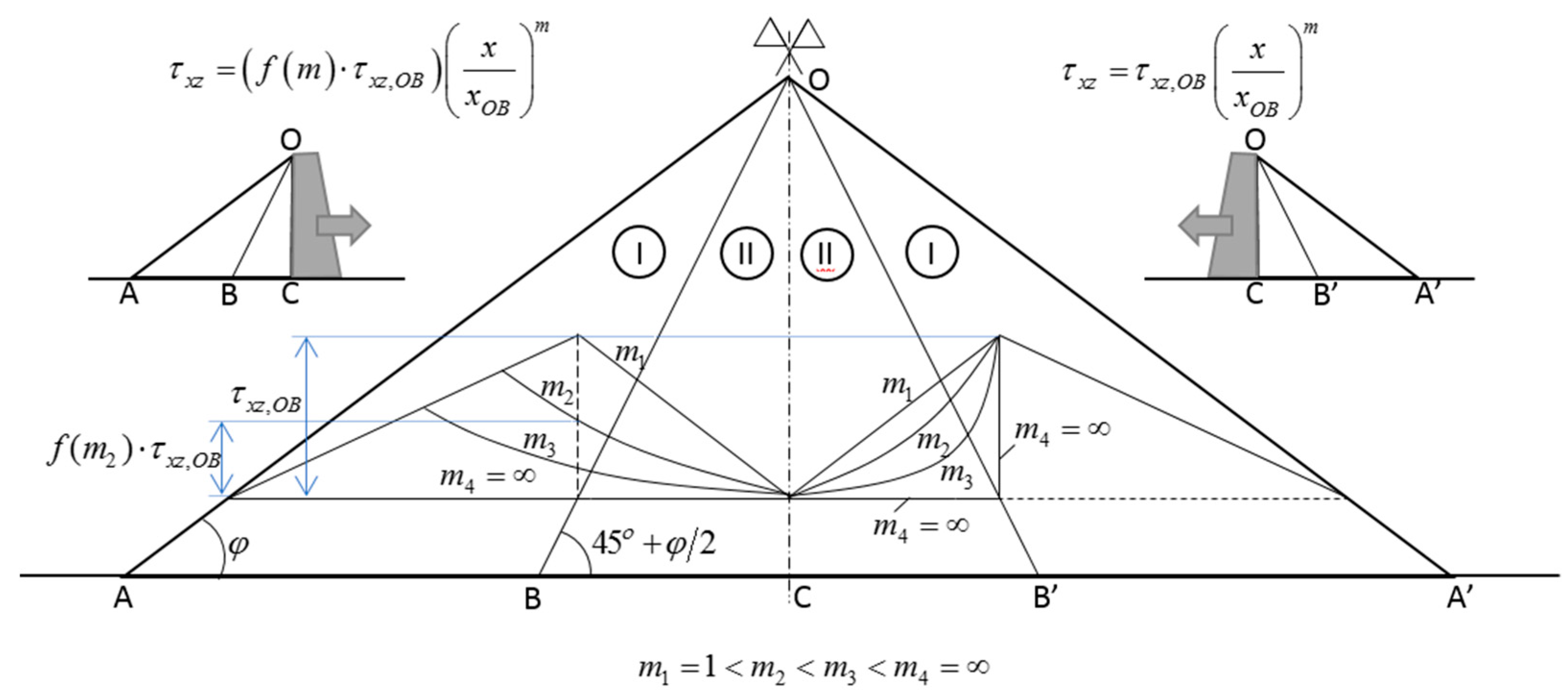
3. The Role of Internal Resistance in Distribution of Horizontal Stress
4. Extension of Cauchy’s First Law of Motion to Deformable Bodies with Internal Resistance and under the Influence of Pseudo-Static Forces
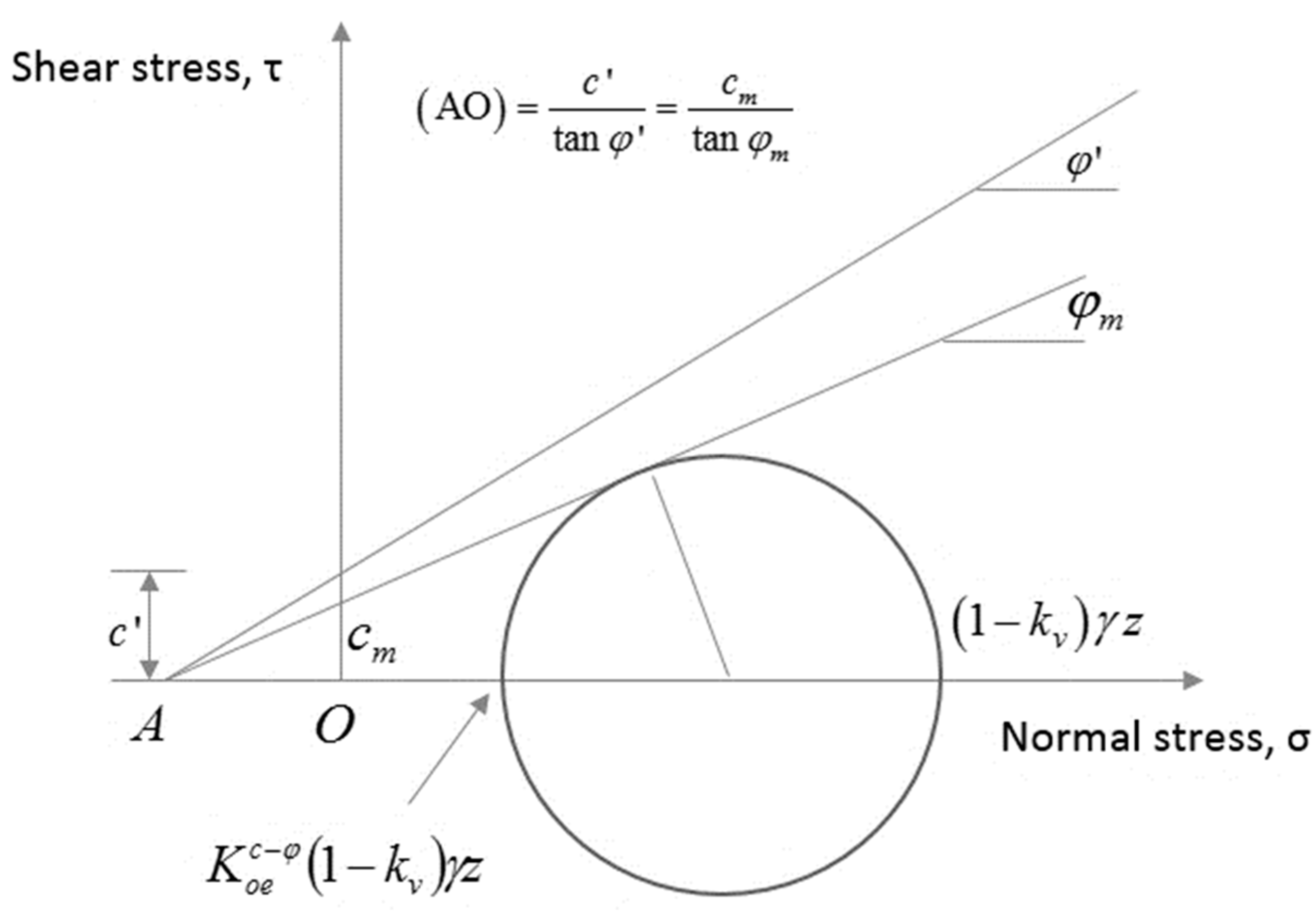
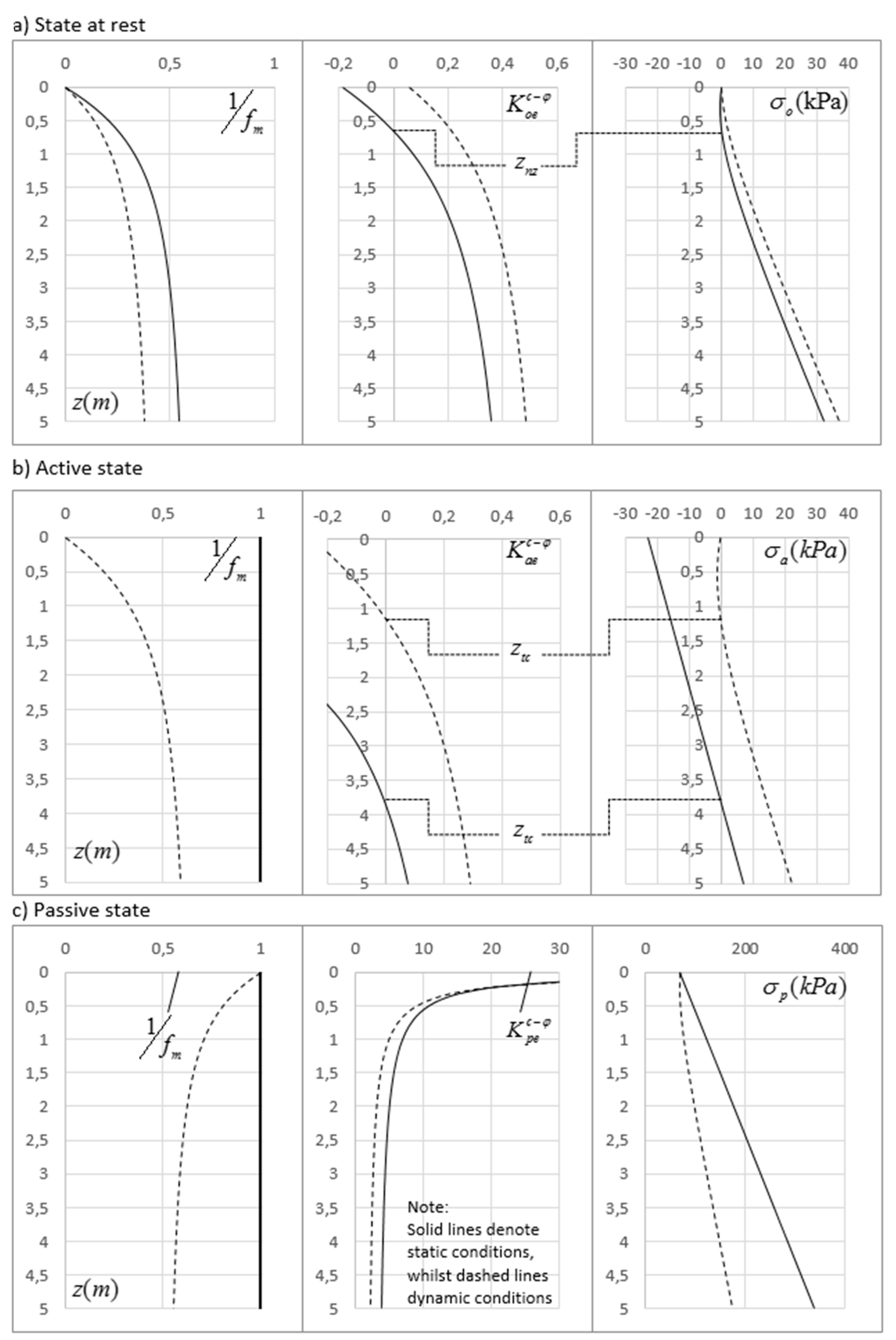
5. Derivation of the Proposed Generalized Coefficient of Earth Pressure at Rest
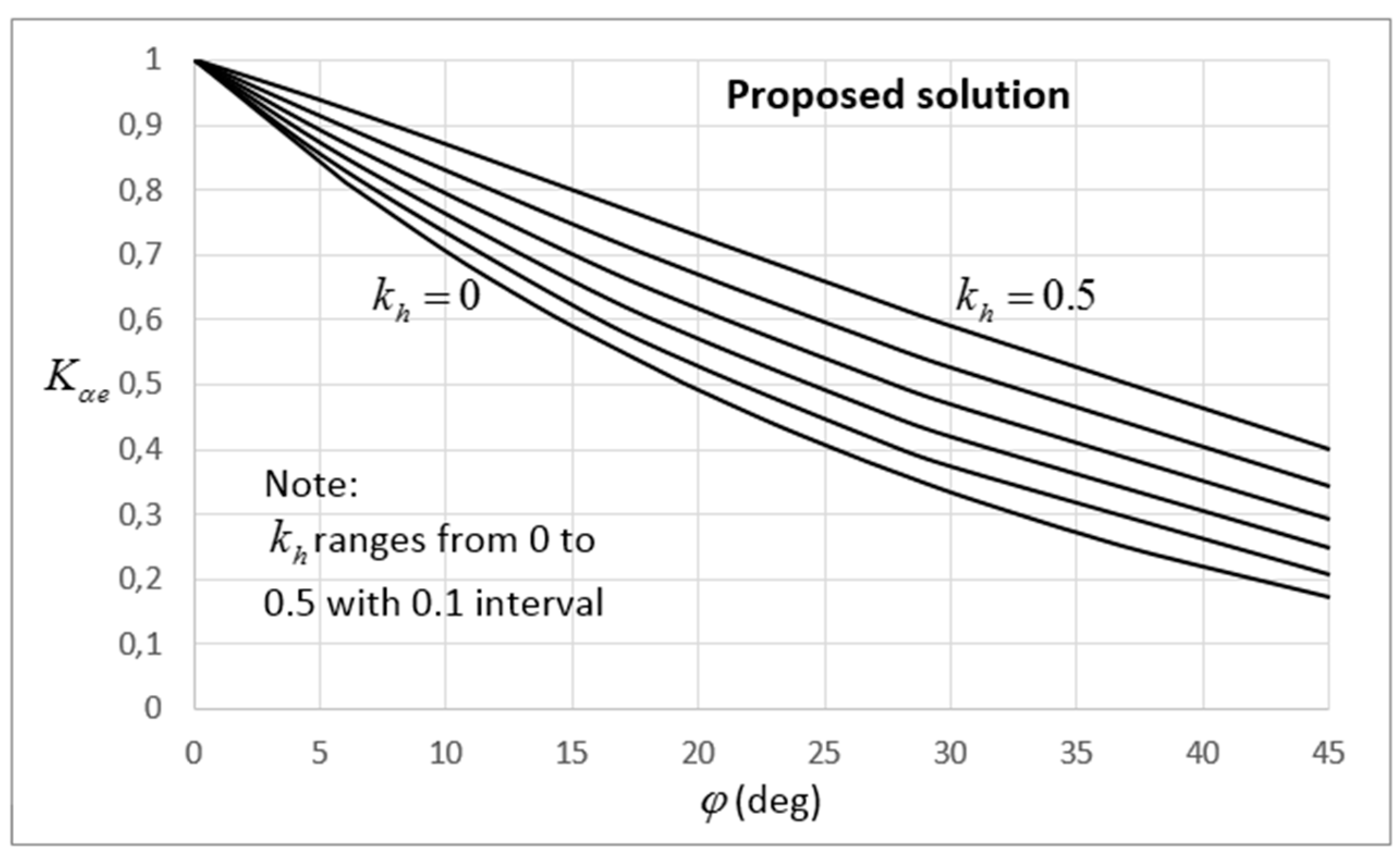
6. The Derived Coefficients of Earth Pressures
7. The “Intermediate” State of Earth Pressure
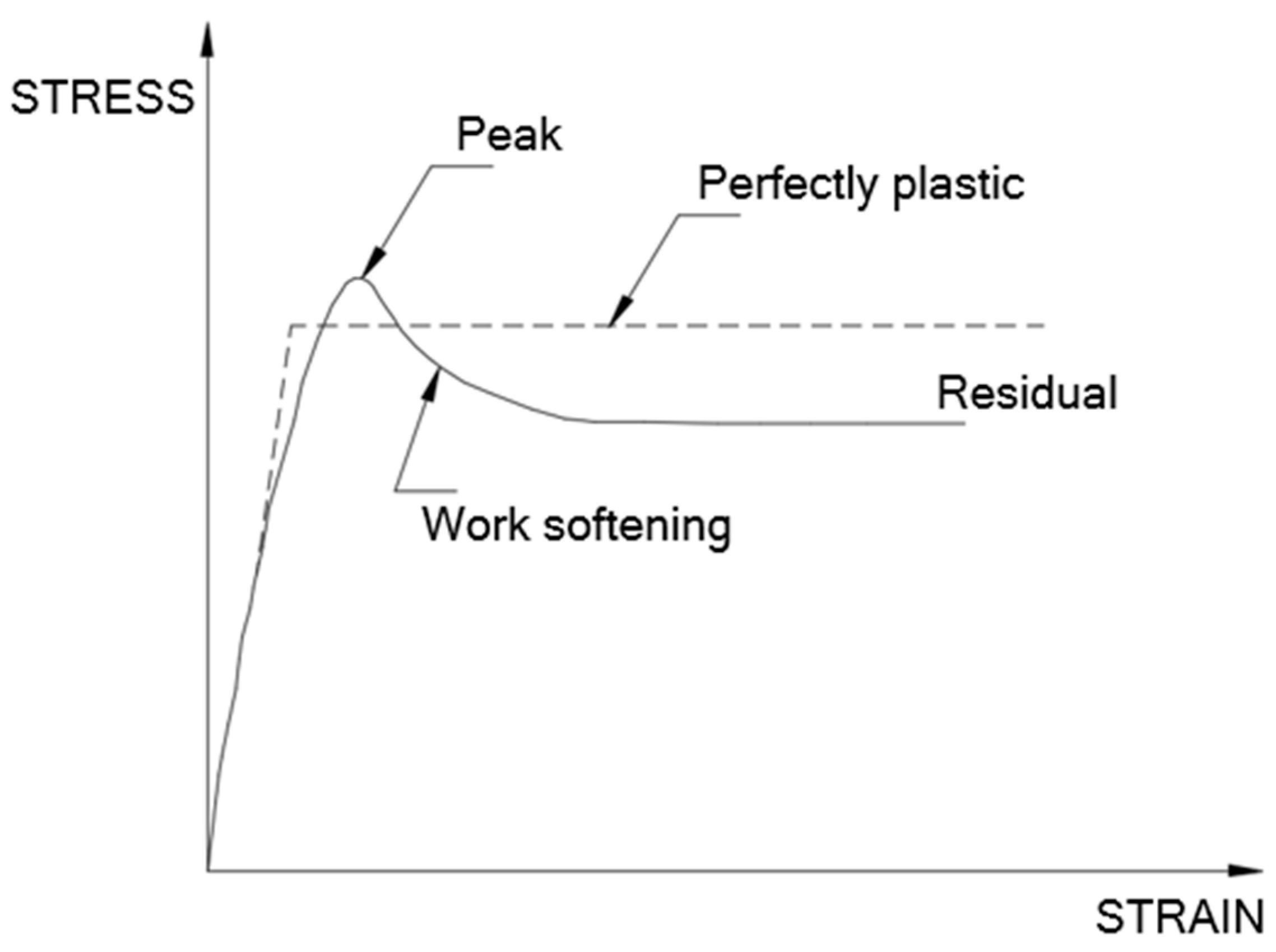
8. The Mobilized Shear Strength of Soil
8.1. The Mobilized Shear Strength of Soil in the State at Rest
8.2. The Mobilized Shear Strength of Soil in the Active and Passive State
8.3. The Mobilized Shear Strength of Soil in the Intermediate State
9. Depth of Neutral Zone (State at Rest) and Tension Crack (Active State)
9.1. Depth of Neutral Zone (State at Rest)
9.2. Depth of Tension Crack (Active State)
10. Discussion
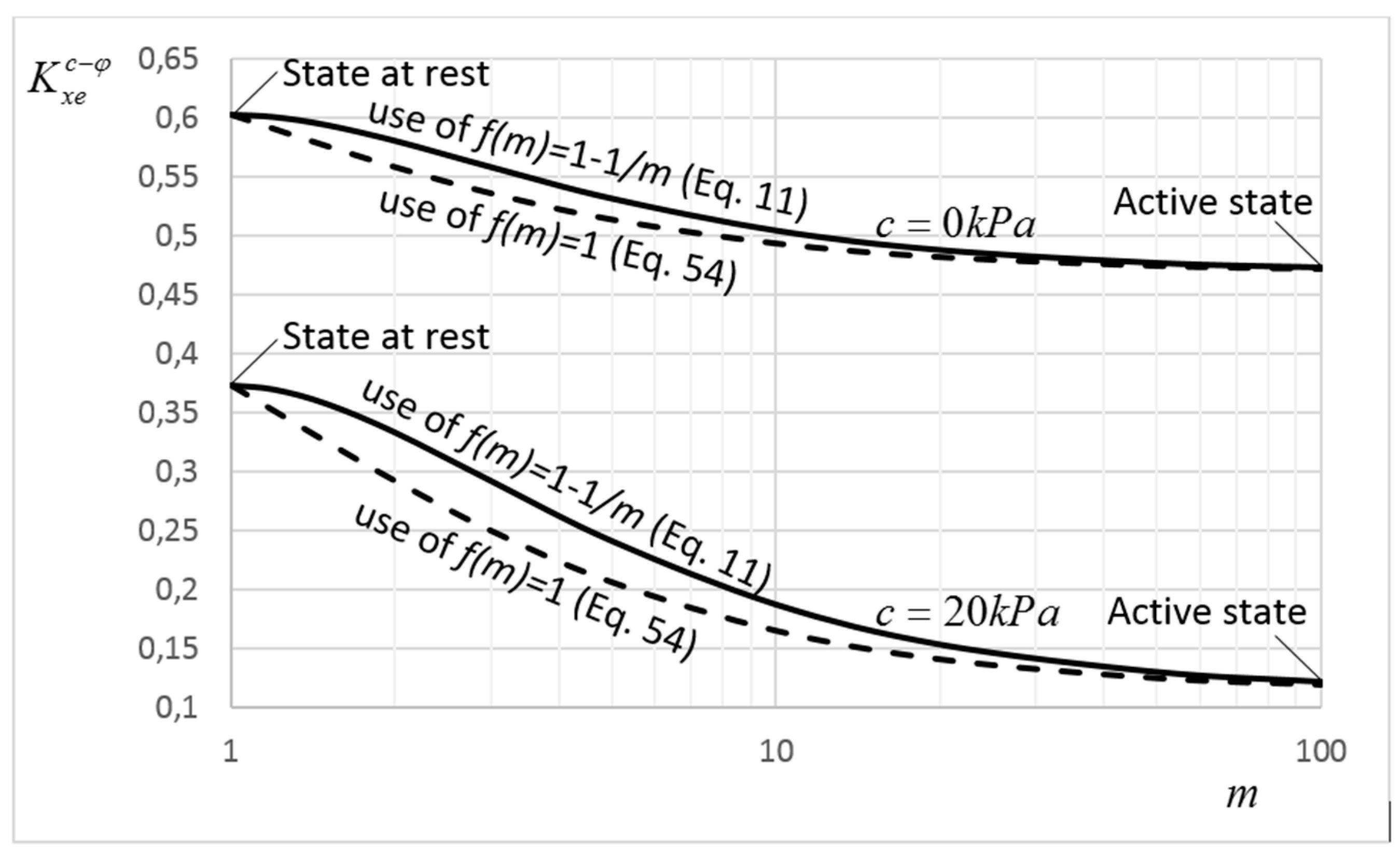
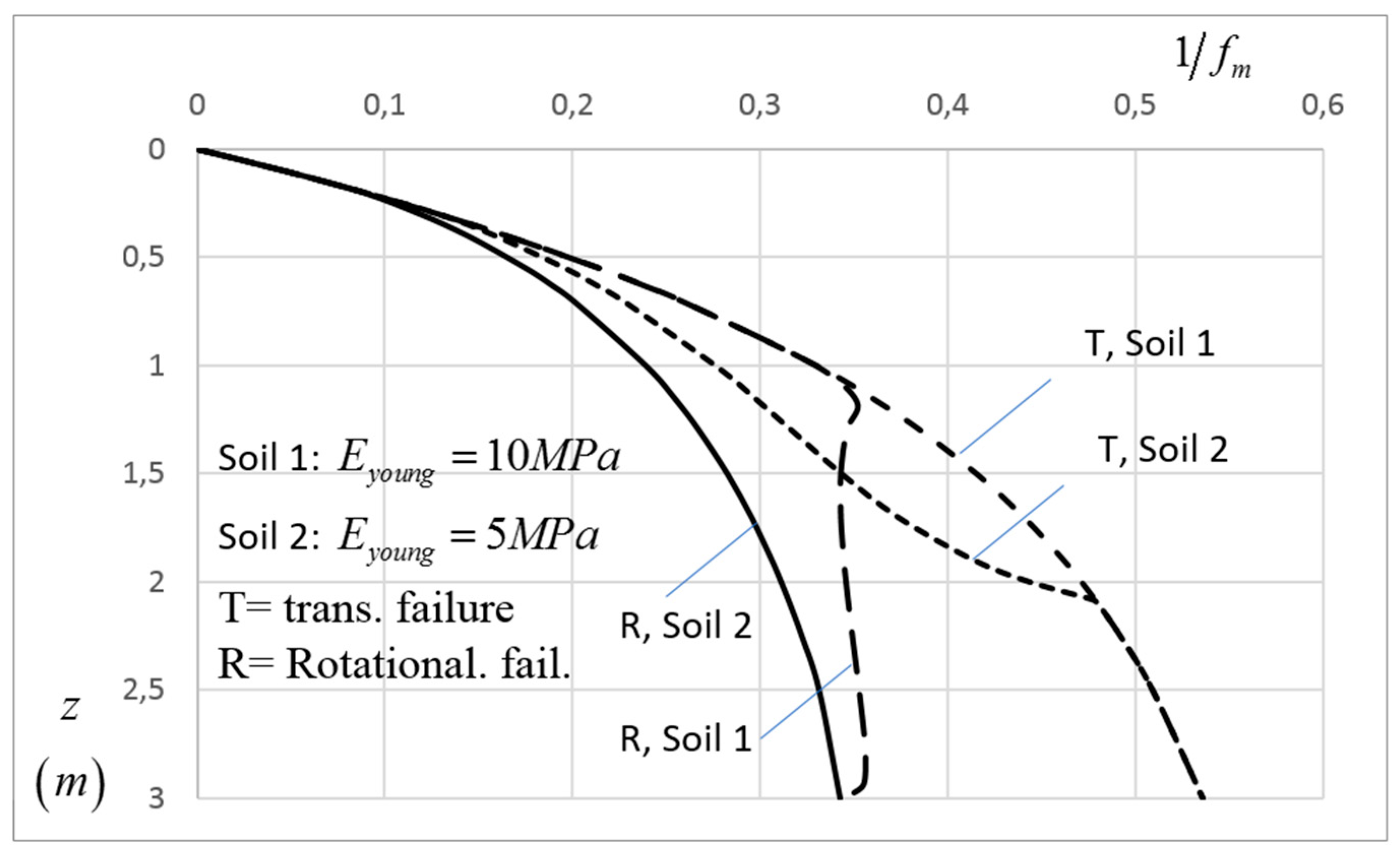
10.1. Choosing a Rational f(m) Function
10.2. Validity of Sand Heap Hypothesis
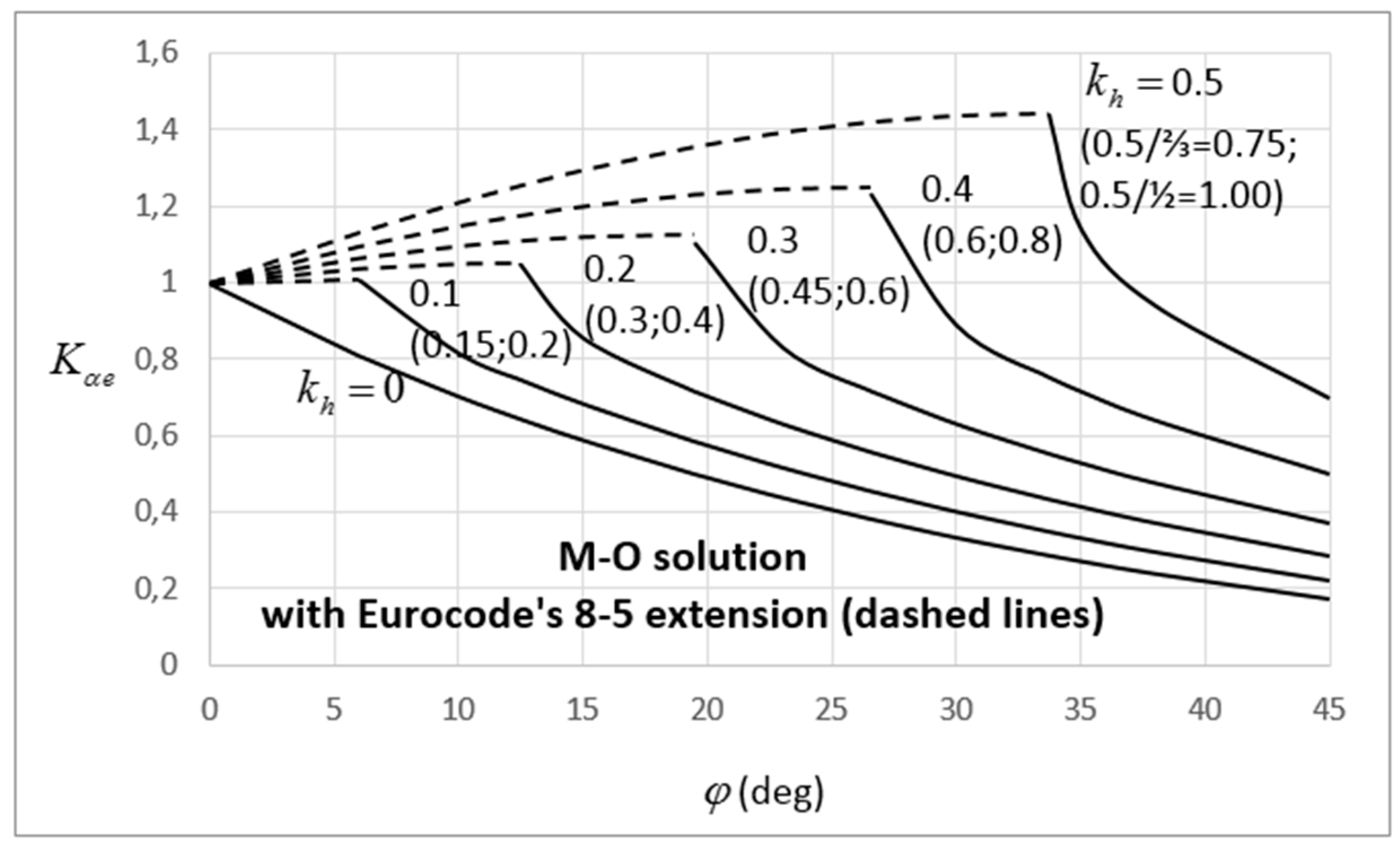
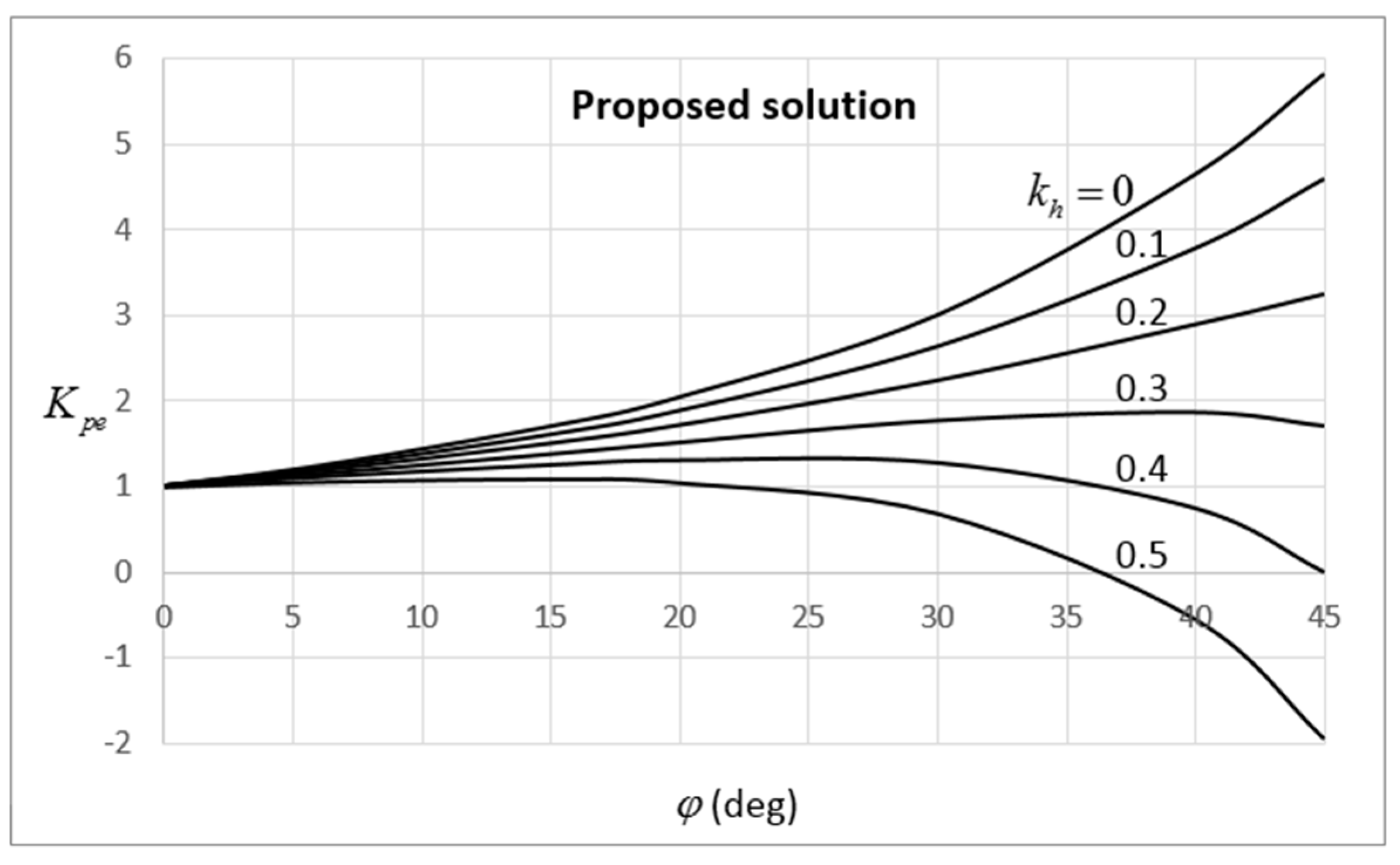
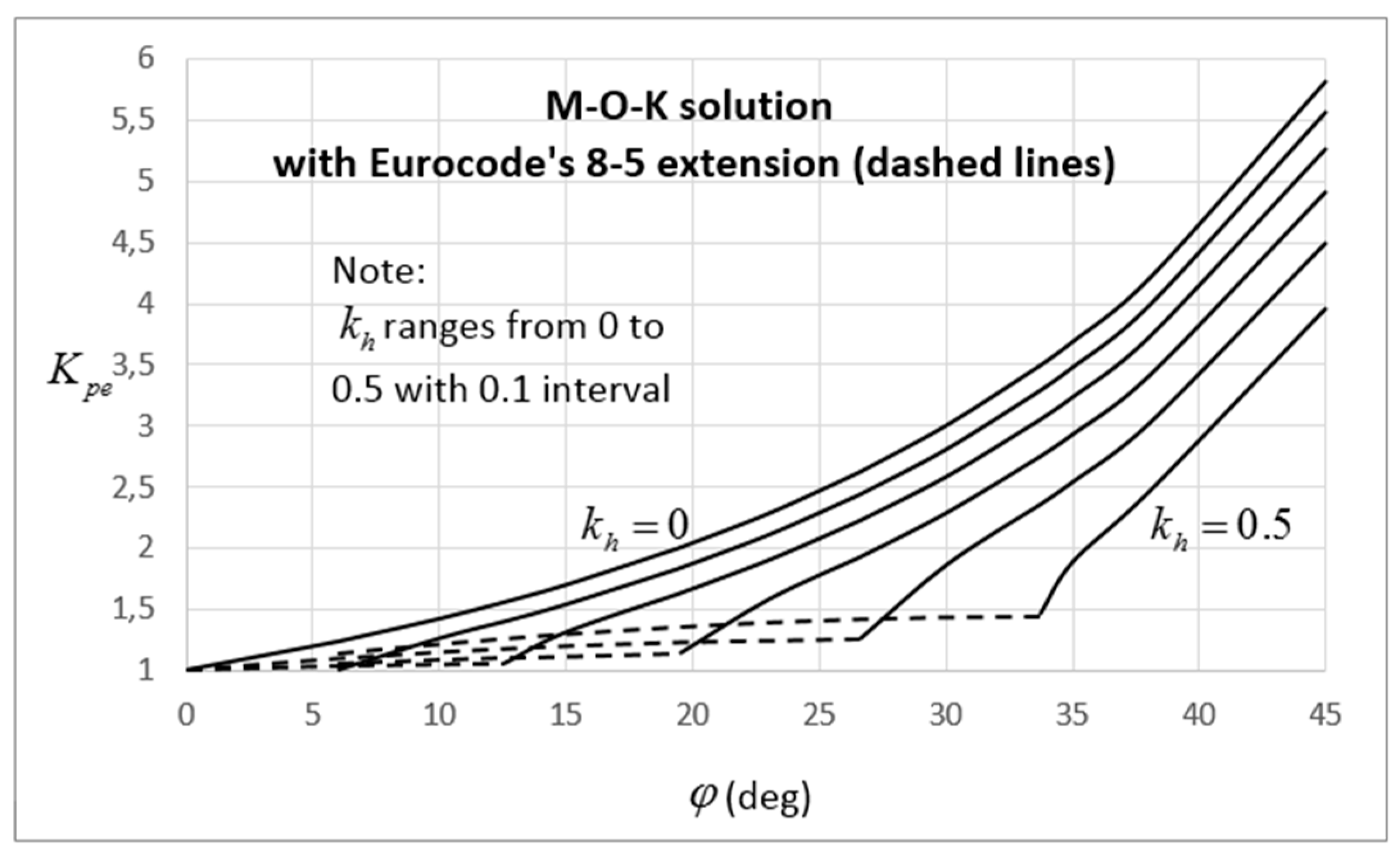
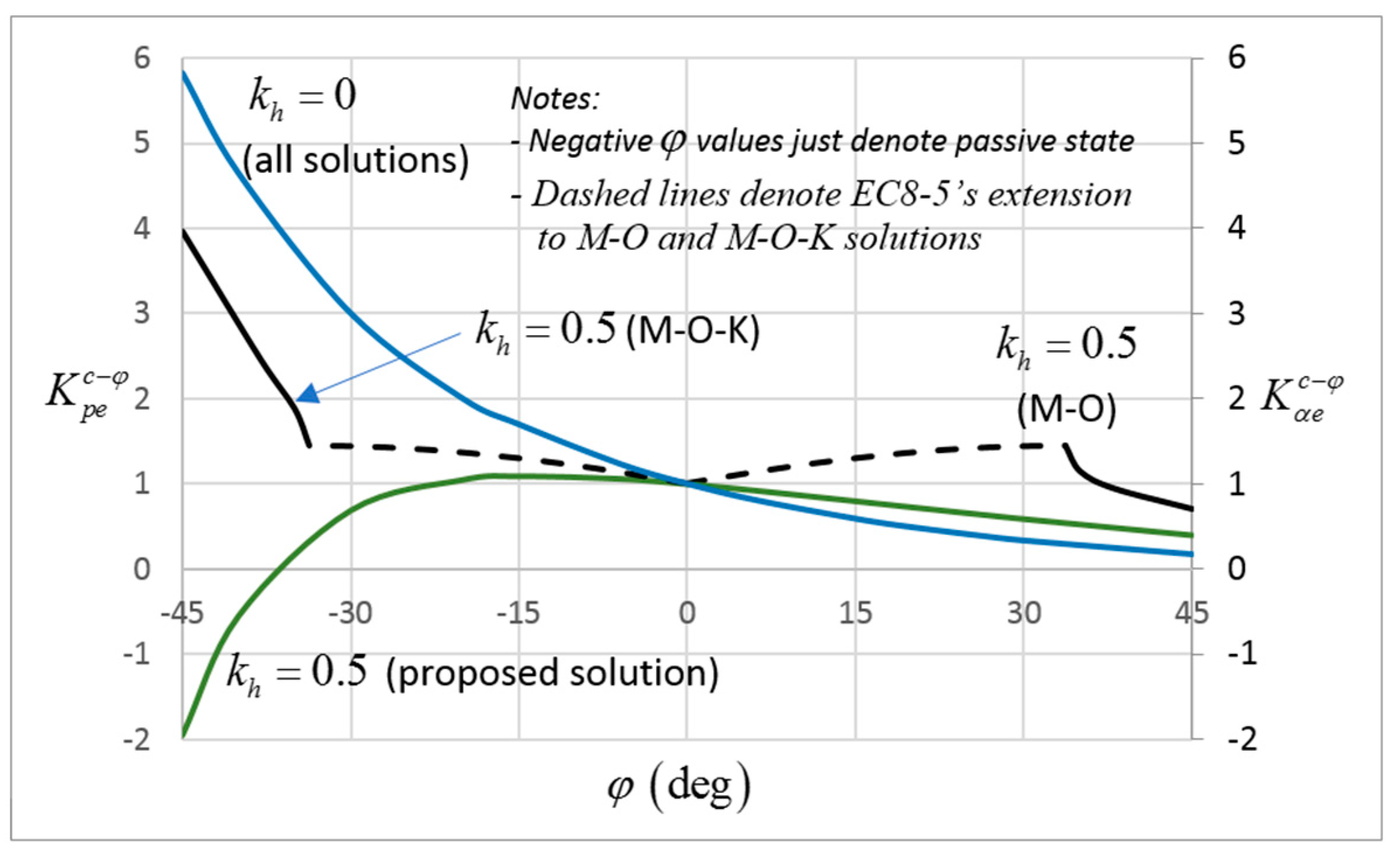
10.3. Comparison of the Proposed Coefficients with Existing Solutions and Experimental Results
10.4. Point of Application of the Resultant Force under Dynamic Conditions
10.5. How Design Codes Treat Dynamic Earth Pressures on Retaining Structures
10.6. Derivation of the Earth Pressure at Rest by the Active Earth Pressure Coefficient
10.7. Earth Pressures Due to External Loading
10.8. The Effect of Consolidation of Soil on the Earth Pressure at Rest
11. Application Examples
11.1. State at Rest, Active State, and Passive State
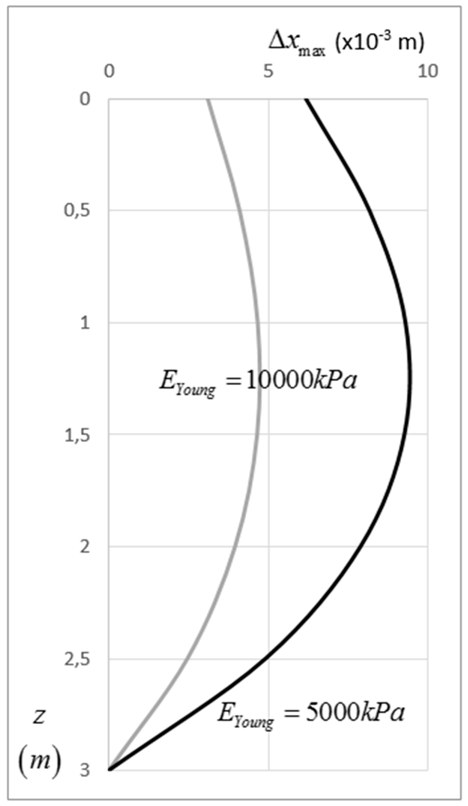
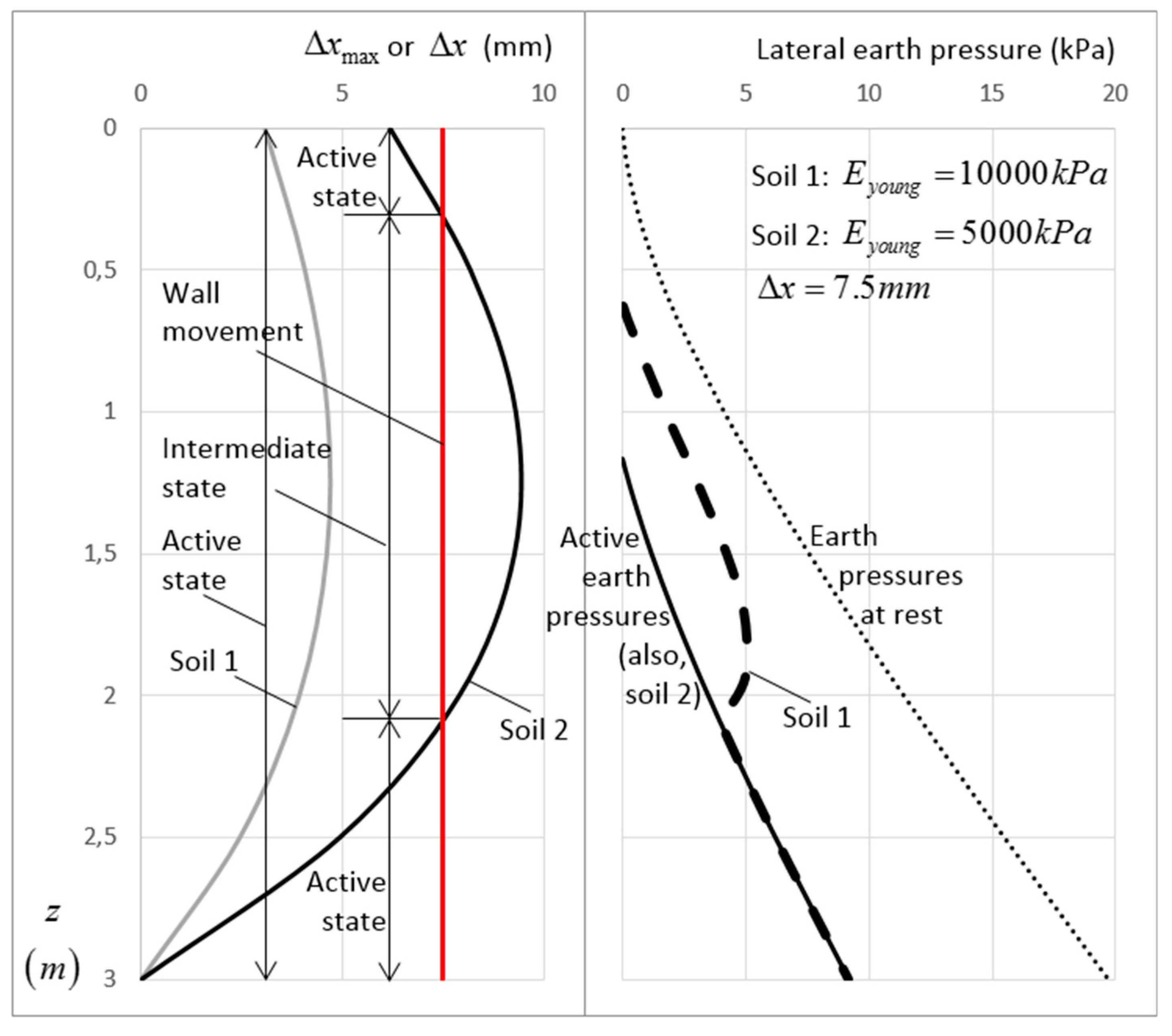
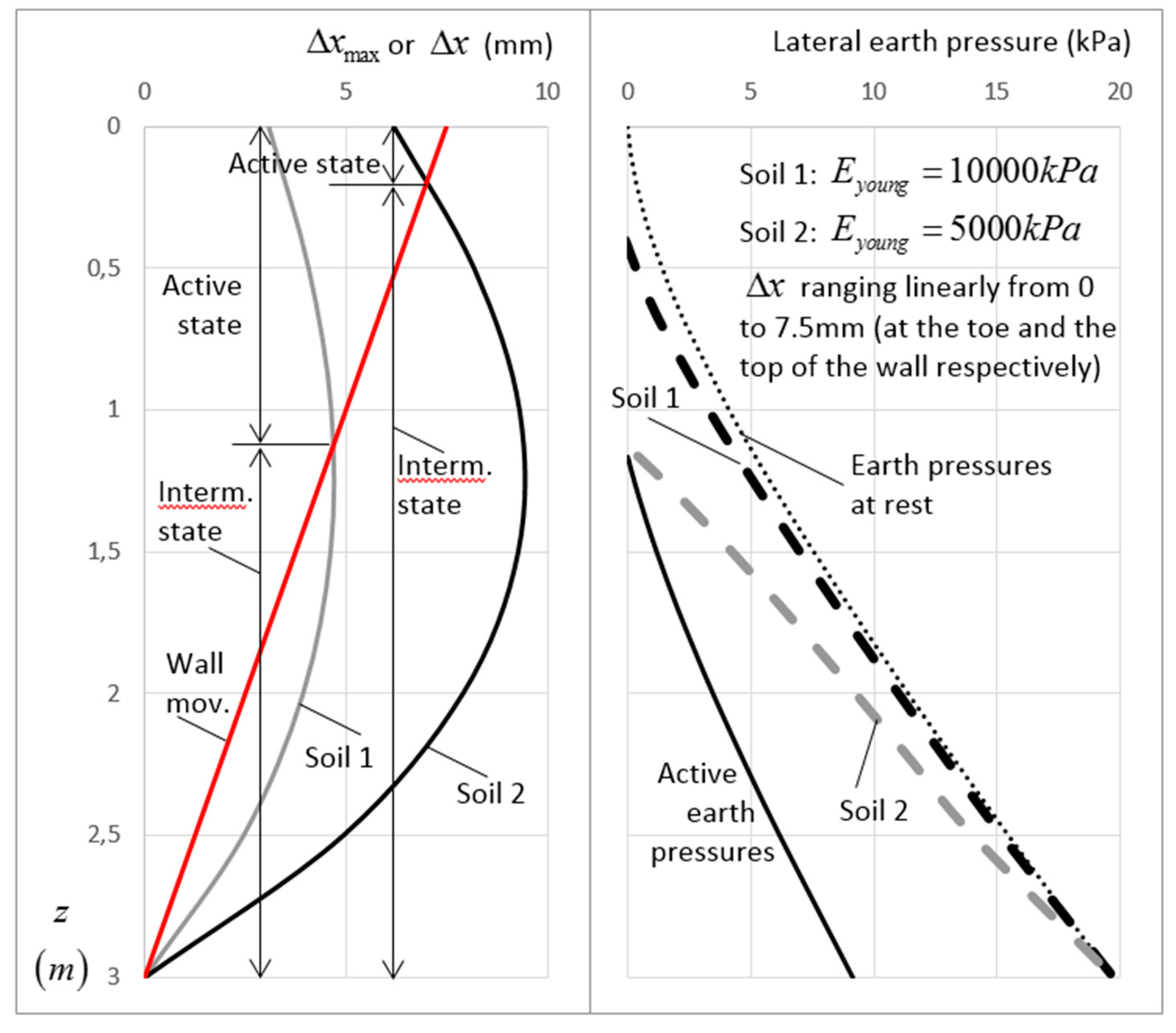
11.2. Intermediate State
12. Summary and Conclusions
Funding
Acknowledgments
Conflicts of Interest
Notation List
| Positive real number | |
| Horizontal pseudo-static acceleration | |
| Inclination angle of sand heap or back slope inclination | |
| Vertical pseudo-static acceleration | |
| Back face inclination angle of the structure with respect to vertical | |
| Unit weight of soil | |
| Overburden stress caused over-consolidation to the underlain soil; this stratum no longer exists e.g., due to erosion | |
| or (depending on the case) | |
| The dynamic pressure increment acting on the wall | |
| Lateral displacement of wall | |
| Lateral displacement of wall corresponding to the active or passive state | |
| The difference between the mobilized friction angle in the active or the passive state and the respective one at the state at rest, that is, or (depending on the case, the difference may be negative) | |
| Angle of friction between structure and soil | |
| Inclination angle of failure plane with respect to horizontal ( for the active state and for the passive state) | |
| Real number (, 1, or 2) | |
| Poisson’s ratio of soil | |
| Coefficient depending only on | |
| Density of the material | |
| Normal stress (it also appears as , , , , , and ) | |
| Vertical stress | |
| Lateral stress | |
| Active earth pressure | |
| Earth pressure at intermediate state (on the active or passive “side”) | |
| Passive earth pressure | |
| Horizontal effective stress | |
| Vertical effective stress | |
| Earth pressure on retaining wall calculated with Finn’s [31] equation taking into account the amount | |
| Pre-consolidation pressure | |
| Earth pressure at rest | |
| Shear stress (it also appears as , and , ) | |
| Mobilized resistance (shear strength) of soil | |
| Friction angle of soil (peak effective value) | |
| Mobilized friction angle of soil (effective value) | |
| The mobilized friction angle of soil at the intermediate state | |
| The mobilized friction angle of soil at the state at rest (it is also referred to as ) | |
| Mobilized friction angle of soil at the state ( for the state at rest, the active, and the passive state, respectively) | |
| Seismic inertia angle | |
| Integral’s constant | |
| Cohesion of soil (peak effective value) | |
| Mobilized cohesion of soil (effective value) | |
| Resultant force of earth pressures at rest | |
| Resultant force of dynamic active earth pressures | |
| Resultant force of dynamic passive earth pressures | |
| Young modulus of soil | |
| , , , and | |
| Body force in the i direction | |
| Mobilization factor of shear strength at the state at rest | |
| Acceleration of gravity | |
| Height of the wall (meaning the height of the retained soil) | |
| Jaky’s coefficient of earth pressure at rest | |
| The generalized coefficient of active earth pressure | |
| The generalized coefficient of earth pressure at rest | |
| The generalized coefficient of passive earth pressure | |
| The generalized coefficient of intermediate earth pressure | |
| Coefficient of lateral earth pressure | |
| It refers to the well-known Coulomb’s active earth pressure coefficient | |
| As above but with zero backfill angle | |
| It refers to the well-known Coulomb’s passive earth pressure coefficient | |
| It refers to the well-known Mononobe–Okabe’s active earth pressure coefficient | |
| It refers to the well-known Kapila’s passive earth pressure coefficient | |
| Seismic coefficient along the in the i direction | |
| Seismic coefficient of horizontal acceleration | |
| Seismic coefficient of vertical acceleration | |
| M-O | It refers to the Mononobe–Okabe solution |
| M-O-K | It refers to Kapila’s solution |
| Real number | |
| Number of planes of the material element resisting to deformation | |
| Normal stress | |
| OCR | Over-consolidation ratio |
| PGA | Peak Ground Acceleration |
| Vertical stress increase at depth z | |
| The reaction force on the assumed Coulomb’s failure plane | |
| Internal resistance of soil in the i direction | |
| Shear stress along the base of Jaky’s sand heap | |
| Shear stress | |
| Imposed seismic force per unit mass in the direction | |
| Acceleration force per unit mass in the direction | |
| Normal stress on the base of Jaky’s sand heap | |
| Weight of Coulomb’s soil wedge | |
| x | x-coordinate |
| x-coordinate on the line OB | |
| z | Depth of soil or z-coordinate |
| Depth of neutral zone |
Appendix A. The Proposed Analysis
Appendix B. Sign Convention
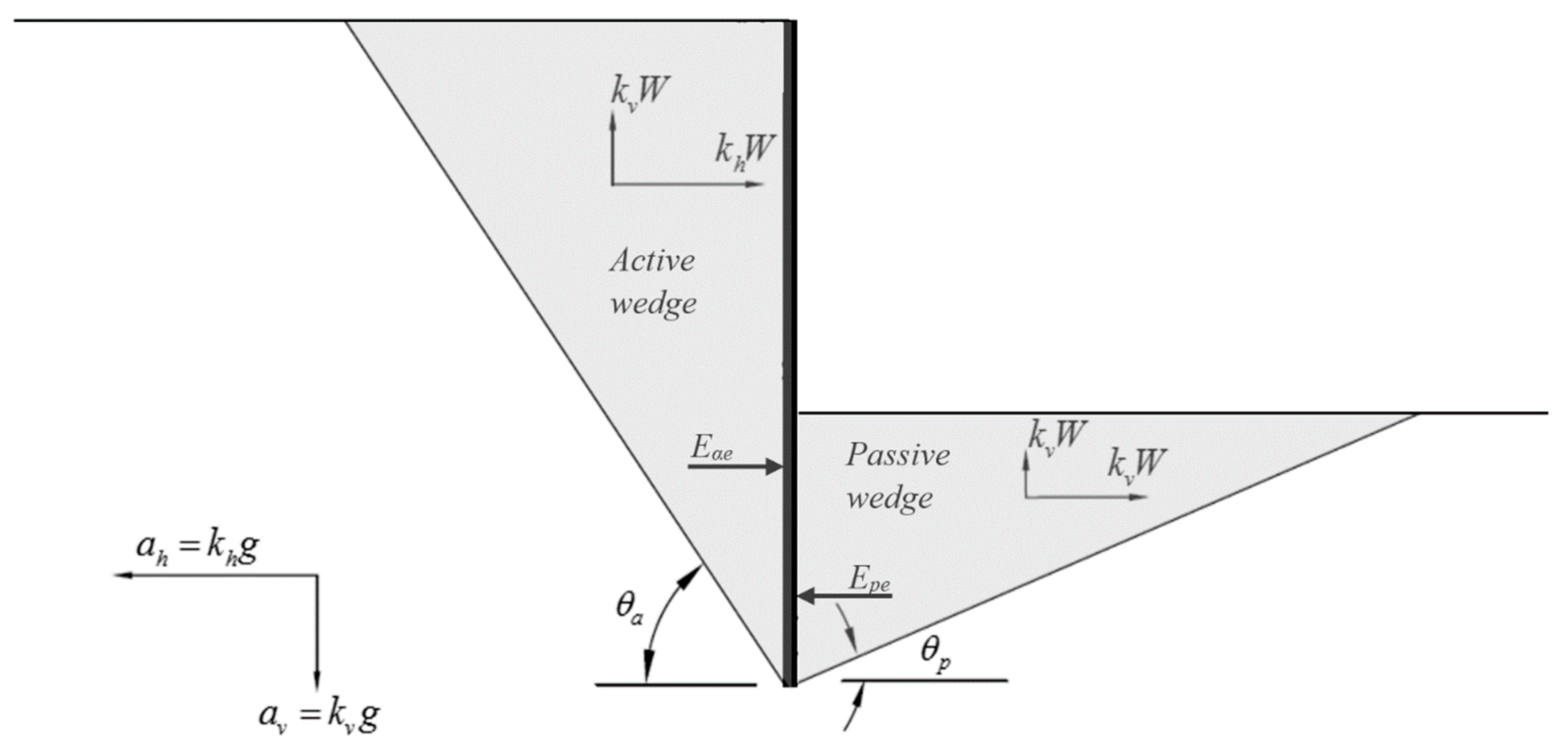
Appendix C. Solution of Equation (36)
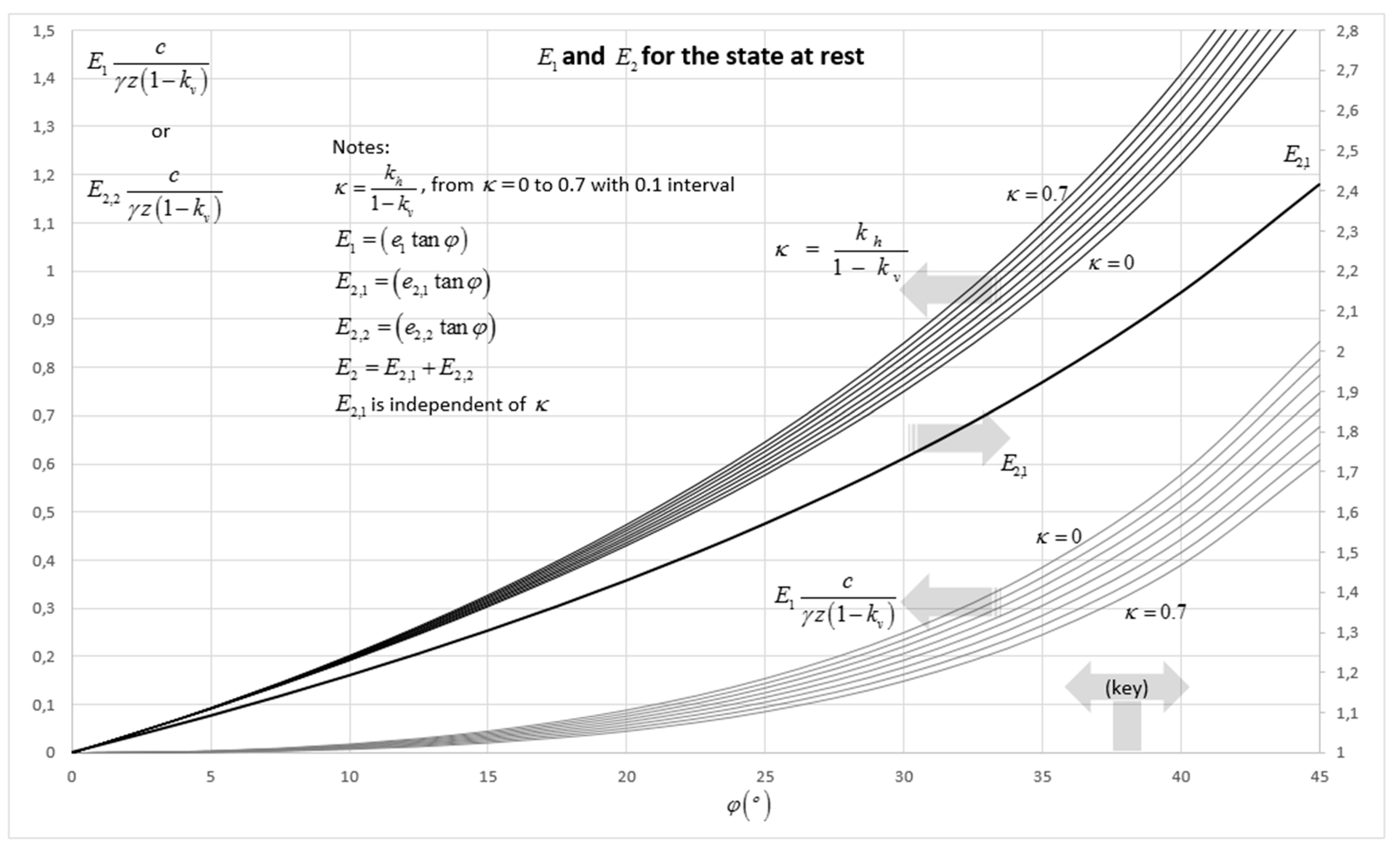
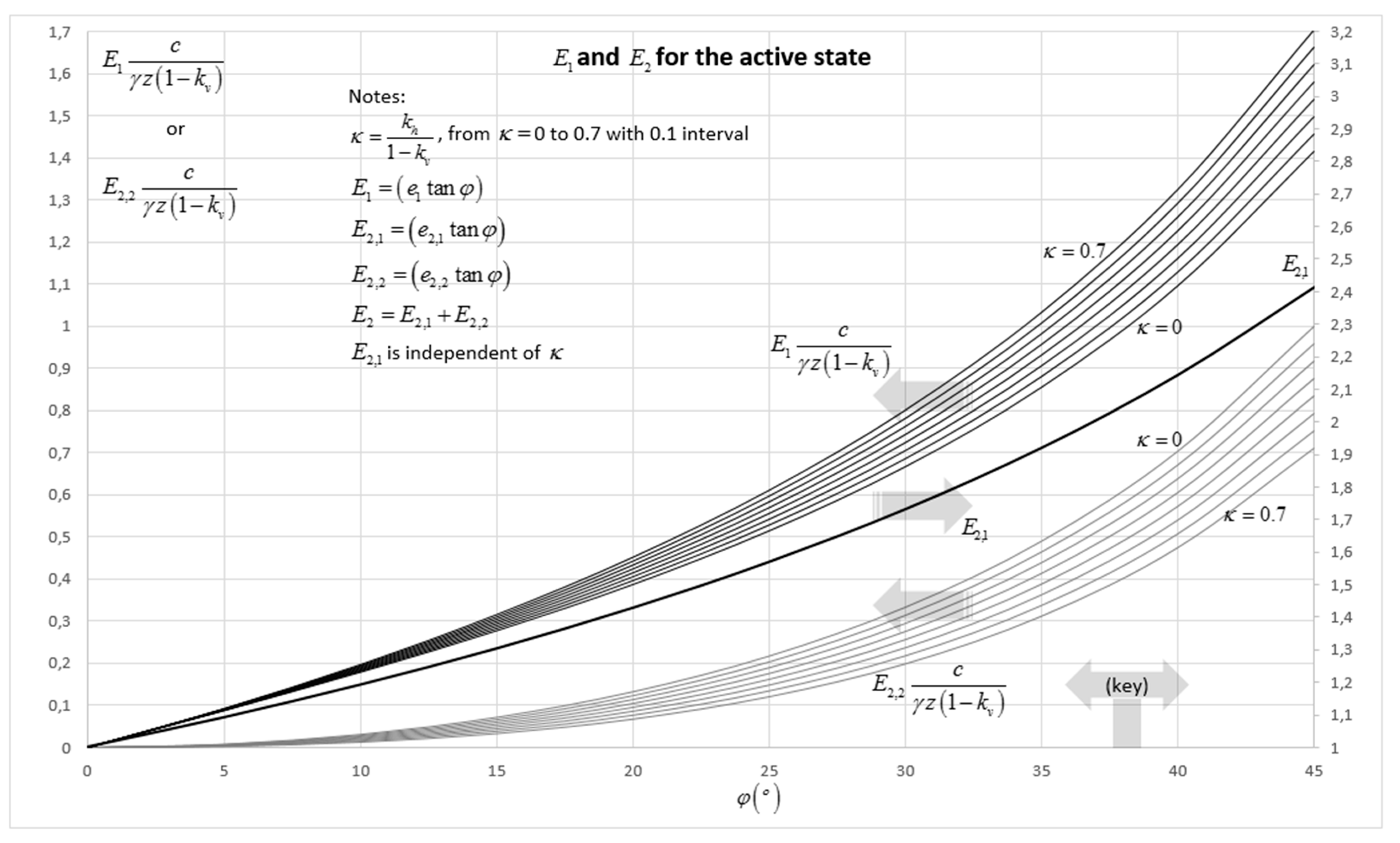
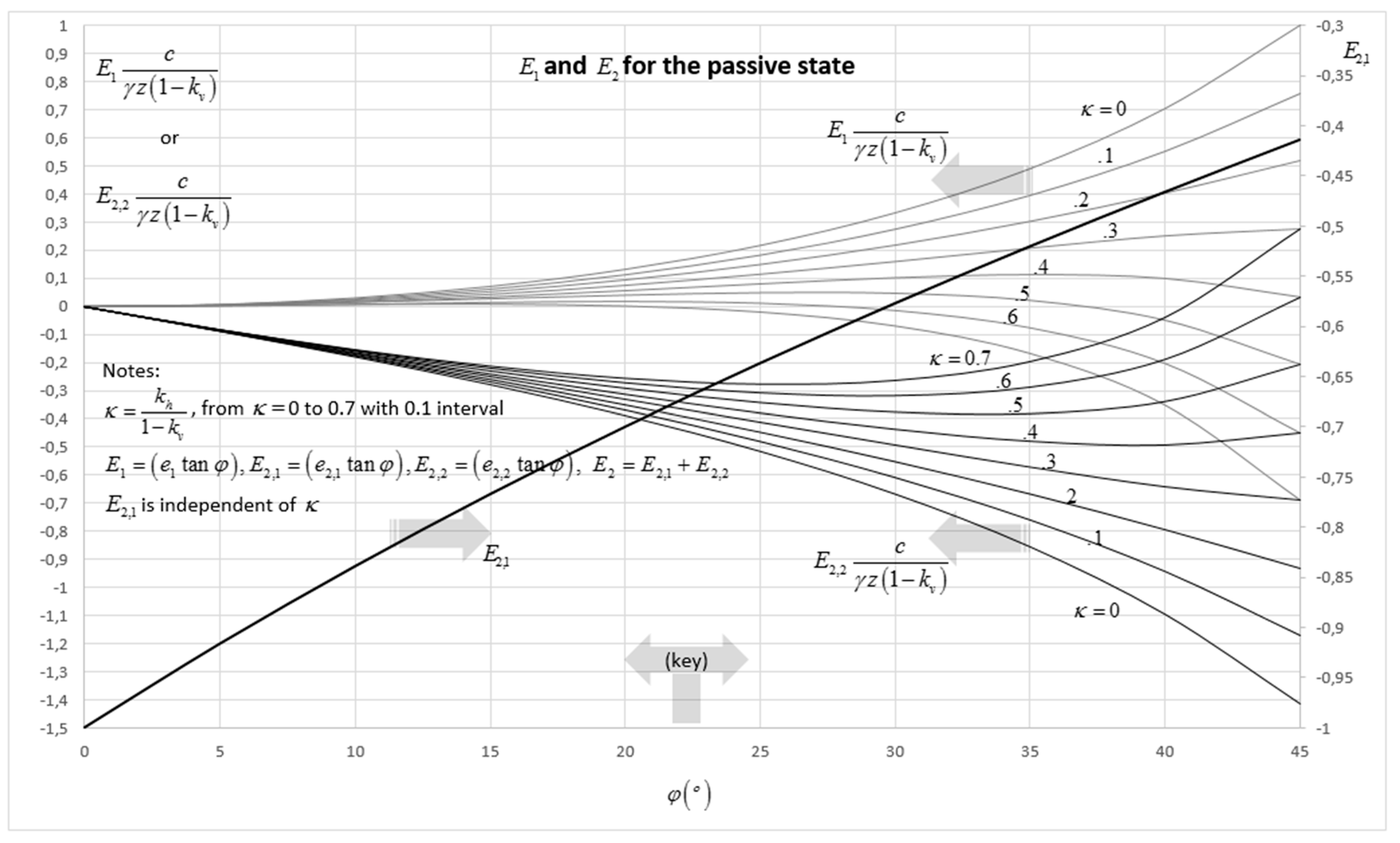
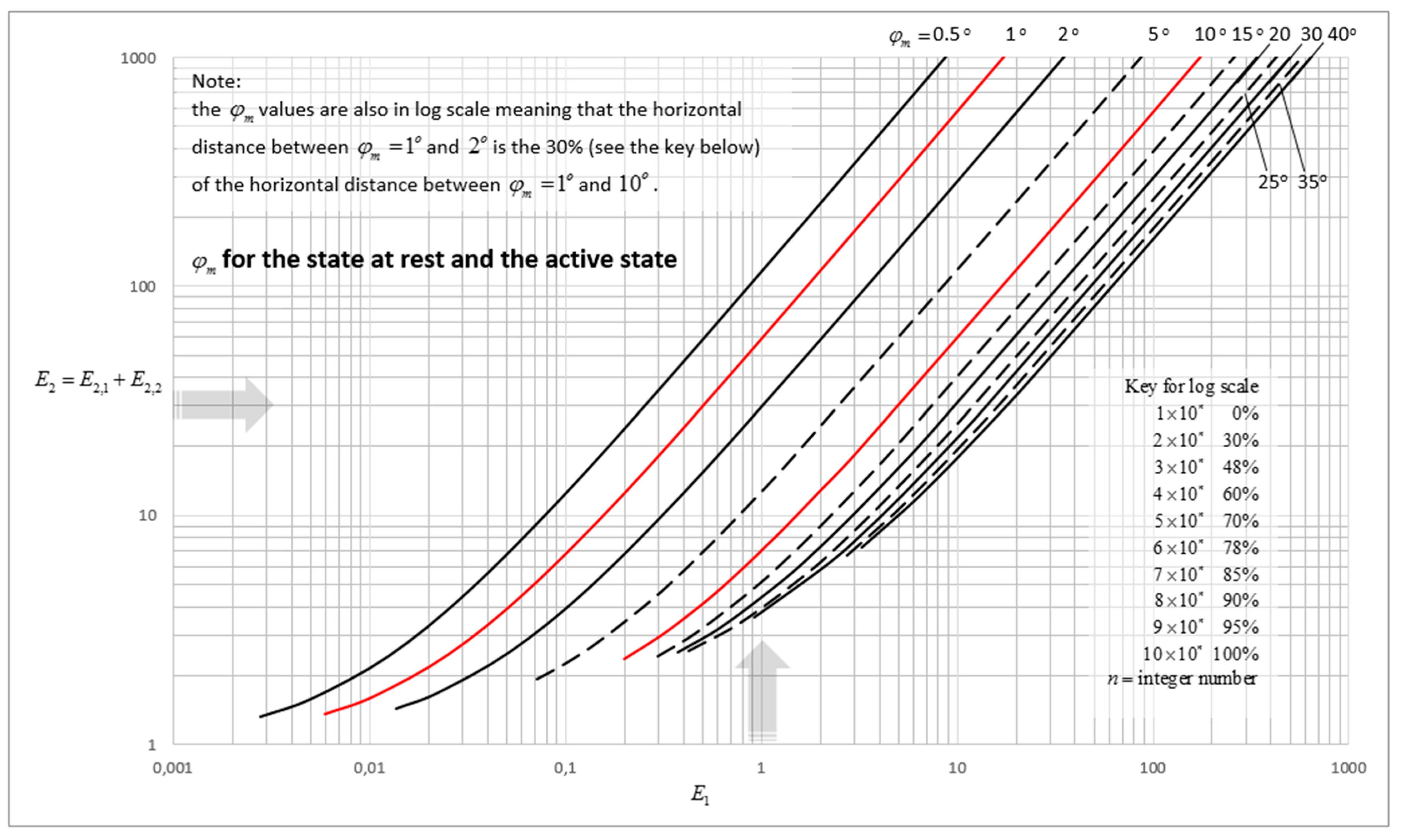
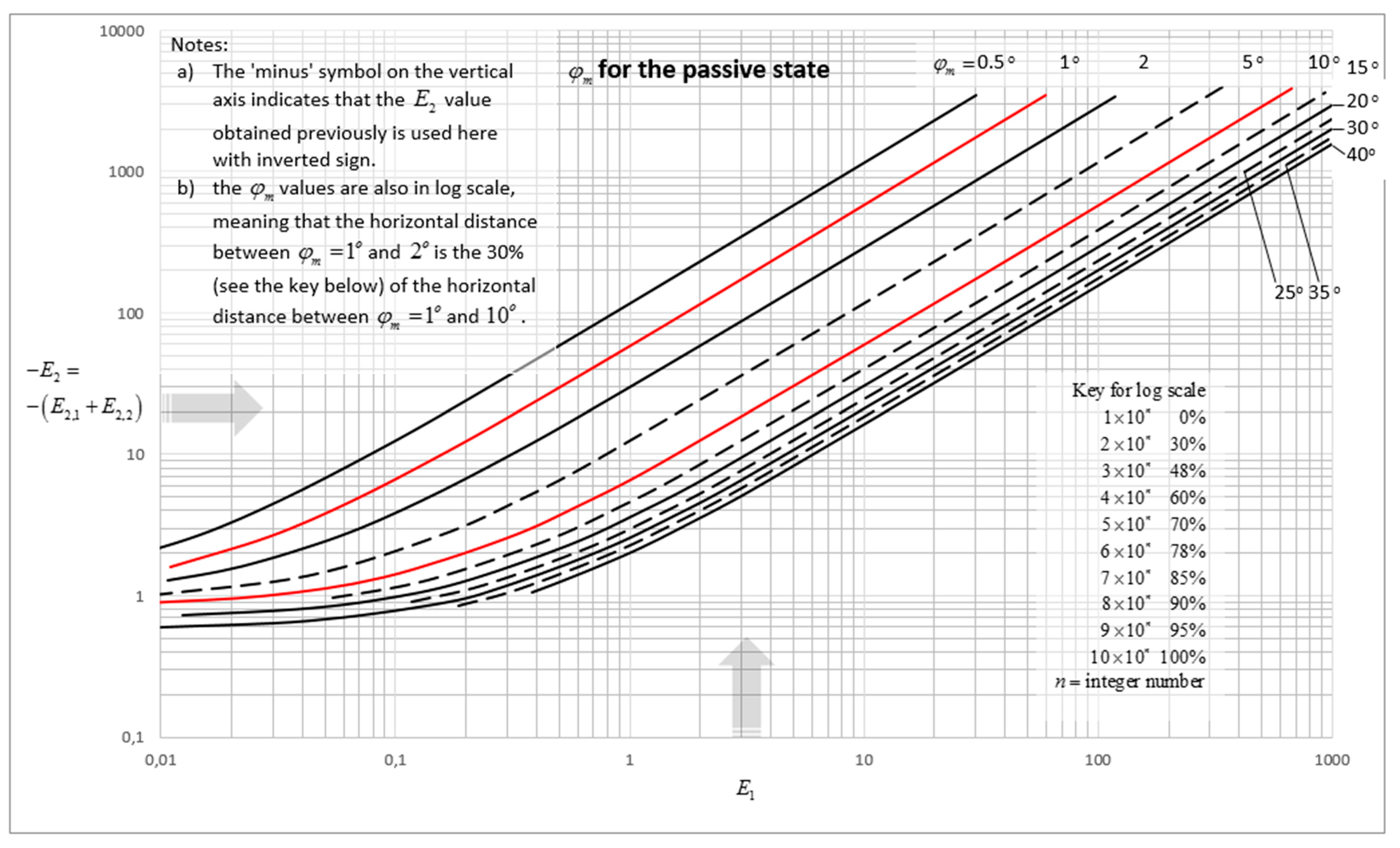
Appendix D. The Parameters e1 and e2 for the Intermediate State on the Passive Side
References
- Gautier, H. Dissertation sur L’epaisseur des Culées des Ponts, sur la Largeur des Piles, sur la Portée des Voussoirs, sur L’effort Et la Pesanteur des Arches À Differens Surbaissemens, Et sur Les Profils de Maçonnerie Qui Doivent Supporter des Chaussées, des Terrasse; Chez André Cailleau: Paris, France, 1717; ISBN 1295197669. [Google Scholar]
- Coulomb, C.A. An attempt to apply the rules of maxima and minima to several problems of stability related to architecture. Mémoires l’Académie, Royale Des Sciences 1776, 7, 343–382. [Google Scholar]
- Rankine, W.J.M., II. On the stability of loose earth. Philos. Trans. R. Soc. Lond. 1857, 147, 9–27. [Google Scholar]
- Bell, A.L. The lateral pressure and resistance of clay and the supporting power of clay foundations. Minutes Proc. Inst. Civ. Eng. 1915, 199, 233–272. [Google Scholar] [CrossRef]
- Muller-Breslau, H. Erddruck Auf Stutzmauert; Alfred Kroner-Verlag: Stuttgart, Germany, 1906. [Google Scholar]
- Caquot, A.I.; Kérisel, J.L. Tables for the Calculation of Passive Pressure, Active Pressure and Bearing Capacity of Foundations; Gauthier-Villars: Paris, France, 1948. [Google Scholar]
- Mononobe, N.; Matsuo, H. On the determination of earth pressures during earthquakes. In Proceedings of the World Engineering Congress, Tokyo, Japan, 22–28 October 1929. [Google Scholar]
- Okabe, S. General theory of earth pressure. Jpn. Soc. Civ. Eng. 1926, 12. [Google Scholar]
- Kapila, J. Earthquake resistant design of retaining walls. In Proceedings of the 2nd Earthquake Symposium; University of Roorkee: Rooekee, India, 1962; pp. 97–108. [Google Scholar]
- Clayton, C.R.I.; Woods, R.I.; Bond, A.J.; Milititsky, J. Earth Pressure and Earth-Retaining Structures; CRC Press: Boca Raton, FL, USA, 2014; ISBN 1482206617. [Google Scholar]
- Jaky, J. The coefficient of earth pressure at rest. J. Soc. Hung. Archit. Eng. 1944, 78, 355–388. [Google Scholar]
- Rowe, P.W. A Stress-Strain Theory for Cohesionless Soil with Applications to Earth Pressures at Rest and Moving Walls. Géotechnique 1954, 4, 70–88. [Google Scholar] [CrossRef]
- Rowe, P.W. General report on papers in Section 1. In Proceedings of the Brussels Conference on Earth Pressure Problems, Brussels, Belgium, September 1958; pp. 25–30. [Google Scholar]
- Hendron, A.J., Jr. The Behavior of Sand in One-Dimensional Compression; Research and Technology Division, Air Force Systems Command, Air Force Weapons Laboratory: Albuquerque, NM, USA, 1963. [Google Scholar]
- Alpan, I. The empirical evaluation of the coefficient K0 and K0R. Soils Found. 1967, 7, 31–40. [Google Scholar] [CrossRef]
- Brooker, E.W.; Ireland, H.O. Earth pressures at rest related to stress history. Can. Geotech. J. 1965, 2, 1–15. [Google Scholar] [CrossRef]
- Schmidt, B. Earth pressures at rest related to stress history. Can. Geotech. J. 1966, 3, 239–242. [Google Scholar] [CrossRef]
- Abdelhamid, M.S.; Krizek, R.J. At-rest lateral earth pressure of a consolidating clay. J. Geotech. Geoenviron. Eng. 1976, 102, 721–738. [Google Scholar]
- Bishop, A.W.; Eldin, A.K.G. The effect of stress history on the relation between and porosity in sand. In Proceedings of the 3rd International Conference Soil Mechanics, Zurich, Switzerland, 16–27 August 1953; pp. 100–105. [Google Scholar]
- Hendron, A.J., Jr. The Behavior of Sand in One-Dimensional Compression. Ph.D. Thesis, University of Illinois, Urbana, IL, USA, 1963. [Google Scholar]
- Abdelhamid, M.S.; Krizek, R.J. At Rest Lateral Earth Pressures of a Consolidating Clay. J. Geotech. Geoenviron. Eng. 1977, 103, 820–821. [Google Scholar]
- Saglamer, A. Soil parameters affecting coefficient of earth pressure at rest of cohesionless soils. In Proceedings of the Istanbul conference on soil/mechanics and Foundation Engineering, Istanbul, Turkey, 31 March–4 April 1975; pp. 9–16. [Google Scholar]
- Slawinski, M.A. Waves and Rays in Elastic Continua; World Scientific: Singapore, 2010. [Google Scholar]
- Hoeg, K.; Christian, J.T.; Whitman, R.V. Settlement of strip load on elastic-plastic soil. J. Soil Mech. Found. Div. 1968, 94, 431–445. [Google Scholar]
- Burland, J.B.; Broms, B.B.; de Mello, V.F.B. Behaviour of foundations and structures. In Proceedings of the 9th International Conference Soil Mechanics and Foundation Engineering, Tokyo, Japan, 10–15 July 1977; pp. 495–546. [Google Scholar]
- Barnes, G. Soil Mechanics: Principles and Practice; Palgrave Macmillan: New York, NY, USA, 2016; ISBN 1137512210. [Google Scholar]
- Landau, L.D.; Lifshitz, E.M.; Sykes, J.B.; Reid, W.H.; Dill, E.H. Theory of Elasticity: Vol. 7 of Course of Theoretical Physics. Phys. Today 1960, 13, 44–46. [Google Scholar] [CrossRef]
- Jaky, J. Pressure in silos. In Proceedings of the 2nd International Conference on Soil Mechanics and Foundation Engineering ICSMFE, London, UK, 21–30 June 1948; pp. 103–107. [Google Scholar]
- Donath, A.D. Untersuchungen veber den Erddruck auf Stuetzwaende; Zeitschrift fuer Bauwesen: Berlin, Germany, 1891. [Google Scholar]
- Richards, R.; Shi, X. Seismic Lateral Pressures in Soils with Cohesion. J. Geotech. Eng. 1994, 120, 1230–1251. [Google Scholar] [CrossRef]
- Finn, W.D. Boundary Values Problems of Soil Mechanics. J. Soil Mech. Found. Div. 1963, 89, 39–72. [Google Scholar]
- Bishop, A.W. The use of the Slip Circle in the Stability Analysis of Slopes. Géotechnique 1955, 5, 7–17. [Google Scholar] [CrossRef]
- Pantelidis, L.; Griffiths, D.V. Integrating Eurocode 7 (load and resistance factor design) using nonconventional factoring strategies in slope stability analysis. Can. Geotech. J. 2013, 51, 208–216. [Google Scholar] [CrossRef]
- Michalowski, R.L. Coefficient of earth pressure at rest. J. Geotech. Geoenviron. Eng. 2005, 131, 1429–1433. [Google Scholar] [CrossRef]
- Pipatpongsa, T.; Vardhanabhuti, B. Analyses of coefficient of lateral earth pressure in wedge-shaped granular mound based on Jaky’s (1944) hypothesis. In Proceedings of the 14th National Conference in Civil Engineering, Nakhon-Ratchsima, Thailand, May 2009; pp. 147–152. [Google Scholar]
- EN1998-5. Eurocode 8: Design of Structures for Earthquake Resistance—Part 5: Foundations, Retaining Structures and Geotechnical Aspects; European Committee for Standardization: Brussels, Belgium, 2004. [Google Scholar]
- AASHTO (American Association of State Highway and Transportation Officials). LRFD Bridge Design Specifications, Customary, U.S. Units, 5th ed.; AASHTO: Washington, DC, USA, 2010. [Google Scholar]
- Seed, H.B.; Whitman., R.V. Design of earth retaining structures for dynamic loads. In Proceedings of the ASCE Specialty Conference-Lateral Stresses in the Ground and Design of Earth Retaining Structures, New York, NY, USA, 22–24 June 1970; pp. 103–147. [Google Scholar]
- Anderson, D.G. Seismic Analysis and Design of Retaining Walls, Buried Structures, Slopes, and Embankments; Transportation Research Board: Washington, DC, USA, 2008; ISBN 0309117658. [Google Scholar]
- Sitar, N.; Mikola, R.G.; Candia, G. Seismically induced lateral earth pressures on retaining structures and basement walls. In Geotechnical Engineering State of the Art and Practice: Keynote Lectures from GeoCongress 2012; Rollins, K., Zekkos, D., Eds.; ASCE Publications: Reston, VA, USA, 2012; pp. 335–358. [Google Scholar]
- Agusti, G.C.; Sitar, N. Seismic Earth Pressures on Retaining Structures in Cohesive Soils; Report No UCB GT 13-02; University of California: Berkeley, CA, USA, August 2013. [Google Scholar]
- Mikola, R.G.; Candia, G.; Sitar, N. Seismic earth pressures on retaining structures and basement walls in cohesionless soils. J. Geotech. Geoenviron. Eng. 2016, 142, 04016047. [Google Scholar] [CrossRef]
- Wagner, N.; Candia, G.; Mikola, R.G.; Sitar, N. Seismic earth pressures—Experiments and Analyses. In Proceedings of the 3rd International Conference Performance Based Design in Earthquake Geotechnical Engineering, Vancouver, BC, Canada, 16–19 July 2017. [Google Scholar]
- Mikola, R.G.; Sitar, N. Seismic Earth Pressures on Retaining Structures in Cohesionless Soils; Report No UCB/CA13-0367; University of California: Berkeley, CA, USA, March 2013. [Google Scholar]
- Mikola, R.G.; Candia, G.; Sitar, N. Seismic earth pressures on retaining structures and basement walls. In Proceedings of the Tenth US National Conference on Earthquake Engineering, Anchorage, AK, USA, 21–25 July 2014. [Google Scholar]
- Sitar, N.; Al Atik, L. Dynamic centrifuge study of seismically induced lateral earth pressures on retaining structures. In Geotechnical Earthquake Engineering and Soil Dynamics IV; Zeng, D., Manzari, M.T., Hiltunen, D.R., Eds.; ASCE Publications: Reston, VA, USA, 2008; pp. 1–11. [Google Scholar]
- Fragaszy, R.J.; Dendy, G.; Higgins, J.D. Seismic Response of Tieback Retaining Walls, Phase I (WA-RD Report No 138.1); Washington State University: Pullman, WA, USA, 1987. [Google Scholar]
- Lew, M.; Sitar, N.; Atik, L. Al Seismic earth pressures: Fact or fiction? In Proceedings of the Earth Retention Conference 3, Bellevue, WA, USA, 1–4 August 2010; pp. 656–673. [Google Scholar]
- Wagner, N.; Sitar, N. Seismic Earth Pressures on Deep Stiff Walls. In Proceedings of the Geotechnical and Structural Engineering Congress, Phoenix, AZ, USA, 14–17 February 2016; pp. 499–508. [Google Scholar]
- Al Atik, L.; Sitar, N. Seismic earth pressures on cantilever retaining structures. J. Geotech. Geoenviron. Eng. 2010, 136, 1324–1333. [Google Scholar] [CrossRef]
- Gazetas, G.; Psarropoulos, P.N.; Anastasopoulos, I.; Gerolymos, N. Seismic behaviour of flexible retaining systems subjected to short-duration moderately strong excitation. Soil Dyn. Earthq. Eng. 2004, 24, 537–550. [Google Scholar] [CrossRef]
- Psarropoulos, P.N.; Klonaris, G.; Gazetas, G. Seismic earth pressures on rigid and flexible retaining walls. Soil Dyn. Earthq. Eng. 2005, 25, 795–809. [Google Scholar] [CrossRef]
- Al Atik, L.; Sitar, N. Development of Improved Procedures for Seismic Design of Buried and Partially Buried Structures; Pacific Earthquake Engineering Research Center: Berkeley, CA, USA, 2007. [Google Scholar]
- Xu, S.-Y.; Kannangara, K.K.P.M. Semi-Analytical Approach to Evaluate Seismic Passive Earth Pressures Considering the Effects of Soil Cohesion and a Curvilinear Failure Surface. J. Geotech. Geoenviron. Eng. 2017, 143, 06017011. [Google Scholar] [CrossRef]
- Building Seismic Safety Council National Earthquake Hazards Reduction Program Recommended Provisions and Commentary for Seismic Regulations for New Buildings and Other Structures (FEMA P-750/2009 Edition): Part I (Provisions) and Part II (Commentary); Federal Emergency Management Agency: Washington, DC, USA, 2009.
- Building Seismic Safety Council NEHRP Recommended Seismic Provisions: Design Examples; FEMA P-751; FEMA: Washington, DC, USA, 2012.
- Venkatramaiah, C. Geotechnical Engineering, 3rd ed.; New Age International: New Delhi, India, 2006; ISBN 812240829X. [Google Scholar]
- Sherif, M.A.; Ishibashi, I.; Lee, C. Do Earth pressure against rigid retaining walls. J. Geotech. Geoenviron. Eng. 1982, 108, 679–695. [Google Scholar]
- Sherif, M.A.; Fang, Y.-S. Dynamic earth pressures on walls rotating about the base. In Proceedings of the 8th WCEE, San Francisco, CA, USA, 21–28 July 1984; pp. 993–1000. [Google Scholar]
- Sherif, M.A.; Fang, Y.-S. Dynamic earth pressures on walls rotating about the top. Soils Found. 1984, 24, 109–117. [Google Scholar] [CrossRef][Green Version]
- Prakash, S.; Basavanna, B.M. Earth pressure distribution behind retaining wall during earthquakes. In Proceedings of the Fourth World Conference on Earthquake Engineering, Santiago, Chile, 13–18 January 1969. [Google Scholar]
- Dunnicliff, J. Geotechnical Instrumentation for Monitoring Field Performance; John Wiley & Sons: New York, NY, USA, 1993; ISBN 0471005460. [Google Scholar]
- Weiler, W.A.; Kulhawy, F.H. Factors affecting stress cell measurements in soil. J. Geotech. Eng. Div. 1982, 108, 1529–1548. [Google Scholar]
- Dave, T.N.; Dasaka, S.M. A review on pressure measurement using earth pressure cell. Int. J. Earth Sci. Eng. 2011, 4, 1031–1034. [Google Scholar]
- Ortiz, L.A.; Scott, R.F.; Lee, J. Dynamic centrifuge testing of a cantilever retaining wall. Earthq. Eng. Struct. Dyn. 1983, 11, 251–268. [Google Scholar] [CrossRef]
- Stadler, A.T. Dynamic Centrifuge Testing of Cantilever Retaining Walls; University of Colorado at Boulder: Boulder, CO, USA, 1996. [Google Scholar]
- Al Atik, L.; Sitar, N. Experimental and Analytical Study of the Seismic Performance of Retaining Structures; Pacific Earthquake Engineering Research Center: Berkeley, CA, USA, 2009. [Google Scholar]
- Chin, C.Y.; Kayser, C. Use of Mononobe-Okabe equations in seismic design of retaining walls in shallow soils. Int. J. Earth Sci. Eng. 2013, 4, 1031–1034. [Google Scholar]
- Kavazanjian, E.; Wang, J.; Martin, G.; Shamsabadi, A.; Lam, I.; Dickenson, S.; Hung, J. LRFD Seismic Analysis and Design of Transportation Geotechnical Features and Structural Foundations (FHWA-NHI-11-032); Federal Highway Administration: Washington, DC, USA, 2011.
- Au-Yeung, Y.S.; Ho, K.K.S. Gravity Retaining Walls Subject to Seismic Loading; Geotechnical Engineering Office, Civil Engineering Department: Valencia, Spain, 1995.
- USACE, U.S. Army Corps of Engineers. Engineering and Design of Retaining and Flood Walls; USACE: Washington, DC, USA, 1989; EM 1110-2-2502. [Google Scholar]
- Wesley, L.D. Fundamentals of Soil Mechanics for Sedimentary and Residual Soils; John Wiley & Sons: New York, NY, USA, 2009; ISBN 0470376260. [Google Scholar]
- Mayne, P.W.; Kulhawy, F.H. K0-OCR relationships in soil. J. Geotech. Eng. 1982, 108, 851–872. [Google Scholar]


© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pantelidis, L. The Generalized Coefficients of Earth Pressure: A Unified Approach. Appl. Sci. 2019, 9, 5291. https://doi.org/10.3390/app9245291
Pantelidis L. The Generalized Coefficients of Earth Pressure: A Unified Approach. Applied Sciences. 2019; 9(24):5291. https://doi.org/10.3390/app9245291
Chicago/Turabian StylePantelidis, Lysandros. 2019. "The Generalized Coefficients of Earth Pressure: A Unified Approach" Applied Sciences 9, no. 24: 5291. https://doi.org/10.3390/app9245291
APA StylePantelidis, L. (2019). The Generalized Coefficients of Earth Pressure: A Unified Approach. Applied Sciences, 9(24), 5291. https://doi.org/10.3390/app9245291




