Analysis of Dynamic Modulation Transfer Function for Complex Image Motion
Abstract
:1. Introduction
2. Modulation Transfer Function (MTF) Calculation Method
2.1. Common Model to Calculate MTF for Any Image Motion
2.2. The MTF for the Mixed Image Motion of Linear Motion and Sinusoidal Motion
3. Analysis of the Analytical MTF Expression for Complex Image Motion
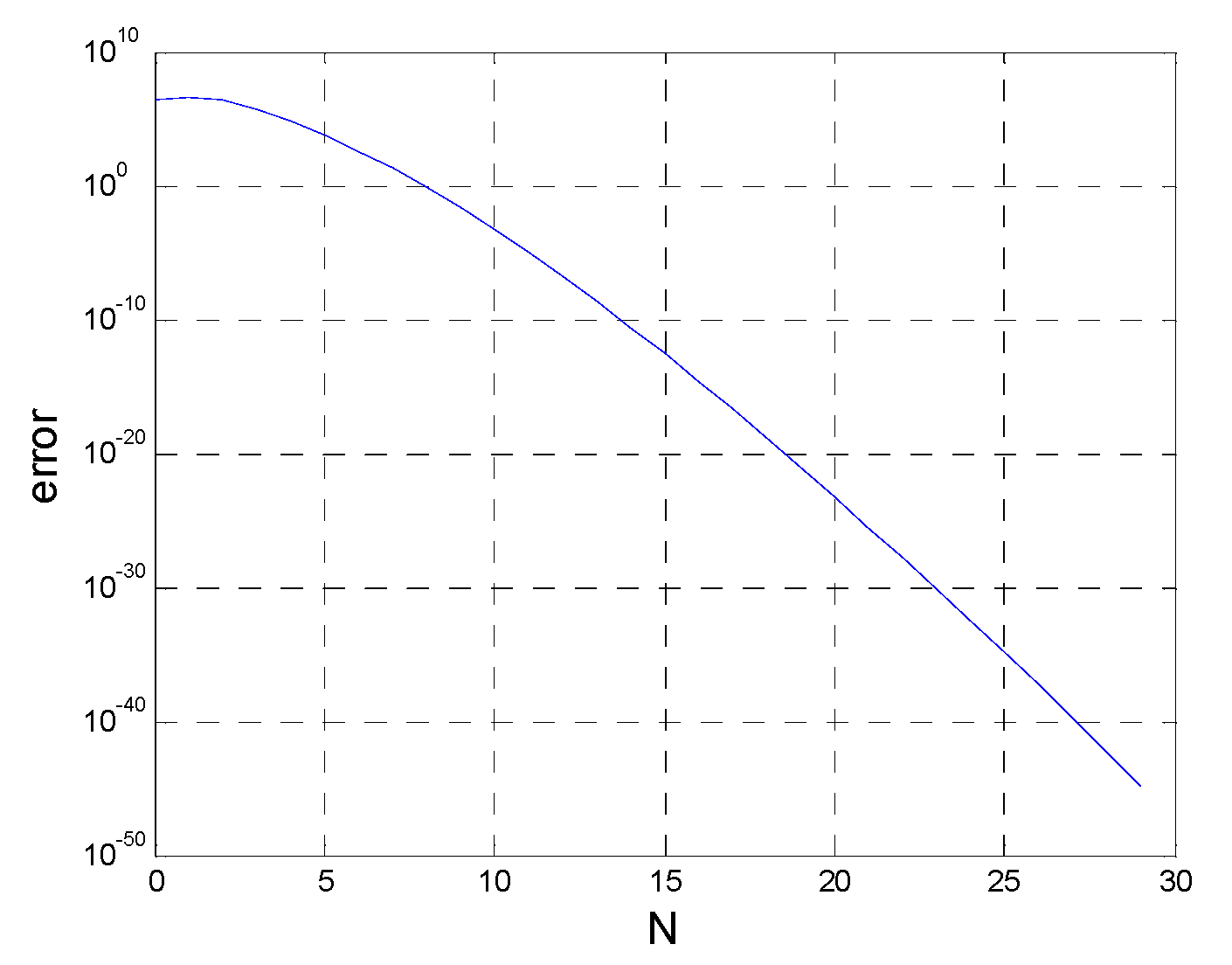
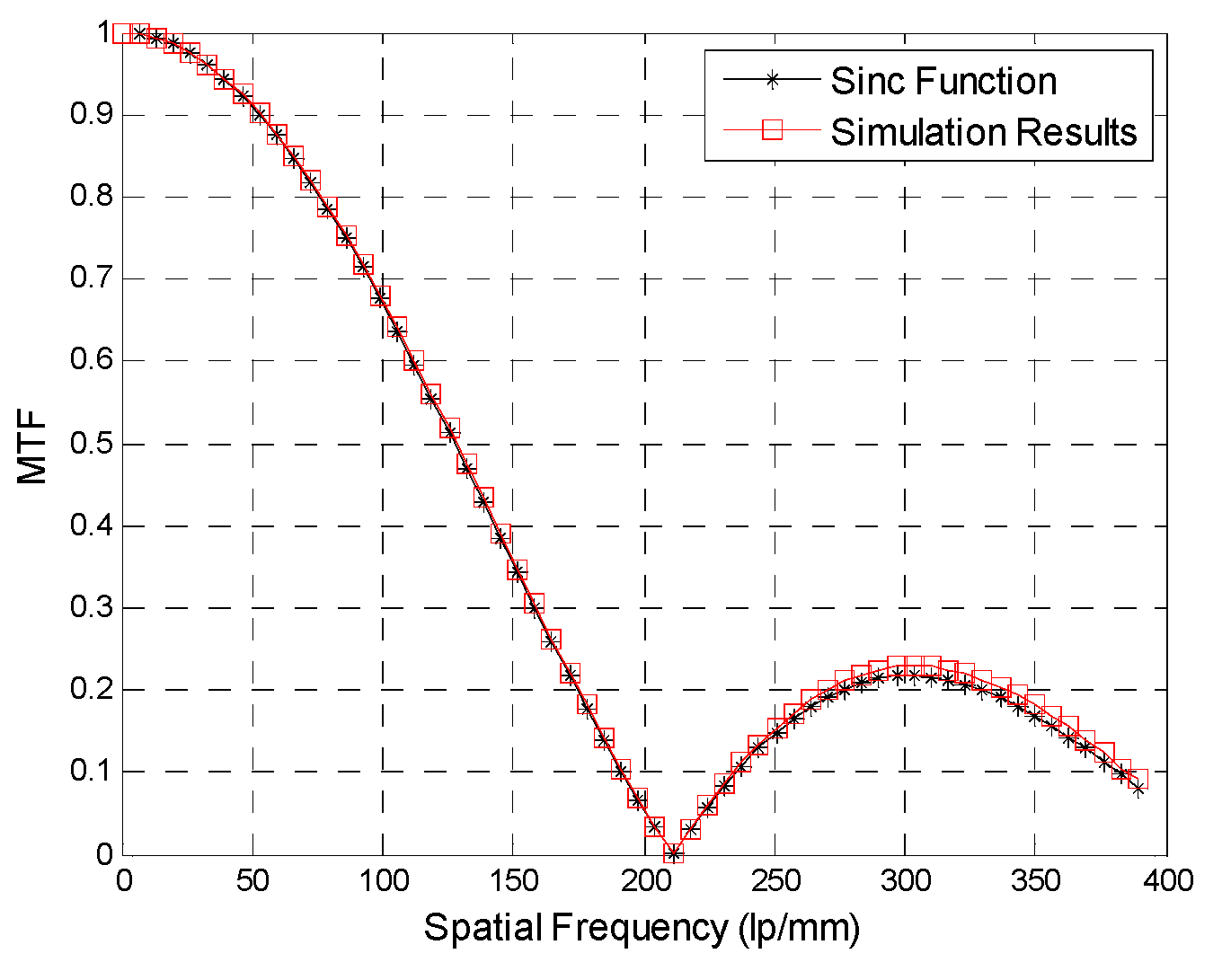
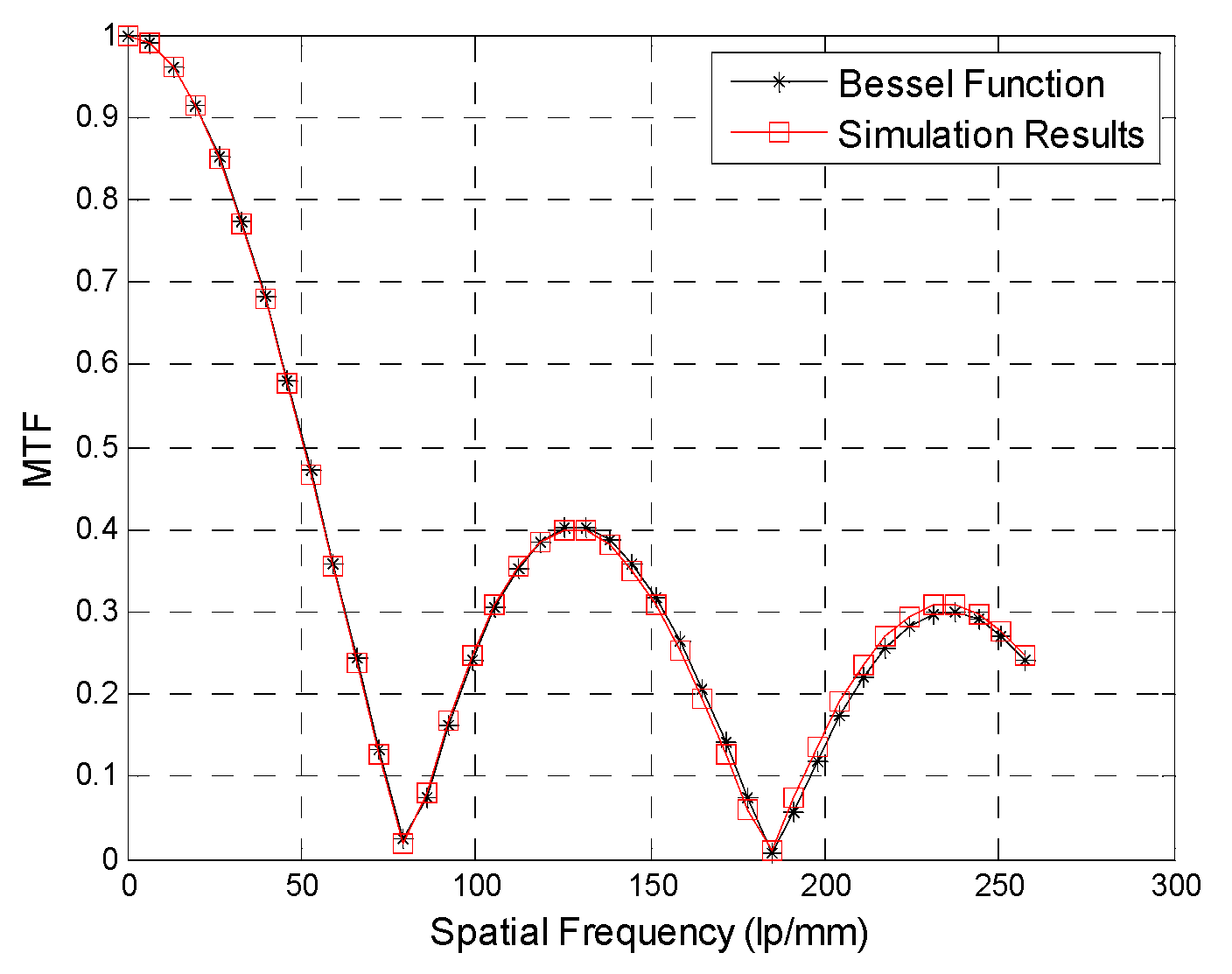
3.1. Convergence of the Approximate Analytical MTF Expression
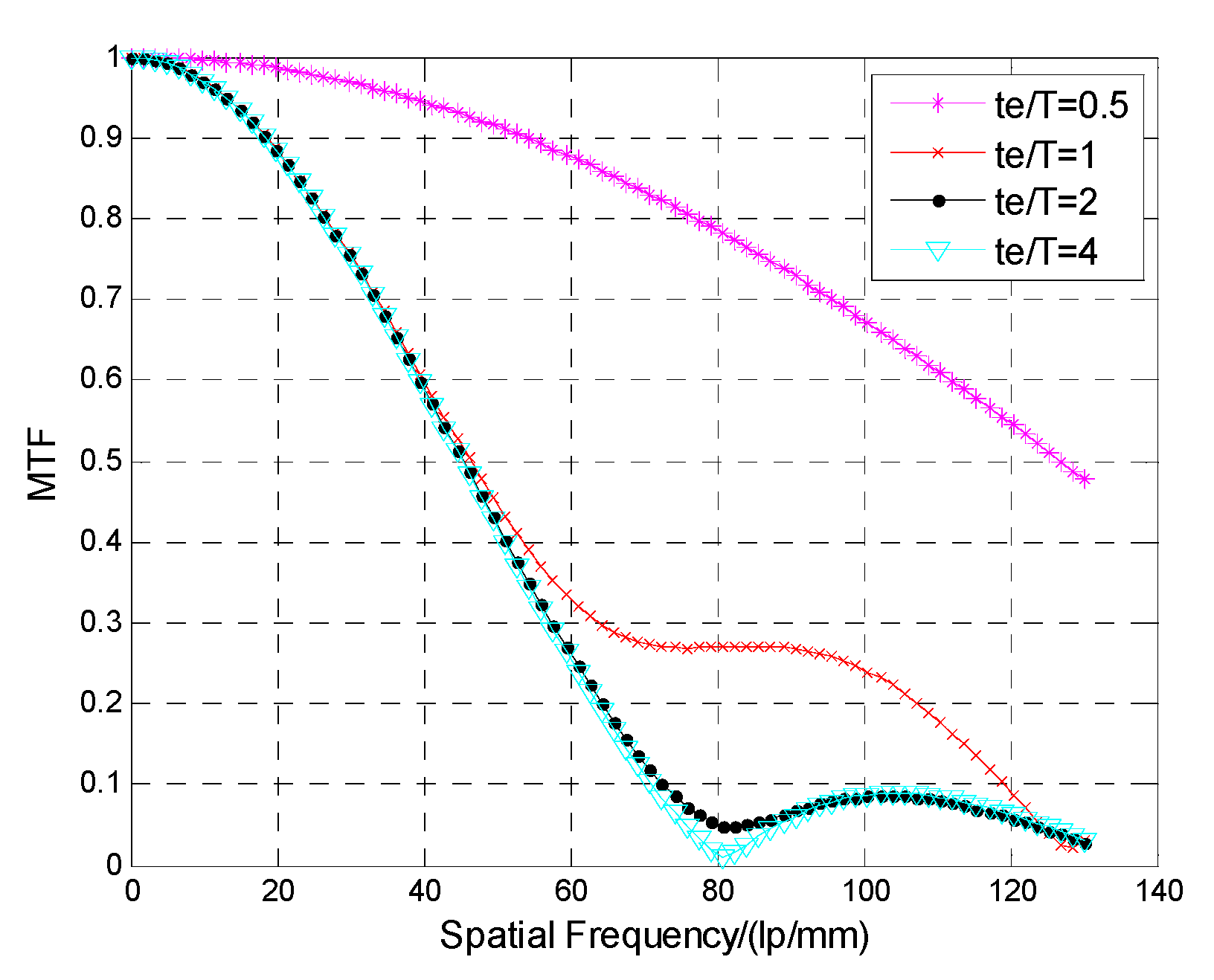
3.2. Expression Analysis of MTF for Image Motion
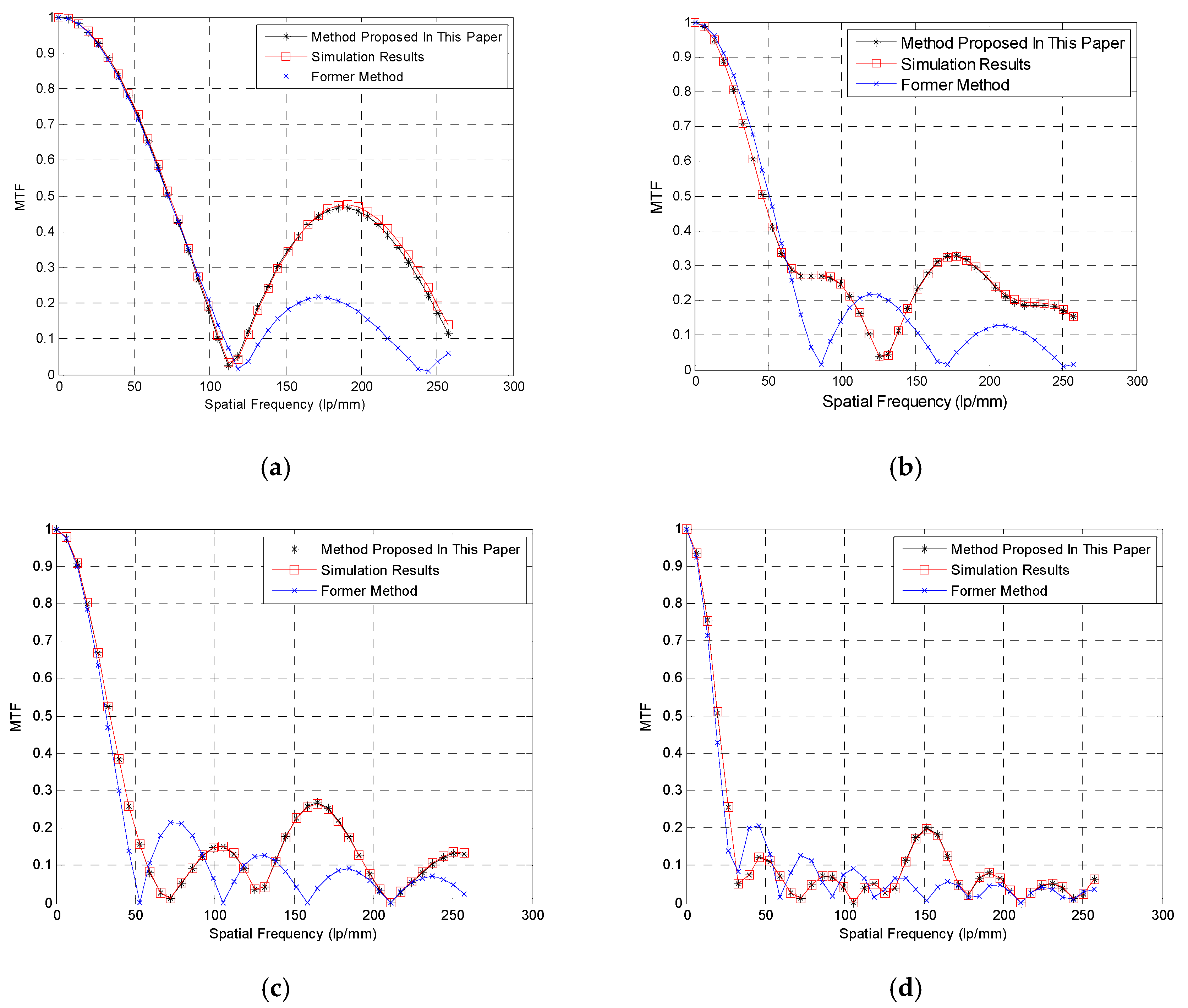
4. Simulation Experiment
4.1. Simulation Method
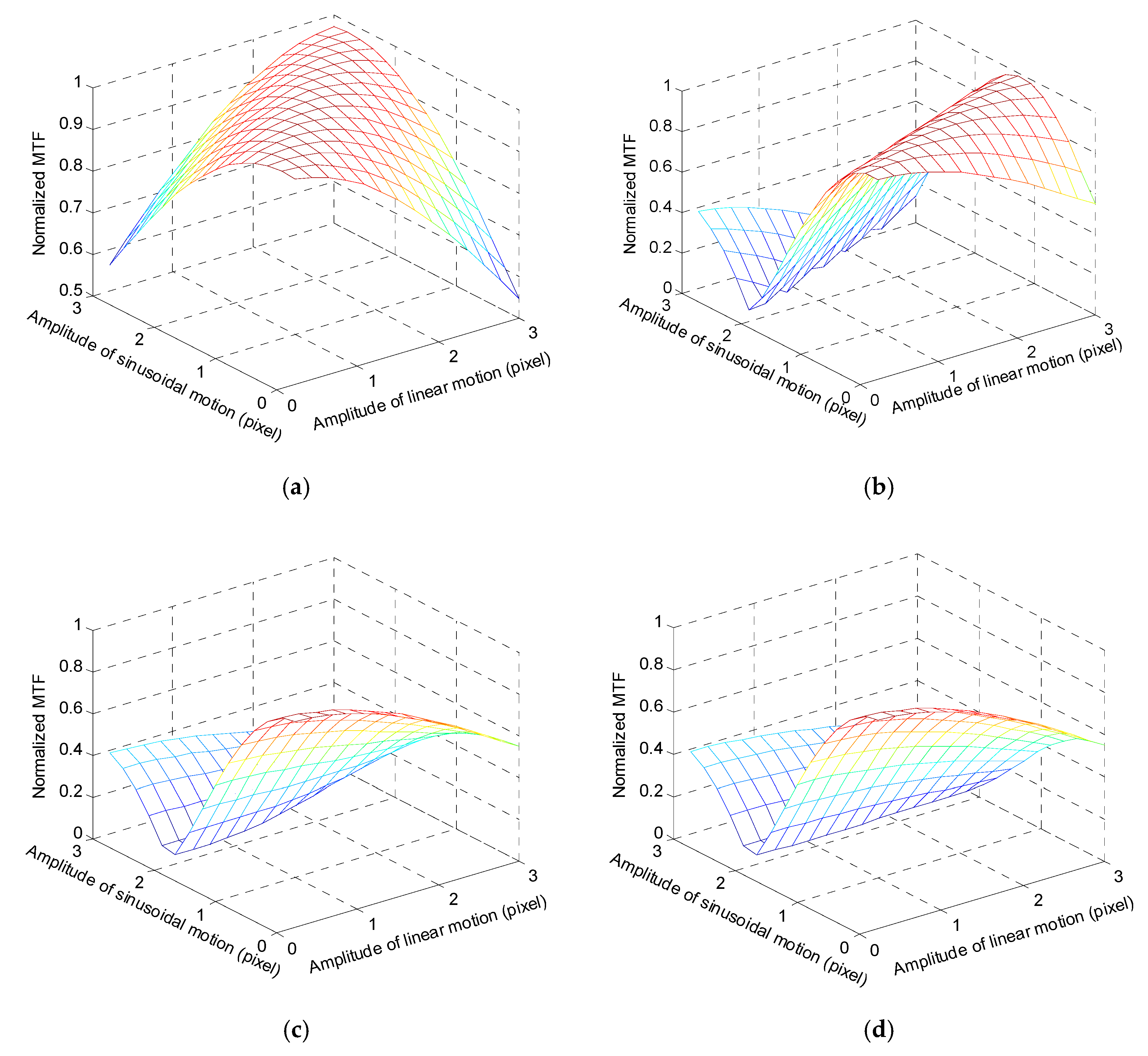
4.2. Simulation Results
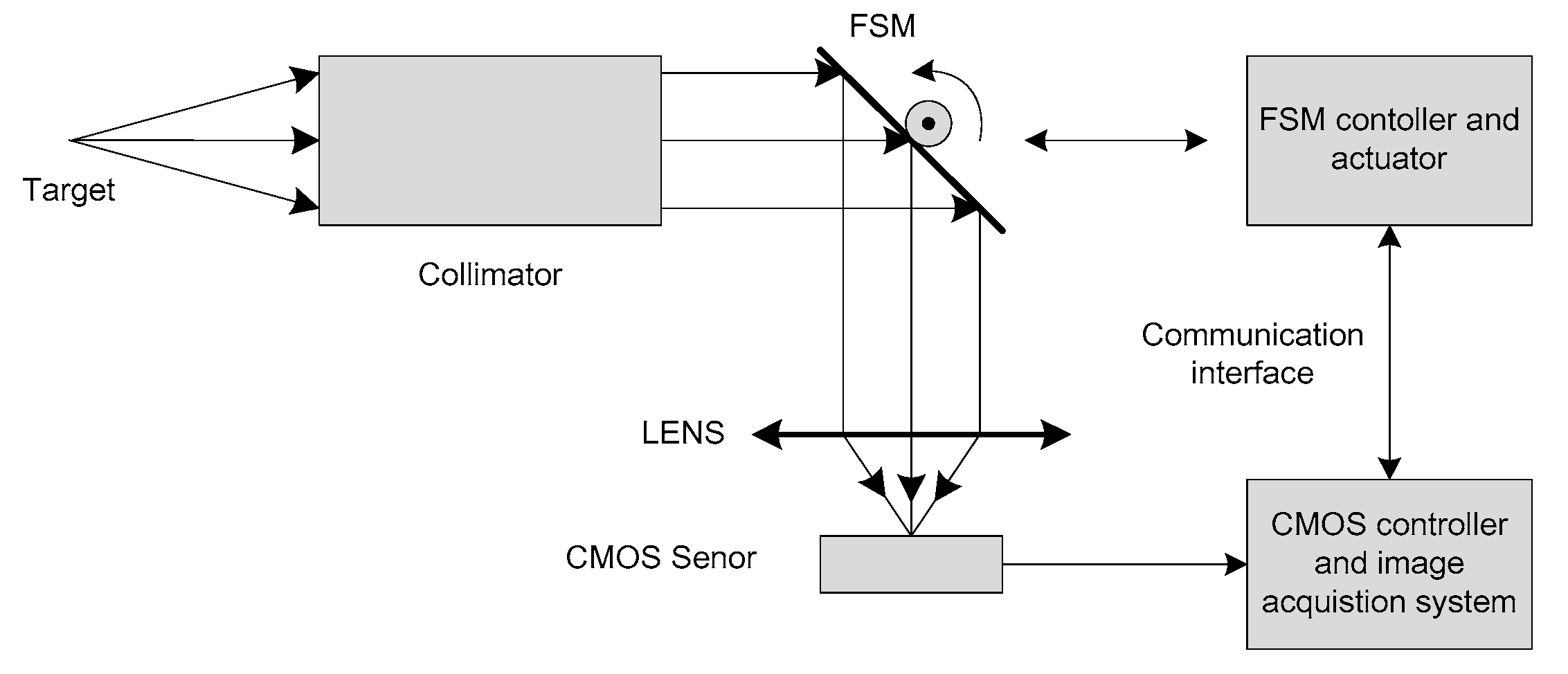
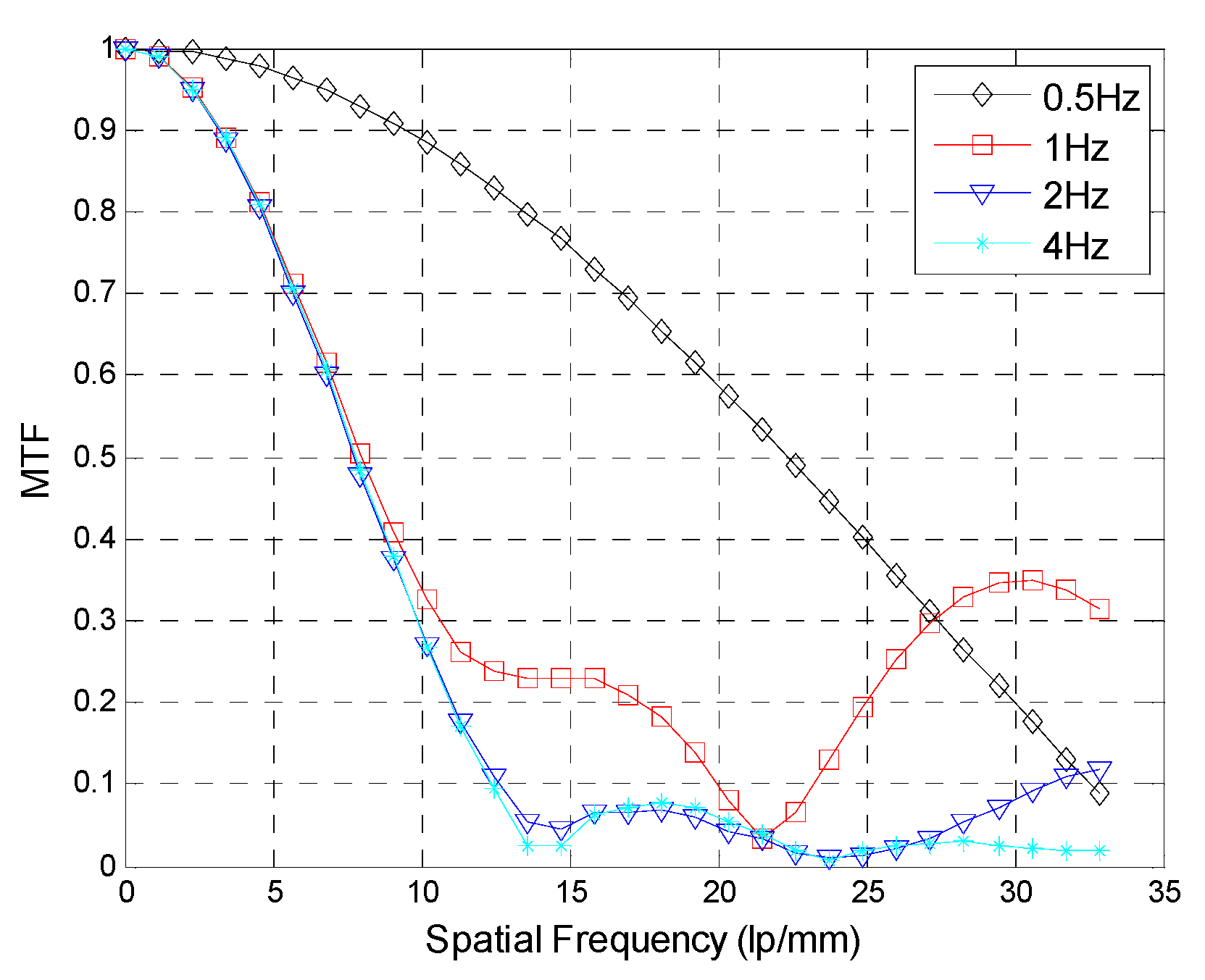
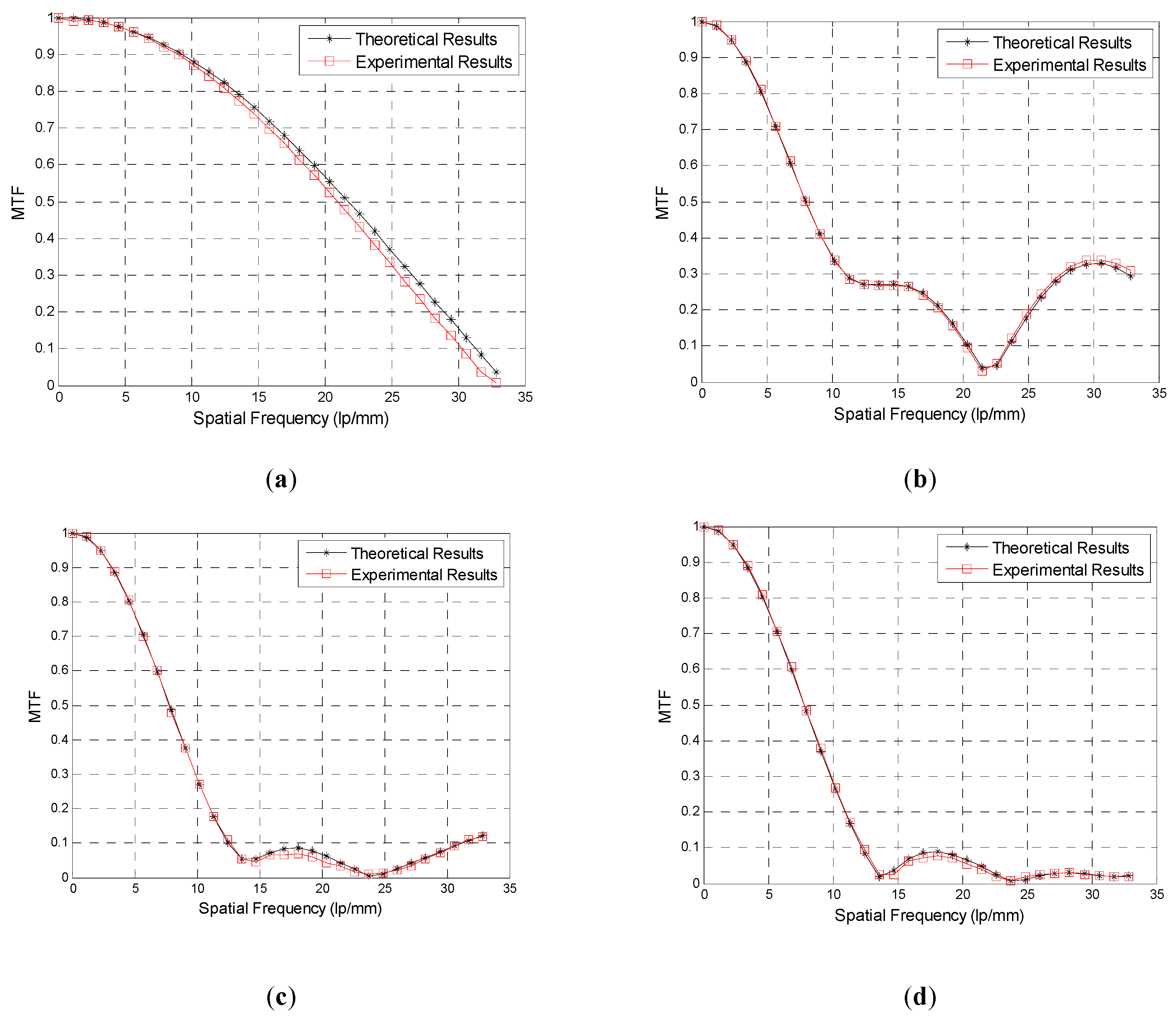
5. Laboratory Experiments for Validation
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Jun, P.; Chengbang, C.; Ying, Z.; Mi, W. Satellite Jitter Estimation and Validation Using Parallax Images. Sensors 2017, 17, 83. [Google Scholar]
- Jin, L.; Fei, X.; Ting, S.; Zheng, Y. Efficient assessment method of on-board modulation transfer function of optical remote sensing sensors. Opt. Express 2015, 23, 6187–6208. [Google Scholar]
- Taiji, L.; Xucheng, X.; Junlin, L.; Chengshan, H.; Kehui, L. A high-dynamic-range optical sensing imaging method for digital TDI CMOS. Appl. Sci. 2017, 7, 1089. [Google Scholar]
- Peng, X.; Qun, H.; Changning, H.; Yongtian, W. Degradation of modulation transfer function in push-broom camera caused by mechanical vibration. Opt. Laser Technol. 2003, 35, 547–552. [Google Scholar]
- Wei, Z.; Hans, Z.; Andreas, S. Wafer-scale fabricated thermo-pneumatically tunable microlenses. Light Sci. Appl. 2014, 3. [Google Scholar] [CrossRef]
- Moojoong, K.; Jaisuk, Y.; Dong-Kwon, K.; Hyunjung, K. Measurement of contrast and spatial resolution for the photothermal imaging method. Appl. Sci. 2019, 9, 1996. [Google Scholar]
- JiaQi, W.; Changxiang, Y. Space optical remote sensor image motion velocity vector computational modeling, error budget and synthesis. Chin. Opt. Lett. 2005, 3, 414–417. [Google Scholar]
- Mark, E.P.; William, G.M. Optical transfer functions, weighting functions, and metrics for images with two-dimensional line-of-sight motion. Opt. Eng. 2016, 55, 063108. [Google Scholar]
- Chenghao, Z.; Zhile, W. Mid-frequency MTF compensation of optical sparse aperture system. Opt. Express 2018, 26, 6973–6992. [Google Scholar]
- Jin, L.; Zilong, L. Using sub-resolution features for self-compensation of the modulation transfer function in remote sensing. Opt. Express 2017, 25, 4018–4037. [Google Scholar]
- Hansung, K.; Heonyong, K.; Moo-Hyun, K. Real-time inverse estimation of ocean wave spectra from vessel-motion sensors using adaptive kalman filter. Appl. Sci. 2019, 9, 2797. [Google Scholar]
- Hadar, O.; Dror, I.; Kopeika, N.S. Image resolution limits resulting from mechanical vibrations. Part IV: Real-time numerical calculation of optical transfer functions and experimental verification. Opt. Eng. 1994, 33, 566–578. [Google Scholar] [CrossRef]
- Yanlu, D.; Yalin, D. Dynamic modulation transfer function analysis of images blurred by sinusoidal vibration. J. Opt. Soc. Korea 2016, 20, 762–769. [Google Scholar]
- Jin, L.; Zilong, L.; Si, L. Suppressing the images smear of the vibration modulation transfer function for remote-sensing optical cameras. Appl. Opt. 2017, 56, 1616–1624. [Google Scholar]
- Adrian, S.; Norman, S.K. Analytical method to calculate optical transfer functions for image motion and vibrations using moments. J. Opt. Soc. Korea 1997, 14, 388–396. [Google Scholar]
- Liude, T.; Tao, W. Calculation of optical transfer function for image motion based on statistical moments. Acta Opt. Sin. 2017, 37. [Google Scholar] [CrossRef]
- Rudoler, S.; Hadar, O.; Fisher, M.; Kopeika, N.S. Image resolution limits resulting from mechanical vibrations Part 2: Experiment. Opt. Eng. 1994, 305, 577–589. [Google Scholar]
- Zhuxi, W.; Dunren, G. Introduction to Special Function; Peking University Press: Beijing, China, 2000; pp. 337–415. [Google Scholar]
- Kun, G.; Lu, H.; Hongmiao, L.; Zeyang, D.; Guoqiang, N.; Yingjie, Z. Analysis of MTF in TDI-CCD subpixel dynamic super-resolution imaging by beam splitter. Appl. Sci. 2017, 7, 905. [Google Scholar]
- Wenbao, G.; YaLin, D. Analysis of influence of vibration on transfer function in optics imaging system. Opt. Precis. Eng. 2009, 17, 314–320. [Google Scholar]
- Yu, J.; Hua, F.; Jiang, W. Distortion evaluation method for the progressive addition lens–eye system. Opt. Commun. 2019, 445, 204–210. [Google Scholar] [CrossRef]
- Xufen, X.; Hongda, F. Regularized slanted-edge method for measuring the modulation transfer function of imaging systems. Appl. Opt. 2018, 57, 6552–6558. [Google Scholar]
- Chin-Ta, Y.; Jyun-Min, S. A study of optical design on 9 × zoom ratio by using a compensating liquid lens. Appl. Sci. 2015, 5, 608–621. [Google Scholar]
- Xufen, X.; Yuncui, Z.; Hongyuan, W.; Wei, Z. Analysis and modeling of radiometric error caused by imaging blur in optical remote sensing systems. Infrared Phys. Technol. 2016, 77, 51–57. [Google Scholar]
- Weiwei, X.; Liming, Z. On-orbit modulation transfer function detection of high resolution optical satellite sensor based on reflected point sources. Acta Opt. Sin. 2017, 37, 0728001-1-8. [Google Scholar] [CrossRef]




| Exposure Time (s) | Our Method | Former Method | ||
|---|---|---|---|---|
| Errors | Running Time (s) | Errors | Running Time (s) | |
| 0.5 | 4.57% | 1.452 | 39.71% | 0.752 |
| 1 | 1.37% | 1.448 | 65.29% | 0.749 |
| 2 | 1.91% | 1.415 | 106.6% | 0.751 |
| 4 | 4.59% | 1.425 | 891.86% | 0.747 |
| The Frequency of Sinusoidal Vibration (Hz) | The Average Relative Error |
|---|---|
| 0.5 | 7.21% |
| 1 | 9.44% |
| 2 | 11.38% |
| 4 | 10.89% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, L.; Yan, C.; Gu, Z.; Li, M.; Li, C. Analysis of Dynamic Modulation Transfer Function for Complex Image Motion. Appl. Sci. 2019, 9, 5142. https://doi.org/10.3390/app9235142
Xu L, Yan C, Gu Z, Li M, Li C. Analysis of Dynamic Modulation Transfer Function for Complex Image Motion. Applied Sciences. 2019; 9(23):5142. https://doi.org/10.3390/app9235142
Chicago/Turabian StyleXu, Lizhi, Changxiang Yan, Zhiyuan Gu, Mengyang Li, and Chenghao Li. 2019. "Analysis of Dynamic Modulation Transfer Function for Complex Image Motion" Applied Sciences 9, no. 23: 5142. https://doi.org/10.3390/app9235142
APA StyleXu, L., Yan, C., Gu, Z., Li, M., & Li, C. (2019). Analysis of Dynamic Modulation Transfer Function for Complex Image Motion. Applied Sciences, 9(23), 5142. https://doi.org/10.3390/app9235142




