Wind Turbine Power Curve Modeling with a Hybrid Machine Learning Technique
Abstract
:Featured Application
Abstract
1. Introduction
2. Popular Power Curve Models
2.1. Parametric Models
2.2. Nonparametric Models
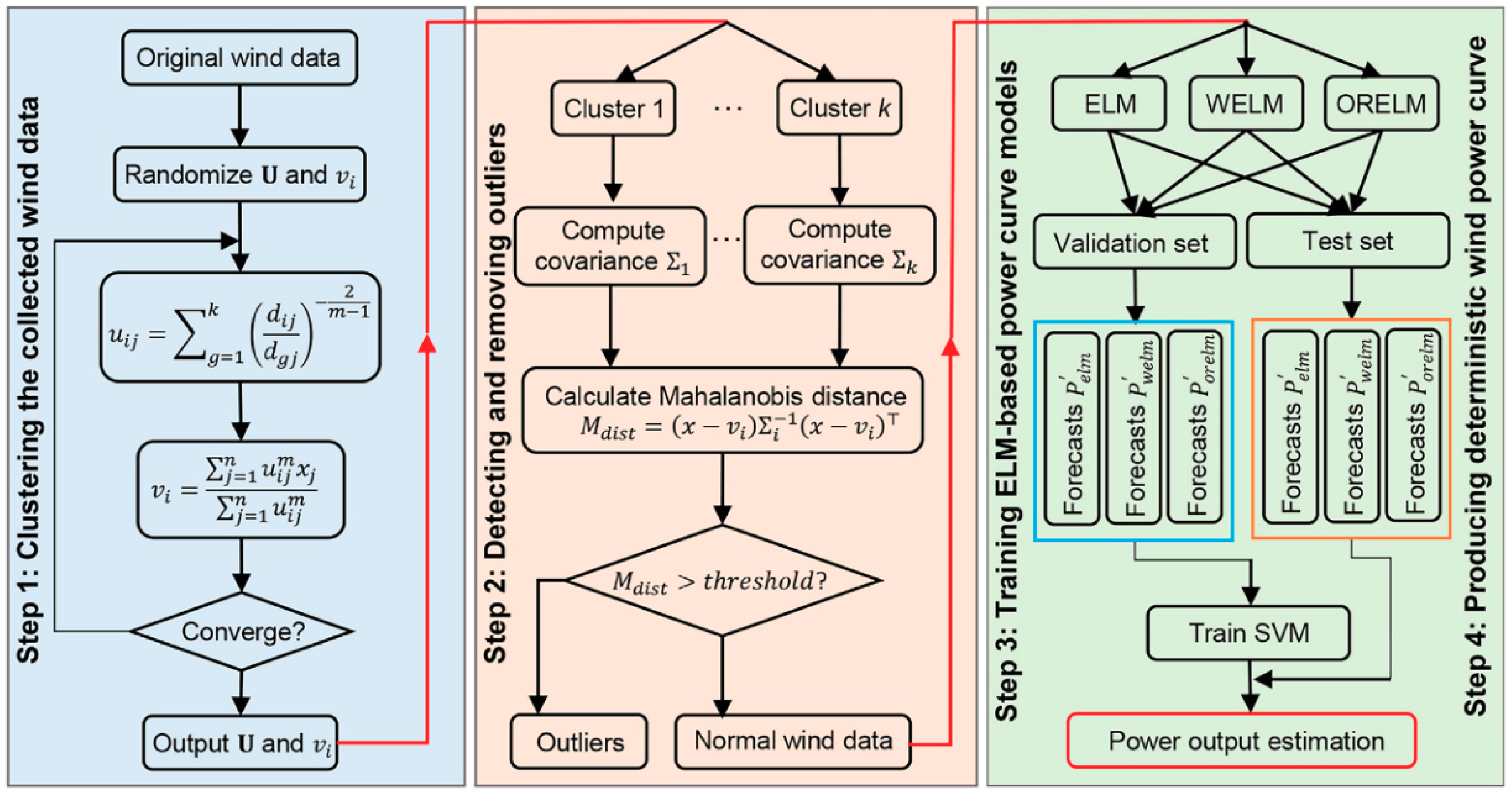
3. Proposed Wind Power Curve Model
3.1. Fuzzy C-Means Clustering
3.2. Extreme Learning Machine and Its Variants
3.2.1. Extreme Learning Machine
3.2.2. Weighted Regularized Extreme Learning Machine (WELM)
3.2.3. Outlier-Robust Extreme Learning Machine (ORELM)
3.3. Support Vector Regression
3.4. Proposed Strategy for Wind Power Curve Modeling
4. Wind Turbine Power Curve Modeling in Different Wind Farms
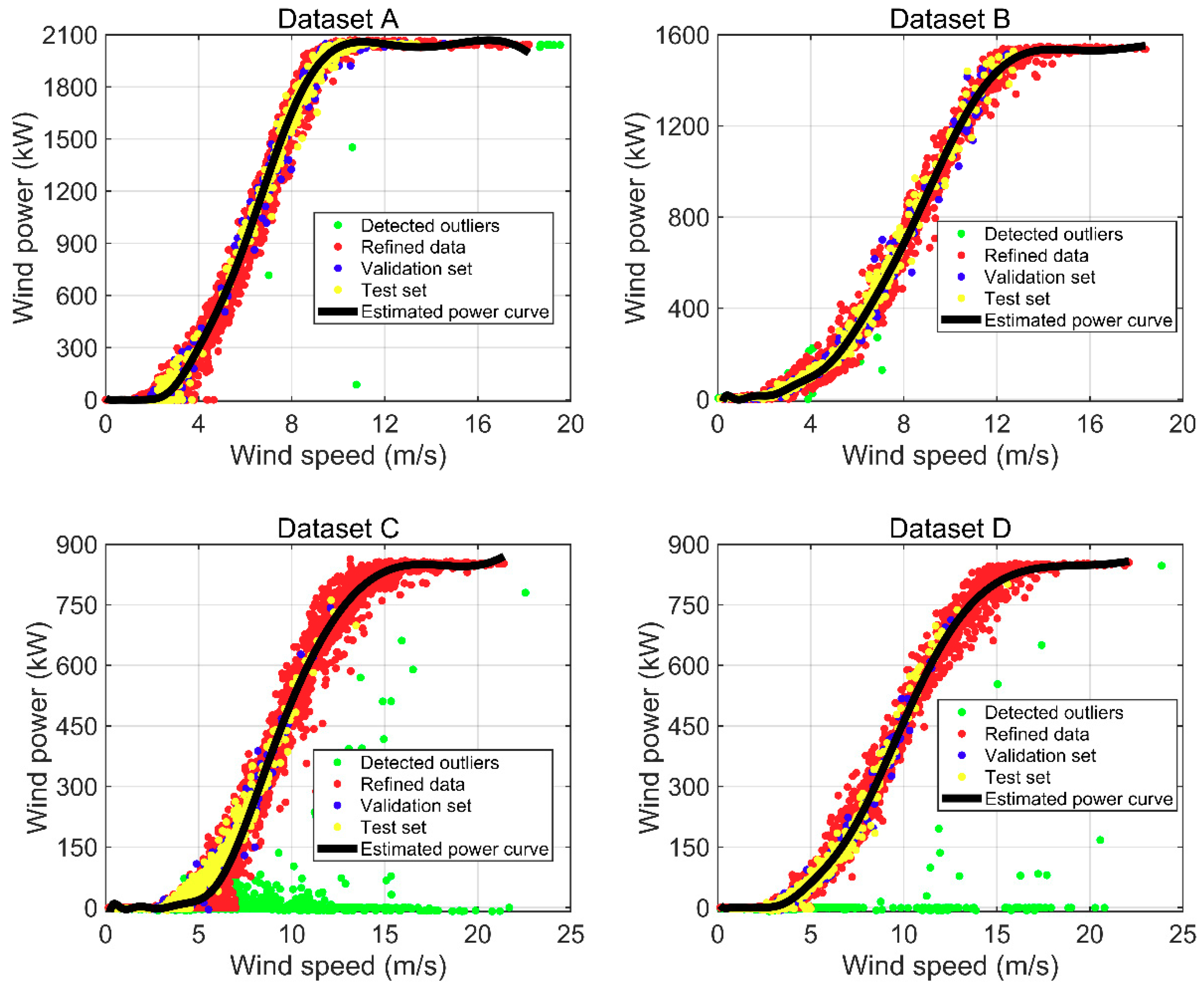
4.1. Data Description
4.2. Experiment Setting
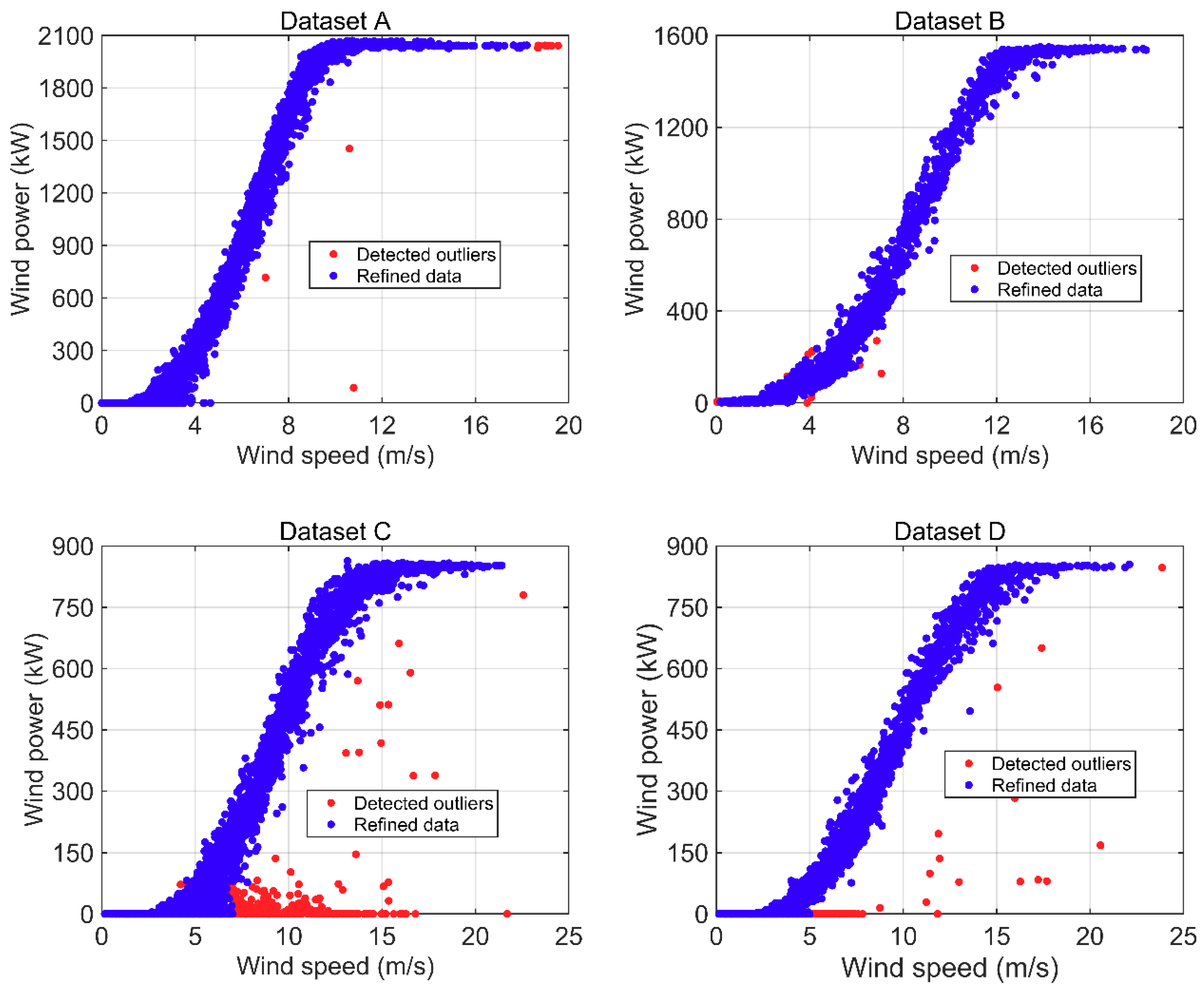
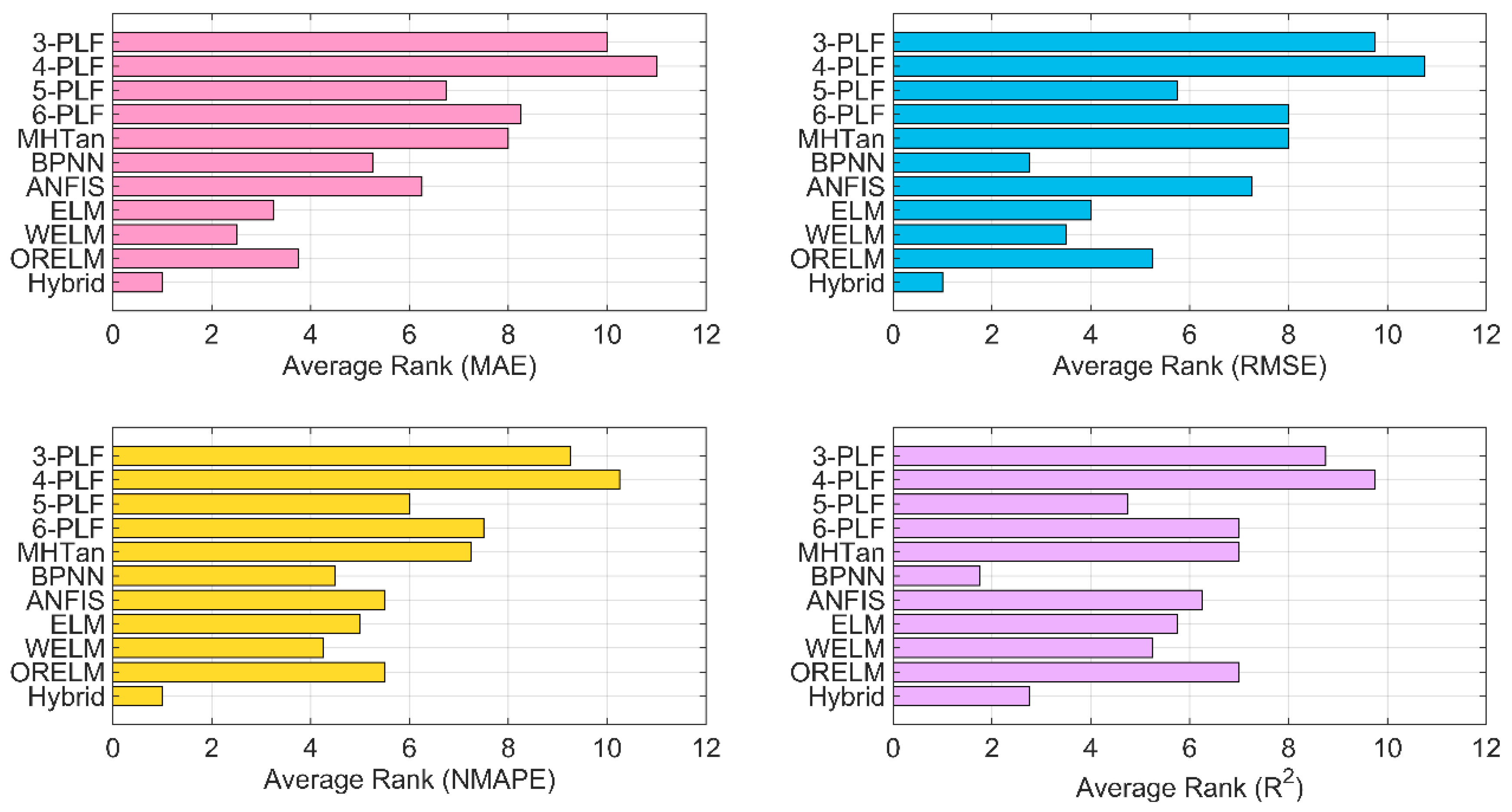
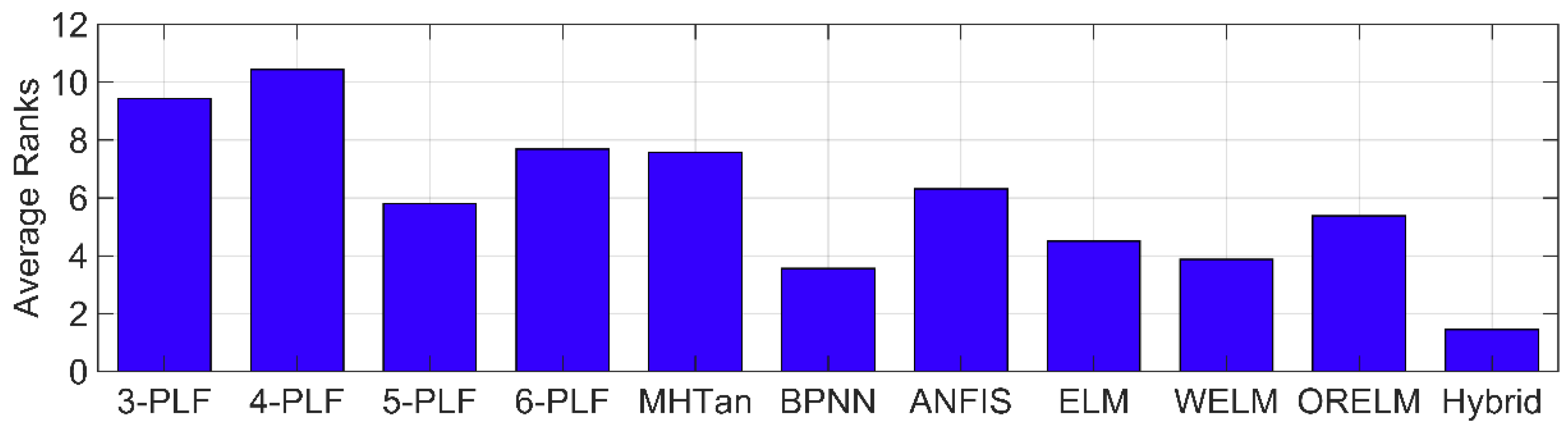
4.3. Results of Wind Turbine Power Curve Modeling
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| WTPC | wind turbine power curve |
| 4-PLF | 4-parameter logistic function |
| 5-PLF | 5-parametrer logistic function |
| 6-PLF | 6-parametrer logistic function |
| MHTan | modified hyperbolic tangent |
| ANN | artificial neural network |
| SVR | support vector regression |
| GP | Gaussian process |
| KNN | K-nearest neighbor model |
| ANFIS | adaptive neuro-fuzzy interference system |
| FCM | fuzzy c-means clustering |
| ELM | extreme learning machine |
| WELM | weighted regularized extreme learning machine |
| ORELM | outlier-robust extreme learning machine |
| BPNN | back-propagation neural network |
| BSA | backtracking search algorithm |
| ALM | Augmented Lagrange Multiplie |
| KKT | Karush-Kuhn-Tucker |
| MAE | mean absolute error |
| RMSE | root mean square error |
| NMAPE | normalized mean absolute percentage error |
| coefficient of determination |
References
- Wang, Y.; Hu, Q.; Li, L.; Foley, A.M.; Srinivasan, D. Approaches to wind power curve modeling: A review and discussion. Renew. Sustain. Energy Rev. 2019, 116, 109422. [Google Scholar] [CrossRef]
- Wang, J.; Song, Y.; Liu, F.; Hou, R. Analysis and application of forecasting models in wind power integration: A review of multi-step-ahead wind speed forecasting models. Renew. Sustain. Energy Rev. 2016, 60, 960–981. [Google Scholar] [CrossRef]
- Wang, Y.; Hu, Q.; Meng, D.; Zhu, P. Deterministic and probabilistic wind power forecasting using a variational Bayesian-based adaptive robust multi-kernel regression model. Appl. Energy 2017, 208, 1097–1112. [Google Scholar] [CrossRef]
- Seo, S.; Oh, S.D.; Kwak, H.Y. Wind turbine power curve modeling using maximum likelihood estimation method. Renew. Energy 2019, 136, 1164–1169. [Google Scholar] [CrossRef]
- Manwell, J.F.; McGowan, J.G.; Rogers, A.L. Wind Energy Explained: Theory, Design and Application; John Wiley & Sons: Hoboken, NJ, USA, 2010. [Google Scholar]
- Carrillo, C.; Montaño, A.O.; Cidrás, J.; Díaz-Dorado, E. Review of power curve modelling for wind turbines. Renew. Sustain. Energy Rev. 2013, 21, 572–581. [Google Scholar] [CrossRef]
- Goretti, G.; Duffy, A.; Lie, T.T. The impact of power curve estimation on commercial wind power forecasts—An empirical analysis. In Proceedings of the 14th International Conference on the European Energy Market (EEM), Dresden, Germany, 6–9 June 2017; pp. 1–4. [Google Scholar]
- Yesilbudak, M. Implementation of novel hybrid approaches for power curve modeling of wind turbines. Energy Convers. Manag. 2018, 171, 156–169. [Google Scholar] [CrossRef]
- Wang, Y.; Hu, Q.; Pei, S. Wind power curve modeling with asymmetric error distribution. IEEE Trans. Sustain. Energy 2019. [Google Scholar] [CrossRef]
- Taslimi-Renani, E.; Modiri-Delshad, M.; Elias, M.F.M.; Rahim, N.A. Development of an enhanced parametric model for wind turbine power curve. Appl. Energy 2016, 177, 544–552. [Google Scholar] [CrossRef]
- Pinson, P.; Nielsen, H.A.; Madsen, H. Robust Estimation of Time-Varying Coefficient Functions-Application to the Modeling of Wind Power Production; Technical University of Denmark, Informatics and Mathematical Modelling: Lyngby, Denmark, 2007. [Google Scholar]
- Sainz, E.; Llombart, A.; Guerrero, J.J. Robust filtering for the characterization of wind turbines: Improving its operation and maintenance. Energy Convers. Manag. 2009, 50, 2136–2147. [Google Scholar] [CrossRef]
- Hernández-Escobedo, Q.; Manzano-Agugliaro, F.; Zapata-Sierra, A. The wind power of Mexico. Renew. Sustain. Energy Rev. 2010, 14, 2830–2840. [Google Scholar] [CrossRef]
- Sohoni, V.; Gupta, S.; Nema, R. A comparative analysis of wind speed probability distributions for wind power assessment of four sites. Turk. J. Electr. Eng. Comput. Sci. 2016, 24, 4724–4735. [Google Scholar] [CrossRef]
- Sohoni, V.; Gupta, S.C.; Nema, R.K. A critical review on wind turbine power curve modeling techniques and their applications in wind based energy systems. J. Energy 2016, 2016, 8519785. [Google Scholar] [CrossRef]
- Lydia, M.; Selvakumar, A.I.; Kumar, S.S.; Kumar, G.E.P. Advanced algorithms for wind turbine power curve modeling. IEEE Trans. Sustain. Energy 2013, 4, 827–835. [Google Scholar] [CrossRef]
- Villanueva, D.; Feijóo, A. Comparison of logistic functions for modeling wind turbine power curves. Electr. Power Syst. Res. 2018, 155, 281–288. [Google Scholar] [CrossRef]
- Marvuglia, A.; Messineo, A. Monitoring of wind farms’ power curves using machine learning techniques. Appl. Energy 2012, 98, 574–583. [Google Scholar] [CrossRef]
- Goudarzi, A.; Davidson, I.E.; Ahmadi, A.; Venayagamoorthy, G.K. Intelligent analysis of wind turbine power curve models. In Proceedings of the IEEE Symposium on Computational Intelligence Applications in Smart Grid (CIASG), Orlando, FL, USA, 9–12 December 2014; pp. 1–7. [Google Scholar]
- Ouyang, T.; Kusiak, A.; He, Y. Modeling wind-turbine power curve: A data partitioning and mining approach. Renew. Energy 2017, 102, 1–8. [Google Scholar] [CrossRef]
- Pandit, R.; Infield, D. Gaussian Process operational curves for wind turbine condition monitoring. Energies 2018, 11, 1631. [Google Scholar] [CrossRef]
- Rogers, T.J.; Gardner, P.; Dervilis, N.; Worden, K.; Maguire, A.E.; Papatheou, E.; Cross, E.J. Probabilistic modelling of wind turbine power curves with application of heteroscedastic Gaussian Process regression. Renew. Energy 2019. [Google Scholar] [CrossRef]
- Wang, Y.; Hu, Q.; Srinivasan, D.; Wang, Z. Wind power curve modeling and wind power forecasting with inconsistent data. IEEE Trans. Sustain. Energy 2019, 10, 16–25. [Google Scholar] [CrossRef]
- Mehrjoo, M.; Jozani, M.J.; Pawlak, M. Wind turbine power curve modeling for reliable power prediction using monotonic regression. Renew. Energy 2020, 147, 214–222. [Google Scholar] [CrossRef]
- Kusiak, A.; Zheng, H.; Song, Z. On-line monitoring of power curves. Renew. Energy 2009, 34, 1487–1493. [Google Scholar] [CrossRef]
- Schlechtingen, M.; Santos, I.F.; Achiche, S. Using data-mining approaches for wind turbine power curve monitoring: A comparative study. IEEE Trans. Sustain. Energy 2013, 4, 671–679. [Google Scholar] [CrossRef]
- Üstüntaş, T.; Şahin, A.D. Wind turbine power curve estimation based on cluster center fuzzy logic modelling. J. Wind Eng. Ind. Aerodyn. 2008, 96, 611–620. [Google Scholar] [CrossRef]
- Stephen, B.; Galloway, S.J.; McMillan, D.; Hill, D.C.; Infield, D.G. A copula model of wind turbine performance. IEEE Trans. Power Syst. 2011, 26, 965–966. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, N.; Lu, H. A novel system based on neural networks with linear combination framework for wind speed forecasting. Energy Convers. Manag. 2019, 181, 425–442. [Google Scholar] [CrossRef]
- Che, J.; Wang, J. Short-term load forecasting using a kernel-based support vector regression combination model. Appl. Energy 2014, 132, 602–609. [Google Scholar] [CrossRef]
- Li, W.; Chang, L. A combination model with variable weight optimization for short-term electrical load forecasting. Energy 2018, 164, 575–593. [Google Scholar] [CrossRef]
- Zheng, L.; Hu, W.; Min, Y. Raw wind data preprocessing: A data-mining approach. IEEE Trans. Sustain. Energy 2015, 6, 11–19. [Google Scholar] [CrossRef]
- Shen, X.; Fu, X.; Zhou, C. A combined algorithm for cleaning abnormal data of wind turbine power curve based on change point grouping algorithm and quartile algorithm. IEEE Trans. Sustain. Energy 2018, 10, 46–54. [Google Scholar] [CrossRef]
- Zhao, Y.; Ye, L.; Wang, W.; Sun, H.; Ju, Y.; Tang, Y. Data-driven correction approach to refine power curve of wind farm under wind curtailment. IEEE Trans. Sustain. Energy 2018, 9, 95–105. [Google Scholar] [CrossRef]
- Huang, G.B.; Zhu, Q.Y.; Siew, C.K. Extreme learning machine: A new learning scheme of feedforward neural networks. IEEE Int. Jt. Conf. Neural Netw. 2004, 2, 985–990. [Google Scholar]
- Deng, W.; Zheng, Q.; Chen, L. Regularized extreme learning machine. In Proceedings of the IEEE Symposium on Computational Intelligence and Data Mining, Nashville, TN, USA, 30 March–2 April 2009; pp. 389–395. [Google Scholar]
- Zhang, K.; Luo, M. Outlier-robust extreme learning machine for regression problems. Neurocomputing 2015, 151, 1519–1527. [Google Scholar] [CrossRef]
- Vapnik, V. The Nature of Statistical Learning Theory; Springer Science & Business Media: Berlin, Germany, 2013. [Google Scholar]
- Bezdek, J.C. Pattern Recognition with Fuzzy Objective Function Algorithms; Springer Science & Business Media: Berlin, Germany, 2013. [Google Scholar]
- Egrioglu, E.; Aladag, C.H.; Yolcu, U. Fuzzy time series forecasting with a novel hybrid approach combining fuzzy c-means and neural networks. Expert Syst. Appl. 2013, 40, 854–857. [Google Scholar] [CrossRef]
- Suykens, J.A.; De Brabanter, J.; Lukas, L.; Vandewalle, J. Weighted least squares support vector machines: Robustness and sparse approximation. Neurocomputing 2002, 48, 85–105. [Google Scholar] [CrossRef]
- Park, J.Y.; Lee, J.K.; Oh, K.Y.; Lee, J.S. Development of a novel power curve monitoring method for wind turbines and its field tests. IEEE Trans. Energy Convers. 2014, 29, 119–128. [Google Scholar] [CrossRef]
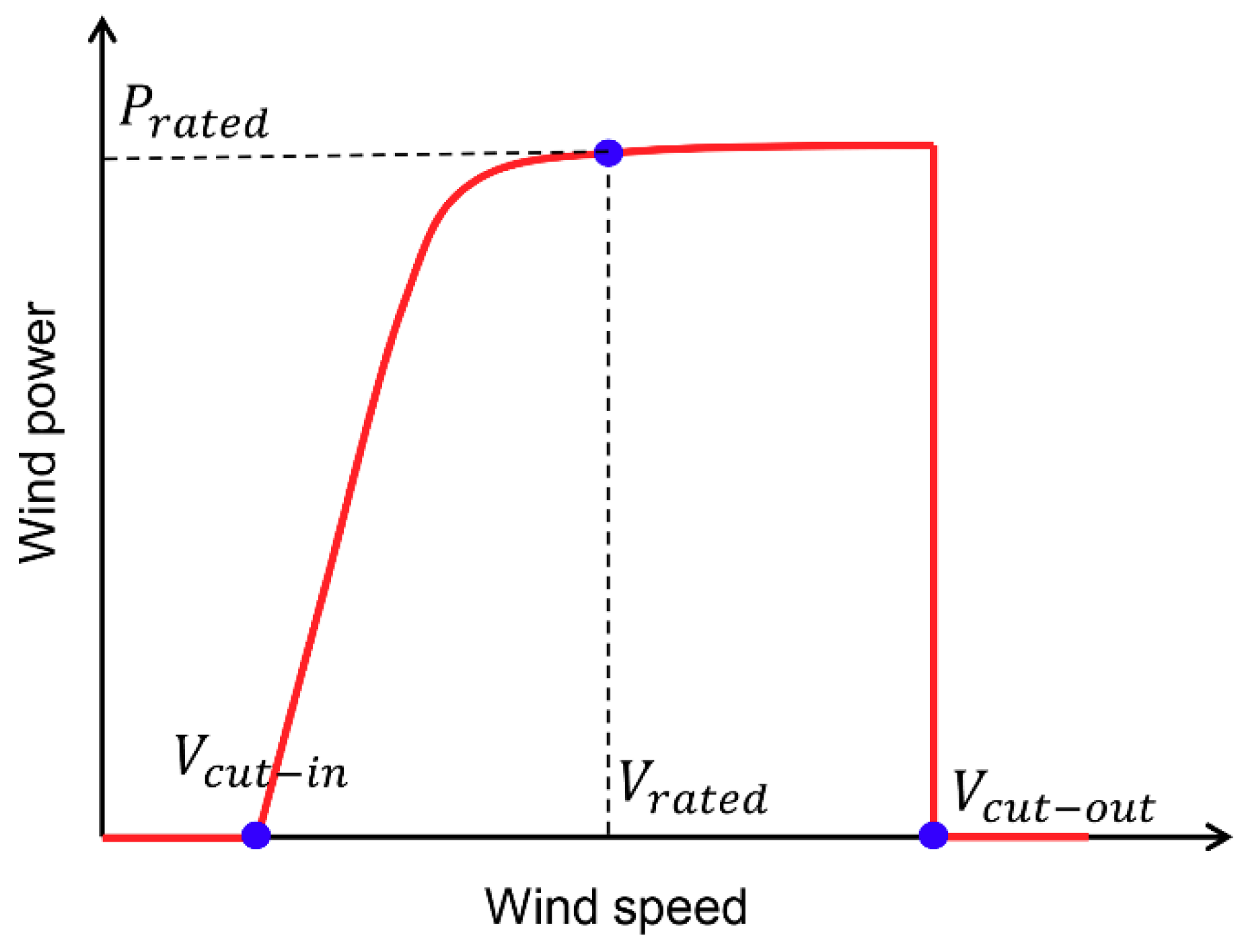
| Model | Expression | Parameters |
|---|---|---|
| 3-PLF | : the capacity of the system; : the rate of increase; : no special mean. | |
| 4-PLF | : the maximum asymptote; : the minimum asymptote; : the inflection point, : means the hill slope. | |
| 5-PLF | : the asymmetric factor; are the same with the parameters in 4-PLF. | |
| 6-PLF | : the lower asymptote; : the upper asymptote; : the growth rate; : the closet asymptote to the maximum growth part of the curve; : the value ; : the value around 1. | |
| MHTan | : nine model parameters. |
| Dataset | All Samples (#) | Training Samples (#) | Validation Samples (#) | Test Samples (#) |
|---|---|---|---|---|
| A | 5500 | 4500 | 400 | 600 |
| B | 6500 | 5500 | 400 | 600 |
| C | 7500 | 6000 | 500 | 1000 |
| D | 6000 | 5000 | 400 | 600 |
| Indicator | Calculation | Description |
|---|---|---|
| MAE | The smaller the better | |
| RMSE | The smaller the better | |
| NMAPE | The smaller the better | |
| The bigger the better |
| Number of Neurons | ELM | WELM | ORELM | |||
|---|---|---|---|---|---|---|
| MAE | NMAPE | MAE | NMAPE | MAE | NMAPE | |
| 20 | 31.1966 | 1.5165 | 30.6275 | 1.4889 | 30.2793 | 1.4720 |
| 40 | 31.3355 | 1.5233 | 30.6819 | 1.4915 | 30.1564 | 1.4660 |
| 60 | 31.2018 | 1.5168 | 30.6325 | 1.4891 | 30.0923 | 1.4629 |
| 80 | 31.2489 | 1.5191 | 30.5587 | 1.4855 | 30.0131 | 1.4590 |
| 100 | 31.1304 | 1.5133 | 30.5600 | 1.4856 | 30.1424 | 1.4653 |
| 120 | 31.1159 | 1.5126 | 30.5568 | 1.4854 | 30.0607 | 1.4613 |
| 140 | 31.1660 | 1.5151 | 30.5901 | 1.4871 | 30.1577 | 1.4660 |
| 160 | 31.2230 | 1.5178 | 30.6028 | 1.4877 | 30.2313 | 1.4696 |
| 180 | 31.2163 | 1.5175 | 30.7079 | 1.4928 | 30.2346 | 1.4698 |
| 200 | 31.2042 | 1.5169 | 30.6600 | 1.4905 | 30.2831 | 1.4721 |
| Number of Neurons | ELM | WELM | ORELM | |||
|---|---|---|---|---|---|---|
| MAE | NMAPE | MAE | NMAPE | MAE | NMAPE | |
| 20 | 19.5752 | 1.2916 | 19.6813 | 1.2986 | 19.3721 | 1.2782 |
| 40 | 19.4678 | 1.2845 | 19.3994 | 1.2800 | 19.1576 | 1.2640 |
| 60 | 19.5612 | 1.2906 | 19.6308 | 1.2952 | 19.4058 | 1.2804 |
| 80 | 19.5769 | 1.2917 | 19.6576 | 1.2970 | 19.3674 | 1.2778 |
| 100 | 19.5334 | 1.2888 | 19.5756 | 1.2916 | 19.4176 | 1.2812 |
| 120 | 19.5381 | 1.2891 | 19.6577 | 1.2970 | 19.9057 | 1.3134 |
| 140 | 19.5528 | 1.2901 | 19.6811 | 1.2985 | 19.9866 | 1.3187 |
| 160 | 19.5555 | 1.2903 | 19.7093 | 1.3004 | 20.1874 | 1.3319 |
| 180 | 19.5723 | 1.2914 | 19.6612 | 1.2972 | 19.7598 | 1.3037 |
| 200 | 19.5538 | 1.2901 | 19.6977 | 1.2996 | 20.1378 | 1.3287 |
| Number of Neurons | ELM | WELM | ORELM | |||
|---|---|---|---|---|---|---|
| MAE | NMAPE | MAE | NMAPE | MAE | NMAPE | |
| 20 | 15.3341 | 2.0665 | 15.3846 | 2.0733 | 16.0515 | 2.1631 |
| 40 | 15.4442 | 2.0813 | 15.6734 | 2.1122 | 16.0831 | 2.1674 |
| 60 | 15.4285 | 2.0792 | 15.4668 | 2.0843 | 16.1864 | 2.1813 |
| 80 | 15.4258 | 2.0788 | 15.4991 | 2.0887 | 16.3482 | 2.2031 |
| 100 | 15.4324 | 2.0797 | 15.4687 | 2.0846 | 16.2203 | 2.1859 |
| 120 | 15.2910 | 2.0606 | 15.3831 | 2.0731 | 15.7288 | 2.1196 |
| 140 | 15.4222 | 2.0783 | 15.7103 | 2.1172 | 16.3020 | 2.1969 |
| 160 | 15.4347 | 2.0800 | 15.4756 | 2.0855 | 16.2555 | 2.1906 |
| 180 | 15.4334 | 2.0798 | 15.4823 | 2.0864 | 16.2622 | 2.1915 |
| 200 | 15.2928 | 2.0609 | 15.5146 | 2.0908 | 15.7213 | 2.1186 |
| Number of Neurons | ELM | WELM | ORELM | |||
|---|---|---|---|---|---|---|
| MAE | NMAPE | MAE | NMAPE | MAE | NMAPE | |
| 20 | 9.7527 | 1.3681 | 9.7187 | 1.3634 | 9.6653 | 1.3559 |
| 40 | 9.7582 | 1.3689 | 9.7191 | 1.3634 | 9.6651 | 1.3559 |
| 60 | 9.7528 | 1.3682 | 9.7150 | 1.3629 | 9.6692 | 1.3564 |
| 80 | 9.7583 | 1.3689 | 9.7179 | 1.3633 | 9.6574 | 1.3548 |
| 100 | 9.7594 | 1.3691 | 9.7182 | 1.3633 | 9.6615 | 1.3554 |
| 120 | 9.7593 | 1.3691 | 9.7186 | 1.3634 | 9.6631 | 1.3556 |
| 140 | 9.7529 | 1.3682 | 9.7156 | 1.3629 | 9.6688 | 1.3564 |
| 160 | 9.7603 | 1.3692 | 9.7197 | 1.3635 | 9.6594 | 1.3551 |
| 180 | 9.7592 | 1.3691 | 9.7186 | 1.3634 | 9.6584 | 1.3549 |
| 200 | 9.7587 | 1.3690 | 9.7188 | 1.3634 | 9.6601 | 1.3552 |
| Dataset | Model | Error Indicator | |||
|---|---|---|---|---|---|
| MAE | RMSE | NMAPE | |||
| A | 3-PLF | 48.4476 | 63.2152 | 2.3528 | 0.9949 |
| 4-PLF | 48.7739 | 63.4799 | 2.3686 | 0.9948 | |
| 5-PLF | 36.5998 | 53.3506 | 1.7774 | 0.9963 | |
| 6-PLF | 45.2280 | 60.8805 | 2.1964 | 0.9952 | |
| MHTan | 42.7914 | 58.3378 | 2.0781 | 0.9956 | |
| BPNN | 32.1661 | 51.2157 | 1.5621 | 0.9966 | |
| ANFIS | 37.3980 | 53.3276 | 1.8162 | 0.9963 | |
| ELM | 32.0219 | 51.4542 | 1.5551 | 0.9966 | |
| WELM | 31.6347 | 52.3488 | 1.5363 | 0.9965 | |
| ORELM | 31.6811 | 53.6236 | 1.5385 | 0.9963 | |
| Hybrid | 30.5422 | 49.7355 | 1.4832 | 0.9968 | |
| B | 3-PLF | 21.7192 | 34.9560 | 1.4212 | 0.9891 |
| 4-PLF | 21.7790 | 34.9837 | 1.4251 | 0.9891 | |
| 5-PLF | 19.9222 | 33.2145 | 1.3036 | 0.9902 | |
| 6-PLF | 20.6772 | 34.6191 | 1.3530 | 0.9894 | |
| MHTan | 20.5743 | 34.2099 | 1.3463 | 0.9896 | |
| BPNN | 19.3444 | 32.8101 | 1.2658 | 0.9904 | |
| ANFIS | 19.3400 | 33.7645 | 1.2655 | 0.9899 | |
| ELM | 19.2145 | 32.9260 | 1.2573 | 0.9904 | |
| WELM | 19.2872 | 33.2975 | 1.2620 | 0.9902 | |
| ORELM | 19.7225 | 34.2069 | 1.2905 | 0.9896 | |
| Hybrid | 18.8438 | 32.0968 | 1.2330 | 0.9909 | |
| Dataset | Model | Error Indicator | |||
|---|---|---|---|---|---|
| MAE | RMSE | NMAPE | |||
| C | 3-PLF | 21.7192 | 34.9560 | 1.4212 | 0.9891 |
| 4-PLF | 21.7790 | 34.9837 | 1.4251 | 0.9891 | |
| 5-PLF | 19.9222 | 33.2145 | 1.3036 | 0.9902 | |
| 6-PLF | 20.6772 | 34.6191 | 1.3530 | 0.9894 | |
| MHTan | 20.5743 | 34.2099 | 1.3463 | 0.9896 | |
| BPNN | 19.3444 | 32.8101 | 1.2658 | 0.9904 | |
| ANFIS | 19.3400 | 33.7645 | 1.2655 | 0.9899 | |
| ELM | 16.0682 | 26.9427 | 2.1093 | 0.9425 | |
| WELM | 15.8361 | 26.6344 | 2.0788 | 0.9438 | |
| ORELM | 15.9102 | 25.9158 | 2.0885 | 0.9468 | |
| Hybrid | 9.0638 | 16.4979 | 1.1898 | 0.9784 | |
| D | 3-PLF | 15.0039 | 19.0627 | 1.8723 | 0.9811 |
| 4-PLF | 15.0733 | 19.1098 | 1.8810 | 0.9810 | |
| 5-PLF | 10.1637 | 16.9569 | 1.2683 | 0.9850 | |
| 6-PLF | 10.1192 | 16.5730 | 1.2628 | 0.9857 | |
| MHTan | 11.1313 | 17.3347 | 1.3891 | 0.9844 | |
| BPNN | 10.0238 | 16.3810 | 1.2509 | 0.9860 | |
| ANFIS | 11.4776 | 20.5935 | 1.4323 | 0.9779 | |
| ELM | 9.8328 | 16.6137 | 1.2270 | 0.9856 | |
| WELM | 9.8043 | 16.4880 | 1.2235 | 0.9858 | |
| ORELM | 9.7503 | 16.5073 | 1.2167 | 0.9858 | |
| Hybrid | 9.4122 | 16.1494 | 1.1745 | 0.9864 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pei, S.; Li, Y. Wind Turbine Power Curve Modeling with a Hybrid Machine Learning Technique. Appl. Sci. 2019, 9, 4930. https://doi.org/10.3390/app9224930
Pei S, Li Y. Wind Turbine Power Curve Modeling with a Hybrid Machine Learning Technique. Applied Sciences. 2019; 9(22):4930. https://doi.org/10.3390/app9224930
Chicago/Turabian StylePei, Shenglei, and Yifen Li. 2019. "Wind Turbine Power Curve Modeling with a Hybrid Machine Learning Technique" Applied Sciences 9, no. 22: 4930. https://doi.org/10.3390/app9224930
APA StylePei, S., & Li, Y. (2019). Wind Turbine Power Curve Modeling with a Hybrid Machine Learning Technique. Applied Sciences, 9(22), 4930. https://doi.org/10.3390/app9224930




