Analysis on the Impacts of Slant Tropospheric Delays on Precise Point Positioning
Abstract
:Featured Application
Abstract
1. Introduction
2. Zenith and Slant Troposphere Modelling Strategy
3. Experiments and Analysis
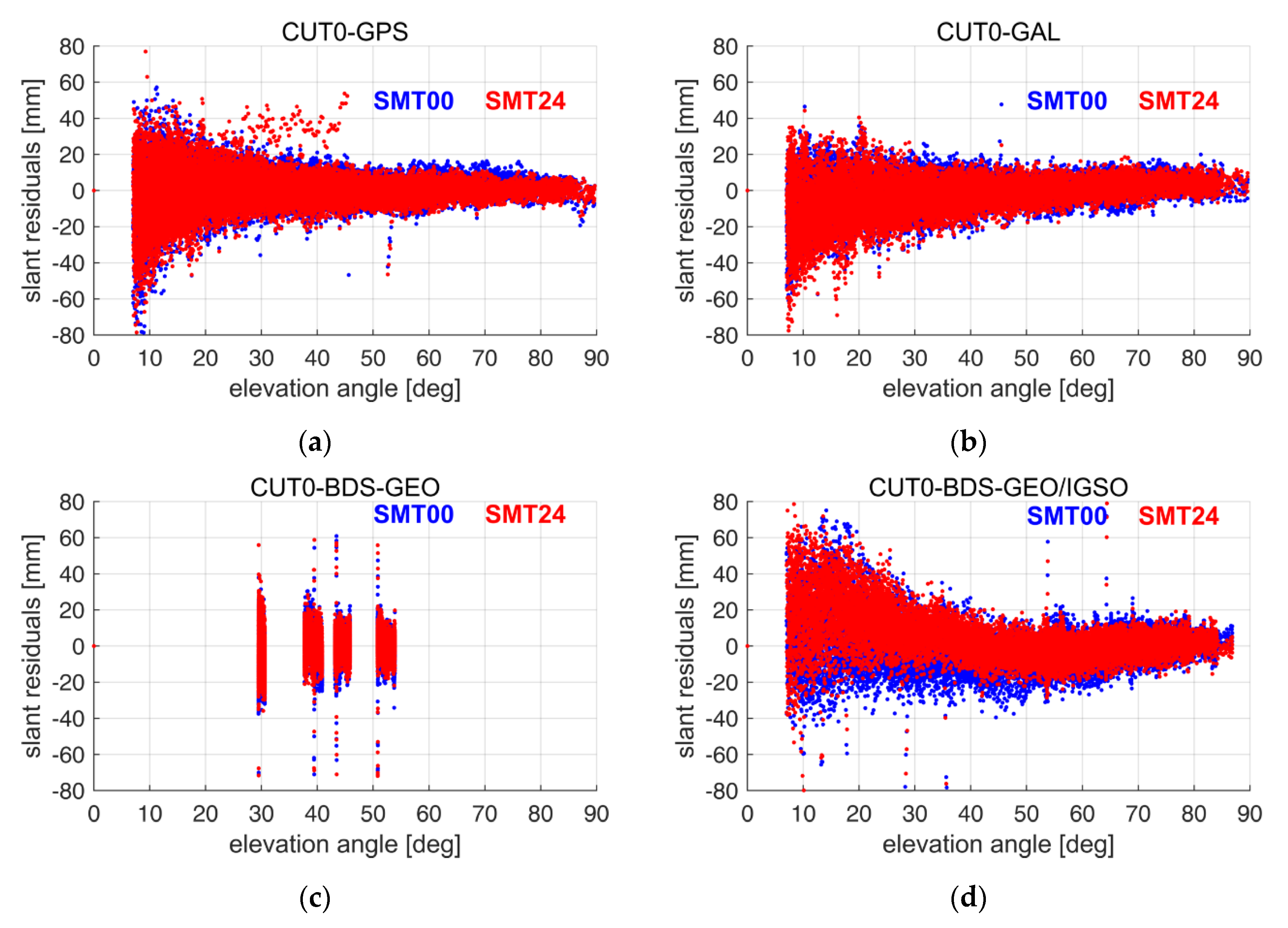
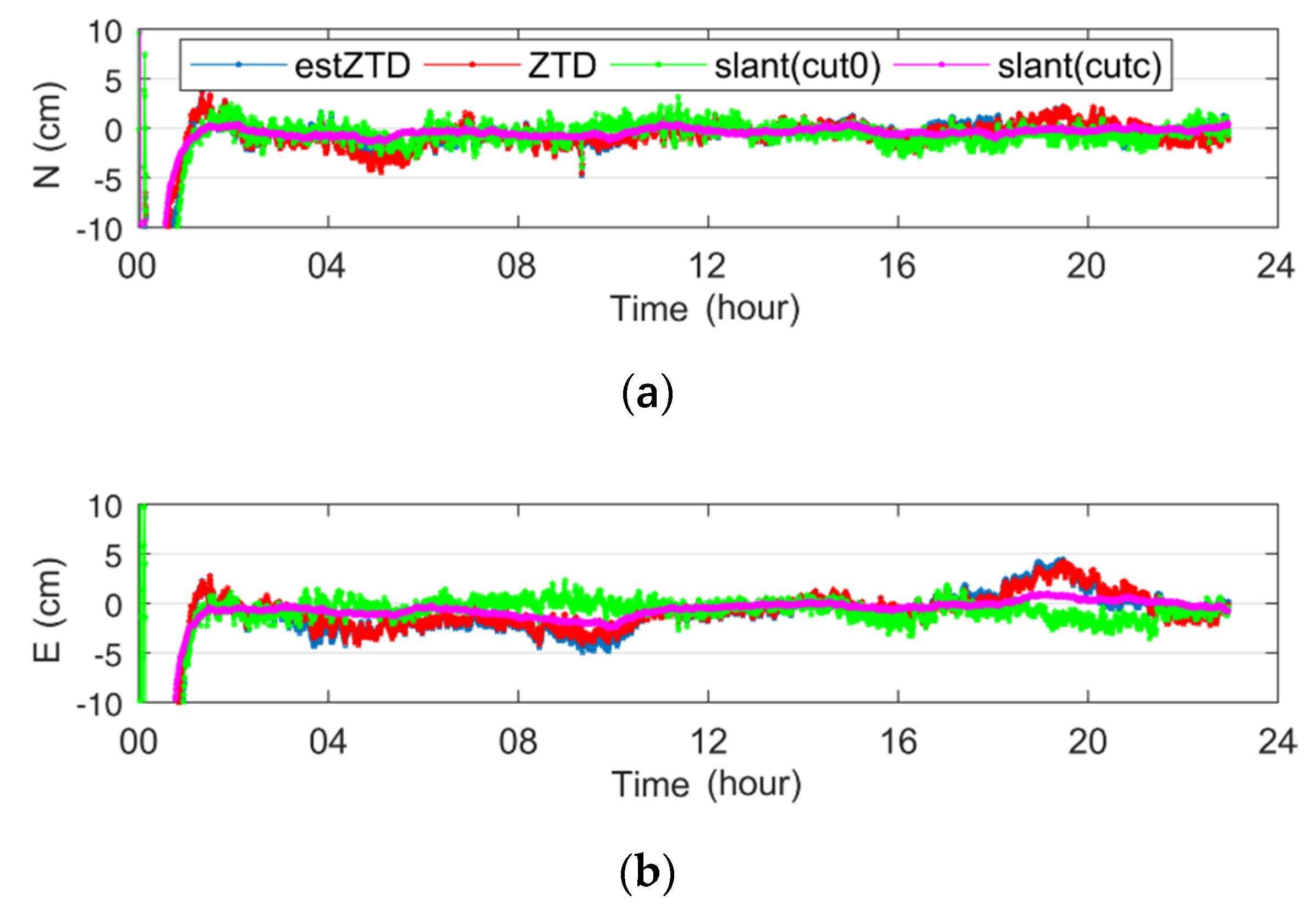
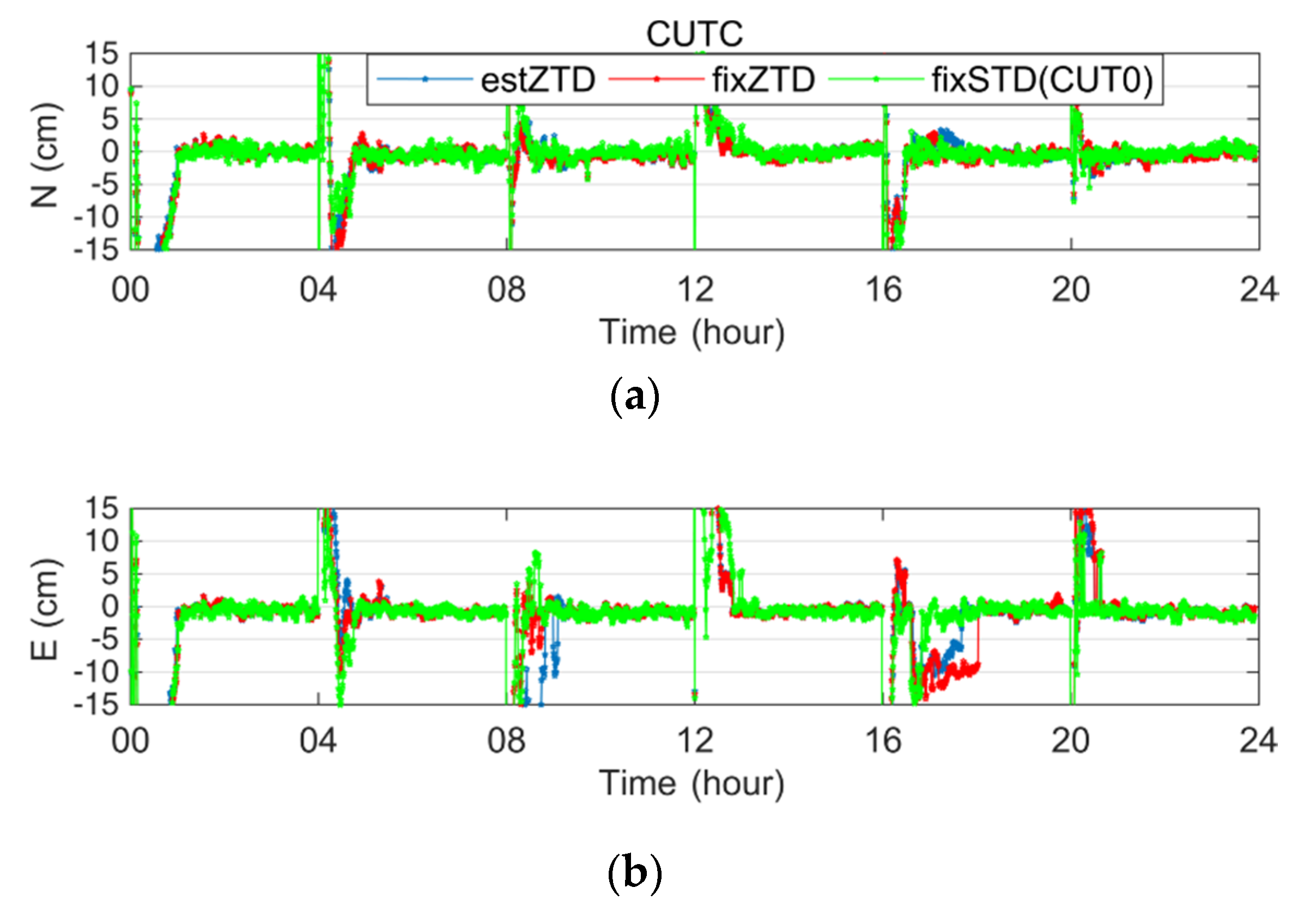
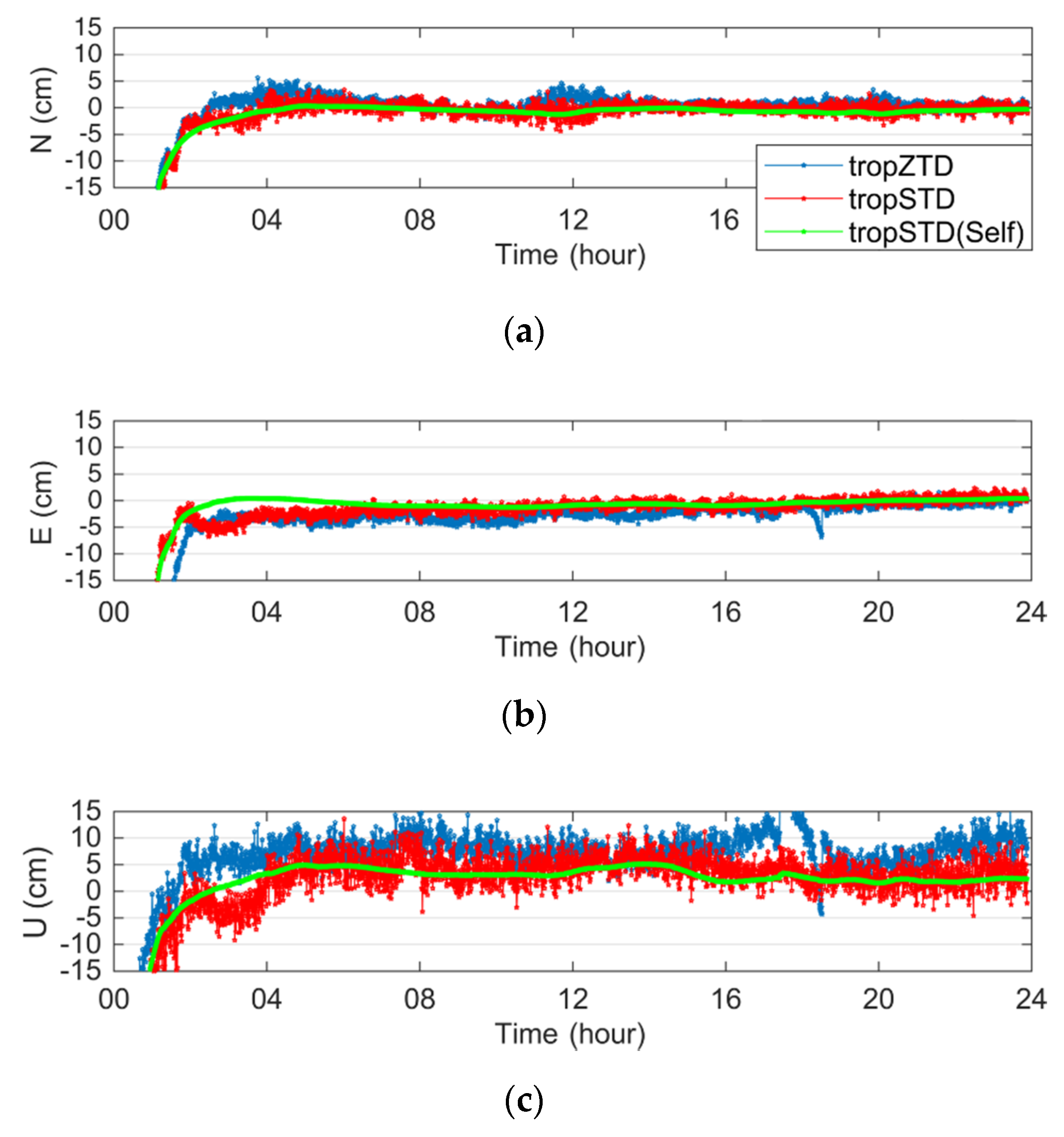
3.1. The Influence of STD on PPP Accuracy
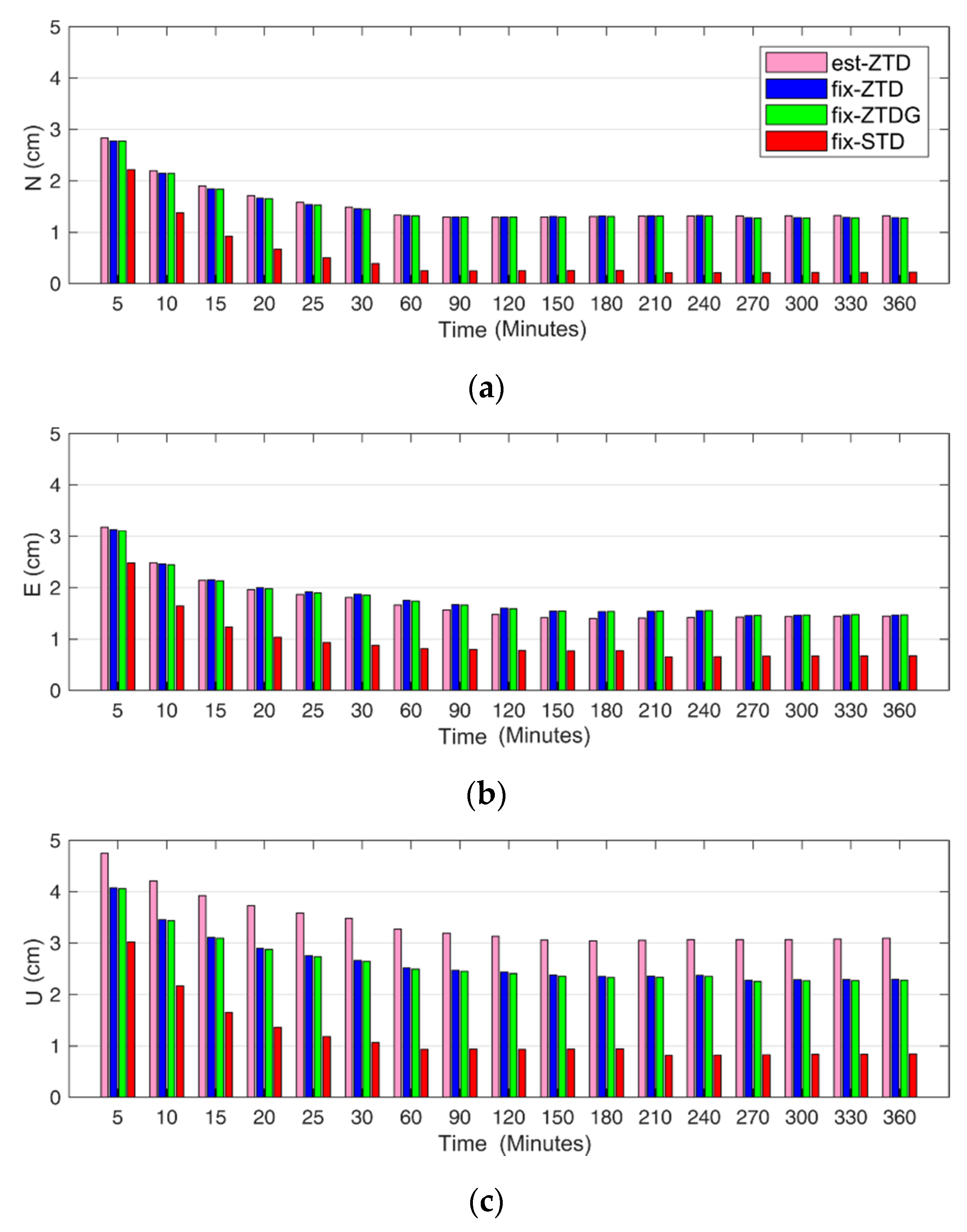
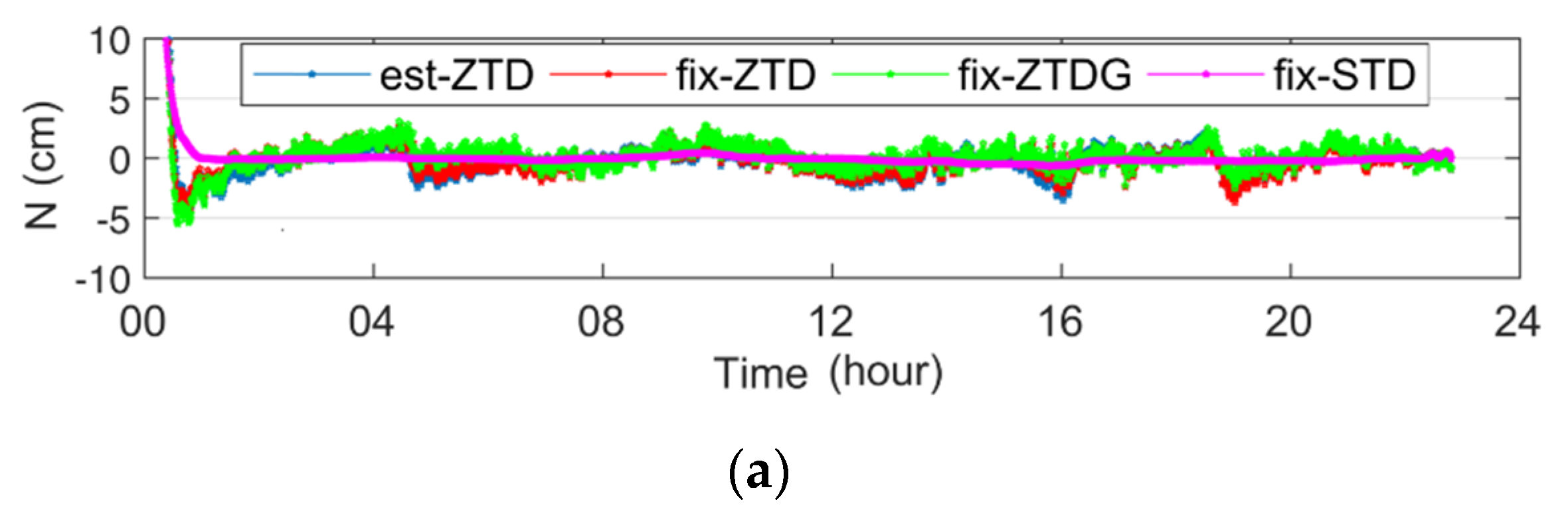
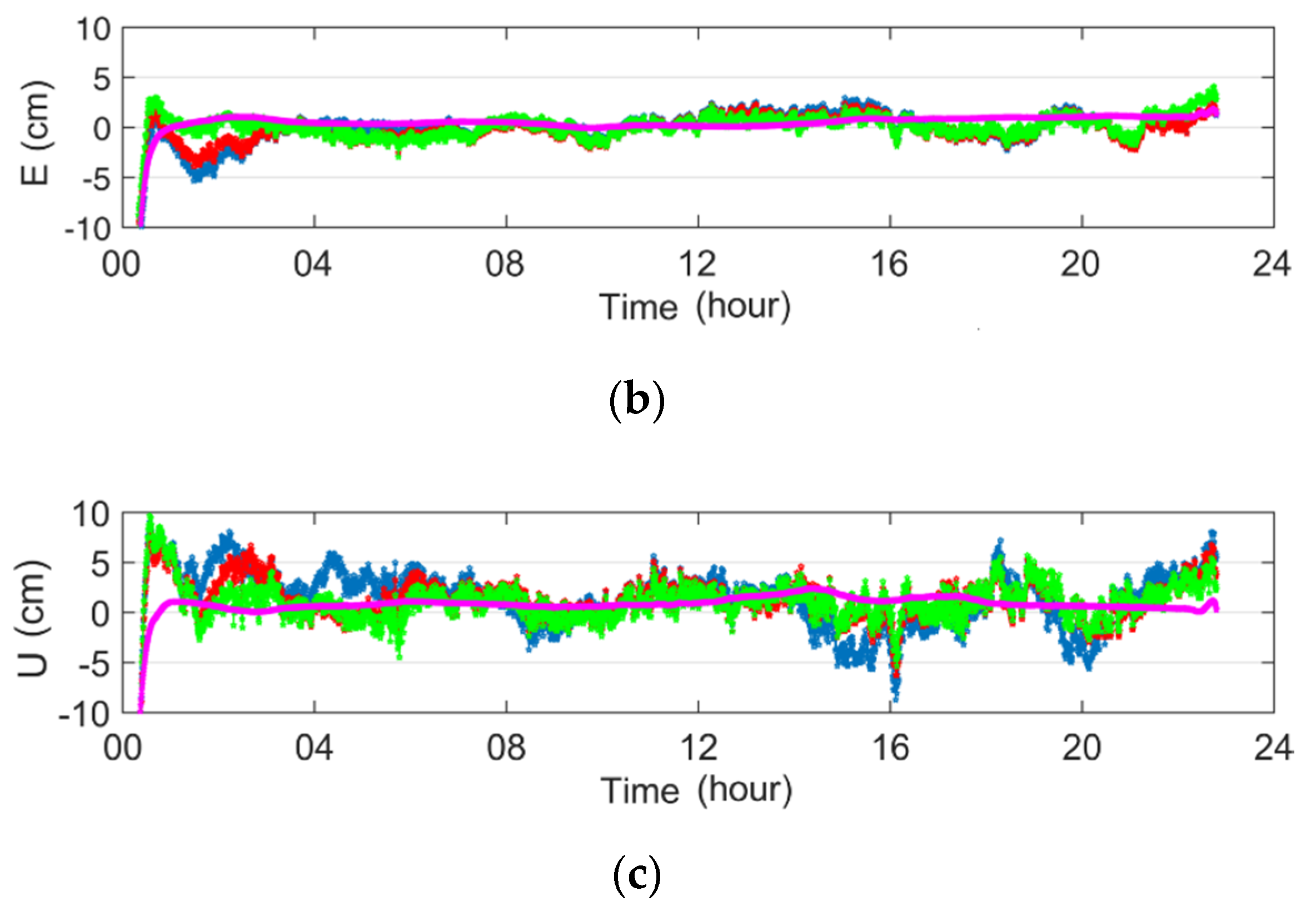
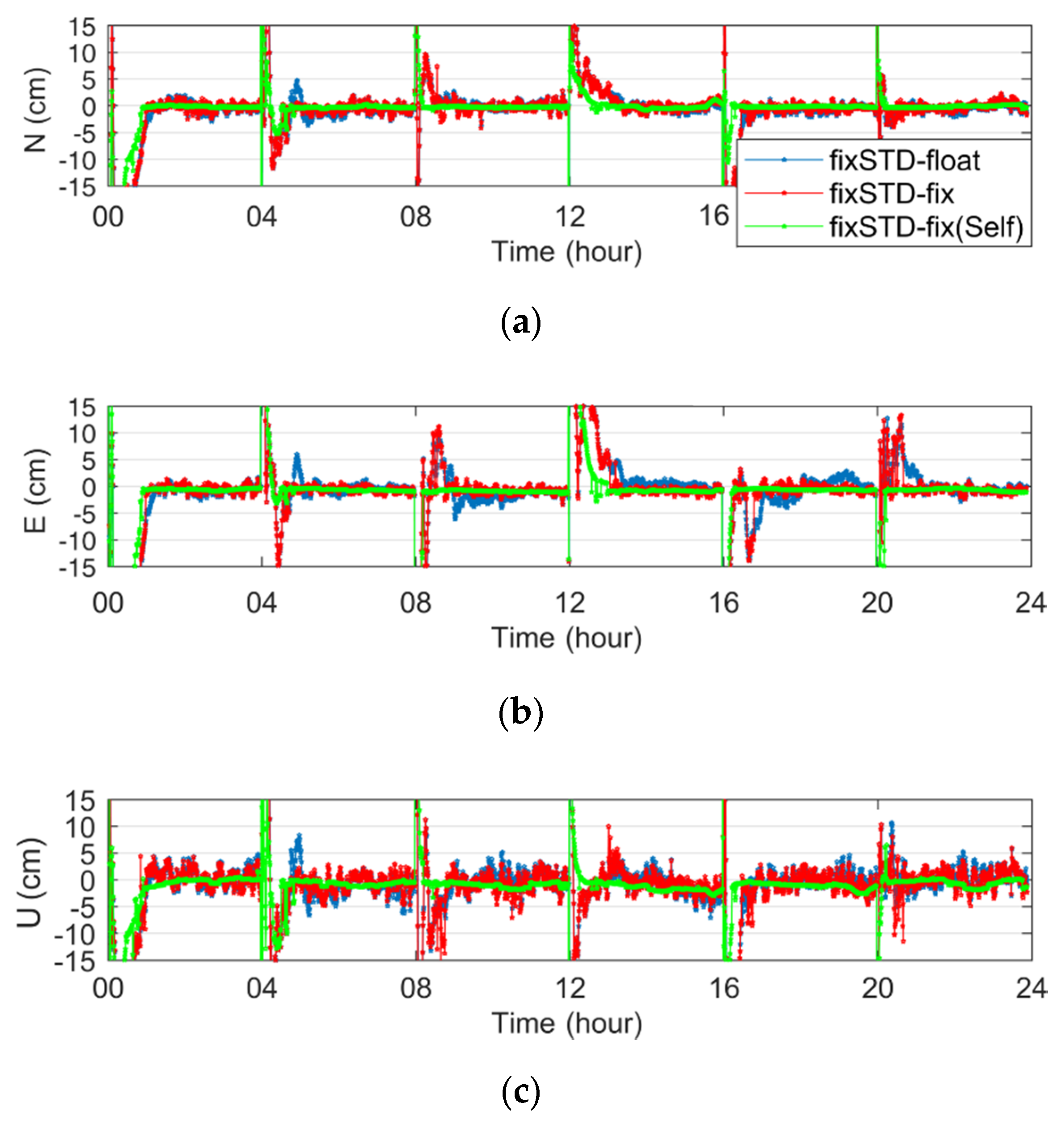
3.2. The Influence of STD on the Parallel PPP Receiver
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Shi, J.; Gao, Y. A troposphere constraint method to improve PPP ambiguity-resolved height solution. J. Navig. 2014, 67, 249–262. [Google Scholar] [CrossRef]
- Jiang, P. The Study of Retrieving 2D/3D Water Vapor Distribution Using Ground-Based GNSS Meteorology. Ph.D. Thesis, Wuhan University, Wuhan, China, 2014. [Google Scholar]
- Dousa, J.; Vaclavovic, P. Real-time zenith tropospheric delays in support of numerical weather prediction applications. Adv. Space Res. 2014, 53, 1347–1358. [Google Scholar] [CrossRef]
- Lu, C.; Zus, F.; Ge, M.; Heinkelmann, R.; Dick, G.; Wickert, J.; Schuh, H. Tropospheric delay parameters from numerical weather models for multi-GNSS precise positioning. Atmos. Meas. Tech. 2016, 9, 5965–5973. [Google Scholar] [CrossRef]
- Lu, C.; Li, X.; Zus, F.; Heinkelmann, R.; Dick, G.; Ge, M.; Wickert, J.; Schuh, H. Improving BeiDou real-time precise point positioning with numerical weather models. J. Geod. 2017, 91, 1019–1029. [Google Scholar] [CrossRef]
- Zhu, K.; Zhao, L.; Wang, W.; Zhang, S.; Liu, R.; Wang, J. Augment BeiDou real-time precise point positioning using ECMWF data. Earth Planets Space 2018, 70, 112. [Google Scholar] [CrossRef]
- Lu, C.; Chen, X.; Liu, G.; Dick, G.; Ge, M.; Wickert, J.; Jiang, X.; Zheng, K.; Schuh, H. Real-time tropospheric delays retrieved from multi-GNSS observations and IGS real-time product streams. Remote Sens. 2017, 9, 1317. [Google Scholar] [CrossRef]
- Lu, C.; Li, X.; Cheng, J.; Dick, G.; Ge, M.; Wickert, J.; Schuh, H. Real-time tropospheric delay retrieval from multi-GNSS PPP ambiguity resolution: Validation with final troposphere products and a numerical weather model. Remote Sens. 2018, 10, 481. [Google Scholar] [CrossRef]
- Hadas, T.; Kaplon, J.; Bosy, J.; Sierny, J.; Wilgan, K. Near-real-time regional troposphere models for the GNSS precise point positioning technique. Meas. Sci. Technol. 2013, 24, 055003. [Google Scholar] [CrossRef]
- Shi, J.; Xu, C.; Guo, J.; Guo, J.; Gao, Y. Local troposphere augmentation for real-time precise point positioning. Earth Planets Space 2014, 66, 30. [Google Scholar] [CrossRef]
- De Oliveira, P.; Morel, L.; Fund, F.; Legros, R.; Monico, J.F.G.; Durand, S.; Durand, F. Modeling tropospheric wet delays with dense and sparse network configurations for PPP-RTK. GPS Solut. 2017, 21, 237–250. [Google Scholar] [CrossRef]
- Lu, C.; Li, X.; Nilsson, T.; Ning, T.; Heinkelmann, R.; Ge, M.; Glaser, S.; Schuh, H. Real-time retrieval of precipitable water vapor from GPS and BeiDou observations. J. Geod. 2015, 89, 843–856. [Google Scholar] [CrossRef]
- Yang, L.; Hill, C.; Moore, T. Numerical weather modeling-based slant tropospheric delay estimation and its enhancement by GNSS data. Geo-Spat. Inf. Sci. 2013, 16, 186–200. [Google Scholar] [CrossRef]
- Bar-Sever, Y.E.; Kroger, P.M.; Borjesson, J.A. Estimating horizontal gradients of tropospheric path delay with a single GPS receiver. J. Geophys. Res. Solid Earth 1998, 103, 5019–5035. [Google Scholar] [CrossRef]
- Kačmařík, M.; Douša, J.; Dick, G.; Zus, G.; Brenot, H.; Möller, G.; Pottiaux, E.; Kapłon, J.; Hordyniec, P.; Václavovic, P.; et al. Inter-technique validation of tropospheric slant total delays. Atmos. Meas. Tech. 2017, 10, 2183–2208. [Google Scholar] [CrossRef]
- Douša, J.; Václavovic, P.; Zhao, L.; Kačmařík, M. New adaptable all-in-one strategy for estimating advanced tropospheric parameters and using real-time orbits and clocks. Remote Sens. 2018, 10, 232. [Google Scholar] [CrossRef]
- Kacmarik, M.; Dousa, J.; Zus, F.; Vaclavovic, P.; Balidakis, K.; Dick, G.; Wickert, J. Sensitivity of GNSS tropospheric gradients to processing options. Ann. Geophys. 2019, 37, 429–446. [Google Scholar] [CrossRef]
- Vaclavovic, P.; Dousa, J. Backward smoothing for precise GNSS applications. Adv. Space Res. 2015, 56, 1627–1634. [Google Scholar] [CrossRef]

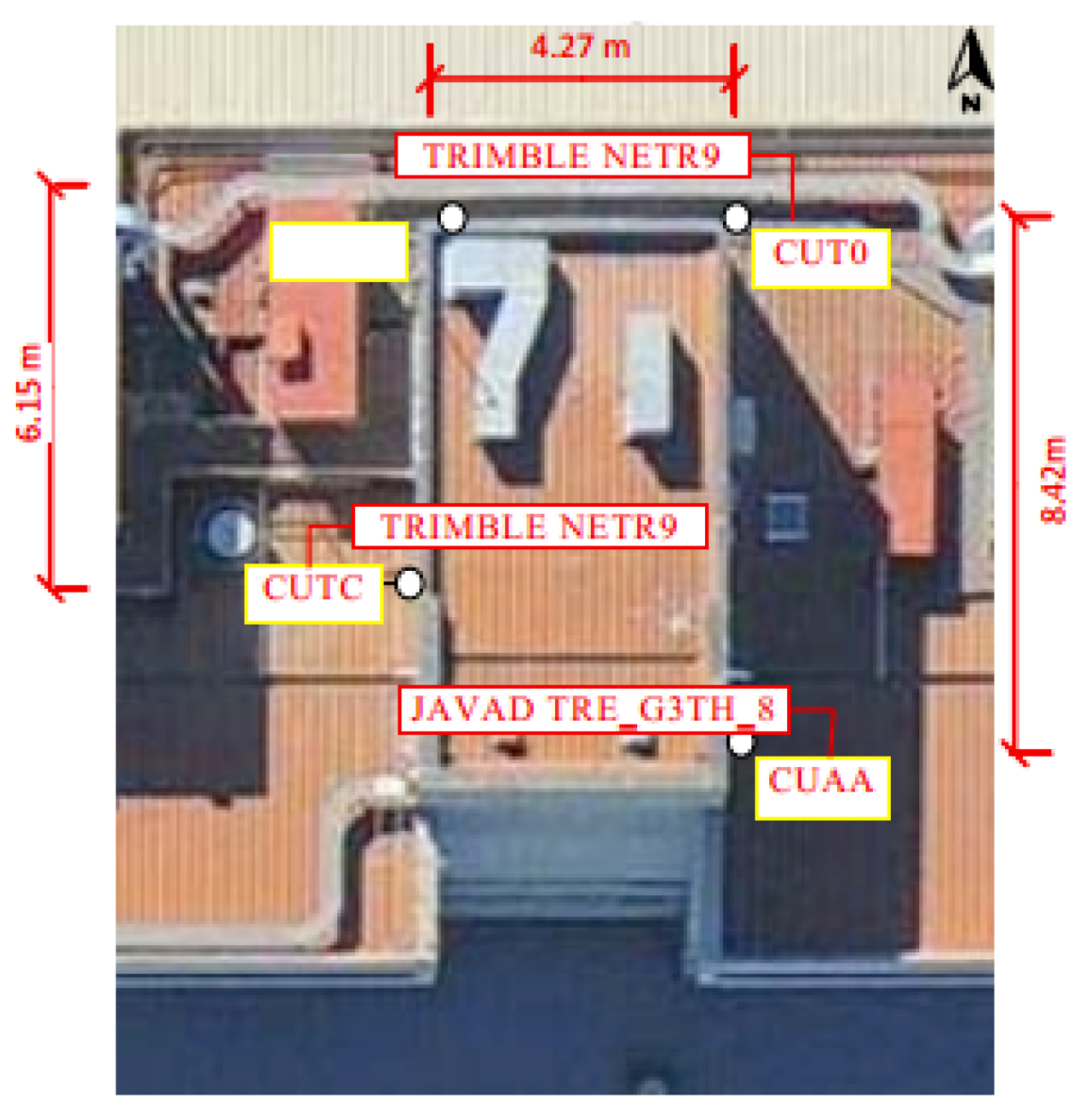


| Item | Strategies |
|---|---|
| Estimator | Forward Kalman/backward smoothing |
| Satellite orbits | Fixed |
| Satellite clock offsets | Fixed |
| Observations | Carrier phase and pseudo-range observations |
| Observation weighting | Elevation-dependent weight |
| Elevation mask angle | Five degrees |
| Zenith troposphere delay | ZHD: Saastamoinen model ZWD: estimated with random-walk Mapping function: Global Mapping Function (GMF) |
| Troposphere gradient | Estimated, epoch-wise random-walk |
| Strategy | Positioning Modes |
|---|---|
| est-ZTD | troposphere is modeled as a parameter |
| fix-ZTD | external zenith tropospheric correction products |
| fix-ZTDG | external zenith tropospheric and horizontal gradient correction products |
| fix-STD | STD correction products considering residuals |
| RMS/m | CUAA | CUTC | ||||
|---|---|---|---|---|---|---|
| North | East | Up | North | East | Up | |
| est-ZTD | 0.0107 | 0.0183 | 0.0351 | 0.0111 | 0.0195 | 0.0372 |
| fix-ZTD | 0.0106 | 0.0160 | 0.0222 | 0.0124 | 0.0174 | 0.0239 |
| fix-STD(CUT0) | 0.0091 | 0.0115 | 0.0174 | 0.0102 | 0.0116 | 0.0187 |
| fix-STD | 0.0052 | 0.0077 | 0.0074 | 0.0052 | 0.0089 | 0.0094 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiong, C.; Yu, L.; Zhao, L. Analysis on the Impacts of Slant Tropospheric Delays on Precise Point Positioning. Appl. Sci. 2019, 9, 4884. https://doi.org/10.3390/app9224884
Xiong C, Yu L, Zhao L. Analysis on the Impacts of Slant Tropospheric Delays on Precise Point Positioning. Applied Sciences. 2019; 9(22):4884. https://doi.org/10.3390/app9224884
Chicago/Turabian StyleXiong, Chunbao, Lina Yu, and Lewen Zhao. 2019. "Analysis on the Impacts of Slant Tropospheric Delays on Precise Point Positioning" Applied Sciences 9, no. 22: 4884. https://doi.org/10.3390/app9224884
APA StyleXiong, C., Yu, L., & Zhao, L. (2019). Analysis on the Impacts of Slant Tropospheric Delays on Precise Point Positioning. Applied Sciences, 9(22), 4884. https://doi.org/10.3390/app9224884





