Abstract
Noninvasive tuning of the mechanical resonance frequencies of suspended parallel nanomembranes in various monolithic arrays is achieved by piezoelectric control of their tensile stress. Parametric amplification of their thermal fluctuations is shown to be enhanced by the piezoelectric actuation and amplification factors of up to 20 dB in the sub-parametric oscillation threshold regime are observed.
1. Introduction
Suspended nano- and micro-resonators are ubiquitous in a wide range of sensing, photonics and telecommunication applications, for many of which a certain degree of tunability of their mechanical properties may be desirable [1,2]. Dynamical tuning of the mechanics can be achieved by modifying the stress of the resonant structures, e.g., capacitively [1,3], electro- [4,5,6] or photo-thermally [7,8,9], by bending [10] or by heating [11]. In general, such a stress control may allow for modifying not only the mechanical resonance frequencies and quality factors, but also the nonlinear response of the resonators [1,12,13,14]. Such a tunability is particularly interesting for arrays consisting of multiple resonators, for instance to match or enhance their collective response and sensing capabilities [15,16,17], to engineer and investigate complex collective dynamics [18,19,20,21,22], or to coherently manipulate phonons between them [23,24,25,26,27,28,29,30,31].
Suspended drum-shaped resonators, made of low loss material such as silicon nitride and possessing high mechanical quality factors, can be efficiently coupled to electromagnetic fields, whether in the optical or microwave/radiofrequency domains [32,33,34,35,36,37,38,39]. Having multiple such membrane resonators [40,41,42,43] simultaneously interacting with cavity fields opens up opportunities for a number of exciting applications, e.g., collectively enhanced optomechanics [44,45,46,47], optomechanical synchronization [48], phonon transport [49,50] or entanglement and multimode squeezing generation [51,52,53,54,55].
We investigate here the tuning of the linear and nonlinear mechanical properties of suspended silicon nitride square drums by the application of a piezoelectrically controlled force to the chip supporting the drums. In this scheme, recently implemented with a single [56] and pairs of membranes [43,57], the compression of the frame caused by the piezoelectric force modifies the tensile stress of the silicon nitride films, thereby allowing for reversibly tuning the mechanical resonance frequencies without deteriorating their quality factors. We report here on the simultaneous tuning of the mechanical resonance frequencies of the membranes of various monolithic double-membrane arrays, and show for instance that the modes of membranes with close resonance frequencies can be tuned to degeneracy by the application of a bias voltage to the piezoelectric element. This tunability would be essential in the abovementioned applications involving optomechanical arrays. In addition to radiation pressure, such drum resonators naturally lend themselves to fluid pressure measurements, and the tuning of their mechanical properties within such compact monolithic arrays would also be highly interesting in connection with the realization of squeeze film pressure sensors [58,59].
Furthermore, as we recently reported in [57], such a piezoelectric stress control allows for enhancing the resonators’ nonlinear response to dynamical actuation. We expand here on this demonstration by performing detailed studies of the parametric excitation of the thermal fluctuations of the fundamental drummodes of two closely lying membranes in a monolithic array, for which amplification factors of up to 20 dB in the sub-parametric oscillation threshold regime are observed. The observed noise spectra and gains are in excellent agreement with the predictions of a simple phase-averaged subthreshold parametric amplification model.
Mechanical parametric amplification [60] being an ubiquitous tool in electro-opto-mechanical systems [61] to investigate and exploit nonlinear dynamics in a wide range of MEMS applications and resonators [1,13,14,17,26,62,63,64,65,66,67,68], the results demonstrated here with suspended silicon nitride drum resonators open up opportunities for interesting applications involving thermomechanical squeezing [27,54,55,56,69,70,71] and amplification [68,72,73] in cavity electro/optomechanics, among others.
2. Electromechanical Resonators and Experimental Setup
The membrane resonators used in this work are commercial [74], high tensile stress (0.7–0.9 GPa), stoichiometric SiN square drums with lateral dimension 500 m and thickness 100 nm, deposited on a Si frame with lateral dimension 5 mm and thickness of either 200 or 500 m. As described in [57] and depicted in Figure 1a,b, three corners of a Si chip were glued by application and curing of a small dab of UV-resist (OrmoComp, Micro resist technology GmbH) onto a piezoelectric ring actuator with 6 mm inner diameter (Noliac NAC2123) to which both dc and ac voltages can be applied. Following the method of [40], double-membrane arrays were made by gluing the two chips together either on top of each other (Figure 1c), so that the intermembrane separation was given by the Si frame thickness (200 m in this case), or with a spacer in between the SiN films setting the separation between the suspended membranes to be m (Figure 1d).
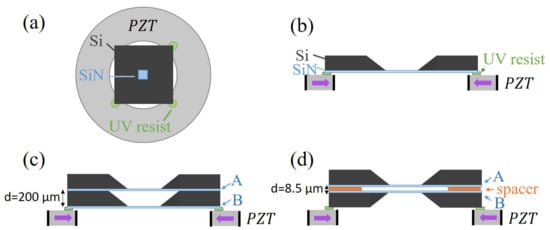
Figure 1.
(a) Top view schematic of the membrane chip mounted on a piezoelectric ring actuator. (b–d) Sideview schematics of the single- or double-membrane electromechanical resonators studied. The purple arrows inside the piezoelectric transducer (PZT) indicate the direction of the compressive force for a positive voltage difference between the outer and inner electrodes.
The vibrations of the membranes can then be measured by monitoring the transmission of monochromatic light ( nm) issued from an external cavity diode laser through a linear Fabry–Perot interferometer constituted by the membrane—or membrane array—and a 50:50 beamsplitter mirror positioned parallel to the membranes at a distance of approximately 7 mm (Figure 2). The fluctuations of the transmitted light are detected with a fast photodiode and analyzed with a narrow resolution bandwidth spectrum analyzer. The wavelength of the light is chosen so as to maximize the sensitivity of the interferometer to the displacement of the membrane modes considered [40]. The mechanical resonance frequencies can be determined by Lorentzian fits to the thermal noise spectrum, typically recorded with a resolution bandwidth (RBW) of 0.5 Hz and averaged 500 times. The mechanical quality factors are determined either from the results of the Lorentzian fits to the thermal noise spectrum, or by performing ringdown spectroscopy of the resonantly excited mode [40,58].
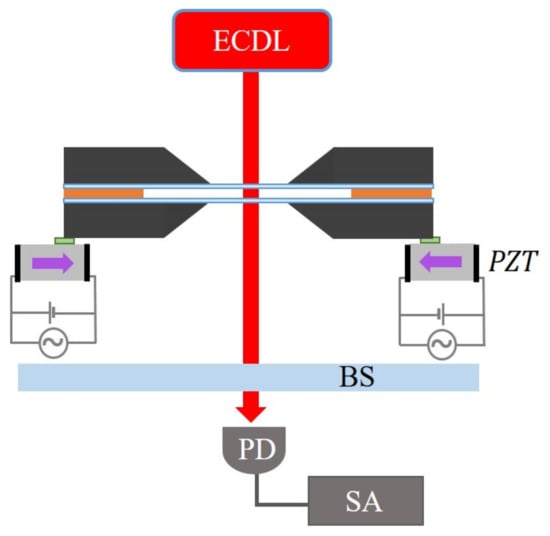
Figure 2.
Schematic experimental setup for the piezoelectric actuation and detection of the membrane vibrations (shown here for the array geometry of Figure 1d). ECDL: external cavity diode laser, BS: beamsplitter mirror, PZT: piezoelectric transducer, PD: photodiode, SA: spectrum analyzer.
3. Mechanical Frequency Tuning
The application of a positive voltage to a single membrane chip with a 200 m-thick frame, as depicted in Figure 1b, results in a reduction of the tensile stress of the SiN film. In this tensile stress-dominated regime the resonance (angular) frequencies of the mechanical modes are to a very good approximation given by
where is the tensile stress, the density of SiN, a the membrane lateral dimension and m, n strictly positive integers, and can thus be tuned by the application of a bias voltage to the piezeoelectric element, as demonstrated in [56]. A linear reduction with of the resonance frequencies of both the fundamental () and a higher order () modes is observed (Figure 3a,b), with frequency shifts of −43 Hz/V and −130 Hz/V, respectively. Furthermore, as shown in Figure 3c, the mechanical quality factors are observed to be only weakly (slight increase for this sample) dependent on the bias voltage.
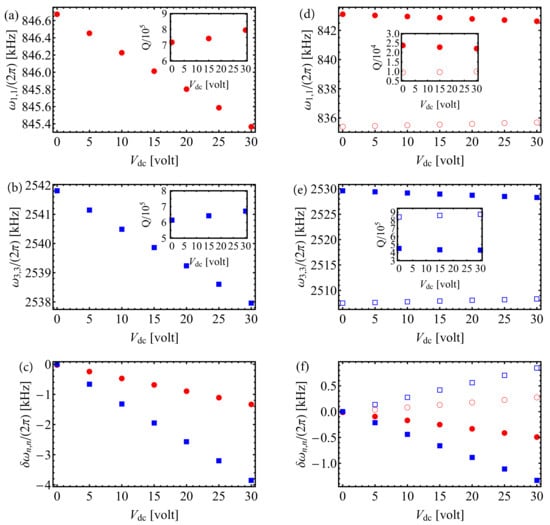
Figure 3.
(a,b) Measured single membrane (1,1) and (3,3) mode frequencies as a function of bias voltage . (c) Corresponding resonance frequencies shifts versus . (d,e) Measured (1,1) and (3,3) mode resonance frequencies of the A (red circles and empty blue squares) and B (red dots and filled blue squares) membranes in a double-membrane array as in Figure 1c, as a function of . (f) Corresponding resonance frequency shifts versus . The error bars are smaller than the size of the data points. The insets in (a,b) and (d,e) show the variations of the mechanical quality factors with .
We now turn to the piezoelectric actuation of double-membrane arrays as depicted in Figure 1c,d. The compression of the piezoelectric transducer (PZT) affects the whole Si frame/SiN films structure. In both geometries the lower (closer to the piezoelectric element) membrane sees its tensile stress decrease when a positive dc-voltage is applied to the PZT, whereas the upper (further away from the piezoelectric element) sees its stress increase. Figure 3d,e shows the variations with the bias voltage of the (1,1) and (3,3) modes of an array with a 200 m-thick frame. Shifts of −16 Hz/V and −44 Hz/V are respectively observed for the (1,1) and (3,3) modes of the lower membrane, and 9 Hz/V and 29 Hz/V for those of the upper membrane. The mechanical quality factors are observed to be essentially independent of the bias voltage (Figure 3f).
Piezoelectric tuning of the modes of a shorter (m) array with thicker frame (500 m) and in the geometry of Figure 1d was also demonstrated and reported in [57]. Figure 4a,b shows the variations with of the resonance frequencies of the (1,1) and (2,2) modes of both membranes. The two membranes of this array exhibit fairly similar bare mechanical properties; for instance, the fundamental modes of the upper (A) and lower (B) membranes have resonance frequencies kHz and kHz, respectively, in absence of biasing. It is then possible to tune them to degeneracy by applying a bias voltage of approximately 56 V, as shown in Figure 4. The mechanical quality factors are also observed to be essentially independent of the bias voltage for this sample [57]. A careful analysis of the evolution of the thermal noise spectra allows furthermore for extracting the intermembrane coupling, as discussed in [57].
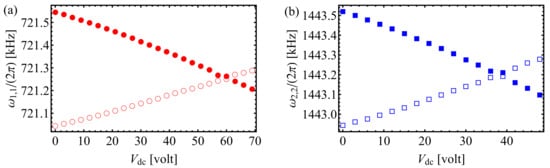
Figure 4.
(a) Measured (1,1) mode resonance frequencies of the A (red circles) and B (red dots) membranes in a double-membrane array as in Figure 1d, as a function of . (b) Measured (2,2) mode resonance frequencies of the A (empty blue squares) and B (filled blue squares) membranes, as a function of .
Having demonstrated the possibility to noninvasively tune the mechanical mode spectrum of such vertically coupled membrane systems, we now turn to their dynamical activation under parametric excitation.
4. Parametric Amplification of the Thermal Fluctuations
4.1. Theoretical Model
We consider a parametric modulation of the spring constant of a normal mode of the form , where is the spring constant in absence of modulation, the normalized modulation amplitude, which is proportional to the applied modulation voltage amplitude and the pump modulation frequency. The classical dynamics of the amplitude around equilibrium, , can be modeled by the following differential equation [60]
where is the bare mechanical resonance frequency of the normal mode considered, m the effective mass of the mode, its damping rate and a thermal noise force arising from the coupling with the thermal environment. For a high quality factor oscillator () and a pump modulation frequency close to the second harmonic frequency, it is convenient to introduce the slowly varying envelope defined by
where the quadratures and are respectively given by the real and imaginary parts of A. Under the rotating wave approximation, Equation (2) yields
where . Fourier transforming Equation (5) using the convention yields
where
The noise spectrum, , of an arbitrary quadrature can be computed using the fact that
such that only and are nonzero and both equal to , where is the Boltzmann constant and T the thermal bath temperature.
If, like in the experiment, one does not keep track of the quadrature angle , one observes an average noise spectrum
given by
At the parametric resonance (), the average noise spectrum in Equation (12) can be simply written as
i.e., the sum of two Lorentzians with HWHMs (half-width at half-maximum) and , corresponding to the noise spectrum of the amplified and deamplified quadratures, respectively. While in general not Lorentzian, the average noise spectrum is, to a good approximation, Lorentzian either at low gains () or close to the parametric threshold , where the contribution of the amplified quadrature noise dominates. At the parametric threshold –or, equivalently, –the linewidth of the noise spectrum diverges (in absence of nonlinearities).
The variance of the amplitude, , is obtained by integrating this one-sided noise spectrum over the positive frequencies
to give the average energy in the mode as
where is the average energy in absence of parametric modulation. In presence of parametric modulation the average energy thus increases with the modulation amplitude as and diverges at the threshold. For a nonzero pump detuning, the amplification is reduced with respect to that on resonance according to Equation (15) and the parametric resonance linewidth depends on both and .
4.2. Experimental Results
Parametric excitation of the membranes of the m-long array, whose dc-actuation was shown in Figure 4, was investigated for different values of the biased voltage by applying a resonant parametric modulation at the second harmonic frequency of the fundamental mode of one of the membranes. The evolution of the noise spectrum of the fundamental modes was then monitored as a function of the modulation voltage amplitude . The bias voltage , which determined the frequency separation between the fundamental mode frequencies (difference between the filled and open circles in Figure 4a), was chosen in such a way that the second harmonic of the excited fundamental mode frequency, or , did not coincide with a (2,2) mode resonance frequency. We verified experimentally that neither the non-resonantly driven (1,1) mode nor the (2,2) modes were excited in presence of the parametric drive.
Figure 5 shows examples of noise spectra of membrane B’s fundamental mode, obtained for a bias voltage corresponding to a frequency separation Hz, and for increasing modulation amplitudes (see Supplementary Materials for the complete spectrum dataset). The modulation amplitudes were normalized to the parametric threshold voltage and the same resolution bandwidth of 0.5 Hz is used for all spectra. The results of Lorentzian fits to the data are also shown. It can be seen that the amplified noise spectra are generally well-approximated by Lorentzians with increasing peak value/area and reduced linewidth, as the parametric modulation amplitude is increased.
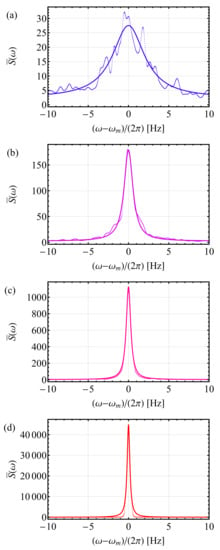
Figure 5.
Average noise spectra of membrane B’s fundamental mode at a bias voltage corresponding to Hz and for different resonant modulation amplitudes corresponding to (a) , (b) , (c) and (d) . The solid lines are the results of Lorentzian fits to the data. The y-axis scale, in arbitrary units, is the same for all figures. The same RBW of 0.5 Hz is used for recording all the spectra.
The average energy is obtained by numerical integration of the spectrum and the energy gain—i.e., the ratio of the average energy for a given to the average energy for —is shown in Figure 6a as a function of . The variations with of the HWHM obtained from the Lorentzian fits is also shown in Figure 6b. The solid line in Figure 6a shows the result of a fit according to Equation (15), while that in Figure 6b shows a linearly decreasing linewidth of the form , where is the HWHM in absence of modulation. As one approaches the threshold, effects due to the finite resolution bandwidth of the spectrum analyzer become visible and the measured linewidth is effectively limited by the RBW. Note that this does not affect the determination of the average energy, however, since the latter is related to the numerical integration of the noise spectrum and is independent of the RBW. Gains in energy of up to 125 (21 dB) were observed for this mode at this particular bias voltage, before the parametric oscillation threshold was reached. Similar behaviors were observed for both fundamental modes and different bias voltages (see Figure 8 and Supplementary Materials), albeit with different gains and thresholds, as will be discussed below.
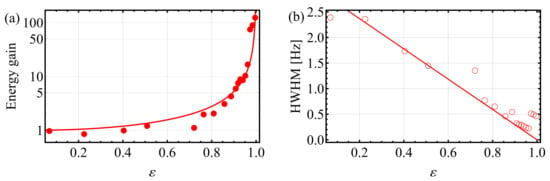
Figure 6.
(a) Energy gain as a function of the normalized parametric modulation amplitude for membrane B’s fundamental mode at a bias voltage corresponding to Hz. The solid line shows the result of a fit according to Equation (15). (b) HWHM of the noise spectra resulting from the Lorentzian fits, as a function of . The solid line shows a linearly decreasing function of the form .
The resonant nature of the parametric excitation was also verified by scanning the modulation voltage frequency around the second harmonic frequency. Figure 7 shows the variation of the energy gain—deduced from the noise spectra as previously—as a function of the pump detuning , for the fundamental mode of membrane B at a bias voltage such that Hz and for two different parametric modulation amplitudes close to the threshold. The solid lines show the theoretical predictions of Equation (15), in which is determined by the zero-detuning value and is the HWHM measured in absence of modulation.
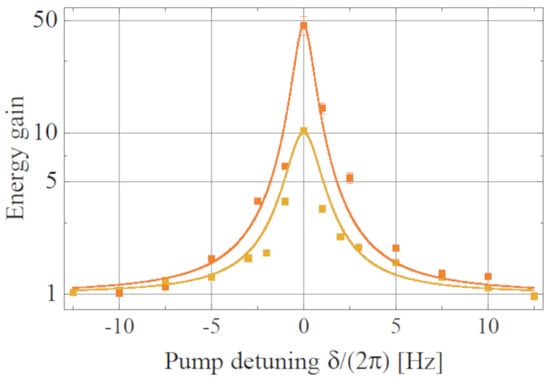
Figure 7.
Energy gain as a function of pump detuning for the fundamental mode of membrane B for Hz and for two modulation voltage amplitudes corresponding to (yellow) and (orange). The solid lines are the theoretical predictions of Equation (15).
We finally investigated the influence of the bias voltage on the resonant parametric amplification of the fundamental modes of both membranes. The energy gains of both modes for different bias voltages are shown in Figure 8 as a function of the resonant modulation amplitude. The amplitude was arbitrarily normalized to the parametric amplification threshold amplitude, mV, of membrane A’s fundamental mode at Hz. One first observes that increasing the bias voltage leads to lower parametric oscillation thresholds for both membranes. Higher thresholds for membrane A than for membrane B at comparable s were also systematically observed. The reasons for this behavior were investigated in detail in [57]. In brief, the lower membrane (B) experiences a direct modulation of its tensile stress at the parametric resonance frequency through the compression of the lower frame. The parametric oscillation threshold can be reached by the application of a moderate modulation voltage. In contrast, such a direct modulation of the SiN film spring constant is much weaker for the upper membrane (A). However, the application of a static compressive force to the chips results in a modification of the nonlinear response/stress of membrane A, which accounts for the lowering of the parametric amplification threshold with the bias voltage. Let us also note that, due to thermal drifts during the measurements, variations in the highest achievable gains close to the threshold were typically observed, so that one cannot rule out that higher subthreshold gain values may be achievable by better temperature control. Let us also remark that, at degeneracy (), the single parametrically excited mode picture breaks down, as the dynamics of the two coupled modes have in principle to be taken into account [27]. However, since the parametric gain for membrane B is substantially stronger than for membrane A, the total amplified noise spectrum becomes quickly dominated by that of membrane B’s fundamental mode, as the modulation amplitude increases. The observed parametric gains and threshold values thus consistently follow those of membrane B.
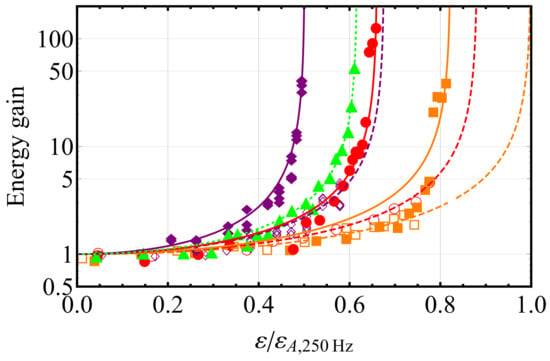
Figure 8.
Energy gains as a function of normalized modulation amplitude for both fundamental modes for increasing , such that Hz (yellow squares), 30 Hz (red circles) and −100 Hz (purple diamonds). The empty and full symbols are for membranes A and B, respectively. The green triangles correspond to the energy gain measured at the degeneracy (). The modulation amplitude is arbitrarily normalized to the threshold amplitude for membrane A’s fundamental mode at Hz. The solid lines show the results of fits to Equation (15).
5. Conclusions
Noninvasive tuning of the mechanical resonance frequencies of suspended square drum resonators in monolithic vertical arrays was demonstrated using a simple scheme where the membrane chips were directly mounted on a piezoelectric ring actuator. The application of a piezoelectrically controlled force to the bottom chip allowed for modifying the tensile stress of the membrane resonators and thereby change their frequencies. For membranes with not too different bare mechanical frequencies, tuning to degeneracy by the application of a dc-voltage to the PZT is possible, as the bottom and top membrane experience opposite frequency shifts with the bias voltage.
Dynamical actuation of both membranes was also demonstrated by the application of an ac-voltage at twice the mechanical resonance frequencies of the fundamental modes of the membranes and observing the parametric amplification of their thermal fluctuations until the parametric oscillation threshold was reached. The experimental observations are well-accounted for by a simple phase-averaged subthreshold parametric oscillator model. Last, the amplification was shown to be enhanced by the simultaneous application of the dc-voltage, which results in higher amplification gains and a lowering of the parametric oscillation thresholds.
Such a tuning of both the linear and nonlinear response of membrane resonators in vertical arrays is promising for exploring collective effects and investigating phonon dynamics in currently investigated optomechanical arrays [40,41,42,43], or for sensing applications [58,59,75].
Supplementary Materials
The following are available at https://www.mdpi.com/2076-3417/9/22/4845/s1, Figure S1: Average noise spectra of membrane B’s fundamental mode for /(2) = 250 Hz and different normalized modulation amplitude (top label of each subplot). The solid lines are the results of Lorentzian fits to the data. Figure S2: Average noise spectra of membrane B’s fundamental mode for /(2) = 30 Hz and different normalized modulation amplitude (top label of each subplot). The solid lines are the results of Lorentzian fits to the data. Figure S3: Average noise spectra of membrane B’s fundamental mode for /(2) = −100 Hz and different normalized modulation amplitude (top label of each subplot). The solid lines are the results of Lorentzian fits to the data. Figure S4: Average noise spectra of membrane A’s fundamental mode for /(2) = 250 Hz and different normalized modulation amplitude (top label of each subplot). The solid lines are the results of Lorentzian fits to the data. Figure S5: Average noise spectra of membrane A’s fundamental mode for /(2) = 30 Hz and different normalized modulation amplitude (top label of each subplot). The solid lines are the results of Lorentzian fits to the data. Figure S6: Average noise spectra of membrane A’s fundamental mode for /(2) = −100 Hz and different normalized modulation amplitude (top label of each subplot). The solid lines are the results of Lorentzian fits to the data. Figure S7: Average noise spectra for /(2) = 0 Hz and different normalized modulation amplitude (top label of each subplot). The solid lines are the results of Lorentzian fits to the data.
Author Contributions
Conceptualization, A.D.; investigation, S.N. and A.N.; data curation, S.N. and A.N. and A.D.; writing—original draft preparation, A.D.; writing—review and editing, S.N. and A.N.; supervision, A.D.; funding acquisition, A.D.
Funding
This research was funded by the Velux Foundations.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ekinci, K.L.; Roukes, M.L. Nanoelectromechanical systems. Rev. Sci. Instrum. 2005, 76, 061101. [Google Scholar] [CrossRef]
- Li, M.; Tang, H.X.; Roukes, M.L. Ultra-sensitive NEMS-based cantilevers for sensing, scanned probe and very high-frequency applications. Nat. Nanotechnol. 2007, 2, 114. [Google Scholar] [CrossRef] [PubMed]
- Kozinsky, I.; Postma, H.W.C.; Bargatin, I.; Roukes, M.L. Tuning nonlinearity, dynamic range, and frequency of nanomechanical resonators. Appl. Phys. Lett. 2006, 88, 253101. [Google Scholar] [CrossRef]
- Jun, S.C.; Huang, X.M.H.; Manolidis, M.; Zorman, C.A.; Mehregany, M.; Hone, J. Electrothermal tuning of Al–SiC nanomechanical resonators. Nanotechnology 2006, 17, 1506–1511. [Google Scholar] [CrossRef]
- Hüttel, A.K.; Steele, G.A.; Witkamp, B.; Poot, M.; Kouwenhoven, L.P.; van der Zant, H.S.J. Carbon Nanotubes as Ultrahigh Quality Factor Mechanical Resonators. Nano Lett. 2009, 9, 2547–2552. [Google Scholar] [CrossRef] [PubMed]
- Barton, R.A.; Storch, I.R.; Adiga, V.P.; Sakakibara, R.; Cipriany, B.R.; Ilic, B.; Wang, S.P.; Ong, P.; McEuen, P.L.; Parpia, J.M.; et al. Photothermal Self-Oscillation and Laser Cooling of Graphene Optomechanical Systems. Nano Lett. 2012, 12, 4681–4686. [Google Scholar] [CrossRef] [PubMed]
- Okamoto, H.; Kamada, T.; Onomitsu, K.; Mahboob, I.; Yamaguchi, H. Optical Tuning of Coupled Micromechanical Resonators. Appl. Phys. Express 2009, 2, 062202. [Google Scholar] [CrossRef]
- Jöckel, A.; Rakher, M.T.; Korppi, M.; Camerer, S.; Hunger, D.; Mader, M.; Treutlein, P. Spectroscopy of mechanical dissipation in micro-mechanical membranes. Appl. Phys. Lett. 2011, 99, 143109. [Google Scholar] [CrossRef]
- Inoue, T.; Anno, Y.; Imakita, Y.; Takei, K.; Arie, T.; Akita, S. Resonance Control of a Graphene Drum Resonator in a Nonlinear Regime by a Standing Wave of Light. ACS Omega 2017, 2, 5792–5797. [Google Scholar] [CrossRef] [PubMed]
- Verbridge, S.S.; Shapiro, D.F.; Craighead, H.G.; Parpia, J.M. Macroscopic Tuning of Nanomechanics: Substrate Bending for Reversible Control of Frequency and Quality Factor of Nanostring Resonators. Nano Lett. 2007, 7, 1728–1735. [Google Scholar] [CrossRef] [PubMed]
- St-Gelais, R.; Bernard, S.; Reinhardt, C.; Sankey, J.C. Swept-Frequency Drumhead Optomechanical Resonators. ACS Photon. 2019, 6, 525–530. [Google Scholar] [CrossRef]
- Almog, R.; Zaitsev, S.; Shtempluck, O.; Buks, E. Signal amplification in a nanomechanical Duffing resonator via stochastic resonance. Appl. Phys. Lett. 2007, 90, 013508. [Google Scholar] [CrossRef]
- Antoni, T.; Makles, K.; Braive, R.; Briant, T.; Cohadon, P.F.; Sagnes, I.; Robert-Philip, I.; Heidmann, A. Nonlinear mechanics with suspended nanomembranes. EPL Europhys. Lett. 2012, 100, 68005. [Google Scholar] [CrossRef]
- Thomas, O.; Mathieu, F.; Mansfield, W.; Huang, C.; Trolier-McKinstry, S.; Nicu, L. Efficient parametric amplification in micro-resonators with integrated piezoelectric actuation and sensing capabilities. Appl. Phys. Lett. 2013, 102, 163504. [Google Scholar] [CrossRef]
- Buks, E.; Roukes, M.L. Electrically tunable collective response in a coupled micromechanical array. J. Microelectromech. Syst. 2002, 11, 802–807. [Google Scholar] [CrossRef]
- Sage, E.; Sansa, M.; Fostner, S.; Defoort, M.; Gély, M.; Naik, A.K.; Morel, R.; Duraffourg, L.; Roukes, M.L.; Alava, T.; et al. Single-particle mass spectrometry with arrays of frequency-addressed nanomechanical resonators. Nat. Commun. 2018, 9, 3283. [Google Scholar] [CrossRef] [PubMed]
- Zhao, C.; Zhou, X.; Pandit, M.; Sobreviela, G.; Du, S.; Zou, X.; Seshia, A. Toward High-Resolution Inertial Sensors Employing Parametric Modulation in Coupled Micromechanical Resonators. Phys. Rev. Appl. 2019, 12, 044005. [Google Scholar] [CrossRef]
- Shim, S.B.; Imboden, M.; Mohanty, P. Synchronized Oscillation in Coupled Nanomechanical Oscillators. Science 2007, 316, 95–99. [Google Scholar] [CrossRef] [PubMed]
- Matheny, M.H.; Grau, M.; Villanueva, L.G.; Karabalin, R.B.; Cross, M.C.; Roukes, M.L. Phase Synchronization of Two Anharmonic Nanomechanical Oscillators. Phys. Rev. Lett. 2014, 112, 014101. [Google Scholar] [CrossRef] [PubMed]
- Deng, G.W.; Zhu, D.; Wang, X.H.; Zou, C.L.; Wang, J.T.; Li, H.O.; Cao, G.; Liu, D.; Li, Y.; Xiao, M.; et al. Strongly Coupled Nanotube Electromechanical Resonators. Nano Lett. 2016, 16, 5456–5462. [Google Scholar] [CrossRef] [PubMed]
- Luo, G.; Zhang, Z.Z.; Deng, G.W.; Li, H.O.; Cao, G.; Xiao, M.; Guo, G.C.; Tian, L.; Guo, G.P. Strong indirect coupling between graphene-based mechanical resonators via a phonon cavity. Nat. Commun. 2018, 9, 383. [Google Scholar] [CrossRef] [PubMed]
- Matheny, M.H.; Emenheiser, J.; Fon, W.; Chapman, A.; Salova, A.; Rohden, M.; Li, J.; Hudoba de Badyn, M.; Pósfai, M.; Duenas-Osorio, L.; et al. Exotic states in a simple network of nanoelectromechanical oscillators. Science 2019, 363. [Google Scholar] [CrossRef] [PubMed]
- Bagheri, M.; Poot, M.; Li, M.; Pernice, W.P.H.; Tang, H.X. Dynamic manipulation of nanomechanical resonators in the high-amplitude regime and non-volatile mechanical memory operation. Nat. Nanotechnol. 2011, 6, 726–732. [Google Scholar] [CrossRef] [PubMed]
- Mahboob, I.; Nishiguchi, K.; Okamoto, H.; Yamaguchi, H. Phonon-cavity electromechanics. Nat. Phys. 2012, 8, 503. [Google Scholar] [CrossRef]
- Faust, T.; Rieger, J.; Seitner, M.J.; Kotthaus, J.P.; Weig, E.M. Coherent control of a classical nanomechanical two-level system. Nat. Phys. 2013, 9, 485. [Google Scholar] [CrossRef]
- Okamoto, H.; Gourgout, A.; Chang, C.Y.; Onomitsu, K.; Mahboob, I.; Chang, E.Y.; Yamaguchi, H. Coherent phonon manipulation in coupled mechanical resonators. Nat. Phys. 2013, 9, 480. [Google Scholar] [CrossRef]
- Mahboob, I.; Okamoto, H.; Onomitsu, K.; Yamaguchi, H. Two-Mode Thermal-Noise Squeezing in an Electromechanical Resonator. Phys. Rev. Lett. 2014, 113, 167203. [Google Scholar] [CrossRef] [PubMed]
- Mathew, J.P.; Patel, R.N.; Borah, A.; Vijay, R.; Deshmukh, M.M. Dynamical strong coupling and parametric amplification of mechanical modes of graphene drums. Nat. Nanotechnol. 2016, 11, 747. [Google Scholar] [CrossRef] [PubMed]
- Chen, C.; Zanette, D.H.; Czaplewski, D.A.; Shaw, S.; López, D. Direct observation of coherent energy transfer in nonlinear micromechanical oscillators. Nat. Commun. 2017, 8, 15523. [Google Scholar] [CrossRef] [PubMed]
- Yang, F.; Rochau, F.; Huber, J.S.; Brieussel, A.; Rastelli, G.; Weig, E.M.; Scheer, E. Spatial Modulation of Nonlinear Flexural Vibrations of Membrane Resonators. Phys. Rev. Lett. 2019, 122, 154301. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.Z.; Song, X.X.; Luo, G.; Su, Z.J.; Wang, K.L.; Cao, G.; Li, H.O.; Xiao, M.; Guo, G.C.; Tian, L.; et al. Coherent Phonon Dynamics in Spatially-Separated Graphene Mechanical Resonators. arXiv 2019, arXiv:1909.11311. [Google Scholar]
- Thompson, J.D.; Zwickl, B.M.; Jayich, A.M.; Marquardt, F.; Girvin, S.M.; Harris, J.G.E. Strong dispersive coupling of a high-finesse cavity to a micromechanical membrane. Nature 2008, 452, 72–75. [Google Scholar] [CrossRef] [PubMed]
- Wilson, D.J.; Regal, C.A.; Papp, S.B.; Kimble, H.J. Cavity Optomechanics with Stoichiometric SiN Films. Phys. Rev. Lett. 2009, 103, 207204. [Google Scholar] [CrossRef] [PubMed]
- Purdy, T.P.; Peterson, R.W.; Regal, C.A. Observation of Radiation Pressure Shot Noise on a Macroscopic Object. Science 2013, 339, 801–804. [Google Scholar] [CrossRef] [PubMed]
- Bagci, T.; Simonsen, A.; Schmid, S.; Villanueva, L.G.; Zeuthen, E.; Appel, J.; Taylor, J.M.; Sørensen, A.; Usami, K.; Schliesser, A.; et al. Optical detection of radio waves through a nanomechanical transducer. Nature 2014, 507, 81. [Google Scholar] [CrossRef] [PubMed]
- Andrews, R.W.; Peterson, R.W.; Purdy, T.P.; Cicak, K.; Simmonds, R.W.; Regal, C.A.; Lehnert, K.W. Bidirectional and efficient conversion between microwave and optical light. Nat. Phys. 2014, 10, 321. [Google Scholar] [CrossRef]
- Yuan, M.; Singh, V.; Blanter, Y.M.; Steele, G.A. Large cooperativity and microkelvin cooling with a three-dimensional optomechanical cavity. Nat. Commun. 2015, 6, 8491. [Google Scholar] [CrossRef] [PubMed]
- Xu, H.; Mason, D.; Jiang, L.; Harris, J.G.E. Topological energy transfer in an optomechanical system with exceptional points. Nature 2016, 80, 537. [Google Scholar] [CrossRef] [PubMed]
- Rossi, M.; Mason, D.; Chen, J.; Tsaturyan, Y.; Schliesser, A. Measurement-based quantum control of mechanical motion. Nature 2018, 563, 53–58. [Google Scholar] [CrossRef] [PubMed]
- Nair, B.; Naesby, A.; Dantan, A. Optomechanical characterization of silicon nitride membrane arrays. Opt. Lett. 2017, 42, 1341–1344. [Google Scholar] [CrossRef] [PubMed]
- Piergentili, P.; Catalini, L.; Bawaj, M.; Zippilli, S.; Malossi, N.; Natali, R.; Vitali, D.; Giuseppe, G.D. Two-membrane cavity optomechanics. N. J. Phys. 2018, 20, 083024. [Google Scholar] [CrossRef]
- Gärtner, C.; Moura, J.P.; Haaxman, W.; Norte, R.A.; Gröblacher, S. Integrated Optomechanical Arrays of Two High Reflectivity SiN Membranes. Nano Lett. 2018, 18, 7171–7175. [Google Scholar] [CrossRef] [PubMed]
- Wei, X.; Sheng, J.; Yang, C.; Wu, Y.; Wu, H. Controllable two-membrane-in-the-middle cavity optomechanical system. Phys. Rev. A 2019, 99, 023851. [Google Scholar] [CrossRef]
- Xuereb, A.; Genes, C.; Dantan, A. Strong Coupling and Long-Range Collective Interactions in Optomechanical Arrays. Phys. Rev. Lett. 2012, 109, 223601. [Google Scholar] [CrossRef] [PubMed]
- Xuereb, A.; Genes, C.; Dantan, A. Collectively enhanced optomechanical coupling in periodic arrays of scatterers. Phys. Rev. A 2013, 88, 053803. [Google Scholar] [CrossRef]
- Seok, H.; Buchmann, L.F.; Singh, S.; Meystre, P. Optically mediated nonlinear quantum optomechanics. Phys. Rev. A 2012, 86, 063829. [Google Scholar] [CrossRef]
- Kipf, T.; Agarwal, G.S. Superradiance and collective gain in multimode optomechanics. Phys. Rev. A 2014, 90, 053808. [Google Scholar] [CrossRef]
- Bemani, F.; Motazedifard, A.; Roknizadeh, R.; Naderi, M.H.; Vitali, D. Synchronization dynamics of two nanomechanical membranes within a Fabry-Perot cavity. Phys. Rev. A 2017, 96, 023805. [Google Scholar] [CrossRef]
- Xuereb, A.; Genes, C.; Pupillo, G.; Paternostro, M.; Dantan, A. Reconfigurable Long-Range Phonon Dynamics in Optomechanical Arrays. Phys. Rev. Lett. 2014, 112, 133604. [Google Scholar] [CrossRef] [PubMed]
- Xuereb, A.; Imparato, A.; Dantan, A. Heat transport in harmonic oscillator systems with thermal baths: application to optomechanical arrays. N. J. Phys. 2015, 17, 055013. [Google Scholar] [CrossRef]
- Bhattacharya, M.; Meystre, P. Multiple membrane cavity optomechanics. Phys. Rev. A 2008, 78, 041801. [Google Scholar] [CrossRef]
- Hartmann, M.J.; Plenio, M.B. Steady State Entanglement in the Mechanical Vibrations of Two Dielectric Membranes. Phys. Rev. Lett. 2008, 101, 200503. [Google Scholar] [CrossRef] [PubMed]
- Nielsen, W.H.P.; Tsaturyan, Y.; Møller, C.B.; Polzik, E.S.; Schliesser, A. Multimode optomechanical system in the quantum regime. Proc. Natl. Acad. Sci. USA 2017, 114, 62. [Google Scholar] [CrossRef] [PubMed]
- Patil, Y.S.; Chakram, S.; Chang, L.; Vengalattore, M. Thermomechanical Two-Mode Squeezing in an Ultrahigh-Q Membrane Resonator. Phys. Rev. Lett. 2015, 115, 017202. [Google Scholar] [CrossRef] [PubMed]
- Pontin, A.; Bonaldi, M.; Borrielli, A.; Marconi, L.; Marino, F.; Pandraud, G.; Prodi, G.A.; Sarro, P.M.; Serra, E.; Marin, F. Dynamical Two-Mode Squeezing of Thermal Fluctuations in a Cavity Optomechanical System. Phys. Rev. Lett. 2016, 116, 103601. [Google Scholar] [CrossRef] [PubMed]
- Wu, S.; Sheng, J.; Zhang, X.; Wu, Y.; Wu, H. Parametric excitation of a SiN membrane via piezoelectricity. AIP Adv. 2018, 8, 015209. [Google Scholar] [CrossRef]
- Naserbakht, S.; Naesby, A.; Dantan, A. Electromechanics in vertically coupled nanomembranes. Appl. Phys. Lett. 2019, 115, 061105. [Google Scholar] [CrossRef]
- Naesby, A.; Naserbakht, S.; Dantan, A. Effects of pressure on suspended micromechanical membrane arrays. Appl. Phys. Lett. 2017, 111, 201103. [Google Scholar] [CrossRef]
- Naserbakht, S.; Dantan, A. Squeeze film pressure sensors based on SiN membrane sandwiches. Sens. Actuators A Phys. 2019, 298, 111588. [Google Scholar] [CrossRef]
- Rugar, D.; Grütter, P. Mechanical parametric amplification and thermomechanical noise squeezing. Phys. Rev. Lett. 1991, 67, 699–702. [Google Scholar] [CrossRef] [PubMed]
- Midolo, L.; Schliesser, A.; Fiore, A. Nano-opto-electro-mechanical systems. Nat. Nanotechnol. 2018, 13, 11–18. [Google Scholar] [CrossRef] [PubMed]
- Turner, K.L.; Miller, S.A.; Hartwell, P.G.; MacDonald, N.C.; Strogatz, S.H.; Adams, S.G. Five parametric resonances in a microelectromechanical system. Nature 1998, 396, 149–152. [Google Scholar] [CrossRef]
- Carr, D.W.; Evoy, S.; Sekaric, L.; Craighead, H.G.; Parpia, J.M. Parametric amplification in a torsional microresonator. Appl. Phys. Lett. 2000, 77, 1545–1547. [Google Scholar] [CrossRef]
- Mahboob, I.; Yamaguchi, H. Piezoelectrically pumped parametric amplification and Q enhancement in an electromechanical oscillator. Appl. Phys. Lett. 2008, 92, 173109. [Google Scholar] [CrossRef]
- Karabalin, R.B.; Masmanidis, S.C.; Roukes, M.L. Efficient parametric amplification in high and very high frequency piezoelectric nanoelectromechanical systems. Appl. Phys. Lett. 2010, 97, 183101. [Google Scholar] [CrossRef]
- Seitner, M.J.; Abdi, M.; Ridolfo, A.; Hartmann, M.J.; Weig, E.M. Parametric Oscillation, Frequency Mixing, and Injection Locking of Strongly Coupled Nanomechanical Resonator Modes. Phys. Rev. Lett. 2017, 118, 254301. [Google Scholar] [CrossRef] [PubMed]
- Huber, J.S.; Rastelli, G.; Seitner, M.; Maximilian, J.; Köbl, J.; Belzig, W.; Dykman, M.I.; Weig, E.M. Squeezing of thermal fluctuations in a driven nanomechanical resonator. arXiv 2019, arXiv:1903.07601. [Google Scholar]
- Bothner, D.; Yanai, S.; Iniguez-Rabago, A.; Yuan, M.; Blanter, Y.M.; Steele, G.A. Cavity electromechanics with parametric mechanical driving. arXiv 2019, arXiv:1908.08496. [Google Scholar]
- Szorkovszky, A.; Doherty, A.C.; Harris, G.I.; Bowen, W.P. Mechanical Squeezing via Parametric Amplification and Weak Measurement. Phys. Rev. Lett. 2011, 107, 213603. [Google Scholar] [CrossRef] [PubMed]
- Farace, A.; Giovannetti, V. Enhancing quantum effects via periodic modulations in optomechanical systems. Phys. Rev. A 2012, 86, 013820. [Google Scholar] [CrossRef]
- Szorkovszky, A.; Brawley, G.A.; Doherty, A.C.; Bowen, W.P. Strong Thermomechanical Squeezing via Weak Measurement. Phys. Rev. Lett. 2013, 110, 184301. [Google Scholar] [CrossRef] [PubMed]
- Lemonde, M.A.; Didier, N.; Clerk, A.A. Enhanced nonlinear interactions in quantum optomechanics via mechanical amplification. Nat. Commun. 2016, 7, 11338. [Google Scholar] [CrossRef] [PubMed]
- Levitan, B.A.; Metelmann, A.; Clerk, A.A. Optomechanics with two-phonon driving. N. J. Phys. 2016, 18, 093014. [Google Scholar] [CrossRef]
- Norcada Inc. Available online: www.norcada.com (accessed on 12 November 2019).
- Naesby, A.; Dantan, A. Microcavities with suspended subwavelength structured mirrors. Opt. Express 2018, 26, 29886–29894. [Google Scholar] [CrossRef] [PubMed]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).