Optimization Based on Product and Desirability Functions for Flow Distribution in Multi-Channel Cooling Systems of Power Inverters in Electric Vehicles
Abstract
1. Introduction
2. Numerical Model and Analysis
2.1. Analysis Model and Governing Equations
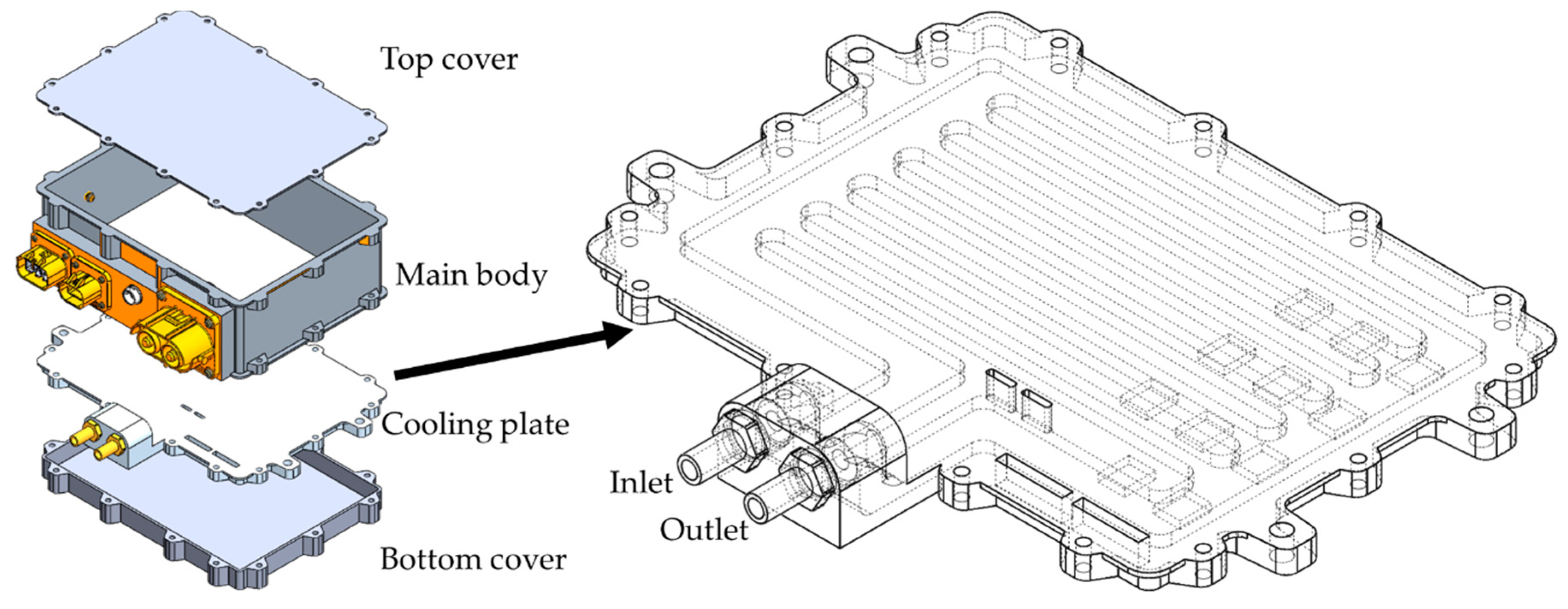
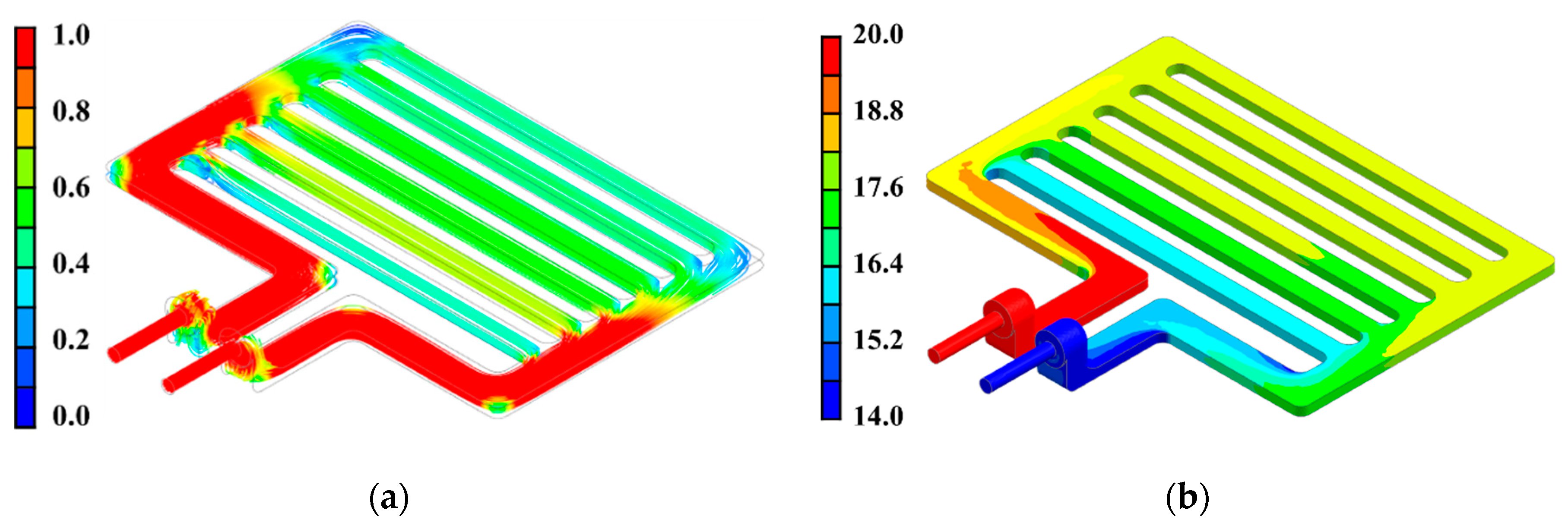
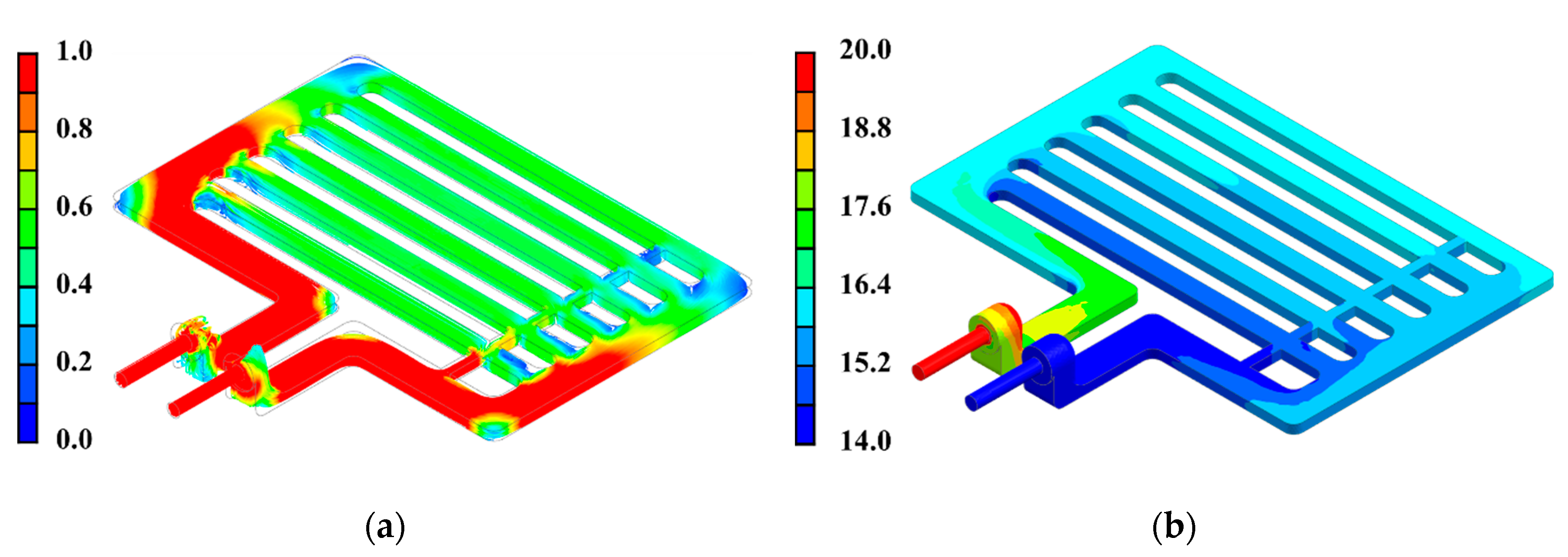
2.2. CFD Analysis of Concept Model and Corresponding Results
3. Optimal OBC Cooling Plate Design and Results
3.1. Experimental Design and Numerical Analysis
3.2. Optimization and Numerical Validation
4. Conclusions
- For the improved prediction accuracy of the optimized approximation values, the product and error distance functions, and normalized functions of the target value to the response were proposed as the optimization functions to ensure target distribution control in each multi-response.
- The effective variables for controlling the distribution of flow rate in each channel of a planar cooling structure include the cooling water inlet volume flow rate, ratio of the width of the rear pipeline to that of the channel, and ratio of the length of the gap between the channel and wall to that of first channel and wall. Among these, the most effective variable was found to be the ratio of the length of the gap between the channel and wall to that of the first channel and wall.
- The product and error distance functions and normalized response functions were applied as the optimization functions to ensure uniform distribution of water in each cooling water channel; it was found that this improved the prediction accuracy of the optimized approximation values.
- The results of surface response optimization using the desirability function with the central composite design approach for our experimental evaluation indicated that the accuracy of optimization could be more significantly improved using a multi-response object function compared with using single-response object functions.
- The proposed method was applied to the cooling system of the OBC/LDC integrated power inverter and was found to be highly effective in controlling uniform flow distribution in each cooling water channel. In particular, the flow uniformity among the different channels using the optimized design was more than or equal to 90% than the initial design model in terms of standard deviation, error distance, and maximum-minimum difference.
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| inlet volume flow rate | |
| length ratio of the gap between the channel and the wall to the first channel | |
| width ratio of the rear pipeline to the channel | |
| desirability function | |
| pressure, Pa | |
| temperature, K | |
| degree of freedom | |
| response for channel i | |
| error distance function | |
| product function | |
| total flow rate | |
| fluid velocity m/s | |
| constant | |
| constant | |
| constant | |
| production of turbulence kinetic energy due to buoyancy, kg/s3-m | |
| production of turbulence kinetic energy due to the mean velocity gradient, kg/s3-m | |
| velocity of inlet, m/s | |
| n | number of responses |
| t | time, s |
| standard deviation | |
| confidence value | |
| dissipation rate of turbulent kinetic energy, m2/s3 | |
| viscosity, Pa-s | |
| density, kg/m3 | |
| turbulent viscosity, Pa-s | |
| turbulent Prandtl number for k | |
| turbulent Prandtl number for ε | |
| importance for response i |
Appendix A
| Trial Run No. | A | B | C | |||
|---|---|---|---|---|---|---|
| Dimension-Less | Unit (mm) | Dimension-Less | Unit (mm) | Dimension-Less | Unit (mm) | |
| 1 | 1.000 | 6.000 | 1.000 | 17.150 | 0.400 | 4.000 |
| 2 | 2.000 | 12.000 | 1.000 | 17.150 | 0.400 | 4.000 |
| 3 | 1.000 | 6.000 | 3.000 | 51.450 | 0.400 | 4.000 |
| 4 | 2.000 | 12.000 | 3.000 | 51.450 | 0.400 | 4.000 |
| 5 | 1.000 | 6.000 | 1.000 | 17.150 | 1.200 | 12.000 |
| 6 | 2.000 | 12.000 | 1.000 | 17.150 | 1.200 | 12.000 |
| 7 | 1.000 | 6.000 | 3.000 | 51.450 | 1.200 | 12.000 |
| 8 | 2.000 | 12.000 | 3.000 | 51.450 | 1.200 | 12.000 |
| 9 | 0.659 | 3.950 | 2.000 | 34.300 | 0.800 | 8.000 |
| 10 | 2.341 | 14.050 | 2.000 | 34.300 | 0.800 | 8.000 |
| 11 | 1.500 | 9.000 | 0.318 | 5.460 | 0.800 | 8.000 |
| 12 | 1.500 | 9.000 | 3.682 | 63.140 | 0.800 | 8.000 |
| 13 | 1.500 | 9.000 | 2.000 | 34.300 | 0.127 | 1.270 |
| 14 | 1.500 | 9.000 | 2.000 | 34.300 | 1.473 | 14.730 |
| 15 | 1.500 | 9.000 | 2.000 | 34.300 | 0.800 | 8.000 |
| Response | Variable | DOF | Sum of Squares | Mean Square Values | F-Value | p-Value |
|---|---|---|---|---|---|---|
| B | 1 | 4.697 | 4.697 | 88.360 | 0.000 | |
| C | 1 | 0.258 | 0.258 | 4.860 | 0.042 | |
| Residuals | 17 | 0.904 | 0.053 | |||
| 0.850 | ||||||
| A | 1 | 0.042 | 0.042 | 5.010 | 0.041 | |
| B | 1 | 0.270 | 0.270 | 31.990 | 0.000 | |
| C | 1 | 0.239 | 0.239 | 28.380 | 0.000 | |
| B × B | 1 | 0.176 | 0.176 | 20.890 | 0.000 | |
| Residuals | 15 | 0.1265 | 0.008 | |||
| 0.850 | ||||||
| B | 1 | 0.006 | 0.006 | 0.300 | 0.592 | |
| B × B | 1 | 0.197 | 0.197 | 9.740 | 0.006 | |
| Residuals | 17 | 0.344 | 0.020 | |||
| 0.370 | ||||||
| B | 1 | 0.137 | 0.137 | 96.240 | 0.000 | |
| C | 1 | 0.048 | 0.048 | 34.040 | 0.000 | |
| B × B | 1 | 0.015 | 0.015 | 10.700 | 0.005 | |
| Residuals | 16 | 0.023 | 0.001 | |||
| 0.90 | ||||||
| A | 1 | 0.018 | 0.018 | 50.220 | 0.000 | |
| B | 1 | 0.371 | 0.371 | 1011.950 | 0.000 | |
| C | 1 | 0.158 | 0.158 | 430.340 | 0.000 | |
| B × B | 1 | 0.151 | 0.1519 | 411.140 | 0.000 | |
| C × C | 1 | 0.003 | 0.003 | 8.700 | 0.011 | |
| B × C | 1 | 0.003 | 0.003 | 9.070 | 0.010 | |
| Residuals | 13 | 0.005 | 0.000 | |||
| 0.990 | ||||||
| A | 1 | 0.039 | 0.039 | 35.240 | 0.000 | |
| B | 1 | 0.558 | 0.558 | 499.670 | 0.000 | |
| C | 1 | 0.223 | 0.223 | 199.340 | 0.000 | |
| B × B | 1 | 0.264 | 0.265 | 236.090 | 0.000 | |
| C × C | 1 | 0.013 | 0.013 | 11.230 | 0.005 | |
| B × C | 1 | 0.005 | 0.005 | 4.490 | 0.054 | |
| Residuals | 13 | 0.015 | 0.001 | |||
| 0.990 | ||||||
| B | 1 | 0.119 | 0.119 | 2.750 | 0.119 | |
| C | 1 | 0.096 | 0.096 | 2.220 | 0.159 | |
| B × B | 1 | 4.128 | 4.128 | 95.410 | 0.000 | |
| C × C | 1 | 0.168 | 0.168 | 3.880 | 0.069 | |
| B × C | 1 | 0.449 | 0.449 | 10.380 | 0.006 | |
| Residuals | 14 | 0.606 | 0.043 | |||
| 0.890 | ||||||
| B | 1 | 0.169 | 0.169 | 13.570 | 0.002 | |
| C | 1 | 0.119 | 0.119 | 9.570 | 0.007 | |
| B × B | 1 | 0.298 | 0.298 | 23.890 | 0.000 | |
| B × C | 1 | 0.138 | 0.138 | 11.020 | 0.005 | |
| Residuals | 15 | 0.187 | 0.012 | |||
| 0.800 | ||||||
References
- Kim, T.H.; Song, H.S.; Lee, B.H.; Lee, C.S.; Kwon, C.S.; Jung, D.Y. Development of the Integrated Power Converter for the Environmentally Friendly Vehicle and Validation of the LDC using Battery HILS. Trans. Korean Inst. Electr. Eng. 2014, 63, 1212–1218. [Google Scholar] [CrossRef]
- Kim, Y.S.; Oh, C.Y.; Sung, W.Y.; Lee, B.K. Topology and Control Scheme of OBC-LDC Integrated Power Unit for Electric Vehicles. IEEE Trans. Power Electron. 2016, 32, 1731–1743. [Google Scholar] [CrossRef]
- Lee, B.K.; Gwak, T.G.; Kim, S.G.; Kim, S.J.; Kim, J.P.; Lee, J.Y. High-efficiency 6.6kW LDC/OBC integration structure for electric vehicles. Korean Inst. Power Electron. 2014, 1, 311–312. [Google Scholar]
- Kim, H.B.; Jeong, J.W.; Bae, S.W.; Kim, J.S. Design and Implementation of 1.8kW Bi-directional LDC with Parallel Control Strategy for Mild Hybrid Electric. Korean Inst. Power Electron. 2017, 22, 75–81. [Google Scholar] [CrossRef][Green Version]
- Lee, I.O. Research on the analysis and improvement of the performance of the phase-shifted full-bridge converter for electric vehicle battery charger applications. Trans. Korean Inst. Power Electron. 2015, 20, 479–490. [Google Scholar] [CrossRef]
- Kim, Y.S.; Oh, C.Y.; Sung, W.Y.; Lee, B.K.; Park, G.C. Optimal design and control of OBC-LDC integrated power unit for electric vehicles. In Proceedings of the 2014 IEEE Applied Power Electronics Conference and Exposition (APEC 2014), Fort Worth, TX, USA, 16 March 2014; pp. 3192–3198. [Google Scholar]
- Ye, B.; Rubel, M.R.H.; Li, H. Design and optimization of cooling plate for battery module of an electric vehicle. Appl. Sci. 2019, 9, 754. [Google Scholar] [CrossRef]
- Brkić, D.; Praks, P. Short overview of early developments of the hardy cross type methods for computation of flow distribution in pipe networks. Appl. Sci. 2019, 9, 2019. [Google Scholar] [CrossRef]
- Yoo, S.Y.; Kim, B.S. A study on the analysis of incompressible and looped flow network using topology constitutive matrix equation. Korean J. Air-Cond. Refrig. Eng. 2010, 22, 573–578. [Google Scholar]
- Kim, B.S.; Yoo, S.Y.; Cho, W.S. Development of analysis program for incompressible looped flow network using constitutive topologic matrix equation. Int. J. Air-Cond. Refrig. 2012, 20, 1–8. [Google Scholar] [CrossRef]
- Niazkar, M.; Afzali, S.H. Analysis of water distribution networks using MATLAB and Excel Spreadsheet: H-Based Methods. Comput. Appl. Eng. Educ. 2017, 25, 129–141. [Google Scholar] [CrossRef]
- Niazkar, M.; Afzali, S.H. Analysis of water distribution networks using MATLAB and Excel Spreadsheet: Q-Based Methods. Comput. Appl. Eng. Educ. 2017, 25, 277–289. [Google Scholar] [CrossRef]
- Moosavian, N.; Jaefarzadeh, M.R. Hydraulic analysis of water supply networks using a modified hardy cross method. Int. J. Eng. Trans. B Appl. 2014, 27, 1331–1338. [Google Scholar] [CrossRef]
- Singh, M.; Kheer, S.K.; Pandita, I.K. Improvement of water distribution networks analysis by topological similarity. Alex. Eng. J. 2016, 55, 1375–1383. [Google Scholar] [CrossRef]
- Noh, J.H.; Lee, H.K.; Ko, D.S.; Hur, D.J. A study on the cooling performance of power converter for eco-friendly vehicle using numerical analysis. J. Comput. Fluid Eng. 2018, 23, 92–101. [Google Scholar] [CrossRef]
- Noh, J.H.; Ko, D.S.; Lee, S.J.; Hur, D.J. Numerical modeling and performance prediction of COS hydrolysis reactor in an integrated gasification fuel cell in terms of thermo-chemical transport phenomena. Appl. Sci. 2018, 8, 1196. [Google Scholar] [CrossRef]
- Park, H.; Yoon, W. Computational fluid dynamics (CFD) modelling and application for sterilization of foods: A review. Processes 2018, 6, 62. [Google Scholar] [CrossRef]
- Ansoni, J.L.; Seleghim, P., Jr. Optimal industrial reactor design: Development of a multiobjective optimization method based on a posteriori performance parameters calculated from CFD flow solutions. Adv. Eng. Softw. 2016, 91, 23–35. [Google Scholar] [CrossRef]
- Li, L.; Cheng, Z.; Lange, C.F. CFD-based optimization of fluid flow product aided by artificial intelligence and design space validation. Math. Probl. Eng. 2018, 1, 1–14. [Google Scholar] [CrossRef]
- Safikhani, H.; Abbassi, A.; Khalkhali, A.; Kalteh, M. Modeling and optimization of nanofluid flow in flat tubes using a combination of CFD and response surface methodology. Heat Transf.-Asian Res. 2014, 44, 377–395. [Google Scholar] [CrossRef]
- Mäkelä, M. Experimental design and response surface methodology in energy applications: A tutorial review. Energy Convers. Manag. 2017, 151, 630–640. [Google Scholar] [CrossRef]
- Jeong, I.J.; Cho, H.W. A weighted mean squared error approach to multiple response surface optimization. J. Korea Acad.-Ind. Coop. Soc. 2013, 14, 625–633. [Google Scholar]
- Lorza, R.; Calvo, M.; Labari, C. Using the multi-response method with desirability functions to optimize the zinc electroplating of steel screws. Metals 2018, 8, 711. [Google Scholar] [CrossRef]
- Jeong, I.J. A posterior preference articulation method to the weighted error minimization approach in multi-response surface optimization. J. Korea Acad.-Ind. Coop. Soc. 2015, 16, 7061–7070. [Google Scholar]
- Mishra, S.K. A brief history of production functions. IUP J. Manag. Econ. 2007, 1, 1–25. [Google Scholar] [CrossRef]
- Chevillard, S. The functions erf and erfc computed with arbitrary precision and explicit error bounds. Inf. Comput. 2012, 216, 72–95. [Google Scholar] [CrossRef]
- Akçay, H.; Anagün, A.S. Multi response optimization application on a manufacturing factor. Math. Comput. Appl. 2013, 18, 531–538. [Google Scholar]
- Seok, W.; Kim, G.H.; Seo, J.; Rhee, S.H. Application of the design of experiments and computational fluid dynamics to bow design improvement. J. Mar. Sci. Eng. 2019, 7, 226. [Google Scholar] [CrossRef]
- Marjavaara, D.; Lundström, S. Response surface-based shape optimization of a Francis draft tube. Int. J. Numer. Methods Heat Fluid Flow 2007, 17, 34–45. [Google Scholar] [CrossRef]
- Wang, K.; Chen, Z. Stepwise regression and all possible subsets regression in education. Electron. Int. J. Educ. Arts Sci. 2016, 2, 60–81. [Google Scholar]



| Function | Parameter | Specification | Unit |
|---|---|---|---|
| Charging (OBC) | Input Voltage | 85~265 | V, AC |
| Input Current | 32 | A | |
| Output Current | 20 | A, DC | |
| Output Power | 7.2 | kW | |
| Power density | 1.44 | kW/L | |
| Inverter (Bidirectional) | Input Voltage | 240~450 | V, DC |
| Output Voltage | 85~265 | V, AC | |
| Output Power | 3.3 | kW | |
| Size | 250 × 180 × 110 | mm |
| Channel | Pressure [kPa] | Velocity [m/s] | Volume Flow [m3/s] | Volume Flow Distribution [%] | Normalized Volume FlowDistribution N [%] |
|---|---|---|---|---|---|
| R1 | 16.198 | 0.396 | 0.020 | 13.187 | 0.791 |
| R2 | 17.200 | 0.667 | 0.033 | 22.223 | 1.333 |
| R3 | 17.676 | 0.579 | 0.029 | 19.315 | 1.159 |
| R4 | 17.932 | 0.493 | 0.025 | 16.442 | 0.987 |
| R5 | 18.074 | 0.442 | 0.022 | 14.739 | 0.884 |
| R6 | 18.108 | 0.423 | 0.021 | 14.094 | 0.846 |
| 0.734 | 0.104 | 0.005 | 3.475 | 0.208 | |
| MM | 1.910 | 0.271 | 0.014 | 9.036 | 0.542 |
| MM Ratio [%] | 10.95 | 54.200 | 54.200 | - | - |
| Variables | Limit | |||
|---|---|---|---|---|
| Dimensionless | SI Units (mm, LPM) | |||
| Lower | Upper | Lower | Upper | |
| A | 1.000 | 2.000 | 6.000 | 12.000 |
| B | 1.000 | 3.000 | 17.150 | 51.450 |
| C | 0.400 | 1.200 | 4.000 | 12.000 |
| Case | Fluid Flow Volume Distribution [Ratio] | SD | Distance Error Function Value | Product Function Value | |||||
|---|---|---|---|---|---|---|---|---|---|
| σ | |||||||||
| 1 | 0.494 | 1.139 | 1.100 | 1.077 | 1.083 | 1.107 | 0.249 | 0.556 | 0.201 |
| 2 | 0.343 | 1.077 | 1.081 | 1.105 | 1.166 | 1.228 | 0.327 | 0.731 | 0.368 |
| 3 | 1.840 | 0.716 | 0.924 | 0.862 | 0.831 | 0.826 | 0.417 | 0.933 | 0.28 |
| 4 | 1.829 | 0.619 | 0.904 | 0.875 | 0.877 | 0.895 | 0.420 | 0.940 | 0.297 |
| 5 | 0.093 | 0.881 | 1.062 | 1.222 | 1.336 | 1.405 | 0.483 | 1.080 | 0.800 |
| 6 | 0.077 | 0.729 | 0.989 | 1.239 | 1.425 | 1.540 | 0.539 | 1.206 | 0.849 |
| 7 | 1.669 | 0.499 | 0.888 | 0.949 | 0.987 | 1.008 | 0.378 | 0.845 | 0.302 |
| 8 | 1.653 | 0.330 | 0.844 | 0.978 | 1.070 | 1.124 | 0.429 | 0.959 | 0.458 |
| 9 | 1.341 | 0.894 | 0.980 | 0.942 | 0.918 | 0.924 | 0.170 | 0.379 | 0.061 |
| 10 | 1.214 | 0.728 | 0.934 | 0.989 | 1.037 | 1.098 | 0.164 | 0.368 | 0.07 |
| 11 | 0.668 | 0.524 | 0.262 | 1.154 | 1.574 | 1.819 | 0.617 | 1.380 | 0.697 |
| 12 | 1.872 | 0.37 | 0.833 | 0.924 | 0.976 | 1.025 | 0.488 | 1.092 | 0.467 |
| 13 | 1.594 | 1.047 | 1.003 | 0.848 | 0.765 | 0.744 | 0.316 | 0.706 | 0.192 |
| 14 | 1.079 | 0.633 | 0.937 | 1.052 | 1.125 | 1.173 | 0.196 | 0.439 | 0.112 |
| 15 | 1.247 | 0.774 | 0.949 | 0.977 | 1.004 | 1.048 | 0.153 | 0.343 | 0.058 |
| Type | A | Regression Equation |
|---|---|---|
| Fluid volume ratio of channel | 0.05 | = 0.265 + 0.5865 B - 0.344 C |
| = 1.091 − 0.1113 A + 0.2977 B − 0.3310 C − 0.1096 B xB | ||
| = 0.495 + 0.484 B − 0.1159 B*B | ||
| = 1.1919 − 0.2287 B + 0.1487 C + 0.03217 B*B | ||
| = 1.2713 + 0.0734 A − 0.5312 B + 0.5188 C + 0.10178 B*B − 0.0925 C*C − 0.0510 B*C | ||
| = 1.3471 + 0.1073 A − 0.6903 B + 0.738 C + 0.13456 B*B − 0.1834 C*C − 0.0626 B*C | ||
| EFV | = 0.123 − 0.419 B + 0.889 C + 0.1425 B*B − 0.3278 B*C | |
| MFV | = 1.775 − 1.750 B + 0.320 C + 0.5325 B*B + 0.672 C*C − 0.592 B*C |
| Case | Object Function Type | Object Function | Target | A | B | C | Composite Desirability |
|---|---|---|---|---|---|---|---|
| M1 | Single Function | 0.000 | - | 2.000 | 0.6437 | 0.9549 | |
| M2 | 0.000 | - | 1.1939 | 0.3498 | 1.0000 | ||
| M3 | Multiple Function | – | 1.000 | 1.067 | 1.6433 | 0.6573 | 0.9603 |
| M4 | –, | 1.000, 0.000 | 1.016 | 1.6717 | 0.6844 | 0.9430 | |
| M5 | –, | 1.000, 0.000 | 1.424 | 1.4579 | 0.4498 | 0.9765 | |
| M6 | –, , | 1.000, 0.000, 0.000 | 1.407 | 1.5607 | 0.5257 | 0.9411 |
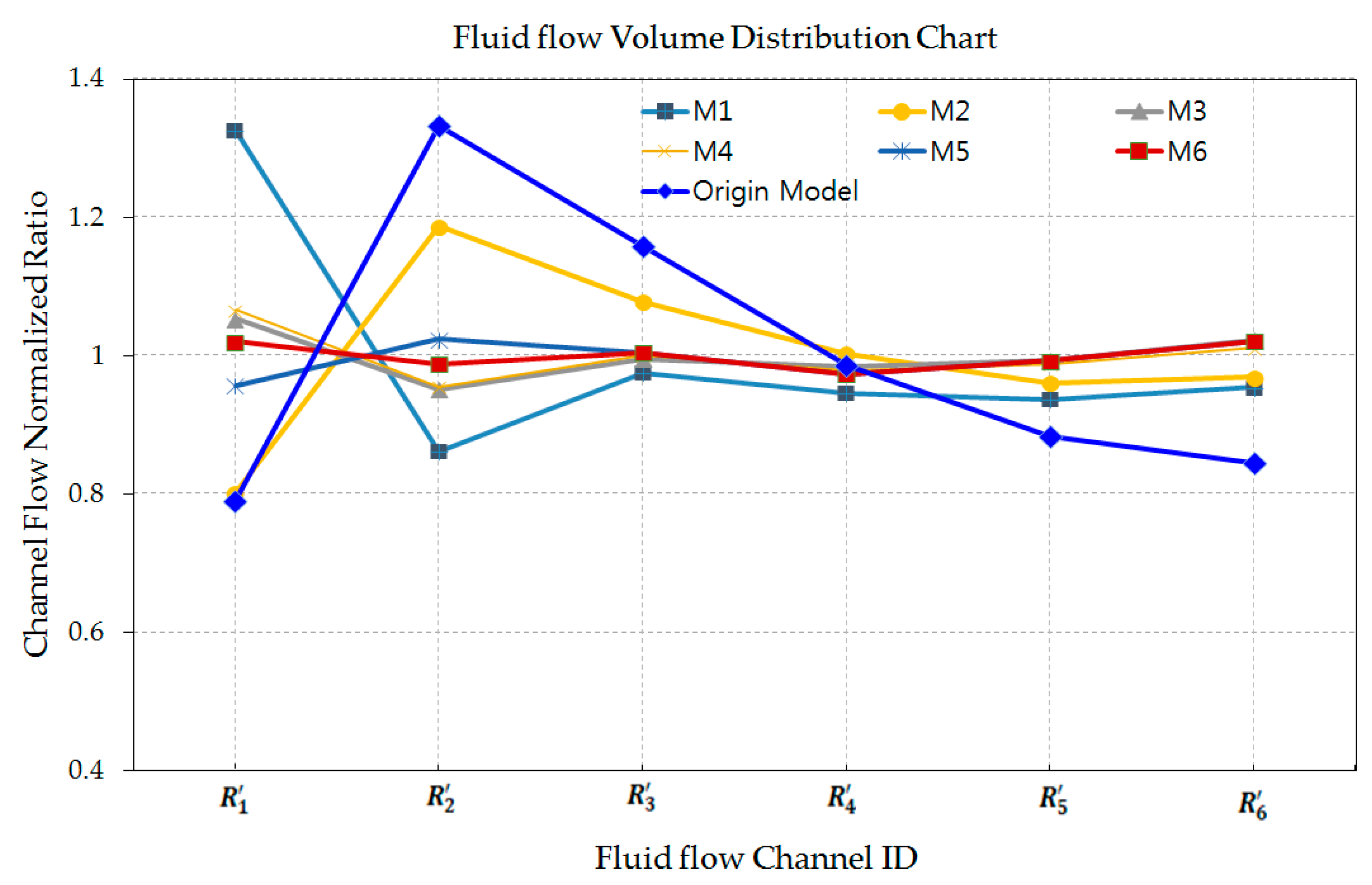
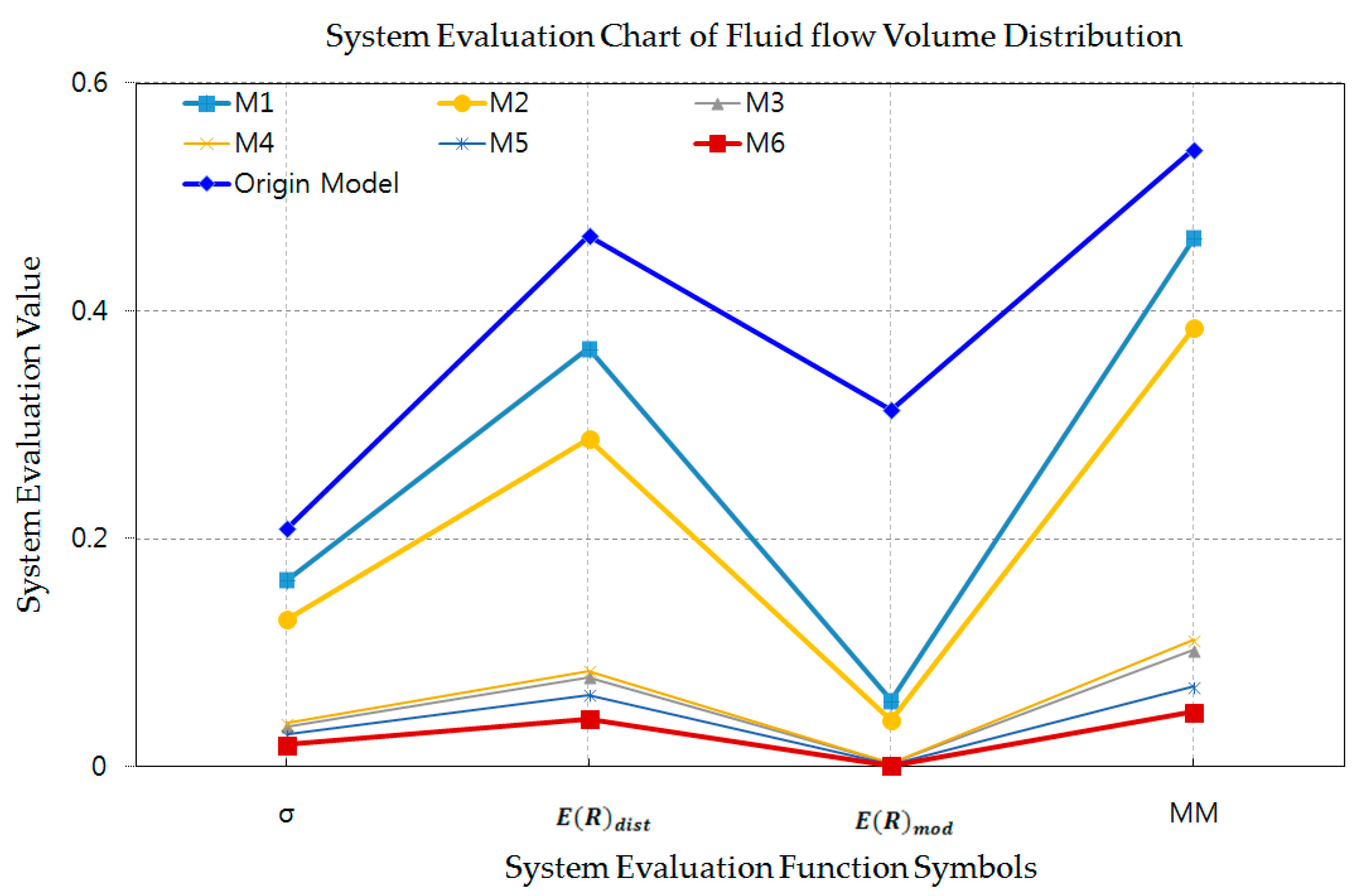
| Case | Fluid Flow Volume Distribution [Ratio] | SD | EFV | MFV | Max-Min | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| σ | MM | |||||||||
| M1 | 1.326 | 0.862 | 0.975 | 0.946 | 0.937 | 0.954 | 0.164 | 0.367 | 0.058 | 0.464 |
| M2 | 0.802 | 1.187 | 1.078 | 1.003 | 0.961 | 0.969 | 0.129 | 0.288 | 0.041 | 0.385 |
| M3 | 1.053 | 0.951 | 0.995 | 0.984 | 0.994 | 1.023 | 0.035 | 0.078 | 0.003 | 0.102 |
| M4 | 1.066 | 0.955 | 1.001 | 0.979 | 0.988 | 1.011 | 0.038 | 0.084 | 0.003 | 0.111 |
| M5 | 0.957 | 1.024 | 1.005 | 0.973 | 0.993 | 1.021 | 0.028 | 0.063 | 0.002 | 0.070 |
| M6 | 1.020 | 0.988 | 1.005 | 0.973 | 0.993 | 1.021 | 0.019 | 0.042 | 0.001 | 0.048 |
| Origin Model | 0.791 | 1.333 | 1.159 | 0.986 | 0.884 | 0.845 | 0.209 | 0.466 | 0.313 | 0.542 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hur, D.-J.; Jeong, S.-H.; Song, S.-I.; Noh, J.-H. Optimization Based on Product and Desirability Functions for Flow Distribution in Multi-Channel Cooling Systems of Power Inverters in Electric Vehicles. Appl. Sci. 2019, 9, 4844. https://doi.org/10.3390/app9224844
Hur D-J, Jeong S-H, Song S-I, Noh J-H. Optimization Based on Product and Desirability Functions for Flow Distribution in Multi-Channel Cooling Systems of Power Inverters in Electric Vehicles. Applied Sciences. 2019; 9(22):4844. https://doi.org/10.3390/app9224844
Chicago/Turabian StyleHur, Deog-Jae, Suk-Hwan Jeong, Seong-Il Song, and Jung-Hun Noh. 2019. "Optimization Based on Product and Desirability Functions for Flow Distribution in Multi-Channel Cooling Systems of Power Inverters in Electric Vehicles" Applied Sciences 9, no. 22: 4844. https://doi.org/10.3390/app9224844
APA StyleHur, D.-J., Jeong, S.-H., Song, S.-I., & Noh, J.-H. (2019). Optimization Based on Product and Desirability Functions for Flow Distribution in Multi-Channel Cooling Systems of Power Inverters in Electric Vehicles. Applied Sciences, 9(22), 4844. https://doi.org/10.3390/app9224844





