Classification of Factors Affecting the Performance of Fully Grouted Rock Bolts with Empirical Classification Systems
Abstract
1. Introduction
2. Materials and Methods
2.1. Rock-Mass Classification System and Rock-Bolt Design
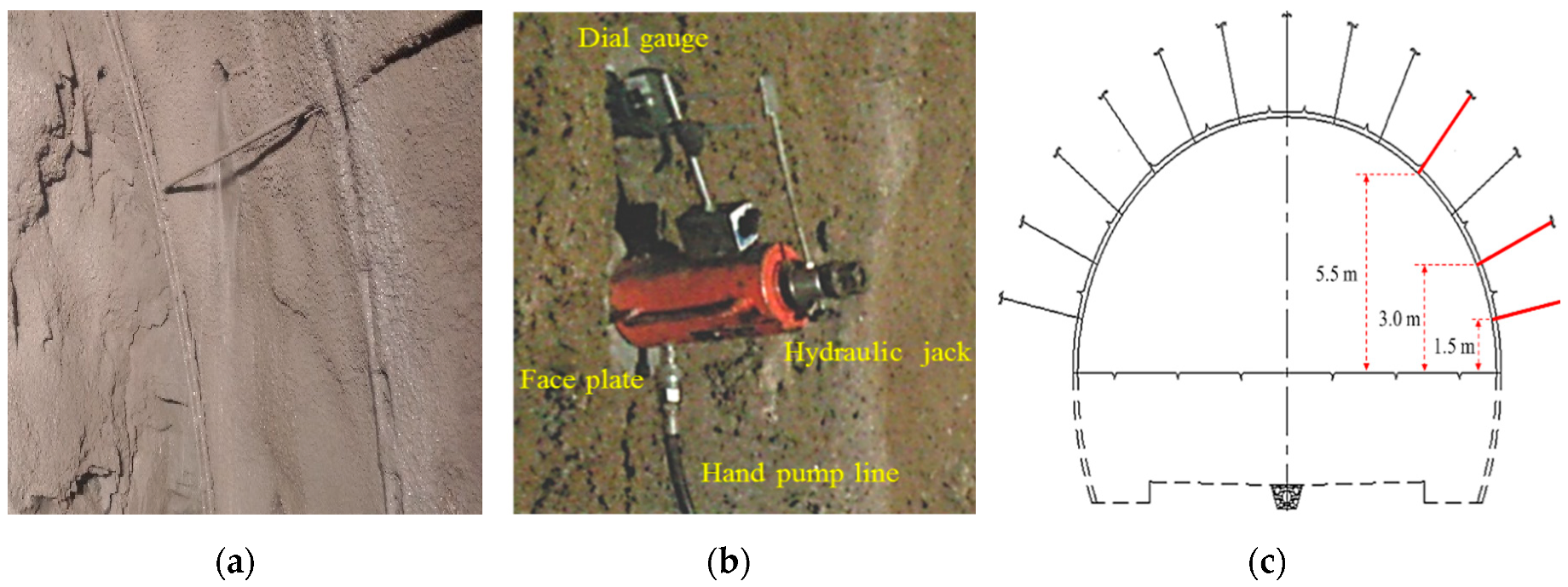
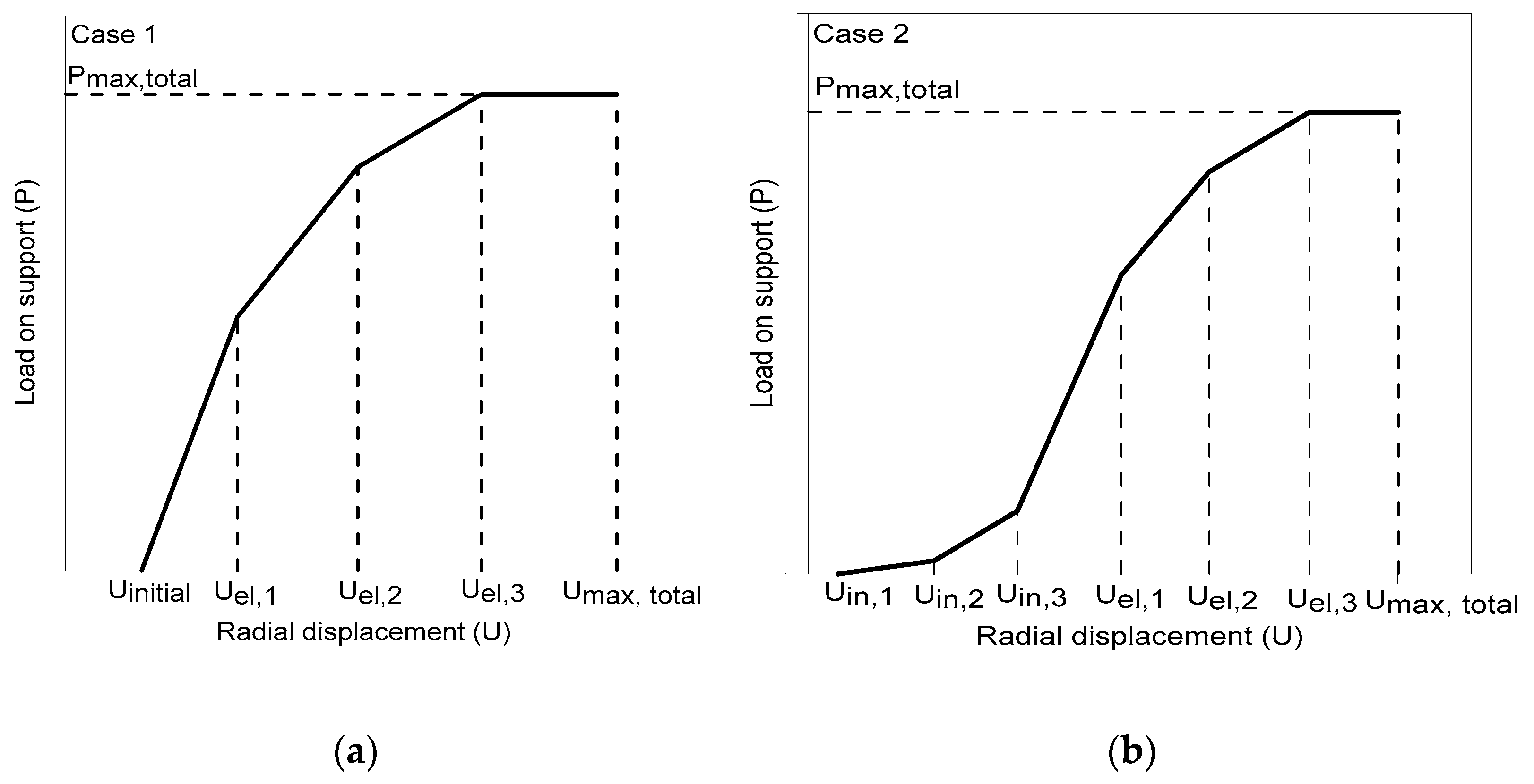
2.2. Field Test Details
3. Results
3.1. Factors Affecting the Performance of Fully Grouted Rock Bolts
- Continuously mechanically coupled (CMC);
- Continuously frictionally coupled (CFC);
- Discretely mechanically or frictionally coupled (DMFC).
3.1.1. Rock-Bolt-Related Factors
Type and Shape
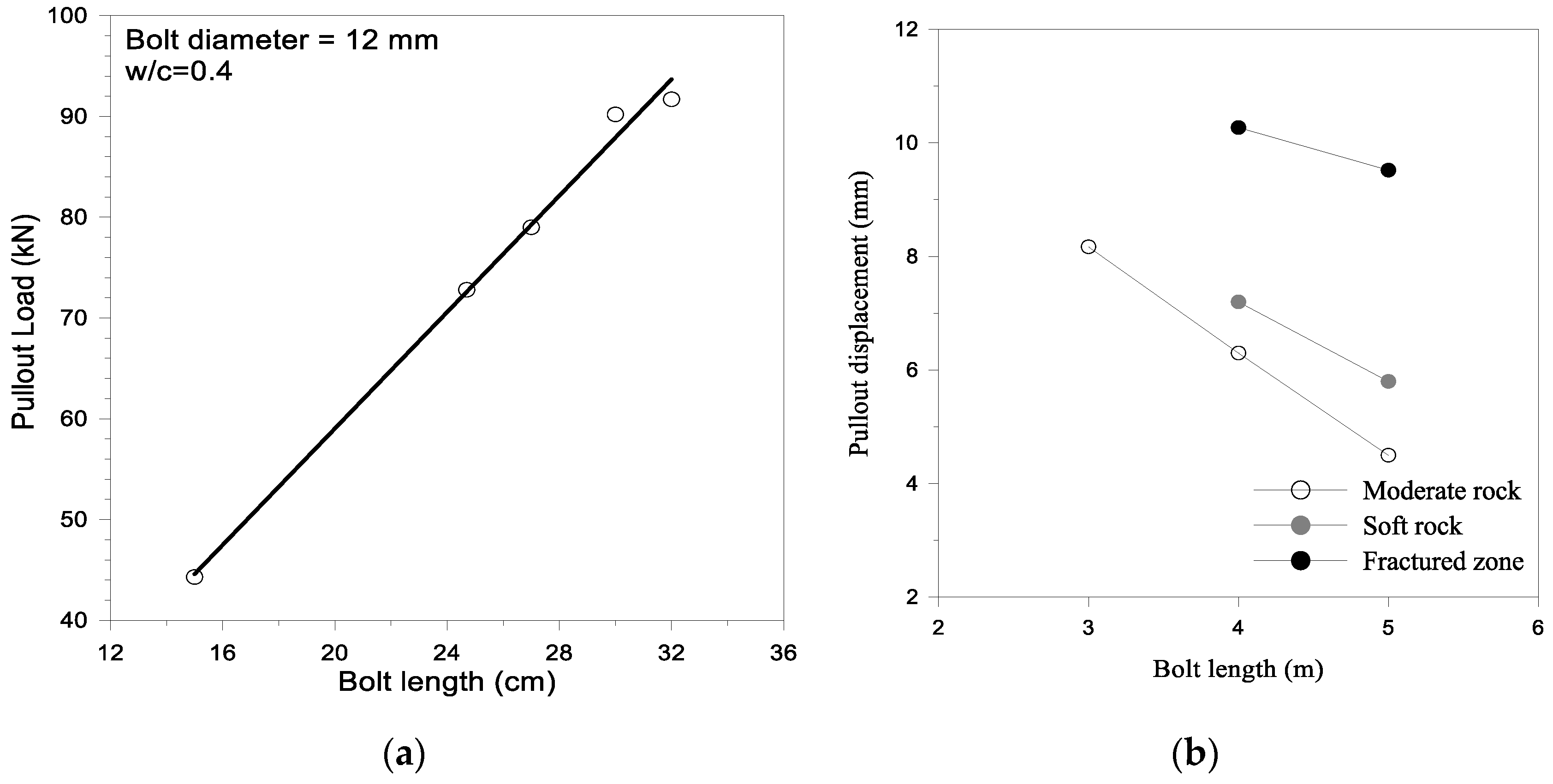
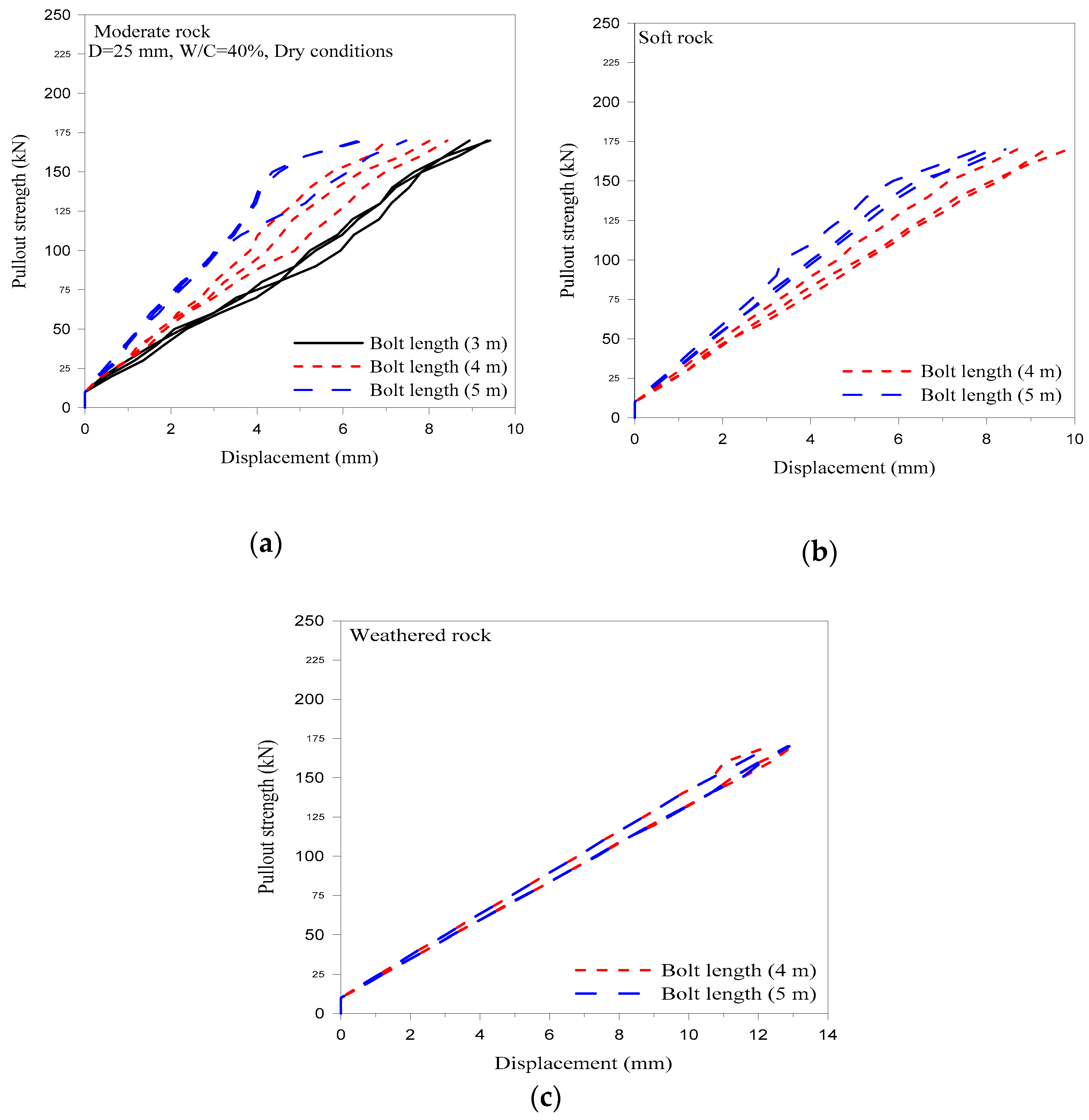
Effect of Rock-Bolt Length
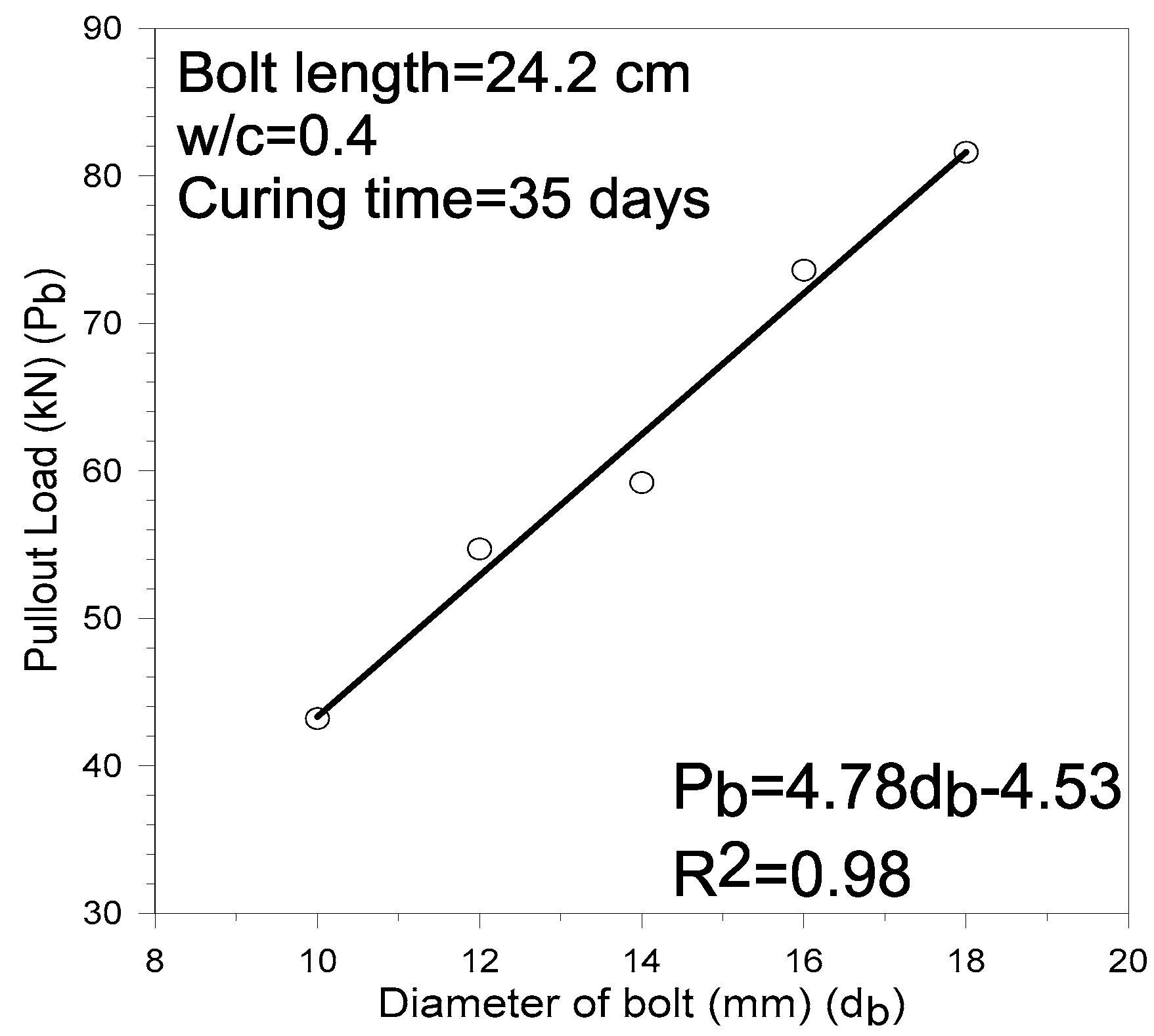
Effect of Bolt and Hole Diameter
Face Plate
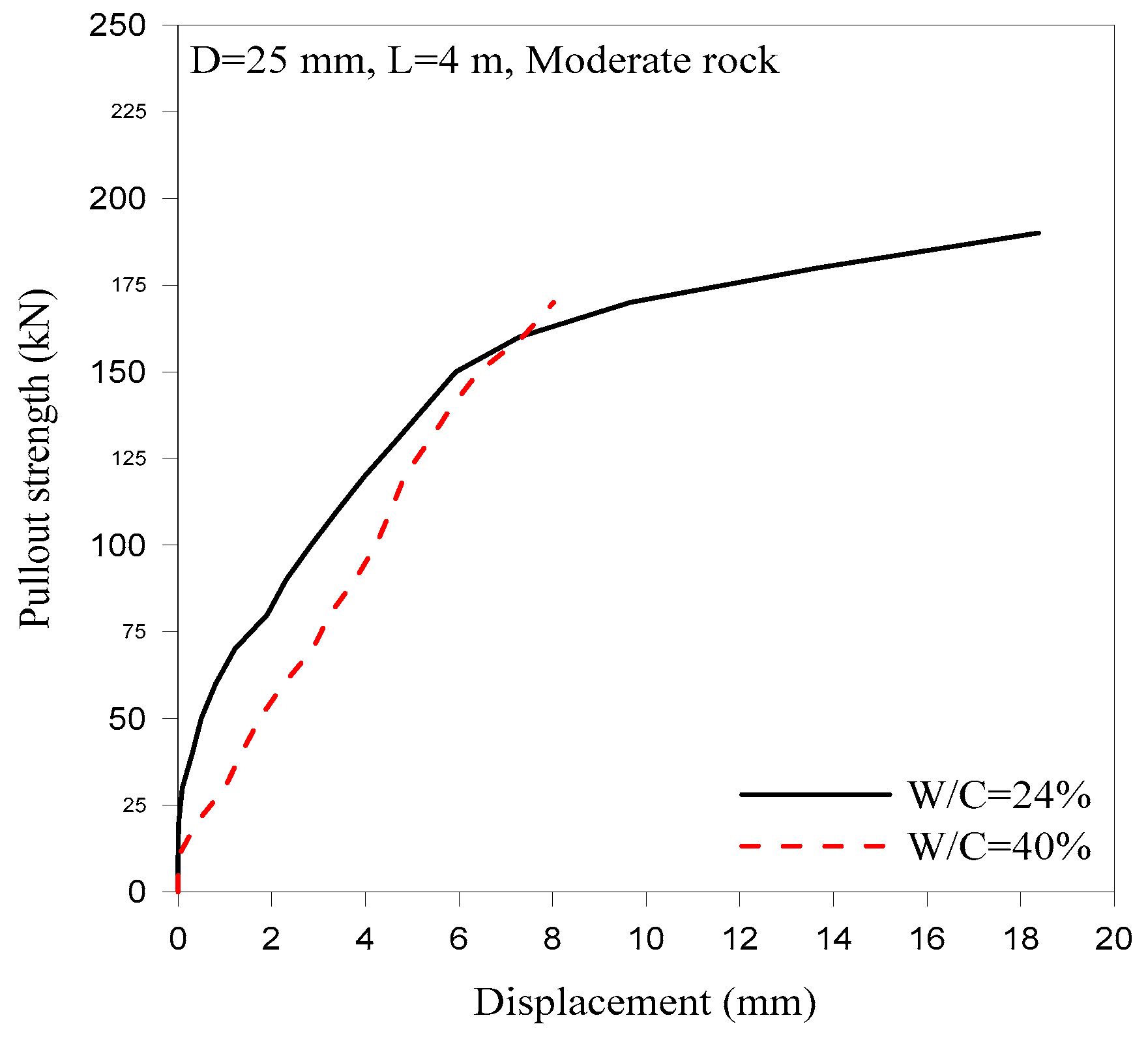
3.1.2. Effect of Grout Properties and Thickness
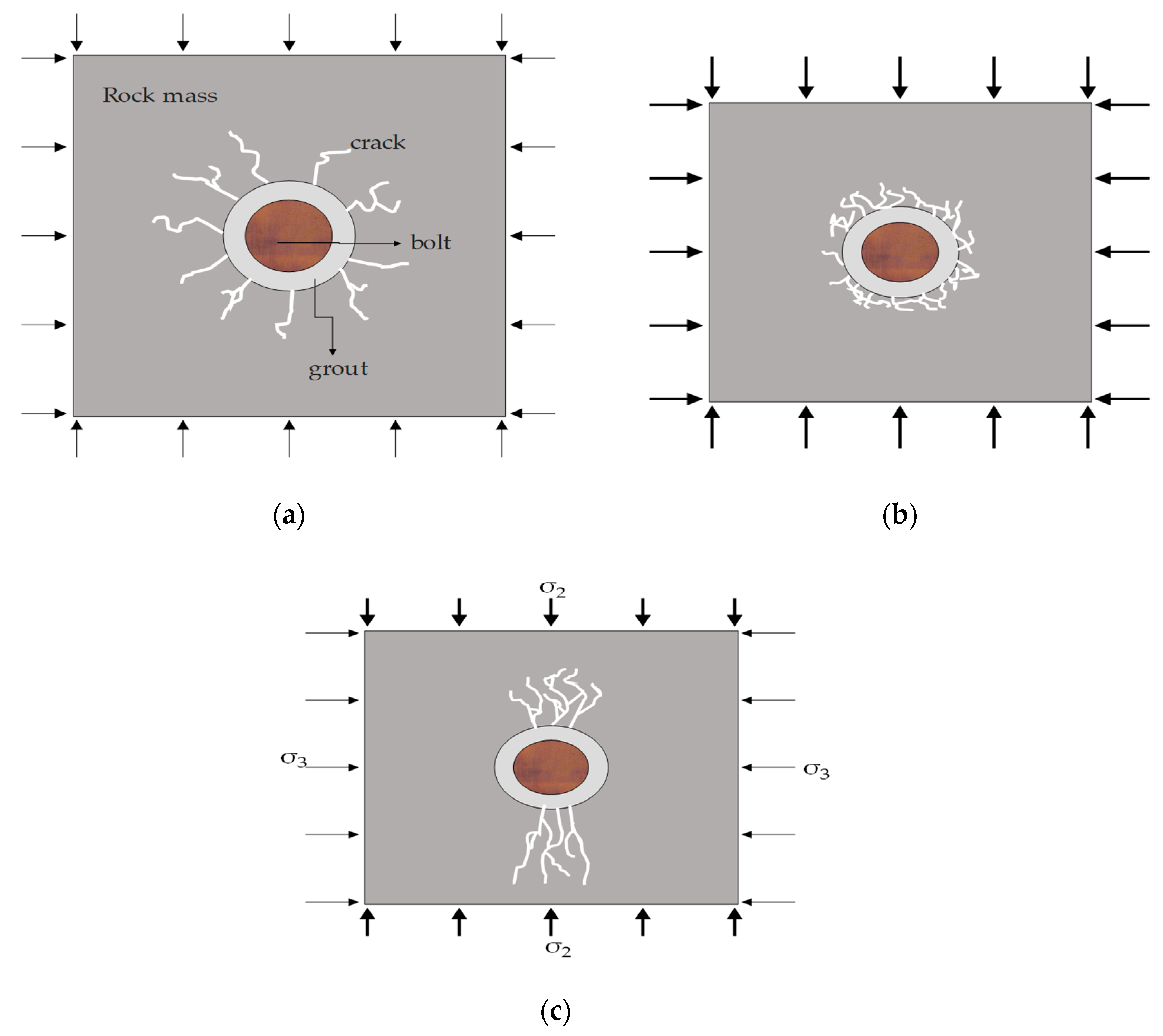
3.1.3. Effect of Stresses
In-Situ Stresses
Induced Stresses
Dynamic Loading
3.1.4. Factors Associated with Installation
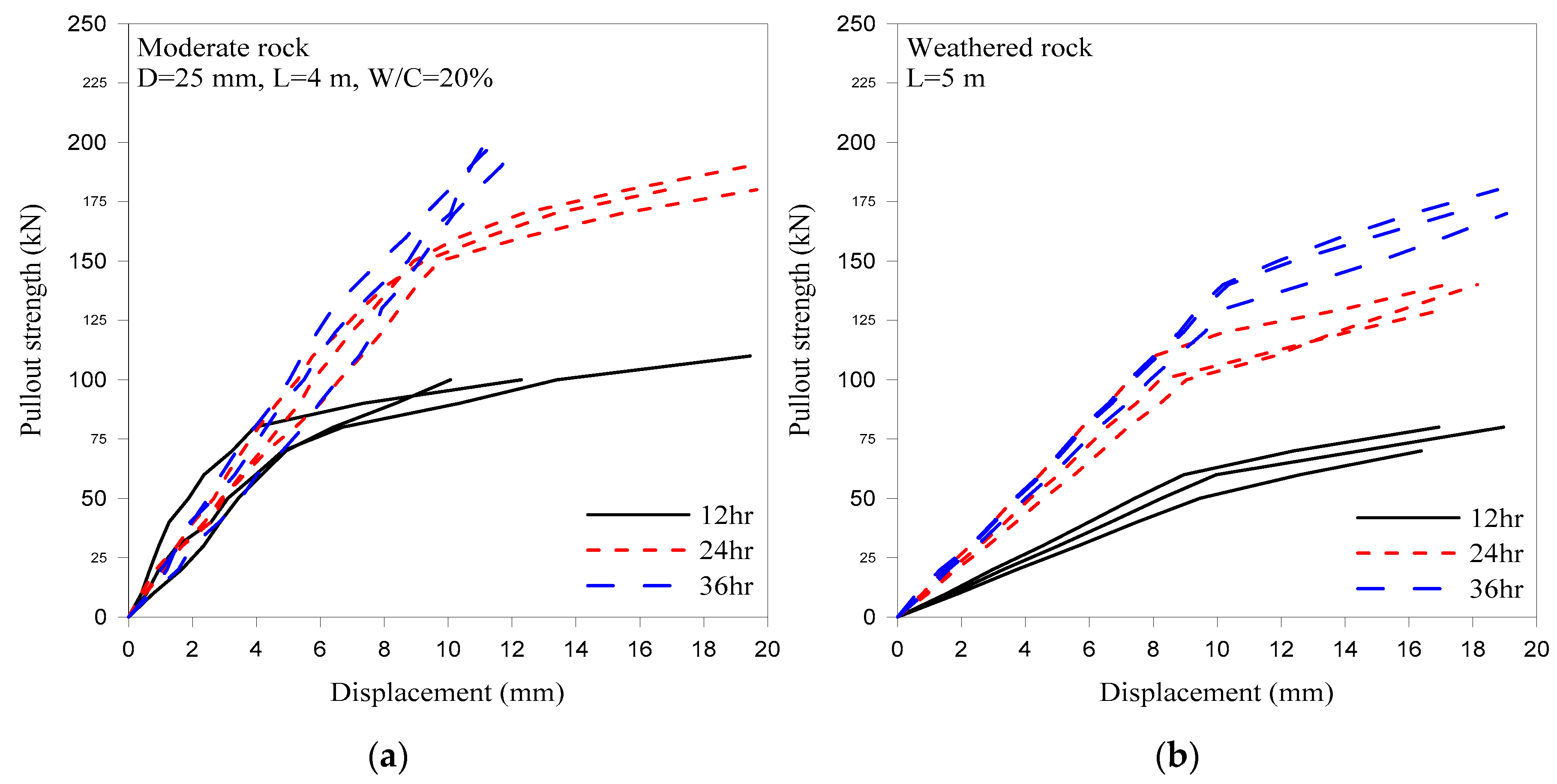
Time of Installation
Effect of Tension
Inclination with Joint
Composite Response
3.1.5. Effect of Rock-Mass Type on the Performance of Fully Grouted Rock Bolt
4. Discussion
5. Conclusions
- The empirical rock-mass classification system proposed 20 mm, fully grouted rock-bolt patterns during tunnel-support design, which is a function of the rock-mass quality and tunnel span. The performance of the rock bolts depends on the efficient load-transfer mechanism, which is determined through the rock-bolt pull-out test.
- Based on the rock-bolt pull-out test, the factors affecting their performance are divided into five groups, and each group is further subdivided, and the effect of pull-out test results is discussed.
- Certain factors, such as rock-mass quality, ground water flow, and stresses, cannot be controlled. As the rock-mass quality decreases, the length effect also decreases in the rock-bolt pull-out test due to the weak bond between the grout and drilled hole’s periphery. In the case of groundwater, inflated steel-tube rock bolts have better performance than fully grouted rock bolts.
- Some parameters are critical for the safe and economic performance of the bolts, i.e., water–cement ratio, rock-bolt length, and time of support installation, and they should be considered in the design of the rock-bolt pattern during underground construction.
- The overall performance of rock bolts in terms of pull-out strength is good in rock mass that is good quality, irrespective of their installation location along the tunnel periphery.
- For the economical and efficient performance of fully grouted rock bolts, the factors investigated in this study should be considered, along with the empirical support patterns using rock-mass classification systems.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bieniawski, Z. Engineering classification of jointed rock masses. Civ. Eng. S. Afr. 1973, 15, 333–343. [Google Scholar]
- Bieniawski, Z.T. Engineering Rock Mass Classifications: A Complete Manual for Engineers and Geologists in Mining, Civil, and Petroleum Engineering; John Wiley & Sons: Hoboken, NJ, USA, 1989. [Google Scholar]
- Barton, N.; Lien, R.; Lunde, J. Engineering classification of rock masses for the design of tunnel support. Rock Mech. 1974, 6, 189–236. [Google Scholar] [CrossRef]
- Grimstad, E.; Barton, N. Updating the Q-System for NMT. In Proceedings of the International Symposium on Sprayed Concrete-Modern Use of Wet Mix Sprayed Concrete for Underground Support, Oslo, Norway, 22–26 October 1993; Norwegian Concrete Association: Oslo, Norway, 1993. [Google Scholar]
- Barton, N. Some new q-value correlations to assist in site characterisation and tunnel design. Int. J. Rock Mech. Min. Sci. 2002, 39, 185–216. [Google Scholar] [CrossRef]
- Palmstrom, A. Rmi-A Rock Mass Characterization System for Rock Engineering Purposes. Ph.D. Thesis, University of Oslo, Oslo, Norway, 1995. [Google Scholar]
- Palmström, A. Recent developments in rock support estimates by the rmi. J. Rock Mech. Tunn. Technol. 2000, 6, 1–19. [Google Scholar]
- Rehman, H.; Naji, A.; Kim, J.-J.; Yoo, H.-K. Empirical evaluation of rock mass rating and tunneling quality index system for tunnel support design. Appl. Sci. 2018, 8, 782. [Google Scholar] [CrossRef]
- Kim, J.; Rehman, H.; Ali, W.; Naji, A.M.; Yoo, H. Weightage effect during back-calculation of rock-mass quality from the installed tunnel support in rock-mass rating and tunneling quality index system. Appl. Sci. 2019, 9, 2065. [Google Scholar] [CrossRef]
- Lowson, A.; Bieniawski, Z. Critical assessment of rmr based tunnel design practices: A practical engineer’s approach. In Proceedings of the SME, Rapid Excavation and Tunnelling Conference, Washington, DC, USA, 23–26 June 2013; pp. 180–198. [Google Scholar]
- NGI. The Q-System, Rock Mass Classification and Support Design. Available online: https://www.ngi.no/eng/Publications-and-library/Books/Q-system (accessed on 9 April 2018).
- Windsor, C. Rock reinforcement systems. Int. J. Rock Mech. Min. Sci. 1997, 34, 919–951. [Google Scholar] [CrossRef]
- Lee, J.; Rehman, H.; Naji, A.; Kim, J.-J.; Yoo, H.-K. An empirical approach for tunnel support design through q and rmi systems in fractured rock mass. Appl. Sci. 2018, 8, 2659. [Google Scholar] [CrossRef]
- Rehman, H.; Naji, A.M.; Kim, J.-J.; Yoo, H. Extension of tunneling quality index and rock mass rating systems for tunnel support design through back calculations in highly stressed jointed rock mass: An empirical approach based on tunneling data from himalaya. Tunn. Undergr. Space Technol. 2019, 85, 29–42. [Google Scholar] [CrossRef]
- Palmstrom, A.; Broch, E. Use and misuse of rock mass classification systems with particular reference to the q-system. Tunn. Undergr. Space Technol. 2006, 21, 575–593. [Google Scholar] [CrossRef]
- Rehman, H.; Naji, A.; Ali, W.; Kim, J.; Abdullah, R.; Yoo, H. Support Design for the Diversion Tunnel of Diamer Basha Dam, Pakistan, Considering The Recent Developments in Empirical Systems; IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2019; p. 012033. [Google Scholar]
- Bieniawski, R.Z.; Aguado, D.; Celada, B.; Rodriquez, A. Forecasting tunnelling behaviour. T T Int. 2011, 39–42. [Google Scholar]
- ASTMD-13e1. Standard Test Method for Rock Bolt Anchor Pull Test; ASTM International: West Conshohocken, PA, USA, 2013. [Google Scholar]
- Dolinar, D.R.; Bhatt, S.K. Trends in roof bolt application. In Proceedings: New Technology for Coal Mine Roof Support; NIOSH: Cincinnat, Hamilton, 2000; pp. 43–51. [Google Scholar]
- Moosavi, M.; Jafari, A.; Khosravi, A. Bond of cement grouted reinforcing bars under constant radial pressure. Cem. Concr. Compos. 2005, 27, 103–109. [Google Scholar] [CrossRef]
- Li, C. A practical problem with threaded rebar bolts in reinforcing largely deformed rock masses. Rock Mech. Rock Eng. 2007, 40, 519–524. [Google Scholar] [CrossRef]
- Li, C.C. A new energy-absorbing bolt for rock support in high stress rock masses. Int. J. Rock Mech. Min. Sci. 2010, 47, 396–404. [Google Scholar]
- Li, C.C.; Stjern, G.; Myrvang, A. A review on the performance of conventional and energy-absorbing rockbolts. J. Rock Mech. Geotech. Eng. 2014, 6, 315–327. [Google Scholar] [CrossRef]
- Kılıc, A.; Yasar, E.; Atis, C. Effect of bar shape on the pull-out capacity of fully-grouted rockbolts. Tunn. Undergr. Space Technol. 2003, 18, 1–6. [Google Scholar] [CrossRef]
- Aziz, N. Bolt surface profiles—An important parameter in load transfer capacity appraisal, Ground Support in Mining and Underground Construction. In Proceedings of the Fifth International Symposium on Ground Support, Perth, Australia, 28–30 September 2004; Taylor & Francis: London, UK, 2004; p. 396. [Google Scholar]
- Barley, A.D.; Windsor, C.R. Recent advances in ground anchor and ground reinforcement technology with reference to the development of the art. In Proceedings of the ISRM International Symposium, 19–24 November 2000; International Society for Rock Mechanics: Lisboa, Portugal, 2000. [Google Scholar]
- Ito, F.; Nakahara, F.; Kawano, R.; Kang, S.-S.; Obara, Y. Visualization of failure in a pull-out test of cable bolts using x-ray ct. Constr. Build. Mater. 2001, 15, 263–270. [Google Scholar] [CrossRef]
- Satola, I. The Axial Load-Displacement Behavior of Steel Strands Used in Rock Reinforcement; Helsinki University of Technology: Espoo, Finland, 2007. [Google Scholar]
- Aziz, N.; Webb, B. Study of load transfer capacity of bolts using short encapsulation push test. In Proceedings of the 2003 Coal Operators, Wollongong, Austrália, 12–14 February 2003. [Google Scholar]
- Signer, S.P. Field Verification of Load-Transfer Mechanics of Fully Grouted Roof Bolts; Bureau of Mines: Pittsburgh, PA, USA, 1990. [Google Scholar]
- Jalalifar, H. A new approach in determining the load transfer mechanism in fully grouted bolts. Ph.D. Thesis, University of Wollongong, Wollongong, Austrália, 2006. [Google Scholar]
- Tao, W.; Chen, C.; Jun, H.; Ting, R. Effect of bolt rib spacing on load transfer mechanism. Int. J. Min. Sci. Technol. 2017, 27, 431–434. [Google Scholar] [CrossRef]
- Osgoui, R.R.; Ünal, E. An empirical method for design of grouted bolts in rock tunnels based on the geological strength index (gsi). Eng. Geol. 2009, 107, 154–166. [Google Scholar] [CrossRef]
- Goris, J. Laboratory evaluation of cable bolt supports. In Proceedings of the 92nd Annual General Meeting of the CIM, Ottawa, ON, Canada, 6–10 May 1990. [Google Scholar]
- Benmokrane, B.; Chennouf, A.; Mitri, H. Laboratory evaluation of cement-based grouts and grouted rock anchors. In International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts; Elsevier: Amsterdam, The Netherlands, 1995; pp. 633–642. [Google Scholar]
- Kılıc, A.; Yasar, E.; Celik, A.G. Effect of grout properties on the pull-out load capacity of fully grouted rock bolt. Tunn. Undergr. Space Technol. 2002, 17, 355–362. [Google Scholar] [CrossRef]
- Kilic, A.; Anil, M. The effects of grout properties to the bolt capacity. In Proceedings of the Sixteenth Mining Congress of Turkey, Ankara, Turkey, 19–22 June 2001. [Google Scholar]
- Ulrich, B.F.; Wuest, W.J.; Stateham, R.M. Relationships between annulus thickness and the integrity of resin-grouted roof bolts. Report of investigations; United States. Bureau of Mines: Washington, DC, USA, 1989. [Google Scholar]
- Tadolini, S. The effects of reduced annulus in roof bolting performance. In Proceedings of the 17th International Conference on Ground Control in Mining, Morgantown, WV, USA, 4–6 August 1998; pp. 230–236. [Google Scholar]
- Li, C.; Stillborg, B. Analytical models for rock bolts. Int. J. Rock Mech. Min. Sci. 1999, 36, 1013–1029. [Google Scholar] [CrossRef]
- Mortazavi, A.; Tabatabaei Alavi, F. A numerical study of the behavior of fully grouted rockbolts under dynamic loading. Soil Dyn. Earthq. Eng. 2013, 54, 66–72. [Google Scholar] [CrossRef]
- Martin, L.B. Theoretical and Experimental Study of Fully Grouted Rockbolts and Cablebolts Under Axial Loads; Ecole Nationale Supérieure des Mines de Paris: Paris, France, 2012. [Google Scholar]
- Martin, L.B.; Hassen, F.H.; Tijani, M.; Noiret, A. A new experimental and analytical study of fully grouted rockbolts. In Proceedings of the 45th US Rock Mechanics/Geomechanics Symposium, San Francisco, CA, USA, 26–29 June 2011; p. ARMA 11-242. [Google Scholar]
- Villaescusa, E.; Varden, R.; Hassell, R. Quantifying the performance of resin anchored rock bolts in the australian underground hard rock mining industry. Int. J. Rock Mech. Min. Sci. 2008, 45, 94–102. [Google Scholar] [CrossRef]
- Campbell, R.; Mould, R. Impacts of gloving and un-mixed resin in fully encapsulated roof bolts on geotechnical design assumptions and strata control in coal mines. Int. J. Coal Geol. 2005, 64, 116–125. [Google Scholar] [CrossRef]
- Rojat, F.; Labiouse, V.; Kaiser, P. Brittle rock failure in the steg lateral adit of the lotschberg base tunnel. Rock Mech. Rock Eng. 2009, 42, 341. [Google Scholar] [CrossRef]
- Shiyong, W.; Manbin, S.; Jian, W. Jinping hydropower project: Main technical issues on engineering geology and rock mechanics. Bull. Eng. Geol. Environ. 2010, 69, 325–332. [Google Scholar] [CrossRef]
- Naji, A.M.; Emad, M.Z.; Rehman, H.; Yoo, H. Geological and geomechanical heterogeneity in deep hydropower tunnels: A rock burst failure case study. Tunn. Undergr. Space Technol. 2019, 84, 507–521. [Google Scholar] [CrossRef]
- Hoek, E.; Marinos, P. Tunnelling in overstressed rock. In Proceedings of the ISRM Regional Symposium-EUROCK 2009, Cavtat, Croatia, 29–31 October 2009; International Society for Rock Mechanics: Lisboa, Portugal, 2009. [Google Scholar]
- Kaiser, P.; Yazici, S.; Nose, J. Effect of stress change on the bond strength of fully grouted cables. In International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts; Elsevier: Amsterdam, The Netherlands, 1992; pp. 293–306. [Google Scholar]
- Stjern, G.; Myrvang, A. The influence of blasting on grouted rockbolts. Tunn. Undergr. Space Technol. 1998, 13, 65–70. [Google Scholar] [CrossRef]
- Jeon, S.-S.; Kim, D.-S.; Jang, Y.-W. Stability assessment of concrete lining and rock bolts of the adjacent tunnel by blast-induced vibration. J. Korean Geotech. Soc. 2007, 23, 33–45. [Google Scholar]
- Brady, B.H.; Brown, E.T. Rock Mechanics: For Underground Mining; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Siang, K.K.; Chon, C.H. Reinforcement mechanisms of rock bolt—A laboratory investigation. Geol. Soc. Malays. 2003, 46, 101–106. [Google Scholar]
- Spang, K.; Egger, P. Action of fully-grouted bolts in jointed rock and factors of influence. Rock Mech. Rock Eng. 1990, 23, 201–229. [Google Scholar] [CrossRef]
- Oreste, P. Analysis of structural interaction in tunnels using the covergence–confinement approach. Tunn. Undergr. Space Technol. 2003, 18, 347–363. [Google Scholar] [CrossRef]
- Unal, E. Development of design guidelines and roof-control standards for coal-mine roofs. Ph. D Thesis, The Pennsylvania State University, State College, PA, USA, 1983. [Google Scholar]
- Li, F.; Quan, X.; Jia, Y.; Wang, B.; Zhang, G.; Chen, S. The experimental study of the temperature effect on the interfacial properties of fully grouted rock bolt. Appl. Sci. 2017, 7, 327. [Google Scholar] [CrossRef]
- Rehman, H.; Ali, W.; Naji, A.; Kim, J.-J.; Abdullah, R.; Yoo, H.-K. Review of rock-mass rating and tunneling quality index systems for tunnel design: Development, refinement, application and limitation. Appl. Sci. 2018, 8, 1250. [Google Scholar] [CrossRef]
- Carranza-Torres, C.; Fairhurst, C. Application of the convergence-confinement method of tunnel design to rock masses that satisfy the hoek-brown failure criterion. Tunn. Undergr. Space Technol. 2000, 15, 187–213. [Google Scholar] [CrossRef]
- Lauffer, H. Gebirgsklassifizierung fur den stol lenbau. Geol. Und Bauwes. 1958, 24, 46–51. [Google Scholar]

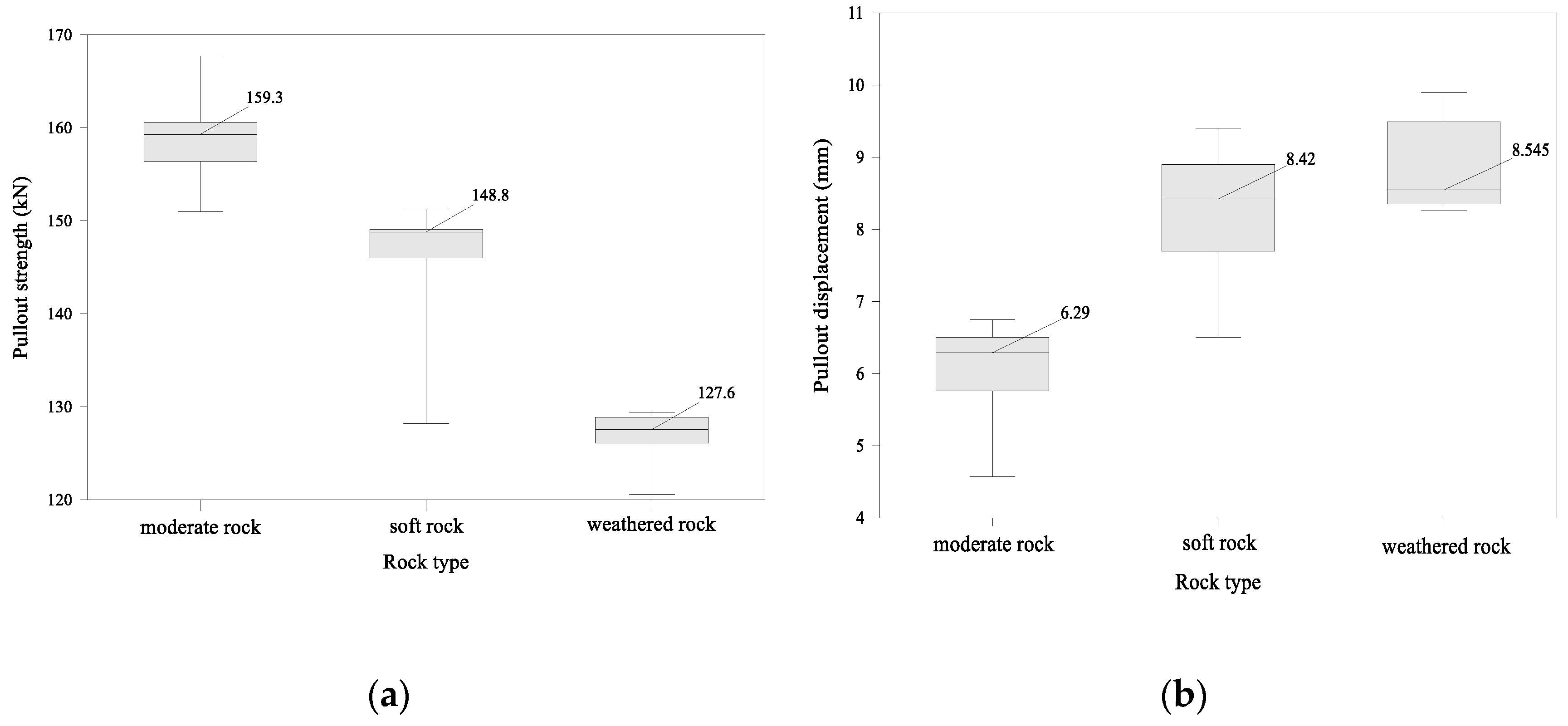
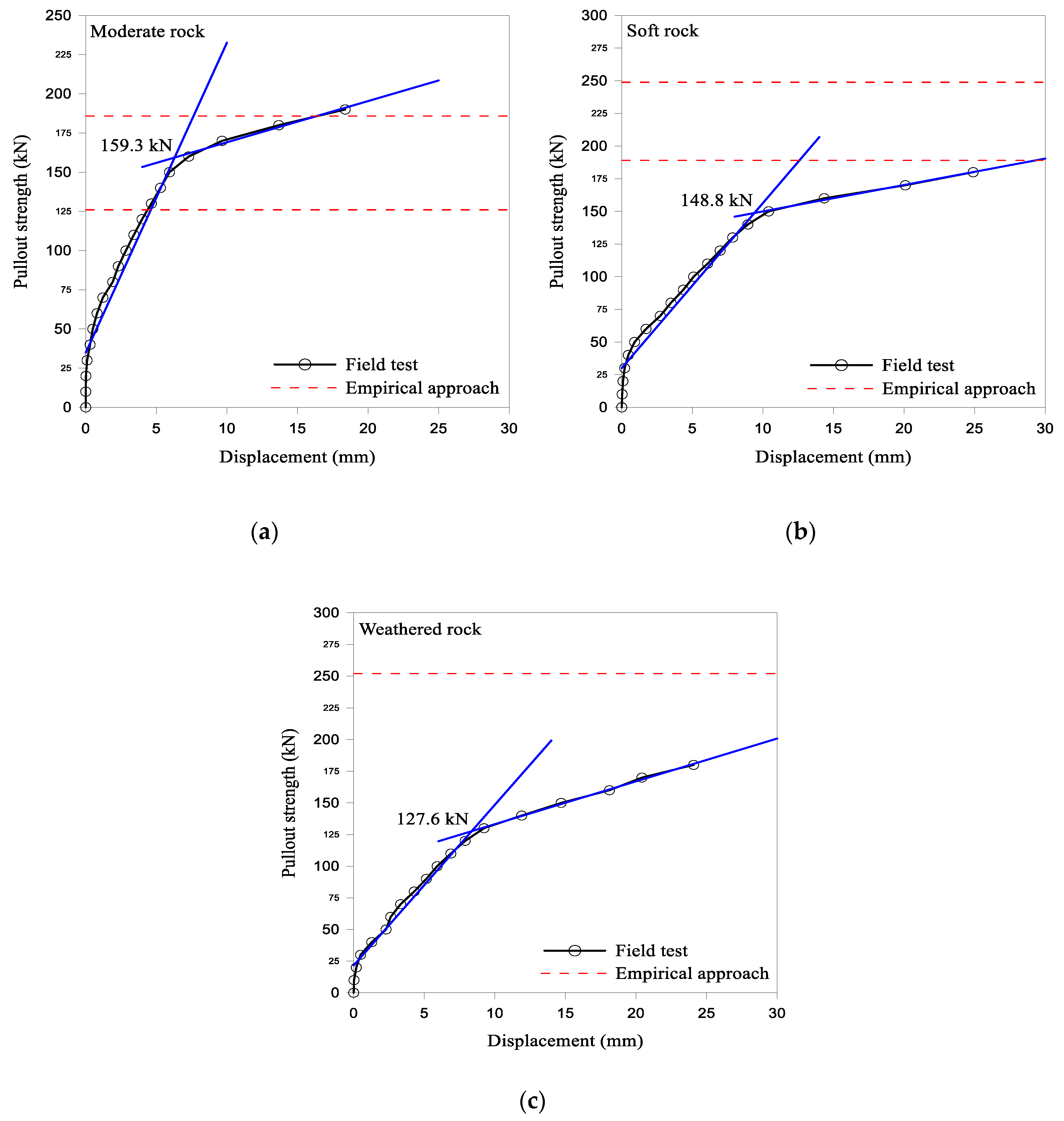
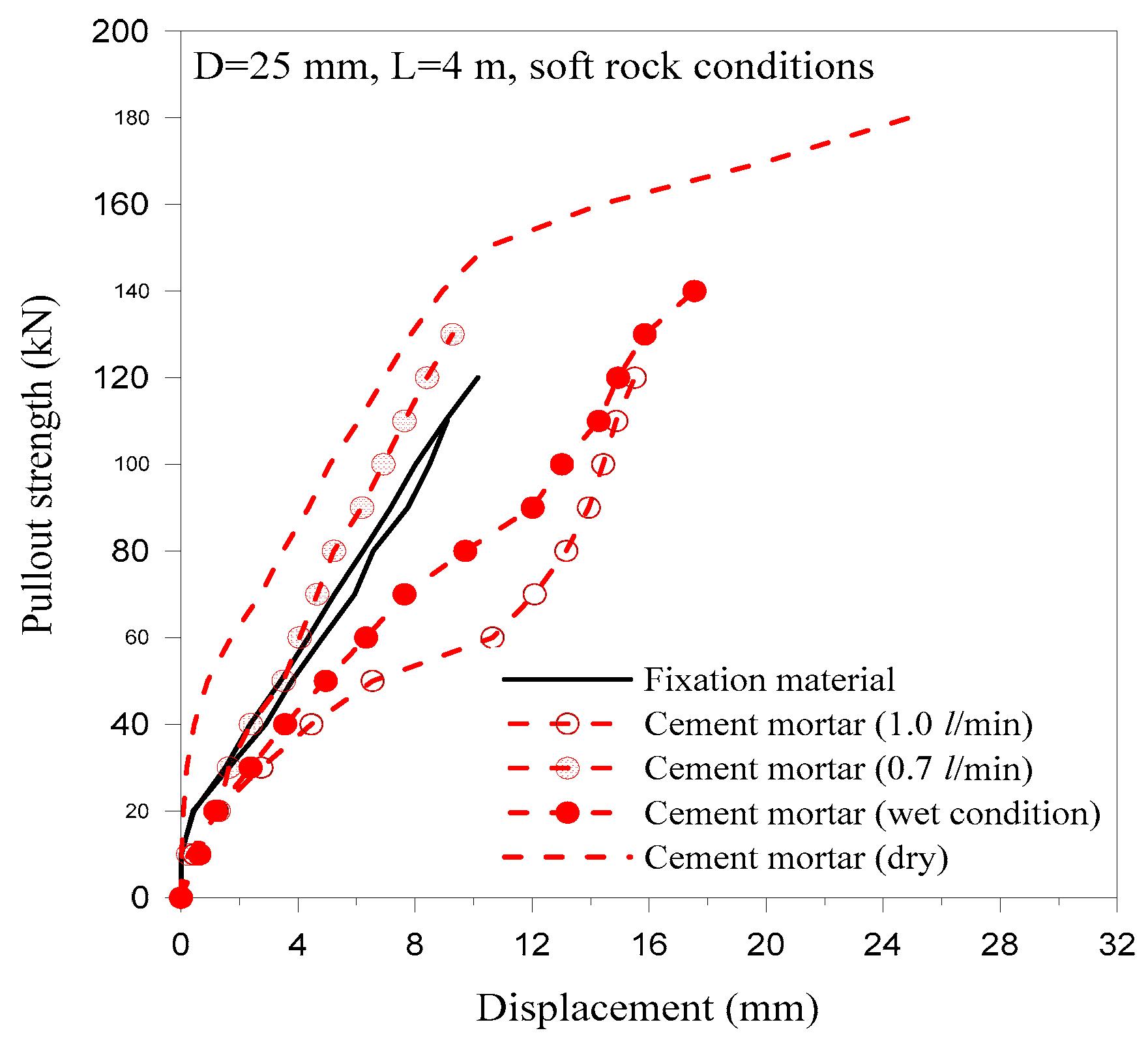
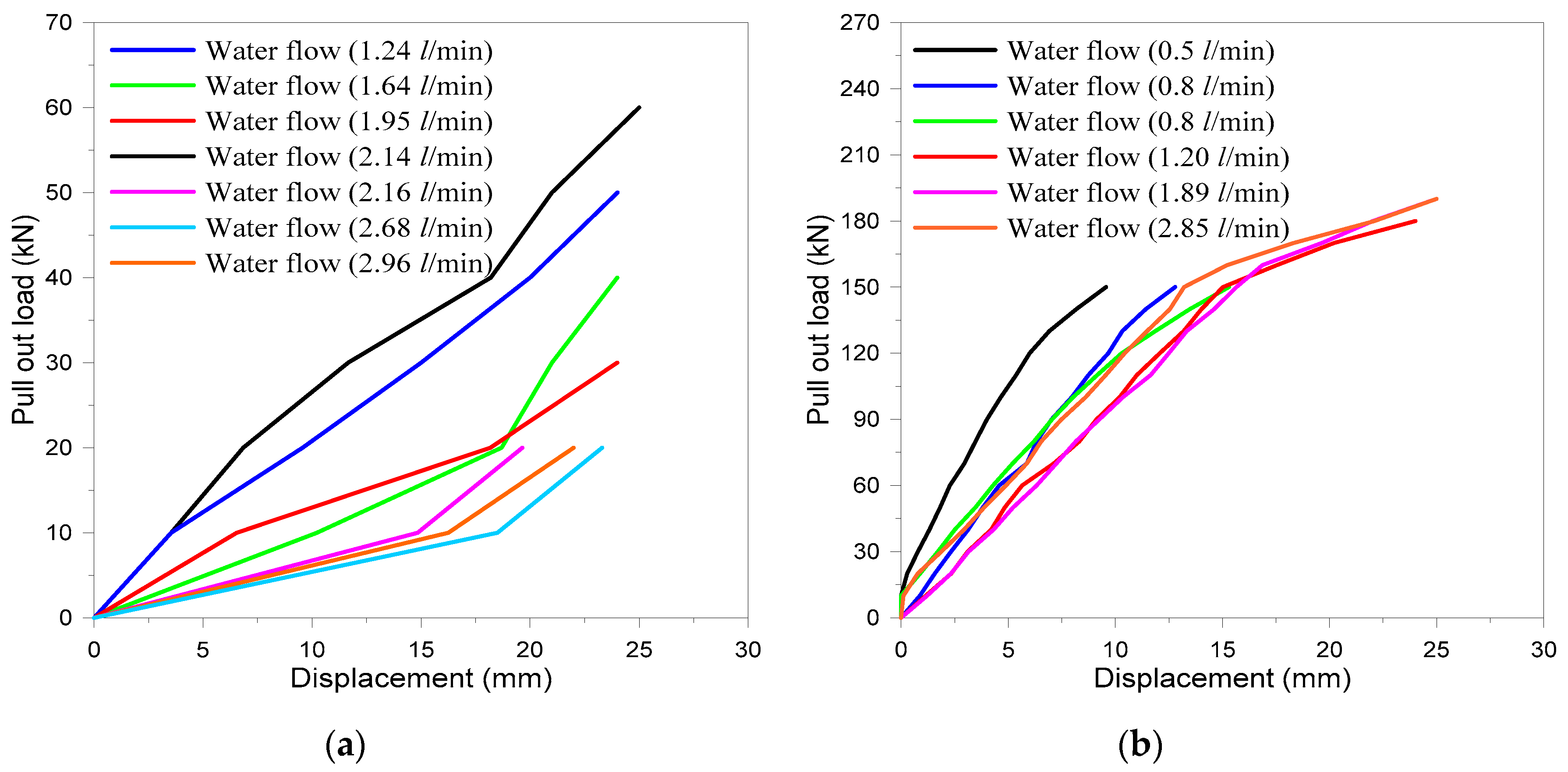
| Rock-Mass Classification System | Rock-Mass Class | ||
|---|---|---|---|
| Weathered Rock Mass | Soft Rock Mass | Moderate Rock Mass | |
| RQD | <25 | 25–50 | 50–75 |
| RMR | <20 | 21–40 | 41–60 |
| Q | <0.1 | 0.1–1 | 1–10 |
| Parameter | |||||
|---|---|---|---|---|---|
| Rock Mass | Rock-Bolt Type | Rock Bolt Length (L) | Curing Time | Grout Type | Ground Water Condition |
| Moderate (50) | Fully grouted (125) | L = 3 m (11) | 12 h (6) | Mortar (103) | Dry (109) |
| Soft (40) | L = 4 m (81) | 24 h (6) | Wet (33) | ||
| Weathered (52) | inflated steel tube (17) | L = 5 m (50) | 36 h (6) | Resin (22) | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, H.; Rehman, H.; Ali, W.; Naji, A.M.; Kim, J.-j.; Kim, J.; Yoo, H. Classification of Factors Affecting the Performance of Fully Grouted Rock Bolts with Empirical Classification Systems. Appl. Sci. 2019, 9, 4781. https://doi.org/10.3390/app9224781
Kim H, Rehman H, Ali W, Naji AM, Kim J-j, Kim J, Yoo H. Classification of Factors Affecting the Performance of Fully Grouted Rock Bolts with Empirical Classification Systems. Applied Sciences. 2019; 9(22):4781. https://doi.org/10.3390/app9224781
Chicago/Turabian StyleKim, Haneol, Hafeezur Rehman, Wahid Ali, Abdul Muntaqim Naji, Jung-joo Kim, Jonguk Kim, and Hankyu Yoo. 2019. "Classification of Factors Affecting the Performance of Fully Grouted Rock Bolts with Empirical Classification Systems" Applied Sciences 9, no. 22: 4781. https://doi.org/10.3390/app9224781
APA StyleKim, H., Rehman, H., Ali, W., Naji, A. M., Kim, J.-j., Kim, J., & Yoo, H. (2019). Classification of Factors Affecting the Performance of Fully Grouted Rock Bolts with Empirical Classification Systems. Applied Sciences, 9(22), 4781. https://doi.org/10.3390/app9224781





