Analogy Study of Center-Of-Pressure and Acceleration Measurement for Evaluating Human Body Balance via Segmentalized Principal Component Analysis

Abstract

The purpose of this research is to investigate the feasibility of evaluating the human’s balancing ability by means of the human body’s swaying acceleration measurements instead of the traditional center-of-pressure (COP) measurement. The COP measurement has been used broadly for assessing the balance ability of patients in hospitals. However, the force plate system which is employed to measure the COP signals of the human body is generally restrictive due to the very high cost as well as the bulky portability. In this study, the balancing ability of the human body was evaluated through the measurements of a capacitive accelerometer. The segmentalized principal components analysis (sPCA) was employed to reduce the influence of the gravity component in acceleration measurement projected onto the horizontal components while the accelerometer inevitably tilts. The signal relationship between the COP and the acceleration was derived, so that the swaying acceleration measurements of human body can be utilized to evaluate the human body’s balancing ability.

1. Introduction

The aging trend of the social population has been a problem in all the developed countries, and hence, healthcare for the elderly has become an essential issue. The decline of balancing ability is one of the important indicators of the aging process of the human body. In addition to being an important indicator of human aging, the balancing ability is also an index for assessing a person’s physical health in medical fields.

The balance of the human body is a sophisticated mechanism. The system that receives the balance-related information consists of three parts: the vision, somatosensory and vestibular system. The vision part provides us with the identification of spatial position, the role of somatosensory is the perception of stimuli on the limbs for the postures and positions and the vestibular system allows us to feel the existence of acceleration in movements. When the human body lacks the balancing ability, the most serious problem is the fall. Therefore, a simple system that can evaluate the balance condition of the human body is definitely beneficial to the balancing ability training and treatment (preventing step) as well as the falling detection (post-mortem remedy step).

The center-of-pressure (COP) has been broadly utilized to evaluate the balancing ability of patients in the fields of clinical medicine and biomedical engineering. The measurements of COP are normally implemented by using the force plate. However, the force-plate-based COP measurement systems are generally highly restrictive due to the very high cost (normally more than 10,000 US dollars) as well as the bulky portability. Therefore, a cheap carry-on device that can be used to estimate the balancing ability of the human body is definitely a merit for the healthcare of the elderly. It is apparent that the swaying dynamics of the human body is related to the balancing ability of the human body. The human body’s sway can be detected in terms of the acceleration, which is able to be measured by the accelerometers. As compared with the force-plate-based COP measurement systems, the accelerometers usually have the advantage of much lower price and convenient portability. The price of a capacitive micro-electro-mechanical system (MEMS) accelerometer may be as low as ten US dollars, and thus the MEMS accelerometers can be integrated inside the cellphones as portable devices.

The studies of utilizing the accelerometers for the swaying measurement have been conducted to assess the balancing ability of the human body. Moe-Nilssen [1] applied the accelerometer to estimate the human body’s balance and extracted the statistical features for discriminating the difference among balance conditions. Furthermore, different experimental cases were set up for the acceleration measurements of balance control [2]. In addition to the accelerometers, the audio-biofeedback (ABF) approach was also utilized to evaluate the sonic influence of different bandwidth for the human body’s balance [3]. Ghasemzadeh et al. [4] investigated the identification of the balance situation through the integration of signals of accelerometer and electromyography (EMG). Their study validated the high correlation between the EMG signal and balance condition of the human body. The acceleration signals were processed by using the wavelet analysis as well as the principal component analysis (PCA) for evaluating the balancing ability of human bodies among the frail, pre-frail and healthy groups [5]. The sample entropy values were utilized to quantify the regularity of COP fluctuations [6]. Their study indicated that the COP fluctuations are more regular for standing than sitting, representing different balance conditions. Huang et al. [7] developed a center-of-pressure and complexity monitoring system (CPCMS) to assess the improvement of human body balance. Their study demonstrated that the CPCMS can achieve similar results to the commercial product. Halicka et al. [8] proposed to examine the effectiveness of visual biofeedback (VBF) signals and accelerometer sensors for improving human balance. They showed that the location of VBF signals had a significant effect on each postural parameter of COP and trunk segments. The approximate entropy values were computed to reflect the amount of irregularity hiding in the COP [9]. The data analysis demonstrated that this method enables us to quantify the postural stability. A point of application (POA) approach was used to determine the accuracy, precision and reliability of COP measurement in a low-cost force plate, called the balance tracking system, and showed an excellent agreement between the POAs and measured COP [10]. In 2018, Adamova et al. [11] used the three-axis accelerometer to quantify the postural stability of patients with cerebellar disorder. Their study demonstrated that the pathological balance control can be identified through the three-dimensional (3D) postural analysis.

Although the COP-based quantification of balancing ability has been employed by medical doctors for decades and is still the major means for evaluating the balance condition of patients, the studies of replacing the COP measurements for balance evaluation have been explored and the feasibility has also been verified. Based on the state-of-art of balance measurement of the human body, a solid and consistent transformation between the COP and acceleration measurements is the crucial step for accurately estimating the balancing ability of the human body. On the other hand, the swaying frequencies of the human body mainly concentrate around the very low-frequency band, as compared to the frequency range of mechanical structural vibration. As for considering the volume, weight, cost and measured bandwidth of the accelerometer, the capacitive accelerometer would be an appropriate one to be bound with the human body and then utilized to measure the swaying acceleration at extremely low frequencies. However, the capacitive accelerometer inherently contains the gravity component on the vertical axis and the gravitation may be projected onto the measurements on the three axes with a time-varying manner, while the bind-in accelerometer tilts along with the human body’s swaying. It is definitely an obstacle and there is difficulty deriving the correlation between the COP signal and acceleration measurement.

Based on the problem statements, the objective of this research is to investigate the feasibility of deriving the transformation from the acceleration measurement to the COP signal, so that the COP-based evaluation of the human body’s balancing ability can be estimated in terms of the swaying acceleration measurements. The empirical mode decomposition (EMD) method [12] was employed to separate the non-stationary acceleration signals and then extract the swaying-related components at the very low-frequency range. With the EMD process, the traditional filtering process in which the central frequency and bandwidth must be first decided would not be needed. The segmentalized PCA (sPCA) was proposed to alleviate the influence of the time-varying gravitation projection onto the acceleration measurements on the three axes. The equilibrium score (EQs) was also estimated through the measured acceleration signals in this research. The results show that high correlation coefficients of more than 0.7 can be obtained between the processed acceleration signals and the COP measurements. The estimated EQs values have mean average percentage error (MAPE) of 4.89 with respect to the EQs values that were calculated by the commercial computer-aid balance testing apparatus.

2. Experiment Design for Relationship Derivation between Acceleration and the Center-of-Pressure (COP)

The sensory organization test (SOT) has been broadly employed to evaluate the balancing ability of the human body in the fields of clinical medicine and biomedical engineering. Among all the external factors that influence the balancing ability of the human body, the majority contains the visual conditions. Based on the SOT, the experimental design in this research contained different visual conditions on a fixed referenced support surface for investigating the effects of the human body’s static balancing ability. The examinees were asked to stand on the force plate associated with five visual conditions, including (1) eyes opening, (2) eyes closing, (3) blank reference swaying, (4) static giddy reference and (5) giddy reference swaying, as tabulated in

Table 1. Visual conditions in the experiment design.

Visual Condition	Expression
C1	Eyes open (no reference)
C2	Eyes closed
C3	Blank reference sway
C4	Static reference with giddy graph
C5	Swayed reference with giddy graph

. The visual conditions of C1 and C2 (eyes opening and closing) mainly assess the balancing ability of the human body with and without the reference. In order to produce the visual perturbation as well as the brain fatigue, three conditions (C3–C5) were conducted in this experiment to investigate the influence of different references upon the balancing ability of the human body. As shown in Figure 1, the referenced wall in the experiment can sway accordingly to simulate the visual conditions C3 to C5. Moreover, the dazzling graph, as shown in Figure 2, was stuck on the referenced wall to produce the factors of visual conditions C4 and C5.

The force plate that the examinee stood on was used to measure the COP locus of the examinee. The force plate measurement system consists of four identical load cells (LDB-30, Jihsense Industril LTD.) and a signal acquisition device (eStrain 4B4V, Chief SI Company). In this experiment, the COP signals were recorded with the sampling rate of 100 Hz. Simultaneously, the capacitive accelerometer (CXL04GP3-R-AL, MEMSIC Inc.) was bound on the waist of the examinee (around the mass center of the human body) to measure the acceleration of human body swaying in the three directions. The acceleration signals were recorded by the data acquisition device (NI 9234) with the same sampling rate as the COP signals. Both the COP loci and acceleration signals of each examinee were measured synchronously for all designated visual conditions with data length of twenty seconds. With the synchronized measurements, the analogy between the COP loci and the acceleration signals of the human body was derived.

3. Processing and Analysis of Measurements

3.1. Signal Separation and Spectrum Analysis

The major difference between the COP and acceleration measurements is the dimension representation. The COP signals, which are recorded through the force plate, consist of the two independent components (in X and Y directions) that are perpendicular to the gravitational direction. According to the SOT, the COP signal in X-direction is defined as the medial-lateral (ML) component and the Y-component is defined as the anterior-posterior (AP) direction. The acceleration signals that are measured by the tri-axial accelerometer consist of the three components in the typical X-Y-Z directions of the Cartesian coordinate system. Since the accelerometer is bound on the human body’s waist and may tilt with human body swaying, the X-Y-Z directions of the tri-axial accelerometer are not fixed in the measurement process.

Through observing the ways that the examinees adjust their posture for balance purposes, both the COP and the acceleration signals have obvious non-stationarity characteristics. The EMD approach that was proposed by Huang et al. [12] is an adaptive data analysis method and can be utilized to separate the non-stationary signals. The EMD process can be simply expressed as:

$$x(t)={\displaystyle \sum _{k=1}^m{c}_k}(t)+r_m(t)$$

(1)

where, x(t) represents any complicated non-stationary signal, c_k(t) is the k-th intrinsic mode function (IMF) of the signal x(t) and r_m(t) is the final residue which can be a constant or the signal mean trend. Based on the concept of EMD, each IMF component satisfies the following conditions [12]: (1) The number of extrema and the number of zero-crossings must be either equal or differ at most by one in the whole data set, and (2) At any point, the mean value of the envelope defined by the local maxima and the envelope defined by the local minima is zeros.

The measurements of COP and acceleration were first decomposed into the IMFs by the EMD method. With the EMD method, the non-stationary COP and acceleration signals can be separated into the independent signal components of different frequency bands. In the experimental process, on the other hand, the external noises or disturbances that are mixed in the measurements may inevitably interfere with the analysis of the COP and the acceleration signals; therefore, it is crucial to remove the uncorrelated signal components from the measurements of COP and acceleration, and reserve the signal components that contain the information correlated to the balancing ability of the human body.

By taking the Hilbert transform of the signal components (IMFs), the analytical signal of c_k(t) can be formed as:

$$z_k(t)=c_k(t)+jH \left\{c_k(t)\right\}=c_k(t)+j{\widehat{c}}_k(t)=A_k(t)e^{j{\varphi }_k(t)}$$

(2)

where, $H\left\{c_k(t)\right\}$ represents the Hilbert transform of c_k(t). The time-dependent amplitude, A_k(t), time-dependent phase, ϕ_k(t), and instantaneous frequency, ω_k(t), of c_k(t) can be formulated as:

$$\begin{array}{c}{A}_k(t)=\sqrt{c_k{(t)}^2+{\hat{c}}_k{(t)}^2}\\ {\varphi }_k(t)={\tan }^{-1}\frac{{\hat{c}}_k(t)}{c_k(t)}\\ {\omega }_k(t)==\frac{d{\varphi }_k(t)}{dt}\end{array}$$

(3)

Therefore, the time-frequency-amplitude distributions of the non-stationary COP and acceleration signals can be expressed as:

$$H(\omega , t)=\sum A_k(t)\cos ({\displaystyle \int {\omega }_k(t)dt})$$

(4)

In order to clearly observe the energy distributions of measurements in the frequency domain, the marginal spectrum of the COP and acceleration signals can be formulated as:

$$S(\omega )={\displaystyle \sum _k{\displaystyle {\int }_0^T{H}_k(\omega , t)} dt}$$

(5)

where, H_k(ω,t) represents the time-frequency distribution of the k-th IMF. The signal compositions and characteristics can then be observed and analyzed within the different frequency scales.

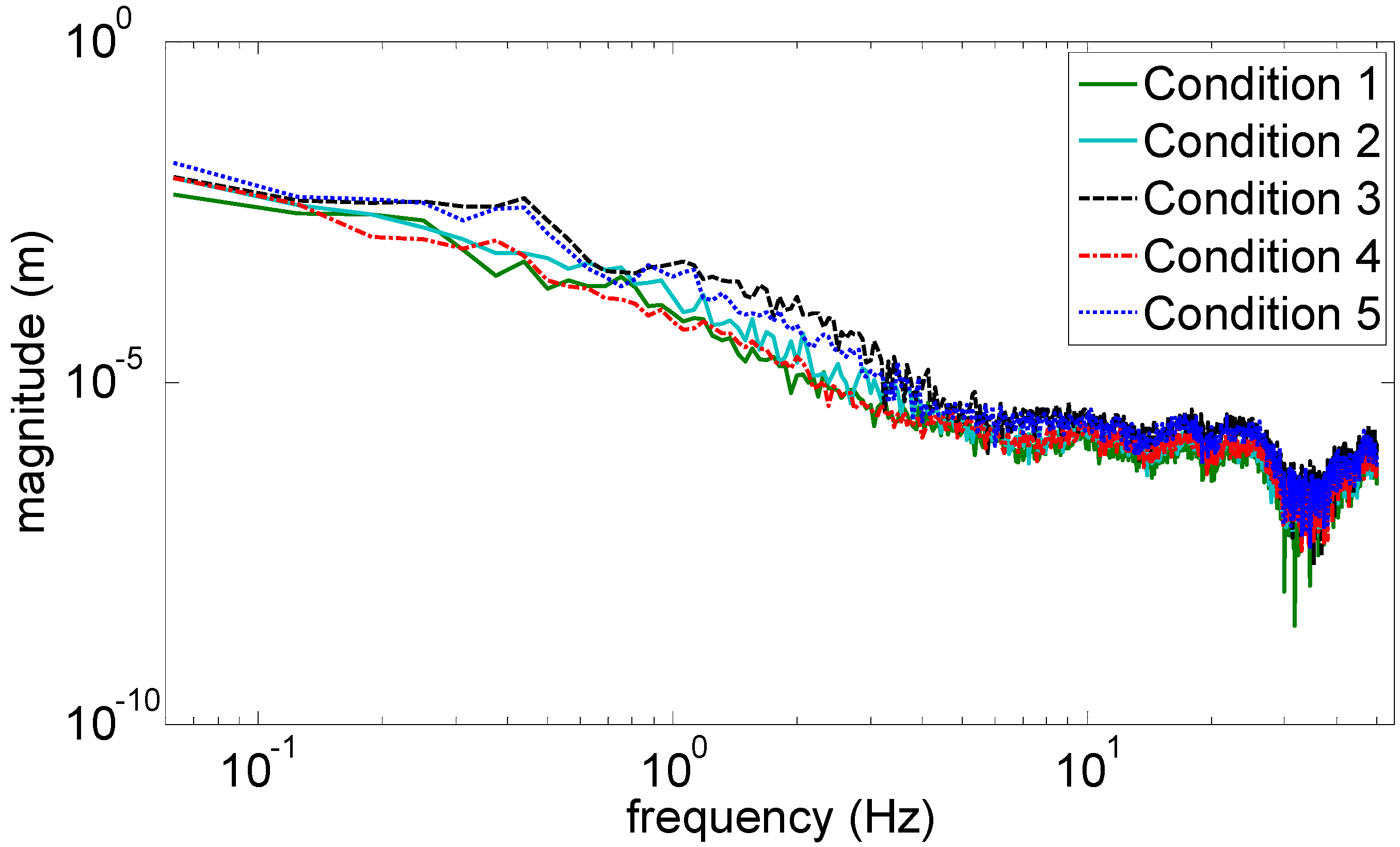
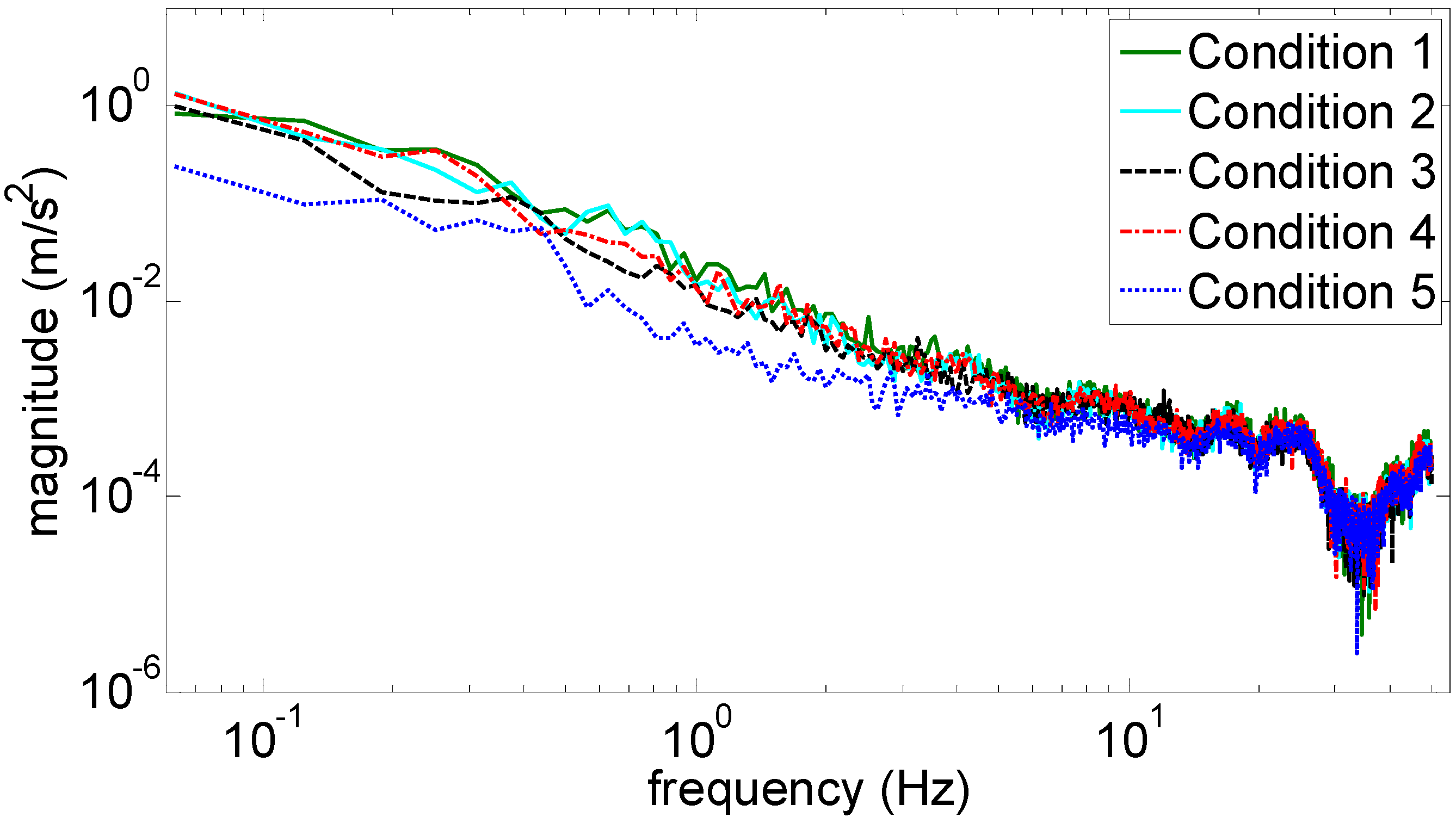
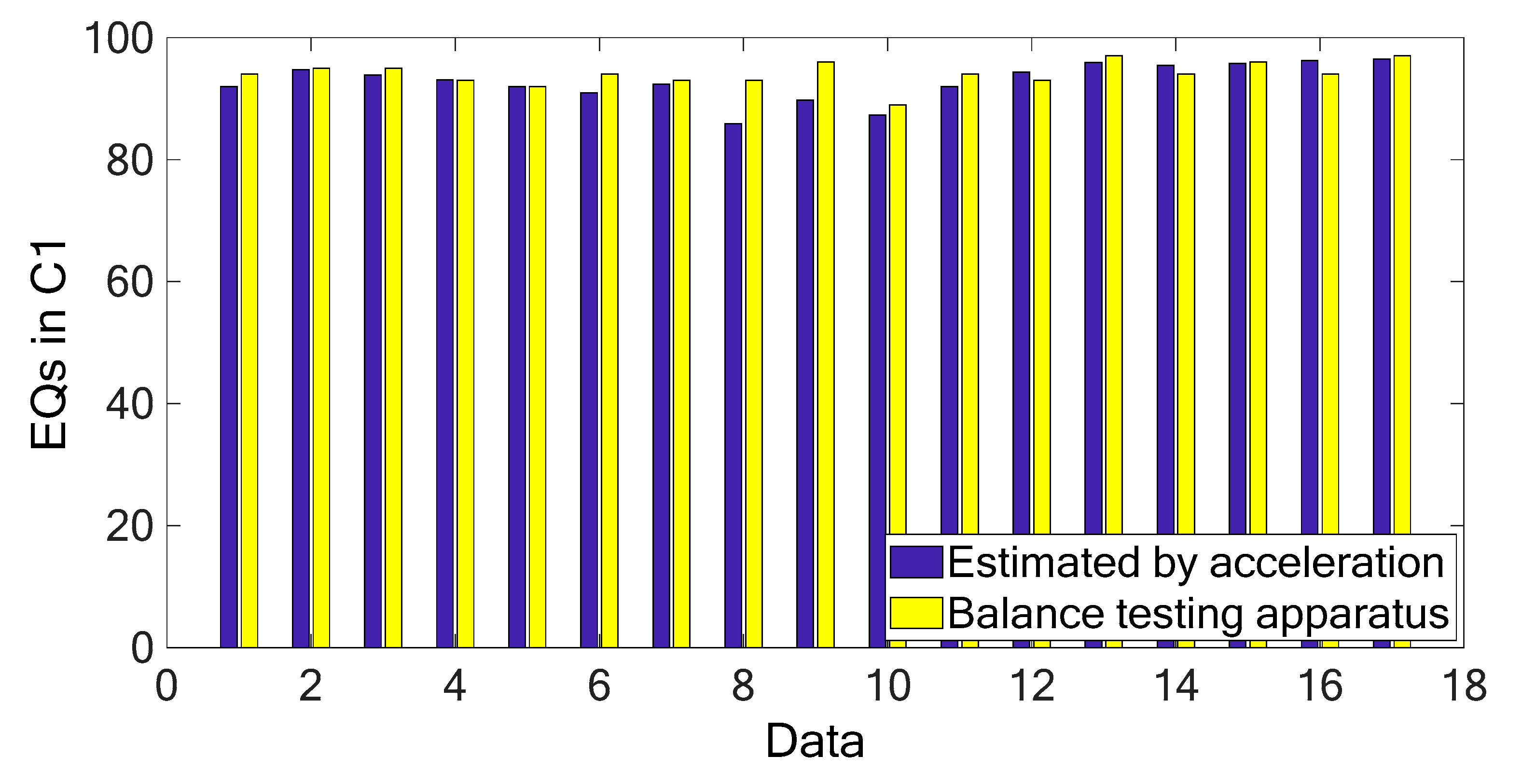
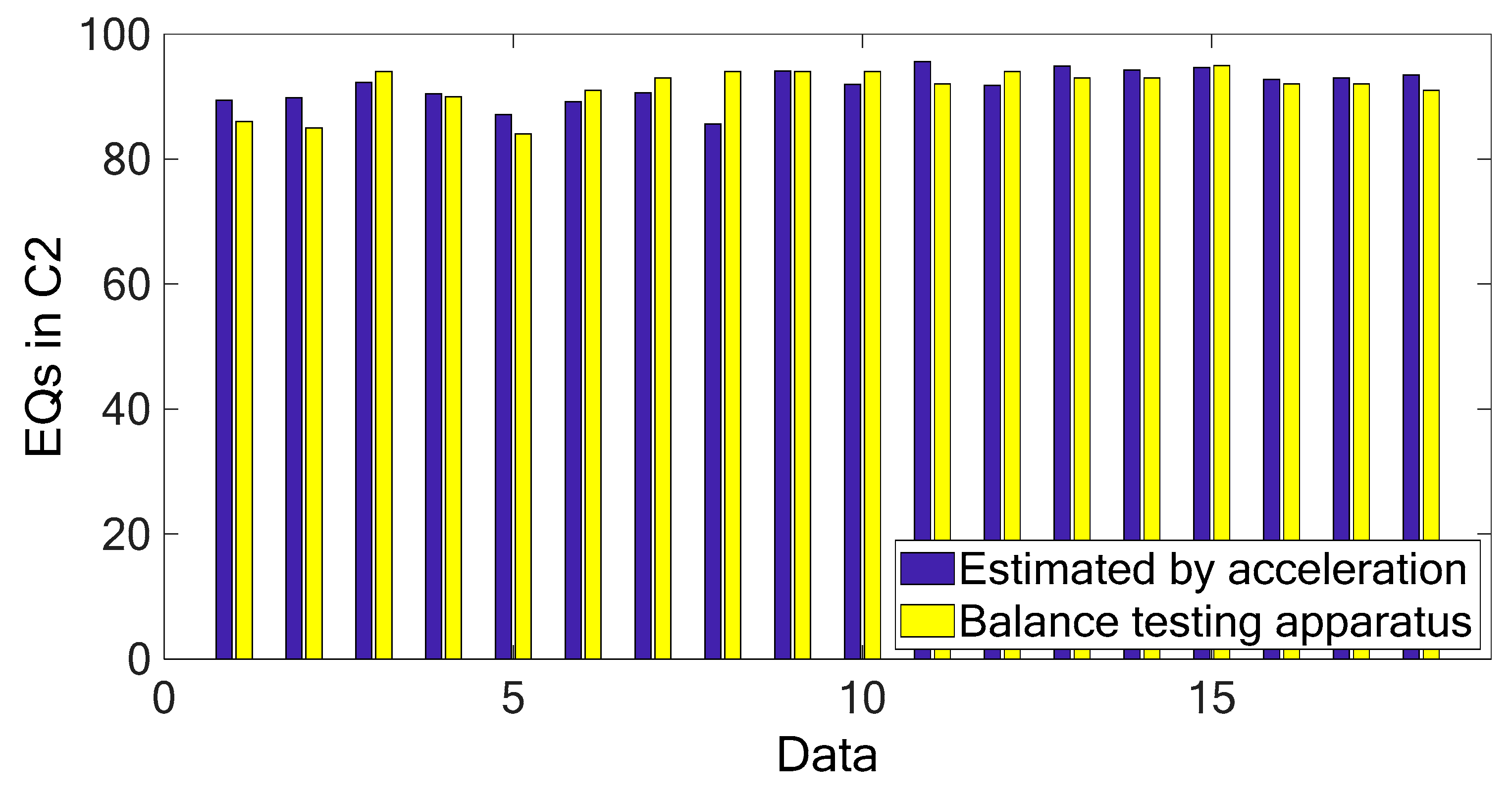
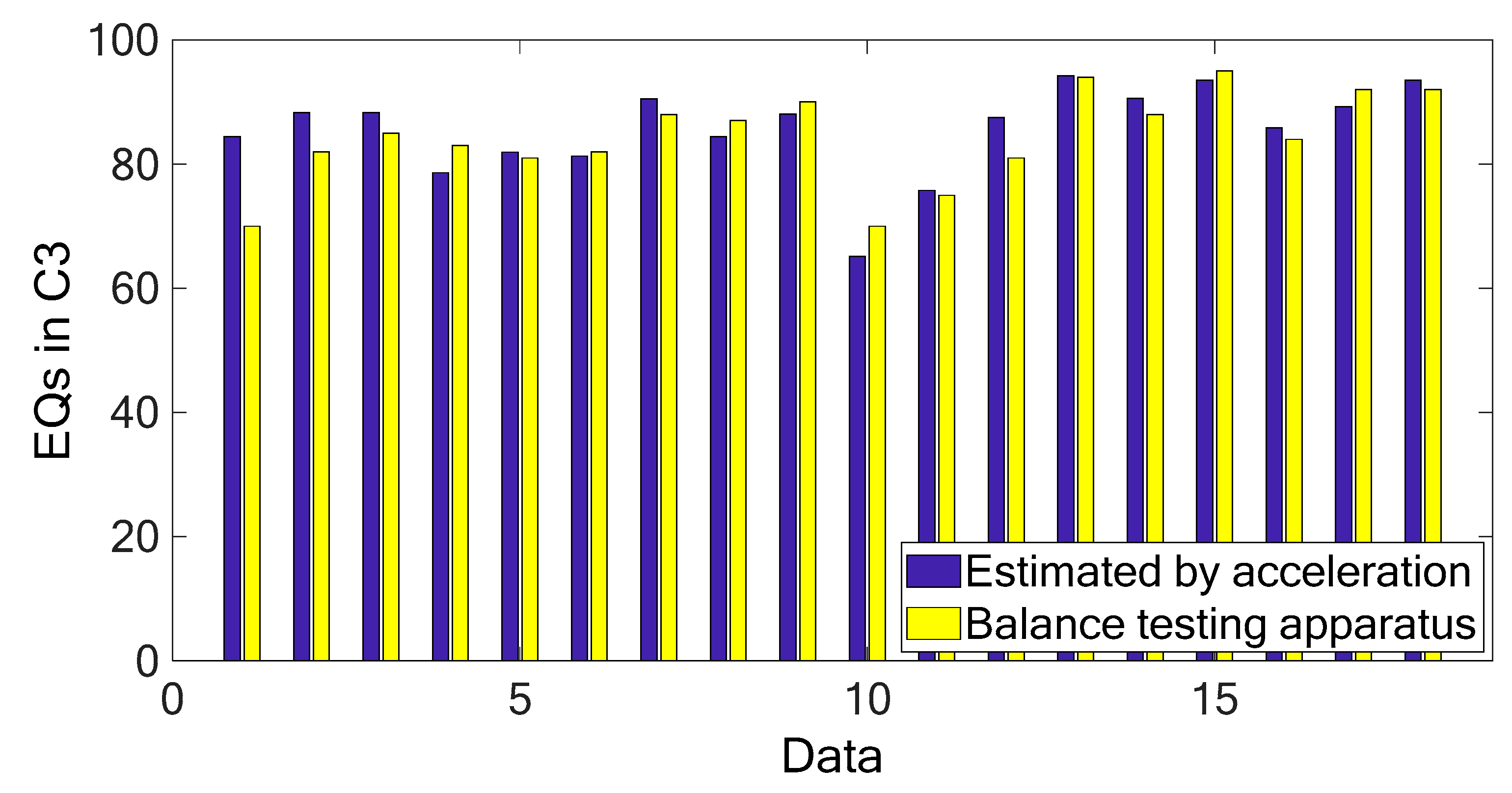
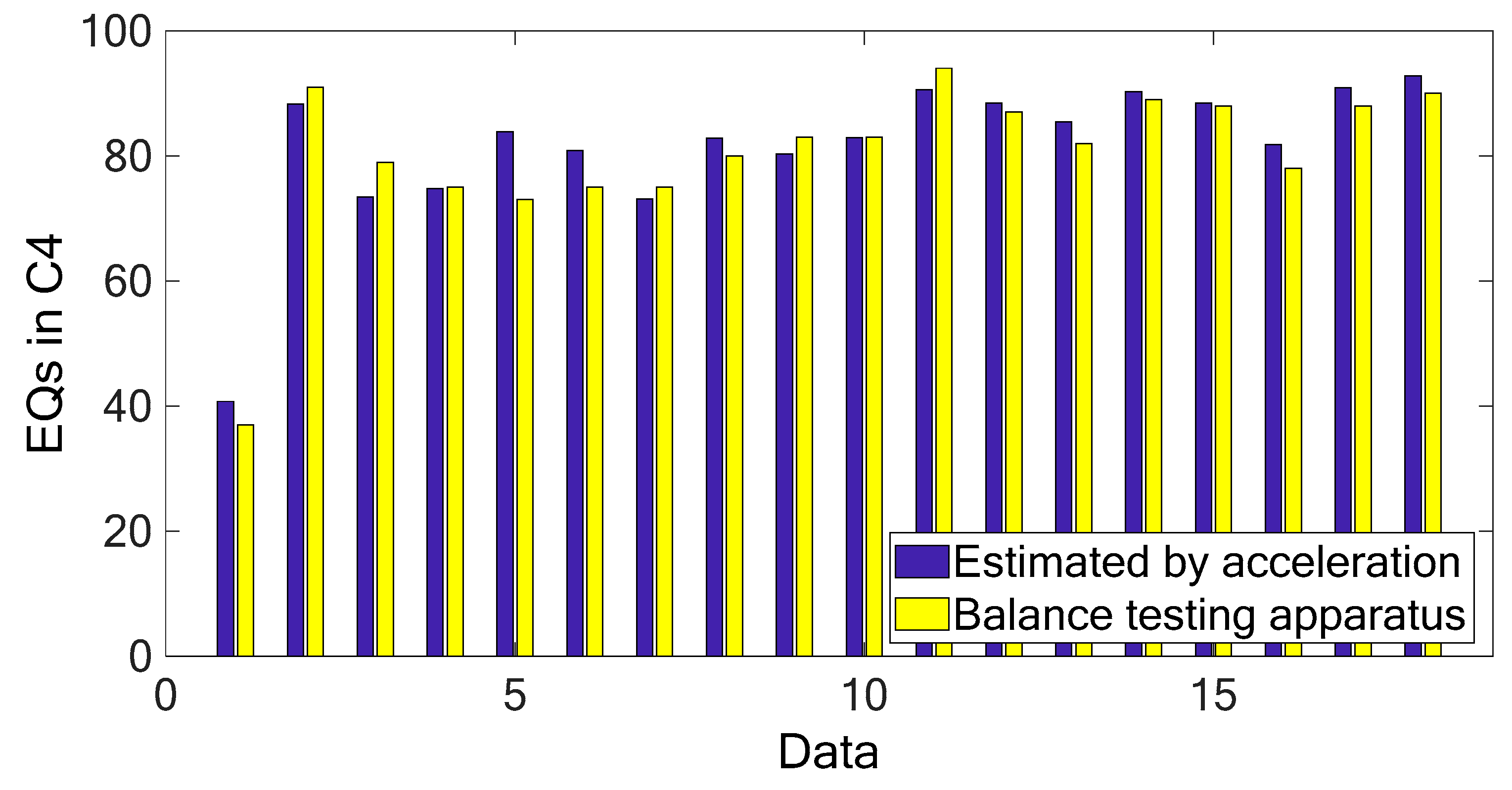
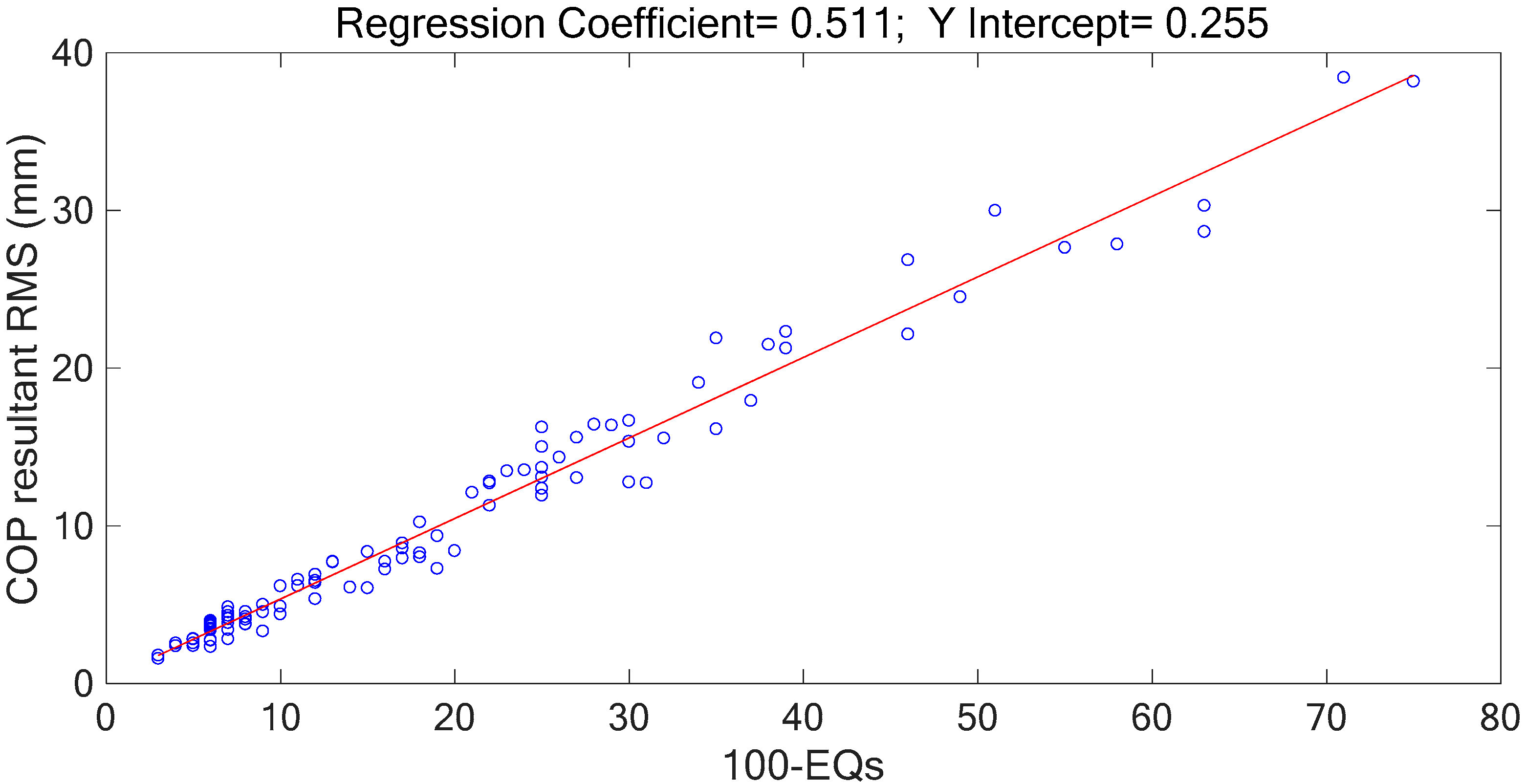
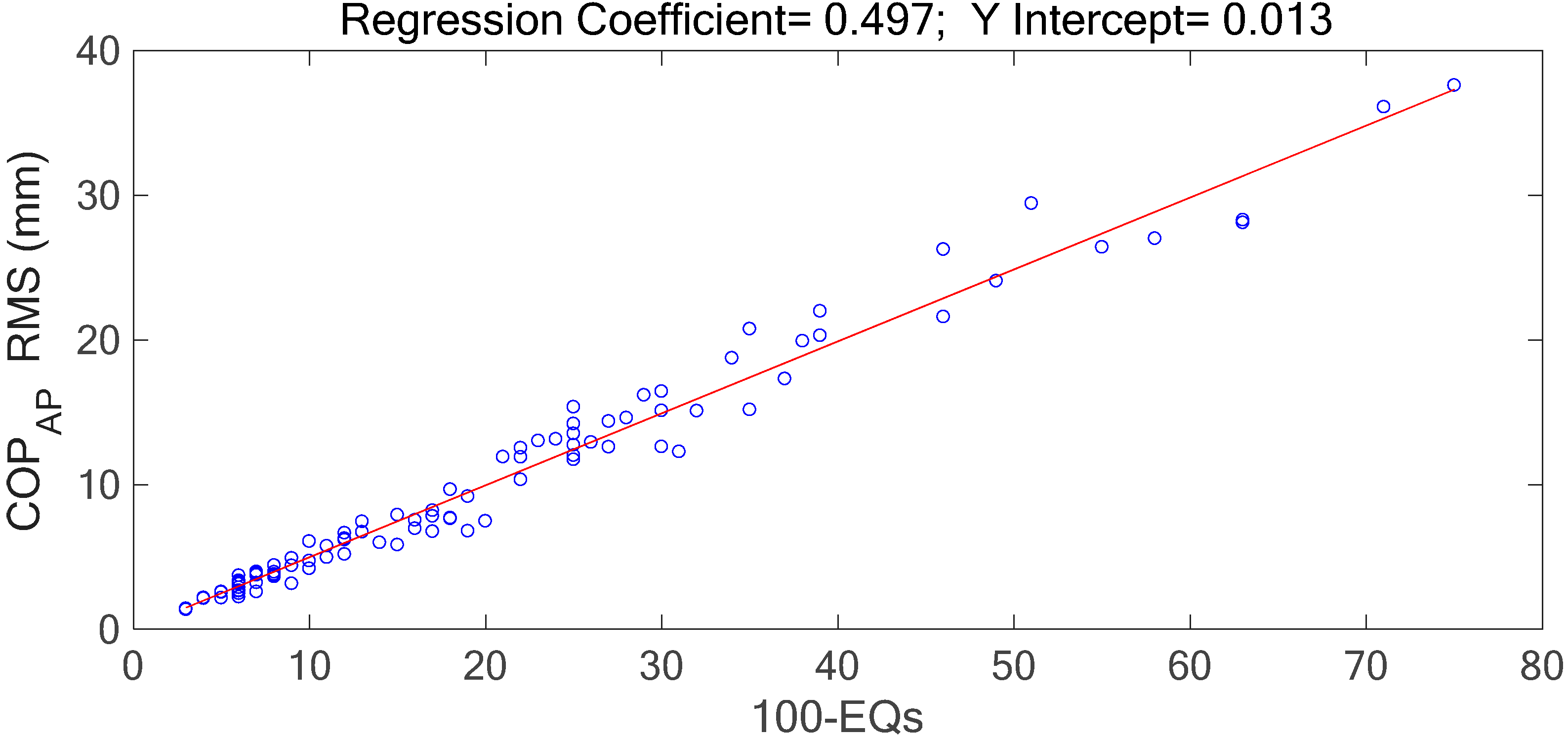
Figure 3 and Figure 4 show the marginal spectra of the COP and acceleration resultants with different experimental visual conditions (as tabulated in Table 1). The marginal spectra of COP and acceleration resultants apparently show that the signal energy concentrates at the low-frequency range. It is intuitive and coincident with the observation that the signal information correlated to the human body’s swaying for balance is found in the signal components of low frequencies. Based on the inference, the signal analysis of COP and acceleration in this research was focused on the IMFs whose bandwidths are within 0–5 Hz.

3.2. Segmentalized Principal Component Analysis (sPCA) for Acceleration Signal

As mentioned before, the frequency characteristics of the human body’s sway mainly focuses on the very low-frequency range, the capacitive accelerometer has satisfactory measurement performance within the bandwidth of very low frequencies, and thus, was utilized to detect the acceleration of the examinee’s body sway in the experiment. However, the bind-in accelerometer inevitably tilted along with the examinee’s body sway and hence, the X-Y-Z directions of the acceleration measurements were time-varying with respect to the fixed reference frame. Furthermore, the measurement of the capacitive accelerometer also includes the constant gravitation (g = 9.81 m/s²) in the vertical direction and thus, the acceleration measurements in the three directions may contain the gravitation projection components while the accelerometer was tilted along with the examinee’s body sway. To the contrary, the COP signal components in ML and AP directions were obtained in the horizontal plane and were independent of the gravitation in the vertical direction. Therefore, it is definitely beneficial for deriving the correlation between the COP and acceleration measurements if the gravitation projection onto the three directions of acceleration signals can be removed.

The concept of PCA that was proposed by Pearson [13] is to convert the measurements in which the variables may be correlated with each other into another sets of variables which are uncorrelated. The sets of variables in the other space are called principal components. The mathematical procedure of PCA is to transform the data sets of measurement into another coordinate system, where the principal components are located through an orthogonal matrix. In this coordinate system, the first principal component has the highest variance, and the subsequent components in turn have as high variance as possible. Therefore, the principal components in the new space are uncorrelated with each other or even orthogonal to each other.

In order to resolve the stated problem of the axial directions variation as well as the gravitation projection issue, and to thereafter derive the relationship between the COP measurement and the acceleration signal, the PCA was employed to process the acceleration signals in this research. The acceleration measurements in X-, Y- and Z-directions were first transformed into another coordinate system where the principal components were located. The principal components in the new coordinate system are theoretically orthogonal to each other, and thus the operation of PCA can reflect the transformed signals in the way of most possible variability in the data [14,15]. In this research, therefore, the variability of acceleration measurements along the three directions was first analyzed.

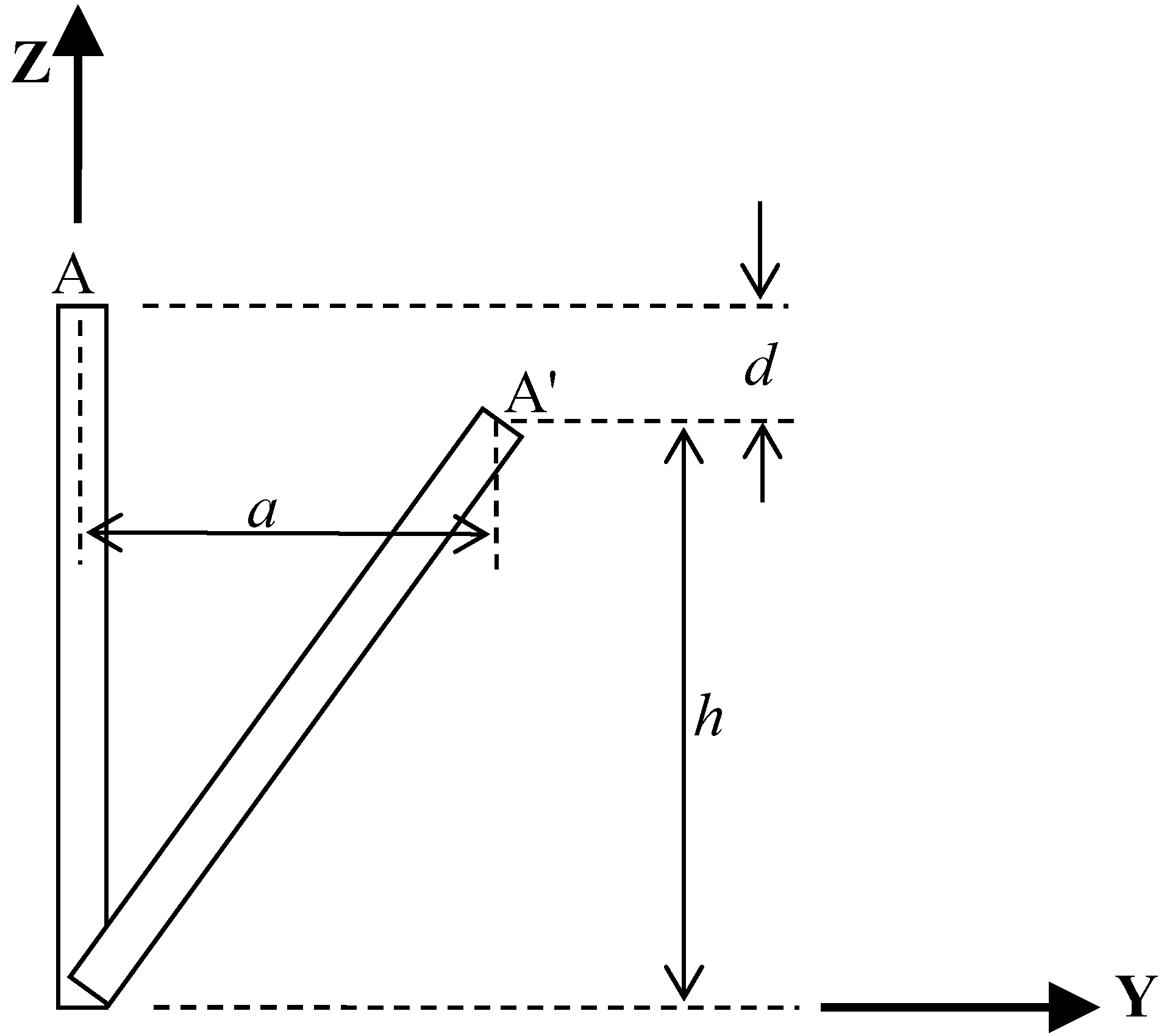
Simply consider that the accelerometer is bound at the point A of the examinee’s waist and sways in the AP direction, as shown in Figure 5. As the examinee sways to maintain the body’s balance status, the accelerometer moves from A to A’, as shown in Figure 5. The acceleration measurements consist of the components perpendicular to the Z-direction as well as the component parallel to the Z-direction. Since the two acceleration components in Y- and Z-direction are proportional to the distance a and d respectively, it can be briefly proven that the acceleration has larger variance in Y-direction than in Z-direction if a is always greater than d. First, assume d > a contradictorily. The distance a in Y-direction can be determined from the geometric relationship, $a=\sqrt{h^2-{(h-d)}^2}$, and hence, $d>\sqrt{h^2-{(h-d)}^2}$. It is easy to derive the contradiction that the condition for d > a implies d > h. Similarly, the same inference can be applied in the X-direction instead of the Y-direction. Therefore, it is reasonable to infer that the acceleration variance in Z-direction is smaller than those in X- and Y-directions.

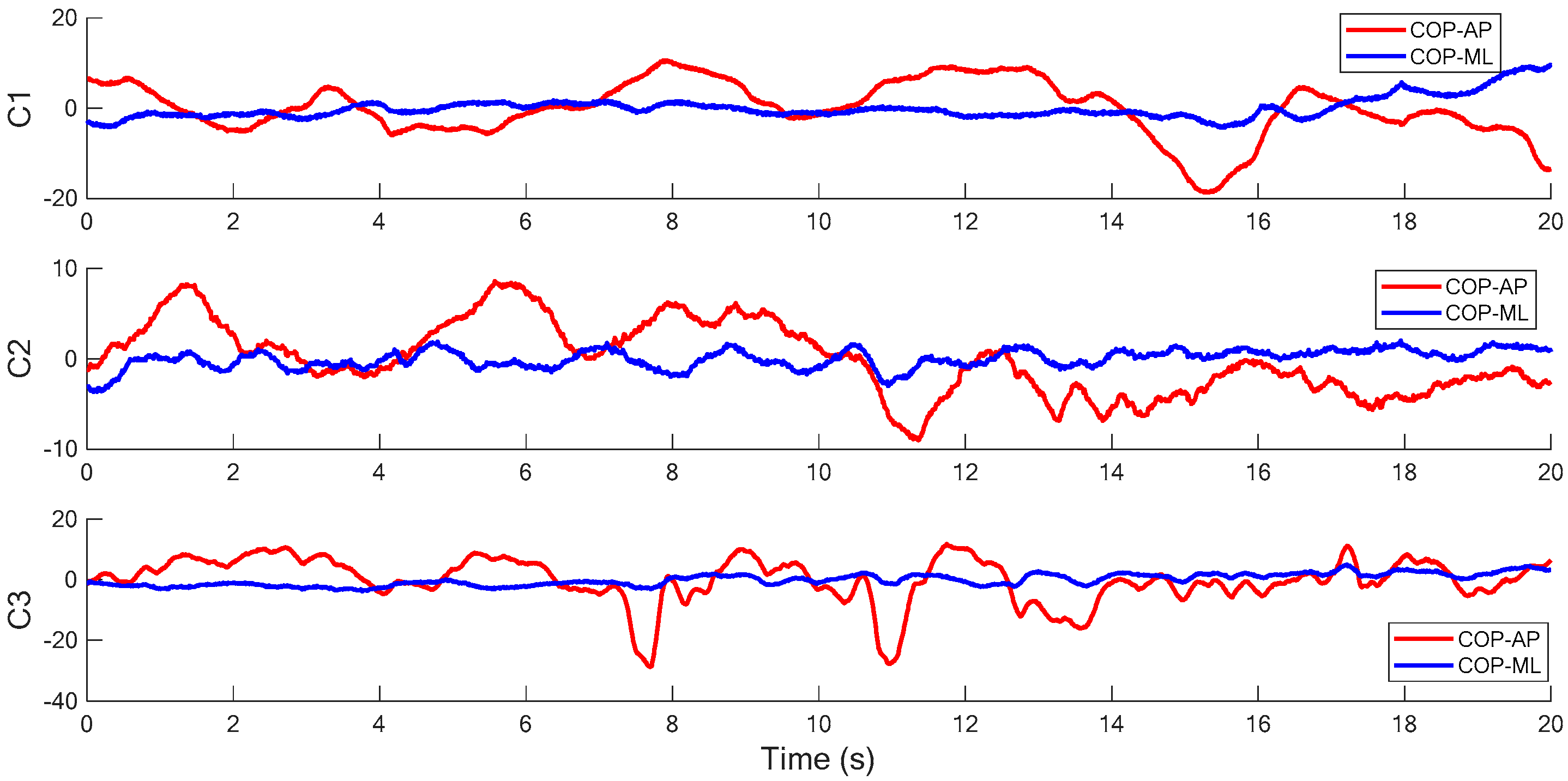
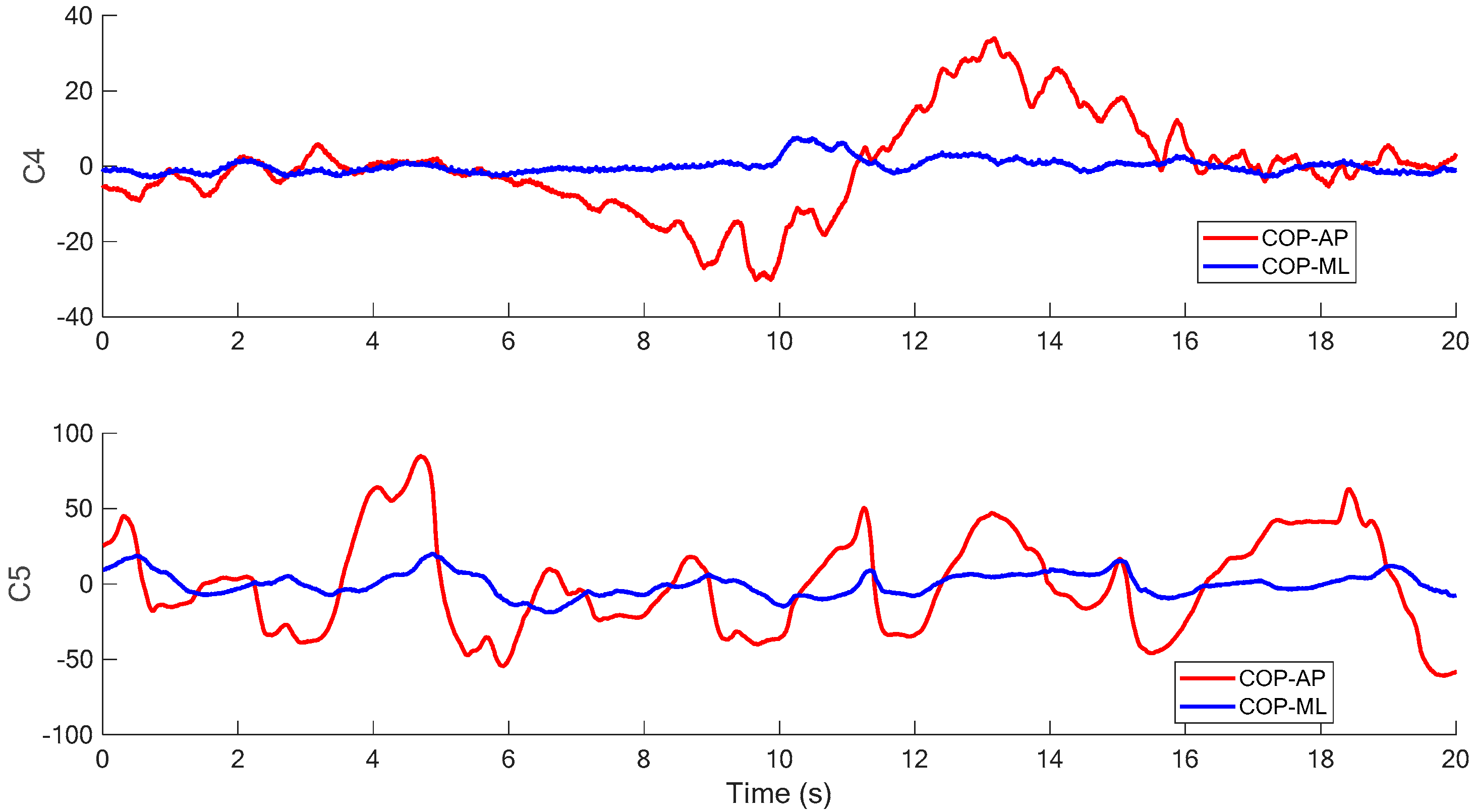
Figure 6 and Figure 7 illustrate the COP measurements of the five visual conditions (Conditions 1 to 5, as shown in Table 1) in the SOT of this research. It is found in the figures that the examinee generally has more sway variance in the AP direction than in the ML direction. A similar phenomenon can also be observed in most of the other COP measurements. The inference is reasonable because the structure of legs and ankles has more capability against the perturbation in the ML direction than in the AP direction while the examinee stands in the normal posture. Therefore, it is assumed in this study that the acceleration measurement in AP direction dominates the balancing characteristics as the examinee sways for most tests.

Based on the concept of PCA, the first principal component corresponds to the COP signal component in the AP direction. The second principal component corresponds to the COP signal component in the ML direction. The third principal component is attributed to the gravitation of the vertical component. This inference was drawn from the fact that the acceleration measurement had less variance in the direction parallel to the gravitation than the directions perpendicular to the gravitation.

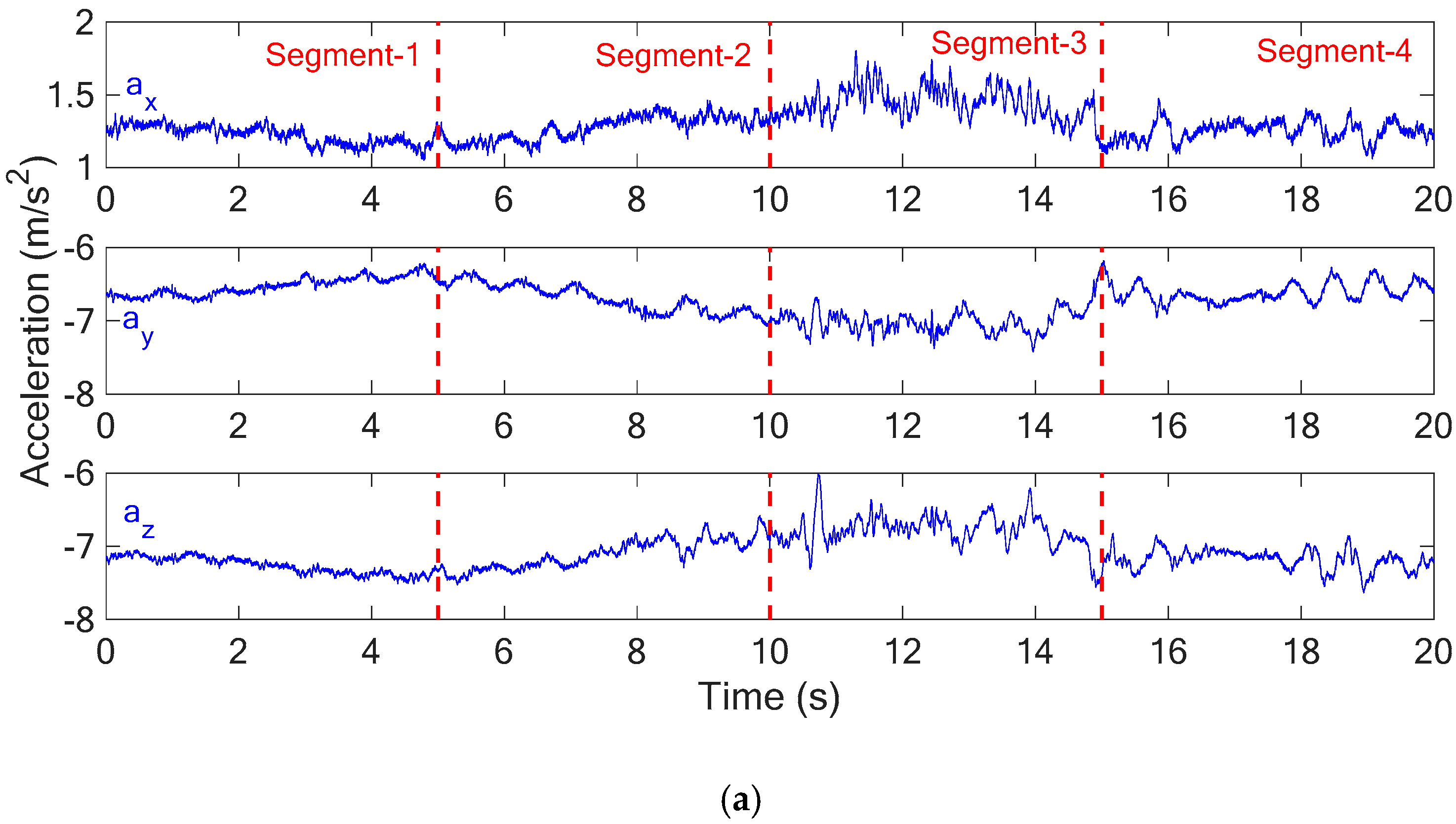
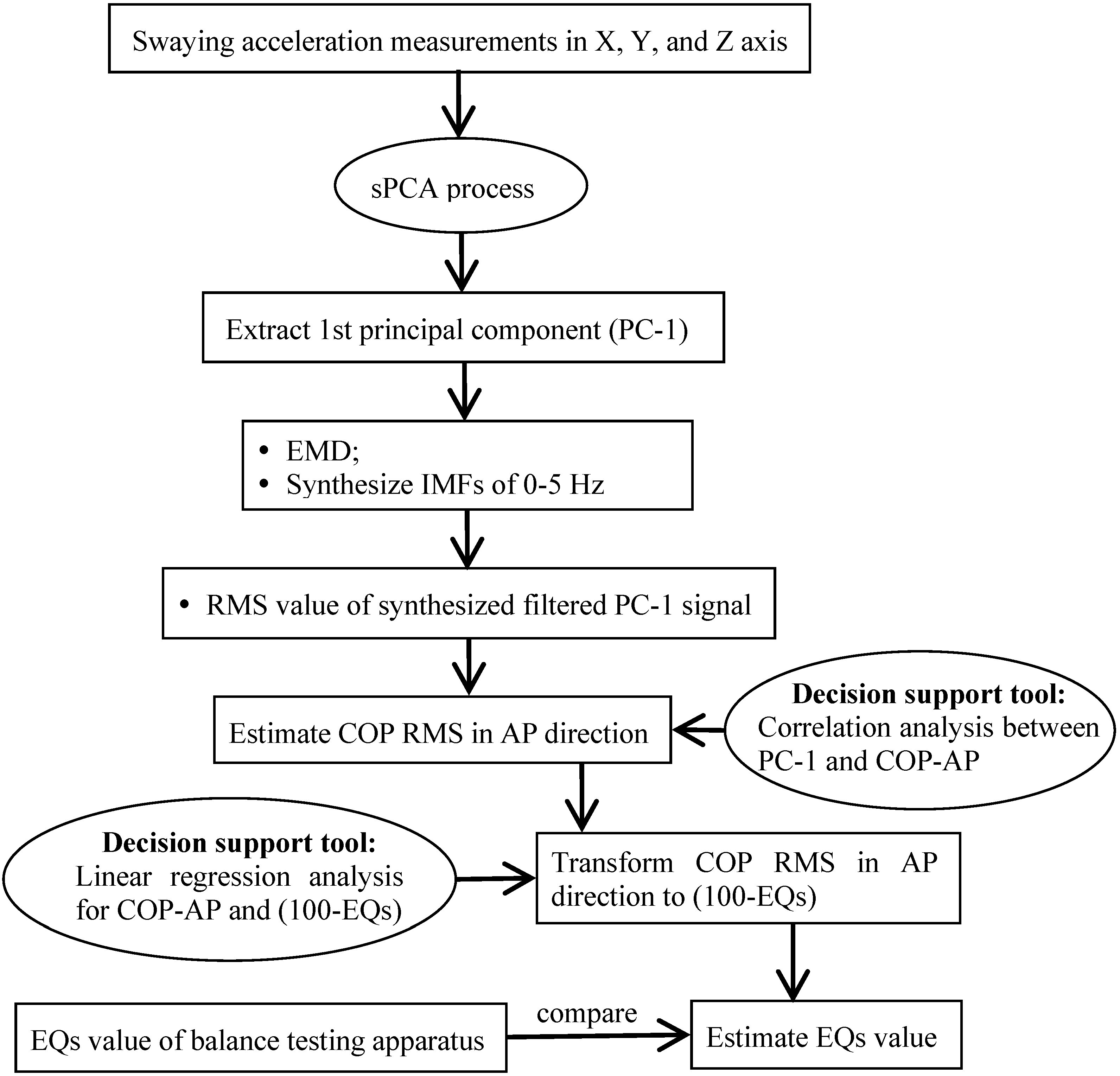
Although the PCA is capable of transforming the acceleration signals into the three principal components corresponding to the AP, ML and vertical directions conceptually, it is, however, apparently unable to reflect the instantaneous variation in the projection of gravitation onto the three measured components in case of the time-varying tilting accelerometer if the PCA is employed to process the signal throughout the whole data length (20 s). In order to address this concern and to deal with the time-varying problem of directivity variation on the oblique accelerometer, the segmentalized PCA (sPCA) was proposed in this research to accurately extract the time-varying components corresponding to the acceleration components that are perpendicular to the gravity at the different instants during the human body’s sway.

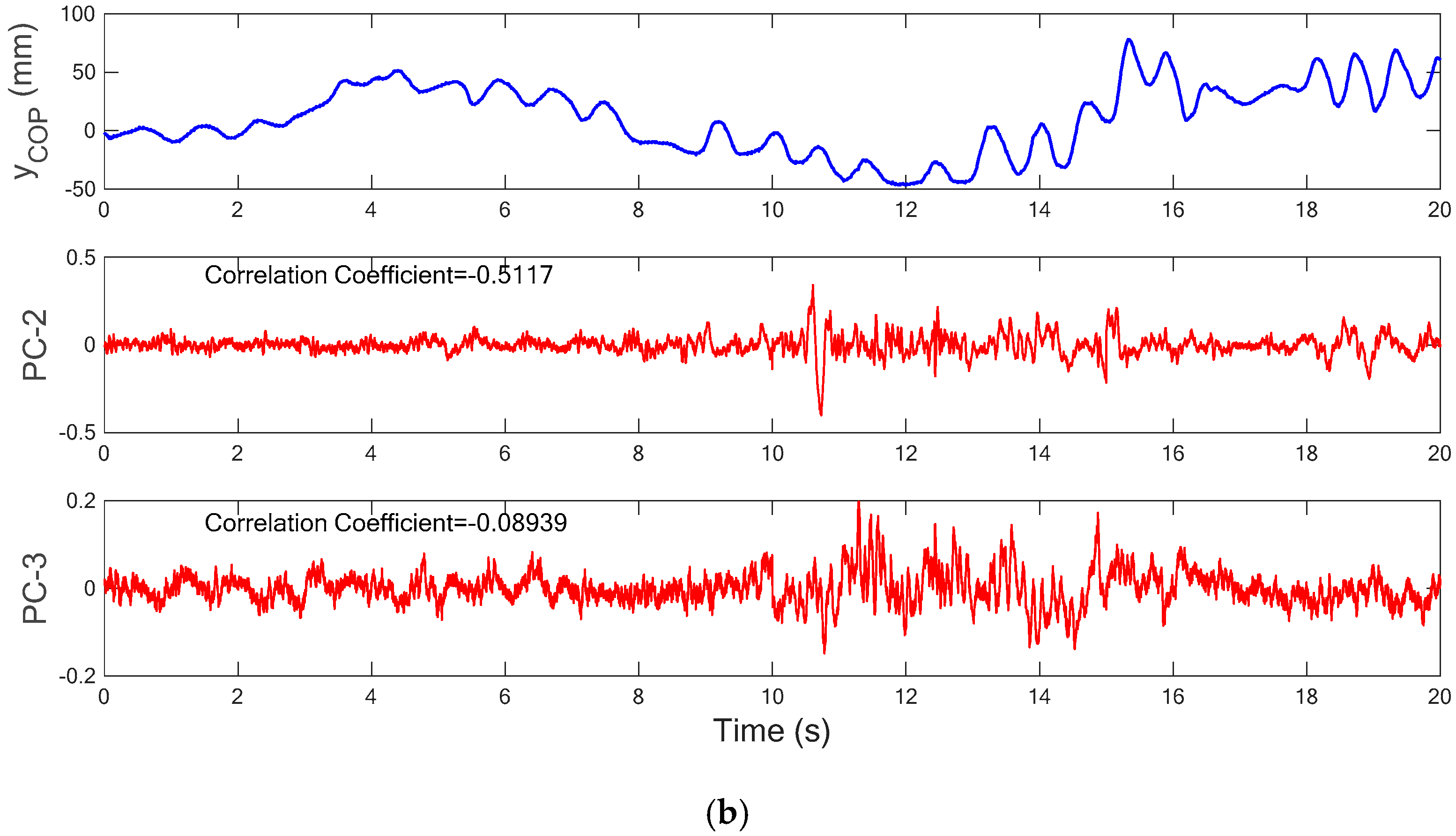
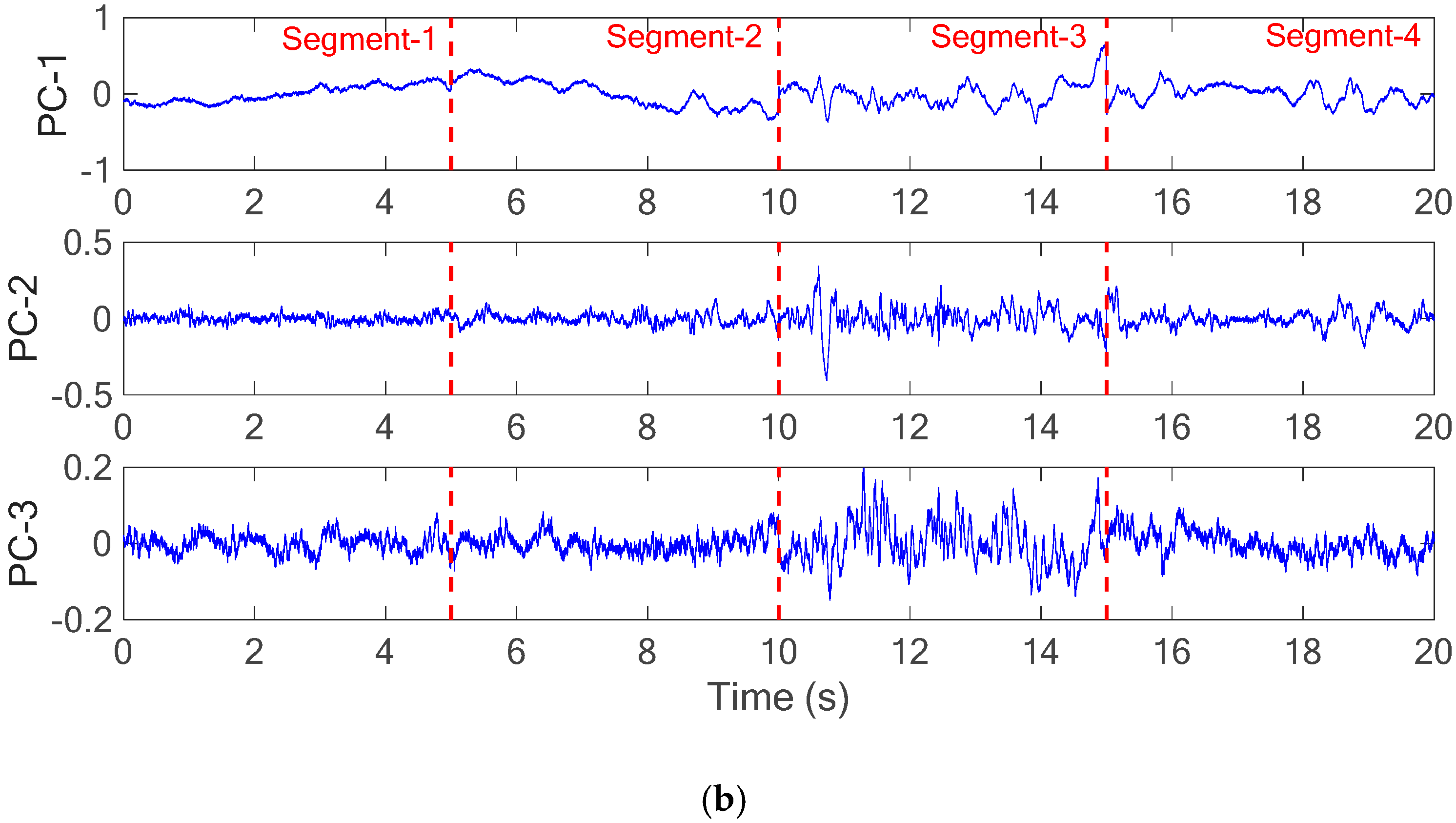
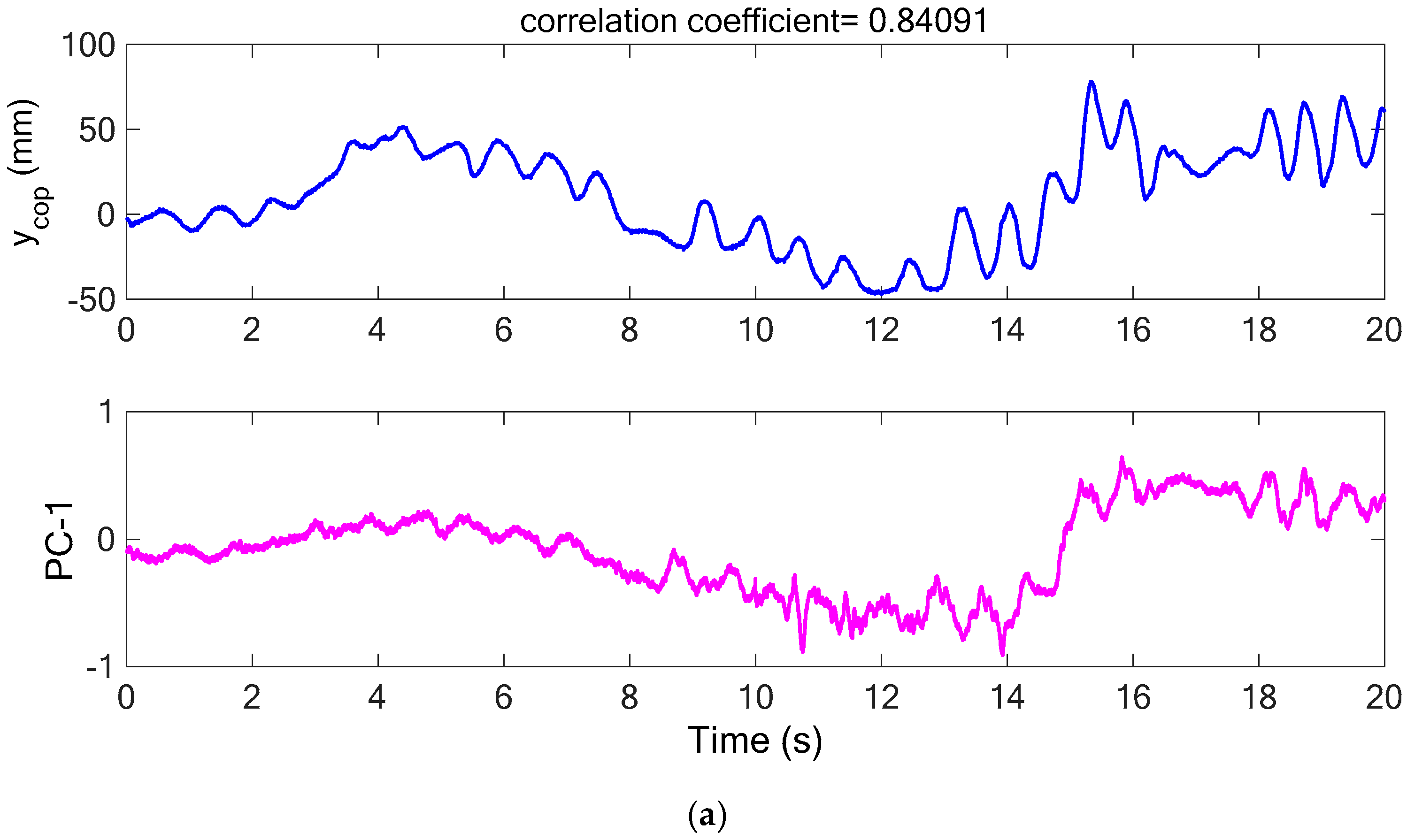
As illustrated in Figure 8a, the acceleration measurements in X-, Y- and Z-directions were divided into four segments and then the PCA was applied for each segment to determine the three principal components (PC-1, PC-2 and PC-3), as shown in Figure 8b. With the connected principal components of each segment, Figure 9a shows the comparison between the COP measurement in the Y-axis (AP) and the first principal component (PC-1) of acceleration signals. It is noted that the PC-1 of the acceleration measurements has similar variation trend with the COP measurement in the AP direction and the correlation coefficient between the two sets of series was calculated as 0.841. As compared with the PC-2 and PC-3 of the acceleration signals, their variation trends are very different from the COP measurement in the AP direction (as shown in Figure 9b), and thus, they have correlation coefficients of −0.512 and −0.089, respectively. The high correlation coefficient between the COP measurement in the AP direction and the PC-1 of the acceleration measurements demonstrates that it is sufficient to accurately predict the COP measurement in the AP direction. Therefore, it is feasible to utilize the processed acceleration measurement to represent the COP signal for evaluating the human body’s balancing ability.

4. Equilibrium Score (EQs) Estimation

A high correlation between the COP in the Y-axis and the first principal component of acceleration signals has been validated in the previous section, and thus it is feasible to use the acceleration measurements representing the COP-based evaluation for human balancing ability. Furthermore, in the field of clinical medicine, the balancing ability of patients is generally assessed through the commercial computer-aid balance testing apparatus in SOT and is broadly quantified in terms of the equilibrium score (EQs). The EQs of patients’ balancing ability is mainly computed through the measurement of COP. The EQs is defined from zero to one hundred. The EQs value of one hundred means an ideal stability while the EQs value of zero represents a tumble. In order to verify the accuracy of analogy between the acceleration measurements and the COP-based EQs evaluation at the balance testing apparatus, the datasets that include the synchronous measurements of body swaying acceleration and COP as well as the EQs evaluation were collected from the Department of Physical Therapy and Assistive Technology in National Yang-Ming University, in which the commercial computer-aid balance testing apparatus was utilized to assess the balancing ability of patients in the five visual conditions. The collected data consisted of 85 sets of acceleration signals and COP measurements that were recorded in the SOT of different examinees. The examinees that had normal balancing abilities in a majority were evaluated through some of C1 to C5 of SOT. All the data were available as the format of digits in text which can be processed and analyzed in MATLAB software.

Before the EQs estimation was investigated, all the collected data was first processed through the correlation analysis to obtain the statistical result of correlation coefficients between the COP measurements and the acceleration signals. Figure 10 shows the results of correlation coefficients between the COP measurements in the AP direction and the three data sets that are the PC-1 of acceleration measurements through the sPCA (with segment length of 1.0 second), the PC-1 of acceleration measurements by using the PCA for the whole signal length, and the original acceleration measurements in the Y-direction, respectively. As shown in the figure, the COP signals in the AP direction have higher overall correlation with the PC-1 of the acceleration measurements with the sPCA process (mean correlation coefficient around 0.78) than the PC-1 through the pure PCA for the whole signal length (mean correlation coefficient around 0.41), as well as the original acceleration measurements in the Y-direction (mean correlation coefficient around 0.40). The correlation analysis apparently shows that the acceleration measurements can be utilized to accurately predict the COP signal in the AP direction through the sPCA, and hence, it is feasible to use the cheap bind-in accelerometer for estimating the human being’s balancing ability instead of the expensive bulky COP measurement system.

Since the transformation from the COP measurement to the EQs is unavailable in this study, the statistical computation can be used to simply derive the relationship between the COP signals and the EQs. Define the swaying level to be (100 EQs). The root-mean-square (RMS) values of COP measurement resultants and the corresponding (100 EQs) values are shown in Figure 11. It is apparent that the transformation between the RMS values of COP measurement resultants and corresponding (100 EQs) values can be derived through the regression analysis. Similar results were also obtained by linear regression to derive the relationship between the RMS values of COP measurements in the AP direction and the corresponding swaying levels, as shown in Figure 12. As shown in these two figures, it is noted that the EQs values can be accurately derived through the linear regression process only using COP measurements in the AP direction.

As mentioned previously, the analysis shows that the COP measurements in the AP direction have high correlation with the first principal component of the acceleration measurements. Therefore, it is feasible to estimate the EQs values through the analysis of the swaying acceleration signals that are measured by the tri-axis capacitive accelerometer. Figure 13 shows the flow chart of signal processing in estimating the EQs values in terms of the acceleration measurements. The human body swaying accelerations were measured by the bind-in tri-axis capacitive accelerometer that is capable of effectively capturing the signals at very low frequencies of human body swaying. The acceleration signals were then processed by using the proposed sPCA to extract the first principal component (PC-1). The signal of PC-1 was separated by the EMD method and the IMFs within the frequency range of 0–5 Hz were synthesized for the further procedure. The RMS value of the synthesized filtered PC-1 signal was calculated and then transformed to estimate the RMS value of COP signal in AP-direction by means of the a priori correlation analysis. Through the a priori linear regression analysis between (100 EQs) and the COP-AP RMS, the EQs values can be estimated. It is noted that the correlation analysis and the linear regression method were utilized as the decision support tools for data transformations among the acceleration signals, COP measurements and (100 EQs) values. The EQs values that were obtained by the commercial computer-aid balance testing apparatus were also utilized to compare with the ones that were estimated from the acceleration measurements. Figure 14, Figure 15, Figure 16, Figure 17 and Figure 18 show the EQs values which were estimated through the acceleration measurements and the EQs values which were obtained by the commercial computer-aid balance testing apparatus in C1 to C5 of SOT. These figures demonstrate that most of the estimated EQs values are close to the EQs values that were obtained by the balance testing apparatus.

Table 2. Mean absolute percentage error (MAPE) of the estimated EQs values in each visual condition of the sensory organization test (SOT).

	C1	C2	C3	C4	C5
MAPE	1.95%	2.56%	4.16%	4.17%	11.63%

shows the mean absolute percentage error (MAPE) of the estimated EQs values in each visual condition of SOT compared with the EQs values that were displayed in the balance testing apparatus, which is defined as:

$$MAPE=\frac{\left|EQ{s}_{est}-EQ{s}_{app}\right|}{EQ{s}_{app}}\times 100\%$$

(6)

where, EQs_est represents the estimated EQs value and EQs_app represents the EQs value displayed in the balance testing apparatus. As shown in Table 2, high accurate EQs estimation can be obtained through the swaying acceleration measurement of the human body as well as the proposed signal processing steps in most of the SOT cases except for some of the cases in C5. The overall accuracy of the estimated EQS values was 95.11%.

5. Conclusions

In this research, the proposed sPCA method was employed to reduce the influence of the measured gravitation component projected onto the horizontal components while the bind-in capacitive accelerometer was utilized to measure the human body’s sway and tilt inevitably. A high correlation between the acceleration measurements and the COP signals of the human body’s sway can thus be derived. Therefore, the acceleration measurements of the human body’s sway can be utilized to represent the human balancing ability with lower hardware expense. Furthermore, the RMS values of COP can be estimated to quantify the EQs values of the human body’s balancing ability in the SOT. The analysis results show that the estimation MAPE of 4.89% can be obtained through the collected SOT data.