Abstract
Numerical simulations were conducted to investigate the transitional characteristics of shock reflections in the dual solution region using laser energy deposition. The numerical approach was validated by comparison to experimental results of the deposition laser energy in front of a blunt model. The simulation results show that the energy deposition in the freestream region can induce a transition of the shock reflection system and the transition characteristics can vary with the position and energy of the laser deposition. As the amount of energy increases, the time required for the transition also increases, and the transition cannot occur when the energy that is applied exceeds a certain level. The time required for the transition can be reduced when the position of energy deposition is moved downstream. The results also show that the transition does not occur regardless of the deposited energy when the laser energy is deposited on the symmetry line.
1. Introduction
In supersonic flow, various types of shock waves are generated depending on the shape of objects that are involved. Research on the shock–shock intersection and shock reflection on a wall has been conducted for many years. Mach reflection and regular reflection can occur at the same freestream Mach number in some supersonic regions [1,2], which are called the dual solution domain. Transitions between regular reflection and Mach reflections were also observed in experimental and numerical studies that were performed in this region. However, the mechanism has not been clearly identified. Hornung et al. [3] and Ben-Dor et al. [4] postulated that the structure of the reflected shock that is generated in the dual solution domain has a hysteresis effect that is influenced by the shape of the shock wave that is generated before it enters the dual solution domain. They also reported that the three-dimensional effect could promote the hysteresis effect.
Various methods have been proposed to avoid unfavorable shock structures and to derive advantageous conditions. The shock structure that is generated around a supersonic vehicle and its strength have a great influence on the performance. In early research, there was an attempt to change the shape of a shock wave by attaching an aerospike structure to the forebody. However, such physical structures have problems such as excessive heat load at the end, additional load at the off-design point, and rotational force when maneuvering. Since then, methods for reducing the load of the object without a physical structure have been proposed, such as the gas-injection technique. However, the equipment size that is required is not affordable for flight, so a technique has been proposed using energy that could be used independently for the operating conditions.
Electromagnetic waves, microwaves, and laser energy are considered possible sources of energy deposition. Azarova et al. [5] investigated the effect of reducing drag by deposition slit-shaped microwaves in front of cone-shaped objects. Hong et al. [6] and Sangtabia et al. [7] performed similar studies using a hemispherical model to investigate the effect of the repetition rate on the drag reduction. Recently, Elias et al. [8] performed an experiment using a femtosecond Laser. Hoang et al. [9,10,11] and Sasoh et al. [12] deposited laser energy at an intake system and examined the effects on the flow control and performance.
Based on a similar principle, the transition from Mach reflection to regular reflection can benefit the performance of high-speed vehicles. Many studies on Mach reflections and regular reflections in supersonic flows have been conducted for this purpose, which can be useful for improving the performance of a supersonic intake. However, few studies have made realistic models or structures to control or generate favorable operating conditions in the supersonic region, although the transition between regular reflection and Mach reflections has been confirmed by many experiments and numerical simulations [4,13,14,15,16,17,18,19].
The aim of this study is to use laser energy deposition to observe the possibility of transitions from Mach reflection to regular reflection in the dual solution region occurring. The results could be used to improve the performance of high-speed vehicles. For this purpose, shock waves were generated using two symmetrical wedges with the same angle, and laser energy was deposited in the freestream region near the shock wave as a disturbance source.
It is reasonable to focus the energy in the freestream region in front of the shock wave to consider a more realistic operating environment. Energy deposition in the area between the shock waves and the wedge surface is less practical because the area can be too small for certain conditions to focus the laser energy. Furthermore, additional factors such as the refraction of the laser beam should be considered. These factors were considered in this study, and changes in the flow structure were observed through computational simulations while changing the position and intensity of the laser energy in the dual solution domain. The characteristics of the transition from Mach reflections to regular reflections were investigated through various energy deposition scenarios.
2. Analysis Methods
2.1. Numerical Techniques
A two-dimensional unsteady Reynolds-averaged Navier-Stokes (RANS) analysis was performed to effectively simulate the generation and transition of shock reflections using symmetry wedges in the dual solution domain. The three-dimensional effect has more impact on the transition from regular reflection to Mach reflection and tends to reduce the height of Mach reflection [4], so two-dimensional studies are used for conservative simulations. Finite Volume Method (FVM) code was developed to simulate high-enthalpy flow with shock waves. According to Mortazavi et al. [20], turbulence has little effect on the generation and transition of the reflected wave, so the viscosity is not considered in this study. The inviscid convection term was calculated by applying the Advection Upstream Splitting Method (AUSMDV) scheme, and the Monotonic Upwind Scheme for Conservation Laws (MUSCL) technique was applied to the interface flux.
Temporal discretization was computed using the fourth-order Runge-Kutta (RK) method, and the T-model proposed by Yan et al. [21] was used to simulate the laser energy that was applied to the flow. This model is well known for simulating the generation of plasma by laser energy deposition and the propagation of blast waves. A high-powered laser is used to generate a blast wave and the laser operates with pulsed discharge. However, the duration of the pulse is only about 10 ns, which is much shorter than the time scale of the flow.
The energy deposition is represented by a symmetric temperature with a Gaussian distribution and the flow density is unchanged because the deposition time is very short. The temperature change of the energy deposition region is expressed as follows:
where r0 is an arbitrary value that is usually defined as the radius of the deposition area, r. The deposition region is assumed to be a sphere and the radius, r, is calculated from its volume. T0 is the peak temperature variation.
The amount of deposited energy E is:
where is the volumetric specific heat, is the freestream density, is the azimuthal angle, and is the swiping angle. The following is then obtained:
2.2. Code Validation
2.2.1. Computational Domain and Flow Conditions
The proposed numerical approach was validated to confirm that it can generate a reasonable solution for the energy deposition, propagation, and interaction between the shocks. It is desirable to compare the results with an experimental case of shock wave reflections in the dual solution domain by energy deposition. However, few experiments have been reported. Furthermore, wind tunnel test results contain flow perturbations, and the shock reflection can be sensitive to small disturbances in the dual solution region. Thus, it is difficult to examine the effects of energy deposition under conditions that are independent of the uncertainty of wind tunnel testing.
Experimental results using laser energy deposition around a sphere model were used to validate the numerical method. Adelgren et al. [22] investigated the propagation of a blast wave due to laser energy deposition and the interaction with the bow shock in front of a sphere model. The Mach number of the freestream is 3.45, the diameter (D) of the sphere is 25.4 mm, and the energy is deposited at 1.0D away from the sphere body. Further details of the flow conditions are shown in Table 1.

Table 1.
Flow conditions in the wind tunnel test (calculated).
Figure 1 shows the grid and boundary conditions that were used in the validation study. The computational domain is extended to 1.3D and only a section of the domain is modeled. Axisymmetric conditions are applied at the centerline and freestream conditions are assigned at the inlet. The properties of the outlet were determined from extrapolation.
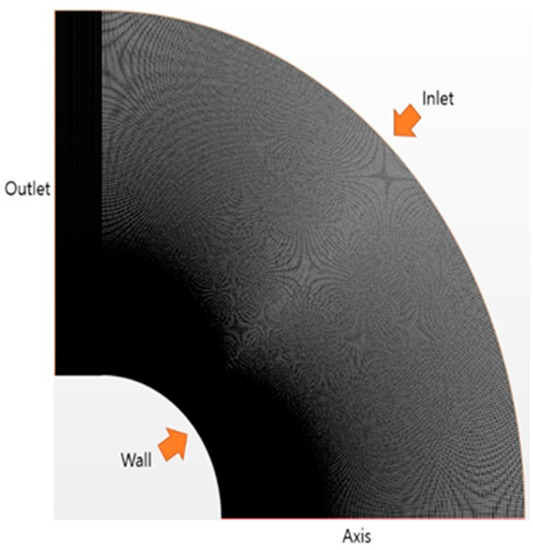
Figure 1.
Computational grid for energy deposition in front of the sphere.
2.2.2. Comparison with the Experimental Results
The amount of energy deposited in the flow can be obtained by Equation (1), however the ratio of the applied energy to the absorbed energy is unknown. In a previous study [23], it was assumed that the same energy is deposited when the simulation shows similar wave propagation and interaction phenomena to that in the experiment. Therefore, a reasonable absorption rate was sought by observing the flow characteristics according to the applied energy and comparing the result with the experiment.
Figure 2 shows Schlieren images from the experiment and simulation. As mentioned, it is hard to determine how much energy is absorbed into the flow, so a parametric study was performed with changes in either the radius of the focus or the deposited energy. The structures of the flow were compared, including the bow shock, reflected shock, blast wave, and vorticity. To do so, numerical Schlieren images were directly superimposed on the experimental results. The images had a fixed aspect ratio and the scale was determined by comparison of the diameter of the sphere.
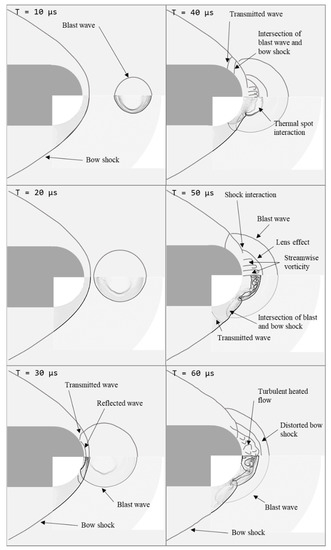
Figure 2.
Comparison between experiment [8] and the simulation results.
The results in Figure 2 were obtained with a radius of about 1.2 mm and energy deposited at 36.78 mJ/pulse. In the experiment, the energy that was applied to the flow was 283 mJ/pulse, which means that the absorbed energy is about 12% of the applied energy. The results showed good agreement with the experimental results in terms of the formation of the blast wave, the propagation, and the interaction with the bow shock in front of the sphere. Furthermore, there was very good agreement between the results of the complex vortex structure due to the lens effect [24], which results from the interaction between the bow shock and a blast wave that was observed at 30 μs after the deposition. In the dual solution problem, the same absorption rate was applied even if the deposition energy changed.
2.3. Shock Reflection in the Dual Solution Domain
2.3.1. Computational Domain
Symmetric wedges with a length of 25.4 mm were used to generate oblique shock waves in the dual solution domain. The boundary conditions and computational grid are shown in Figure 3. The grid was generated using a one-side hyperbolic tangent function, which produced a cluster near the end of the wedges in the expansion zone. The minimum size of the grid was 2.0 × 105– m, which was determined based on the validation test. Even if the angle of the wedges changes, the freestream Mach number and the minimum height of the contraction zone remain the same. The flow parameters are shown in Table 2.

Figure 3.
Computational grid for the shock reflection study.

Table 2.
Flow conditions for the shock reflection study.
2.3.2. Shock Reflection in the Dual Solution Domain
When the freestream velocity exceeds a critical Mach number (about 2.202), it is theoretically possible for both regular reflection and Mach reflections to occur at the same Mach number [25,26,27]. This region is known as the dual solution domain, which lies between the von Neumann and detachment criteria. Figure 4 shows the shock reflection region as a function of the wedge angle in the range of the freestream Mach number. At Mach 3.45, the dual solution was obtained when the wedge had an angle of 20 to 24°.
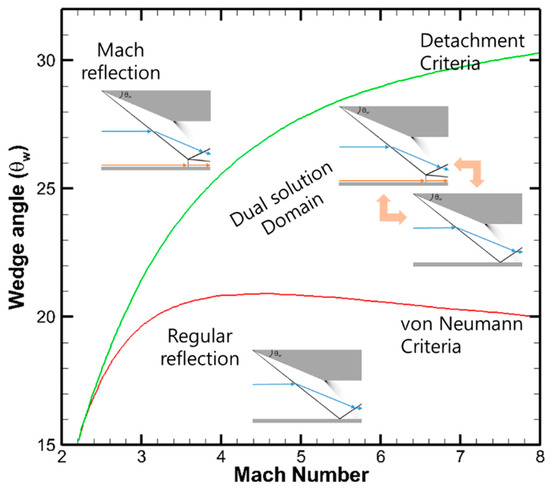
Figure 4.
Domains of possible shock reflection configurations.
Figure 5 shows the oblique shock and the following reflected shock for wedge angles of 23° and 24°. When the wedge angles are between 21° and 23°, the flow structure and the characteristics of the reflected shock wave are the same, but as the wedge angle increases, the angle of the oblique shock wave also increases and reflection occurs upstream. The results suggest that the two symmetric oblique shocks emanating from the opposite wedge generate regular reflection when the wedge angle is less than 23°. However, Mach reflection is observed when the wedge angle is larger than 23°. This is consistent with the observation in previous theoretical studies that Mach reflections are favorable in the vicinity of the detachment criteria.
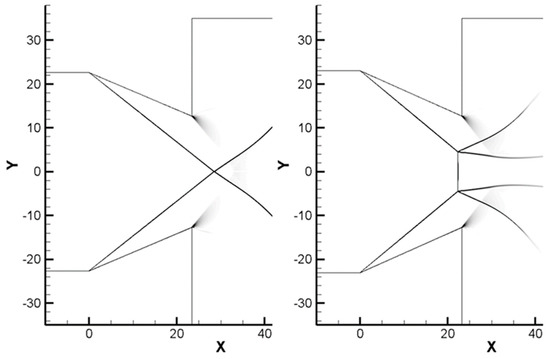
Figure 5.
Regular reflection (left, 23° wedge), Mach reflection (right, 24° wedge).
2.3.3. Transition from Regular Reflection to Mach Reflection
Theoretically, shockwave reflections in the dual solution domain could be regular or Mach reflections, but the mechanisms for determining the reflection characteristics are not fully understood. However, experiments were performed while changing either the distance between the wedges, the angle of the wedges, or inflow conditions, which showed that the probability of transition from regular reflection to the Mach reflections is high when there is a disturbance in the pressure or density upstream [28,29].
In the present study, the transition occurred when the fluctuation of the pressure in the freestream region was intentionally applied to the wedges with angles less than 23°. The fluctuation is about 20% of its undisturbed value, which is similar to the value from previous research [4]. Comparing Figure 5 to Figure 6 shows that the regular reflection changed to Mach reflection for the same wedge angle of 23°. Once the transition occurred, the Mach reflections were maintained, even after the disturbance passed through the computational domain. Figure 6 shows the results of the transition for wedge angles of 22° and 23°. As the wedge angle increases, the height of the Mach reflection also increases because the interaction of the shock waves occurs upstream as the angle of the oblique shock wave increases.

Figure 6.
Transition of shock reflection for the 1D gap (left, 22° wedge/right, 23° wedge).
The reflection characteristics of oblique shock waves in the dual solution domain are influenced by the angle of the wedge and the freestream conditions [18,30]. However, few studies have been performed on the effect of the distance between wedges. To observe the effect of the distance between wedges, the same amount of artificial pressure disturbance was applied upstream of the domain and the distance between the wedges was increased by 5 mm (~0.2D). In Figure 7, the same transition phenomena due to the disturbance were observed, however the position of the Mach reflection moved downstream due to the crossing position of the oblique shock wave moving downstream. Furthermore, the height of the Mach reflection was decreased as the distance between the wedges increased. It is expected that the transition from Mach reflection to regular reflection by a disturbance could be obtained more easily when the distance between two wedges is larger because the height of the Mach reflection is reduced. Therefore, wedges with a larger distance were implemented in this study.
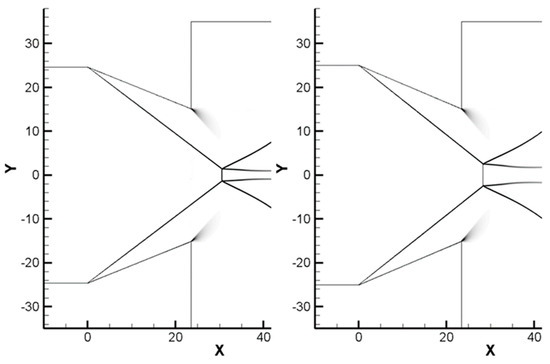
Figure 7.
Transition of shock reflection for the 1.2D gap (left, 22° wedge/right, 23° wedge).
3. Analysis of the Transition between Shock Reflections
In general, the presence of Mach reflections at a supersonic inlet increases the non-uniformity of the flow and the total pressure loss, which is undesirable for the performance of a vehicle. Therefore, it is common for most supersonic intakes to be designed so that regular reflections occur. Thus, it is meaningful for the Mach reflection to change into a regular reflection when a Mach reflection has occurred at the supersonic inlet under certain conditions. A numerical simulation was conducted with different positions and amounts of energy deposition.
As shown in Figure 8, three points were selected based on the streamwise distance from the edge of the wedge at 0 mm, 10 mm, and 20 mm. A wedge angle of 22° was used for the transition study. First, Mach reflection was induced by generating perturbation upstream as mentioned in Section 2.3.3
. Next, the energy was deposited at different points to find the possible transition from the Mach reflection back to regular reflection. As mentioned, the deposition is focused near the shock wave, but for position (c), the focus is on the centerline to compare the effect of symmetric deposition.
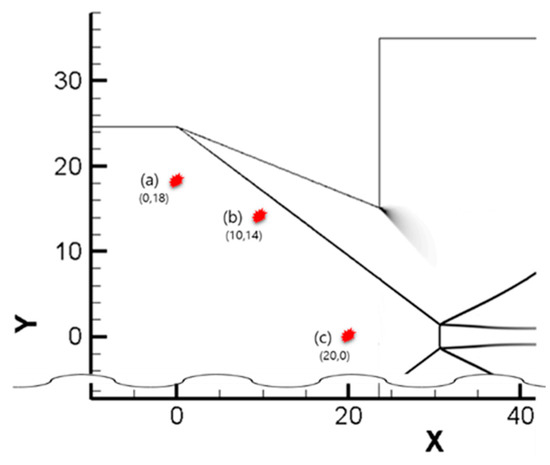
Figure 8.
Location of energy deposition.
3.1. Position (a)
Figure 9 shows the result of applying 107.5 mJ of energy upstream of the wedges (point (a) in Figure 8). The shock wave structure from the upper wedge collapses due to the blast wave that is generated by the energy deposition and the disturbance is also propagated in a part of the oblique shock wave that is generated from the lower wedge. At this time (T = 40 μs), the Mach reflections temporarily disappear due to the interaction between the oblique shock wave and the blast wave and then the disturbance from the energy deposition passes the computational domain (T = 120 μs). The blast wave that is caused by the energy deposition temporarily changes the symmetric shock structure into an asymmetric one.

Figure 9.
Interaction between blast wave and oblique shock, deposition upstream of the wedges. Energy: 107.5 mJ.
At 100 μs, two slip lines are observed: an upper slip line that meets the blast wave through the oblique shock from the lower wedge and a lower slip line from the Mach reflection that is generated by the interaction with the blast wave and the lower oblique shock. The Mach reflection that is generated by the interaction between the blast wave and the oblique shock has the form of a right running shock. The behavior of the blast wave propagating along with the upper wedge from 100 to 240 μs was examined in detail. The wave from the deposition initially propagates upstream and then downstream along with the flow over time and intersects with the flow of the preceding blast wave. This wave passes through Mach reflections between 200 and 240 μs, which creates a temporary shock wave structure that is similar to the one that developed when the angle of the upper wedge decreased.
According to a previous study [4], to induce a transition from Mach reflection to regular reflection in a steady flow, it is necessary to generate conditions in which the Mach reflection is not maintained, such as by reducing the wedge angle or increasing the freestream Mach number. In this study, the wedge is symmetrical, but the wave structure is temporarily asymmetrical due to the energy deposition. Thus, when the overall Mach reflection (oMR) changes to an overall regular reflection (oRR), there should be a moment when there are direct Mach reflection (DiMR) and inversed Mach reflection (InMR) structures (right or left running shocks) [31,32]. The definition of the oMR, oRR, DiMR, and InMR are described by Courant et al. [33].
Although this study was performed with an unsteady flow, the results show that a transition occurs under similar conditions. The preceding blast waves interacted with the oblique shock that is generated from the lower wedge and produced temporarily asymmetric Mach reflections. The subsequent blast wave induces a transition by generating a shock structure, which is similar to the structure that could be generated by installing a wedge with a smaller angle than the one suggested in the von Neumann criteria. It is assumed that the transition is terminated after about 600 us, however unlike in Figure 5 (left), a slip line was observed after the reflection point, which suggests that little disturbance remains.
Figure 10 shows the results from when the deposition energy is increased to 215 mJ at the same location (position (a)). Even though the energy level was increased, the phenomena are almost the same, including the collapse of the Mach reflection, regeneration, and the transition. In this case, as the deposited energy increases, the velocity of the blast wave increases, so the collapse of the reflected shock structure begins earlier than in the previous conditions. However, the last interaction between the blast wave and the Mach reflection occurs at 200 to 240 μs, which is nearly the same as in Figure 9. Distortion of the reflected shock is also observed. However, due to the generation of strong blast waves, the duration of the disturbance affecting the flow is increased and the transient Mach reflection remains longer during the regeneration process. Because of this effect, the time required for the complete transition is 1.5 times longer than in the previous conditions.
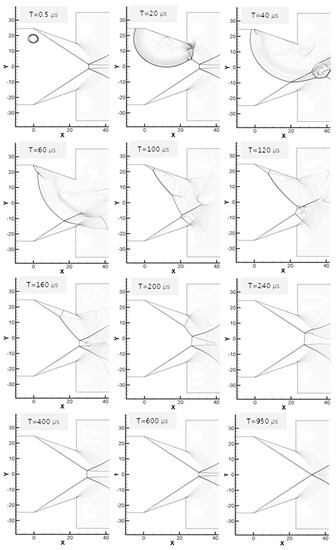
Figure 10.
Interaction between blast wave and oblique shock, deposition upstream of the wedges. Energy: 215.0 mJ.
Figure 11 shows the results for when the deposited energy is increased to 420 mJ. Different shock regeneration characteristics from the previous conditions are observed. In these conditions, the disturbance influences the oblique shock wave that is generated in the lower wedge as the intensity of the blast wave increases (T = 30 μs). As the blast waves reaching the lower wedge are reflected, superimposition and reflection of the complex shock waves develop near the wedge surface, which does not occur in the previous cases. The change of the reflection characteristics of the shock wave in this region is considered to play a major role in forming multiple normal shock waves downstream.
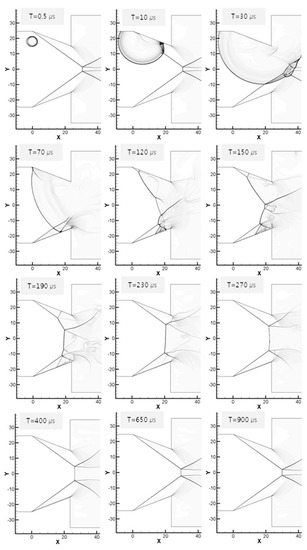
Figure 11.
Interaction between blast wave and oblique shock, deposition upstream of the wedges. Energy: 430.0 mJ.
Compared to the two preceding cases with lower laser energy, the main difference is in the location where the final interaction occurs. In previous cases, multiple shock interaction between the blast wave and reflected shock occurs from T = 40 μs to T = 120 μs, but it lasts to 230 μs for this case. The interaction is almost finished and the shock structure becomes stable before it contacts the last blast wave, which propagated upstream. Thus, the only effect of the intersect wave is changing the impinging shock angle. However, in the case of the highest energy, there is still much interaction left when the last blast wave passes the interaction region, and a strong Mach reflection develops in the contraction zone. Because there is no reason for the transition, the Mach reflection remains in the domain.
In addition, the interaction between the blast wave and shock wave does not continue in the expansion zone and the interference with the rarefaction wave generated at the tip of the wedge is not observed. This was assumed to contribute to the transition by changing the flow speed. It is concluded that even if the energy is deposited at the same position, the characteristics of shock wave interactions can be different for varying energy levels. In particular, the transition does not occur when too much energy is deposited to avoid Mach reflections near the von Neumann criteria of the dual solution domain and it could also be speculated that the transition could be induced efficiently by decreasing the energy.
3.2. Position (b)
Mouton et al. [30] conducted a study on the transition of regular reflection to Mach reflections by changing the location of the deposition between the wedge surface and oblique shock. A similar analysis was performed by moving the deposition position inside the contraction region (position (b) in Figure 8) to examine the effect of the position of the laser energy deposition on the transition characteristics. Figure 12 shows the computational results from when 107.5 mJ of energy is deposited at position (b). The intermediate collapse and regeneration process of the shock wave due to the blast wave can be considered to be qualitatively the same as the result of position (a). However, as the time for the blast wave to reach the upper oblique shock wave decreases, the last intersection of the blast wave and Mach reflection occurs between 150 μs and 180 μs in the expanded region.
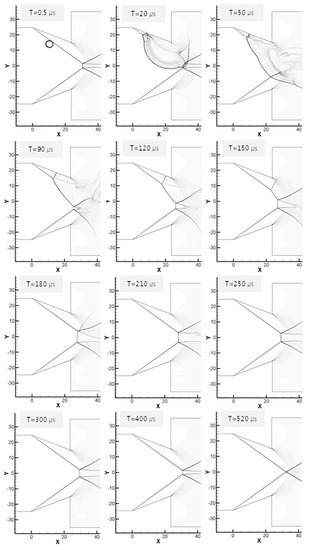
Figure 12.
Interaction between blast wave and oblique shock, deposition at the middle of the upper wedge. Energy: 107.5 mJ.
In these conditions, the transition occurs very slowly compared to the case of position (a), even after the disturbance disappears. However, the time for the transition to the regular reflection to be completed decreases by about 80 μs from T = 600 μs to T = 520 μs. It seems that this mainly results from the time difference of when the blast wave begins to interact with the oblique shock wave. Thus, it is expected that moving the focus of energy deposition into the contraction zone may contribute to promoting the transition from Mach reflection to regular reflection.
Figure 13 shows the results from doubling the energy of the laser to 215 mJ. Compared to Figure 12, the time that is required to complete the transition is increased due to the formation of a strong blast wave, which is the same tendency that was obtained from the result for position (a). In this case, disturbances from the blast wave passed through the computational domain faster than in the case of position (a). Compared with Figure 10, the transition time is 800 μs, which is 150 μs less than the energy applied to position (a). Thus, by moving the energy deposition point downstream from position (a) to position (b) in Figure 8, the transition can be promoted.
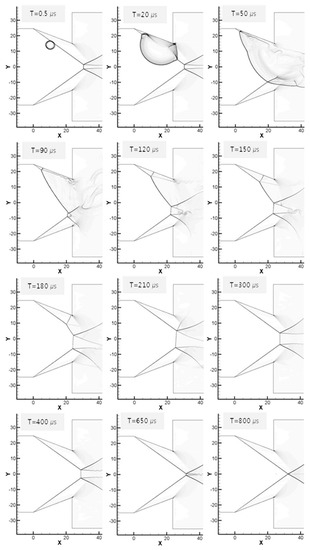
Figure 13.
Interaction between blast wave and oblique shock, deposition at the middle of the upper wedge. Energy: 215.0 mJ.
The deposition energy was increased further to 430 mJ, as shown in Figure 14. The simulation results are very similar to those in Figure 11. As the strong blast wave reaches the lower wedge surface, the reflected wave from this region influences the shock wave regeneration process. Similar to Figure 11, multiple normal shock waves are generated on the wedge. In this case, Mach reflection is maintained after the regeneration of the shock wave, which supports the previous claim that excessive energy deposition may have a negative impact on the shock wave transition in the dual solution domain.

Figure 14.
Interaction between blast wave and oblique shock, deposition at the middle of the upper wedge. Energy: 430.0 mJ.
Considering that a transition occurs at 215 mJ despite the strong Mach reflections, the following differences can be found in the simulation results. The final state of the shock reflection seems to be significantly affected by the position of the Mach reflection that occurs during the transition process. This means that a complex shock system that is caused by a disturbance should undergo interference from an expansion wave that is generated at the end of the wedge for a transition of the shock system. This is supported by the results obtained with 430 mJ of energy, where the effect of a disturbance only ends at the contraction zone. In that case, there is no interference with the expansion wave before it was stabilized and no transition is produced.
3.3. Position (c)
From the results thus far, it is expected that moving the deposition position downstream and not using excessive energy will be effective for the shock reflection transition, especially from Mach reflection to regular reflection. The focus of the laser energy was moved further downstream and on the centerline (point (c) in Figure 8). Figure 15, Figure 16 and Figure 17 show the results from when energy levels of 107.5 mJ, 215.0 mJ, and 430.0 mJ are applied. In this case, the shock wave disturbance due to the blast wave occurs in only a short interval of T = 10–160 μs.
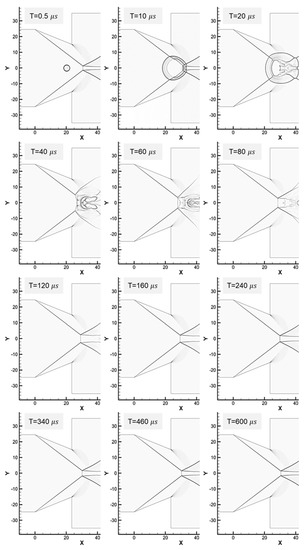
Figure 15.
Interaction between blast wave and oblique shock, deposition downstream of the wedges. Energy: 107.5 mJ.
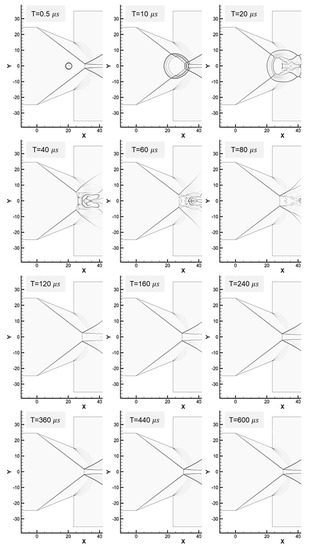
Figure 16.
Interaction between blast wave and oblique shock, deposition downstream of the wedges. Energy: 215.0 mJ.
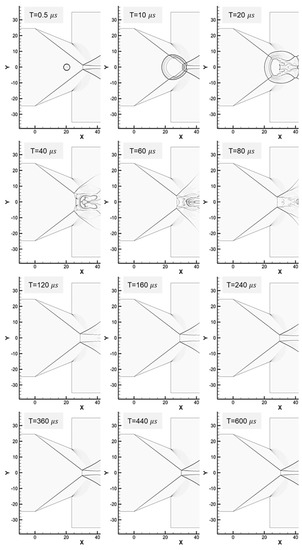
Figure 17.
Interaction between blast wave and oblique shock, deposition downstream of the wedges. Energy: 430.0 mJ.
As shown in the figures, no transition occurred under these deposition conditions. When 107.5 mJ of energy was deposited, the transition was not observed even though the interaction between the blast wave and the oblique shock wave continued up to the expansion zone. In contrast, when the energy was increased further, the interaction was terminated in the contraction zone. It seems that the difference in the transition characteristics resulted from the location of the deposition. In other words, when the focus was placed on the centerline, the structures of the shock waves from both wedges were changed at the same time, which is similar to the phenomena observed in the case of 430.0 mJ of energy at other positions. This concurrent distortion prevents the generation of an asymmetrical shock structure.
The residence time of the blast wave in the computational domain was also reduced as energy was deposited downstream. This results in Mach reflection after the disturbance passes the domain. This means that when introducing symmetrical disturbance, the transition from Mach reflection to regular reflection is not achieved regardless of the deposited energy. From these results, it is assumed that there is an optimal position that can cause a transition within a minimum time in the contraction section. Furthermore, even with a structurally symmetrical double wedge, it is possible to induce the transition by temporarily creating a virtual asymmetric wedge by selecting the energy deposition position unevenly.
4. Discussion
In this study, numerical studies on the transition characteristics with energy deposition were performed to avoid Mach reflections in the dual solution domain. A two-dimensional unsteady analysis was performed to efficiently simulate the flow around a symmetric geometry. In comparison with the experiment results using a hemisphere model, the proposed numerical method showed good agreement in the flow structures, such as the shock and blast wave propagation and reflections. In addition, the conditions under which Mach or regular reflection occurred in the dual solution domain were in good agreement with the theoretical study.
The computational results show that it is possible to transition from Mach reflections to regular reflections through energy deposition at an asymmetric location. The preceding blast waves that were generated by the energy deposition interacted with the oblique shock from the wedge and disrupted the Mach reflections. During the regeneration of the shock waves, the blast wave induces regular reflection, which has a similar effect to changing the wedge angle to below the von Neumann criteria through several additional interactions. The results showed that the transition occurred faster as the focus moved into the contraction zone when the same energy was deposited.
However, when more energy was deposited, the shock wave structure collapsed sooner, but the total time that was required for flow stabilization was increased due to the generation of a strong blast wave. As the level of energy increased further, the transition did not occur. The entire disruption of the shock system by strong blast waves prevented the local shock angle variation in the regeneration process. The results suggest that the expansion wave also plays a role in the transition. This tendency is maintained for different focal locations. However, when the focus of energy deposition lies on the symmetry axis, no transition occurs regardless of the energy level because the shock system is not changed to an asymmetric configuration by a disturbance.
These results suggest that the shock wave transition phenomena in the dual solution domain are affected by both the amount and the location of the energy. It is also expected that there is an optimal location for energy deposition that depends on the operating conditions and the shape of the structure. However, this study mainly focused on the feasibility of the proposed technique and the investigation of the transient shock wave characteristics by laser energy deposition. Thus, the effect of various parameters needs further investigation, including the freestream conditions, the length of the wedge, asymmetric arrangements, and three-dimensional effects.
Author Contributions
Conceptualization, S.K. and H.J.L.; methodology, S.K. and H.J.L.; software, S.K. and Y.K.; validation, S.K., Y.K., and H.J.L.; formal analysis, S.K.; investigation, S.K. and H.J.L.; resources, H.J.L.; data curation, S.K. and Y.K.; writing—original draft preparation, S.K. and Y.K.; writing—review and editing, H.J.L.; visualization, S.K. and Y.K.; supervision, H.J.L.; project administration, H.J.L.; funding acquisition, H.J.L.
Funding
This work was supported by the National Research Foundation of Korea (NRF) Grant, which is funded by the Government of Korea (MIST) (2017R1C1B5076748).
Conflicts of Interest
The authors declare no conflict of interest.
References
- von Neumann, J. Refraction, Intersection and Reflection of Shock Waves; NavOrd Report No. 203-45; Naval Ordnance Laboratory: White Oak, MD, USA, 1945. [Google Scholar]
- von Neumann, J. Oblique Reflection of Shocks; Explosives Research Report 12; Bureau of Ordinance: Washington, DC, USA, 1943. [Google Scholar]
- Hornung, H.G.; Oertel, H.; Sandeman, R.J. Transition to Mach reflection of shock waves in steady and pseudo-steady flow with and without relaxation. J. Fluid Mech. 1979, 90, 541–560. [Google Scholar] [CrossRef]
- Ben-Dor, G.; Ivanov, M.; Vasilev, E.I.; Elperin, T. Hysteresis processes in the regular reflection↔Mach reflection transition in steady flows. Prog. Aerosp. Sci. 2002, 38, 347–387. [Google Scholar] [CrossRef]
- Azarova, O.A.; Knight, D.D. An approach of drag force decrease for combined cylinder AD bodies under the action of microwave and laser energy deposition. Aerosp. Sci. Technol. 2017, 64, 154–160. [Google Scholar] [CrossRef]
- Yanji, H.; Diankai, W.; Qian, L.; Jifie, Y. Interaction of single-pulse laser energy with bow shock in hypersonic flow. Chin. J. Aeronaut. 2014, 27, 241–247. [Google Scholar]
- Sangtabi, A.R.; Ramiar, A.; Ranjbar, A.A.; Abdollahzadeh, M.; Kianifar, A. Influence of repetitive laser pulse energy depositions on supersonic flow over a sphere, cone and oblate spheroid. Aerosp. Sci. Technol. 2018, 76, 81–82. [Google Scholar] [CrossRef]
- Elias, P.; Severac, N.; Luyssen, J.; Tobeli, J.; Lambert, F.; Bur, R.; Houard, A.; Andre, Y.; Albert, S.; Mysyrowicz, A.; et al. Experimental investigation of linear energy deposition using femtosecond laser filamentation in a M = 3 supersonic flow. In Proceedings of the 2018 Joint Propulsion Conference, Cincinnati, OH, USA, 9–11 July 2018. [Google Scholar]
- Pham, H.S.; Myokan, M.; Tamba, T.; Iwakawa, A.; Sasoh, A. Impacts of energy deposition on flow characteristics over an inlet. In Proceedings of the 47th AIAA Fluid Dynamics Conference, Denver, CO, USA, 5–9 June 2017. [Google Scholar]
- Liu, H.; Yan, C.; Zhao, Y.; Wang, S. Active control method for restart performances of hypersonic inlets based on energy addition. Aerosp. Sci. Technol. 2019, 85, 481–494. [Google Scholar] [CrossRef]
- Pham, H.S.; Myokan, M.; Tamba, T.; Iwakawa, A.; Sasoh, A. Effects of repetitive laser energy deposition on supersonic duct flows. AIAA J. 2018, 56, 542–553. [Google Scholar] [CrossRef]
- Sasoh, A.; Kim, J.H.; Yamashita, K.; Sakai, T. Supersonic aerodynamic performance of truncated cones with repetitive laser pulse energy depositions. Shock Waves 2014, 24, 59–67. [Google Scholar] [CrossRef]
- Ivanov, M.S.; Gimelshein, S.F.; Beylich, A.E. Hysteresis effect in stationary reflection of shock waves. Phys. Fluids 1995, 7, 685–687. [Google Scholar] [CrossRef]
- Ivanov, M.S.; Zeitoun, D.; Vuillon, J.; Gimelshein, S.F.; Markelov, G.N. Investigation of the hysteresis phenomena in steady shock reflection using kinetic and continuum methods. Shock Waves 1996, 5, 341–346. [Google Scholar] [CrossRef]
- Ivanov, M.S.; Markelov, G.N.; Kudryavtsev, A.N.; Gimelshein, S.F. Numerical analysis of shock wave reflection transition in steady flows. AIAA J. 1998, 36, 2079–2086. [Google Scholar] [CrossRef]
- Chpoun, A.; Ben-Dor, G. Numerical confirmation of the hysteresis phenomenon in the regular to the Mach reflection transition in steady flows. Shock Wave 1995, 5, 199–204. [Google Scholar] [CrossRef]
- Ben-Dor, G.; Elperin, T.; Li, H.; Vasiliev, E.I. The influence of downstream-pressure on the shock wave reflection phenomenon in steady flows. J. Fluid Mech. 1999, 386, 213–232. [Google Scholar] [CrossRef]
- Ivanov, M.S.; Ben-Dor, G.; Elperin, T.; Kudryavtsev, A.N.; Khotyanovsky, D. Mach-number-variation-induced hysteresis in steady flow shock wave reflections. AIAA J. 2001, 39, 972–974. [Google Scholar] [CrossRef]
- Onofri, M.; Nasuti, F. Theoretical considerations on shock reflections and their implications on the evaluation of air intake performance. Shock Waves 2001, 11, 151–156. [Google Scholar] [CrossRef]
- Mortazavi, M.; Knight, D. Numerical simulation of energy deposition in a viscous supersonic flow past a hemisphere. In Proceedings of the 53rd Aerospace Sciences Meeting, Kissimmee, FL, USA, 5–9 January 2015. [Google Scholar]
- Yan, H.; Adelgren, R.G.; Bouszko, M.; Ivanov, M.; Kudryavtsec, A.; Khotyanovsky, D.; Elliott, G.S.; Knight, D. Laser energy deposition in quiescent air. In Proceedings of the 41st Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 6–9 January 2003. [Google Scholar]
- Adelgren, R.G.; Yan, H.; Elliott, G.S.; Knight, D.; Beutner, T.J.; Zheltovodov, A.A. Control of Edney IV interaction by pulsed laser energy deposition. AIAA J. 2005, 43, 256–269. [Google Scholar] [CrossRef]
- Mortazavi, M.; Knight, D. Numerical simulation of energy deposition in a supersonic flow past a hemisphere. In Proceedings of the 52nd Aerospace Sciences Meeting and Exhibit, National Harbor, MD, USA, 13–17 January 2014. [Google Scholar]
- Georgievskii, P.Y.; Levin, V.A. Unsteady interaction of a sphere with atmospheric temperature inhomogeneity at supersonic speed. Fluid Dyn. 1993, 28, 568–574. [Google Scholar] [CrossRef]
- Hornung, H.G.; Robinson, M.I. Transition from regular to Mach reflection of shock waves. Part 2. The steady flow criterion. J. Fluid Mech. 1982, 128, 155–164. [Google Scholar] [CrossRef]
- Molder, S. Particular conditions for the termination of regular reflection of shock waves. Can. Aeronaut. Space J. 1979, 25, 44–49. [Google Scholar]
- Ben-Dor, G. Shock Wave Reflection Phenomena; Springer: New York, NY, USA, 2007. [Google Scholar]
- Henderson, L.F.; Lozzi, A. Further experiments and transition of Mach reflection. Experiments and transition of Mach reflection. J. Fluid Mech. 1979, 68, 139–158. [Google Scholar] [CrossRef]
- Chpoun, A.; Passerel, D.; Li, H.; Ben-Dor, G. Reconsideration of oblique shock wave reflection in steady flows. Part 1. Experimental investigation. J. Fluid Mech. 1995, 301, 19–35. [Google Scholar] [CrossRef]
- Mouton, C.A. Transition between Regular Reflection and Mach Reflection in the Dual-Solution Domain. Ph.D. Thesis, California Institute of Technology, Pasadena, CA, USA, 2007. [Google Scholar]
- Li, H.; Chpoun, A.; Ben-Dor, G. Analytical and experimental investigations of the reflection of asymmetric shock waves in steady flows J. Fluid Mech. 1999, 390, 25–43. [Google Scholar] [CrossRef]
- Ivanov, M.S.; Ben-Dor, G.; Elperin, T.; Kudryavtsec, A.; Khotyanovsky, D. The reflection of asymmetric shock waves in steady flows: A numerical investigation. J. Fluid Mech. 2002, 469, 71–87. [Google Scholar] [CrossRef]
- Courant, R.; Friedrichs, K.O. Hypersonic Flow and Shock Waves, 5th ed.; Springer: New York, NY, USA, 1999. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).