Dynamic Analysis of Modified Duffing System via Intermittent External Force and Its Application
Abstract
1. Introduction
2. Duffing Oscillator Description
3. Design and Dynamic Characteristic Analysis of MD System
3.1. Design of MD System with Intermittent External Force
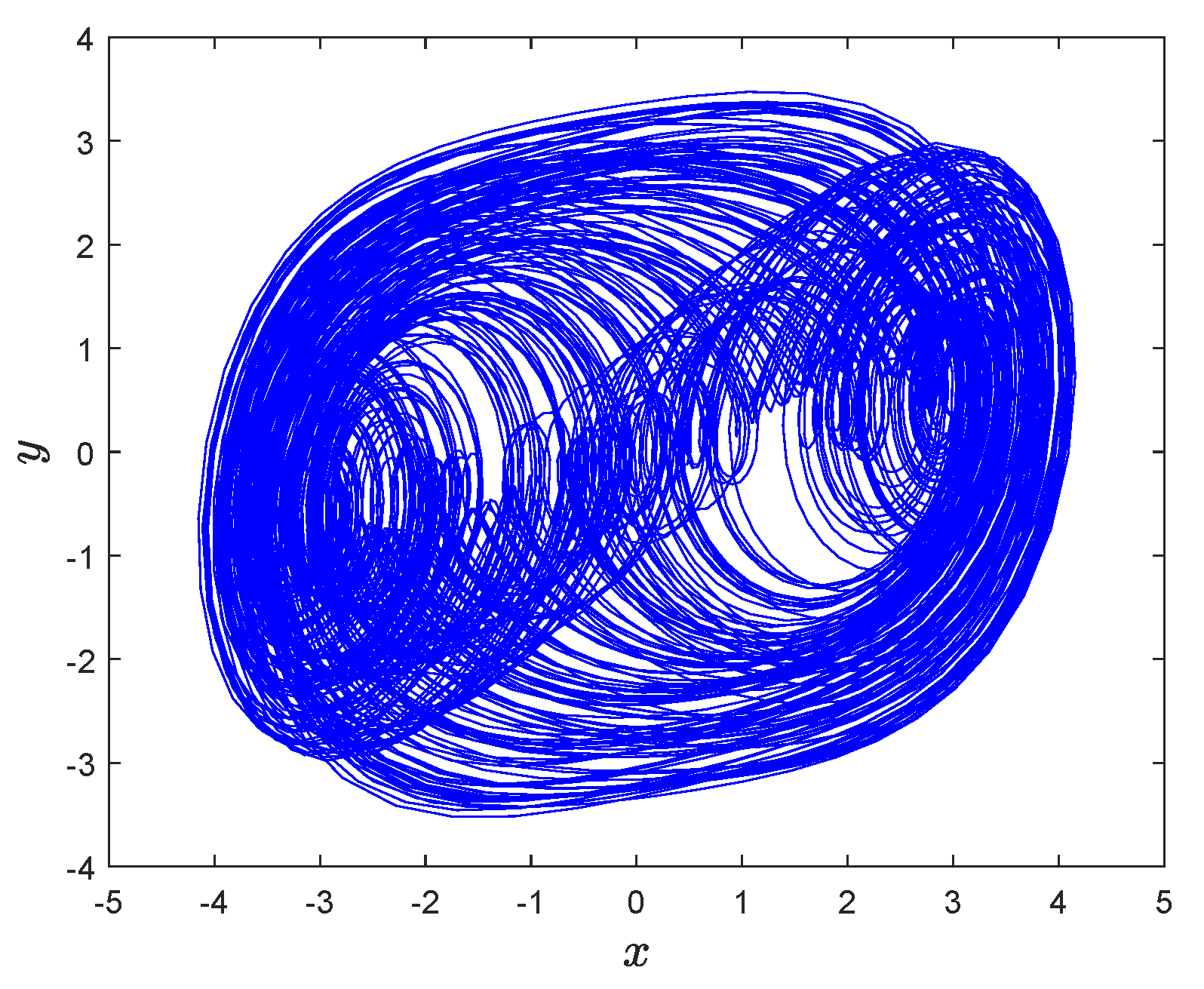
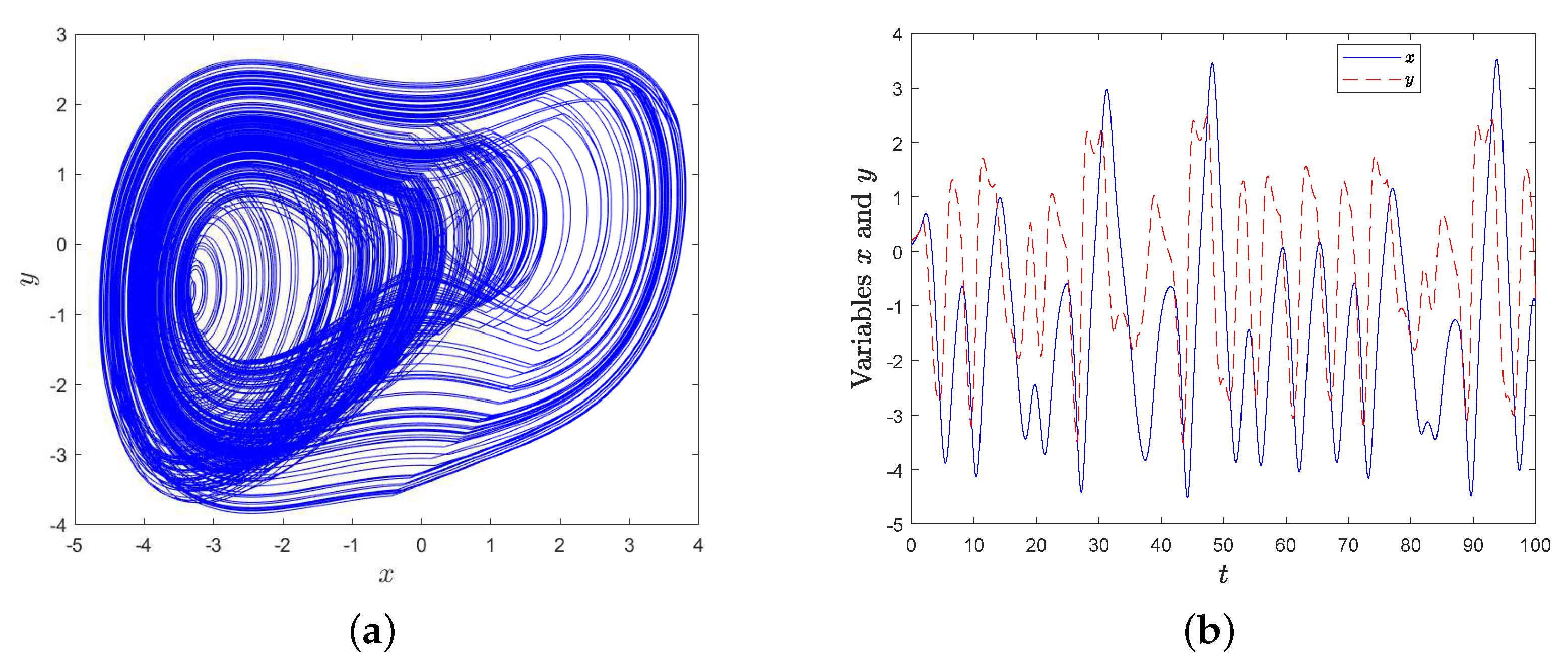
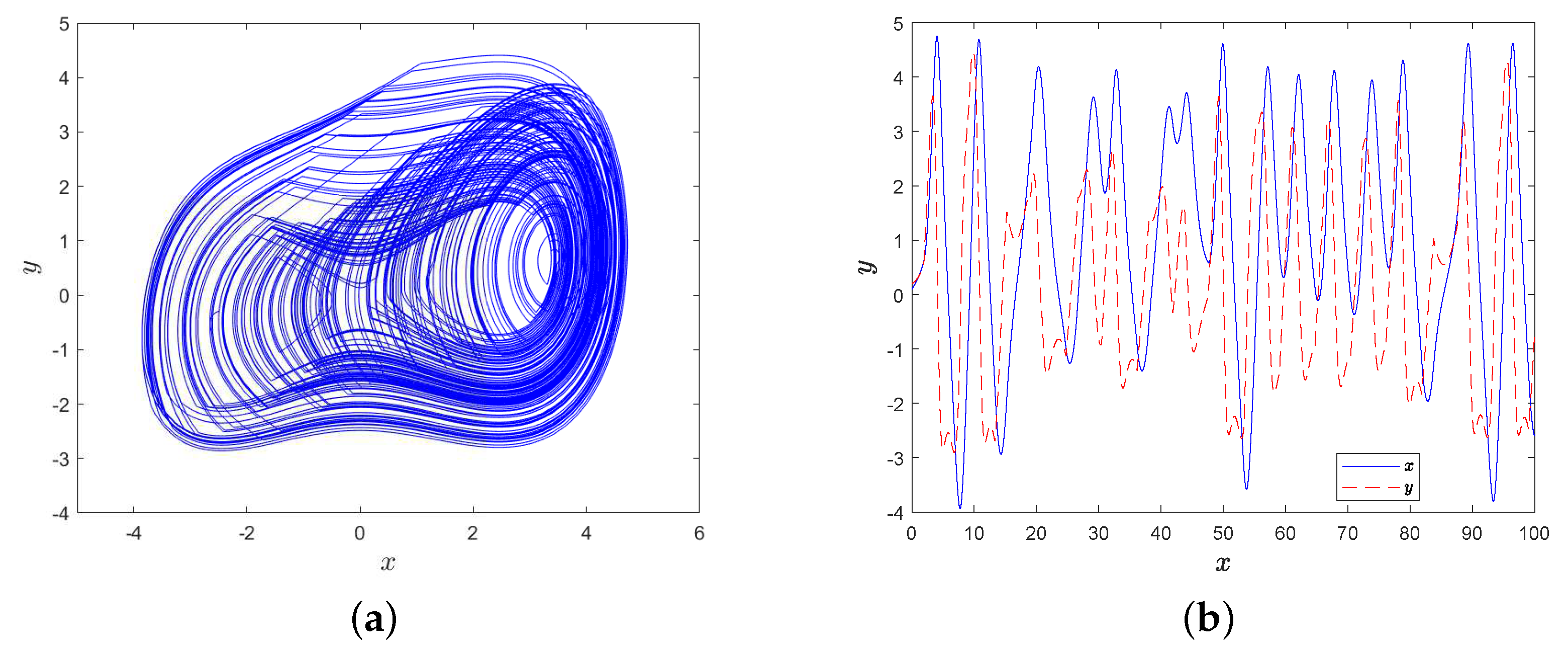
3.2. Simulation Experiment of MD System with Intermittent External Force
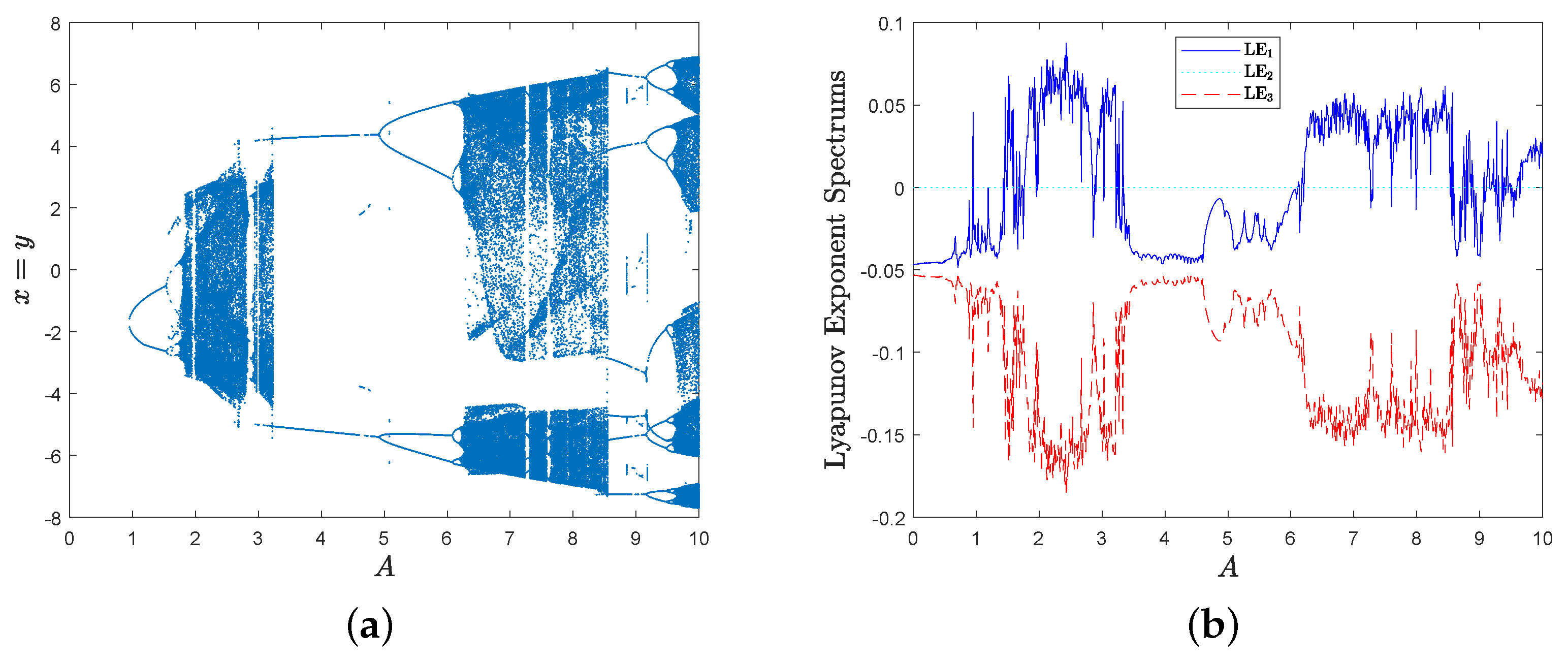
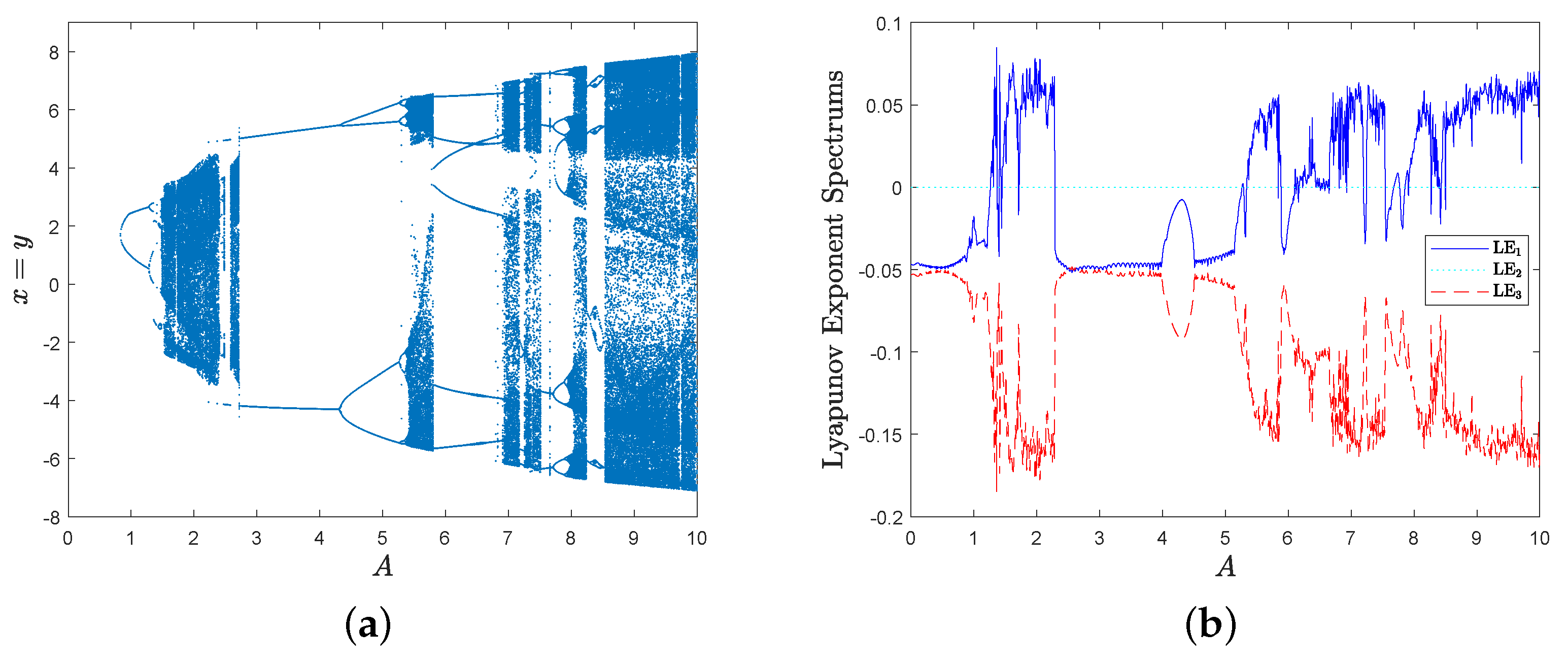
3.3. Dynamics Analysis of MD System with Respect to Parameter A
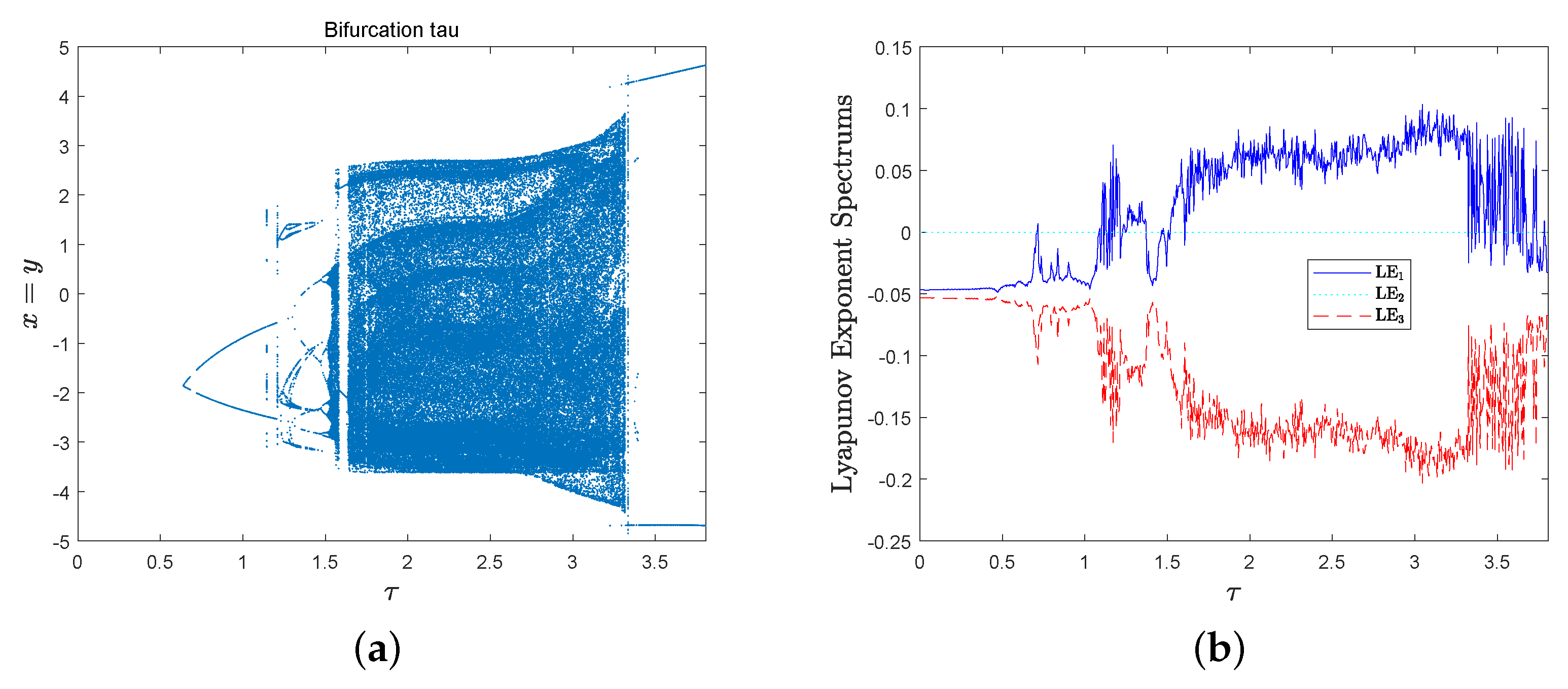
3.4. Dynamics Analysis of MD System with Respect to Parameter
3.5. Dynamics Analysis of MD System with Respect to Parameter
4. Algorithm Design and Information-Encryption Application
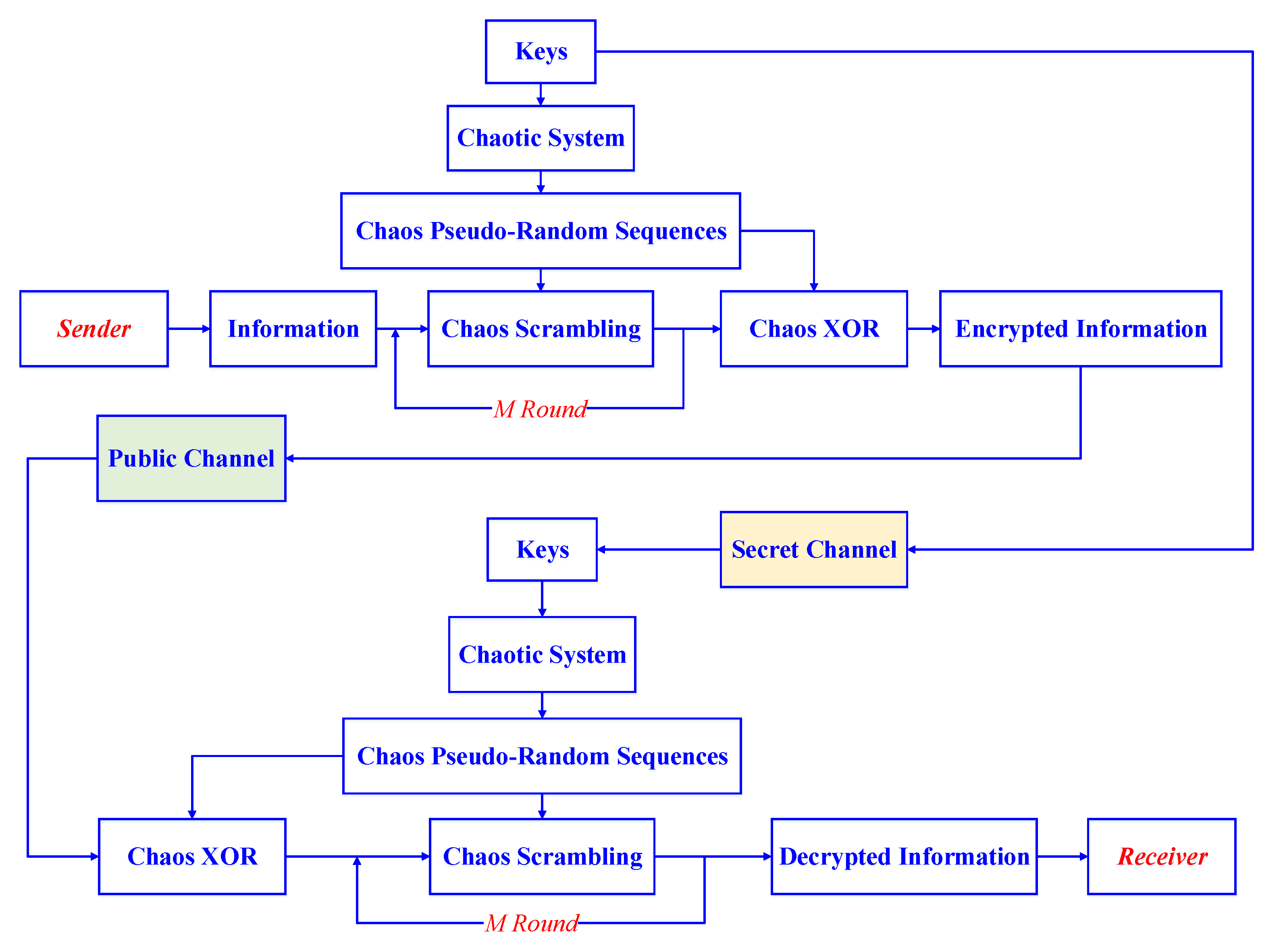
4.1. Algorithm Design
4.2. Simulation Experiment
4.3. Key Sensitivity and Key Space
4.4. NIST Test
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Kolen, M.J. The Duffing Equation—Nonlinear Oscillators and Their Behaviour; John Wiley & Sons, Ltd.: West Sussex, UK, 2011; pp. 1–63. ISBN 9780470977835. [Google Scholar]
- Chen, G.R.; Ueta, T. Yet another chaotic attractor. Int. J. Bifurcat. Chaos 1999, 9, 1465–1466. [Google Scholar] [CrossRef]
- Lü, J.H.; Chen, G.R. A new chaotic attractor coined. Int. J. Bifurcat. Chaos 2002, 12, 659–661. [Google Scholar] [CrossRef]
- Chen, Q.G.; Chen, G.R. A chaotic system with one saddle and two stable node-foci. Int. J. Bifurcat. Chaos 2008, 18, 1393–1414. [Google Scholar]
- Yang, Q.G.; Wei, Z.C.; Chen, G.R. An unusual 3D autonomous quadratic chaotic system with two stable nodefoci. Int. J. Bifurcat. Chaos 2010, 20, 1061–1083. [Google Scholar] [CrossRef]
- Novak, S.; Frehlich, R.G. Transition to chaos in the Duffing oscillator. Phys. Rev. A 1982, 26, 3660–3663. [Google Scholar] [CrossRef]
- Vincent, U.E.; Kenfack, A. Synchronization and bifurcation structures in coupled periodically forced non-identical Duffing oscillators. Phys. Scripta 2008, 77, 045005. [Google Scholar] [CrossRef]
- Chabreyrie, R.; Aubry, N. Switching chaos on/off in Duffing oscillator. arXiv 2011, arXiv:1108.4118. [Google Scholar]
- Kozlowski, J.; Parlitz, U.; Lauterborn, W. Bifurcation analysis of two coupled periodically driven Duffing oscillators. Phys. Rev. E 1995, 51, 1861–1867. [Google Scholar] [CrossRef]
- Sabarathinam, S.; Volos, C.K.; Thamilmaran, K. Implementation and study of the nonlinear dynamics of a memristor-based duffing oscillator. Nonlinear Dyn. 2017, 87, 37–49. [Google Scholar] [CrossRef]
- Niknam, A.; Farhang, K. Friction-induced vibration in a two-mass damped system. J. Sound Vibrat. 2019, 456, 454–475. [Google Scholar] [CrossRef]
- Li, C.; Sprott, J.C.; Yuan, Z.; Li, H. Constructing chaotic systems with total amplitude control. Int. J. Bifurcat. Chaos 2015, 25, 1530025. [Google Scholar] [CrossRef]
- Yu, S.M.; Tang, W.K.S.; Lü, J.H.; Chen, G.R. Generation of n × m-wing Lorenz-like attractors from a modified Shimizu-Morioka model. IEEE Trans. Circuits Syst.-II 2008, 55, 1168–1172. [Google Scholar] [CrossRef]
- Pham, V.-T.; Jafari, S.; Wang, X.; Ma, J. A chaotic system with different shapes of equilibria. Int. J. Bifurcat. Chaos 2016, 26, 1650069. [Google Scholar] [CrossRef]
- Zhang, F.C.; Liao, X.F.; Zhang, G.Y. Qualitative behaviors of the continuous-time chaotic dynamical systems describing the interaction of waves in plasma. Nonlinear Dyn. 2017, 88, 1623–1629. [Google Scholar] [CrossRef]
- Sun, J.; Lu, C.; Yuan, X. Lagrange stability for impulsive Duffing equations. J. Diff. Equ. 2019, 266, 6924–6962. [Google Scholar]
- Varshney, V.; Sabarathinam, S.; Prasad, A.; Thamilmaran, K. Infinite number of hidden attractors in memristor-based autonomous duffing oscillator. Int. J. Bifurcat. Chaos 2018, 28, 1850013. [Google Scholar] [CrossRef]
- Vaidyanathan, S. Anti-synchronization of Duffing double-well chaotic oscillators via integral sliding mode control. Int. J. ChemTech Res. 2016, 9, 297–304. [Google Scholar]
- Kabziński, J. Synchronization of an uncertain Duffing oscillator with higher order chaotic systems. Int. J. Appl. Math. Comput. Sci. 2018, 28, 625–634. [Google Scholar] [CrossRef]
- Wang, X.; Pham, V.-T.; Volos, C. Dynamics, circuit design, and synchronization of a new chaotic system with closed curve equilibrium. Complexity 2017, 2017, 7138971. [Google Scholar] [CrossRef]
- Pham, V.-T.; Jafari, S.; Volos, C.; Giakoumis, A.; Vaidyanathan, S.; Kapitaniak, T. A chaotic system with equilibria located on the rounded square loop and its circuit implementation. IEEE Trans. Circuits Syst.-II 2016, 63, 878–882. [Google Scholar] [CrossRef]
- Li, C.; Xu, X.; Ding, Y.; Dou, B. Weak photoacoustic signal detection based on the differential Duffing oscillator. Int. J. Modern Phys. B 2018, 32, 1850103. [Google Scholar] [CrossRef]
- Wang, G.; He, S. A quantitative study on detection and estimation of weak signals by using chaotic Duffing oscillators. IEEE Trans. Circuits Syst.-I 2003, 50, 945–953. [Google Scholar] [CrossRef]
- Li, C.; Luo, G.; Li, C. A parallel image encryption algorithm based on chaotic Duffing oscillators. Multimedia Tools Appl. 2018, 77, 19193–19208. [Google Scholar] [CrossRef]
- Zapateiro, M.; Vidal, Y.; Acho, L. A secure communication scheme based on chaotic duffing oscillators and frequency estimation for the transmission of binary-coded messages. Communicat. Nonlinear Sci. Numer. Simul. 2014, 19, 991–1003. [Google Scholar] [CrossRef]
- Nicolis, C. Climatic responses to systematic time variations of parameters: A dynamical approach. Nonlin. Processes Geophys. 2018, 25, 649–658. [Google Scholar] [CrossRef]
- Nicolis, C. Self-oscillations and predictability in climate dynamics. Tellus 1984, 36, 1–10. [Google Scholar] [CrossRef][Green Version]
- Nicolis, C. Irreversible thermodynamics of a simple atmospheric flow model. Int. J. Bifurcation Chaos 2002, 12, 2557–2566. [Google Scholar] [CrossRef]
- Kwasniok, F. Analysis and modelling of glacial climate transitions using simple dynamical systems. Philos. Trans. Math. Phys. Eng. Sci. 2013, 371, 1–22. [Google Scholar] [CrossRef]
- Nicolis, G.; Nicolis, C. Stochastic resonance, self-organization and information dynamics in multistable systems. Entropy 2016, 18, 172. [Google Scholar] [CrossRef]
- Zaher, A.A. Duffing oscillators for secure communication. Comput. Electr. Eng. 2018, 71, 77–92. [Google Scholar] [CrossRef]
- Chen, G.R.; Mao, Y.B.; Chui, C.K. A symmetric image encryption scheme based on 3D chaotic cat maps. Chaos Solit. Fract. 2004, 21, 749–761. [Google Scholar] [CrossRef]
- Kwok, H.S.; Tang, W.K.S. A fast image encryption system based on chaotic maps with finite precision representation. Chaos Solit. Fract. 2007, 32, 1518–1529. [Google Scholar] [CrossRef]
- Liu, X.; Song, Y.; Jiang, G.P. Hierarchical bit-level image encryption based on chaotic map and feistel network. Int. J. Bifurcat. Chaos 2019, 29, 1950016. [Google Scholar] [CrossRef]
- Preishuber, M.; Hütter, T.; Katzenbeisser, S.; Uhl, A. Depreciating motivation and empirical security analysis of chaos-based image and video encryption. IEEE Trans. Informat. Forensics Secur. 2018, 13, 2137–2150. [Google Scholar] [CrossRef]
- He, J.; Yu, S.; Cai, J. Topological horseshoe analysis for a three-dimensional anti-control system and its application. Optik 2016, 127, 9444–9456. [Google Scholar] [CrossRef]
- Zhang, Y.Q.; Wang, X.Y. Analysis and improvement of a chaos-based symmetric image encryption scheme using a bit-level permutation. Nonlinear Dyn. 2014, 77, 687–698. [Google Scholar] [CrossRef]
- Wang, X.Y.; Li, P.; Zhang, Y.Q.; Liu, L.Y.; Zhang, H.; Wang, X. A novel color image encryption scheme using dna permutation based on the lorenz system. Multimedia Tools Appl. 2017, 77, 6243–6265. [Google Scholar] [CrossRef]
- Ashwin, P.; Camp, C.; Von der Heydt, A. Chaotic and non-chaotic response to quasiperiodic forcing: Limits to predictability of ice ages paced by Milankovitch forcing. Dyn. Stat. Clim. Syst. 2018, 3, 1–30. [Google Scholar]
- Li, C.; Feng, B.; Li, S.; Kurths, J.; Chen, G. Dynamic analysis of digital chaotic maps via state-mapping networks. IEEE Trans. Circuits Syst.-I 2019, 66, 2322–2335. [Google Scholar] [CrossRef]
- Li, C.; Zhang, Y.; Xie, E.Y. When an attacker meets a cipher-image in 2018: A year in review. J. Inf. Security Appl. 2019, 48, 102361. [Google Scholar] [CrossRef]
- He, J.; Cai, J. Design of a new chaotic system based on Van der Pol oscillator and its encryption application. Mathematics 2019, 7, 743. [Google Scholar] [CrossRef]
- Murillo-Escobar, M.A.; Cruz-Hernndez, C.; Cardoza-Avendaño, L.; Méndez-Ramrez, R. A novel pseudorandom number generator based on pseudorandomly enhanced logistic map. Nonlinear Dyn. 2017, 87, 407–425. [Google Scholar] [CrossRef]




| One Parameter Error of Initial Conditions | Whether Original Image Recovered Successfully or Not | One Parameter Error of Initial Conditions | Whether Original Image Recovered Successfully or Not |
|---|---|---|---|
| No | No | ||
| No | No | ||
| No | No | ||
| No | No |
| Statistical Tests | p-Value |
|---|---|
| Frequency | 0.5341 |
| Block frequency | 0.1453 |
| Cumulative sums | 0.6082 |
| Runs | 0.1626 |
| Longest run | 0.6163 |
| Rank | 0.8514 |
| FFT | 0.9915 |
| Nonoverlapping templates | 0.4491 |
| Overlapping templates | 0.9114 |
| Universal | 0.9558 |
| Approximate entropy | 0.4944 |
| Random excursions | 0.4273 |
| Random excursions variant | 0.9982 |
| Linear complexity | 0.4166 |
| Serial | 0.8513 |
| Success | All |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, J.; Cai, J. Dynamic Analysis of Modified Duffing System via Intermittent External Force and Its Application. Appl. Sci. 2019, 9, 4683. https://doi.org/10.3390/app9214683
He J, Cai J. Dynamic Analysis of Modified Duffing System via Intermittent External Force and Its Application. Applied Sciences. 2019; 9(21):4683. https://doi.org/10.3390/app9214683
Chicago/Turabian StyleHe, Jianbin, and Jianping Cai. 2019. "Dynamic Analysis of Modified Duffing System via Intermittent External Force and Its Application" Applied Sciences 9, no. 21: 4683. https://doi.org/10.3390/app9214683
APA StyleHe, J., & Cai, J. (2019). Dynamic Analysis of Modified Duffing System via Intermittent External Force and Its Application. Applied Sciences, 9(21), 4683. https://doi.org/10.3390/app9214683