Coordinated Formation Design of Multi-Robot Systems via an Adaptive-Gain Super-Twisting Sliding Mode Method
Abstract
:Featured Application
Abstract
1. Introduction
- The multiple-input-multiple-output dynamics of the formation problem were formulated.
- An adaptive-gain super-twisting sliding mode control method was developed by the formation maneuvers of uncertain multi-robot systems.
- The control method is with the guaranteed closed-loop stability in the sense of Lyapunov.
- The adaptive gains were theoretically bounded even if the boundaries of the uncertainties and disturbances were unknown.
2. Modelling
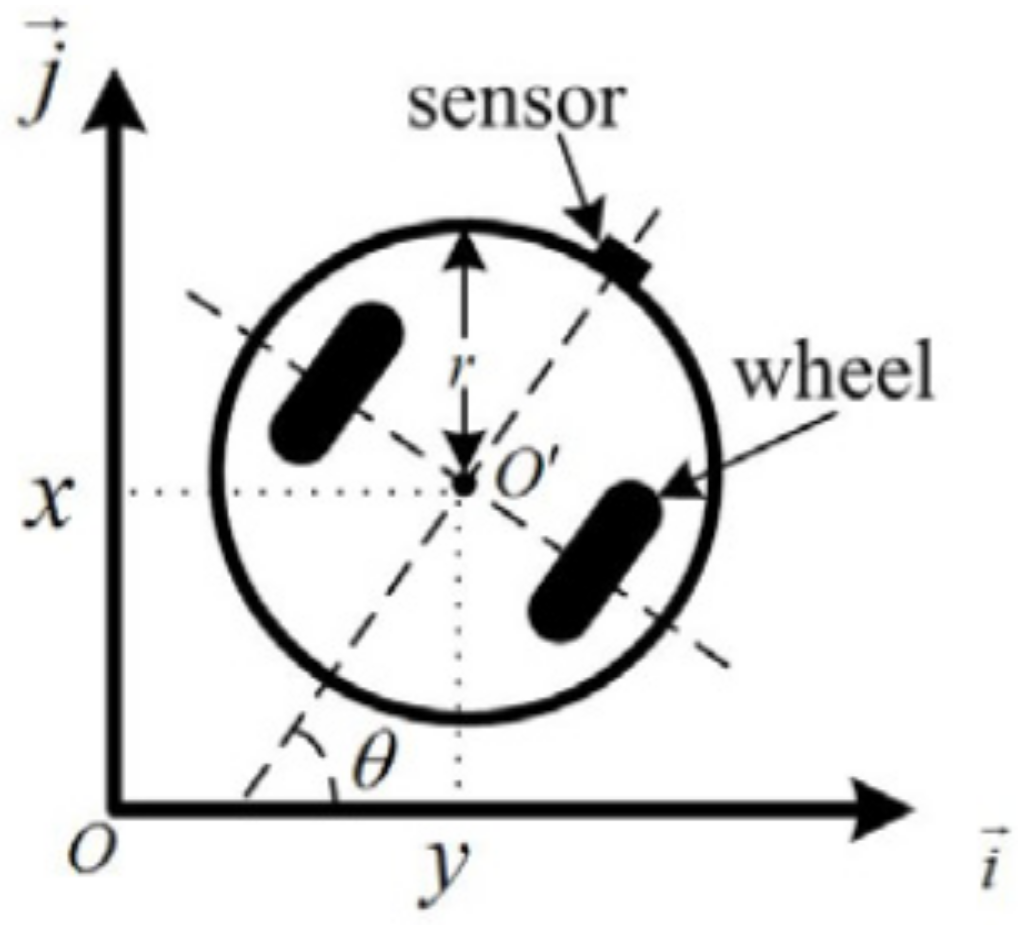
2.1. Model of a Robot
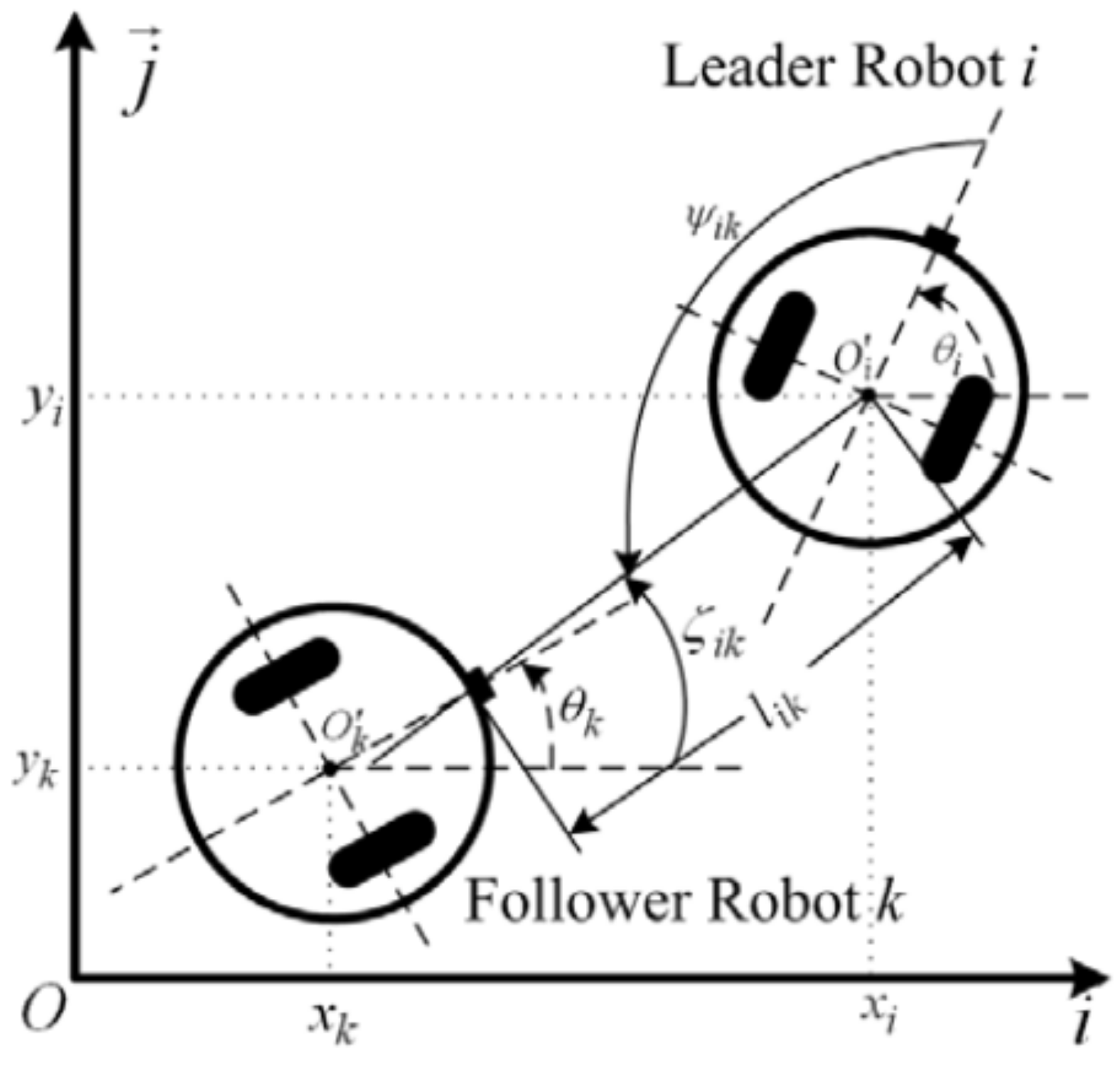
2.2. Model of a Leader-Follower Formation Pair
3. Control Design
3.1. Sliding Mode Design and Its Input-Output Dynamics
3.2. Adaptive-Gain Super-Twisting Sliding Mode Design
3.3. Stability Analysis of the Closed-Loop Control System
- a parameterso thatsatisfies (25) ifat t = 0;Hereis an arbitrary positive constant and is determined by (23).
- a finite timeso that the sliding modes ofare reached in the finite timeregarding to the adaptive-gain super-twisting sliding mode control method, that is,, and. Here,and.
- bothandare bounded.
4. Implementation
4.1. Multi-Robot Simulation Platform
4.2. Simulation Results
4.2.1. String Formation When Moving along a Circular Trajectory
4.2.2. String Formation When Moving along an S-Shape Trajectory
4.2.3. String Formation When Moving Along a Straight Trajectory
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Guillet, A.; Lenain, R.; Thuilot, B.; Martinet, P. Adaptable robot formation control: Adaptive and predictive formation control of autonomous vehicles. IEEE Robot Autom. Mag. 2014, 21, 28–39. [Google Scholar] [CrossRef]
- Dai, Y.Y.; Qian, D.W.; Lee, S. Multiple robots motion control to transport an object. Filomat 2018, 32, 1547–1558. [Google Scholar] [CrossRef] [Green Version]
- Dey, A.; Son, L.H.; Kumar, P.K.K.; Selvachandran, G.; Quek, S.G. New concepts on vertex and edge coloring of simple vague graphs. Symmetry 2018, 10, 373. [Google Scholar] [CrossRef]
- Qian, D.W.; Tong, S.W.; Guo, J.R.; Lee, S.G. Leader-follower-based formation control of non-holonomic mobile robots with mismatched uncertainties via integral sliding mode. Proc. Inst. Mech. Eng. Part I J. Syst. Control Eng. 2015, 229, 559–569. [Google Scholar] [CrossRef]
- Qian, D.W.; Tong, S.W.; Li, C.D. Observer-based leader-following formation control of uncertain multiple agents by integral sliding mode. Bull. Pol. Acad. Sci. Tech. Sci. 2017, 65, 35–44. [Google Scholar] [CrossRef] [Green Version]
- Dai, Y.; Kim, Y.; Wee, S.; Lee, D.; Lee, S. Symmetric caging formation for convex polygonal object transportation by multiple mobile robots based on fuzzy sliding mode control. ISA Trans. 2016, 60, 321–332. [Google Scholar] [CrossRef]
- Herman, P.; Adamski, W. Non-adaptive velocity tracking controller for a class of vehicles. Bull. Pol. Acad. Sci. Tech. Sci. 2017, 65, 459–468. [Google Scholar] [CrossRef] [Green Version]
- Loria, A.; Dasdemir, J.; Jarquin, N.A. Leader-follower formation and tracking control of mobile robots along straight paths. IEEE Trans. Control Syst. Technol. 2016, 24, 727–732. [Google Scholar] [CrossRef]
- Kamalova, A.; Navruzov, S.; Qian, D.; Lee, S.G. Multi-Robot exploration based on multi-objective grey wolf optimizer. Appl. Sci. 2019, 9, 2931. [Google Scholar] [CrossRef]
- Li, C.D.; Yi, J.Q.; Wang, H.K.; Zhang, G.Q.; Li, J.Q. Interval data driven construction of shadowed sets with application to linguistic word modeling. Inf. Sci. 2020, 507, 503–521. [Google Scholar] [CrossRef]
- Cheng, L.; Wang, Y.; Ren, W.; Hou, Z.G.; Tan, M. On convergence rate of leader-following consensus of linear multi-agent systems with communication noises. IEEE Trans. Autom. Control 2016, 61, 3586–3592. [Google Scholar] [CrossRef]
- Dey, A.; Pradhan, R.; Pal, A.; Pal, T. A genetic algorithm for solving fuzzy shortest path problems with interval type-2 fuzzy arc lengths. Malayas. J. Comput. Sci. 2018, 31, 255–270. [Google Scholar] [CrossRef]
- Li, C.D.; Gao, J.L.; Yi, J.Q.; Zhang, G.Q. Analysis and design of functionally weighted single-input-rule-modules connected fuzzy inference systems. IEEE Trans. Fuzzy Syst. 2018, 26, 56–71. [Google Scholar] [CrossRef]
- Qian, D.W.; Xi, Y.F. Leader-follower formation control for multiple robots via derivative and integral terminal sliding mode. Appl. Sci. 2018, 8, 1045. [Google Scholar] [CrossRef]
- Dey, A.; Pal, A.; Pal, T. Interval type 2 fuzzy set in fuzzy shortest path problem. Mathematics 2016, 4, 62. [Google Scholar] [CrossRef]
- Dey, A.; Son, L.H.; Pal, A.; Long, H.V. Fuzzy minimum spanning tree with interval type 2 fuzzy arc length: Formulation and a new genetic algorithm. Soft Comput. 2019. [Google Scholar] [CrossRef]
- Li, Z.; Yuan, W.; Chen, Y.; Ke, F.; Chu, X.; Chen, C.P. Neural-dynamic optimization-based model predictive control for tracking and formation of nonholonomic multirobot systems. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 6113–6122. [Google Scholar] [CrossRef]
- Chen, X.; Jia, Y. Adaptive leader-follower formation control of non-holonomic mobile robots using active vision. IET Contr. Theory Appl. 2015, 9, 1302–1311. [Google Scholar] [CrossRef]
- Liao, T.L.; Chan, W.S.; Yan, J.J. Distributed adaptive dynamic surface formation control for uncertain multiple quadrotor systems with interval type-2 fuzzy neural networks. Trans. Inst. Meas. Control 2019, 41, 1861–1879. [Google Scholar] [CrossRef]
- Luy, N.T. Distributed cooperative H∞ optimal tracking control of MIMO nonlinear multi-agent systems in strict-feedback form via adaptive dynamic programming. Int. J. Control 2018, 91, 952–968. [Google Scholar] [CrossRef]
- Utkin, V.I. Sliding Modes in Control and Optimization, 2nd ed.; Springer: Berlin, Germany, 1992. [Google Scholar]
- Qian, D.W.; Li, C.D.; Lee, S.G.; Ma, C. Robust formation maneuvers through sliding mode for multi-agent systems with uncertainties. IEEE/CAA J. Autom. Sin. 2018, 5, 342–351. [Google Scholar] [CrossRef]
- Qian, D.W.; Tong, S.W.; Li, C.D. Leader-following formation control of multiple robots with uncertainties through sliding mode and nonlinear disturbance observer. ETRI J. 2016, 38, 1008–1018. [Google Scholar] [CrossRef]
- Nair, R.R.; Karki, H.; Shukla, A.; Behera, L.; Jamshidi, M. Fault-tolerant formation control of nonholonomic robots using fast adaptive gain nonsingular terminal sliding mode control. IEEE Syst. J. 2018, 13, 1006–1017. [Google Scholar] [CrossRef]
- Utkin, V. Discussion aspects of high-order sliding mode control. IEEE Trans. Autom. Control 2015, 61, 829–833. [Google Scholar] [CrossRef]
- Chalanga, A.; Kamal, S.; Fridman, L.M.; Bandyopadhyay, B.; Moreno, J.A. Implementation of super-twisting control: Super-twisting and higher order sliding-mode observer-based approaches. IEEE Trans. Ind. Electron. 2016, 63, 3677–3685. [Google Scholar] [CrossRef]
- Defoort, M.; Floquet, T.; Kokosy, A.; Perruquetti, W. Sliding-mode formation control for cooperative autonomous mobile robots. IEEE Trans. Ind. Electron. 2008, 55, 3944–3953. [Google Scholar] [CrossRef]
- Shtessel, Y.; Taleb, M.; Plestan, F. A novel adaptive-gain supertwisting sliding mode controller: Methodology and application. Automatica 2012, 48, 759–769. [Google Scholar] [CrossRef]








© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qian, D.; Zhang, G.; Chen, J.; Wang, J.; Wu, Z. Coordinated Formation Design of Multi-Robot Systems via an Adaptive-Gain Super-Twisting Sliding Mode Method. Appl. Sci. 2019, 9, 4315. https://doi.org/10.3390/app9204315
Qian D, Zhang G, Chen J, Wang J, Wu Z. Coordinated Formation Design of Multi-Robot Systems via an Adaptive-Gain Super-Twisting Sliding Mode Method. Applied Sciences. 2019; 9(20):4315. https://doi.org/10.3390/app9204315
Chicago/Turabian StyleQian, Dianwei, Guigang Zhang, Jiarong Chen, Jian Wang, and Zhimin Wu. 2019. "Coordinated Formation Design of Multi-Robot Systems via an Adaptive-Gain Super-Twisting Sliding Mode Method" Applied Sciences 9, no. 20: 4315. https://doi.org/10.3390/app9204315
APA StyleQian, D., Zhang, G., Chen, J., Wang, J., & Wu, Z. (2019). Coordinated Formation Design of Multi-Robot Systems via an Adaptive-Gain Super-Twisting Sliding Mode Method. Applied Sciences, 9(20), 4315. https://doi.org/10.3390/app9204315



