A Multi-Level Optimization Method for Elastic Constants Identification of Composite Laminates
Abstract
Featured Application
Abstract
1. Introduction
2. Multi-Level Optimization Method
Subject to gk(x) ≤ 0; k = 1, 2, …, 2N
Subject to gk*(x) ≤ 0; k = 1, 2, …., 2N
3. Numerical Examples of Global Minimum Determination
4. Elastic Constants Identification of Composite Laminate
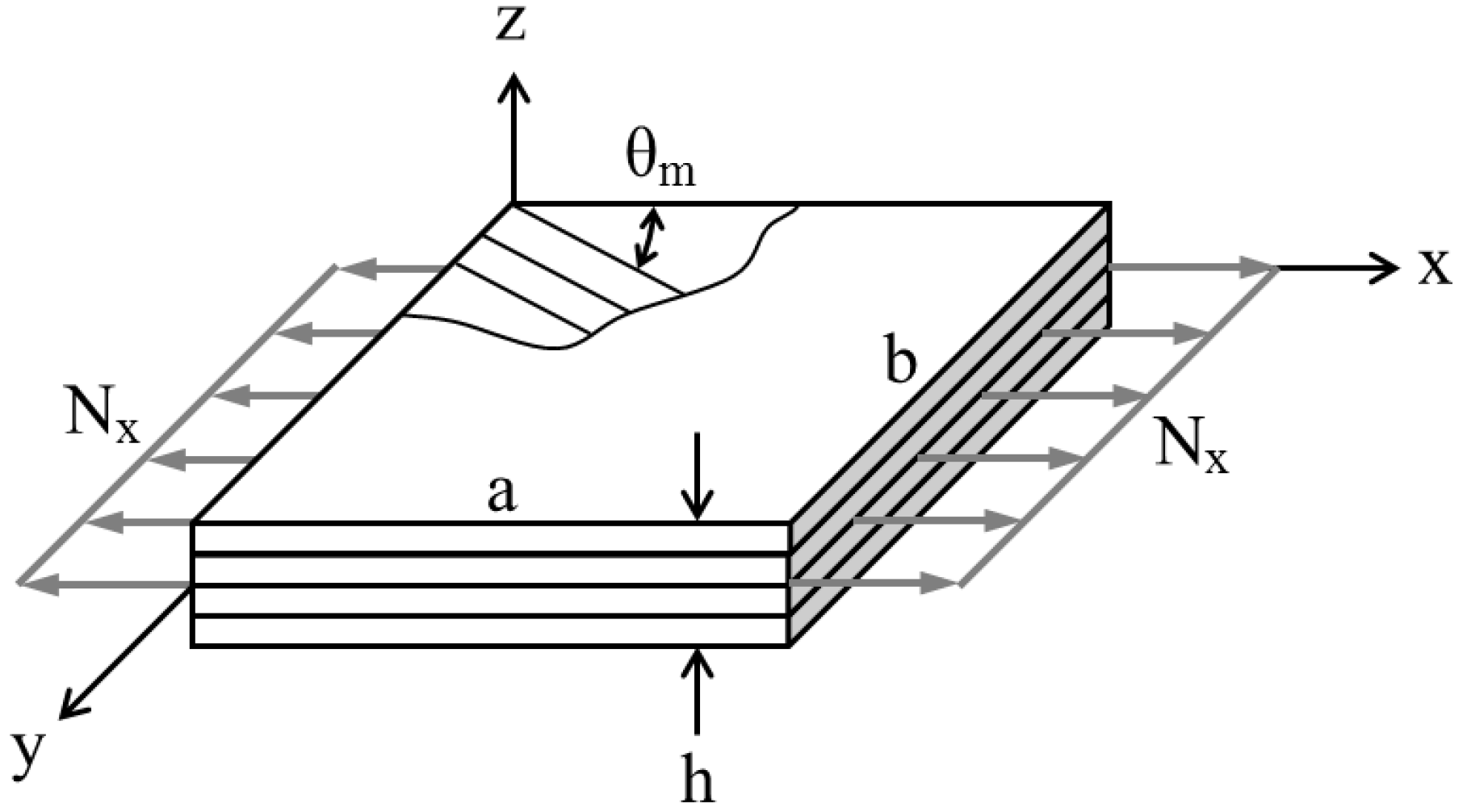
4.1. Strain Analysis of Symmetric Composite Laminate under Axial Load
4.2. Formulation of Elastic Constants Identification
4.3. Numerical Examples
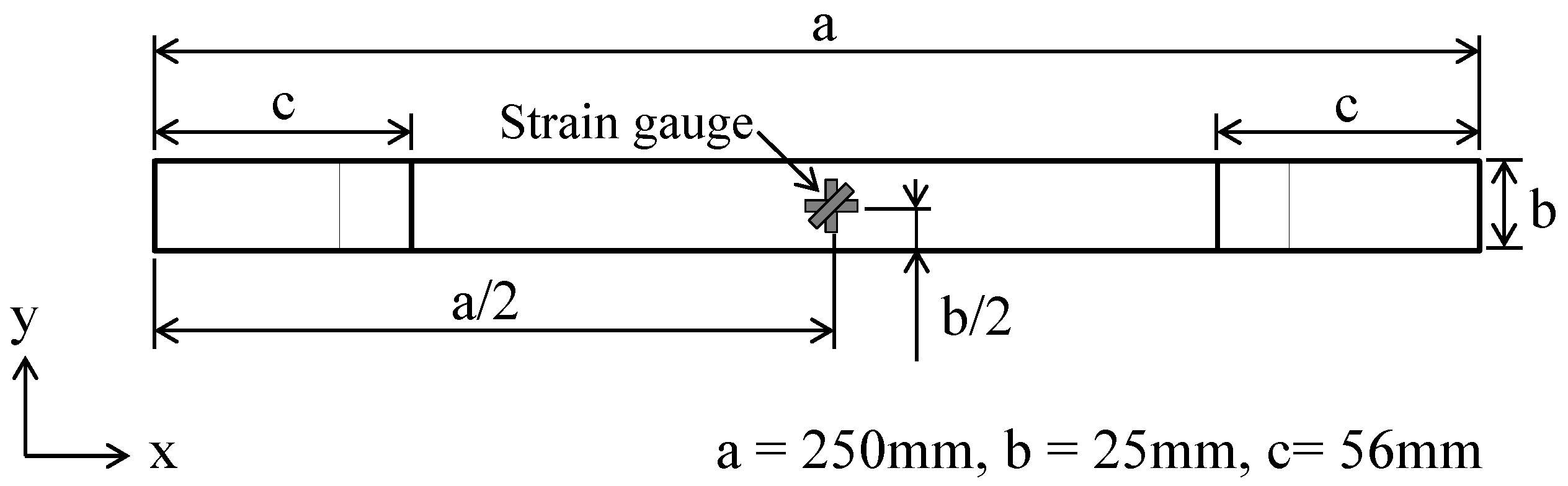
5. Experimental Study
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Pagnotta, L. Recent progress in identification methods for the elastic characterization of materials. Int. J. Mech. 2008, 2, 129–140. [Google Scholar]
- Gibson, R.F. Modal vibration response measurements for characterization of composite materials and structures. Compos. Sci. Technol. 2000, 60, 2769–2780. [Google Scholar] [CrossRef]
- Grédiac, M.; Fournier, N.; Paris, P.A.; Surrel, Y. Direct identification of elastic constants of anisotropic plates by modal analysis: Experimental results. J. Sound Vib. 1998, 210, 643–659. [Google Scholar] [CrossRef]
- De Wilde, W.P.; Sol, H. Anisotropic material identification using measured resonant frequencies of rectangular composite plates. Compos. Struct. 1987, 4, 317–324. [Google Scholar]
- Bledzki, A.K.; Kessler, A.; Rikards, R.; Chate, A. Determination of elastic constants of glass/epoxy unidirectional laminates by the vibration testing of plates. Compos. Sci. Technol. 1999, 59, 2015–2024. [Google Scholar] [CrossRef]
- Lee, C.R.; Kam, T.Y. Identification of mechanical properties of elastically restrained laminated composite plates using vibration data. J. Sound Vib. 2006, 295, 999–1016. [Google Scholar] [CrossRef]
- Banerjee, B. Elastic parameter identification of plate structures using modal response: An ECE based approach. J. Eng. Mech. 2016, 142, 04015059. [Google Scholar] [CrossRef]
- Mishra, A.K.; Chakraborty, S. Determination of material parameters of FRP plates with rotational flexibility at boundaries using experimental modal testing and model updating. Exp. Mech. 2015, 55, 803–815. [Google Scholar] [CrossRef]
- Geymonat, G.; Pagano, S. Identification of mechanical properties by displacement field measurement: A variational approach. Meccanica 2003, 38, 535–545. [Google Scholar] [CrossRef]
- Grédiac, M.; Pierron, F.; Surrel, Y. Novel procedure for complete in-plane composite characterization using a single T-shaped specimen. Exp. Mech. 1999, 39, 142–149. [Google Scholar] [CrossRef]
- Avril, S.; Bonnet, M.; Bretelle, A.S.; Grédiac, M.; Hild, F.; Ienny, P.; Latourte, F.; Lemosse, D.; Pagano, S.; Pagnacco, E. Overview of identification methods of mechanical parameters based on full-field measurements. Exp. Mech. 2008, 48, 381–402. [Google Scholar] [CrossRef]
- Wang, W.T.; Kam, T.Y. Elastic constants identification of shear deformable laminated composite plates. ASCE J. Eng. Mech. 2001, 127, 1117–1123. [Google Scholar] [CrossRef]
- Diveyev, B.; Butiter, I.; Shcherbina, N. Identifying the elastic moduli of composite plates by using high-order theories. 2. Theoretical-experimental approach. Mech. Compos. Mater. 2008, 44, 207–216. [Google Scholar] [CrossRef]
- Bruno, L.; Felice, G.; Pagnotta, L.; Poggialini, A.; Stigliano, G. Elastic characterization of orthotropic plates of any shape via static testing. Int. J. Solids Struct. 2008, 45, 908–920. [Google Scholar] [CrossRef][Green Version]
- Lecompte, D.; Smits, A.; Sol, H.; Vantomme, J.; Van Hemelrijck, D. Mixed numerical-experimental technique for orthotropic parameter identification using biaxial tensile tests on cruciform specimens. Int. J. Solids Struct. 2007, 44, 1643–1656. [Google Scholar] [CrossRef]
- Hematiyan, M.R.; Khosravifard, A.; Shiah, Y.C.; Maletta, C.; Pagnotta, L. A new stable inverse method for identification of the elastic constants of a three-dimensional generally anisotropic solid. Int. J. Solids Struct. 2017, 106, 240–250. [Google Scholar] [CrossRef]
- Kam, T.Y.; Chen, C.M.; Yang, S.H. Material characterization of laminated composite materials using a three-point-bending technique. Compos. Struct. 2009, 88, 624–628. [Google Scholar] [CrossRef]
- Chen, C.M.; Kam, T.Y. Elastic constants identification of composite materials using a single angle-ply laminate. ASCE J. Eng. Mech. 2006, 132, 1187–1194. [Google Scholar] [CrossRef]
- Chen, C.M.; Kam, T.Y. Elastic constants identification of symmetric angle-ply laminates via a two-level optimization approach. Compos. Sci. Technol. 2007, 67, 698–706. [Google Scholar] [CrossRef]
- Snyman, J.A. A new and dynamic method for unconstrained minimization. Appl. Math. Model. 1982, 6, 449–462. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R.C. Particle swarm optimization. In Proceedings of the IEEE International Conference on Neural Networks, the University of Western Australia, Perth, Australia, 27 November–1 December 1995; pp. 1942–1948. [Google Scholar]
- Vanderplaats, G.N. Numerical Optimization Techniques for Engineering Design: With Applications; McGraw-Hill Inc.: New York, NY, USA, 1984. [Google Scholar]
- Parsopoulos, K.E.; Vrahatis, M.N. Particle Swarm Optimization Method for Constrained Optimization Problems. Intell. Technol. Theory Appl. New Trends Intell. Technol. 2002, 76, 214–220. [Google Scholar]
- Hu, X.; Eberhart, R. Solving constrained nonlinear optimization problems with particle swarm optimization. In Proceedings of the sixth world multiconference on systemics, cybernetics and informatics, Orlando, FL, USA, 14–18 July 2002; pp. 203–206. [Google Scholar]
- Snyman, J.A.; Fatti, L.P. A multi-start global minimization algorithm with dynamic search trajectories. J. Optim. Theory Appl. 1987, 54, 121–141. [Google Scholar] [CrossRef]
- The Mathworks. Matlab, The Language of Technical Computing, Version R2014a; The Mathworks: Natick, MA, USA, 2014. [Google Scholar]
- Swanson, S.R. Introduction to Design and Analysis with Advanced Composite Materials; Prentice-Hall International, Inc.: Upper Saddle River, NJ, USA, 1997. [Google Scholar]
- ASTM. Standards and Literature References for Composite Materials, 2nd ed.; ASTM: West Conshohocken, PA, USA, 1990. [Google Scholar]

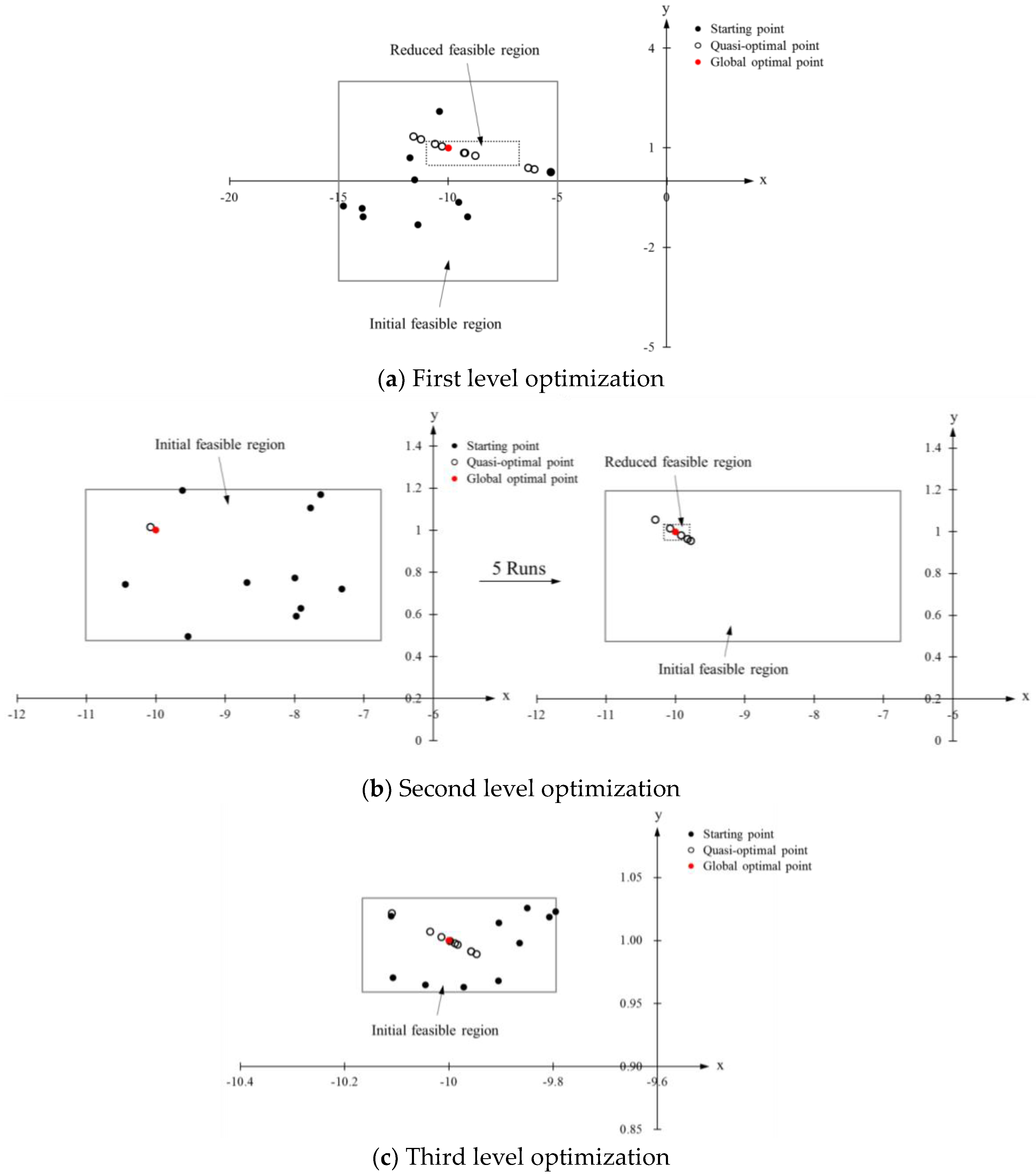
| Function | Level | Variable | ||
|---|---|---|---|---|
| x | y | |||
| Schaffer function (−100 ≤ x ≤ 100, −100 ≤ y ≤ 100) | Actual | 0.00 | 0.00 | |
| 1st | Mean (μ) | −6.89 × 10−5 | 1.50 × 10−5 | |
| Standard deviation (σ) | 3.50 × 10−4 | 2.65 × 10−5 | ||
| 2nd | Mean (μ) | 1.53 × 10−7 | 1.73 × 10−7 | |
| Standard deviation (σ) | 6.27 × 10−7 | 5.73 × 10−7 | ||
| 3rd | Identified | −7.95 × 10−8 | 3.29 × 10−7 | |
| Bukin function (I) (−15 ≤ x ≤ −5, −3 ≤ y ≤ 3) | Actual | −10.00 | 1.00 | |
| 1st | Mean (μ) | −8.88 | 0.83 | |
| Standard deviation (σ) | 2.13 | 0.360 | ||
| 2nd | Mean (μ) | −9.98 | 1.00 | |
| Standard deviation (σ) | 0.19 | 0.04 | ||
| 3rd | Identified | −10.0 | 1.00 | |
| Bukin function (II) (−100 ≤ x ≤ 100, −100 ≤ y ≤ 100) | Actual | −10.0 | 1.00 | |
| 1st | Mean (μ) | −4.27 | 1.10 | |
| Standard deviation (σ) | 9.58 | 1.64 | ||
| 2nd | Mean (μ) | −9.98 | 1.00 | |
| Standard deviation (σ) | 0.54 | 0.11 | ||
| 3rd | Identified | −10.0 | 1.00 | |
| Function | Methods | Identified Design Variable | |
|---|---|---|---|
| x | y | ||
| Schaffer function (−100 ≤ x ≤ 100, −100 ≤ y ≤ 100) | Actual | 0.00 | 0.00 |
| MSGO | 9.98 × 10−5 | 1.42 × 10−5 | |
| PS | −8.85 × 10−1 | −6.33 × 10−1 | |
| GA | −1.90 × 10−3 | −2.09 × 10−2 | |
| MLOM (Present) | −7.95 × 10−8 | 3.29 × 10−7 | |
| Bukin function (I) (−15 ≤ x ≤ −5, −3 ≤ y ≤ 3) | Actual | −10.00 | 1.00 |
| MSGO | −9.97 | 0.99 | |
| PS | −10.00 | 1.00 | |
| GA | −8.13 | 0.66 | |
| MLOM (Present) | −10.0 | 1.00 | |
| Bukin function (II) (−100 ≤ x ≤ 100, −100 ≤ y ≤ 100) | Actual | −10.00 | 1.00 |
| MSGO | −9.27 | 0.86 | |
| PS | −9.76 | 0.95 | |
| GA | 0.86 | 0.01 | |
| MLOM (Present) | −10.0 | 1.00 | |
| Level 1 | Material Constant | ||||
|---|---|---|---|---|---|
| E1 (GPa) | E2 (GPa) | ν12 | G12 (GPa) | ||
| No. | Actual | Actual | 8.11 | 0.31 | 5.22 |
| 1 | Starting point | 323.83 | 5.470 | 0.240 | 8.163 |
| Lowest local minimum | 138.75 | 10.126 | 0.298 | 5.080 | |
| 2 | Starting point | 440.60 | 6.235 | 0.428 | 5.819 |
| Lowest local minimum | 138.62 | 8.057 | 0.298 | 5.190 | |
| 3 | Starting point | 423.37 | 6.992 | 0.164 | 9.102 |
| Lowest local minimum | 138.65 | 8.262 | 0.296 | 5.173 | |
| 4 | Starting point | 38.41 | 6.472 | 0.432 | 1.908 |
| Lowest local minimum | 138.61 | 8.283 | 0.300 | 5.183 | |
| 5 | Starting point | 174.31 | 8.895 | 0.451 | 4.871 |
| Lowest local minimum | 137.84 | 9.625 | 0.366 | 5.335 | |
| 6 | Starting point | 28.28 | 11.457 | 0.158 | 6.655 |
| Lowest local minimum | 139.08 | 9.948 | 0.270 | 4.994 | |
| 7 | Starting point | 466.51 | 4.205 | 0.460 | 2.226 |
| Lowest local minimum | 138.78 | 7.244 | 0.275 | 5.174 | |
| 8 | Starting point | 368.32 | 6.533 | 0.163 | 3.714 |
| Lowest local minimum | 138.45 | 6.739 | 0.309 | 5.284 | |
| 9 | Starting point | 23.15 | 2.677 | 0.209 | 7.166 |
| Lowest local minimum | 137.72 | 7.448 | 0.384 | 5.442 | |
| 10 | Starting point | 300.78 | 9.360 | 0.367 | 7.618 |
| Lowest local minimum | 138.55 | 7.955 | 0.304 | 5.212 | |
| Mean (Quasi-optimal design variable μ) | 138.50 (0.00%) * | 8.369 (3.19%) | 0.310 (0.03%) | 5.207 (−0.25%) | |
| Standard deviation σ | 0.40 | 1.11 | 0.03 | 0.12 | |
| Coefficient of variation | 0.29 | 13.21 | 11.19 | 2.29 | |
| Level 2. | Material Constant | ||||
|---|---|---|---|---|---|
| E1 (GPa) | E2 (GPa) | ν12 | G12 (GPa) | ||
| Actual | 138.50 | 8.11 | 0.31 | 5.22 | |
| Particle group No. | |||||
| Identified | 1 | 138.28 | 8.302 | 0.331 | 5.271 |
| 2 | 138.54 | 7.797 | 0.304 | 5.219 | |
| 3 | 138.59 | 8.044 | 0.301 | 5.198 | |
| 4 | 138.52 | 8.259 | 0.309 | 5.210 | |
| 5 | 138.38 | 8.760 | 0.323 | 5.228 | |
| Mean (Quasi-optimal design variable μ) | 138.46 (−0.03%) * | 8.233 (1.51%) | 0.314 (1.17%) | 5.225 (0.10%) | |
| Standard deviation σ | 0.11 | 0.32 | 0.01 | 0.02 | |
| Coefficient of variation | 0.08 | 3.88 | 3.61 | 0.48 | |
| Level 3 | Material Constant | |||
|---|---|---|---|---|
| E1 (GPa) | E2 (GPa) | ν12 | G12 (GPa) | |
| Actual | 138.50 | 8.11 | 0.31 | 5.22 |
| Identified | 138.47 (−0.02%) * | 8.185 (0.93%) | 0.313 (0.97%) | 5.225 (0.09%) |
| Method | Material Constant | |||
|---|---|---|---|---|
| E1 (GPa) | E2 (GPa) | ν12 | G12 (GPa) | |
| Actual | 138.5 | 8.11 | 0.31 | 5.22 |
| MSGO | 138.29 (−0.15%) * | 7.678 (−5.33%) | 0.329 (6.03%) | 5.291 (1.35%) |
| PS | 140.09 (1.15%) | 10.048 (23.90%) | 0.180 (−41.98%) | 4.677 (−10.39%) |
| GA | 136.81 (−1.22%) | 7.232 (−10.82%) | 0.467 (50.72%) | 5.657 (8.38%) |
| Present method (3 Levels) | 138.47 (−0.02%) | 8.185 (0.93%) | 0.313 (0.97%) | 5.225 (0.09%) |
| Actual Elastic Constant | |||||||
| E1 (GPa) | E2 (GPa) | ν12 | G12 (GPa) | ||||
| Material type | A. Carbon/epoxy | 146.50 | 9.22 | 0.30 | 6.84 | ||
| B. Scotchply® 1002 E-glass/epoxy | 38.60 | 8.27 | 0.26 | 4.14 | |||
| Given Strain | |||||||
| εx (με) | εy (με) | ε45 (με) | |||||
| [0°/±45°]s Laminate (Fx = 0.5 kN) | A. Carbon/epoxy | 210.6170 | −149.9256 | 28.5322 | |||
| B. Scotchply® 1002 E-glass/epoxy | 579.4597 | −269.9758 | 154.7419 | ||||
| Material Type | Material Constant | |||||
|---|---|---|---|---|---|---|
| E1 (GPa) | E2 (GPa) | ν12 | G12 (GPa) | |||
| A. Carbon/epoxy | Actual | 146.50 | 9.22 | 0.30 | 6.84 | |
| Level | ||||||
| 1st | Mean (Identified) | 146.49 | 9.507 | 0.293 | 6.818 | |
| Standard deviation | 0.89 | 0.67 | 0.07 | 0.22 | ||
| 2nd | Mean (Identified) | 146.500 (0%) | 9.228 (0.09%) | 0.300 (0%) | 6.838 (−0.03%) | |
| Standard deviation | 0.18 | 0.06 | 0.01 | 0.05 | ||
| B. Scotchply® 1002 E-glass/epoxy | Actual | 38.60 | 8.27 | 0.26 | 4.14 | |
| Level | ||||||
| 1st | Mean (Identified) | 38.42 | 7.993 | 0.271 | 4.196 | |
| Standard deviation | 1.37 | 2.14 | 0.07 | 0.26 | ||
| 2nd | Mean (Identified) | 38.60 (0%) | 8.161 (−1.3%) | 0.264 (1.5%) | 4.147 (0.17%) | |
| Standard deviation | 0.21 | 0.60 | 0.02 | 0.07 | ||
| Material Type | Level 3 | Material Constant | |||
|---|---|---|---|---|---|
| E1 (GPa) | E2 (GPa) | ν12 | G12 (GPa) | ||
| A. Carbon/epoxy | Actual | 146.5 | 9.22 | 0.30 | 6.84 |
| Mean (Identified) | 146.50 (0.00%) * | 9.220 (0.00%) | 0.300 (−0.06%) | 6.839 (−0.01%) | |
| B. Scotchply® 1002 E-glass/epoxy | Actual | 38.6 | 8.27 | 0.26 | 4.14 |
| Mean (Identified) | 38.59 (−0.01%) | 8.197 (−0.88%) | 0.263 (0.99%) | 4.146 (0.15%) | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, C.Y.; Kam, T.Y. A Multi-Level Optimization Method for Elastic Constants Identification of Composite Laminates. Appl. Sci. 2019, 9, 4267. https://doi.org/10.3390/app9204267
Huang CY, Kam TY. A Multi-Level Optimization Method for Elastic Constants Identification of Composite Laminates. Applied Sciences. 2019; 9(20):4267. https://doi.org/10.3390/app9204267
Chicago/Turabian StyleHuang, Chien Yang, and Tai Yan Kam. 2019. "A Multi-Level Optimization Method for Elastic Constants Identification of Composite Laminates" Applied Sciences 9, no. 20: 4267. https://doi.org/10.3390/app9204267
APA StyleHuang, C. Y., & Kam, T. Y. (2019). A Multi-Level Optimization Method for Elastic Constants Identification of Composite Laminates. Applied Sciences, 9(20), 4267. https://doi.org/10.3390/app9204267





