Improving Electric Energy Consumption Prediction Using CNN and Bi-LSTM
Abstract
1. Introduction
2. Related Works
3. Materials and Methods
3.1. Acronym
| EECP | The electric energy consumption prediction |
| CNN | Convolutional Neural Network |
| Bi-LSTM | Bi-directional Long Short-Term Memory |
| IHEPC | The individual household electric power consumption dataset |
| LSTM | Long Short-Term Memory |
| RNN | Recurrent neural network |
| MSE | Mean Square Error |
| RMSE | Root Mean Square Error |
| MAE | Mean Absolute Error |
| MAPE | Mean Absolute Percentage Error |
| MLP | The Multilayer perceptron |
| ReLU | The Rectified Linear Unit |
| EECP-CBL | The Electric Energy Consumption Prediction model utilizing the combination of CNN and Bi-LSTM |
3.2. Datasets
3.3. The EECP-CBL Model
4. Experiments
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Lin, J.C.W.; Shao, Y.; Fournier-Viger, P.; Hamido, F. BILU-NEMH: A BILU neural-encoded mention hypergraph for mention extraction. Inf. Sci. 2019, 496, 53–64. [Google Scholar] [CrossRef]
- Djenouri, Y.; Belhadi, A.; Lin, J.C.W.; Cano, A. Adapted K-Nearest Neighbors for Detecting Anomalies on Spatio-Temporal Traffic Flow. IEEE Access 2019, 7, 10015–10027. [Google Scholar] [CrossRef]
- Nguyen, T.N.; Lee, S.; Nguyen-Xuan, H.; Lee, J. A novel analysis-prediction approach for geometrically nonlinear problems using group method of data handling. Comput. Methods Appl. Mech. Eng. 2019, 354, 506–526. [Google Scholar] [CrossRef]
- Nguyen, T.N.; Thai, H.C.; Luu, A.T.; Nguyen-Xuan, H.; Lee, J. NURBS-based postbuckling analysis of functionally graded carbon nanotube-reinforced composite shells. Comput. Methods Appl. Mech. Eng. 2019, 347, 983–1003. [Google Scholar] [CrossRef]
- Nguyen, N.T.; Thai, C.H.; Nguyen-Xuan, H.; Lee, J. Geometrically nonlinear analysis of functionally graded material plates using an improved moving Kriging meshfree method based on a refined plate theory. Compos. Struct. 2018, 193, 268–280. [Google Scholar] [CrossRef]
- Nguyen, N.P.; Hong, S.K. Sliding Mode Thau Observer for Actuator Fault Diagnosis of Quadcopter UAVs. Appl. Sci. 2018, 8, 1893. [Google Scholar] [CrossRef]
- Nguyen, N.P.; Hong, S.K. Fault-tolerant control of quadcopter UAVs using robust adaptive sliding mode approach. Energies 2019, 12, 95. [Google Scholar] [CrossRef]
- Le, T.; Vo, M.T.; Vo, B.; Lee, M.Y.; Baik, S.W. A hybrid approach using oversampling technique and cost-sensitive learning for bankruptcy prediction. Complexity 2019. [Google Scholar] [CrossRef]
- Le, T.; Vo, B.; Fujita, H.; Nguyen, N.T.; Baik, S.W. A fast and accurate approach for bankruptcy forecasting using squared logistics loss with GPU-based extreme gradient boosting. Inf. Sci. 2019, 494, 294–310. [Google Scholar] [CrossRef]
- Le, T.; Le, H.S.; Vo, M.T.; Lee, M.Y.; Baik, S.W. A Cluster-Based Boosting Algorithm for Bankruptcy Prediction in a Highly Imbalanced Dataset. Symmetry 2018, 10, 250. [Google Scholar] [CrossRef]
- Le, T.; Lee, M.Y.; Park, J.R.; Baik, S.W. Oversampling techniques for bankruptcy prediction: Novel features from a transaction dataset. Symmetry 2018, 10, 79. [Google Scholar] [CrossRef]
- Hemanth, D.J.; Anitha, J.; Náaji, A.; Geman, O.; Popescu, D.E.; Le, H.S. A Modified Deep Convolutional Neural Network for Abnormal Brain Image Classification. IEEE Access 2019, 7, 4275–4283. [Google Scholar] [CrossRef]
- Le, T.; Baik, S.W. A robust framework for self-care problem identification for children with disability. Symmetry 2019, 11, 89. [Google Scholar] [CrossRef]
- Hoang, V.L.; Le, H.S.; Khari, M.; Arora, K.; Chopra, S.; Kumar, R.; Le, T.; Baik, S.W. A New Approach for construction of Geo-Demographic Segmentation Model and Prediction Analysis. Comput. Intell. Neurosci. 2019. [Google Scholar] [CrossRef]
- Park, D.; Kim, S.; An, Y.; Jung, J.Y. LiReD: A Light-Weight Real-Time Fault Detection System for Edge Computing Using LSTM Recurrent Neural Networks. Sensors 2018, 18, 2110. [Google Scholar] [CrossRef] [PubMed]
- Huang, C.J.; Kuo, P.H. A Deep CNN-LSTM Model for Particulate Matter (PM2.5) Forecasting in Smart Cities. Sensors 2018, 18, 2220. [Google Scholar] [CrossRef]
- Ran, X.; Shan, Z.; Fang, Y.; Lin, C. An LSTM-Based Method with Attention Mechanism for Travel Time Prediction. Sensors 2019, 19, 861. [Google Scholar] [CrossRef]
- Lin, J.C.W.; Shao, Y.; Zhou, Y.; Pirouz, M.; Chen, H.C. A Bi-LSTM mention hypergraph model with encoding schema for mention extraction. Eng. Appl. Artif. Intell. 2019, 85, 175–181. [Google Scholar] [CrossRef]
- Oliveira, E.M.; Oliveira, F.L. Forecasting mid-long term electric energy consumption through bagging ARIMA and exponential smoothing methods. Energy 2018, 144, 776–788. [Google Scholar] [CrossRef]
- Wu, D.C.; Amini, A.; Razban, A.; Chen, J. ARC algorithm: A novel approach to forecast and manage daily electrical maximum demand. Energy 2018, 154, 383–389. [Google Scholar] [CrossRef]
- Krishnan, M.; Sakthivel, R.; Vishnuvarthan, R. Neural network based optimization approach for energy demand prediction in smart grid. Neurocomputing 2018, 273, 199–208. [Google Scholar]
- Fayaz, M.; Kim, D. A Prediction Methodology of Energy Consumption Based on Deep Extreme Learning Machine and Comparative Analysis in Residential Buildings. Electronics 2018, 7, 222. [Google Scholar] [CrossRef]
- Bouktif, S.; Fiaz, A.; Ouni, A.; Serhani, M.A. Optimal Deep Learning LSTM Model for Electric Load Forecasting using Feature Selection and Genetic Algorithm: Comparison with Machine Learning Approaches. Energies 2018, 11, 1636. [Google Scholar] [CrossRef]
- Tanveer, A.; Huanxin, C.; Yabin, G.; Jiangyu, W. A comprehensive overview on the data driven and large scale based approaches for forecasting of building energy demand: A review. Energy Build. 2018, 165, 301–320. [Google Scholar]
- Moon, J.; Kim, Y.; Son, M.; Hwang, E. Hybrid Short-Term Load Forecasting Scheme Using Random Forest and Multilayer Perceptron. Energies 2018, 11, 3283. [Google Scholar] [CrossRef]
- Johannesen, N.J.; Kolhe, M.; Goodwin, M. Relative evaluation of regression tools for urban area electrical energy demand forecasting. J. Clean. Prod. 2019, 218, 555–564. [Google Scholar] [CrossRef]
- Divina, F.; Torres, M.G.; Goméz Vela, F.A.; Noguera, J.L.V. A Comparative Study of Time Series Forecasting Methods for Short Term Electric Energy Consumption Prediction in Smart Buildings. Energies 2019, 12, 1934. [Google Scholar] [CrossRef]
- Bouazza, K.E.; Deabes, W.A. Smart Petri Nets Temperature Control Framework for Reducing Building Energy Consumption. Sensors 2019, 19, 2441. [Google Scholar] [CrossRef]
- Kim, J.; Moon, J.; Hwang, E.; Kang, P. Recurrent inception convolution neural network for multi short-term load forecasting. Energy Build. 2019, 194, 328–341. [Google Scholar] [CrossRef]
- Hebrail, G.; Berard, A. Individual Household Electric Power Consumption Data Set. UCI Machine Learning Repository. Available online: https://archive.ics.uci.edu/ml/datasets/individual+household+electric+power+consumption (accessed on 1 September 2019).
- Kim, T.Y.; Cho, S.B. Predicting residential energy consumption using CNN-LSTM neural networks. Energy 2019, 182, 72–81. [Google Scholar] [CrossRef]
- Gers, F.A.; Schmidhuber, J.; Cummins, F. Learning to Forget: Continual Prediction with LSTM. Neural Comput. 2000, 12, 2451–2471. [Google Scholar] [CrossRef] [PubMed]
- Graves, A.; Schmidhuber, J. Framewise phoneme classification with bidirectional LSTM and other neural network architectures. Neural Netw. 2005, 18, 602–610. [Google Scholar] [CrossRef] [PubMed]
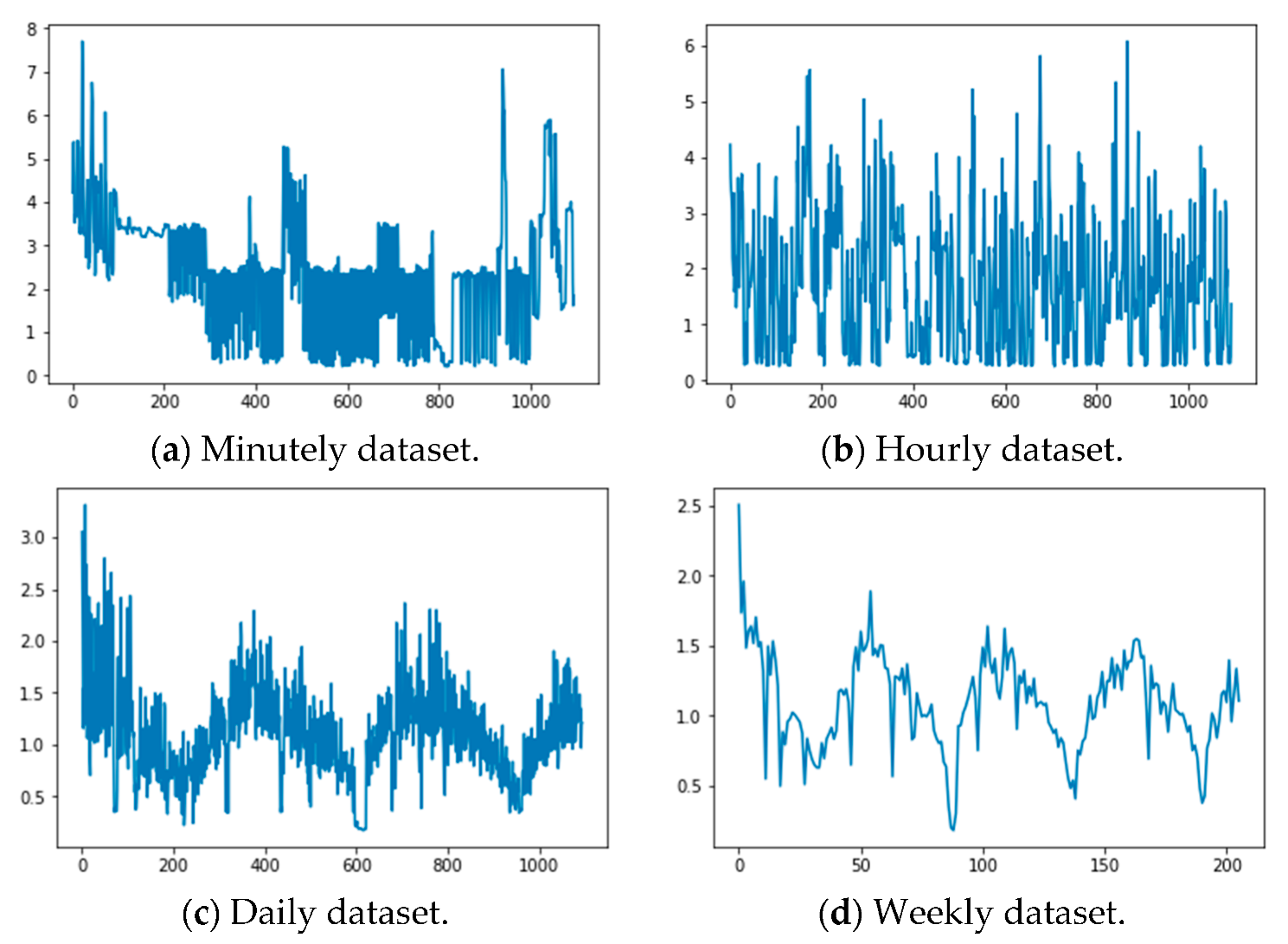
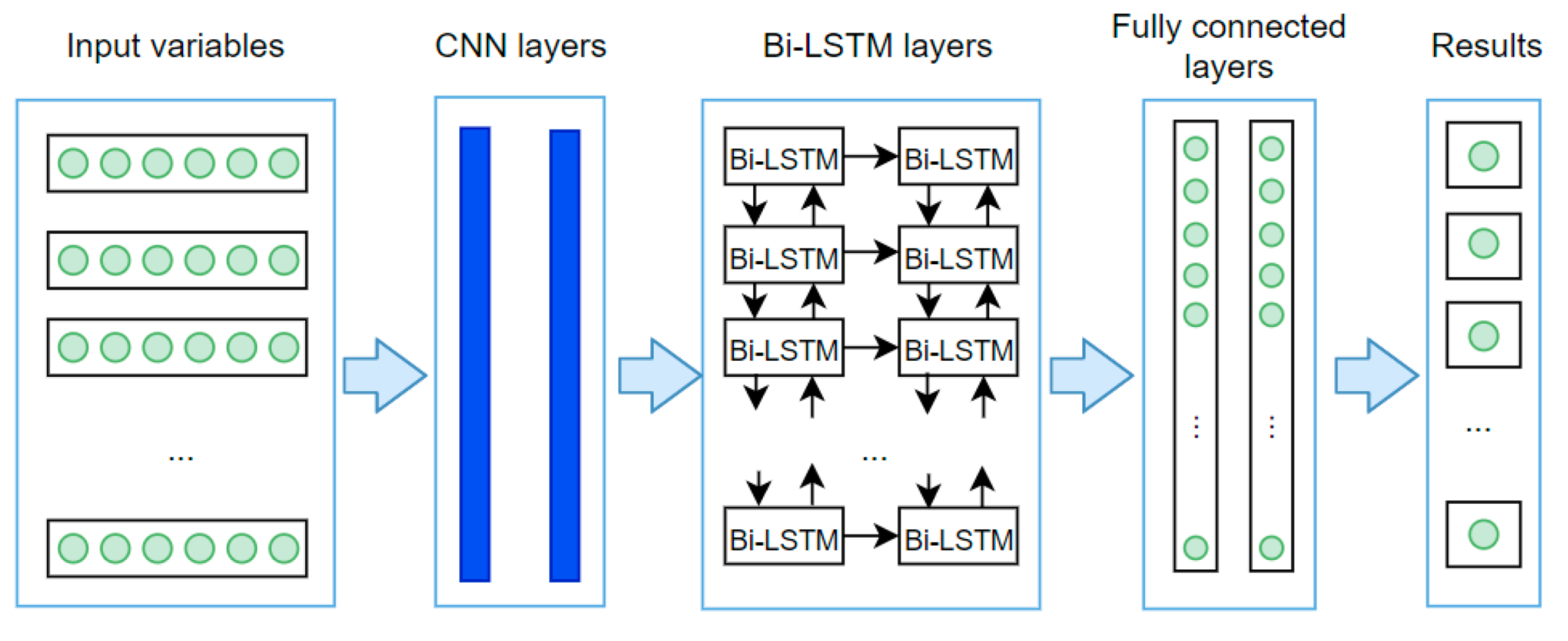
| # | Variable | Description |
|---|---|---|
| 1 | Day | A value from 1 to 31 |
| 2 | Month | A value from 1 to 12 |
| 3 | Year | A value from 2006 to 2010 |
| 4 | Hour | A value from 0 to 23 |
| 5 | Minute | A value from 1 to 60 |
| 6 | Global active power | The household global minute-averaged active power (in kilowatt) |
| 7 | Global reactive power | The household global minute-averaged reactive power (in kilowatt) |
| 8 | Voltage | The minute-averaged voltage (in volt) |
| 9 | Global intensity | The household global minute-averaged current intensity (in ampere) |
| 10 | Sub metering 1 | This variable corresponds to the kitchen, containing mainly a dishwasher, an oven and a microwave, hot plates being not electric, but gas powered (in watt-hour of active energy) |
| 11 | Sub metering 2 | This variable corresponds to the laundry room, containing a washing machine, a tumble-drier, a refrigerator and a light (in watt-hour of active energy) |
| 12 | Sub metering 3 | This variable corresponds to an electric water heater and an air conditioner (in watt-hour of active energy) |
| #No | Layer Type | Neurons | Parameters |
|---|---|---|---|
| 1 | Convolution1D | (None, None, 6, 64) | 192 |
| 2 | MaxPooling1D | (None, None, 3, 64) | 0 |
| 3 | Convolution1D | (None, None, 2, 64) | 8256 |
| 4 | MaxPooling1D | (None, None, 1, 64) | 0 |
| 5 | Flatten | (None, None, 64) | 0 |
| 6 | Bi-LSTM | (None, None, 128) | 66,048 |
| 7 | Bi-LSTM | (None, 128) | 98,816 |
| 8 | Fully connected layer | (None, 128) | 16,512 |
| 9 | Dropout | (None, 128) | 0 |
| 10 | Fully connected layer | (None, 1) | 129 |
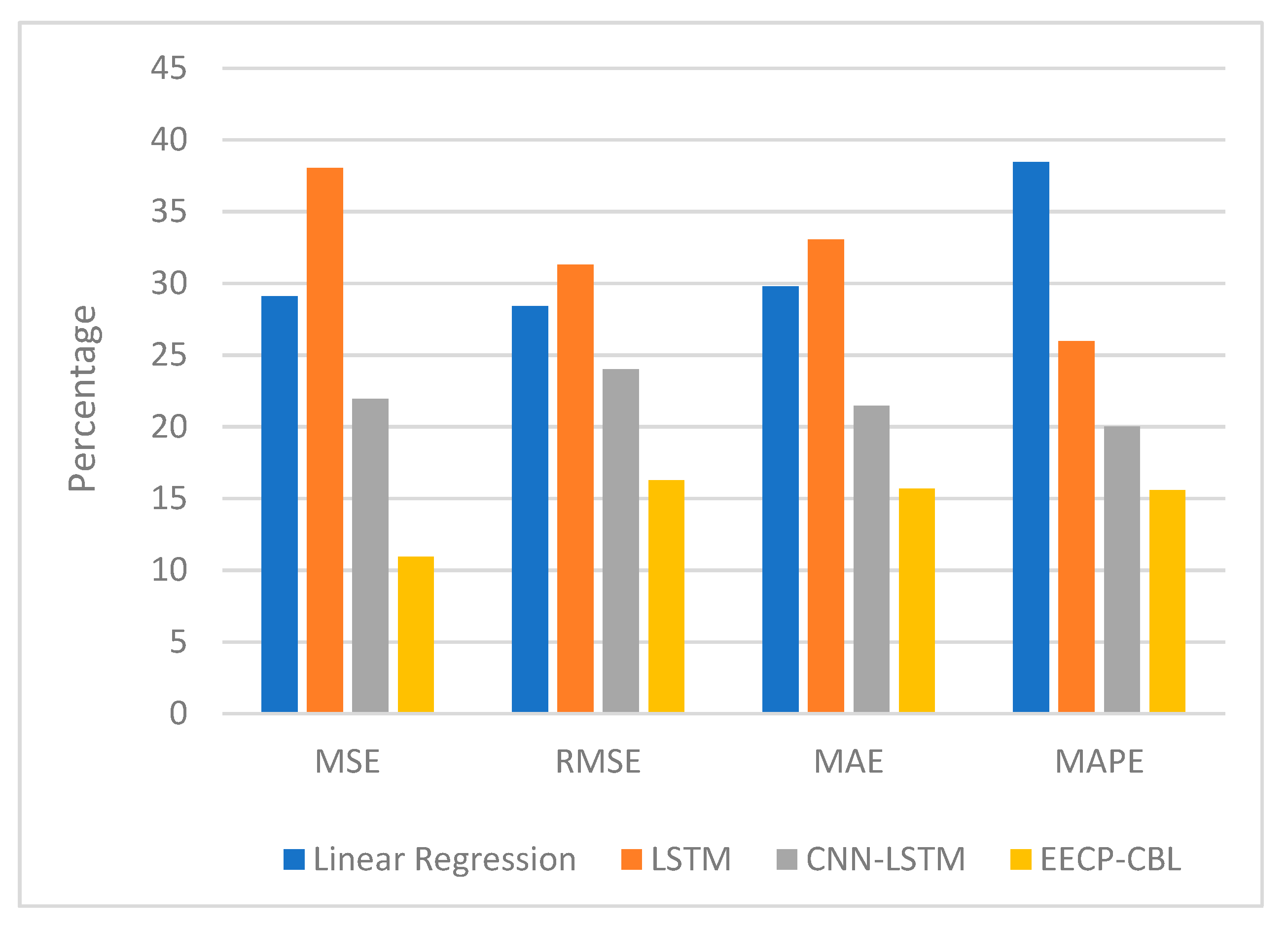
| #No | Model | MSE | RMSE | MAE | MAPE | Training Time (s) | Predicting Time (s) |
|---|---|---|---|---|---|---|---|
| 1 | Linear Regression | 0.405 | 0.636 | 0.418 | 74.52 | 1028 | 37.48 |
| 2 | LSTM | 0.748 | 0.865 | 0.628 | 51.45 | 6880 | 114.26 |
| 3 | CNN-LSTM | 0.374 | 0.611 | 0.349 | 34.84 | 2070 | 62.99 |
| 4 | EECP-CBL | 0.051 | 0.225 | 0.098 | 11.66 | 3950 | 43.83 |
| #No | Model | MSE | RMSE | MAE | MAPE | Training Time (s) | Predicting Time (s) |
|---|---|---|---|---|---|---|---|
| 1 | Linear Regression | 0.425 | 0.652 | 0.502 | 83.74 | 692.12 | 2.88 |
| 2 | LSTM | 0.515 | 0.717 | 0.526 | 44.37 | 2281.50 | 5.95 |
| 3 | CNN-LSTM | 0.355 | 0.596 | 0.332 | 32.83 | 820.70s | 2.31 |
| 4 | EECP-CBL | 0.298 | 0.546 | 0.392 | 50.09 | 1296.34 | 1.87 |
| #No | Model | MSE | RMSE | MAE | MAPE | Training Time (s) | Predicting Time (s) |
|---|---|---|---|---|---|---|---|
| 1 | Linear Regression | 0.253 | 0.503 | 0.392 | 52.69 | 27.83 | 1.32 |
| 2 | LSTM | 0.241 | 0.491 | 0.413 | 38.72 | 106.06 | 2.97 |
| 3 | CNN-LSTM | 0.104 | 0.322 | 0.257 | 31.83 | 42.35 | 1.91 |
| 4 | EECP-CBL | 0.065 | 0.255 | 0.191 | 19.15 | 61.36 | 0.71 |
| #No | Model | MSE | RMSE | MAE | MAPE | Training Time (s) | Predicting Time (s) |
|---|---|---|---|---|---|---|---|
| 1 | Linear Regression | 0.148 | 0.385 | 0.320 | 41.33 | 11.23 | 1.48 |
| 2 | LSTM | 0.105 | 0.324 | 0.244 | 35.78 | 24.42 | 3.66 |
| 3 | CNN-LSTM | 0.095 | 0.309 | 0.238 | 31.84 | 14.12 | 2.06 |
| 4 | EECP-CBL | 0.049 | 0.220 | 0.177 | 21.28 | 20.7 | 0.4 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Le, T.; Vo, M.T.; Vo, B.; Hwang, E.; Rho, S.; Baik, S.W. Improving Electric Energy Consumption Prediction Using CNN and Bi-LSTM. Appl. Sci. 2019, 9, 4237. https://doi.org/10.3390/app9204237
Le T, Vo MT, Vo B, Hwang E, Rho S, Baik SW. Improving Electric Energy Consumption Prediction Using CNN and Bi-LSTM. Applied Sciences. 2019; 9(20):4237. https://doi.org/10.3390/app9204237
Chicago/Turabian StyleLe, Tuong, Minh Thanh Vo, Bay Vo, Eenjun Hwang, Seungmin Rho, and Sung Wook Baik. 2019. "Improving Electric Energy Consumption Prediction Using CNN and Bi-LSTM" Applied Sciences 9, no. 20: 4237. https://doi.org/10.3390/app9204237
APA StyleLe, T., Vo, M. T., Vo, B., Hwang, E., Rho, S., & Baik, S. W. (2019). Improving Electric Energy Consumption Prediction Using CNN and Bi-LSTM. Applied Sciences, 9(20), 4237. https://doi.org/10.3390/app9204237









