Predicting Student Grades Based on Their Usage of LMS Moodle Using Petri Nets
Abstract
:1. Introduction
2. Related Work
The Basic Concept of Petri Nets
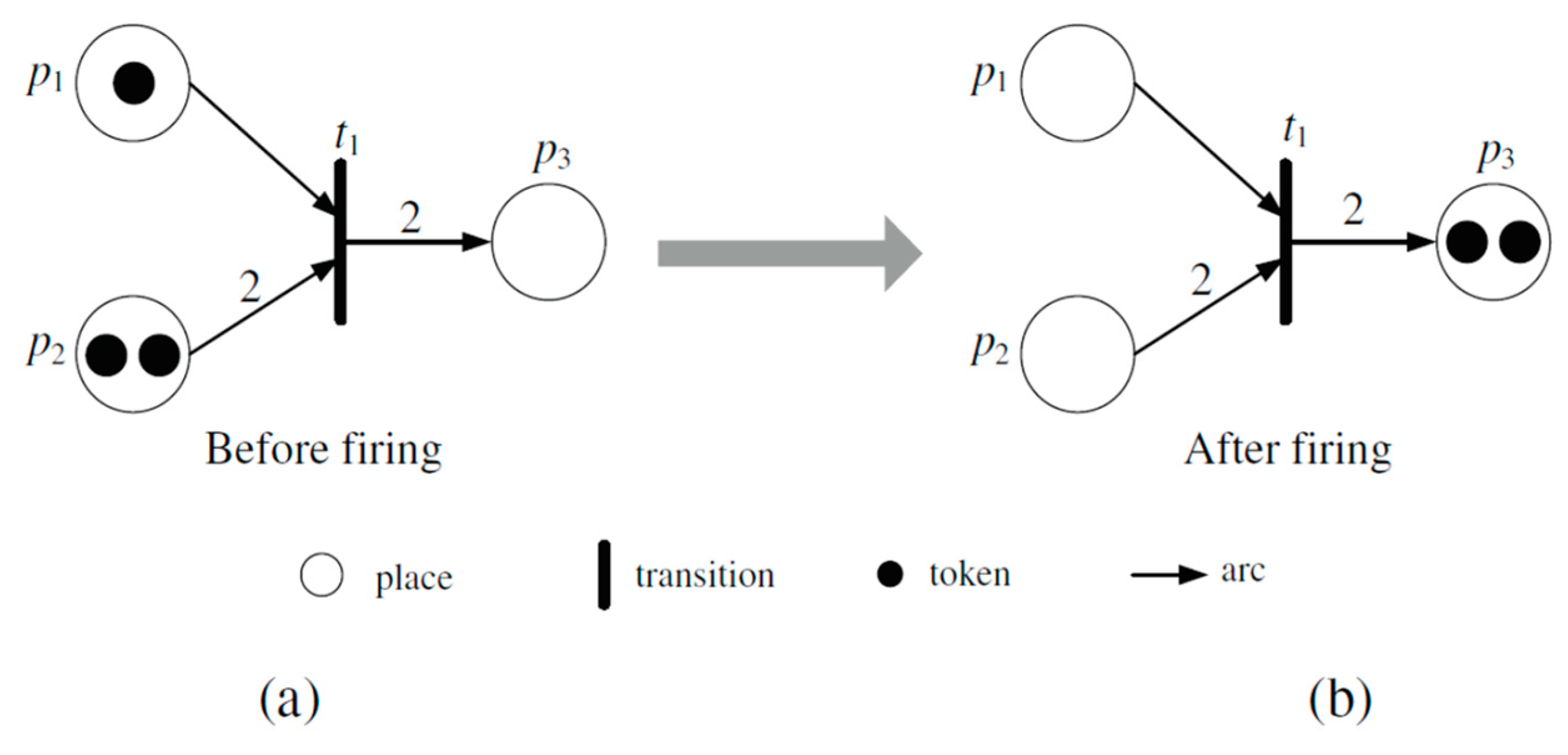
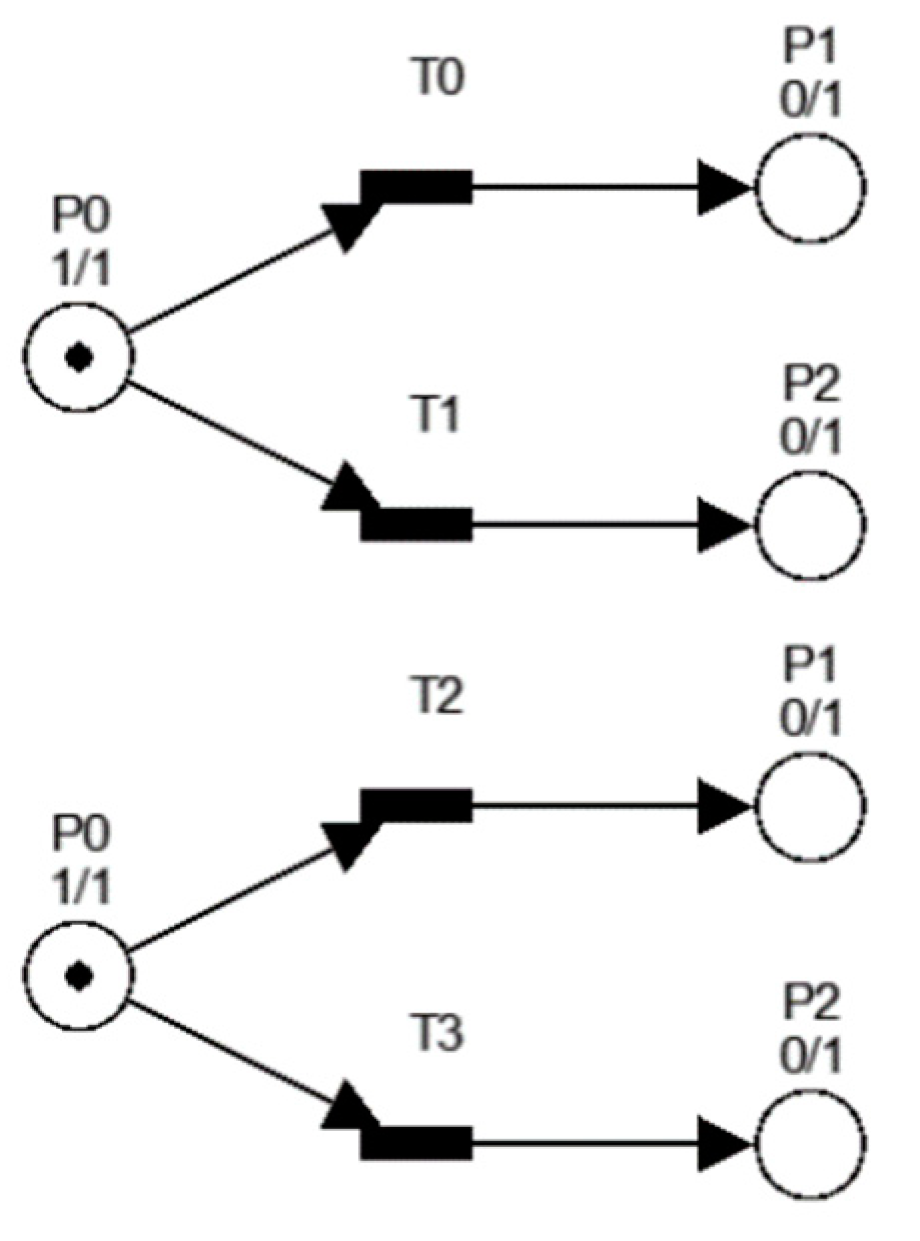
- P = {p1,p2,…,pm} is a finite set of places. A place represents a circle, such as p1,p2 and p3 in Figure 1.
- T = {t1,t2,…,tn} is a finite set of transitions. A transition represents a bar, such as t1 in Figure 1. The intersection of P and T is an empty set, while the union of P and T is not an empty set, i.e., P∩T = ∅ and T∪P ≠ ∅.
- A⊆(PxT)∪(TxP) is a set of arcs connecting places and transitions, such as the arrowhead from p1 to t1 depicted in Figure 1.
- W:A→{1,2,3,…} is a weight function, whose weight value is positive integers. Arcs, i.e., arrowhead, are labeled with weights. For example, in Figure 1, the arrowhead from t1 to p3, which is labeled with “2”, is denoted as W(t1,p3) = 2. When the weight is unity and/or “1”, the label of arc is usually omitted, e.g., W(p1,t1) = 1 is omitted in Figure 1.
- M0:P→{0,1,2,3,…} is the initial marking. If there are k tokens inside place pi, it is said that pi is marked with k tokens. For example, in Figure 1a, p1 is marked with one token, which is denoted as M(p1) = 1. p2 is marked with two tokens, which is denoted as M(p2) = 2. If Figure 1a is the initial status, the initial marking is denoted as M0(p1,p2,p3) = {1,2,0}.
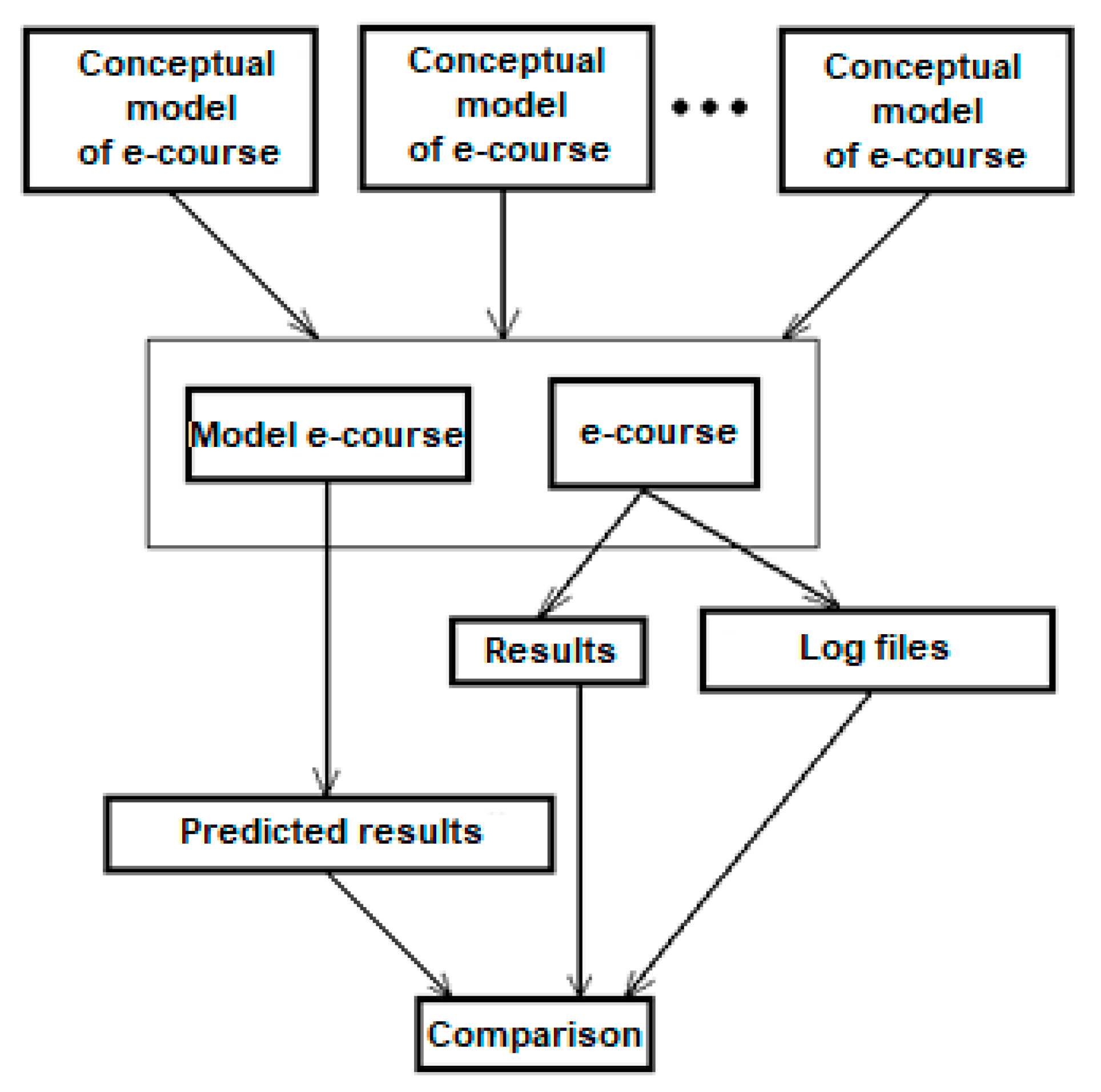
3. Materials and Methods
- A design of student behavior models in a virtual learning environment, i.e., study of materials in individual parts of the course, models of logical functions, loop models, condition models, deadlocks, etc. that could simulate the student behavior in the virtual education system and its subsequent rating.
- After creating the appropriate educational models, it was possible to create a new e-course and test it with the models created for the e-course.
- A creation of an e-course from the proposed Petri Network models.
- After result evaluation of the real e-course using models designed for the e-course, it was possible to find out which parts of the e-course were most used for study and especially which parts contributed the most to the better grades of the students.
3.1. Modeling Uncertainty with Petri Nets
3.2. Observing Student Movement in LMS
- Time
- User name
- Affected user
- Event context
- Component
- Event name
- Description
- Source
- IP
4. Results and Discussion
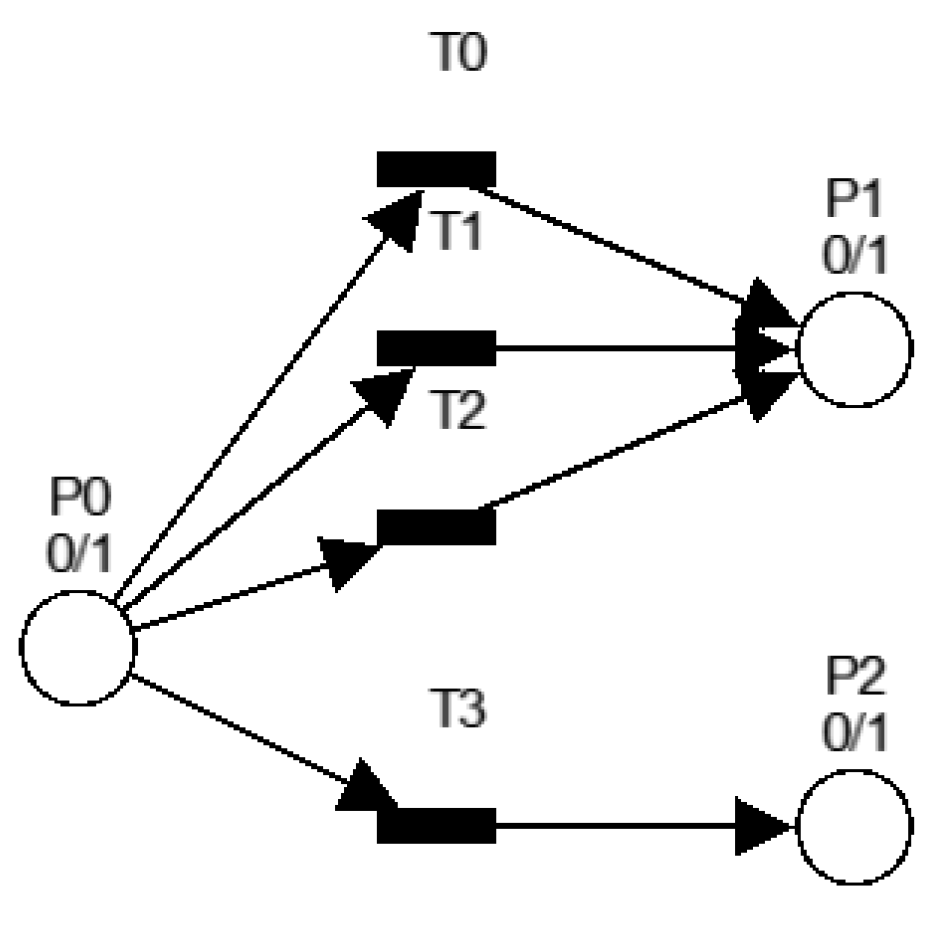
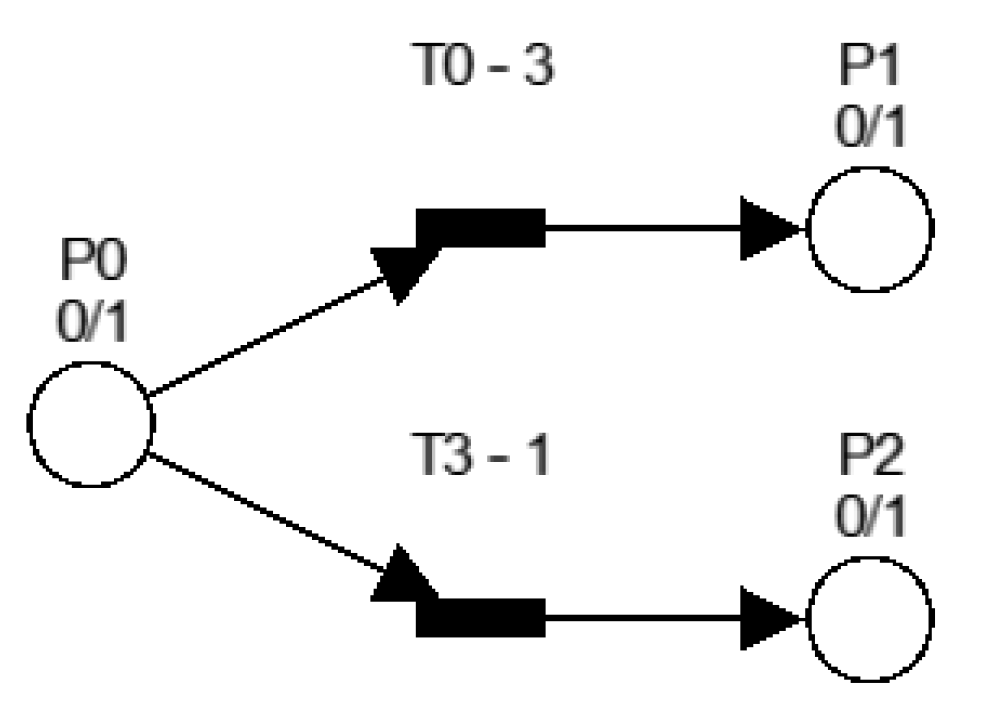
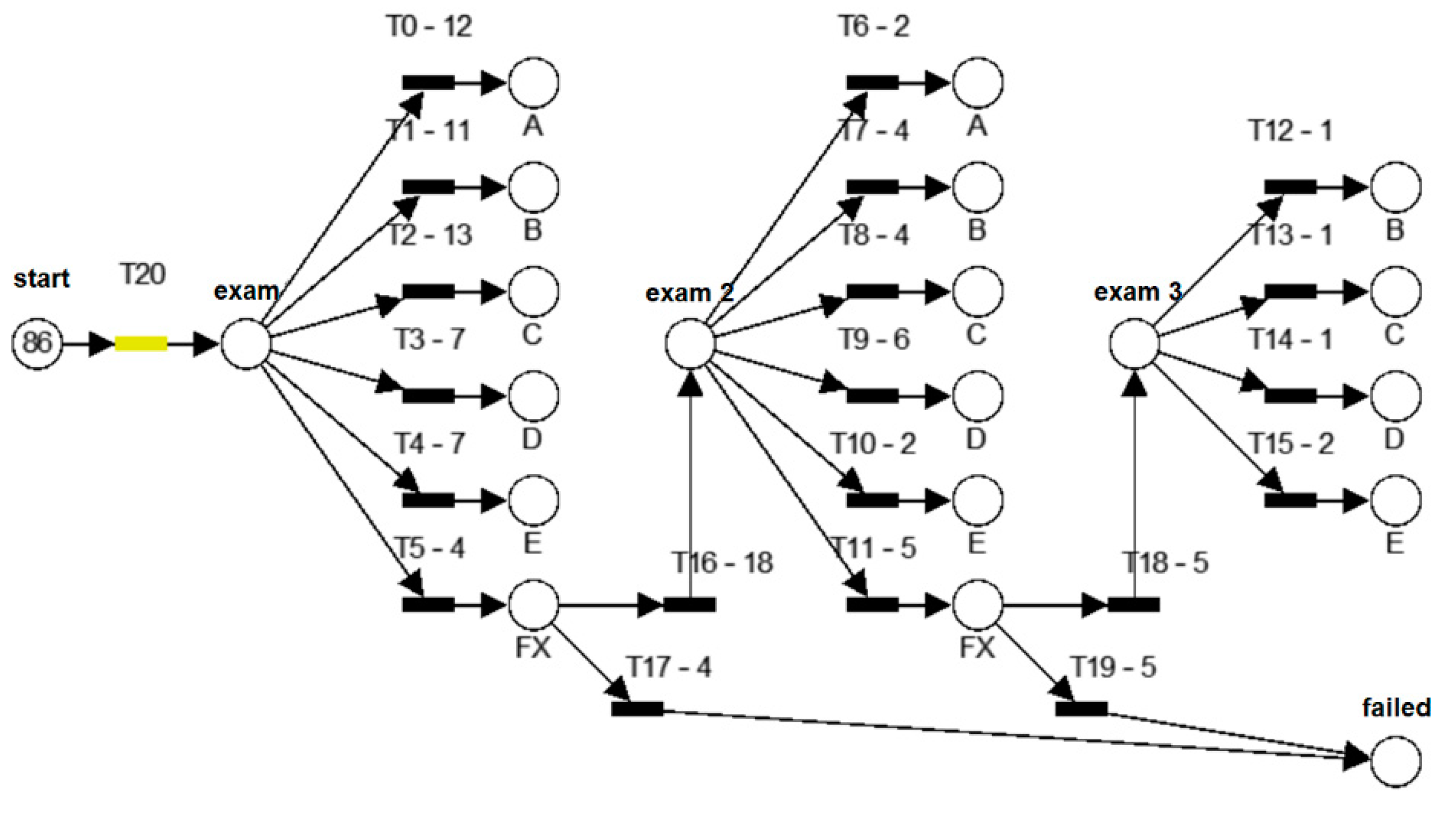
4.1. Model of the Final Exam in Petri Nets
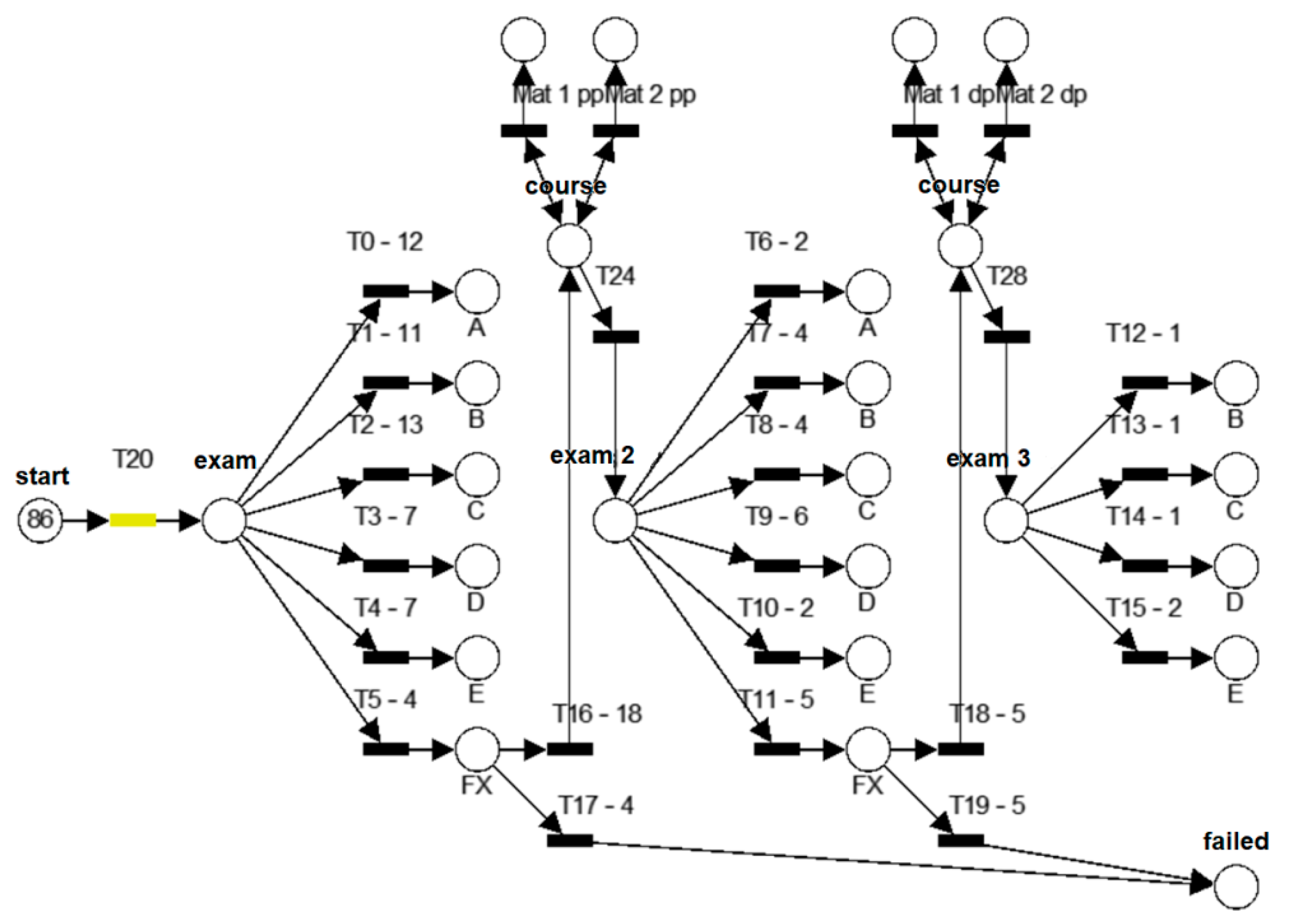
4.2. Model of Grade Prediction
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Holub, M.; Bieliková, M. An inquiry into the utilization of behavior of users in personalized Web. J. Univers. Comput. Sci. 2011, 17, 1830–1853. [Google Scholar]
- Kim, E.; Park, H.; Jang, J. Development of a Class Model for Improving Creative Collaboration Based on The Online Learning System (Moodle) in Korea. J. Open Innov. Technol. Mark. Complex. 2019, 5, 67. [Google Scholar] [CrossRef]
- Costello, E. Opening up to open source: Looking at how Moodle was adopted in higher education. Open Learn. J. Open Distance e-Learn. 2013, 28, 187–200. [Google Scholar] [CrossRef]
- Hew, K.F.; Huang, B.; Chu, K.W.S.; Chiu, D.K. Engaging Asian students through game mechanics: Findings from two experiment studies. Comput. Educ. 2016, 92, 221–236. [Google Scholar] [CrossRef]
- Zhou, L.; Chen, L.W.; Fan, Q.M.; Ji, Y.L. Students’ Perception of Using Digital Badges in Blended Learning Classrooms. Sustainability 2019, 11, 18. [Google Scholar] [CrossRef]
- Kc, D. Evaluation of Moodle Features at Kajaani University of Applied Sciences—Case Study. Procedia Comput. Sci. 2017, 116, 121–128. [Google Scholar] [CrossRef]
- Molnar, G. The Impact of Modern ICT-Based Teaching and Learning Methods in Social Media and Networked Environment. In Proceedings of the 11th International Scientific Conference on Distance Learning in Applied Informatic (DiVAi), Sturovo, Slovakia, 2–4 May 2016; Wolters Kluwer Cr a S: Strašnice, Czechia, 2016; pp. 341–350. [Google Scholar]
- Molnár, G.; Benedek, A. ICT related tasks and challenges in the new model of technical teacher training. In Proceedings of the Eighth International Multi-Conference on Computing in the Global Information Technology (ICCGI), Nice, France, 21–26 July 2013; IARIA: Barcelona, Spain, 2013; pp. 40–44. [Google Scholar]
- Juhaňák, L.; Zounek, J.; Rohlíková, L. Using process mining to analyze students’ quiz-taking behavior patterns in a learning management system. Comput. Hum. Behav. 2019, 92, 496–506. [Google Scholar] [CrossRef]
- Romero, C.; Cerezo, R.; Bogarín, A.; Sánchez-Santillán, M. Educational process mining: A tutorial and case study using Moodle data sets. In Data Mining and Learning Analytics: Applications in Educational Research; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2016; pp. 1–28. [Google Scholar]
- Romero, C.; Ventura, S. Educational data mining: A review of the state of the art. IEEE Trans. Syst. Man Cybern. Part C (Appl. Rev.) 2010, 40, 601–618. [Google Scholar] [CrossRef]
- Romero, C.; Ventura, S.; Pechenizkiy, M.; Baker, R.S. Handbook of Educational Data Mining; CRC Press: Boca Raton, FL, USA, 2010. [Google Scholar]
- Trcka, N.; Pechenizkiy, M.; van der Aalst, W. Process mining from educational data. In Handbook of Educational Data Mining; CRC Press: Boca Raton, FL, USA, 2010; pp. 123–142. [Google Scholar]
- Reimann, P.; Yacef, K. Using process mining for understanding learning. In Handbook of Design in Educational Technology; Routledge: Abingdon, UK, 2013; pp. 472–481. [Google Scholar]
- Reimann, P.; Markauskaite, L.; Bannert, M. e-R esearch and learning theory: What do sequence and process mining methods contribute? Br. J. Educ. Technol. 2014, 45, 528–540. [Google Scholar] [CrossRef]
- Chang, Y.-C.; Huang, Y.-C.; Chu, C.-P. B2 model: A browsing behavior model based on High-Level Petri Nets to generate behavioral patterns for e-learning. Expert Syst. Appl. 2009, 36, 12423–12440. [Google Scholar] [CrossRef]
- Balogh, Z.; Turcani, M.; Magdin, M. The possibilities of using Petri Nets for realization of a universal model of educational process. In Proceedings of the 2013 IEEE 14th International Conference on Information Reuse and Integration (IRI), San Francisco, CA, USA, 14–16 August 2013; pp. 162–169. [Google Scholar]
- Balogh, Z.; Turcani, M. Possibilities of Modelling Web-Based Education Using IF-THEN Rules and Fuzzy Petri Nets in LMS. In Informatics Engineering and Information Science, Pt I; AbdManaf, A., Zeki, A., Zamani, M., Chuprat, S., ElQawasmeh, E., Eds.; Springer: Berlin, Germany, 2011; Volume 251, pp. 93–106. [Google Scholar]
- Klimeš, C.; Balogh, Z. Modelovanie Procesov Pomocou Petriho Sietí; Fakulta prírodných vied; UKF Nitra: Nitra, Slovakia, 2012. [Google Scholar]
- Kucharik, M.; Balogh, Z. Evaluation of fuzzy Petri nets with the tool TransPlaceSim. In Proceedings of the 10th IEEE International Conference on Application of Information and Communication Technologies (AICT), Baku, Azerbaijan, 12–14 October 2016. [Google Scholar]
- Campos-Rebelo, R.; Costa, A.; Gomes, L. Finding learning paths using Petri nets modeling applicable to e-learning platforms. In Proceedings of the 3rd IFIP WG 5.5/SOCOLNET Doctoral Conference on Computing, Electrical and Industrial Systems, DoCEIS 2012, Costa de Caparica, Portugal, 27–29 February 2012; Volume 372, pp. 151–160. [Google Scholar]
- Chen, S.M. Representing fuzzy knowledge using extended fuzzy Petri nets. In Proceedings of the 2nd International Symposium on Uncertainty Modeling and Analysis, College Park, MD, USA, USA, 25–28 April 1993; pp. 339–346. [Google Scholar]
- Mtibaa, S.; Tagina, M. A Petri-Net model based timing constraints specification for e-learning system. In Proceedings of the 2012 International Conference on Education and e-Learning Innovations, Sousse, Tunisia, 1–3 July 2012. [Google Scholar]
- Murata, T. Petri Nets: Properties, Analysis and Applications. Proc. IEEE 1989, 77, 541–580. [Google Scholar] [CrossRef]
- Jensen, K. Colored petri nets. Lect. Notes Comput. Sci. 1987, 254, 248–299. [Google Scholar] [CrossRef]
- Kodamana, H.; Raveendran, R.; Huang, B. Mixtures of Probabilistic PCA with Common Structure Latent Bases for Process Monitoring. IEEE Trans. Control Syst. Technol. 2019, 27, 838–846. [Google Scholar] [CrossRef]
- Tian, Y.; Wang, X.Z.; Jiang, Y.; You, G.H. A Distributed Probabilistic Coverage Sets Configuration Method for High. Density WSN; Ieee: New York, NY, USA, 2017; pp. 2312–2316. [Google Scholar]
- Dehban, A.; Jamone, L.; Kampff, A.R.; Santos-Victor, J. A Deep Probabilistic Framework for Heterogeneous Self-Supervised Learning of Affordances; Ieee: New York, NY, USA, 2017; pp. 476–483. [Google Scholar]
- Kuchárik, M.; Balogh, Z. Modeling of Uncertainty with Petri Nets. In 11th Asian Conference on Intelligent Information and Database Systems (ACIIDS 2019); Nguyen, N.T., Gaol, F.L., Nguyen, N.T., Trawinski, B., Hong, T.P., Eds.; Springer: Berlin, Germany, 2019; Volume 11431, pp. 499–509. [Google Scholar]
- Dobashi, K. Automatic data integration from Moodle course logs to pivot tables for time series cross section analysis. In Knowledge-Based and Intelligent Information & Engineering Systems; ZanniMerk, C., Frydman, C., Toro, C., Hicks, Y., Howlett, R.J., Jain, L.C., Eds.; Elsevier Science Bv: Amsterdam, The Netherlands, 2017; Volume 112, pp. 1835–1844. [Google Scholar]
- Fang, Y.; Huang, Z. An improved algorithm for session identification on web log. In Proceedings of the 2010 International Conference on Web Information Systems and Mining (WISM 2010), Sanya, China, 23–24 October 2010; Volume 6318, pp. 53–60. [Google Scholar]
- Benko, L.; Reichel, J.; Munk, M. Analysis of student behavior in virtual learning environment depending on student assessments. In Proceedings of the 13th IEEE International Conference on Emerging eLearning Technologies and Applications (ICETA), Stary Smokovec, Slovakia, 26–27 November 2015. [Google Scholar]
- Maheswara Rao, V.V.R.; Valli Kumari, V.; Raju, K.V.S.V.N. An intelligent system for web usage data preprocessing. In Proceedings of the 1st International Conference on Computer Science and Information Technology, CCSIT 2011, Bangalore, India, 2–4 January 2011; Volume 131, pp. 481–490. [Google Scholar]
- Štencl, M.; Štastný, J. Neural network learning algorithms comparison on numerical prediction of real data. In Proceedings of the 16th International Conference on Soft Computing Mendel, Brno, Czech Republic, 23–25 June 2010; pp. 280–285. [Google Scholar]

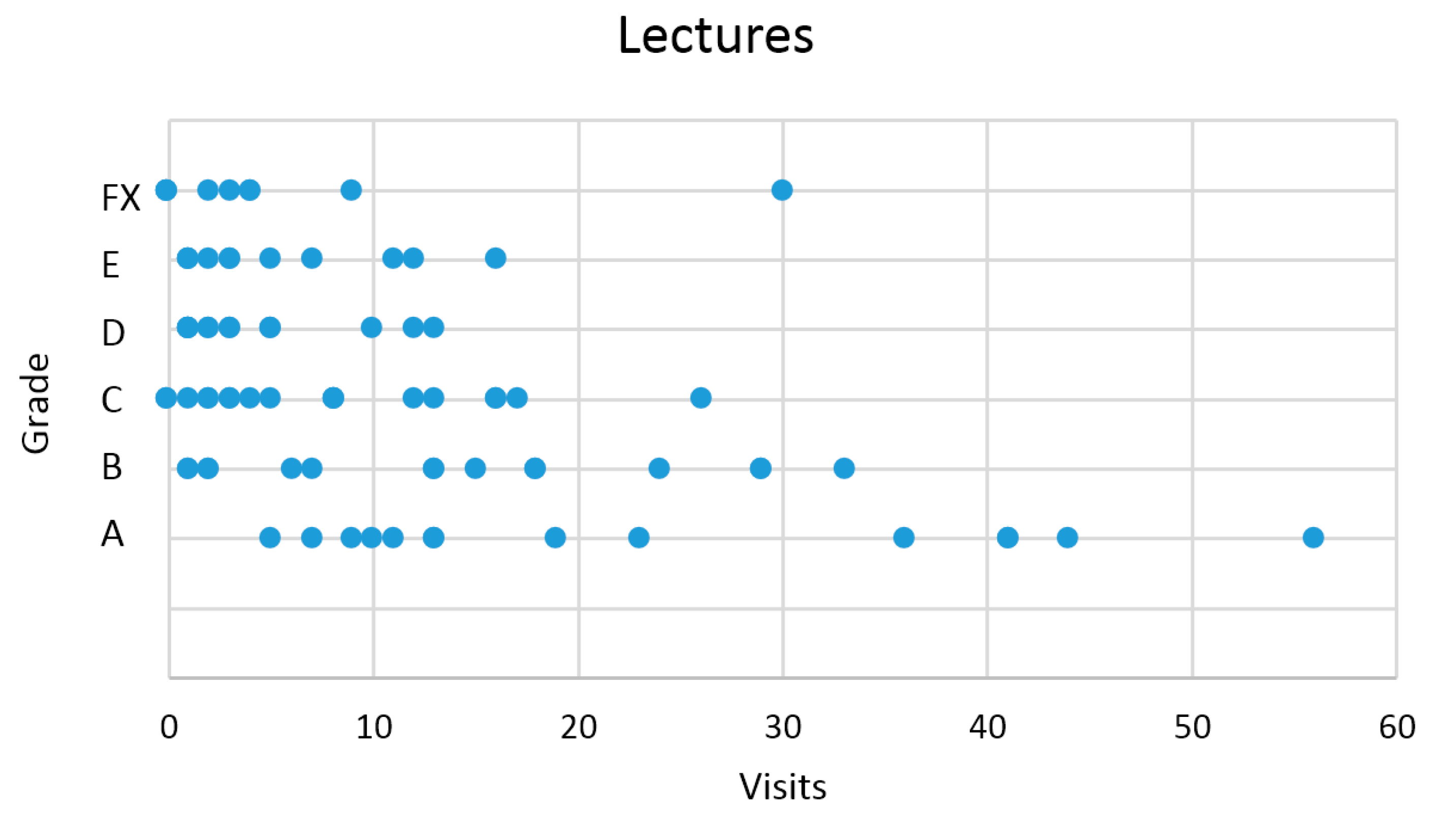

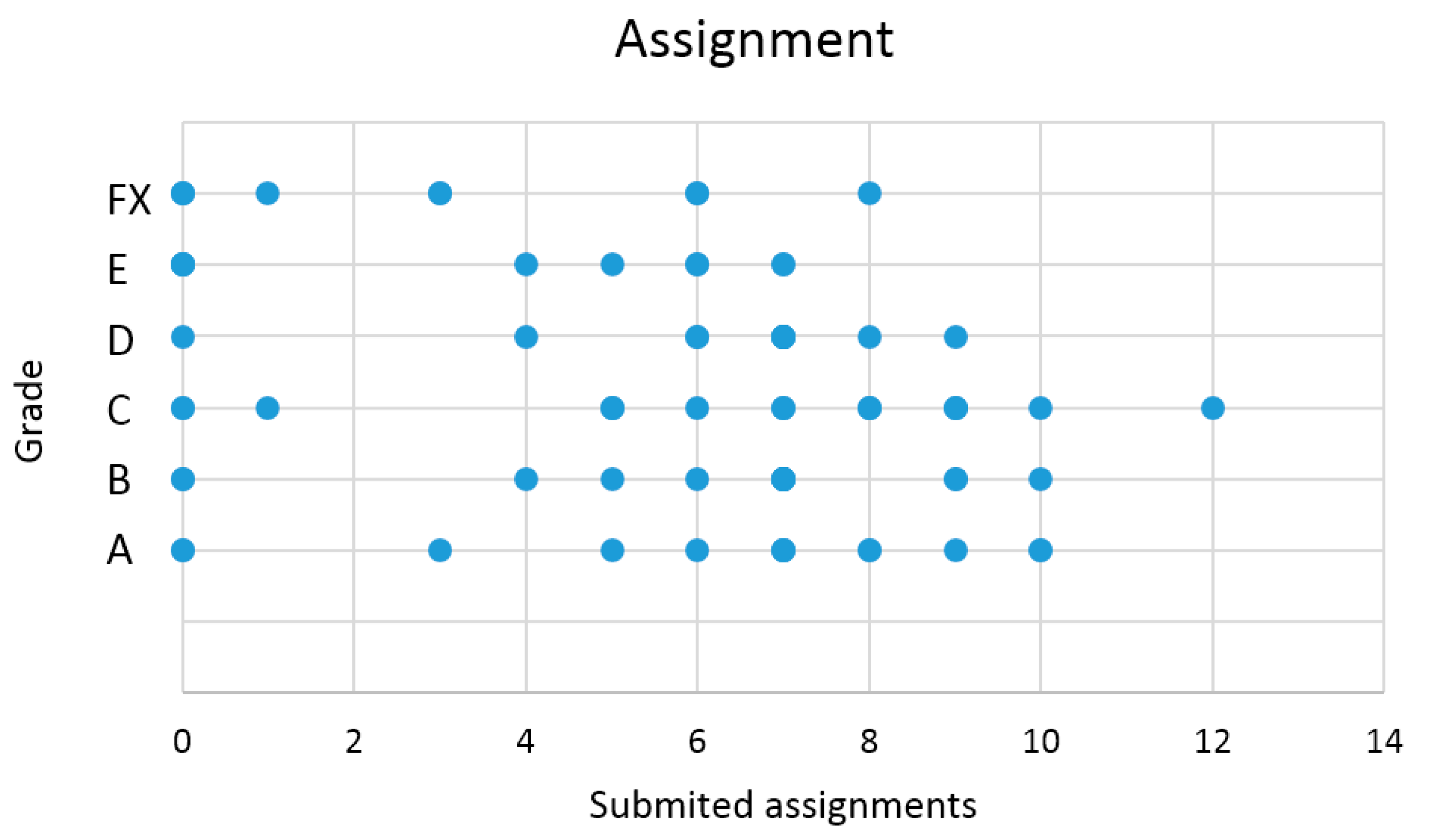
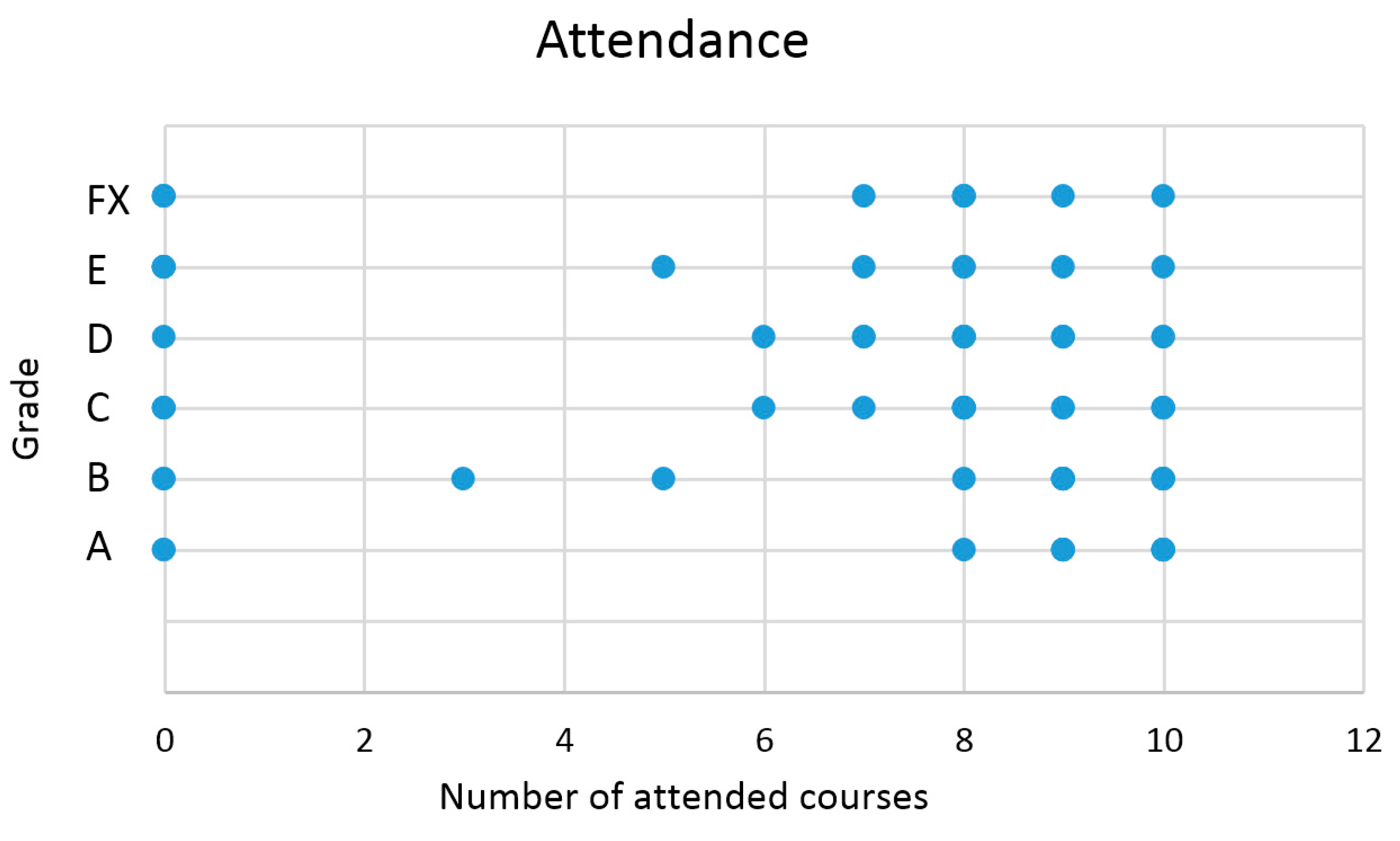
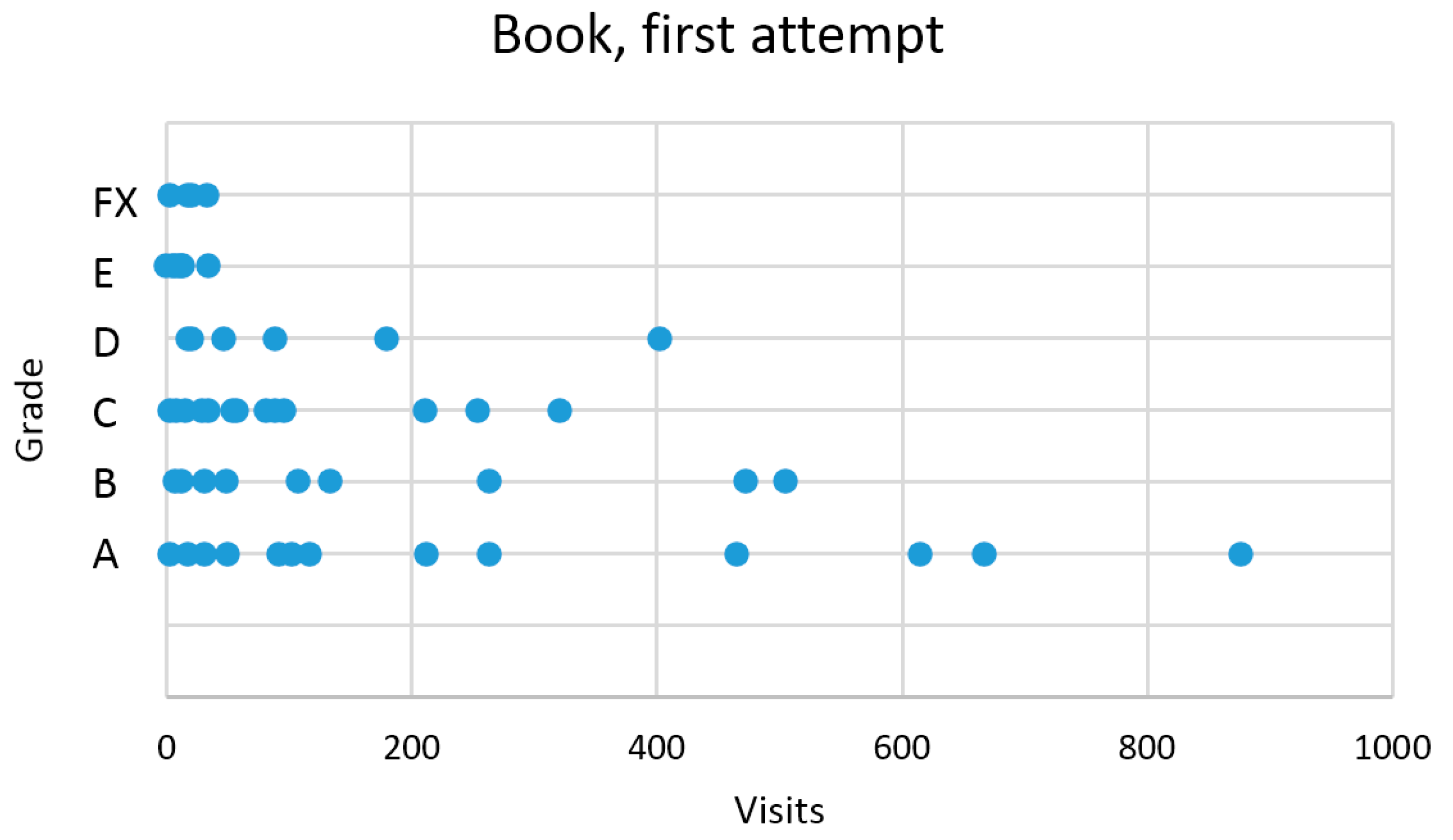
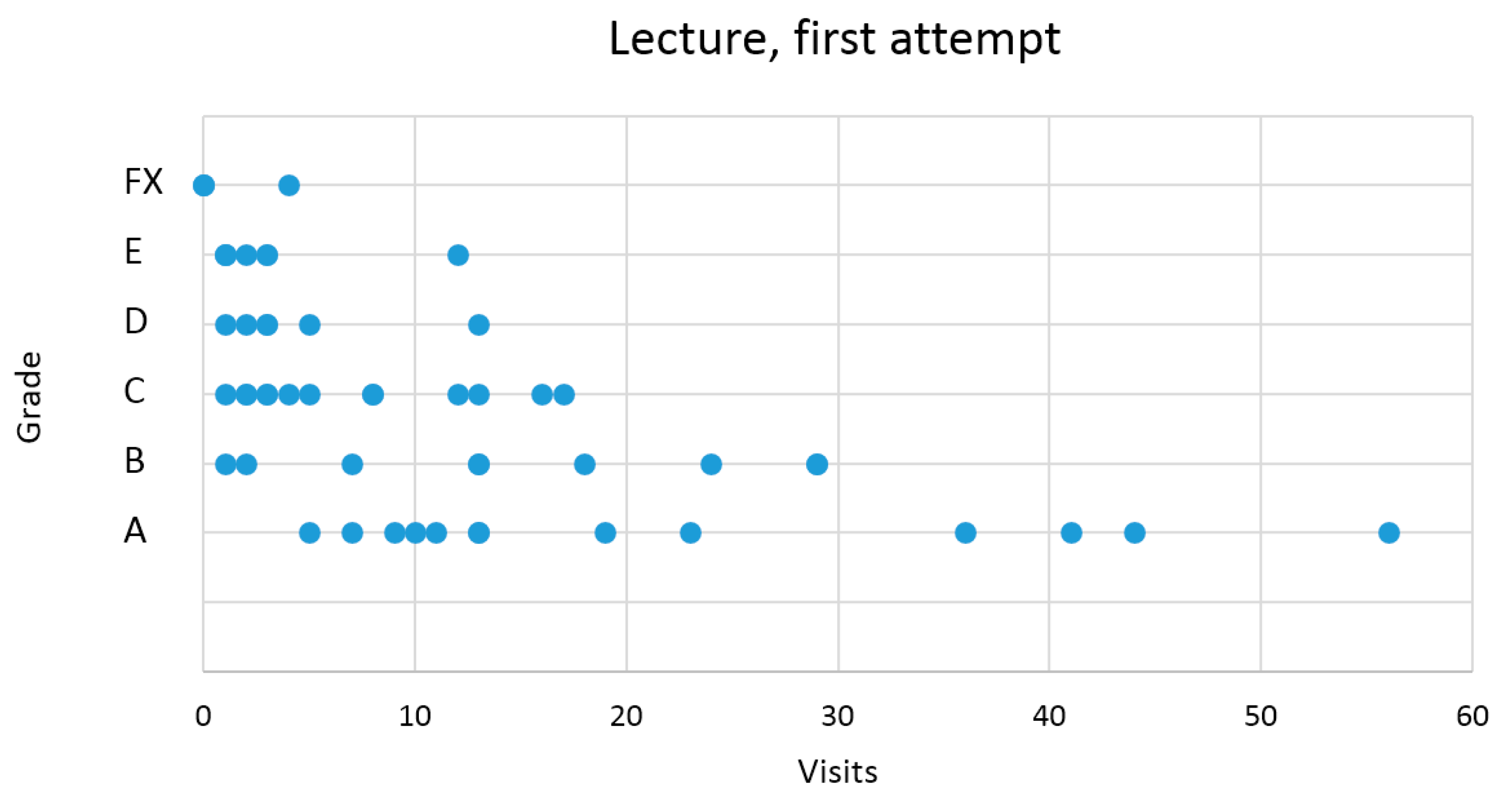
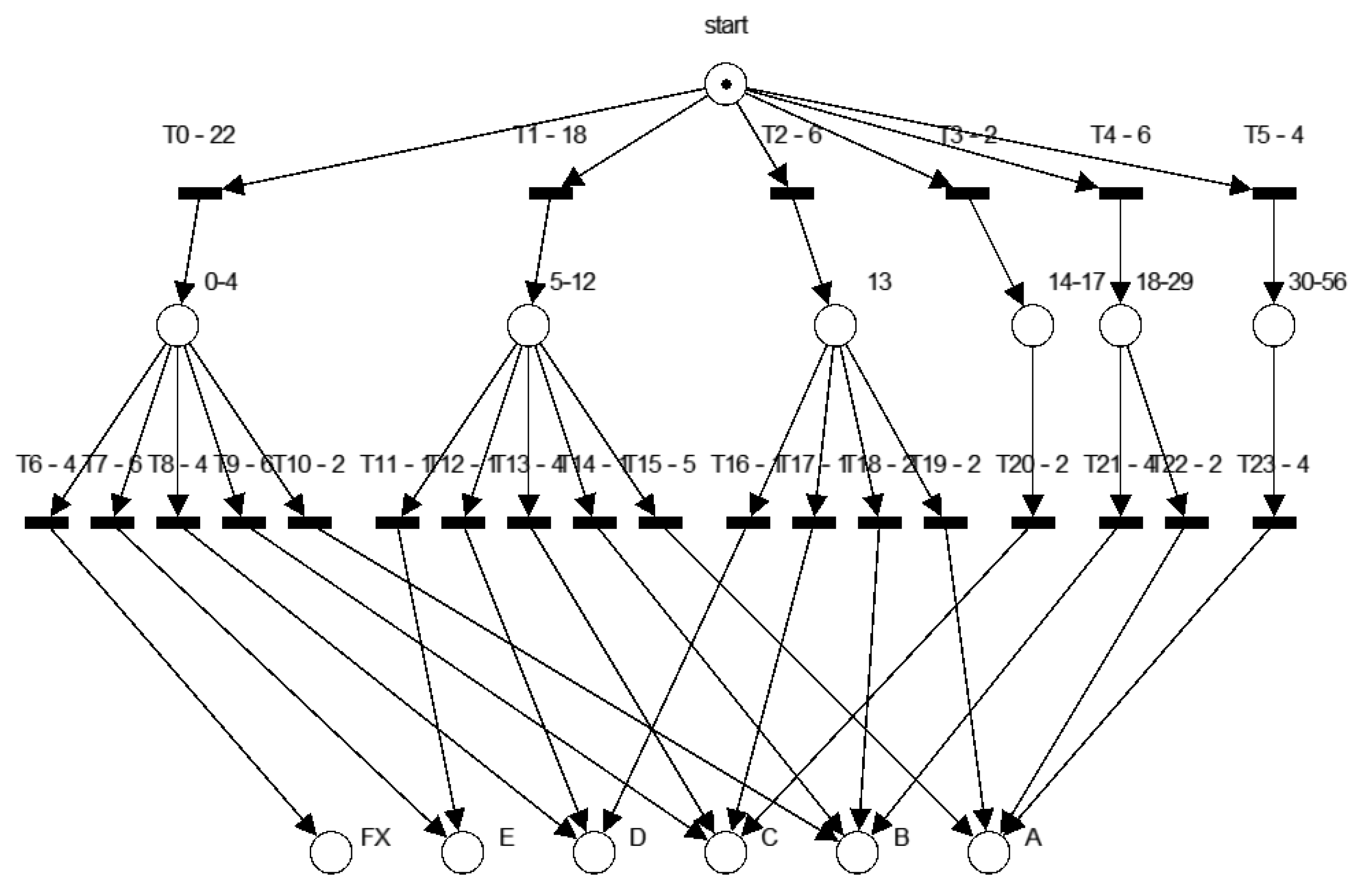
| Visits | 0..4 | 5..12 | 13 | 14..17 | 18..29 | 30..56 |
| Students | 22 | 18 | 6 | 2 | 6 | 4 |
| A | 0 | 5 | 2 | 0 | 2 | 4 |
| B | 2 | 1 | 2 | 0 | 4 | 0 |
| C | 6 | 4 | 1 | 2 | 0 | 0 |
| D | 4 | 1 | 1 | 0 | 0 | 0 |
| E | 6 | 1 | 0 | 0 | 0 | 0 |
| FX | 4 | 0 | 0 | 0 | 0 | 0 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Balogh, Z.; Kuchárik, M. Predicting Student Grades Based on Their Usage of LMS Moodle Using Petri Nets. Appl. Sci. 2019, 9, 4211. https://doi.org/10.3390/app9204211
Balogh Z, Kuchárik M. Predicting Student Grades Based on Their Usage of LMS Moodle Using Petri Nets. Applied Sciences. 2019; 9(20):4211. https://doi.org/10.3390/app9204211
Chicago/Turabian StyleBalogh, Zoltán, and Michal Kuchárik. 2019. "Predicting Student Grades Based on Their Usage of LMS Moodle Using Petri Nets" Applied Sciences 9, no. 20: 4211. https://doi.org/10.3390/app9204211
APA StyleBalogh, Z., & Kuchárik, M. (2019). Predicting Student Grades Based on Their Usage of LMS Moodle Using Petri Nets. Applied Sciences, 9(20), 4211. https://doi.org/10.3390/app9204211





