Featured Application
The 2-2 piezoelectric composite bilaminated vibrator with lower resonance frequency and larger vibration displacement used for making low frequency acoustic transducer.
Abstract
A piezoelectric composite vibrator with a bilaminated structure is designed and fabricated, in this work by applying bending vibration to increase vibration displacement and reduce resonance frequency. The finite element software ANSYS (ANSYS, Inc. USA) is used to simulate the 2-2 and 1-3 piezoelectric composite bilaminated vibrators under free boundary condition and optimize their design. Simulation results show that the vibration displacement of the 2-2 vibrator is higher than that of the 1-3 vibrator, and the resonance frequency of the former is lower than the latter. Five pieces each of the 2-2 and piezoelectric ceramic vibrators are prepared. In addition, simulation and experimental results indicate that the vibration displacement of the 2-2 vibrator increases by 2.3 times, whereas its resonance frequency decreases by nearly 100 Hz, in comparison with those of the piezoelectric ceramic bilaminated vibrator.
1. Introduction
In the past 30 years, due to the rapid development of science and technology, low-frequency transducers have been more and more applied in sonar system and Marine science research. As a part of sonar systems, transducers have played a very important role in underwater sounding, locating, object recognition, communication, navigation, remote control, seabed remote sensing (bottom, stratum, landform), searching for oil and gas, and developing mineral resources. Piezoelectric vibrator is the core element of low frequency transducer. Reducing the resonant frequency and increasing the vibration displacement are the key technologies in the study of low frequency transducers. Bilaminated piezoelectric vibrators have several advantages, such as low resonance frequency, small size, light weight, and simple structure, and are an ideal low-frequency vibration sound source. Several studies on bilaminated vibrators made of piezoelectric ceramics and trilaminar vibrators made of piezoelectric ceramics and metal sheets have been reported. Woollett developed a theory of bimorph and trilaminar modifications of circular plate transducers for underwater applications. The approach used in his work was based on presenting deflection curves under flexure using a polynomial function, and Rayleigh’s principle for the cases of simply supported and clamped boundary conditions [1]. Aronov studied the effective electromechanical coupling coefficient and resonant frequency of bilaminated and trilaminated circular plate transducers by using the energy method [2,3]. Zhang et al. presented a general solution of displacement, resonance, and free-field voltage sensitivity for metal piezoceramic bimorph transducers with a fixed boundary [4]. He et al. derived the displacement distribution function and resonance frequency equation of a piezoelectric ceramic bimorph, and studied the influence of the vibrator’s radius on resonance frequency and vibration displacement [5]. Ding et al. studied the circular composite piezoelectric vibrator and calculated and analyzed the relationship among resonance frequency, the effective electromechanical coupling coefficient, and the size of the vibrator [6]. Zhang studied three laminated plate transducers under three different boundary conditions, and derived the expressions of the resonance frequency and the effective electromechanical coupling coefficient by using the Raleigh method. In this study, numerical calculations and finite element simulations of the resonance frequency and the effective electromechanical coupling coefficient of the transducer varying with structural parameters were performed [7]. Zhang et al. studied the radiation impedance of a thin circular flat plate in flexural vibration with a free boundary, and the results showed that the radiation impedance was the function of the wave number κ, the radius α, and the nodal line [8].
Studies on the performance of rectangular piezoelectric laminated vibrators are limited. Lin studied the flexural vibration of a piezoelectric ceramic rectangular thin plate. Under the boundary conditions of free edges and simply supported edges, the resonance frequency equations were derived, and the relationship between the vibrational modes and geometrical dimensions was analyzed [9]. Qiao et al. studied the resonance frequencies of a rectangular trilaminar vibrator under five boundary conditions [10]. Zheng et al. determined the effects of modifying the transducer’s physical size and other performance parameters on its frequency character and radiation property [11]. Mansoor et al. found that the sensitivity and amplitude of a piezoelectric metal/ceramic composite transducer could be improved by changing the thickness of the piezoelectric material and the spatial distribution of the vibrator [12]. However, the improvement of a vibrator’s piezoelectric properties by changing the material structure, especially via fabricating a bilaminated vibrator through piezoelectric composite materials, have yet to be reported. Piezoelectric composite material is a new material with piezoelectric effect, which is composed of at least one piezoelectric phase material and non-piezoelectric phase material in a certain connecting way. Piezoelectric composites have been widely studied and applied since their advent because of their advantages. Piezoelectric composites are classified according to their connectivity. Each component phase can be self-connected in a 0-, 1-, 2-, or 3-dimensional manner. If the composite consists of two component phases, there are 10 kinds of connectivity, namely 0-0, 0-1, 0-2, 0-3, 1-1, 1-2, 1-3, 2-2, 2-3, 3-3 [13,14]. So far, the development and application of piezoelectric composites have a history of nearly 50 years. In the mid-1970s, the Material Laboratory of Pennsylvania State University began to study the application of piezoelectric composites in underwater acoustics, and developed 1-3 piezoelectric composites. R.E. Newnham, D.P. Skinner, K.A. Klicker, T.R. Gururaja, and H.P. Savakus have done a lot of theoretical and experimental research, and tested the properties of piezoelectric composites with different volume percentages [15,16,17]. Since the early 1980s, B.A. Auld and Y. Wang of Stanford University in California, USA, have established the theoretical model of 1-3 piezoelectric composites with periodic arrangement of PZT (Lead zirconate titanate) columns, and analyzed the transverse structural modes [18]. W. A. Smith of Philips Laboratory in New York, USA, has done similar work [19]. At the same time, many countries have also carried out piezoelectric composite research, such as Helen L.W. Chan in Australia [20] and Hiroshi Takeuchi in Japan [21]. Some researchers have also fabricated transducers using piezoelectric composites, such as Chitose Nakaya in Japan, G. Hayward and R. Hamilton in Britain. Zhuang et al. developed 3-3 piezoelectric composites for broadband transducers [22]. Shui et al. participated in the production of 1-3 piezoelectric composites. Wang et al. made hydrophones with 0-3 piezoelectric composites [23]. Geng developed 1-3 and 2-2 piezoelectric composites and made them for nondestructive testing and water immersion detection, P-wave and S-wave transducers for damage and lithology measurement [24]. An underwater parametric array source transducer composed of PZT/thin-polymer composite were fabricated by Hwang et al. [25]. Kuznetsova et al. used a nanocomposite polymeric layer to increase the efficiency of ultrasound radiation into the liquid by antisymmetric zero-order (A0) Lamb waves propagating in piezoelectric plates [26]. Among many piezoelectric composites, 1-3 and 2-2 piezoelectric composites have been extensively studied. Piezoelectric composites have many advantages that ordinary piezoelectric materials do not possess [27]: (1) The acoustic impedance of piezoelectric materials with low acoustic impedance is much larger than that of water, which greatly limits its application in water and ultrasound. The acoustic impedance of composites can be greatly reduced due to the presence of polymer with very low density, which is about a quarter of that of ordinary PZT materials. When piezoelectric composites are used to make transducers, it is easy to find the corresponding sound absorbing materials as backing, and make the transducers easy to match with water or human tissues. In addition, the acoustic impedance of piezoelectric composites can be controlled by changing the volume fraction of PZT phase to match different media. Therefore, piezoelectric composites have broad application prospects in water immersion testing, oil logging, and medical ultrasound. (2) The low quality factor. The piezoelectric composites with low quality factor is 2–3 orders of magnitude lower than that of ordinary PZT, which is due to the greater attenuation of polymers. The low quality factor makes the piezoelectric composite material very suitable for making broadband narrow pulse transducer. (3) The dielectric constant of piezoelectric composites is much lower than that of ordinary PZT because of the low dielectric constant of polymers. As a result, the electrostatic capacitance of the piezoelectric composite material is smaller, and the input impedance of the transducer is higher when it works, so it has higher sensitivity of the receiving voltage. In addition, the low electrostatic capacitance makes the charging and discharging time shorter. Using piezoelectric composite materials, the transducer with larger first wave amplitude can be fabricated. Therefore, it has been widely used in these fields. (4) Piezoelectric constants dh and gh of high hydrostatic pressure. In underwater acoustic applications, the hydrostatic piezoelectric constant dh = d33 + 2d31 of ordinary PZT. Because d33 is approximately equal to −2d31, dh is very small. In piezoelectric composites, d31 is reduced by controlling the volume fraction of PZT phase, thus dh is increased. The dielectric constant of piezoelectric composites is very small, which makes gh = dh/ε much larger than that of ordinary PZT. Therefore, piezoelectric composite materials are ideal materials for hydrophones. (5) Smaller plane electromechanical coupling coefficient. In piezoelectric composites, PZT columns are coupled by polymers, and the plane electromechanical coupling coefficient of PZT columns is smaller than that of ordinary PZT columns. Therefore, the radial mode in piezoelectric composites is weaker than that in ordinary PZT, which makes the energy more concentrated on the thickness mode, which improves the time response of the pulse to a certain extent. (6) Flexible polymers, such as epoxy resins, are more flexible at high temperatures, which can make piezoelectric composites into some specific shapes to meet the special requirements of practical applications. In the past, in the fabrication of focusing transducers, acoustic lenses were added to the surface of PZT or piezoelectric single crystal to narrow or focus the sound beam at a certain point in space. Using piezoelectric composites, spherical or cylindrical concave surfaces with certain curvature can be pressed at high temperatures, so that sound waves can be directly focused at the center of curvature, generating point or line focused beams, thus avoiding the trouble of making sound lenses and calculating the location of focus. At the same time, it can reduce the loss caused by the acoustic lens and improve the sensitivity of the transducer. In the present work, piezoelectric composite materials were used to replace piezoelectric ceramics to fabricate a bilaminated vibrator, improve the vibration displacement, and reduce the resonance frequency.
2. Structure of the Bilaminated Piezoelectric Composite Vibrator
The structure of the bilaminated piezoelectric composite vibrator is shown in Figure 1. The vibrator was prepared using two layers of a piezoelectric composite with an opposite polarization direction in the z-axis, and the circuit in parallel.
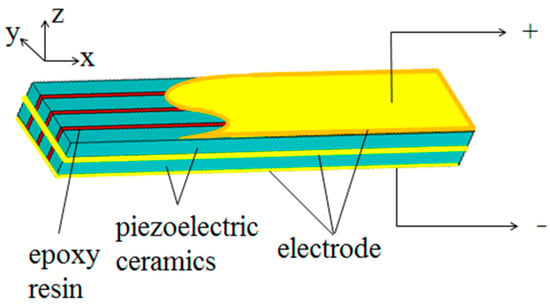
Figure 1.
Structure of the piezoelectric composite bilaminated vibrator.
As shown in Figure 2a, when the polarization direction in the z-axis of the upper and lower piezoelectric plates is opposite, the power supply is connected in series. As shown in Figure 2b, when the polarization direction in the z-axis of the upper and lower piezoelectric plates is the same, the power supply is connected in parallel [28,29,30].
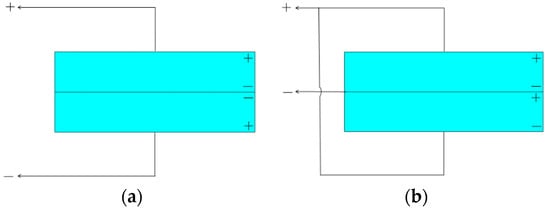
Figure 2.
Schematic of the series and parallel arrangements of the piezoelectric layers. (a) Parallel arrangement. (b) Series arrangement.
Under electric field excitation, when one layer is elongated at a certain time, the other is shortened, and the entire bilaminated vibrator produces a bending vibration, which is the working principle of the bending vibration.
When a slip occurs between the two piezoelectric composites, the performance of the bilaminated vibrator is considerably reduced. Thus, the plywood must be thin, strong, and stable. Bonding piezoelectric composites with low-temperature epoxy resin is suitable, and proper pressure should be applied in curing the epoxy resin.
In the present work, 2-2 and 1-3 type piezoelectric composites were composed of piezoelectric ceramics and epoxy resin, a bilaminated vibrator was studied. Figure 3a shows the 2-2 piezoelectric composite, which was fabricated with 2D-connected piezoelectric ceramic and 2D-connected epoxy resin. Figure 3b shows the 1-3 piezoelectric composite, which was prepared with a 1D-connected piezoelectric ceramic and 3D-connected epoxy resin. The composite electrode was perpendicular to the upper and lower surfaces of the z-axis. The thickness direction (longitudinal) of the composite material was at the z-axis, and the transverse directions were the x- and y-axes [31,32,33,34].

Figure 3.
Structures of the 2-2 and 1-3 type piezoelectric composite. (a) 2-2 type. (b) 1-3 type.
3. Finite Element Simulation of the Piezoelectric Composite Bilaminated Vibrator
The 2-2 and 1-3 piezoelectric composite were simulated under free boundary condition via the finite element method to select a bilaminated piezoelectric composite vibrator. The electrical and vibration characteristics of the piezoelectric composites were analyzed using the finite element analysis software ANSYS. The size of the 2-2 and 1-3 piezoelectric composites was 49.5 mm in length, 9.5 mm in width, and 2 mm in height, and the volume percentage of the piezoelectric ceramics was 0.8. First, the finite element simulation models of the 2-2 and 1-3 piezoelectric composite bilaminated vibrators were established in accordance with the solid structure, as shown in Figure 4. Blue represents the piezoelectric phase and red represents the polymer phase. Second, material parameters of the piezoelectric ceramics and epoxy resins were shown in Table 1 [35]. The anisotropic PZT-5 piezoelectric ceramics were selected as the piezoelectric phase and the solid element Solid5 was selected as the element type. The material parameters included density, stiffness matrix, piezoelectric constant matrix, and dielectric constant matrix. The polymer phase is made of high polymer epoxy resin. The unit type is Solid45. Solid45 is used for three-dimensional solid structure model.

Figure 4.
Finite element models of the 2-2 and 1-3 piezoelectric composite bilaminated vibrators. (a) 2-2. (b) 1-3.

Table 1.
Material parameters of the piezoelectric ceramics and epoxy resins
The grid size was set to 1/10 of the wavelength at the central frequency in the finite element model [36].
In the present study, 1 and 0 V were applied to the top and bottom of the model at the z-axis direction. No constraints are imposed. The frequency range was 4000–6600 Hz, which was divided into 260 substeps with a 10 Hz interval between each step. The damping coefficient is set as 0.02, and the admittance curve of the piezoelectric vibrator is obtained. The calculation results are shown in Figure 5. The series resonance frequency, parallel resonance frequency, and bandwidth of the vibrator were obtained from the admittance curve, as shown in Table 2.
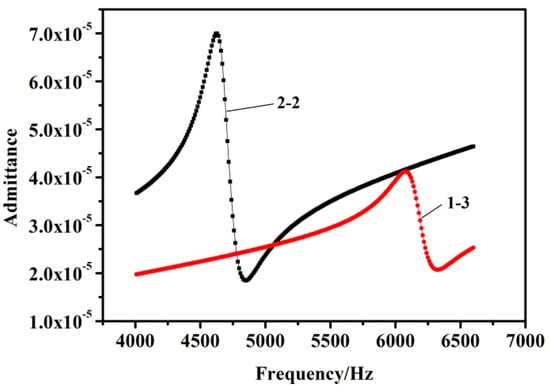
Figure 5.
Admittance curve of the 2-2 and 1-3 piezoelectric composite bilaminated vibrators.

Table 2.
Results of the finite element simulation.
The effective electromechanical coupling coefficients of the 2-2 and 1-3 vibrators were calculated using Equation (1) [30,37], where fs and fp refer to the series resonance frequency and the parallel resonance frequency, respectively. The results are listed in Table 2.
As shown in Figure 5, the series resonance frequency of the 2-2 vibrator was 4630 Hz, whereas that of the 1-3 vibrator was 5320 Hz. Furthermore, the bandwidth of the 2-2 vibrator increased 1.8 times in comparison with that of the 1-3 vibrator.
Figure 6 shows the vibration modes of the two kinds of composites, different colors represent different displacements. In Figure 6a, the largest displacement appeared at the center of the upper and lower surfaces of the 2-2 vibrator. The result is similar to that of the 1-3 vibrator in Figure 6b. In Figure 7, the maximum vibration displacement of the 2-2 vibrator at the resonance point was 7.87 × 10−11 m, and that of the 1-3 vibrator was 3.72 × 10−11 m, where the driving voltage was 1 V. Moreover, the maximum vibration displacement of the 2-2 vibrator was twice greater than that of the 1-3 vibrator, suggesting that the 2-2 composite is superior to the 1-3 composite in the preparation of the piezoelectric composite bilaminated vibrator.

Figure 6.
Displacement deformation graph of the 2-2 and 1-3 piezoelectric composite bilaminated vibrators. (a) 2-2. (b) 1-3.
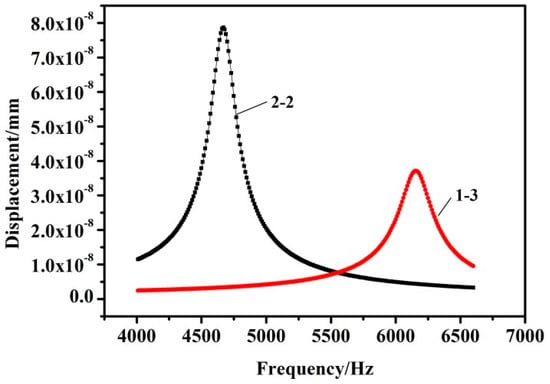
Figure 7.
Vibration displacement curves of the 2-2 and 1-3 type piezoelectric composite bilaminated vibrators.
The structure of the bilaminated piezoelectric ceramic bilaminated vibrator is shown in Figure 8. The vibrator was prepared using two layers of a piezoelectric ceramic with an opposite polarization direction in the z-axis, and the circuit in parallel. The piezoelectric ceramic bilaminated vibrator (hereinafter referred to as ‘ceramic vibrator’) was also simulated through a finite element method, to analyze the differences between its property and that of the 2-2 vibrator. The size of the piezoelectric ceramic was 49.5 mm in length, 9.5 mm in width, and 2 mm in height, and the volume percentage of the piezoelectric ceramics was 1. First, the finite element simulation model of the piezoelectric ceramic bilaminated vibrator was established in accordance with the solid structure, as shown in Figure 9. Second, material parameter of the piezoelectric ceramics was shown in Table 1. The grid size was set to 1/10 of the wavelength at the central frequency in the finite element model.
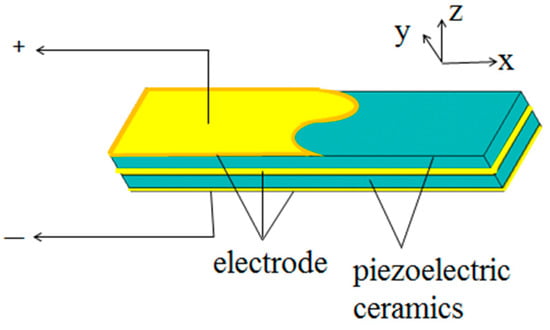
Figure 8.
Structure of the piezoelectric ceramic bilaminated vibrator.

Figure 9.
Finite element model of the piezoelectric ceramic bilaminated vibrator.
In the present study, 1 and 0 V were applied to the top and bottom of the model at the z-axis direction. No constraints are imposed. The frequency range was 4000–6600 Hz, which was divided into 260 substeps with a 10 Hz interval between each step. The damping coefficient is set as 0.02, and the admittance curve of the piezoelectric vibrator is obtained. The results are shown in Figure 10a,b, showing that the series resonance frequency of the 2-2 vibrator is smaller, and the vibration displacement as well as the bandwidth of the 2-2 vibrator are larger than those of the ceramic vibrator.
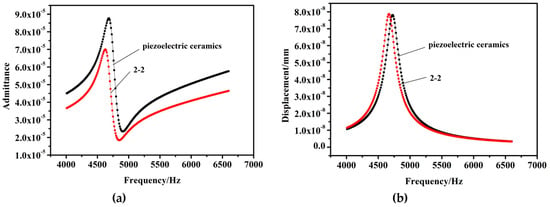
Figure 10.
(a) Admittance curves of the 2-2 piezoelectric composite bilaminated vibrator and the ceramic vibrator. (b) Vibration displacement curves of the 2-2 piezoelectric composite bilaminated vibrator and the ceramic vibrator.
4. Fabrication and Performance Test of the Bilaminated Vibrator
On the basis of the finite element simulation results, the 2-2 piezoelectric composite was selected to prepare a bilaminated vibrator. The ceramic vibrator with the same shape and size was also prepared in the present work to compare its performance with that of the traditional one.
The 2-2 piezoelectric composite bilaminated vibrator comprised a piezoelectric phase, a polymer phase, and surface electrodes with the following structural parameters length = 49.5 mm, width = 9.5 mm, height = 2 mm, column width = 2 mm, and joint-cutting width = 0.5 mm. The PZT5 piezoelectric ceramic, 618 epoxy resin, and silver paste were selected as the piezoelectric phase, polymer phase, and surface electrode, respectively. The 2-2 piezoelectric composite was prepared via the “slice and fill” method [38,39,40]. The preparation process is shown in Figure 11.
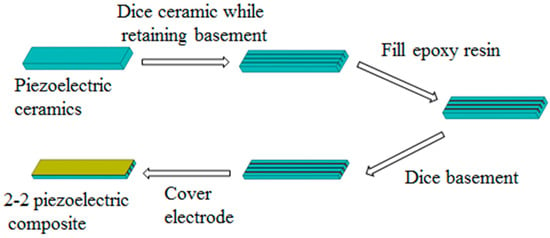
Figure 11.
Preparation technology of the 2-2 piezoelectric composite.
The detailed preparation procedure is described as follows [41,42,43].
1. A piezoelectric ceramic block was cut into strips along the width directions of the ceramic block. The piezoelectric ceramic block was not cut through the whole thickness, and a common base was retained. The polarization direction of the piezoelectric ceramic block was parallel to the thickness direction of the ceramic.
2. The epoxy resin was cast into the piezoelectric ceramic strips.
3. The piezoelectric ceramic sample was inverted, and the ceramic base was cut precisely along the grooves between the piezoelectric ceramic strips.
4. The top and bottom surfaces of the composite were polished and cleaned using acetone, and a thin layer of silver on the surfaces as electrodes were coated via magnetron sputtering.
The composite samples were fabricated in accordance with the above preparation method, as shown in Figure 12.

Figure 12.
Image of the fabricated 2-2 piezoelectric composites.
The 2-2 piezoelectric composite bilaminated vibrator is composed of two identical 2-2 piezoelectric composites bonded with epoxy resin in the opposite direction of polarity. As shown in Figure 1, the structure size of the 2-2 piezoelectric composites is 49.5 × 9.5 × 2 mm, and its volume fraction is 0.8 (2 mm in width of ceramic column and 0.5 mm in width of the epoxy resin).
2-2 piezoelectric composite bilaminated vibrator samples, as shown in Figure 13, were fabricated.

Figure 13.
Image of the 2-2 piezoelectric composite bilaminated vibrator samples.
The bilaminated piezoelectric ceramic vibrator structure (length = 49.5 mm, width = 9.5 mm, and height = 2 mm), which is made from PZT5 piezoelectric ceramic, is shown in Figure 8.
The preparation process is shown in Figure 14. The upper and lower surfaces of the piezoelectric ceramics were polished flat, and the samples were scrubbed with alcohol. The detailed preparation procedure is described as follows.

Figure 14.
Preparation technology of the piezoelectric ceramic vibrator.
1. After drying, the samples were placed in the sample table of an ultrahigh vacuum multitarget magnetron sputtering instrument the upper surfaces were sputtered, and the samples were reversed for reverse sputtering.
2. Two identical piezoelectric ceramic vibrators were bonded with epoxy resin in the opposite direction of polarity.
The piezoelectric ceramic bilaminated vibrator samples, as shown in Figure 15, were fabricated.

Figure 15.
Image of the piezoelectric ceramic bilaminated vibrator samples.
Five groups of 2-2 piezoelectric composite bilaminated vibrator samples were tested using an Agilent 4294 A impedance analyzer. The admittance curves and impedance curves were selected to obtain the series resonance frequency fs (the frequency corresponding to the maximum admittance mode) and the parallel resonance frequency fp (the frequency corresponding to the maximum impedance mode). The bandwidth was also read. The parameters of the five groups of 2-2 piezoelectric composite bilaminated vibrator samples were measured via the above test method. The results are shown in Table 3. The electromechanical coupling coefficients of the 2-2 piezoelectric composite bilaminated vibrator listed in Table 3 were calculated using Equation (1).

Table 3.
Performance parameters of the 2-2 piezoelectric composite bilaminated vibrator
A laser Doppler vibrometer (PSV-400 Polytec Inc., Germany) equipped with software analysis system to achieve 2D and 3D animation display and data analysis. It was used to observe the actual vibration of the five groups of 2-2 piezoelectric composite bilaminated vibrator samples under free boundary condition. The vibration dynamic diagram was shown in Figure 16, which indicated that the vibration displacement at the center of the upper and lower surfaces was the largest. The center point was selected, and the vibration displacement curve was read. The maximum vibration displacement of each group vibrator was listed in Table 3.
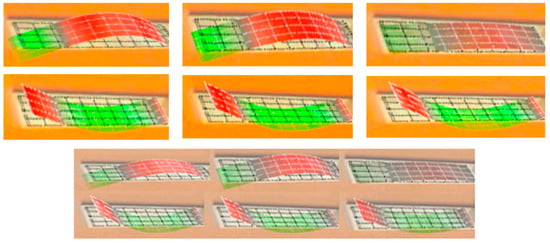
Figure 16.
Image of the vibration dynamic diagram.
In accordance with the above measurement methods, five groups of piezoelectric ceramic bilaminated vibrators were measured using an impedance analyzer and a laser Doppler vibrometer. The series resonance frequency fs, parallel resonance frequency fp, bandwidth B, electromechanical coupling coefficient, and maximum vibration displacement are listed in Table 4.

Table 4.
Performance parameters of the ceramic vibrators
The average piezoelectric parameters of the 2-2 and ceramic vibrators are shown in Table 5.

Table 5.
Comparison of the average piezoelectric parameters of the 2-2 and ceramic vibrators
The admittance and vibration displacement curves of the 2-2 and ceramic vibrators obtained by experiments are shown in Figure 17a,b, respectively.
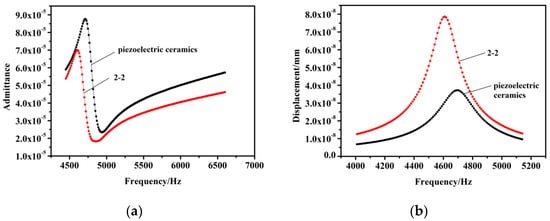
Figure 17.
(a) Admittance curves of the 2-2 and ceramic vibrators. (b) Vibration displacement curves of the 2-2 and ceramic vibrators.
Table 5 and Figure 17 show that the resonance frequency of the 2-2 piezoelectric composite bilaminated vibrator is lower than that of the ceramic vibrator. The maximum vibration displacement of the 2-2 piezoelectric composite bilaminated vibrator is 2.297 times that of the ceramic one. The effective electromechanical coupling coefficients and bandwidth of the 2-2 piezoelectric composite bilaminated vibrator are larger than those of the ceramic one.
Comparing Figure 10a with Figure 17a, it can be seen that the shape and intensity of the corresponding peaks of the vibration modes on the admittance–frequency curve obtained by the harmonic response analysis are consistent with the actual measurement. The results of finite element analysis are basically in accordance with the variation law of the actual test results, with an error of about 0.04%. We can also see from Figure 10b and Figure 17b that the results of ANSYS calculation of vibration displacement of piezoelectric ceramic double-layer plate oscillator are far greater than the actual measured values. This is because when ANSYS calculates and analyses, it is assumed that the material is uniform and without defects, and the actual material will inevitably have defects. The deformation of piezoelectric material mainly depends on the piezoelectric strain constant d33 of the material. However, the theoretical parameters used in ANSYS simulation calculation in this paper have errors with the actual material parameters, which need to be further studied. However, the ANSYS calculation results of vibration displacement of 2-2 type piezoelectric composite bi-laminate vibrator basically coincide with the actual test results. The reason is that the piezoelectric strain constant of bi-laminate oscillator increases rapidly with the addition of polymer phase. The strain of composite bi-laminate vibrator is mainly determined by Young’s modulus and volume percentage of polymer phase. Therefore, the piezoelectric strain constant d33 has little effect on the corresponding variables of the PZT ceramic column under the same electric field strength.
5. Discussion
Compared with piezoelectric ceramics, the piezoelectric composites have lower longitudinal wave velocity; materials with low longitudinal wave velocity can achieve a low resonance frequency with small thickness. Therefore, the resonance frequency of the 2-2 piezoelectric composite bilaminated vibrators is lower than that of the ceramic vibrator. Compared with that of piezoelectric ceramics, the stiffness of piezoelectric composites is smaller. As such, under the same electric intensity, piezoelectric composites can produce large deformation, thereby generating a remarkable vibration displacement [35].
6. Conclusions
In this work, a 2-2 piezoelectric composite bilaminated vibrator consisting of two 2-2 piezoelectric composites bonded in opposite polarity direction was prepared. 2-2 and 1-3 vibrators were analyzed under free boundary condition via finite element simulation, showing that the 2-2 vibrator could achieve higher vibration displacement and lower resonance frequency compared with the 1-3 vibrator. Furthermore, 2-2 and ceramic vibrators were fabricated and tested. The experimental results showed that the vibration displacement of the 2-2 vibrator was 2.29 times higher than that of the ceramic vibrator, and the resonance frequency was reduced by 1.02 times; moreover, the bandwidth was expanded by 1.19 times. Thus, the 2-2 vibrator has remarkable advantages in terms of piezoelectric properties in comparison with the ceramic vibrator.
Author Contributions
Conceptualization, X.L., L.W. and C.Z.; Data Curation, X.L.; Formal Analysis, X.L., C.Z. and Y.Z.; Funding Acquisition, L.W. and C.Z.; Investigation, X.L., C.Z. and R.S.; Methodology, X.L., C.Z., S.H. and Y.Z.; Project Administration, L.W.; Resources, L.W.; Software, X.L. and C.Z.; Supervision, L.W.; Validation, X.L. and C.Z.; Visualization, X.L.; Writing—Original Draft Preparation, X.L.; Writing—Review and Editing, X.L., L.W. and R.S.
Funding
This work was supported by the National Natural Science Foundation of China (no. 61871043, no. 61771060), and the Science & Technology Key Project of Beijing Municipal Institutions (no. KZ201911232023), the Sensor Key Laboratory Open Fund of Beijing (no. 2019CGKF004).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Woollett, R.S. Theory of the Piezoelectric Flexural DISK Transducer with Applications to Underwater Sound; Research Report #490; U.S. Navy Underwater Sound Laboratory: New London, CT, USA, 5 December 1960. [Google Scholar]
- Aronov, B.S. The energy method for analyzing the piezoelectric electroacoustic transducers II. Acoust. Soc. Am. 2005, 118, 627–637. [Google Scholar] [CrossRef]
- Aronov, B.S. Nonuniform piezoelectric circular plate flexural transducers with underwater applications. Acoust. Soc. Am. 2015, 138, 1570. [Google Scholar] [CrossRef] [PubMed]
- Jinduo, Z.; Guidong, L.; Fuhu, L. Analysis and calculation on receiving characteristics of the bimorph flexural transducers. Tech. Acoust. 1999, 18, 107–110. [Google Scholar]
- Xiping, H.; Qiang, L. Piezoelectric ceramic bimorph in bending vibration. J. Jishou Univ. 2017, 38, 13–18. [Google Scholar] [CrossRef]
- Shaohu, D.; Ting, Z. Bending vibration analysis of the circular composite piezoelectric vibrator. Basic Sci. J. Text. Univ. 2007, 20, 172–175. [Google Scholar] [CrossRef]
- Ningning, Z. Research on flexural vibration characteristics of three laminated piezoelectric transducers. Tech. Acoust. 2017, 36, 383–389. [Google Scholar] [CrossRef]
- Pin, Z.; Xiping, H.; Yanjun, W. Radiation impedance of thin circular flat plate in flexural vibration with free boundary. J. Shanxi Norm. Univ. 2007, 35, 31–34. [Google Scholar] [CrossRef]
- Shuyu, L. Study on natural vibration and resonance frequency of rectangular radiators in flexural vibration. J. Shanxi Norm. Univ. 2000, 28, 40–46. [Google Scholar] [CrossRef]
- Wenxiao, Q.; Xiaohua, C.; Fei, Z. Effect of boundary conditions on vibration modes of bending vibrator in acoustic logging. Sci. China Ser. D Earth Sci. 2008, 38, 174–179. [Google Scholar] [CrossRef]
- Lin, Z.; Weijun, L.; Dong, W. The design of sandwich dipole transducer based on finite element method. Well Logging Technol. 2009, 33, 106–109. [Google Scholar] [CrossRef]
- Mansoor, M.B.; KÖble, S.; Wangwong, T.; Woias, P.; Goldschmidtböing, F. Design, characterization and sensitivity analysis of a piezoelectric ceramic/metal composite transducer. Micromachines 2017, 8, 271. [Google Scholar] [CrossRef]
- Uchino, K. Advanced Piezoelectric Material: Science and Technology, 2nd ed.; Woodhead Publishing: Duxford, UK, 2017. [Google Scholar]
- Newnham, R.E.; Skinner, D.P.; Cross, L.E. Connectivity and piezoelectric-pyroelectric composites. Mater. Res. Bull. 1978, 13, 525–536. [Google Scholar] [CrossRef]
- Klicker, K.A.; Biggers, J.V.; Newnham, R.E. Composites of PZT and Epoxy for Hydrostatic Transducer Applications. J. Am. Ceram. Soc. 1981, 64, 5–9. [Google Scholar] [CrossRef]
- Gururaja, T.R.; Schulze, W.A.; Shrout, T.R.; Safari, A.; Cross, L.W.E. High frequency applications of PZT/polymer composite materials. Ferroelectrics 1981, 39, 1245–1248. [Google Scholar] [CrossRef]
- Savakus, H.P.; Klicker, K.A.; Newnham, R.E. PZT-epoxy piezoelectric transducers: A simplified fabrication procedure. Mater. Res. Bull. 1981, 16, 677–680. [Google Scholar] [CrossRef]
- Auld, B.A.; Kunkel, H.A.; Shui, Y.A.; Wang, Y. Dynamic Behavior of Periodic Piezoelectric Composites. In Proceedings of the 1983 Ultrasonics Symposium, Atlanta, GA, USA, 31 October–2 November 1983; pp. 554–558. [Google Scholar] [CrossRef]
- Smith, W.A.; Shaulov, A.; Auld, B.A. Tailoring the properties of composite piezoelectric materials for medical ultrasonic transducers. IEEE Ultrason. Symp. 1985, 642–647. [Google Scholar] [CrossRef]
- Chan, H.L.W.; Unsworth, J. Effect of thinning and ceramic width on properties of 1−3 PZT/EPOXY composites. Ferroelectr. Lett. Sect. 1986, 6, 133–137. [Google Scholar] [CrossRef]
- Takeuchi, H.; Nakaya, C.; Katakura, K. Medical Ultrasonic Probe Using PZT/Polymer Composite. In Proceedings of the IEEE 1984 Ultrasonics Symposium, Dallas, TX, USA, 14–16 November 1984; pp. 507–510. [Google Scholar] [CrossRef]
- Yongqiu, Z.; Yuanguang, H.; Qichang, X. Sandwich PZT/polymer composite transducer. Ferroelectrics 1983, 49, 241–249. [Google Scholar] [CrossRef]
- Jialing, Z.L.; Likun, W.; Fuxue, Z. Preparation of large area 0-3 piezoelectric composites for hydrophone. Piezoelectr. Acoustoopt. 1999, 21. [Google Scholar] [CrossRef]
- Xuecang, G.; Mingxuan, L. Study on 1-3 piezoelectric PZT/epoxy composite material and transducer for ultrasonic transducer. Appl. Acoust. 1991, 10, 10–14. [Google Scholar]
- Hwang, Y.; Ahn, H.; Nguyen, D.-N.; Kim, W.; Moon, W. An underwater parametric array source transducer composed of PZT/thin-polymer composite. Sens. Actuators A Phys. 2018, 279, 601–616. [Google Scholar] [CrossRef]
- Kuznetsova, I.E.; Zaitsev, B.D.; Borodina, I.A.; Shikhabudinov, A.M.; Teplykh, A.A.; Etoungh, D.M.; Feuillard, G. The effect of nanocomposite polymeric layer on the radiation of antisymmetric zero-order Lamb wave in a piezoelectric plate contacting with liquid. J. Appl. Phys. 2013, 113, 224507. [Google Scholar] [CrossRef]
- Changjiu, D.; Mingxuan, L. 1-3 Piezo-Composite materials. Appl. Acoust. 1995, 14, 2–7. [Google Scholar] [CrossRef]
- Abdollahi, A.; Arias, I. Constructive and destructive interplay between piezoelectricity and flexoelectricity in flexural sensors and actuators. J. Appl. Mech. 2015, 82, 121003-1–121003-4. [Google Scholar] [CrossRef]
- Koyama, D.; Kashihara, Y.; Hatanaka, M.; Nakamura, K.; Matsukawa, M. Movable optical lens array using ultrasonic vibration. Sens. Actuators A 2016, 237, 35–40. [Google Scholar] [CrossRef]
- Guidong, L.; Jinduo, Z.; Renqian, W. Piezoelectric Transducers and Arrays; Peking University Press: Beijing, China, 2005; pp. 172–173. [Google Scholar]
- Newnhan, R.E. Composite piezoelectric transducers. Mater. Eng. 1980, 2, 93–106. [Google Scholar]
- Mendiola, J.; Jimenez, B. Review of recent work on ferroelectric composite systems. Ferroelectrics 1984, 53, 159–166. [Google Scholar] [CrossRef]
- Gururaja, T.R. Piezoelectric Composite Materials for Ultrasonic Transducer Applications. IEEE Trans. Sonics Ultrason. 1985, 32, 481–498. [Google Scholar] [CrossRef]
- Ting, R.Y. Evaluation of new piezoelectric composite materials for hydrophone applications. Ferroelectrics 1986, 67, 143. [Google Scholar] [CrossRef]
- Chao, Z. Research on Three-Phase Piezocomposite and Curved Surface Transducer. Ph.D. Thesis, Beijing University of Posts and Telecommunications, Beijing, China, 2019. [Google Scholar]
- Lei, Q. Research on Transducer with Broad Beamwidth. Ph.D. Thesis, Beijing University of Posts and Telecommunications, Beijing, China, 2010. [Google Scholar]
- Li, L. Research on 1-3 Series Piezoelectric Composite and Underwater Transducer 1-3. Ph.D. Thesis, Beijing University of Posts and Telecommunications, Beijing, China, 2008. [Google Scholar]
- Hongwei, W.; Likun, W.; Yonghong, Z. 2-2 type piezoelectric composite pipe frequency simulation and fabrication and performance test. Electron. Compon. Mater. 2015, 34, 1–4. [Google Scholar] [CrossRef]
- Jikang, Y.; Guoyou, G.; Jialin, S.; Jingchao, C.; Jiatao, Z. Preparation of piezoelectric composites. J. Kunming Univ. Sci. Technol. 2000, 6. [Google Scholar] [CrossRef]
- Xiao, F. Study on Fabrication and Properties of 2-2 Piezoelectric Composites. Master’s Thesis, Wuhan University of Technology, Wuhan, China, 2012. [Google Scholar]
- Yanjun, Z.; Likun, W.; Lei, Q. Finite element analysis and experimental study on 1-3 piezoelectric composites with modified polymer phase. Ferroelectrics 2019, 537, 223–236. [Google Scholar] [CrossRef]
- Xing, L.; Likun, W.; Chao, Z.; Yanjun, Z. The effect of piezoelectric ceramic volume fraction on the thickness vibration characteristics of 1-3 piezocomposites. Ferroelectrics 2018, 531, 84–91. [Google Scholar] [CrossRef]
- Xing, L.; Likun, W.; Chao, Z.; Yanjun, Z. Effect of ceramic volume fraction on the performance of the 1-3 composite transducers. Piezoelectr. Acoustoopt. 2019, 41, 396–400. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).