Dynamics of a Turbine Blade with an Under-Platform Damper Considering the Bladed Disc’s Rotation
Abstract
:Featured Application
abstract
1. Introduction
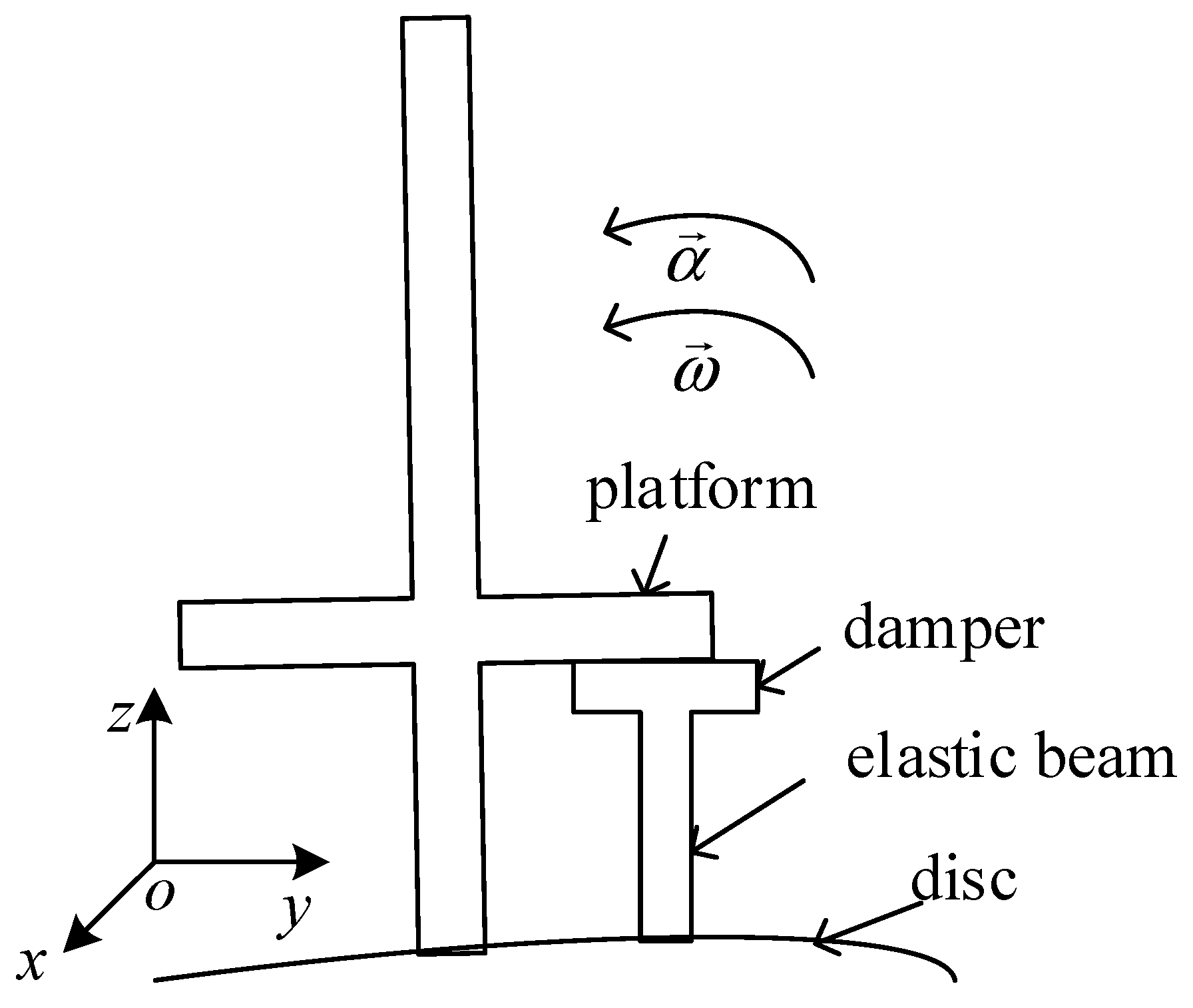
2. Mechanical Model and Dynamics Equations
2.1. Blade-Damper Model
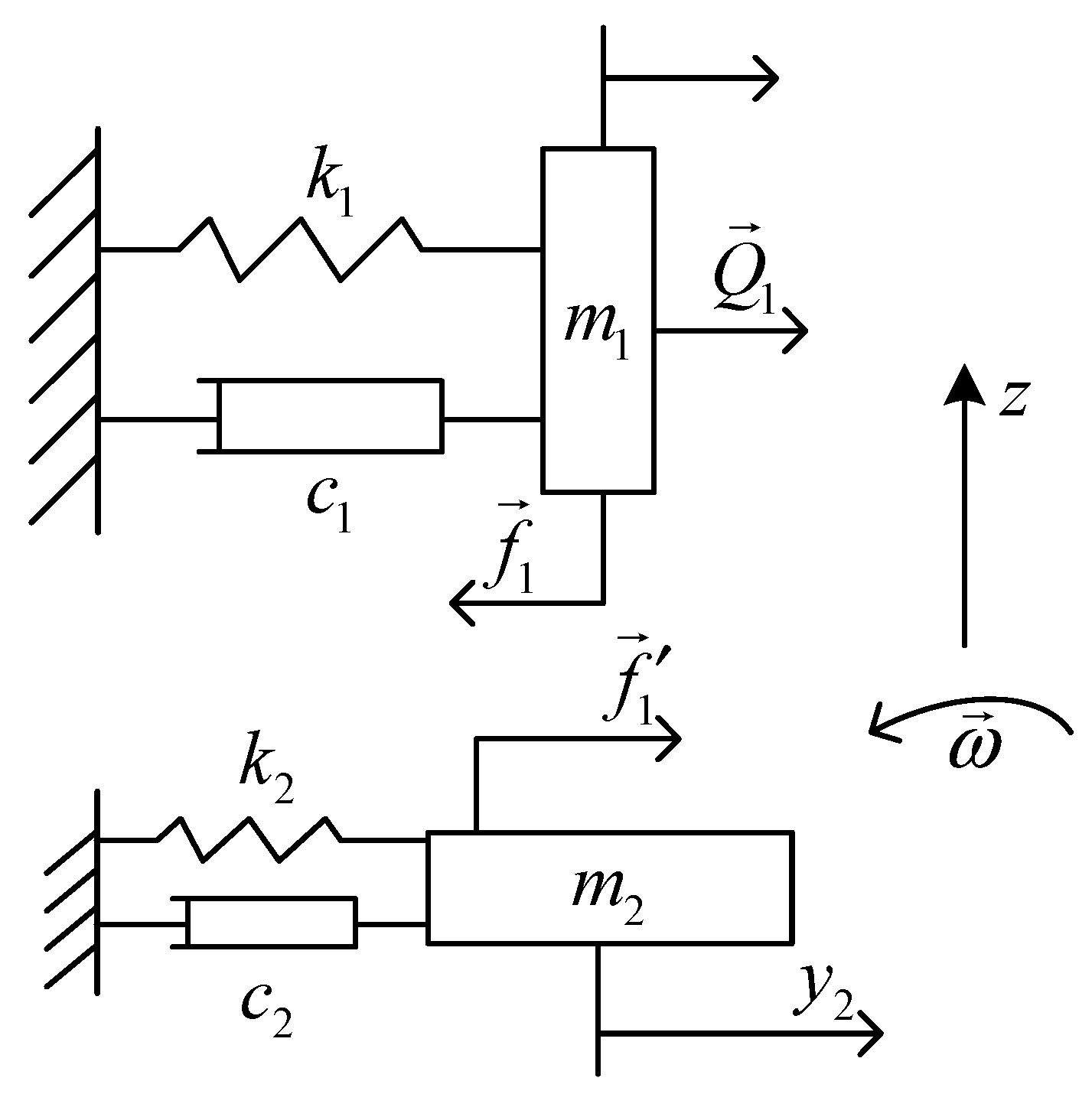
2.2. The Dynamics Equations of Blade-Coupled Vibration
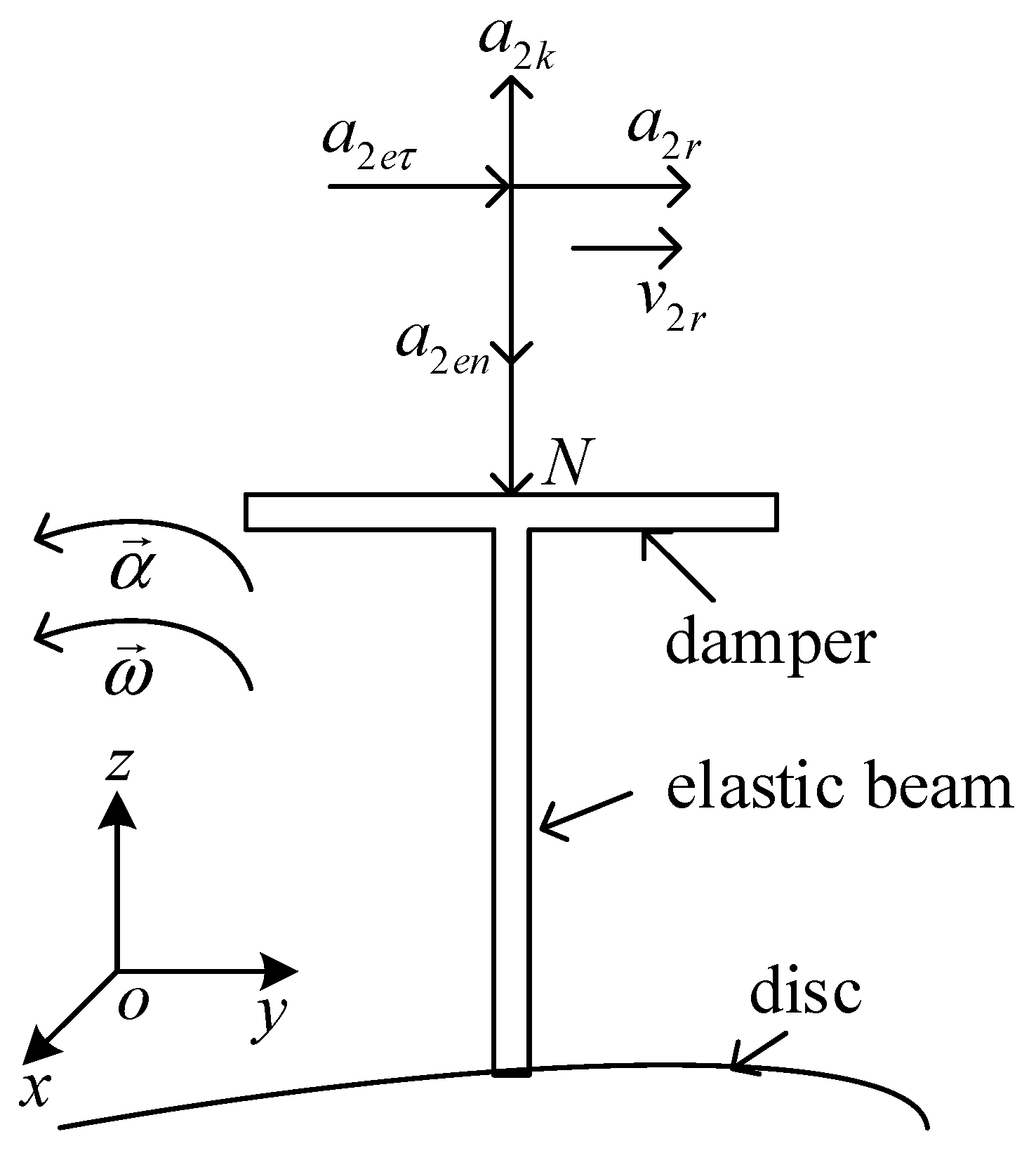
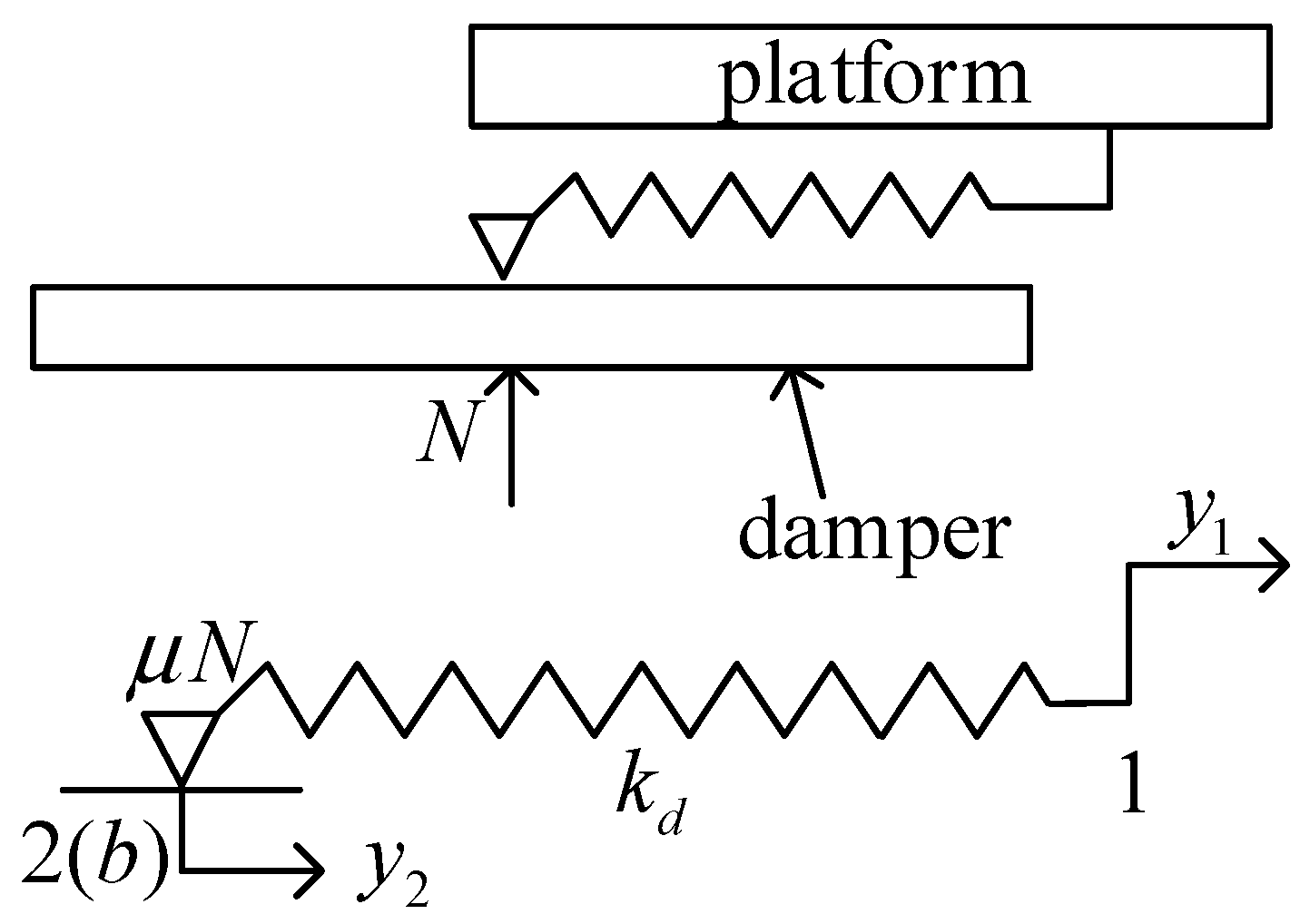
2.3. Normal Pressure and Dry Friction Force
2.3.1. Normal Pressure
2.3.2. Dry Friction Force
3. Numerical Simulation
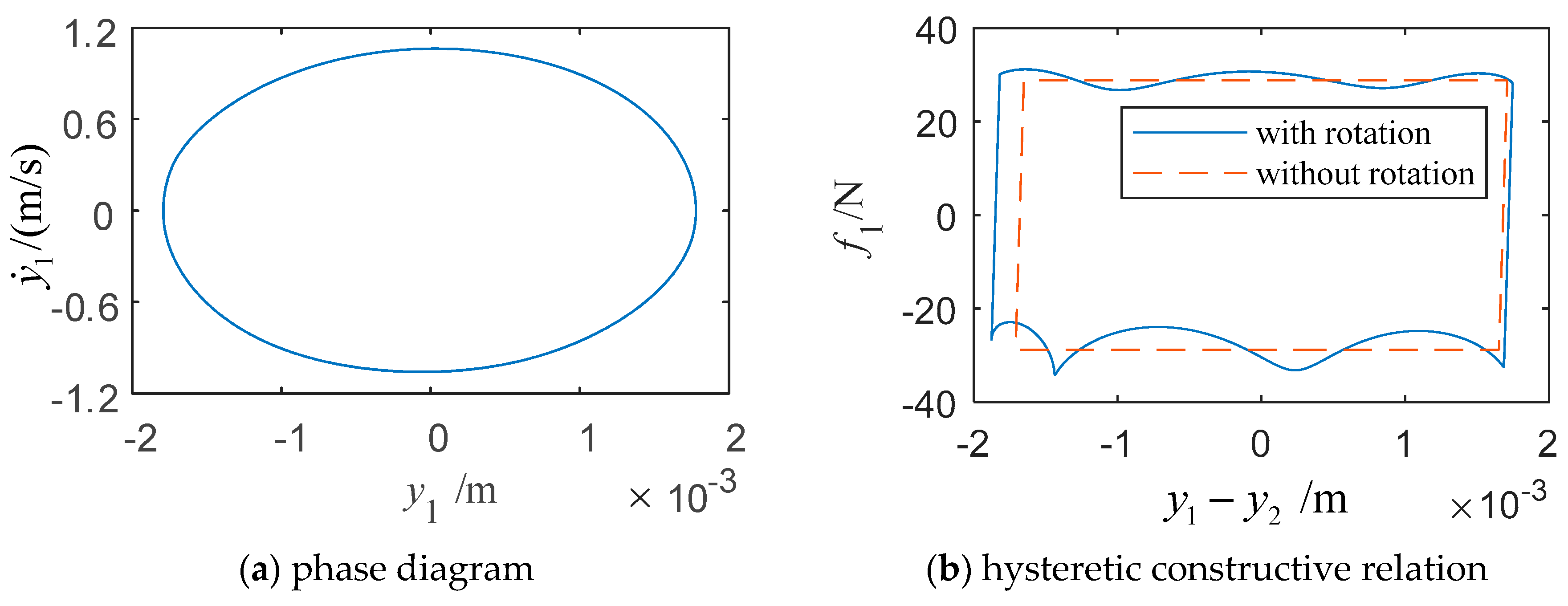
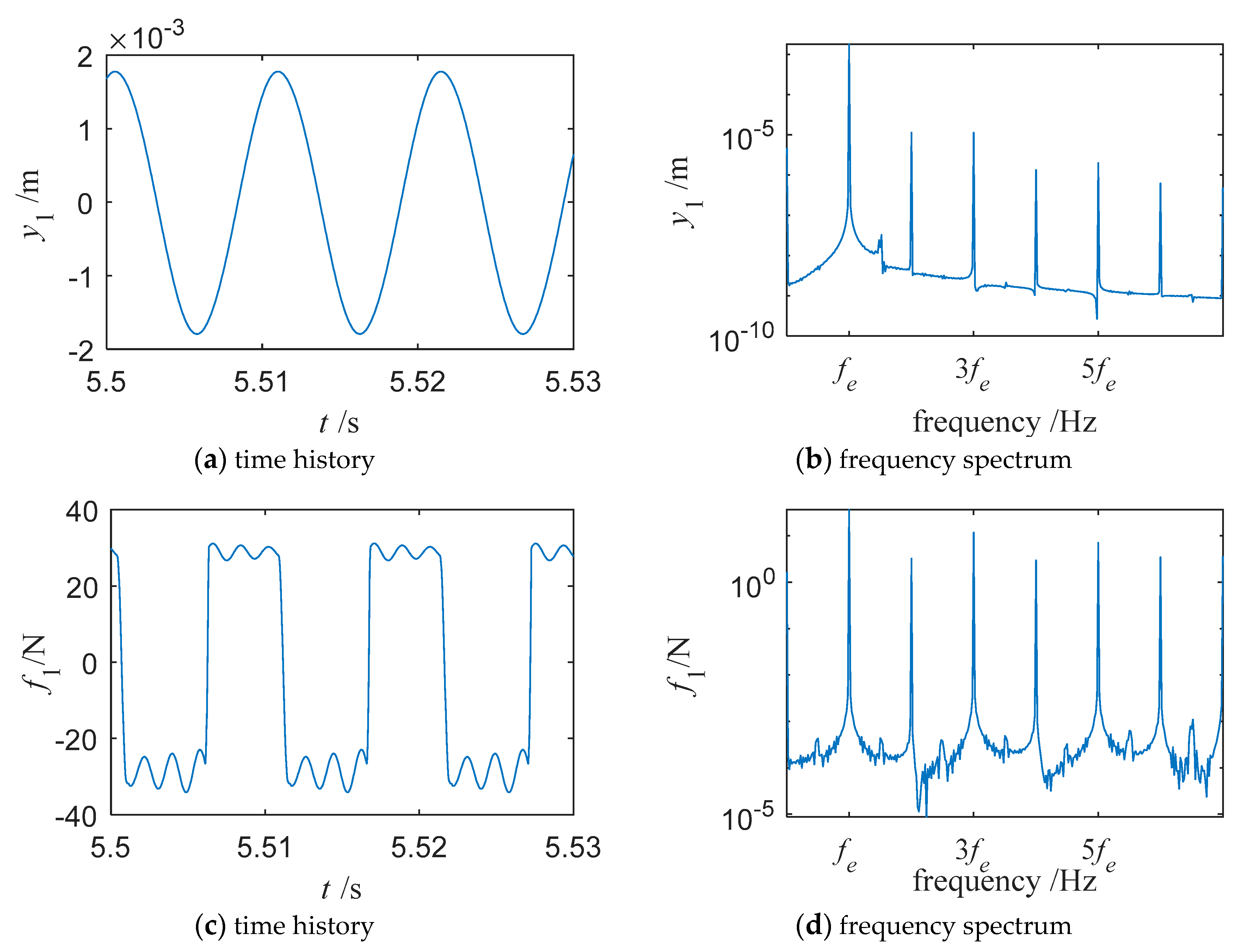
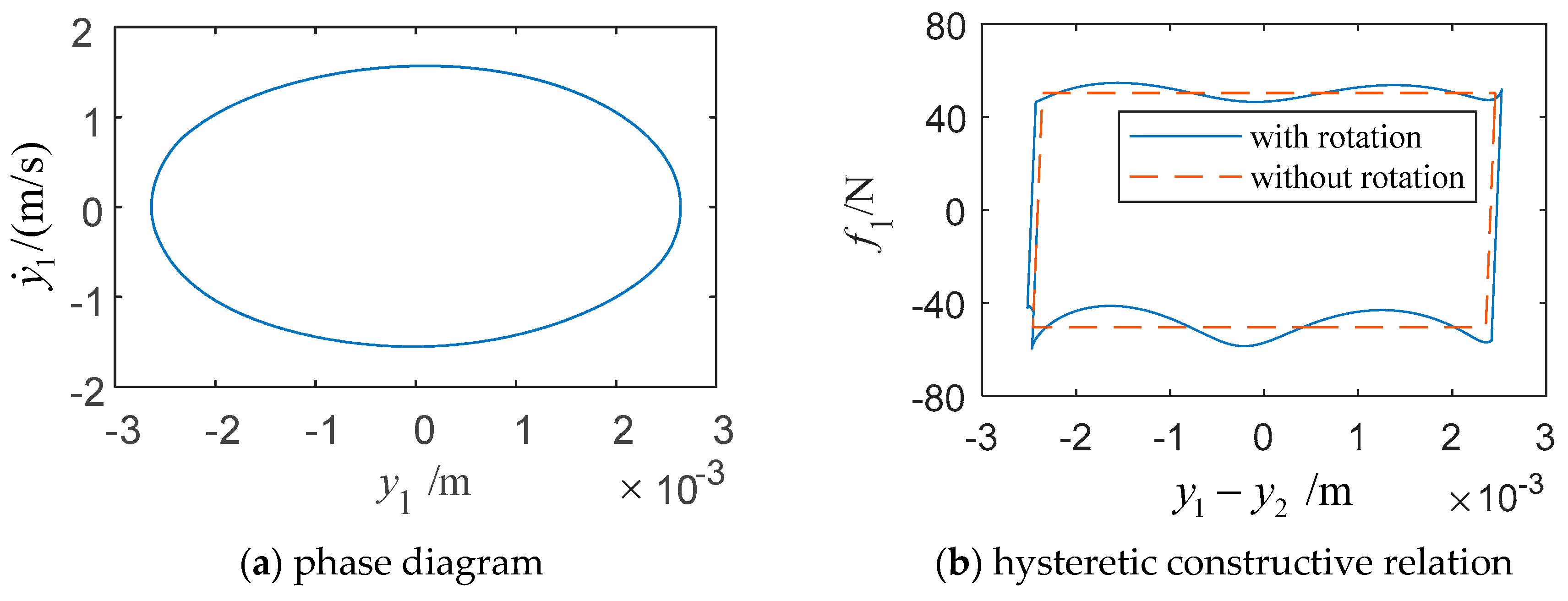
3.1. The Analysis of the Vibration Response’s Characteristics
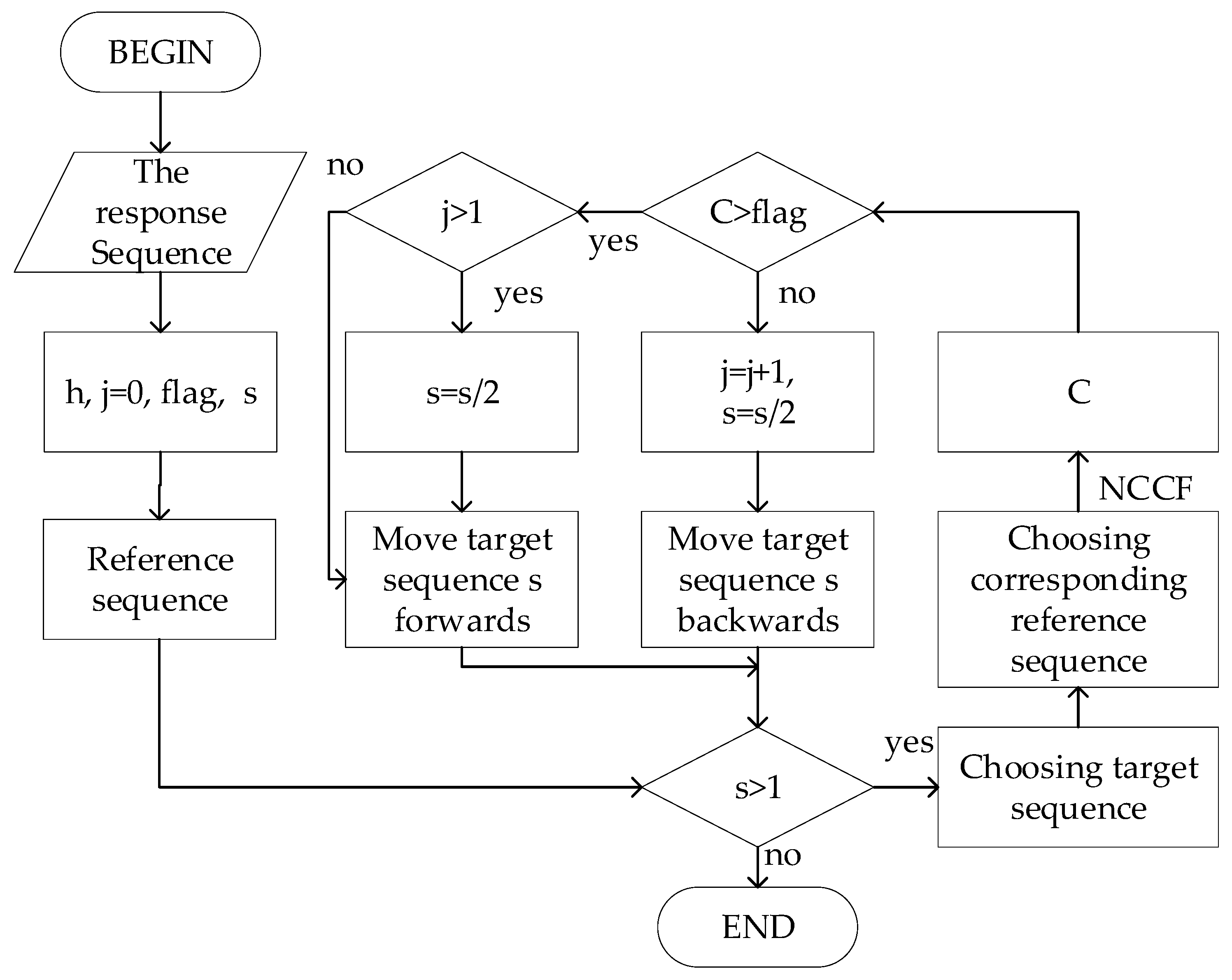
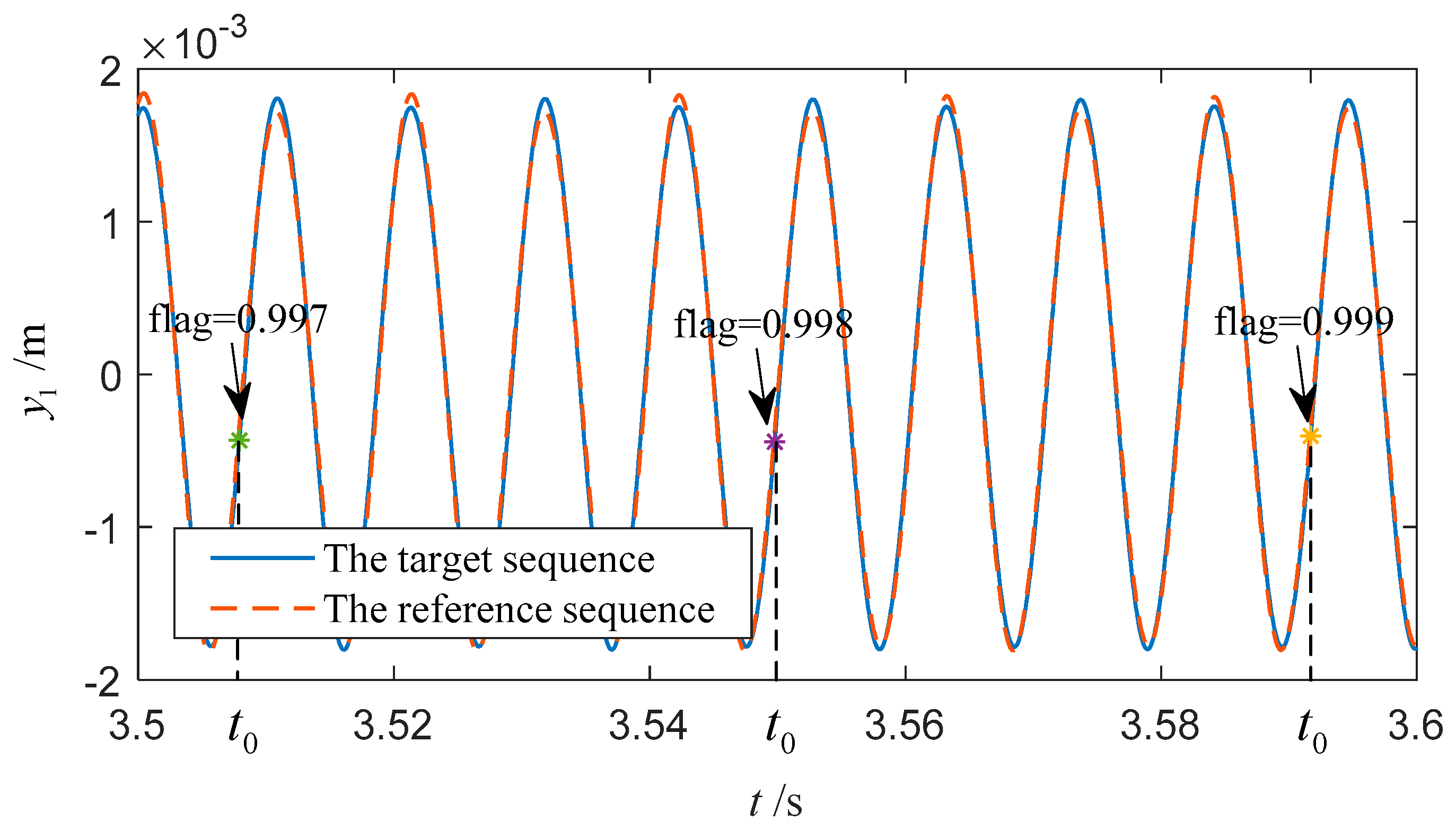
3.2. The Decision of Steady-State of the Blade
3.3. The Vibration Reduction Characteristics of the System
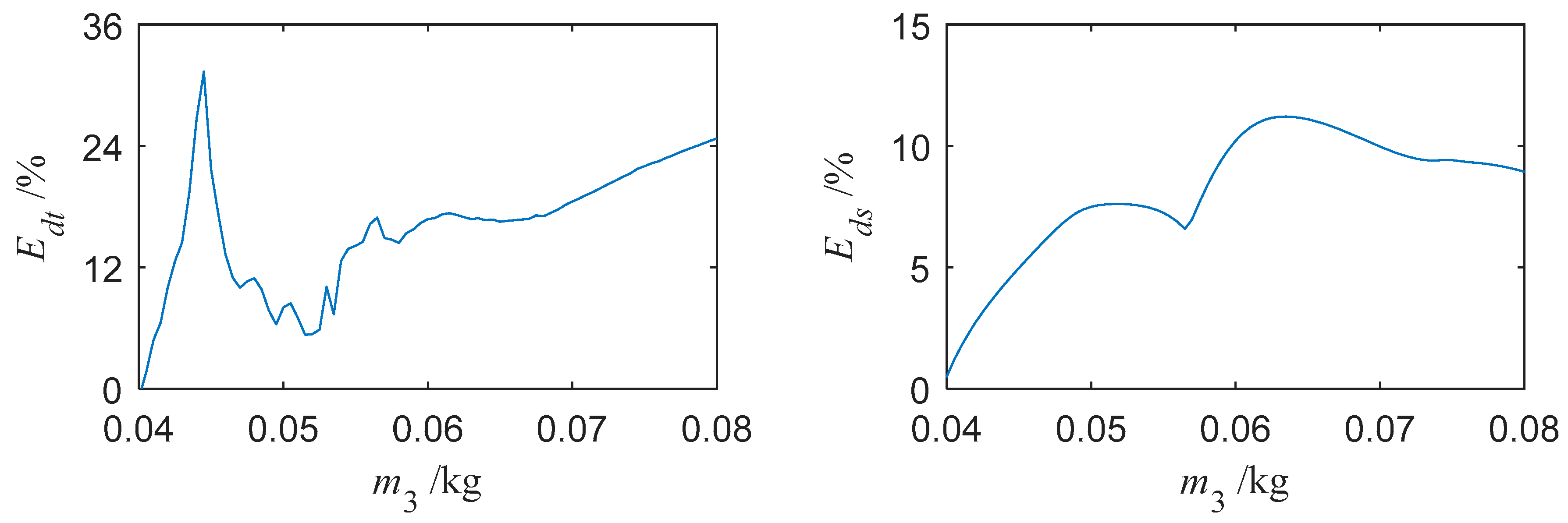
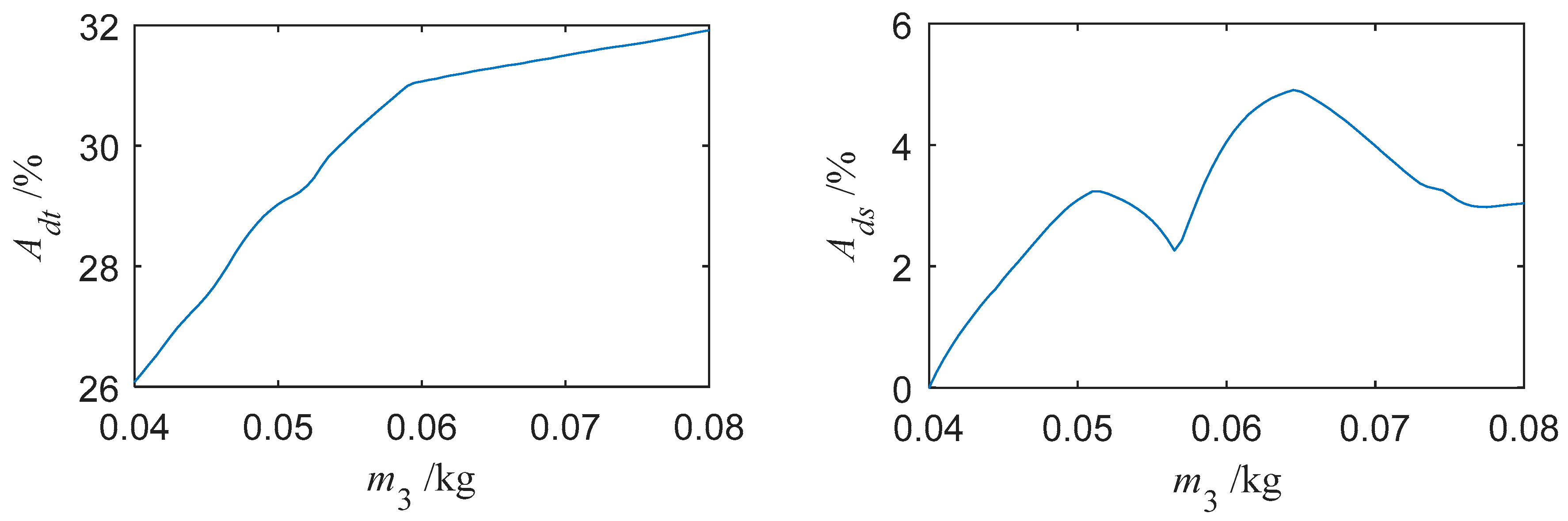
3.3.1. The Effect of Damper Mass on the Vibration Reduction
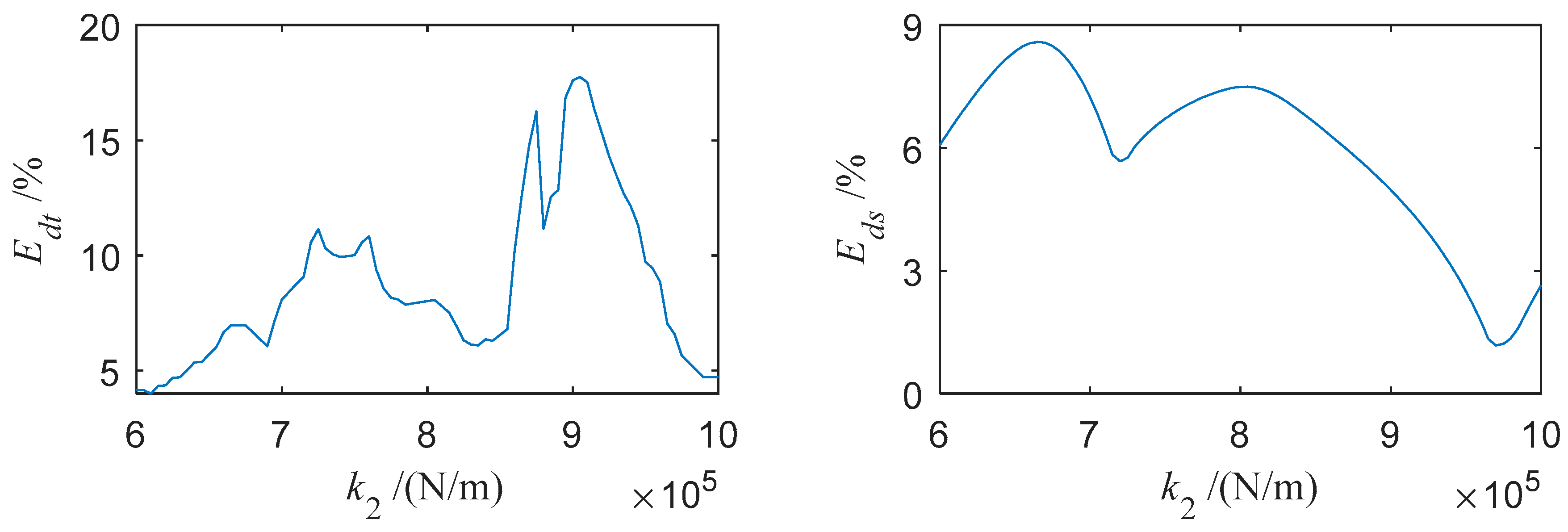
3.3.2. The Effect of a Damper’s Vibrational Stiffness on the Vibration Reduction
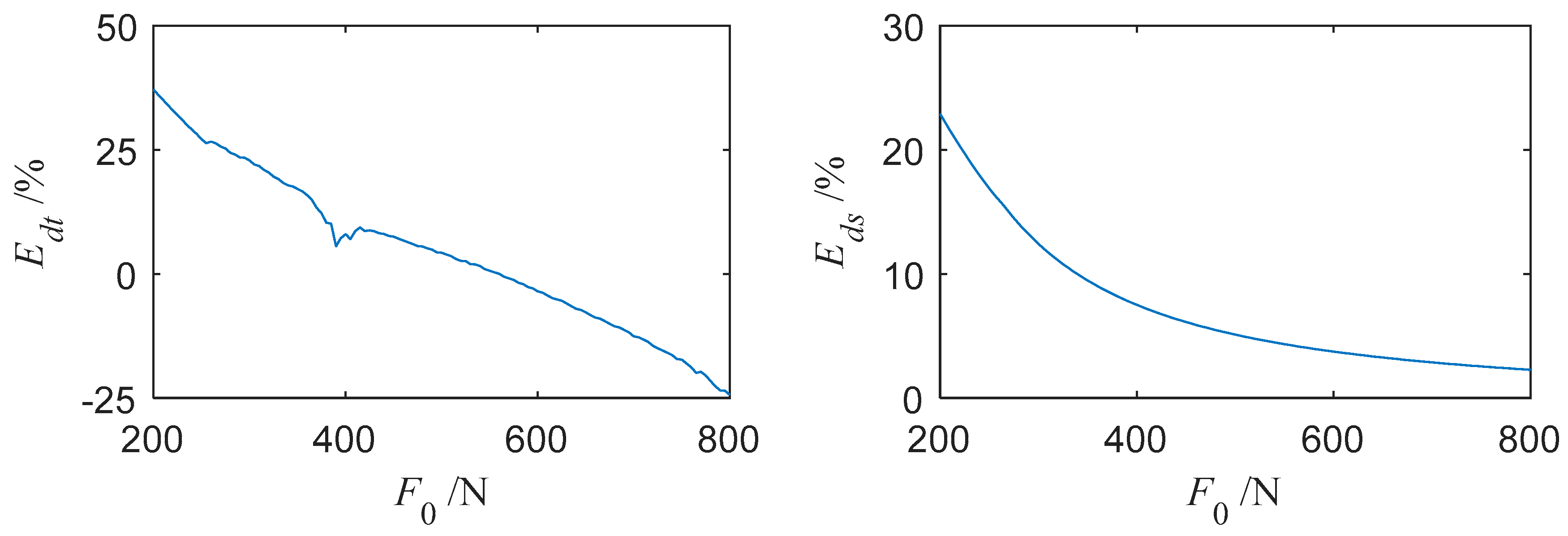
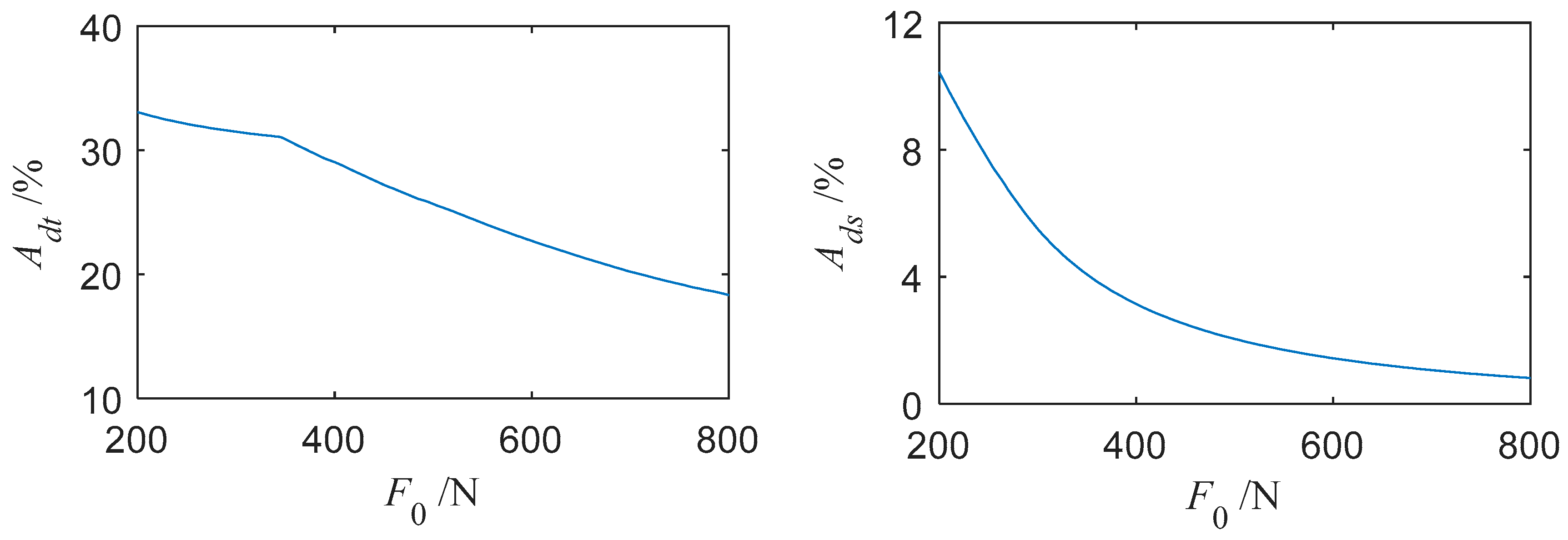
3.3.3. The Effect of External Excitation Amplitude on the Vibrational Reduction
4. Conclusions
- The dynamic model and analysis method presented in this paper are effective to study the influence of a bladed disc’s rotation on the dynamic characteristics of a turbine blade. The changes of the convective inertial force and Coriolis inertial force during the rotation of the bladed disc have a significant influence on the hysteretic constructive relationship of friction-relative displacement and the characteristics of the system dynamics.
- When the friction contact surface is not detached, changing the damper mass, the damper vibration stiffness, and the external excitation amplitude, results in only higher harmonics in the system response and friction force, and in the system’s response, bifurcation and chaos cannot be observed.
- With proper parameters, adding a platform damper will make the turbine blade’s vibration reduce obviously. When the steady-state response is periodic, the reduction law of the average power of blade vibration and the maximum absolute value of the steady-state response are basically the same. However, reduction laws of the average power of blade vibration and the maximum absolute value of the transient response are different. With some parameters, the reduction effect of the transient response may be negative. Greater normal pressure would be needed to keep the damper working well when the external excitation amplitude increases.
- In engineering, the vibrational reduction effects of the steady-state response and the transient response should be analyzed comprehensively in the under platform-damper design.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Qin, J.; Yan, Q.; Huang, W.C. Literature survey of dry friction damper model and analysis method for depressing vibration of rotating blade. Adv. Aeronaut. Sci. 2018, 34, 25–33. [Google Scholar]
- Menq, C.H.; Chidamparam, P. Friction damping of two-dimensional motion and application in vibration control. J. Sound Vib. 1991, 144, 427–447. [Google Scholar] [CrossRef]
- Sanliturk, K.Y.; Ewins, D.J. Modelling two-dimensional friction contact and its application using harmonic balance method. J. Sound Vib. 1996, 193, 511–523. [Google Scholar] [CrossRef]
- Xia, F. Modelling of a two-dimensional Coulomb friction oscillator. J. Sound Vib. 2003, 265, 1063–1074. [Google Scholar] [CrossRef]
- Shan, Y.C. Investigation on the Vibration Control of Turbo-Machine Blade by Dry Friction Damping. Ph.D. Thesis, Beihang University, Beijing, China, 2002. [Google Scholar]
- Shan, Y.C.; Zhu, Z.G. Theoretical and numerical methods for solving friction force of circular motion in contact plane. J. Aerosp. Power 2006, 17, 447–450. [Google Scholar]
- Ma, H.; Xie, F.; Nai, H.; Wen, B. Vibration characteristics analysis of rotating shrouded blades with impacts. J. Sound Vib. 2016, 378, 92–108. [Google Scholar] [CrossRef]
- He, B.; Ouyang, H.; Ren, X.; He, S. Dynamic response of a simplified turbine blade model with under-platform dry friction dampers considering normal load variation. Appl. Sci. 2017, 7, 228. [Google Scholar] [CrossRef]
- Botto, D.; Umer, M. A novel test rig to investigate under-platform damper dynamics. Mech. Syst. Signal Proc. 2018, 100, 344–359. [Google Scholar] [CrossRef]
- Botto, D.; Gastadi, C.; Gola, M.M.; Umer, M. An experimental investigation of the dynamics of a blade with two under-platform dampers. J. Eng. Gas Turbines Power 2018, 140, 032504. [Google Scholar] [CrossRef]
- Umer, M.; Botto, D. Measurement of contact parameters on under-platform dampers coupled with blade dynamics. Int. J. Mech. Sci. 2019, 159, 450–458. [Google Scholar] [CrossRef]
- Liao, M.F.; Li, Y.; Song, M.B.; Wang, S.J. Dynamics modeling and numerical analysis of rotor with elastic support/dry friction dampers. Trans. Nanjing Univ. Aeronaut. 2018, 35, 69–83. [Google Scholar]
- Qi, W.K.; Gao, D.P. Study of vibration response analysis method for the dry friction damping systems. J. Aerosp. Power 2006, 21, 167–173. [Google Scholar]
- Qi, W.K.; Gao, D.P. Microslip study on friction damping and its application in design of vibration reductions. Acta Aeronaut. Astronaut. 2006, 27, 74–78. [Google Scholar]
- Stein, G.J.; Zahoranský, R.; Múčka, P. On dry friction modeling and simulation in kinematically excited oscillatory systems. J. Sound Vib. 2008, 311, 74–96. [Google Scholar] [CrossRef]
- Allara, M. A model for the characterization of friction contacts in turbine blades. J. Sound Vib. 2009, 320, 527–544. [Google Scholar] [CrossRef]
- Sayed, B.A.; Chatelet, E.; Baguet, S.; Jacquet-Richardet, G. Dissipated energy and boundary condition effects associated to dry friction on the dynamics of vibrating structures. Mech. Mach. Theory 2011, 46, 79–491. [Google Scholar] [CrossRef]
- He, S.W.; Ren, X.M.; Qin, W.Y. A method for reducing the blade vibration of platform damper using the macro-micro slip model. J. Northwest. Polytech. Univ. 2012, 27, 282–288. [Google Scholar]
- Gastaldi, C.; Gola, M.M. On the relevance of a microslip contact model for under-platform dampers. Int. J. Mech. Sci. 2016, 115, 145–156. [Google Scholar] [CrossRef]
- Lou, Y.; Jiang, X.; Wang, Y. Modeling of microslip friction and its application in the analysis of under-platform damper. Int. J. Aeronaut. Space 2018, 19, 388–398. [Google Scholar]
- Wang, B.L.; Zhang, X.M.; Wei, H.T. Harmonic balance method for nonlinear vibration of dry friction oscillator with Iwan model. J. Aerosp. Power 2013, 28, 1–9. [Google Scholar]
- Chen, L.; Sun, L. Steady-state analysis of cable with nonlinear damper via harmonic balance method for maximizing damping. J. Struct. Eng. 2016, 143, 04016172. [Google Scholar] [CrossRef]
- Zhang, D.; Fu, J.; Zhang, Q.; Hong, J. An effective numerical method for calculating nonlinear dynamics of structures with dry friction: Application to predict the vibration response of blades with under-platform dampers. Nonlinear Dyn. 2017, 88, 223–237. [Google Scholar] [CrossRef]
- He, B.; Ouyang, H.; He, S.; Ren, X. Stick–slip vibration of a friction damper for energy dissipation. Adv. Mech. Eng. 2017, 9, 1–13. [Google Scholar] [CrossRef]
- Yu, H.; Xu, Y.; Sun, X. Analysis of the non-resonance of nonlinear vibration isolation system with dry friction. J. Mech. Sci. Technol. 2018, 32, 1489–1497. [Google Scholar] [CrossRef]
- Shang, G.B.; Xu, Z.L.; Xiao, J.F. A microslip dry friction model with variable normal load. J. Vib. Eng. 2016, 29, 444–451. [Google Scholar]
- Xu, C.; Li, D.W.; Chen, X.Q.; Wang, D. Vibration analysis for a micro-slip frictional system considering variable normal load. J. Vib. Shock 2017, 36, 122–127. [Google Scholar]


| Parameters | Values | Parameters | Values |
|---|---|---|---|
| 0.5 kg | 1 N s/m | ||
| 4 × 105 N/m | 1 N s/m | ||
| 1 × 106 N/m | 0.01 m | ||
| 600 rad/s | 0.01 m | ||
| 0.2 |
| Parameters | Values |
|---|---|
| 0.049 kg | |
| 0.04 kg | |
| 6×105 N/m | |
| 400 N |
| Parameters | Values |
|---|---|
| 0.079 kg | |
| 0.07 kg | |
| 8 × 105 N/m | |
| 600 N |
| Parameters | Values |
|---|---|
| 0.04 kg~0.08 kg | |
| 8 × 105 N/m | |
| 400 N |
| Parameters | Values |
|---|---|
| 0.059 kg | |
| 0.05 kg | |
| 6 × 105 N/m~1 × 106 N/m | |
| 400 N |
| Parameters | Values |
|---|---|
| 0.059 kg | |
| 0.05 kg | |
| 8 × 105 N/m | |
| 200 N~800 N |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, S.; Jia, W.; Yang, Z.; He, B.; Zhao, J. Dynamics of a Turbine Blade with an Under-Platform Damper Considering the Bladed Disc’s Rotation. Appl. Sci. 2019, 9, 4181. https://doi.org/10.3390/app9194181
He S, Jia W, Yang Z, He B, Zhao J. Dynamics of a Turbine Blade with an Under-Platform Damper Considering the Bladed Disc’s Rotation. Applied Sciences. 2019; 9(19):4181. https://doi.org/10.3390/app9194181
Chicago/Turabian StyleHe, Shangwen, Wenzhen Jia, Zhaorui Yang, Bingbing He, and Jun Zhao. 2019. "Dynamics of a Turbine Blade with an Under-Platform Damper Considering the Bladed Disc’s Rotation" Applied Sciences 9, no. 19: 4181. https://doi.org/10.3390/app9194181
APA StyleHe, S., Jia, W., Yang, Z., He, B., & Zhao, J. (2019). Dynamics of a Turbine Blade with an Under-Platform Damper Considering the Bladed Disc’s Rotation. Applied Sciences, 9(19), 4181. https://doi.org/10.3390/app9194181







