Reduced-Complexity Artificial Neural Network Equalization for Ultra-High-Spectral-Efficient Optical Fast-OFDM Signals
Abstract
:1. Introduction
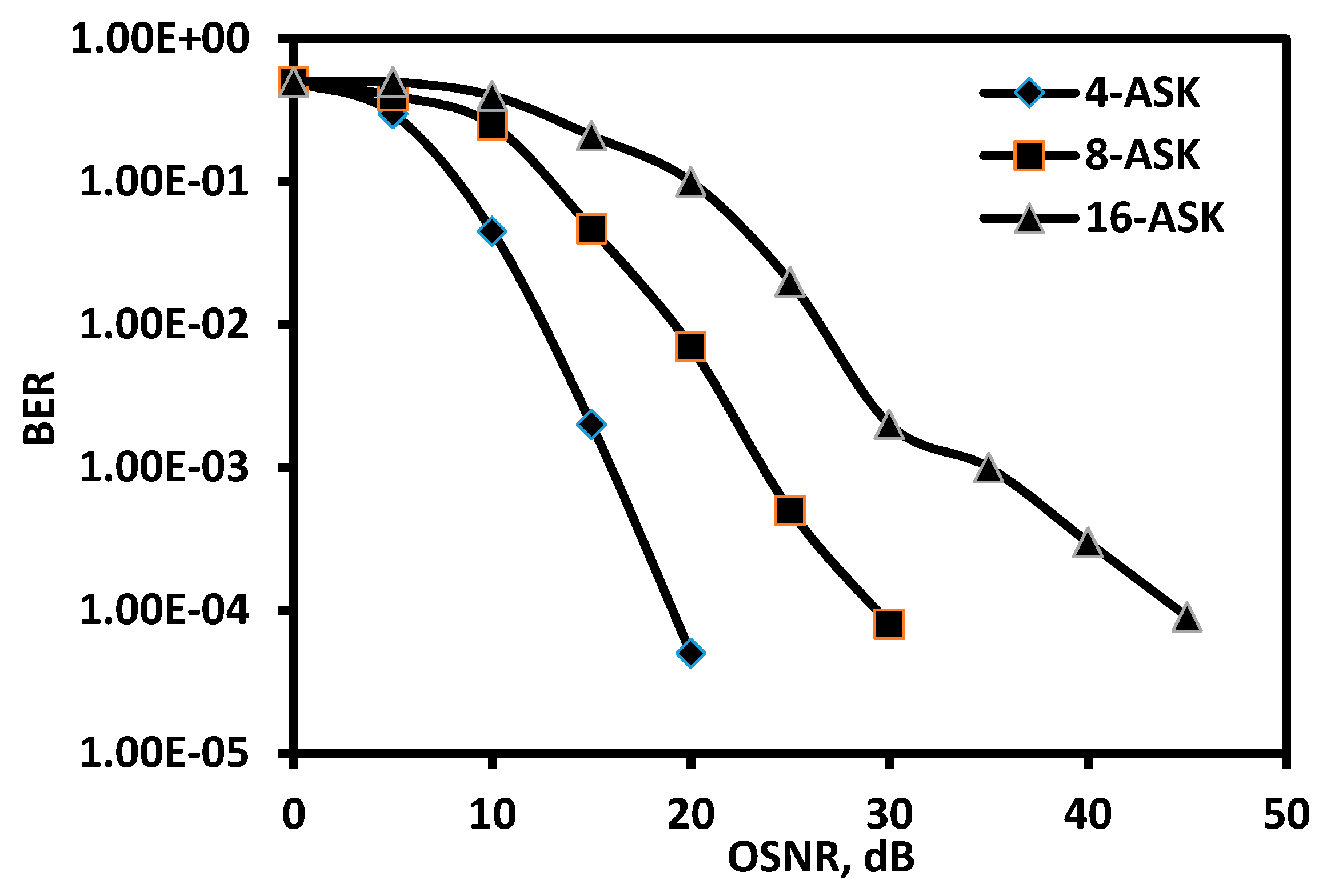
2. Impact of Directed-Detected Optical Fast-OFDM Signals over AWGN Using Linear Equalization
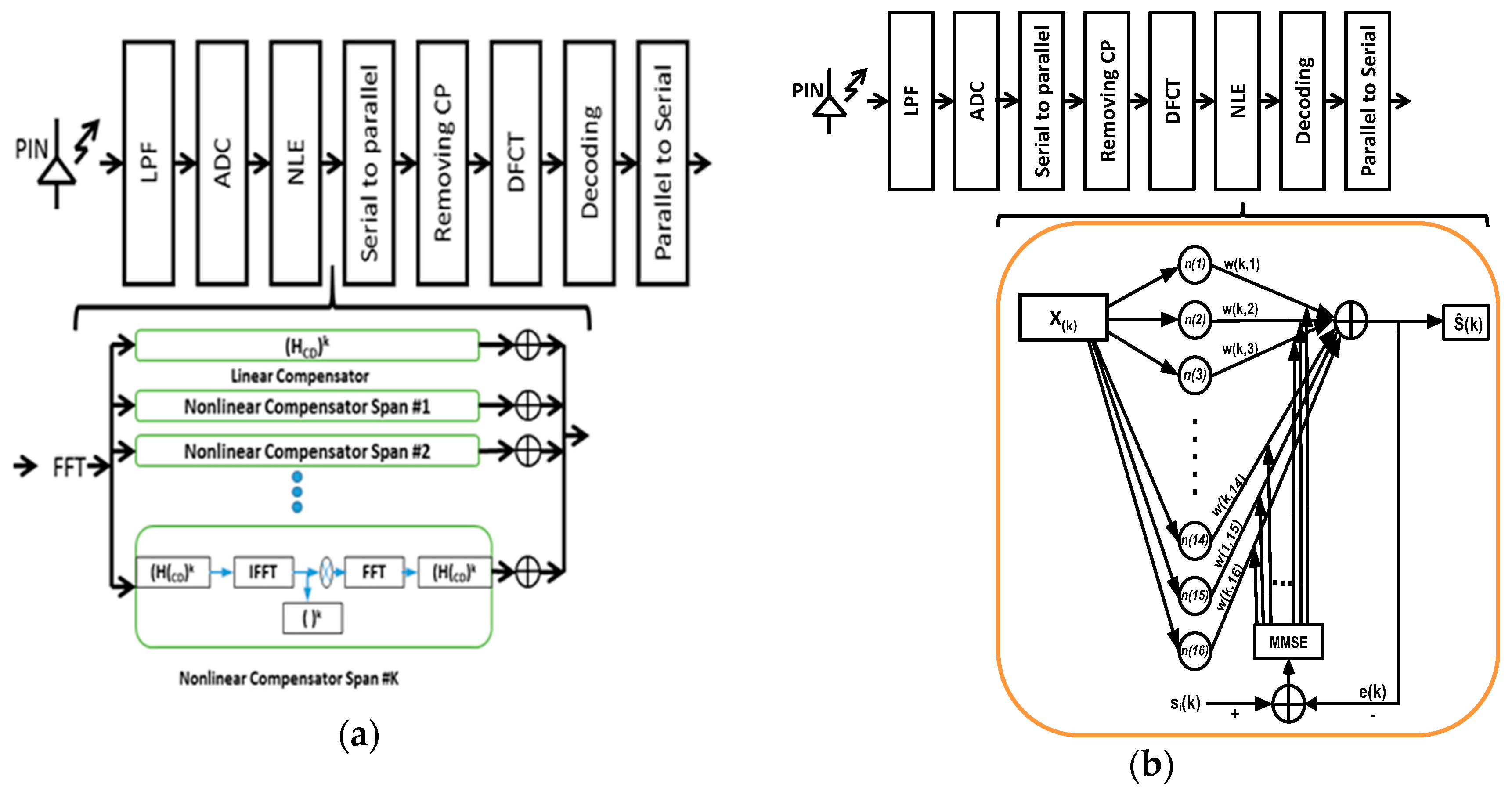
3. ANN and IVSTF Nonlinear Equalizers
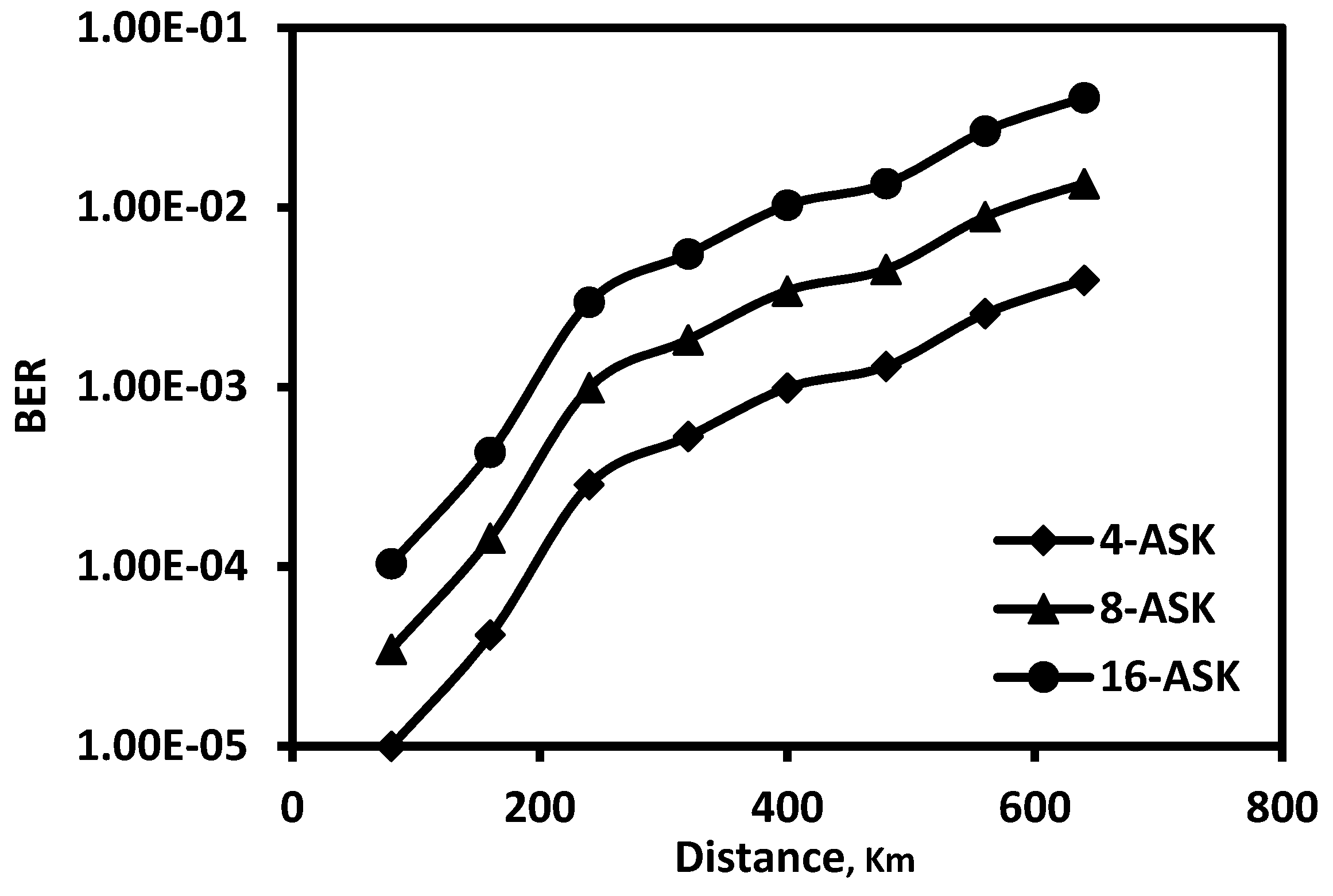
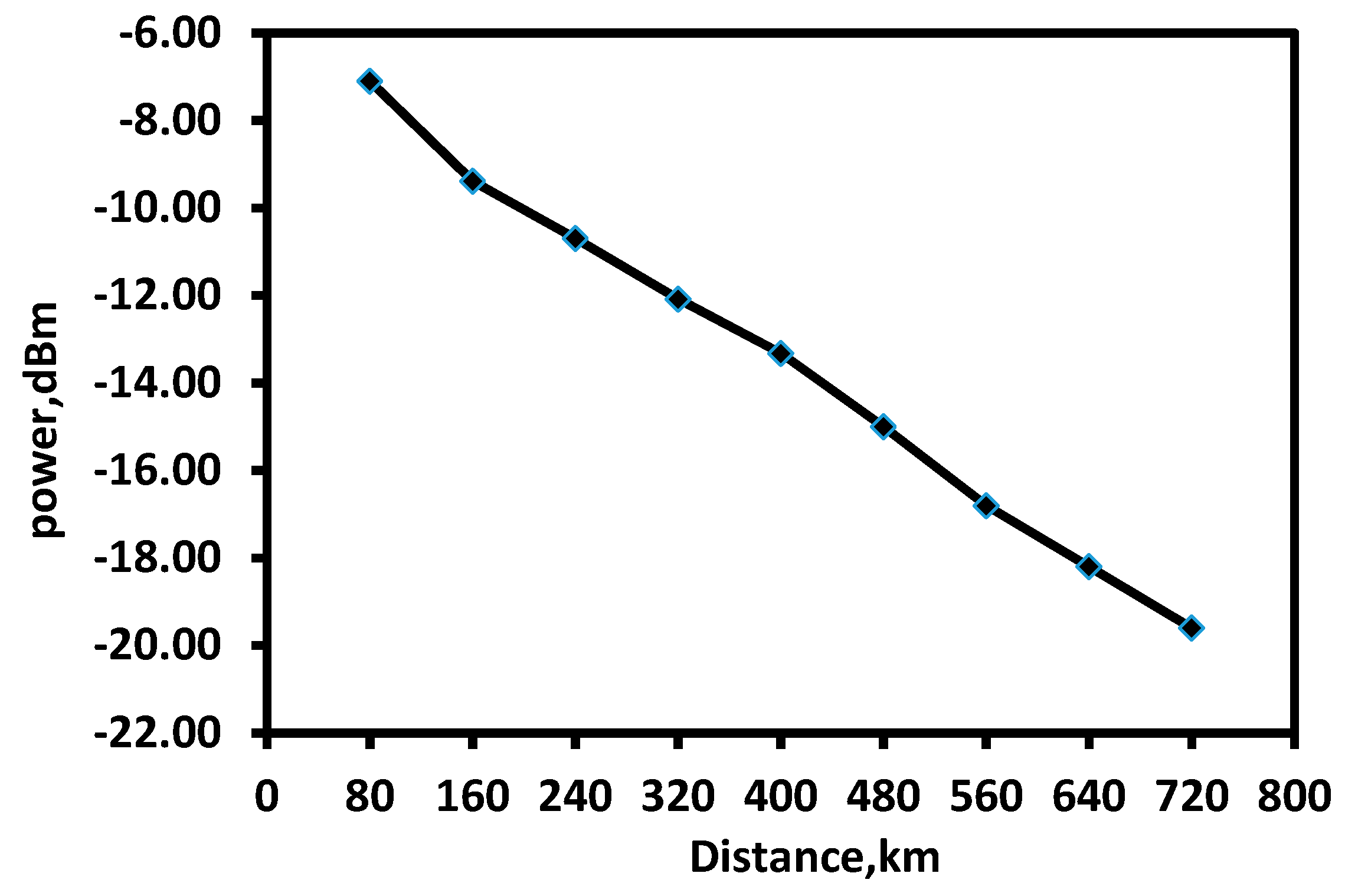
4. Direct-Detected Optical Fast-OFDM System Model Equipped with NLEs and Performance over SMF
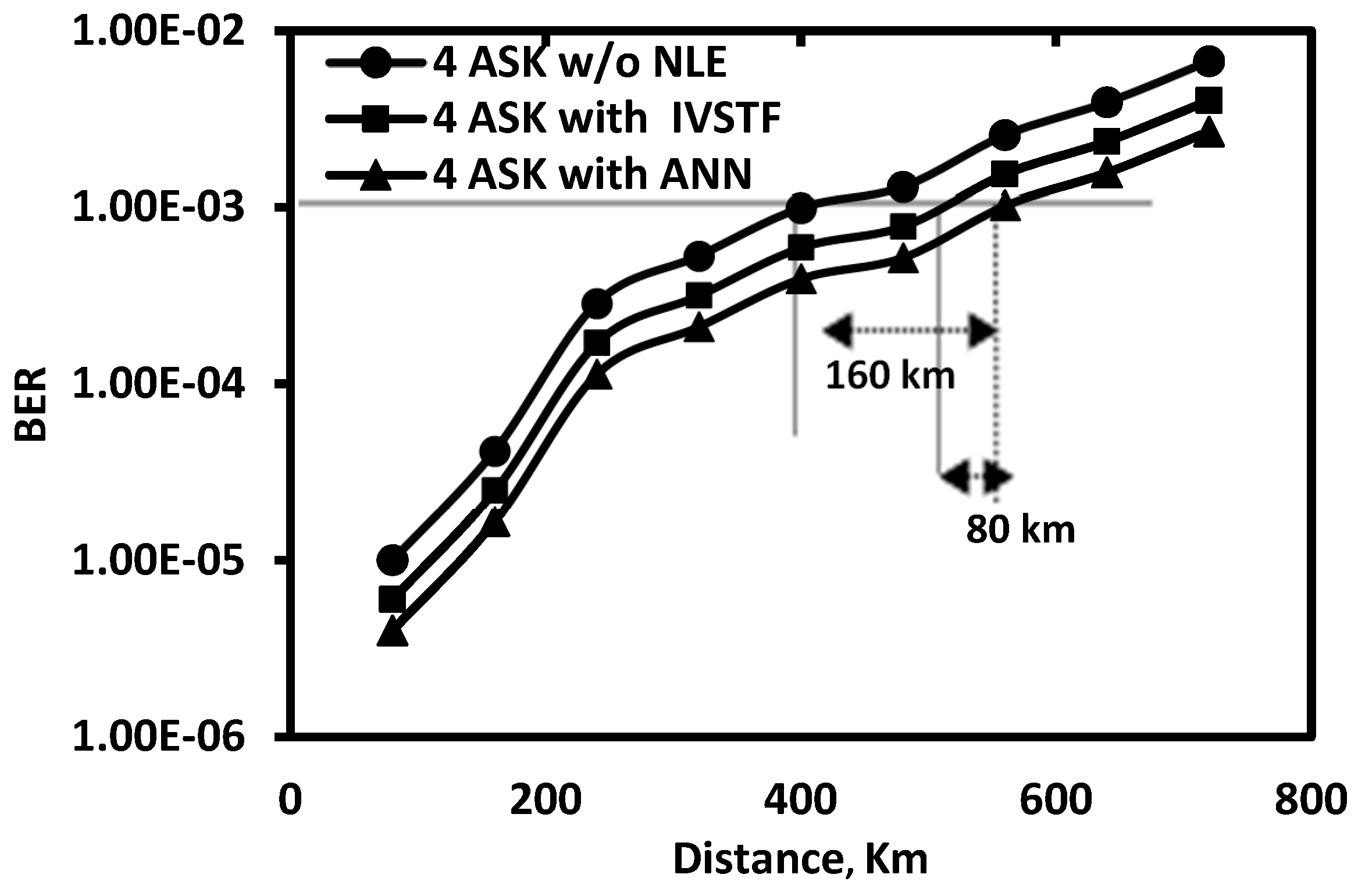
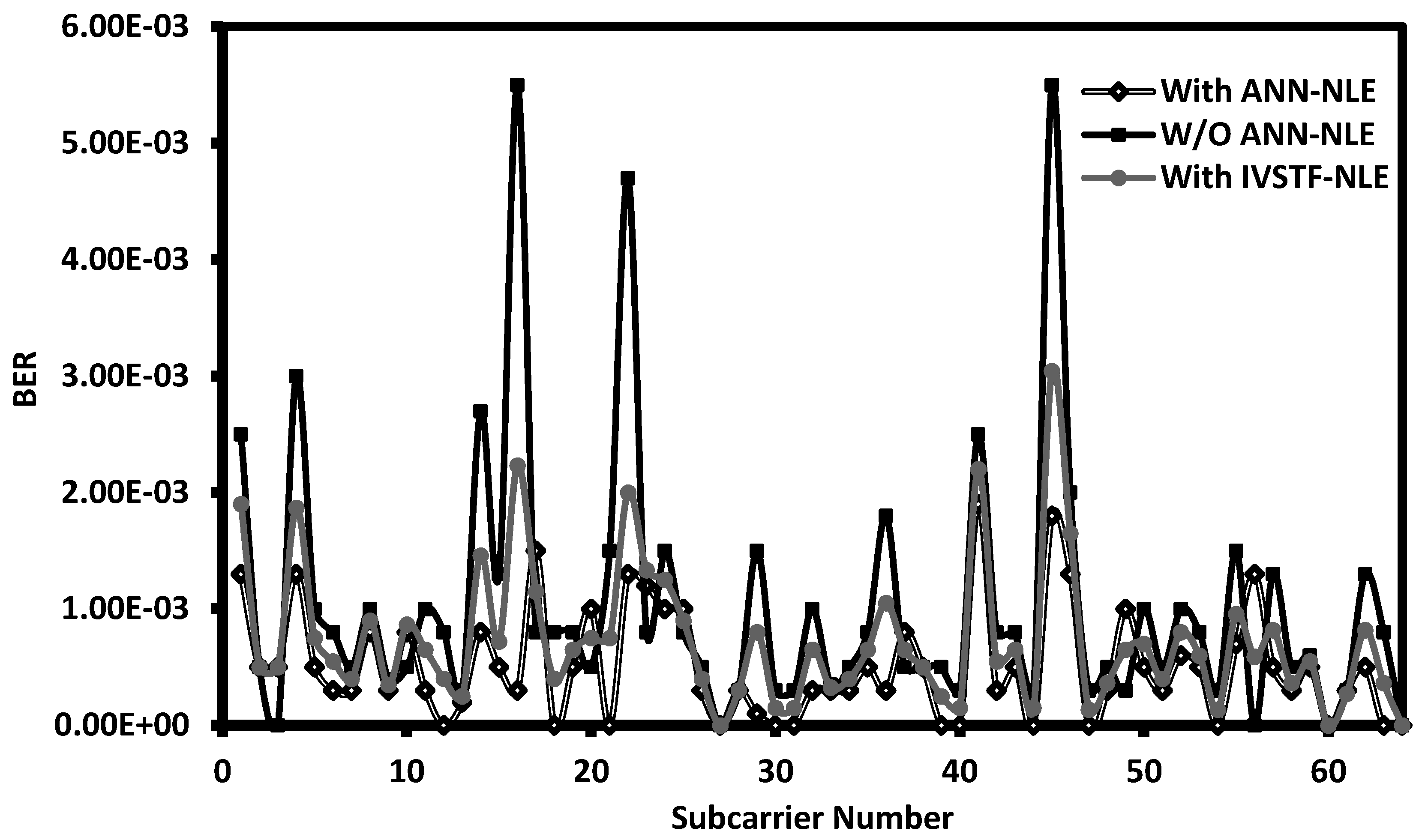
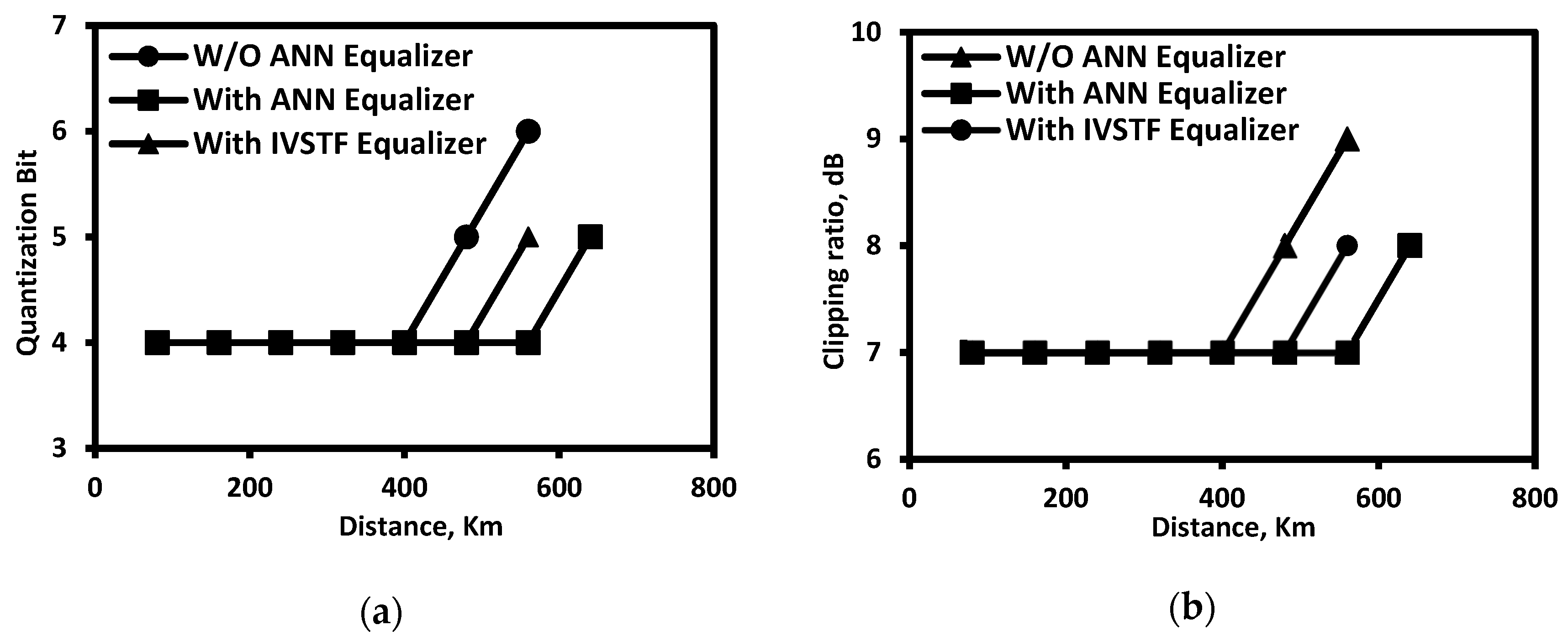
5. ANN vs. IVSTF in Direct-Detected Optical Fast-OFDM
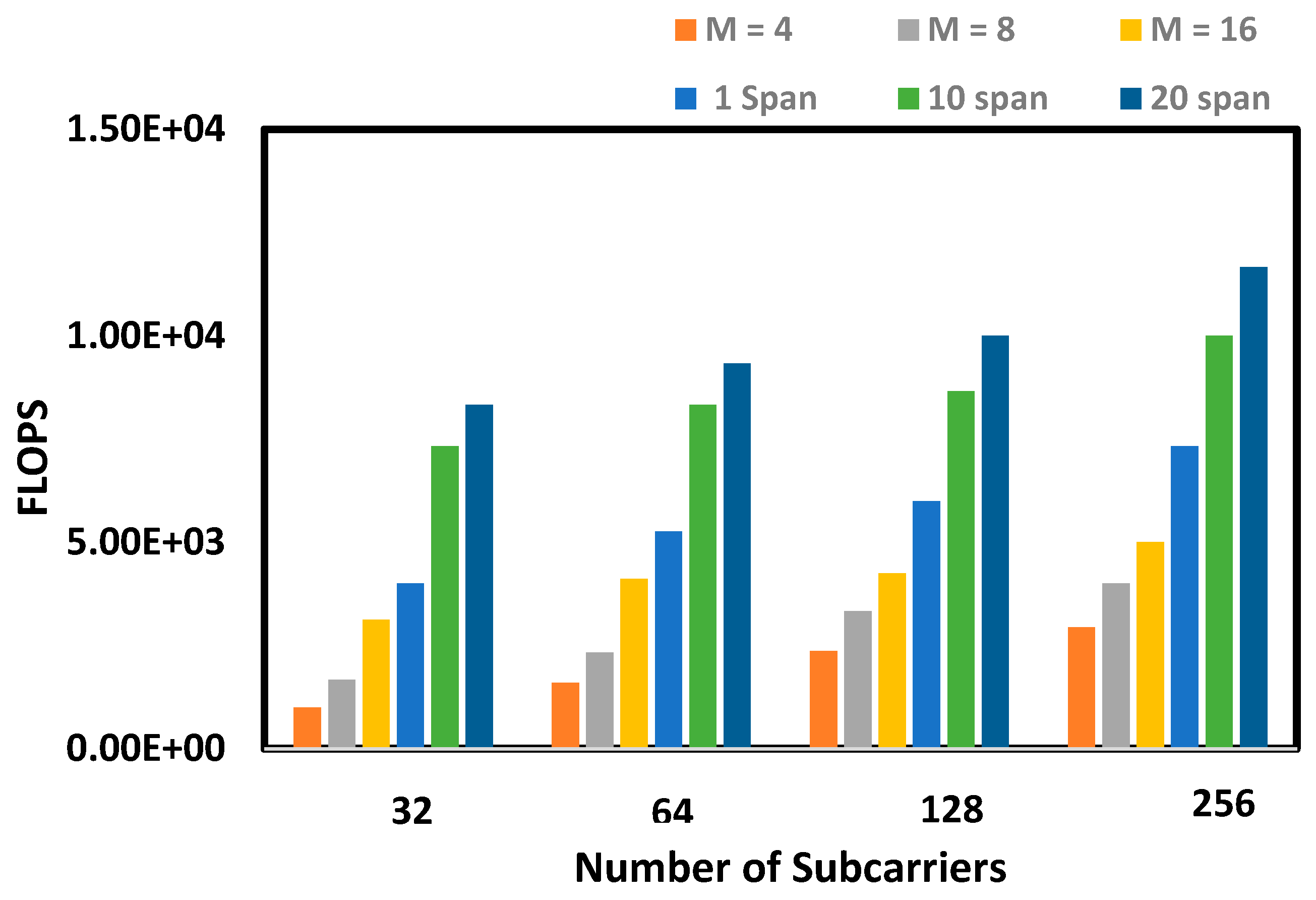
6. Computational Complexity Analysis
7. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Jansen, S.L.; Morita, I.; Schenk, C.W.; Takeda, N.; Tanaka, H. Coherent Optical 25.8-Gb/s OFDM Transmission over 4160-km SSMF. IEEE J. Lightw. Technol. 2008, 26, 6–15. [Google Scholar] [CrossRef]
- Pratt, W.K. Laser Communication Systems, 1st ed.; John Wiley & Sons: New York, NY, USA, 1969. [Google Scholar]
- Li, K.; Darwazeh, I. System performance comparison of Fast-OFDM with overlapping MC-DS-CDMA and MT-CDMA systems. In Proceedings of the 6th International Conference on Information, Communications & Signal Processing, Singapore, 10–13 December 2007; pp. 1–4. [Google Scholar]
- Ibrahim, S.K.; Jian, Z.; Rafique, D.; O’Dowd, J.A.; Ellis, A.D. Demonstration of world-first experimental optical Fast OFDM system at 7.174 Gbit/s and 14.348 Gbit/s. In Proceedings of the European Conference and Exhibition on Optical Communication (ECOC), Torino, Italy, 19–23 September 2010; pp. 1–3. [Google Scholar]
- Zhao, J.; Ibrahim, S.K.; Rafique, D.; Gunning, P.; Ellis, A.D. Symbol synchronization exploiting the symmetric property in optical Fast OFDM. IEEE Photonics Technol. Lett. 2011, 23, 594–596. [Google Scholar] [CrossRef]
- Giacoumidis, E.; Tsokanos, A.; Mouchos, C.; Zardas, G.; Alves, C.; Wei, J.L.; Tang, J.M.; Gosset, C.; Jaouën, Y.; Tomkos, I. Extensive comparisons of optical Fast-OFDM and conventional optical OFDM for local and access networks. J. Opt. Commun. Netw. 2012, 4, 724–733. [Google Scholar] [CrossRef]
- Jarajreh, M.A.; Ghassemlooy, Z.; Ng, W.P. Improving the chromatic dispersion tolerance in long-haul fibre links using the coherent optical orthogonal frequency division multiplexing. IET Microw. Antennas Propag. 2010, 6, 651–658. [Google Scholar] [CrossRef]
- Gao, G.; Zhang, J.; Gu, W. Analytical Evaluation of Practical DBP-Based Intra-Channel Nonlinearity Compensators. IEEE Photonics Technol. Lett. 2013, 25, 717–720. [Google Scholar] [CrossRef]
- Liu, L.; Li, L.; Huang, Y.; Cui, K.; Xiong, Q.; Hauske, F.N.; Xie, C.; Cai, Y. Intrachannel Nonlinearity Compensation by Inverse Volterra Series Transfer Function. IEEE J. Lightw. Technol. 2012, 30, 310–316. [Google Scholar] [CrossRef]
- Lowery, A.J. Fiber nonlinearity pre- and post-compensation for long-haul optical links using OFDM. Opt. Exp. 2007, 15, 12965–12970. [Google Scholar] [CrossRef]
- Giacoumidis, E.; Aldaya, I.; Jarajreh, M.A.; Tsokanos, A.; Le, S.T.; Farjady, F.; Ellis, A.D.; Doran, N.J. Volterra-based Reconfigurable Nonlinear Equalizer for Dual-Polarization Multi-Band Coherent OFDM. IEEE Photonics Technol. Lett. 2014, 26, 1383–1386. [Google Scholar] [CrossRef]
- Giacoumidis, E.; Mhatli, S.; Nguyen, T.; Le, S.; Aldaya, I.; Ellis, A.; Mccarthy, M.; Eggleton, B. Comparison of DSP-based nonlinear equalizers for intra-channel nonlinearity compensation in coherent optical OFDM. Opt. Lett. 2016, 41, 2509–2512. [Google Scholar] [CrossRef]
- Giacoumidis, E.; Lin, Y.; Wei, J.; Aldaya, I.; Tsokanos, A.; Barry, B. Harnessing machine learning for fiber-induced nonlinearity mitigation in long-haul coherent optical OFDM. Future Internet 2019, 11, 2. [Google Scholar] [CrossRef]
- Jarajreh, M.A.; Giacoumidis, E.; Aldaya, I.; Le, S.T.; Tsokanos, A.; Ghassemlooy, Z.; Doran, N.J. Artificial neural network nonlinear equalizer for coherent optical OFDM. IEEE Photonics Technol. Lett. 2015, 27, 387–390. [Google Scholar] [CrossRef]
- Zhao, J. Multi-Tap Equalization for Performance Improvement in Optical Fast OFDM Systems. IEEE Photonics Technol. Lett. 2015, 27, 42–45. [Google Scholar] [CrossRef]
- Zidan, M.; Abdel-Aty, A.; El-shafei, M.; Feraig, M.; Al-Sbou, Y.; Eleuch, H.; Abdel-Aty, M. Quantum Classification Algorithm Based on Competitive Learning Neural Network and Entanglement Measure. Appl. Sci. 2019, 9, 1277. [Google Scholar] [CrossRef]
- Walczak, S. An empirical analysis of data requirements for financial forecasting with neural networks. J. Manag. Inf. Syst. 2001, 17, 203–222. [Google Scholar]
- Yue, F.; Chai, T. Neural-network-based nonlinear adaptive dynamical decoupling control. IEEE Trans. Neural Netw. 2007, 18, 921–925. [Google Scholar] [CrossRef] [PubMed]
- Mellit, A.; Eleuch, H.; Benghanem, M.; Elaoun, C.; Massi Pavan, A. An adaptive model for predicting of global, direct and diffuse hourly solar irradiance. Energy Convers. Manag. 2010, 51, 771–782. [Google Scholar] [CrossRef]
- Nsiri, B.; Mhatli, S.; Mallouki, N.; Ghanbarisabagh, M.; Giacoumidis, E.; Ammar, M.; Bouallègue, A.; Attia, R. Nonlinearity mitigation of optical Fast-OFDM signals using a Wiener-Hammerstein electrical equalizer. In Proceedings of the Science and Information Conference (SAI), London, UK, 28–30 July 2015; pp. 1056–1061. [Google Scholar]
- Savazzi, P.; Favalli, L.; Costamagna, E.; Mecocci, A. A suboptimal approach to channel equalization based on the nearest neighbor rule. IEEE J. Sel. Areas Commun. 1998, 16, 1640–1648. [Google Scholar] [CrossRef]
- Rajbhandari, S.; Ghassemlooy, Z.; Angelova, M. Effective denoising and adaptive equalization of indoor optical wireless channel with artificial light using the discrete wavelet transform and artificial neural network. IEEE J. Lightw. Technol. 2009, 27, 4493–4500. [Google Scholar] [CrossRef]
- Charalabopoulos, G.; Stavroulakis, P.; Aghvami, A.H. A frequency-domain neural network equalizer for OFDM. In Proceedings of the GLOBECOM, San Francisco, CA, USA, 1–5 December 2003; pp. 571–575. [Google Scholar]
- Giacoumidis, E.; Ibrahim, S.K.; Zhao, J.; Wei, J.L.; Tang, J.M.; Ellis, A.D.; Tomkos, I. Effect of ADC on the Performance of Optical Fast-OFDM in MMF/SMF-Based Links. In Proceedings of the Electromagnetics Research Symposium (PIERS), Suzhou, China, 12–16 September 2011; pp. 402–406. [Google Scholar]
- Riedmiller, M.; Braun, H.A. Direct adaptive method for faster backpropagation learning: The RPROP Algorithm. In Proceedings of the IEEE International Conference on Neural Networks (ICNN), San Francisco, CA, USA, 28 March–1 April 1993; pp. 586–591. [Google Scholar]
- Chen, E.; Tao, R.; Zhao, X. Channel equalization for OFDM system based on the BP Neural network. In Proceedings of the IEEE International Conference on Signal Processing (ICSP), Beijing, China, 16–20 November 2006. [Google Scholar]
- Benvenuto, N.; Piazza, F. On the complex backpropagation algorithm. IEEE Trans. Signal Proc. 1992, 40, 967–969. [Google Scholar] [CrossRef]
- Giacoumidis, E.; Wei, J.L.; Yang, X.L.; Tsokanos, A.; Tang, J.M. Adaptive modulation-enabled WDM impairment reduction in multi-channel optical OFDM transmission systems for next generation PONs. IEEE Photonics 2010, 2, 130–140. [Google Scholar] [CrossRef]
- Giacoumidis, E.; Jarajreh, M.A.; Sygletos, S.; Le, S.T.; Tsokanos, A.; Hamié, A.; Pincemin, E.; Jaouën, Y.; Farjady, F.; Ellis, A.D.; et al. Dual-polarization multi-band OFDM transmission and transceiver limitations for up to 500 Gb/s in uncompensated long-haul links. Opt. Exp. 2014, 22, 10975–10986. [Google Scholar] [CrossRef]
- Giacoumidis, E.; Le, S.T.; Aldaya, I.; Wei, J.L.; McCarthy, M.E.; Doran, N.J.; Eggleton, B.J. Experimental Comparison of Artificial Neural Network and Volterra based Nonlinear Equalization for CO-OFDM. In Proceedings of the OSA Optical Fiber Communication Conference and Exposition and the National Fiber Optic Engineers Conference (OFC/NFOEC), San Francisco, CA, USA, 20–24 March 2016. [Google Scholar]
| Parameter | Description & Unit |
|---|---|
| Signal modulation format | 4-, 8-, 16-ASK |
| Signal data bit-rate | 9.69, 14.53, 19.37 Gb/s |
| Operating wavelength | 1550 nm |
| Number of sub-carriers | 64 |
| Cyclic prefix (CP) length | 25% |
| Forward-error-correction | 7% |
| ANN training vector length | 5% |
| Photo-detector type | PIN |
| PIN sensitivity | −19 dBm |
| DAC/ADC sampling rate | 6.25 GS/s |
| DAC/ADC quant. bits | 7 |
| DAC/ADC clipping ratio | 13 dB |
| LPF roll-off function | Bessel-Thomson |
| LPF 3 dB bandwidth (order) | 3 GHz (2nd order) |
| EDFA gain (noise figure) | 16 dB (6 dB) |
| SSMF span (length) | 8 (80 km) |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
A. Jarajreh, M. Reduced-Complexity Artificial Neural Network Equalization for Ultra-High-Spectral-Efficient Optical Fast-OFDM Signals. Appl. Sci. 2019, 9, 4038. https://doi.org/10.3390/app9194038
A. Jarajreh M. Reduced-Complexity Artificial Neural Network Equalization for Ultra-High-Spectral-Efficient Optical Fast-OFDM Signals. Applied Sciences. 2019; 9(19):4038. https://doi.org/10.3390/app9194038
Chicago/Turabian StyleA. Jarajreh, Mutsam. 2019. "Reduced-Complexity Artificial Neural Network Equalization for Ultra-High-Spectral-Efficient Optical Fast-OFDM Signals" Applied Sciences 9, no. 19: 4038. https://doi.org/10.3390/app9194038
APA StyleA. Jarajreh, M. (2019). Reduced-Complexity Artificial Neural Network Equalization for Ultra-High-Spectral-Efficient Optical Fast-OFDM Signals. Applied Sciences, 9(19), 4038. https://doi.org/10.3390/app9194038




