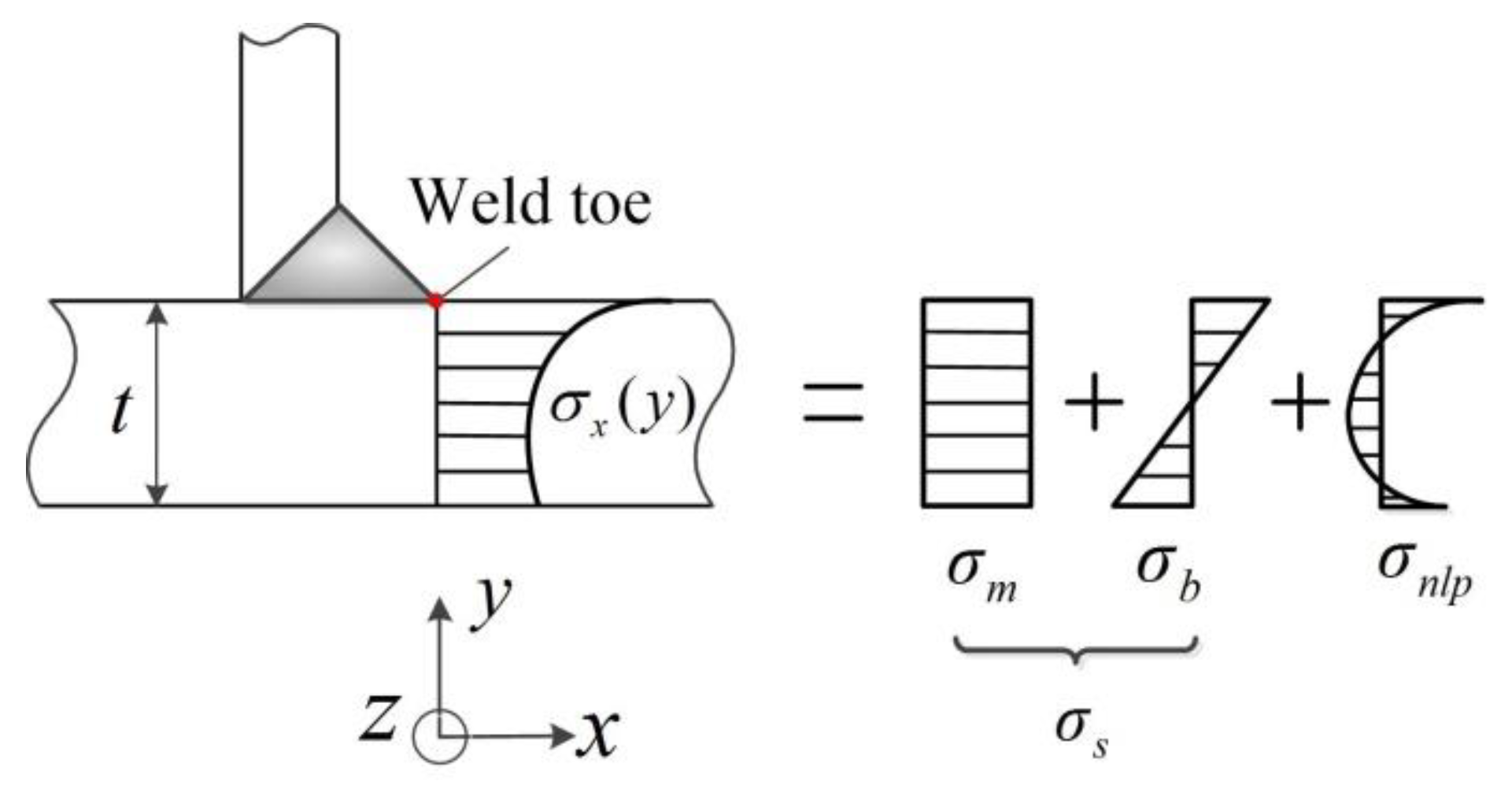
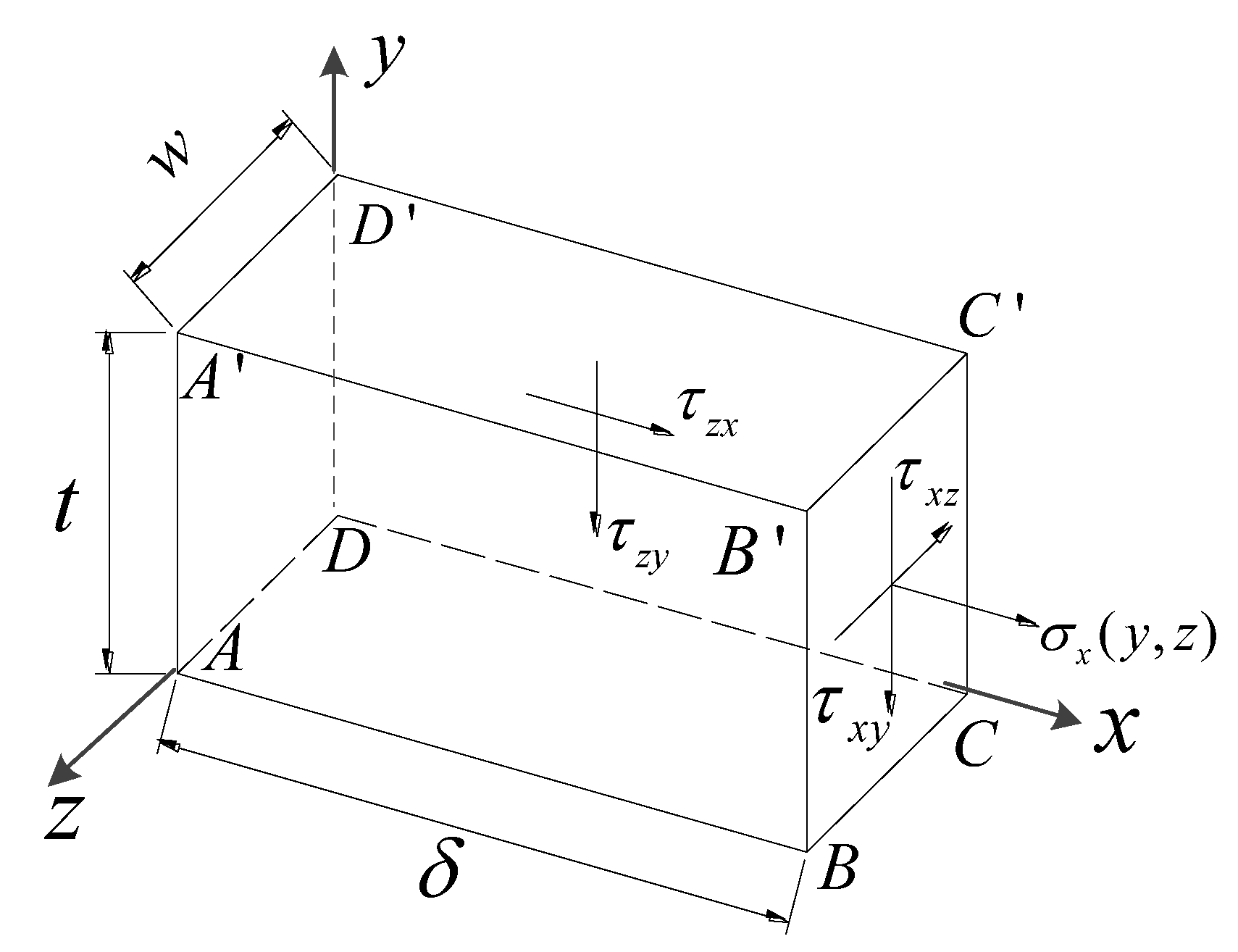
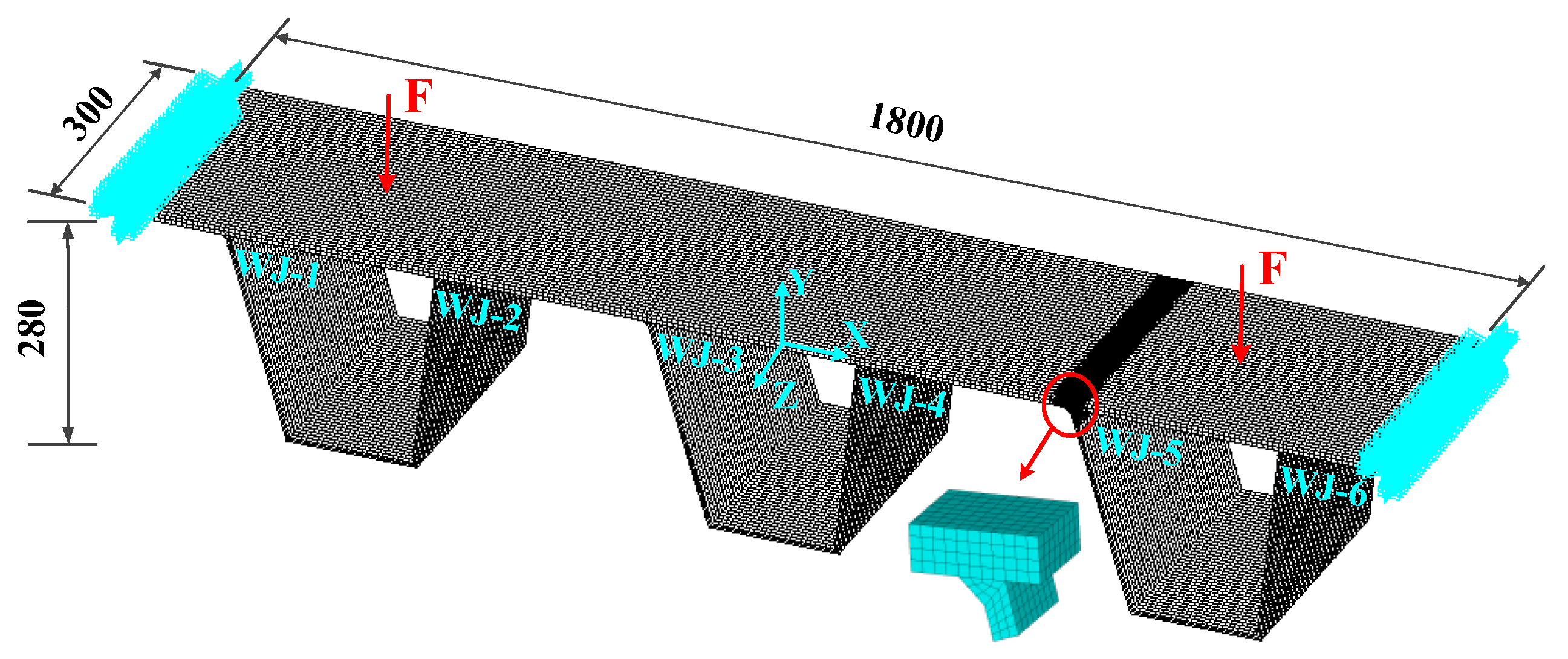
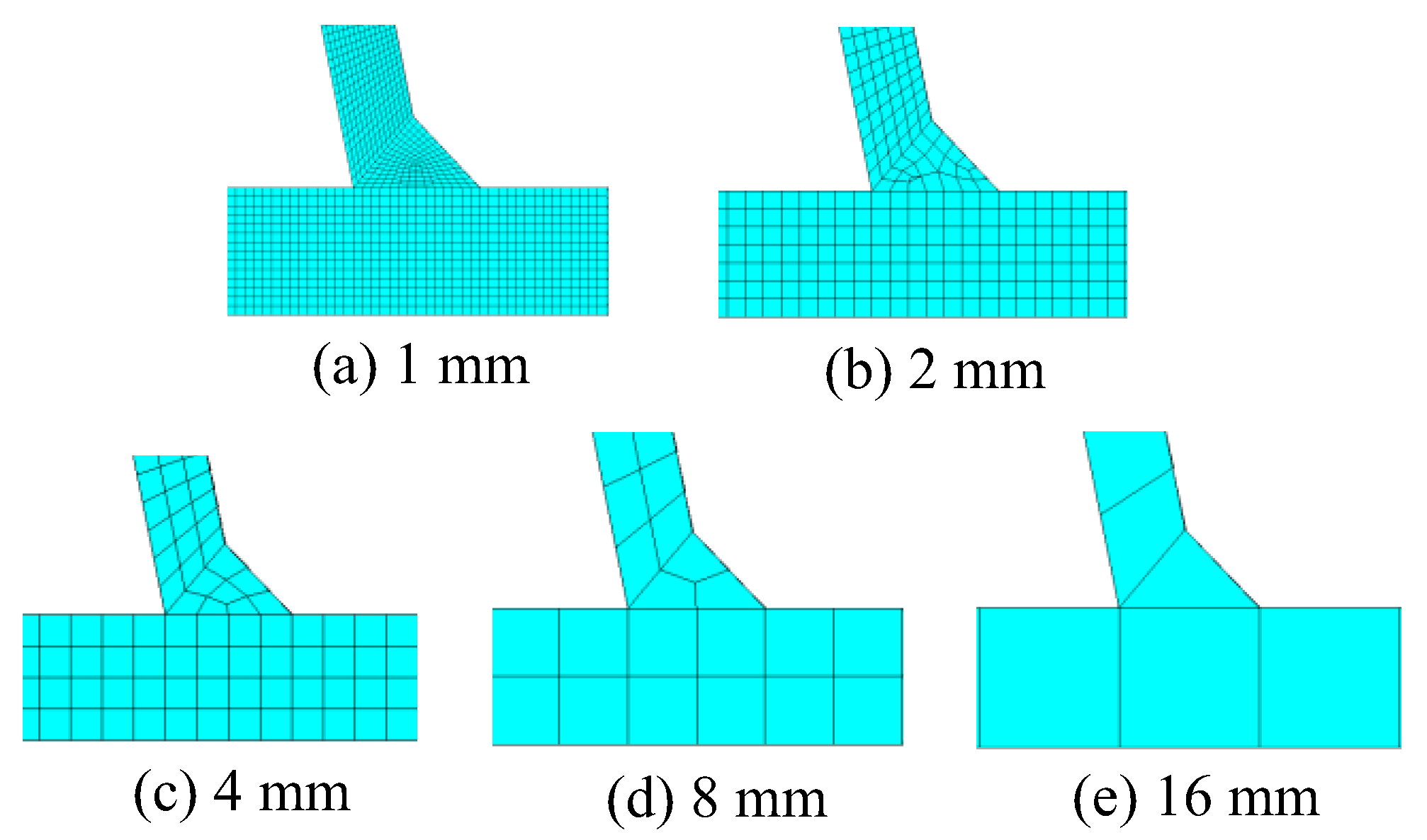
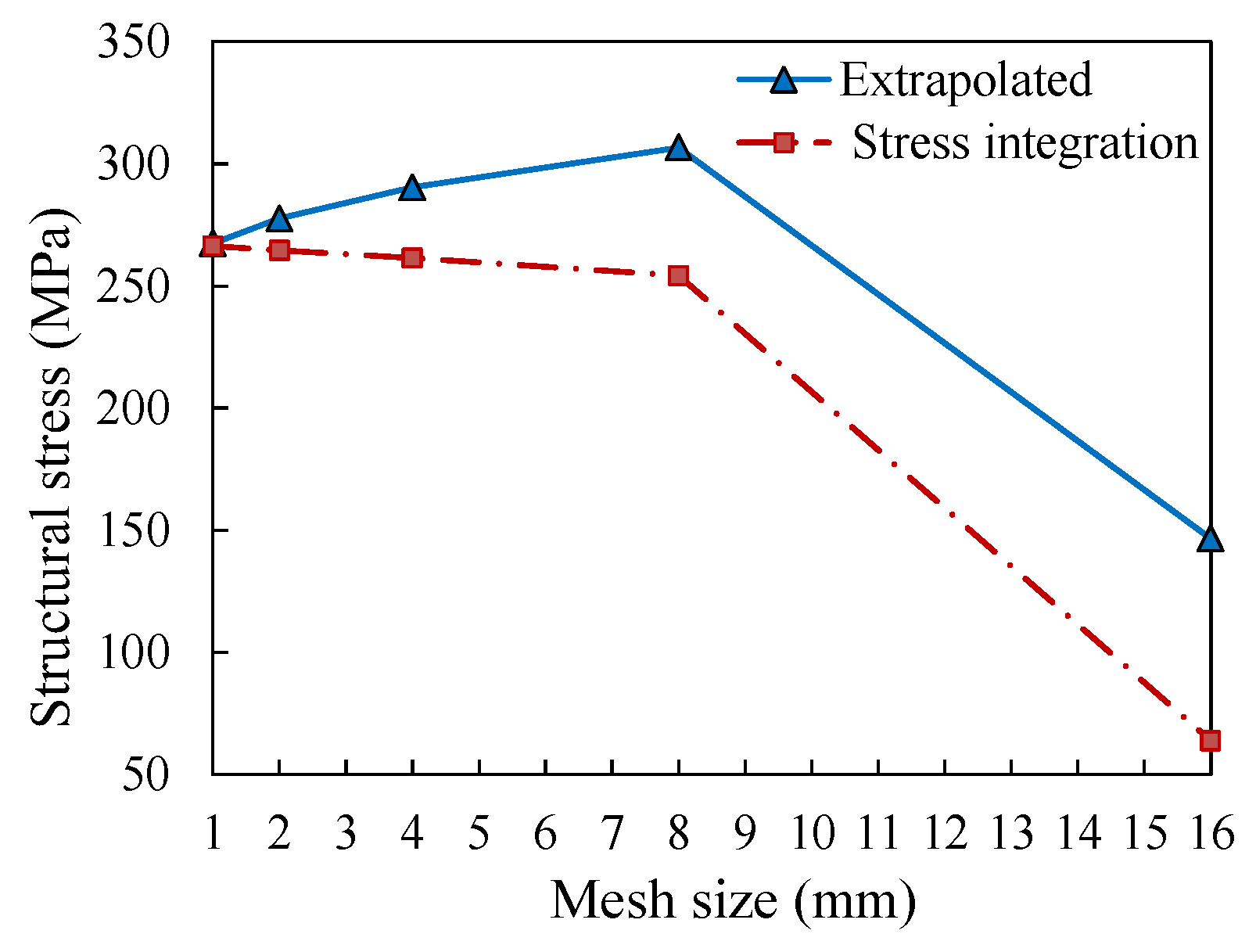
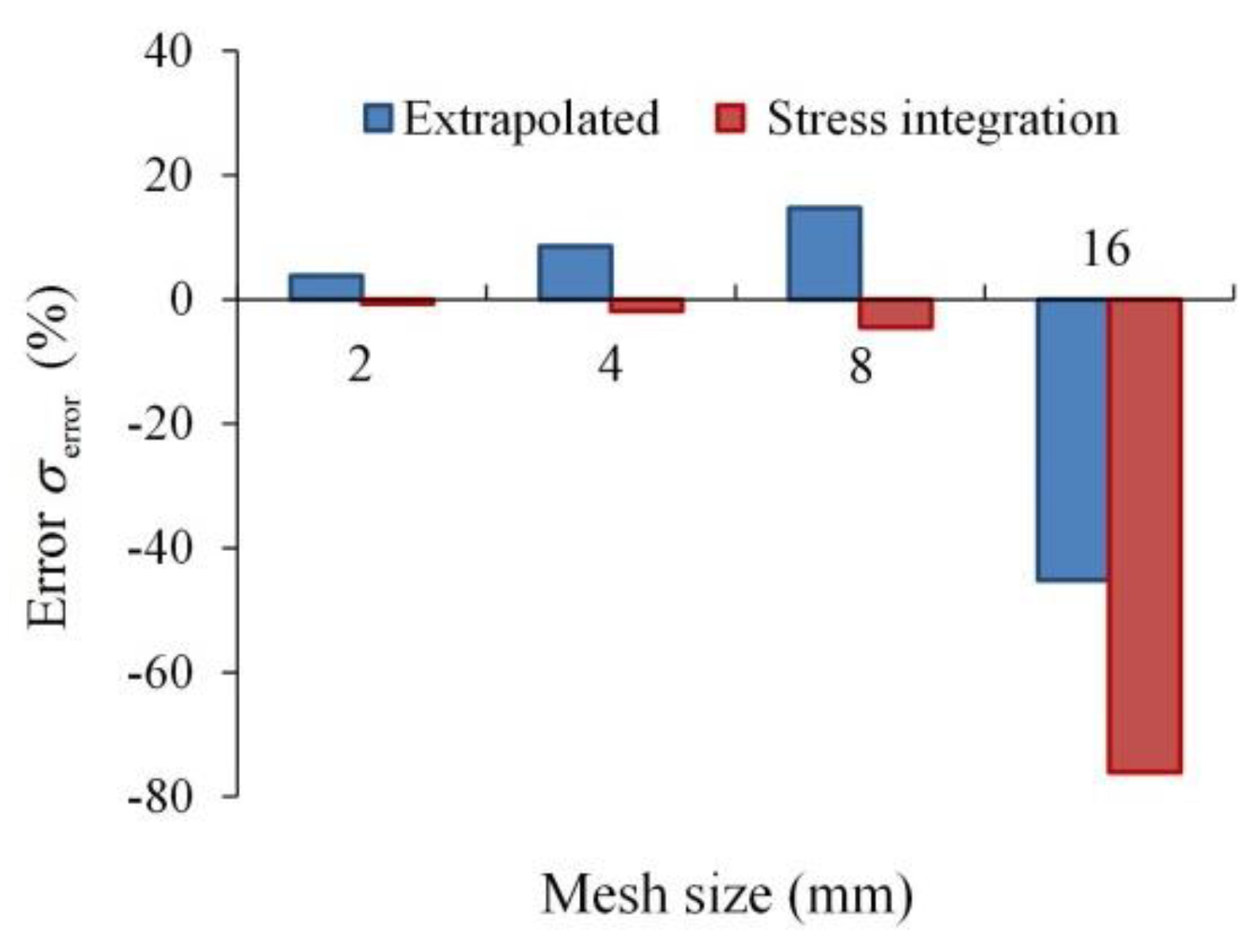
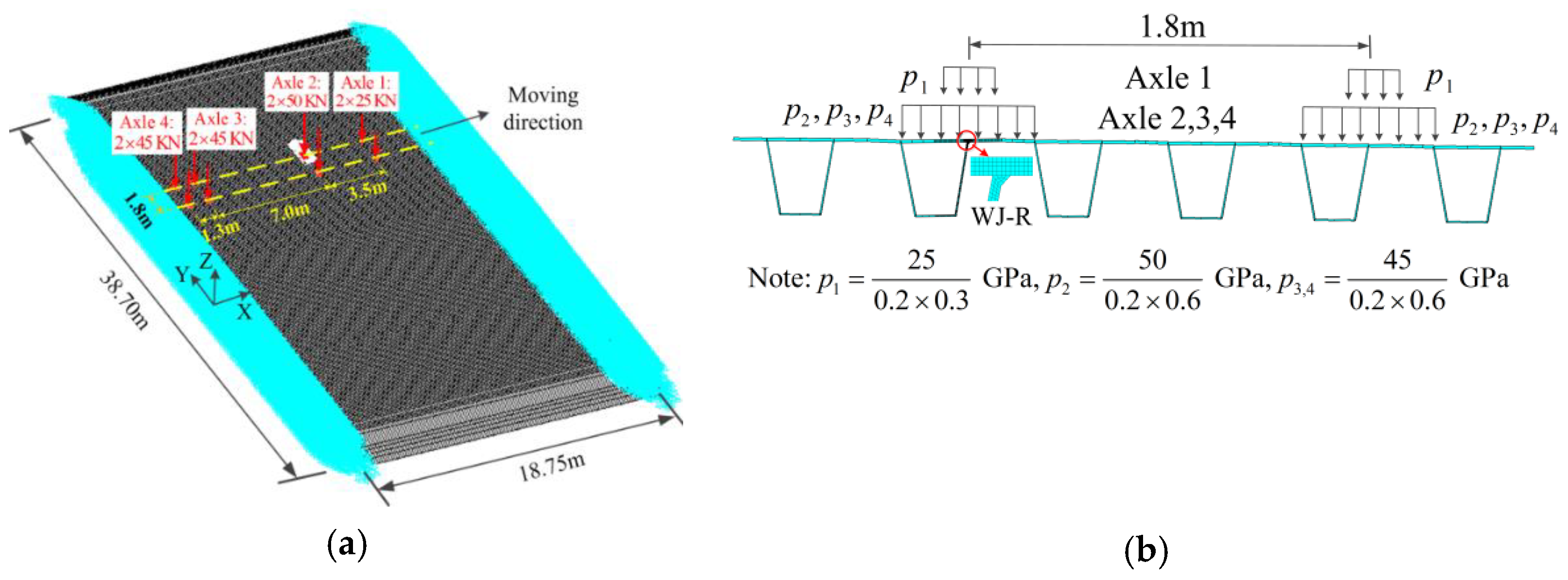
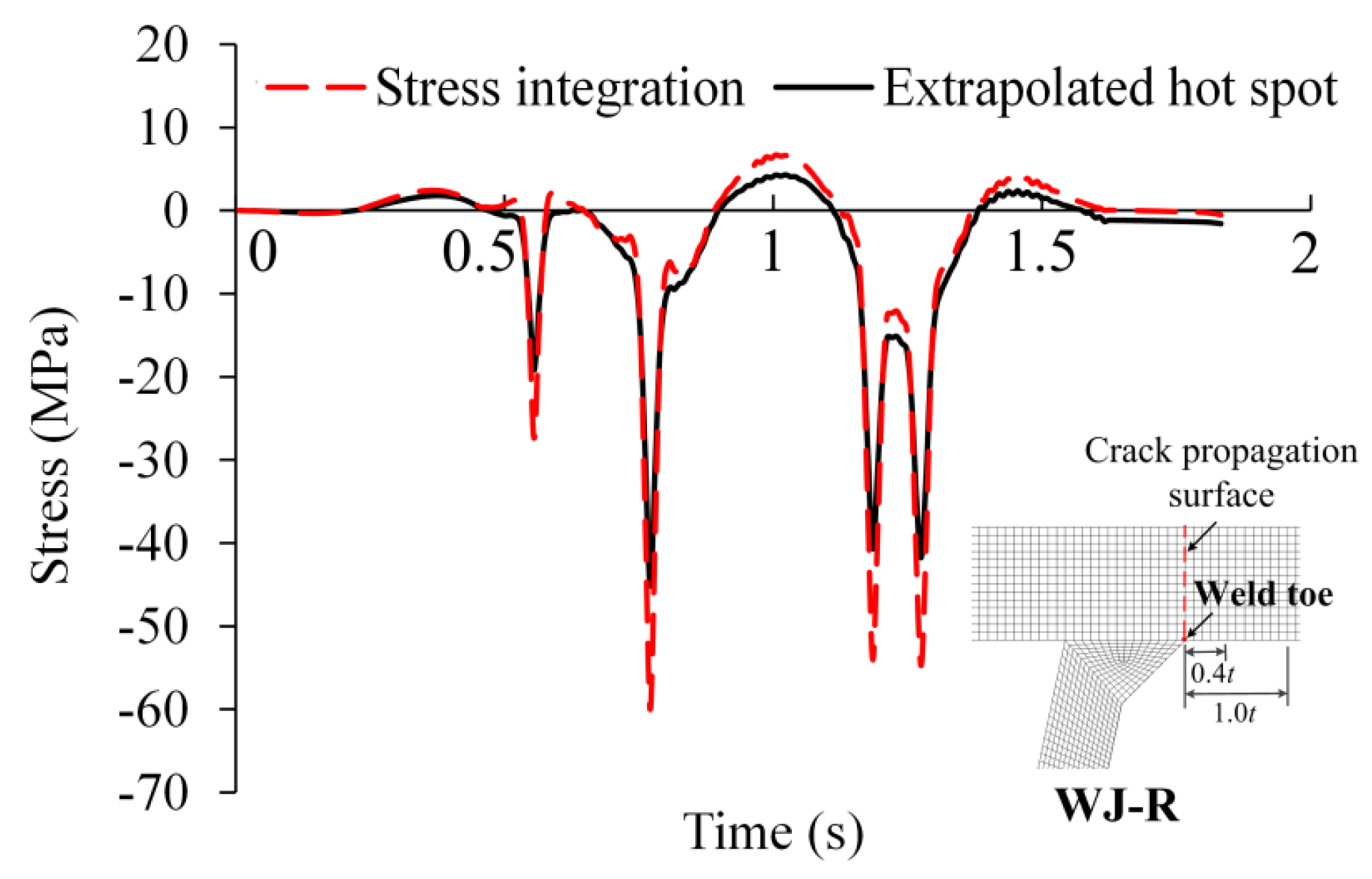
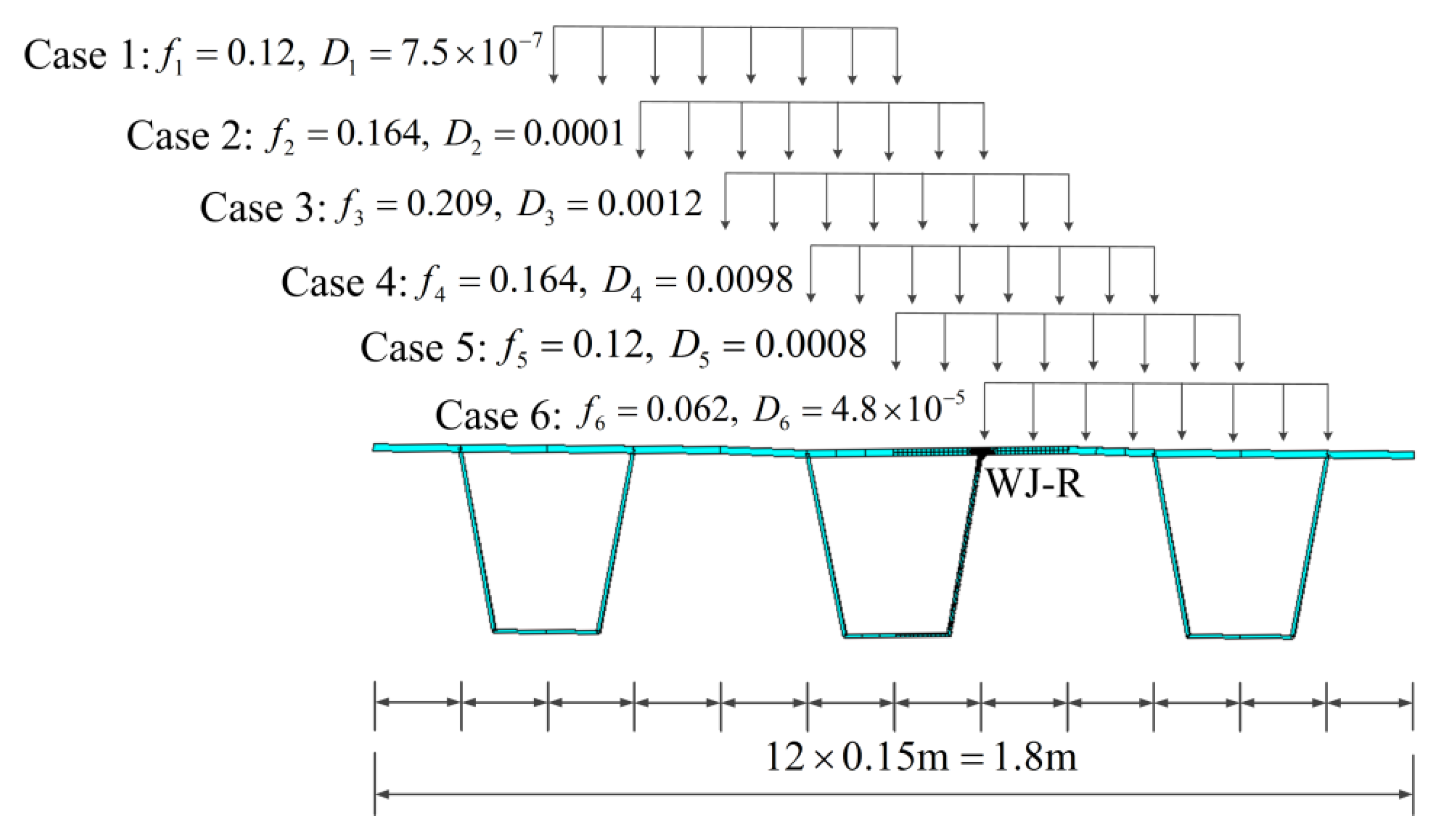
1. Introduction
Due to their light weight, high bearing capacity and short installation time, orthotropic steel decks (OSDs) have been widely used in long-span steel bridges, suspension bridges, and cable-stayed bridges [
1,
2]. However, in some cases, some welded joints of OSDs have shown serious fatigue cracks shortly after the bridge was opened to traffic [
3,
4]. For example, after 1.5 to 2 years of the Bronx-Whitestone Bridge being in use, cracks were found in the welded joints of the deck ribs by visual inspection, and the cracks continued to expand [
3]. Located in the Yangtze River Delta, an area with the heaviest traffic in China, the Jiangyin Yangtze River Bridge experienced fatigue cracks only nine years after its construction.
Figure 1 reveals fatigue cracking in the Jiangyin Yangtze River Bridge. As presented in the figure, many cracks initiated from the weld toe between the deck and the U-rib, which caused serious orthotropic steel deck and pavement damage. Therefore, it is important to evaluate the fatigue life of deck-to-rib welded joints in orthotropic steel decks using appropriate approaches.
At present, the main approaches used for steel bridge fatigue life evaluation [
5,
6,
7] include the nominal stress approach, the extrapolation hot spot stress approach, and equivalent structural stress approach. The nominal stress approach has been applied to some bridge design codes [
8,
9], but it adopts different S-N curves for different welded joint types, and it is difficult to determine the location of nominal stress points of complex structure joints accurately with this approach [
10]. The extrapolated hot spot stress approach [
11,
12] only needs a unified S-N curve for different welded joints. However, it needs a fine mesh to achieve more accurate results due to its mesh sensitivity, and it is difficult to establish a uniform hot spot extrapolation formula for different weld toe types. The equivalent structural stress approach was proposed by Dong et al. [
13,
14], and is mesh insensitive. That is, accurate results can be obtained using a coarser mesh, and computational efficiency is improved. Moreover, for different weld joint types, a unified master S-N curve stress can be used for fatigue life evaluation [
13]. To calculate the structural stresses, for the shell elements, Dong et al. provided an approach based on the nodal force [
14]. That is, the structural stress is calculated using the nodal force and moment at the weld toe. For solid elements, the structural stress calculation based on stress integration is adopted. Dong et al. provided the stress integration formula of two-dimensional (2D) solid elements [
15], and Feng et al. further provided the stress integration formula of three-dimensional (3D) solid elements [
16,
17]. That is, the stress on the reference surface, which is at a certain distance from the weld toe, is first extracted from FEM and integrated, and then the structural stress at the crack propagation surface is calculated through the equilibrium equation. There are three parameters in the formula of the stress integration approach: The plate thickness, the isolation body width, and the distance between the crack propagation surface and the reference surface. Understanding of the influence of the deck thickness on fatigue life was provided by Dong et al. [
13]. However, the influences of the other two parameters have not been given in previous studies. Therefore, in the present study, the stress integration approach of 3D solid elements is further studied, and the influences of calculated parameters on the results are investigated. The master S-N curve given by Dong et al. is mainly used for low-cycle fatigue evaluation [
18], and the slope of the curve remains unchanged. However, the bridge fatigue life evaluation under actual traffic load belongs to the high cycle fatigue problem, with low stress amplitude [
19]. The slope of S-N curve changes from low to high cycles in the fatigue design codes, such as Eurocode3 [
9] and the International Institute of Welding (IIW) [
12]. Therefore, the slope of the master S-N curve at high cycles and its influence on the bridge fatigue life are also discussed in the present study.
The studies on the fatigue behaviors of rib-to-deck welded joints in orthotropic steel decks using equivalent structural stress have been given by Li et al. [
20] and Wang et al. [
21]. However, these research efforts on the fatigue performance of rib-to-deck welded joints in OSDs occurred under experimental conditions. In the present study, the research is oriented towards an actual bridge: Jiangyin Bridge. The actual bridge model and fatigue vehicle load model are given, and the vehicle daily traffic volume data were obtained through bridge structural health monitoring.
The change of the weld size affects the fatigue performance of welded joints. Zhang et al. [
22] pointed out that one of the main methods to improve the weld joint fatigue properties is to change the weld size. The new improving deck-rib welding details in OSDs include increasing the size of the weld itself and increasing the thickness of the U-rib edge close to the weld seam, both of which increase the distance from the weld toe to the weld root. The parameters, including the relative weld height and deck toe flank angle, have an effect on the weld root notch stress intensity factors for rib-to-deck welded joints, as proposed by Luo et al. [
23]. They also investigated the fatigue performance of an innovative rib-to-deck welded joint which has an increased weld depth due to the rolled U-rib with thickened edges [
24]. The rolled U-ribs with thickened edges may significantly change the stress distribution around the rib-to-deck joint. Heng et al. [
25] evaluated the fatigue performance of the rib-to-deck welded joints in OSDs with thickened edge U-ribs (TEUs) and investigated the effects of weld penetration and the open angle of the rib-to-deck joints. The findings showed that as the penetration depth in TEU specimens decreased from 12 to 4 mm, the maximum notch stress was only increased by 2.8%. The use of TEUs significantly improved the robustness of the welded joints in terms of sensitivity to variations in the weld penetration. The appropriate increases in the open angle of the rib-to-deck joints in OSDs with TEUs further improved fatigue performances. Wang et al. [
26] pointed out that increasing the weld size is effective in improving the fatigue performance within a certain range. The transition angle and radius between the weld and the deck have an important impact on the fatigue strength of butt weld joints. When the transition angle is fixed (i.e., the weld shape remains the same), the weld fatigue strength does not change with the weld width and height. Cao et al. [
27] highlighted that the open angle between the deck and weld seam had a significant effect on the effective notch stress at the weld toe. Therefore, in the present study, the weld geometry size was measured in the experiment, which was within the range of the weld manufacturing errors, without any treatment, such as thickening of the U-rib or enlarging of the weld seam. The influence of the weld size differences caused by weld manufacturing errors on the fatigue performance of the deck-rib welding details in the OSD of Jiangyin Bridge is discussed based on the stress integration approach.
In order to improve the fatigue performance of the weld seams, scholars have put forward different treatment methods, such as ultrasonic treatment, the crack stop hole treatment, the grinding treatment, and so on. The ultrasonic impact is an effective method to decrease welding residual stress and thereby improve the fatigue strength of welds for steel bridges [
28,
29,
30]. The crack stop hole treatment could reduce stress concentration and prevent cracks from growing [
31,
32]. The grinding treatment effectively increases the transitional radius of the welds and reduces the stress concentration without changing the local microstructure, which improves the fatigue life of deck-rib welding details. Furthermore, the influence of the grinding radius and depth of the local stress field at the weld toe have been studied [
33,
34]. In the present study, a new grinding type is proposed, and the influence of the grinding radius on the fatigue life is discussed based on the stress integration approach.
Scholars have different opinions on the effect of the weld penetration rate on the fatigue life of weld joints. Plotting fatigue test results in an S-N diagram showed that specimens with weld melt-through (WMT) seem to have slightly lower fatigue strengths than 80% partial joint penetration (80% PJP) specimens, but the difference is more likely to be within the usual scatter of test data, which means that both details have comparable fatigue strength [
2]. Sim and Uang [
35] suggested that a shallower weld penetration (for example, an 80% PJP) appears to have a slightly higher fatigue resistance than a deeper one (for example, a 100% weld penetration). Fu et al. pointed out that an increased penetration rate can decrease the crack-propagation rate and enhance fatigue life [
36]. Cao et al. showed that fatigue cracks initiate from the weld toe inside the rib in 100% penetration specimens, but from the weld root inside the rib in 75% penetration specimens [
27]. Therefore, based on the stress integration approach, the fatigue life of the deck-rib weld details under 80% partial penetration and 100% full penetration were compared in the present study.
In this paper, two parameters and the mesh sensitivity of the stress integration approach for 3D solid elements were first analyzed. Then, the applicability of a master S-N curve of the equivalent structural stress approach was verified based on the experimental data of the deck-rib weld details in the OSD. Finally, the multi-scale finite element model (FEM) of Jiangyin Bridge was established, and the bridge fatigue life calculation steps based on the stress integration approach were given. The influence of the slope of the master S-N curve at high cycles on the bridge fatigue life is discussed. Further, the influence of the weld parameters on the fatigue life of deck-rib welding details in the OSD of Jiangyin Bridge was analyzed based on the stress integration approach, including: (1) The influence of the weld size change caused by weld manufacturing errors on the bridge fatigue life is analyzed based on the measured weld size in the experiment; (2) a new grinding treatment type is proposed, and the influence of the grinding radius on fatigue life is analyzed; and (3) the fatigue life of deck-rib welding details under 80% partial penetration and 100% full penetration are compared.
4. Experimental Verification of the Master S-N Curve
Figure 9 presents the static-load experimental device [
37]. The loading force generated by the jack was equally distributed by the distribution beam on the deck plate of the specimen. Therefore, the bending moment of the specimen was consistent between two loading points. The resistance-type strain gauges with the length of 10 mm and the width of 2 mm were adopted as strain-measurement sensors. Due to the symmetry of the structural geometry shape and load,
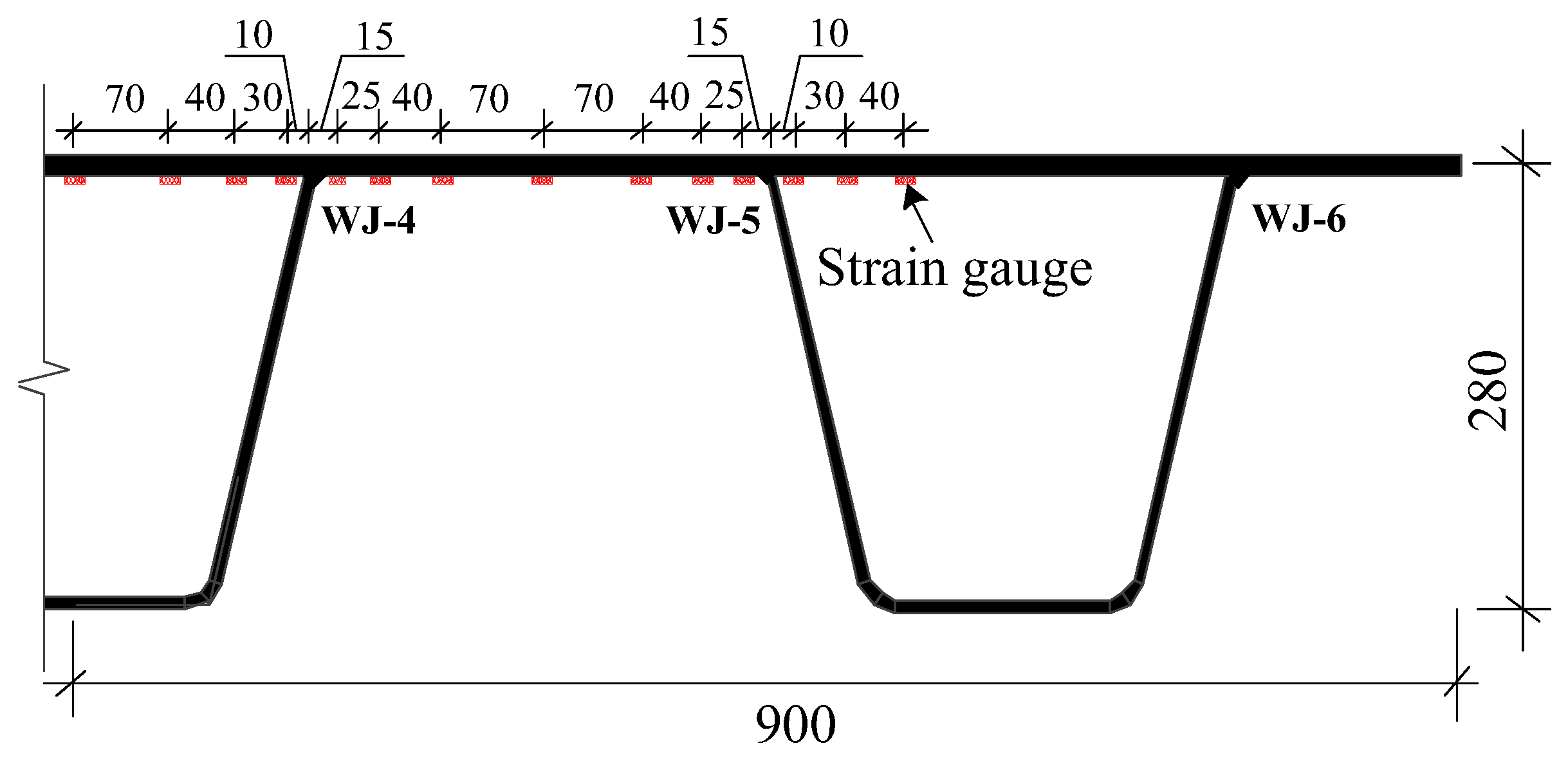
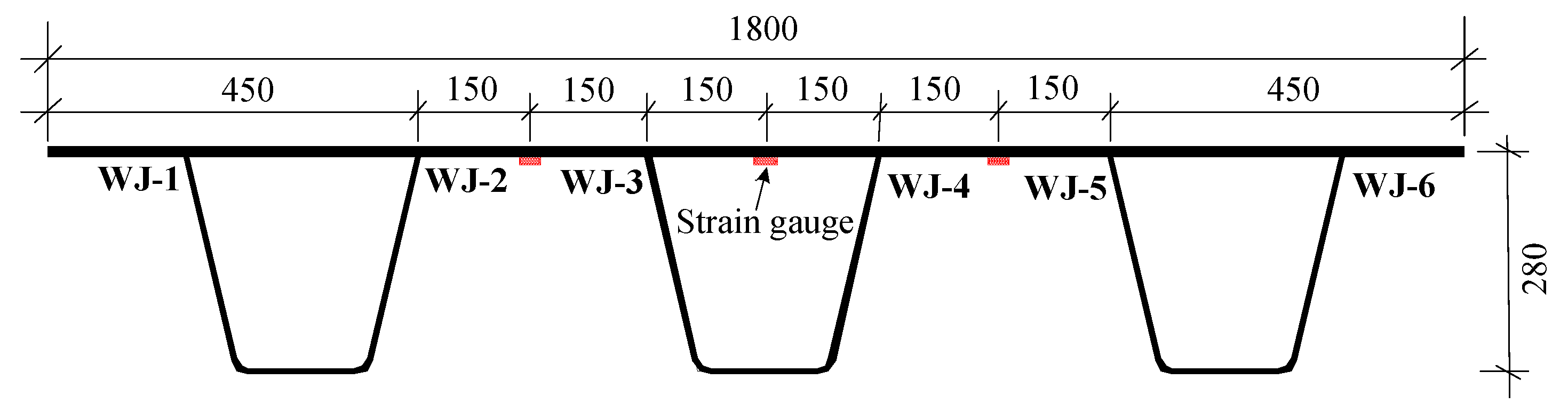
Figure 10 shows the strain gauges distribution of half of the specimen. In this figure, the uniaxial strain gauge was adopted with sensitive grid size of 10 mm
3 mm, a resistance value of 120 Ω and a sensitivity coefficient of 2.06. Fourteen strain gauges were distributed on the bottom of the deck, as shown in
Figure 10.
Figure 11 shows a comparison between the numerical simulation results and experiment results of the 3U deck-rib component. The experimental study of the deck-rib welding details was undertaken by Ding et al. [
37], as shown in
Figure 9 and
Figure 10. The geometric dimensions, boundary conditions and loading forces of FEM were the same with that of the experiment, as shown in
Figure 4. The deck and rib thickness were 16 mm and 8 mm, respectively. The simple support constraints were applied to the left and right ends of the model, and the static-load concentrated force F was 18 KN. In
Figure 11, the path of the deck near the weld side at the cross-section Z = 150 mm was selected. The horizontal coordinate X is shown in
Figure 4, and the vertical coordinate is the transverse stress
. In the figure, the curve and the dots represent the numerical simulation results and the experimental results, respectively. The experimental results are the transverse stresses measured by the strain gauges in
Figure 10.
Figure 11 shows that the maximum value of the numerical simulation results is approximately 294 MPa at the weld toe. The second largest value is approximately 254 MPa at the weld root. The minimum value is approximately 54 MPa. This value was obtained between the weld toe and root (6 mm from the weld root). The experimental results are in good agreement with the numerical simulation results, except for the stress at the weld toe and root. Since the stresses at the weld toe and root cannot be measured in this experiment, the numerical simulation results are considered reliable.
Figure 12 presents the strain gauges distribution in the fatigue experiments [
36]. The strain gauges are used to measure nominal stress and located in the middle of two adjacent weld seams, as show in
Figure 12.
Table 2 shows the experiment results of the 3U deck-rib component [
37]. The fatigue cracks were all located at the weld toes, and most of them were on the welds of WJ-2 and WJ-5, which are symmetrical positions. In this table, the fatigue life and nominal stress values were obtained from the fatigue experiments [
37]. The equivalent stress range
at the weld toe, which has been calculated by Equation (8), was obtained from the corresponding FEM shown in
Figure 4.
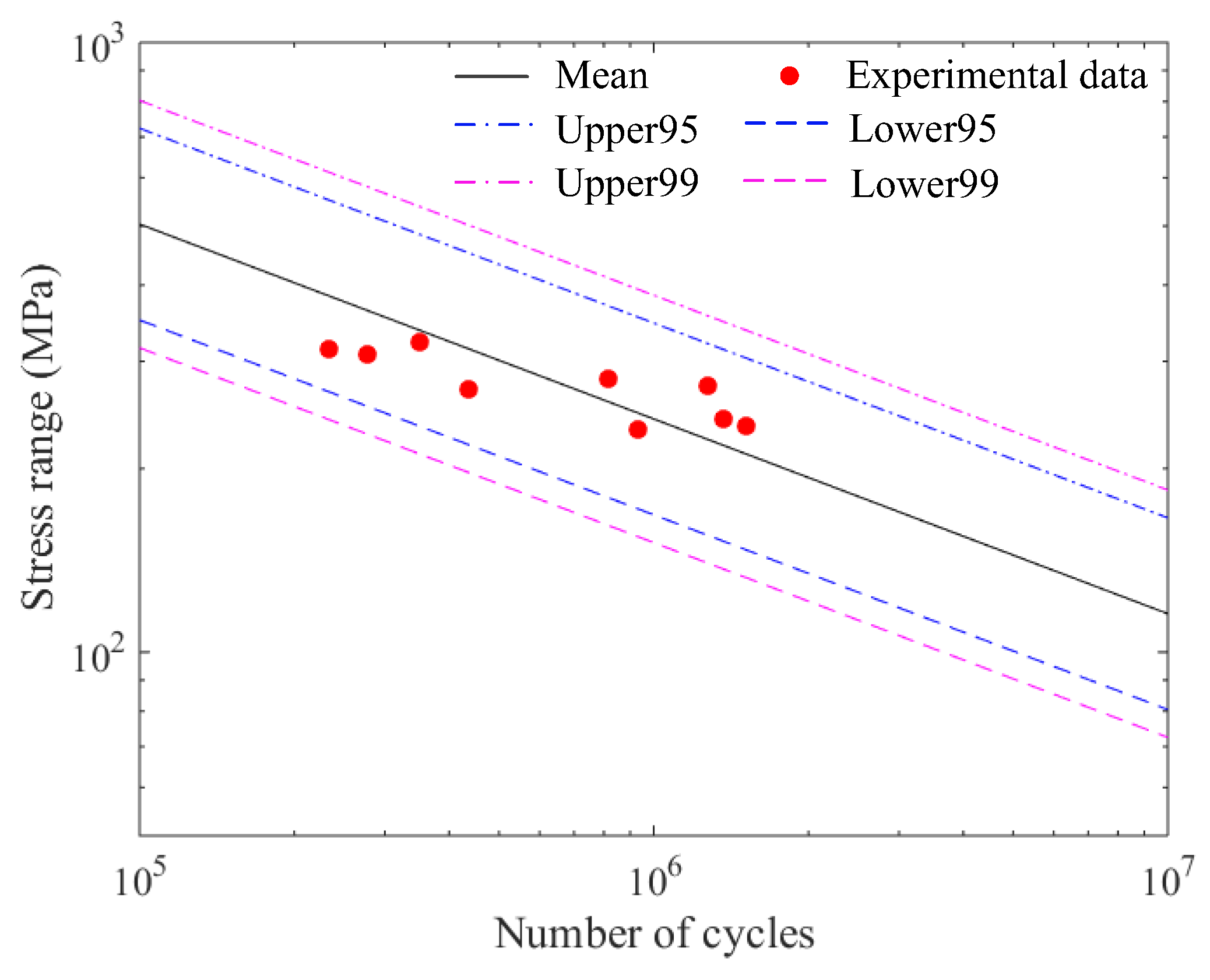
Figure 13 shows the experimental verification of the master S-N curve for the OSD based on the stress integration approach. The equation of the master S-N curve is shown in Equation (10). In
Figure 13, the vertical coordinate is the equivalent structural stress range
, and the dots are the experiment data of the equivalent structural stress range in
Table 1.
Figure 13 shows that the experimental data points are around the mean S-N curve, and all the experiment data points are within the 95% survival rate master S-N curves. Therefore, the master S-N curve with the lower 95% survival rate can be used for the fatigue evaluation of the deck-rib welding details in the OSD under a non-high cycle (
), as shown in Equation (10), where
.
6. Influence of Weld Parameters on the Fatigue Life of Deck-Rib Welding Details in the OSD
6.1. Influence of Weld Size on the Bridge Fatigue Life
Figure 19 shows the measurement of deck-rib weld sizes in the experiment. In
Figure 19,
and
are the three sides of the weld triangle. The measured weld sizes are listed in
Table 5.
and
are the three angles calculated by
and
, as shown in
Figure 16. The mean, minimum and maximum values of the weld size are shown in
Table 6.
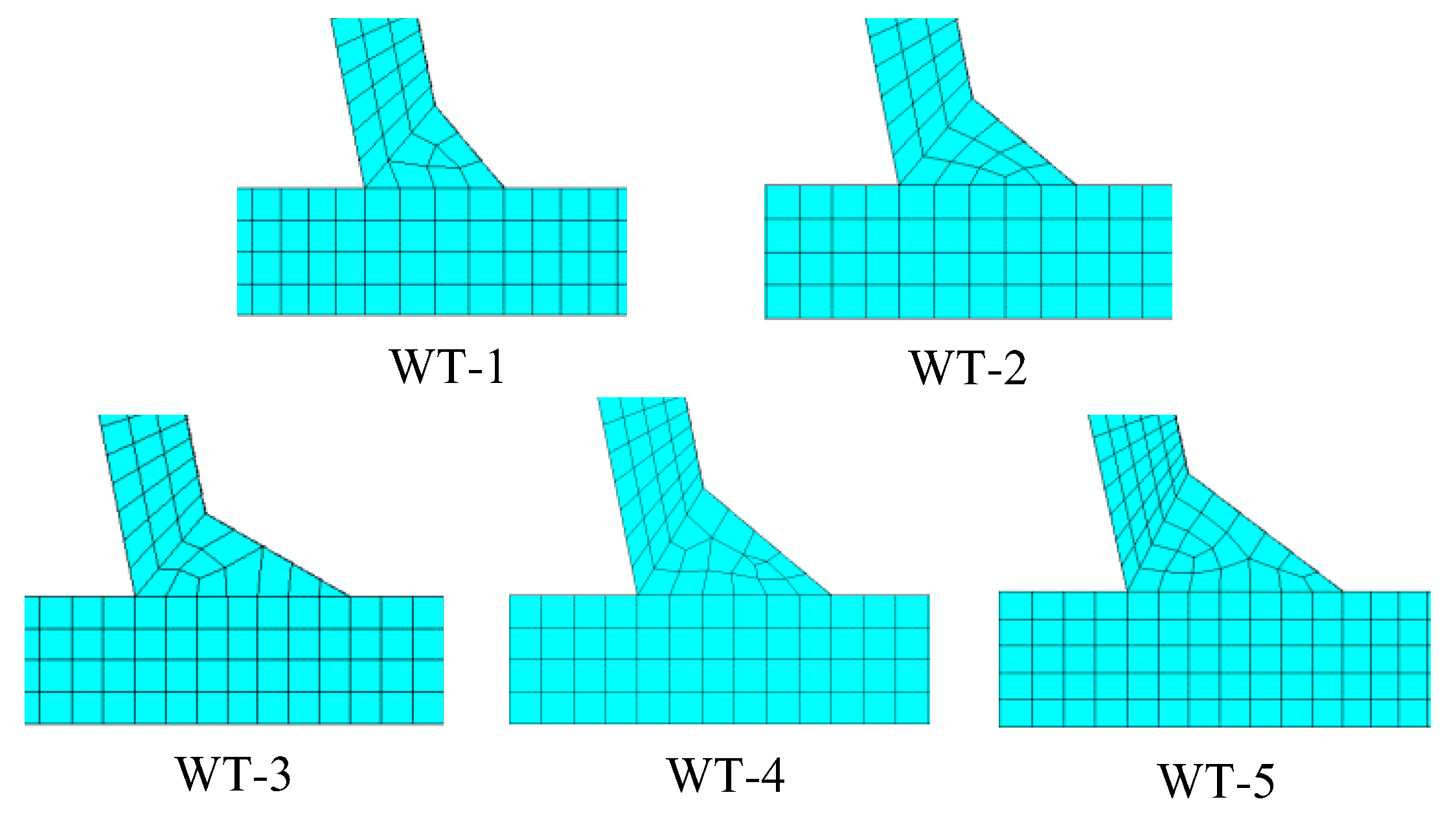
Since the measured actual weld size is discrete, which is mainly caused by weld manufacturing errors, five representative weld types (WTs) were selected in the present study, as shown in
Figure 20 and
Table 7. In
Table 7: (1) The angle
remains at 100 degrees. The size of weld type 4 (WT-4) is close to the mean value in
Table 6. The length
of WT-1 and WT-5 are close to the minimum value and maximum value in
Table 6, respectively, and the rest of the values are within the extreme range. (2) A comparison of WT-1, WT-2 and WT-3 shows that the length
increases successively when the length
remains unchanged. That is, the angle
between the deck and rib decreases by 10 degrees successively. (3) A comparison of WT-2, WT-4 and WT-5 shows that the weld angles remain the same, and the length of three sides increases by an equal proportion of 25% successively. That is, the weld area increases by 56% successively. (4) The length
of WT-5 is approximately equal to that of WT-3, and the length of
is extended by 56%.
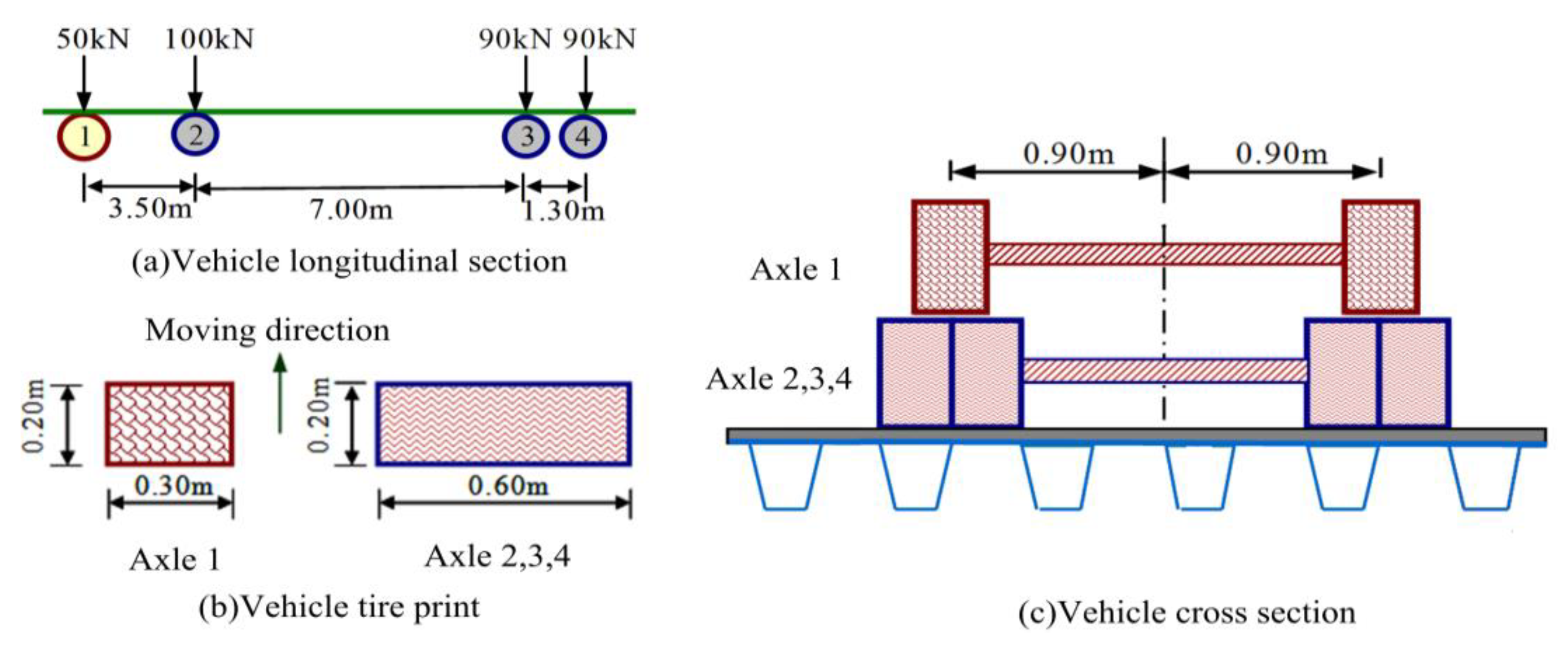
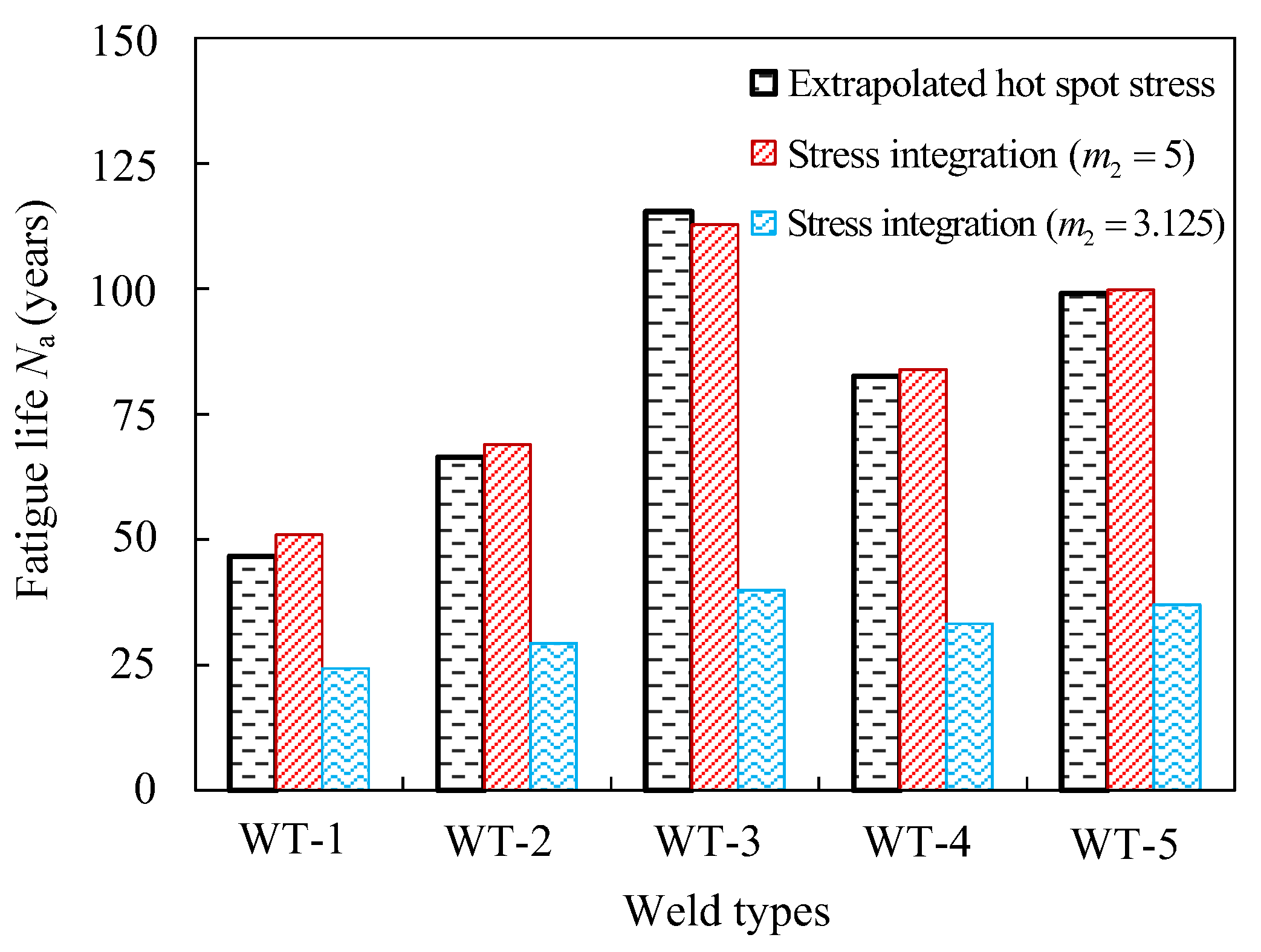
Figure 21 shows the variation of fatigue life with the weld size under the standard vehicle load in
Figure 15. In
Figure 21,
is the slope of the master S-N curve at high cycles
using the stress integration approach. The fatigue life calculation steps are shown in
Section 5.4, and the fatigue life of WT-4 is shown in
Table 4.
(1) The fatigue life of the stress integration approach with slope is close to that of the extrapolated hot spot stress approach. However, the fatigue life with slope is less than half that of the extrapolated hot spot stress approach. Therefore, the slope of the master S-N curve at high cycles significantly affects the bridge fatigue life, and the slope is more reasonable.
(2) The fatigue lives of WT-1, WT-2, WT-3, WT-4 and WT-5 are approximately 51 years, 69 years, 113 years, 84 years and 100 years, respectively, and only reach approximately 100 years under a standard vehicle load. Thus, the change of the weld size can obviously affect the bridge fatigue life. The fatigue life of the most favorable condition, WT-3, is 2.2 times that of the most unfavorable, WT-1.
(3) The comparison of WT-1, WT-2 and WT-3 shows that the fatigue life increases obviously with the decrease of the angle between the weld and the deck. The fatigue life increases by approximately 50% with the decrease of angle by 10 degrees.
(4) The comparison of WT-2, WT-4 and WT-5 shows that when the weld angles remain the same, the fatigue life increases with the increase of the weld area. The fatigue life increases by approximately 20% with the weld area increasing by 56% (or the length of three sides increasing by 25% with the same proportions).
(5) The comparison of WT-3 and WT-5 shows that the fatigue life decreases with the increase of , when the length of is approximately equal. The fatigue life decreases by approximately 12% with the increase of , by 56%. Although the weld area increases in this case, the fatigue life decreases due to the increased angle between the deck and the weld.
(6) Therefore, the change of weld size caused by weld manufacturing errors can obviously affect the actual bridge fatigue life. The fatigue life of five different weld types varies from 51 years to 113 years under a standard vehicle load. The weld fatigue life increases with the decrease of the angle between the deck and the rib and the increase of the weld area. The most favorable weld type is WT-3, with the angle of 30 degrees and the area of 48 mm2.
6.2. Grinding Treatment
It can be seen from the results in the previous section that the decrease of the angle between the deck and the weld can significantly improve the fatigue life of the deck-rib welding details. The reason is that the stress concentration at the weld toe decreases with the decrease of the angle between the weld and the deck. For the same reason, grinding treatment can also reduce the stress concentration at the weld by smoothing the transition between the deck and the weld.
6.2.1. Influence of Grinding Types
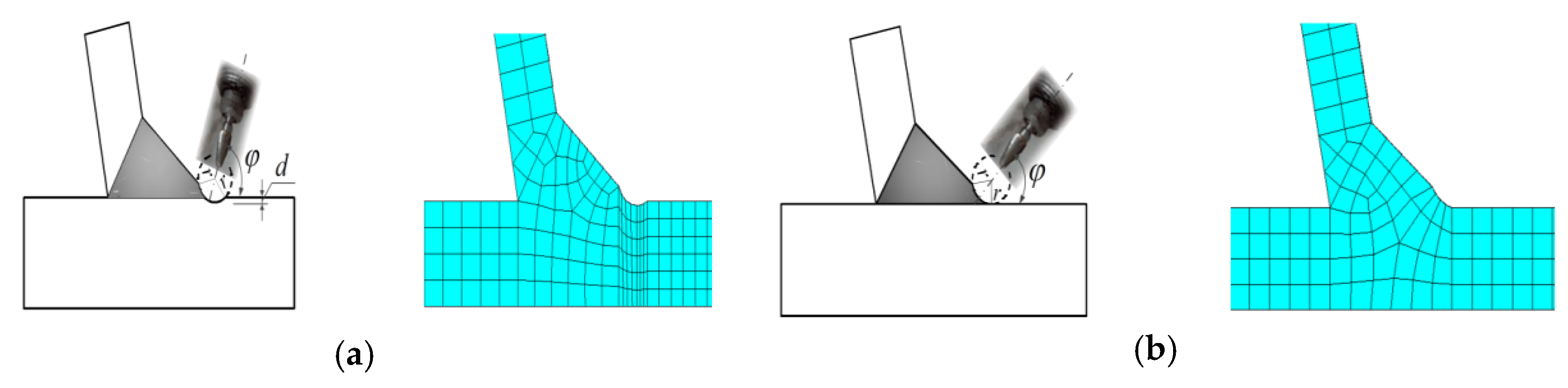
The two grinding types and their FEMs are shown in
Figure 22. In
Figure 22, the parameters
,
and
are the grinding radius, grinding depth, and the angle between the axial direction of the grinder head and the deck, respectively. These parameters for two grinding types are shown in
Table 8. The grinding radius
r and depth of grinding type 1 (GT1) are 3 mm and 0.5 mm, respectively, and the grinding arc intersects with the deck [
34]. The grinding type 2 (GT2) is a new grinding type proposed in the present study. The grinding radius
is also 3 mm and the grinding depth
is 0. that is, the grinding arc is tangent to the deck without weakening the deck. In the grinding treatment process, the main difference between GT2 and GT1 is the angle
between the axial direction of the grinder head and the deck. Nonetheless, how to accurately control the angle is a key issue to be considered in the experiment design. A comparison of different grinding types is shown in
Table 8.
Table 8 shows the comparison of different grinding types. For GT1, the equivalent structural stress
increases by 5.75% and the fatigue life
decreases by 25% compared with the non-grinding type. For GT2, the equivalent structural stress
decreases by 1.88% and the fatigue life
increases by 10% compared with the non-grinding type. Since GT2 can reduce the stress concentration at the weld toe without weakening the deck section, it is more conducive to improving the fatigue life of the weld.
6.2.2. Influence of Grinding Radius
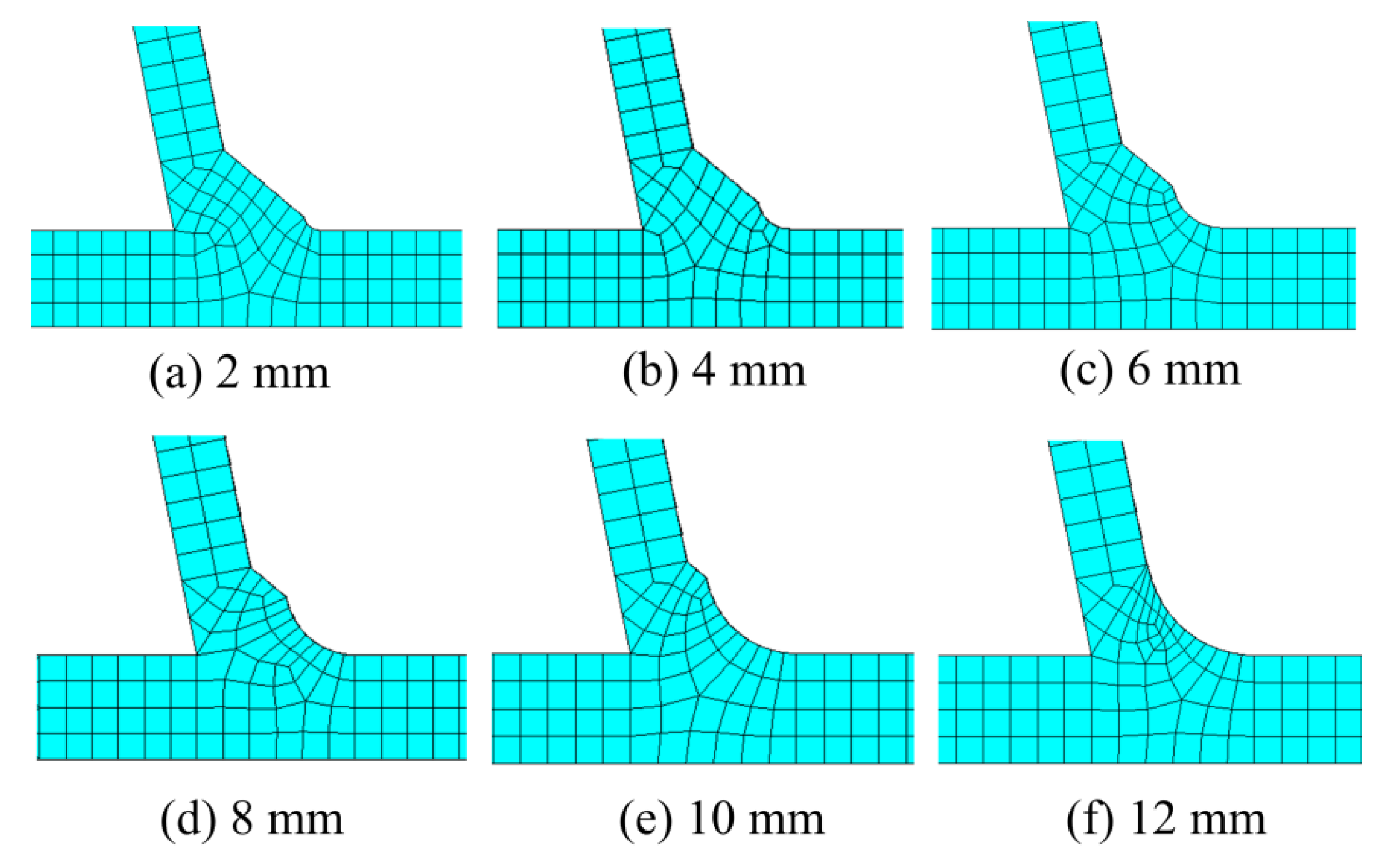
Figure 23 shows the finite element models with different grinding radii of GT2 under WT-4. In
Figure 23, 12 mm is the maximum grinding radius to ensure that both the deck and the rib are not weakened. For WT-1, WT-2, WT-3, WT-4 and WT-5, the maximum grinding radius is 6 mm, 8 mm, 14 mm, 12 mm and 14 mm, respectively. After the grinding treatment, all the welds meet the requirements in the code that the height of the weld throat is not less than the thickness of the rib [
38].
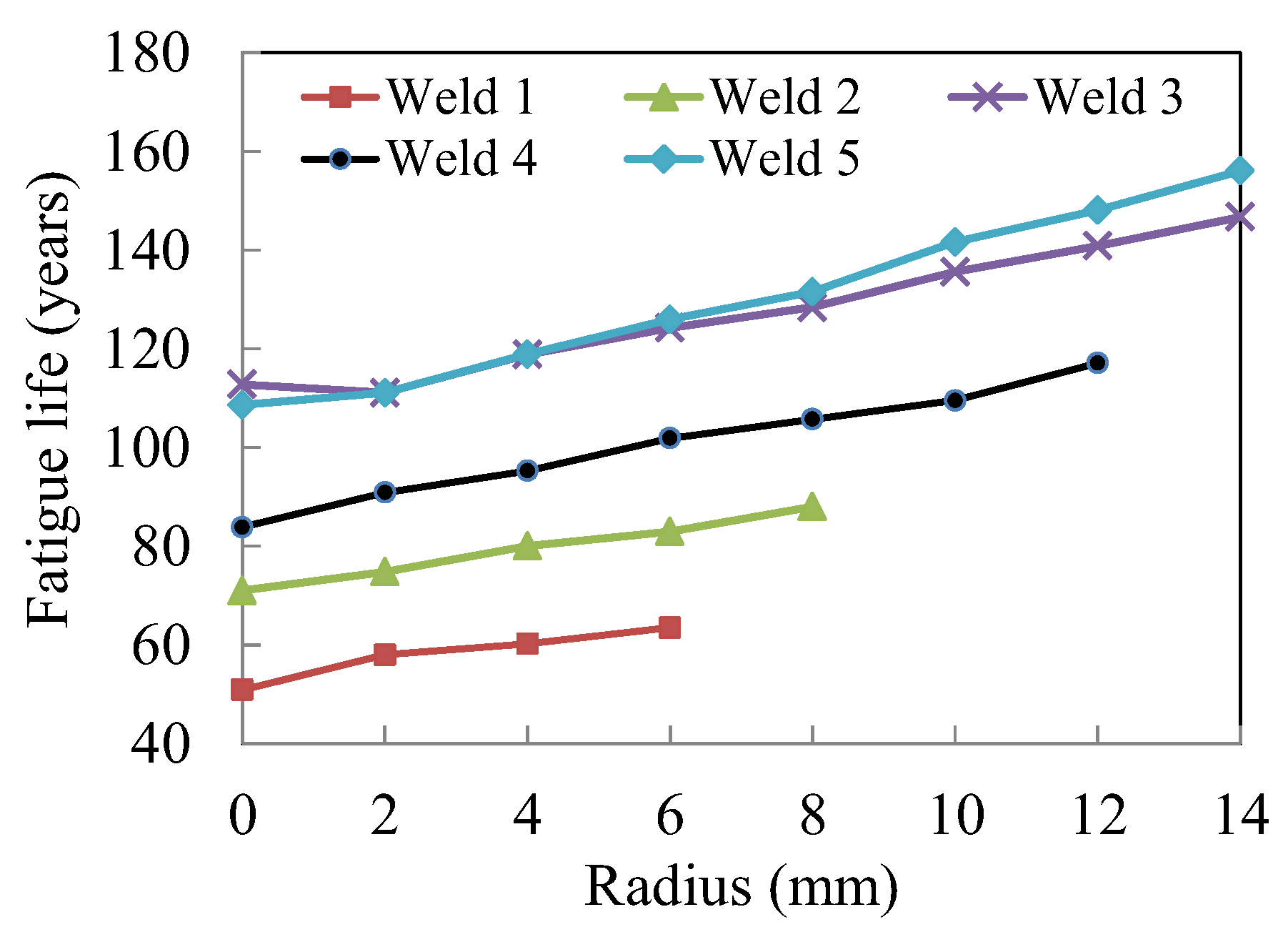
According to the fatigue life calculation steps in
Section 5.4, the variation of the fatigue life with the grinding radius for GT2 under different weld types is shown in
Figure 24. In this figure:
(1) A comparison of WT-1, WT-2 and WT-3 shows that when the grinding radius changes from 0 to 2 mm, the fatigue life of WT-1, WT-2 and WT-3 increases by 14%, 5% and −1.5%, respectively. This indicates that the grinding treatment has an obvious effect on increasing fatigue life when the angle between the deck and the weld is large.
(2) When the grinding radius is greater than 2 mm, the curves of the fatigue life as they vary with the grinding radius under different weld types are almost parallel, which indicates that when the grinding radius is large, the influence of the grinding radius on the fatigue life has little relation to the weld type.
(3) For different weld types, when the grinding radius is greater than 2 mm, the fatigue life at the weld toe increases with the increase of the grinding radius. The fatigue life increases by approximately 5% when the grinding radius increases by 2 mm.
(4) A larger grinding radius is conducive to improving the bridge fatigue life, but at the same time, it can increase the weakening of the weld seam itself, which may lead to cracks in the weld throat. Therefore, further experimental research is needed to select an appropriate grinding radius which both ensures fatigue cracks do not appear in the weld throat and maximizes the fatigue life at the weld toe.
6.3. Influence of the Weld Penetration Rate
The penetration rate of the deck-rib welding details shall not be lower than 80% in the code [
8]. To study the influence of the weld penetration rate on the bridge fatigue life, a FEM of 80% partial penetration and 100% full penetration for WT-4 are shown in
Figure 25. According to the fatigue life calculation steps in
Section 5.4, the structural stress and fatigue life of 80% partial penetration and 100% full penetration at the weld toe were calculated, as shown in
Table 9. Compared with 100% full penetration, the structural stress
and equivalent structural stress
of the weld toe under 80% partial penetration were reduced by approximately 1.3%, and the fatigue life
increased by approximately 5.6%. Therefore, the fatigue life of 80% partial penetration is slightly higher than that of 100% full penetration.