3. Background
Deduction in classical mathematical statistics is based on random samples drawn from a given population. In an alternative approach, derived from the Bayes’ theorem [
5,
6,
7,
8,
9], deduction can be based not only on a random sample, but also on a priori information. The
a posteriori information is generated from these two sets of data. A priori knowledge may refer to expert knowledge, deriving from earlier investigations whose results are known, but not for the entire dataset. The character of knowledge does not allow us to take advantage of it in the classical approach. Therefore, the Bayesian approach should be used. If the same data can be used in both cases, classical and Bayesian analysis would give similar conclusions. In its most basic form, the Bayes theorem presents the dependence of the conditional probability of event
A on condition
B and the conditional probabilities of event
B on condition
A, provided that event
A is completed and the probability of event
A and its complement, which can be expressed in the following form:
. The formula above is generalized to a situation in which the occurrence of many mutually exclusive events is considered, and not as in the given relationship between only event
A and its complement:
. Here,
f(θ) means a function of the
a priori probability density of parameter
θ, while
f(x|θ) is a function of reliability, i.e., a function of the density of the conditional observation result at a given value of
θ. The symbol
Ω used under the integral indicates a set of possible values of the estimated parameter
θ. To the left of the formula is the density function of the
a posteriori probability of the parameter
θ, after observing the result of the sample x. Thus, based on Bayes’ theorem, the function of the a priori probability density of parameter
θ is updated, using information from the sample. The population parameters to be estimated, e.g., parameter
θ (for example mean, standard deviation, specified type element fraction) are treated differently in the two cases. In the classical approach, parameter values are specific but remain unknown. In the Bayesian analysis, they are treated as random variables.
For random variables with a continuous probability distribution, Bayes’ theorem may be presented as follows:
f(θ|x)—a posteriori density function of parameter θ, after sample result x has been observed
f(θ)—a priori distribution density function of parameter θ;
Ω—set of possible values of parameter θ.
Therefore, based on Bayes’ theorem, the a priori density function of parameter θ is updated with the use of information from the sample.
In the present paper, Bayesian analysis has been adopted for a case, in which the unknown distribution of parameter
θ is to be estimated, and
θ is the mean in a normal population. The population standard deviation
σ0 is known. It is derived from a priori knowledge that the mean
θ is a normal random variable with parameters
m1 and
σ1. If, in turn, the average of an
n-element sample drawn from the population is equal to
m2, the
a posteriori distribution of the random variable
θ is also normal, with the mean
m and standard deviation
σ, calculated as follows:
The presented Bayes’ theorem gives a valuable practical possibility of the successive inclusion of new information coming from consecutively drawn random samples. During a consecutive step, knowledge about the posterior distribution of parameter θ is treated as a priori knowledge of this parameter. Including new portions of information does not affect the final result.
When the probability distribution of the examined parameter is estimated, a credible set of the parameter can be constructed. The credible set (the highest posterior density set) is an interval, to which the value of the parameter drops with a defined probability. This is the analog of a confidence interval concept that is used in classical statistical analysis. The confidence interval predicts the unknown value of the parameter with an assumed probability.
The selection of parameters requires careful and cautious use of statistical analysis, including the use of the Bayesian approach. In Bayesian statistical analysis, results of research from the soil of the analyzed sites were subsequently included. In the calculations, it was stated that the final result is independent of the order of the objects. In addition, the mean values of the unit weight of organic soils, Pliocene clays, and boulder clays are the same in the case of classical analysis and the Bayesian approach.
Bayesian analysis (i.e., Equations (1)–(3)) is performed in order to provide an a posteriori probability distribution function for model parameters, the most likely thickness of layers of the soil, and its unit weight. Here, the asymptotic technique is used to estimate the posterior model parameters. The asymptotic technique includes an approximation of the
a posteriori probability function as a Gaussian probability distribution function (PDF), and the
a posteriori probability distribution function for model parameters is a combined Gaussian probability distribution function with a mean value equal to the most probable posterior probability distribution function [
10]. The asymptotic technique was successfully used in previous studies to interpret the undrained shear strength of mineral and organic soils from DMT tests.
In the Bayesian approach, some preliminary knowledge about the distribution of parameter values is modified after confronting the data. Using the a priori distribution and knowledge about the sample taken, a new parameter distribution is determined, which takes into account both the original a priori beliefs and the empirical data obtained. An important characteristic of the Bayesian approach is that the sequential modification of knowledge about the distribution of the tested parameter gives the same result as in the case, when all doses of information are included in the conclusion at once—that is, if successively taken samples are treated as one larger sample. It also implies that the order of attaching new portions of information is arbitrary. Therefore, a question should be answered: When is the Bayesian approach worth applying in practice—that is, when will the classical approach not give better results? The classical approach will not give better results when the a priori information is only in the form of results of the analyses, but the tests on the basis of which these analyses were made are no longer available (therefore, it is impossible to extend the data sample based on which the inference is made in the classic way).
The application of statistical analysis of the test results in geotechnical design by the Bayesian approach allows for taking into account the influence of the distance of the test site from the designed object.
Previous statistical methods mostly using the least squares estimation, used data from field and laboratory studies as a closed number of random variables to determine the expected values, variances, and correlations for a given expression as a function of the random variable. The main disadvantage of the least squares method used to estimate the parameters is the difficulty in the representation of knowledge about the expected values of parameters, which should result from the estimation process. There has been significant progress in parameter estimation, as shown by increasingly numerous examples of applications in various fields, such as Bayesian analysis, in which a set of test results may be increased by new data—and on this basis, the probability of occurrence may be determined.
Bayesian approaches were used in the analysis presented in this paper. A total of 56 samples with an undisturbed structure were used for determining the unit weight test results, and the corresponding DMT measurements were taken into account. In laboratory tests, soil samples taken with thin “Shelby”-type samplers with dimensions of Ø 88.9 mm were used. In the laboratory, specimen samples for oedometer and triaxial test measurements with dimensions of 50 mm × 100 mm were cut out of soils with a non-disturbed structure taken with the SHELBY cylinder. Combining the measurement of soil unit weight with the structure of the sample—85 mm × 15 mm, h = 50 mm—the unit weight of the natural soil was calculated. Results of the DMT test, which allowed to determine the p0 and p1 values, were compared with results obtained from laboratory tests of the selected samples, obtaining a mean square relative deviation (MRSD) below 10%. Based on the collected results both from laboratory and dilatometer tests (DMT) examinations, a data set was developed (a regional database and a general database) in the form of a table.
5. Previous Methods of Determining Soil Unit Weight
Soil total unit weight (γ
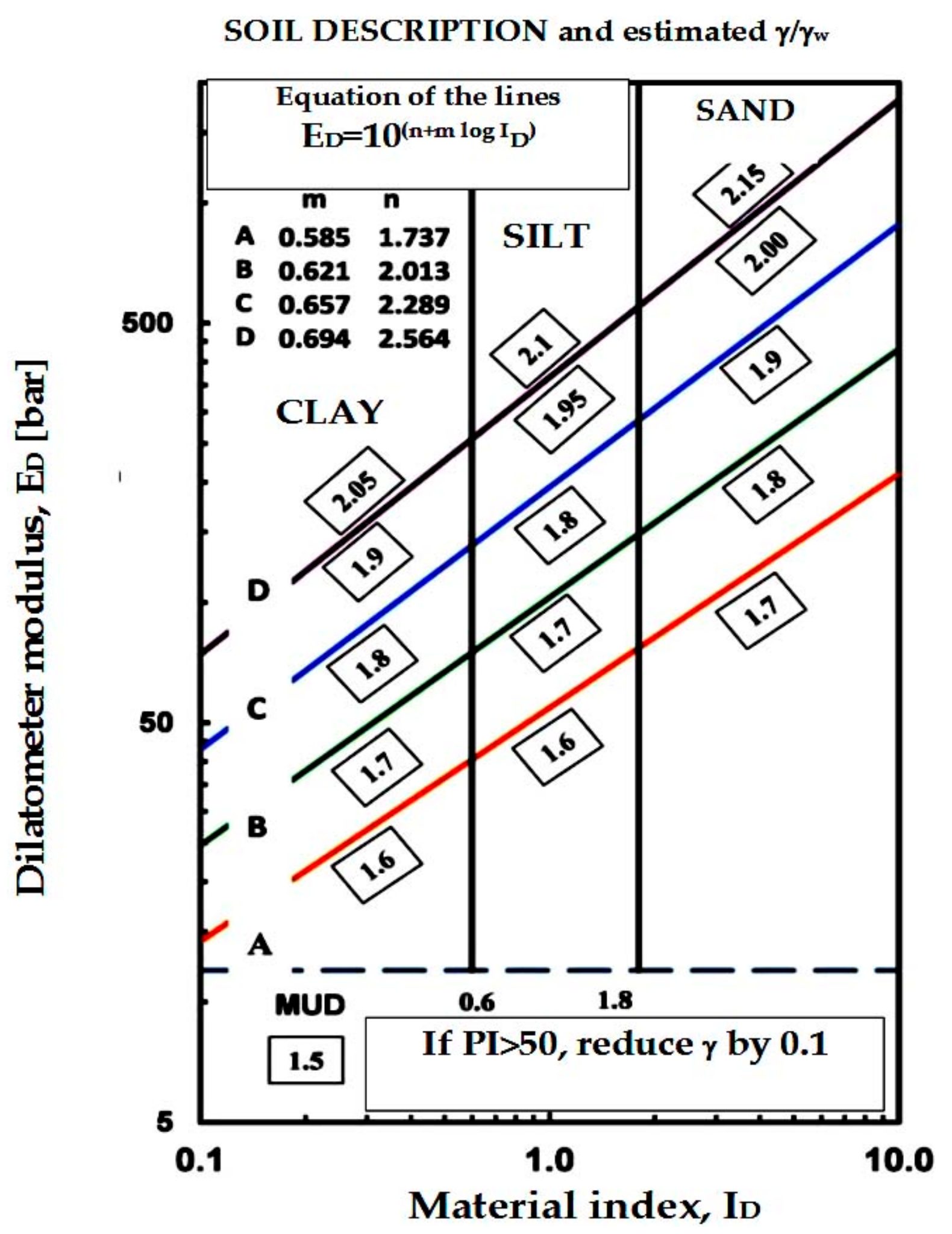
t) is classified as the basic physical characteristics of both mineral and organic soils. This feature is most often determined in laboratory tests. Recently, many formulas appeared in the literature to determine the soil total unit weight on the basis of in situ tests, e.g., cone penetration tests (CPTU) and DMT investigations. The article describes the dependencies between (γ
t) and parameters determined from dilatometer tests (DMT). Although so far no database for (γ
t) has been presented, Marchetti and Crapps [
25] have suggested that it should be estimated according to the
ID and
ED values (
Figure 1).
Similarly, a relationship was developed for the results of DMT tests to assess the soil total unit weight. These dependencies are presented in Equation (8) [
26,
27]:
where: ρ = (γ
T/(γ
w), and σ
atm =100 kPa is atmospheric pressure.
So far, attempts have been made to estimate the soil unit weight based on DMT tests for selected types of mineral soils [
28,
29] or to develop new dependencies between the total unit weight and DMT indexes [
30]. These studies focused mainly on natural clays with a soft or hard consistency. These soils are homogeneous, which is often associated with high groundwater level.
Ozer et al. [
30,
31] proposed a correlation to estimate the total unit weight in terms of
p1 pressure from DMT. This model provides a fairly accurate prediction of laboratory results for soft to medium compact clays from the “Lake Bonneville” valley. The formula is as follows:
Ouyang and Mayne [
32] found that there is a relationship between soil total unit weight (
γt), contact pressure (
p0), and depth (
z) for clays in the range from normally consolidated (NC) to lightly preconsolidated (LOC), with soft to hard consistency. The newly defined slope parameter (
mp0 =
Δp0/
Δz) with a forced intersection equal to 0 has been set for homogeneous inorganic clays. It was found to be related with soil unit weight, as expressed by the following formulas in Equations (11) and (12):
where:
The cited authors have stated that in the case of inorganic clays, these formulas (Equations (11) and (12)) do not give adequate results for OL (Organic Low liquid limit) or OH (Organic High liquid limit) soils, or soils with a significant organic content. The values are based on data obtained mainly from inorganic and non-sensitive clays.
6. Geotechnical Conditions of the Test Sites
This paper includes the test results of mineral and organic subsoils obtained from the Antoniny, Koszyce, and Mielimąka sites located in the Noteć river valley in the Wielkopolska province, the Nielisz site located in the Wieprz river valley in the Lublin province, and the SGGW Campus and Stegny sites located in Warsaw, where the Department of Geotechnical Engineering SGGW is located, and where a laboratory and field testing program has been carried out under and outside of the main dam embankment [
33,
34] (
Figure 2). The grain-size distribution curve obtained from laboratory tests for mineral soils from these sites is presented in
Table 1 (
Figure 3). All the test sites are located in Poland.
This paper presents the test results of mineral and organic subsoils obtained from the following sites: Antoniny, Koszyce, Nielisz, Stegny and Warsaw University of Life Sciences (WULS)-SGGW Campus. The Antoniny test embankment was designed and performed in the frame of cooperation between the Department of Geotechnical Engineering SGGW and the
Swedish Geotechnical Institute (SGI). The physical properties of soil from the Antoniny site were determined during earlier WULS-SGGW tests [
33,
34,
35,
36]. The Koszyce test dam is located in the Ruda river valley. In the central part of the dam subsoil, a layer of soft organic soils was discovered. The organic soils are Quaternary deposits of an oxbow lake [
33,
34]. The Nielisz site is located in the Wieprz river valley in the Lublin province, the SGGW Campus site is located within the Department of Geotechnical Engineering SGGW, and the Stegny site is located in Warsaw, where a laboratory and field testing program was performed under and outside the main dam embankment [
34,
35]. The area of the SGGW campus is located in the southern part of Warsaw in the Ursynów commune. It is limited by: the Nowoursynowska street 166 from the north-east, Ciszewskiego street from the south-west, Rosoła street from the south-east, and the area of forts, behind which the Służewiecka valley runs, from the north-east. At a distance of about 700 m from the plot, toward the north-east, runs the edge of the Vistula escarpment (nature protection area). At a distance of about 700 m to the south-west runs Warsaw Metro I line [
37]. The “Stegna” experimental field was founded by an academic center, following two research projects of the Scientific Research Committee implemented by the Department of Engineering Geology of the University of Warsaw and the Department of Geoengineering SGGW at the Warsaw University of Life Sciences. It is located in the southern part of the city of Warsaw, in the Mokotów district, at the Stegny housing estate. The soils that are subject to the presented research are Mio-Pliocene clays, belonging to the Poznań Formation. The location of all analyzed objects is shown in
Figure 2. The index properties of mineral and organic soils and the grain size distribution curve obtained from laboratory tests for mineral soils from the described sites are presented in
Table 1 and
Figure 3.
Table 2 was compiled based on the results obtained from the analysis of well profiles and dilatometer tests. It contains data used to compare the unit weight of mineral and organic soils obtained from laboratory tests based on DMT results from the Antoniny, Koszyce, Nielisz, Stegny and WULS-SGGW campus sites. Data of dilatometer test readings (DMT), effective vertical stresses
σvo, water pressure
uo, and soil unit weight (
γ) from laboratory tests were collected for each study site. Individual soil fractions (
fclay,
fsilt and
fsand) and corresponding pressures from the dilatometer, such as pressures (
p0,
p1) and dilatometer indexes (
ID,
KD and
ED), were also collected. The preconsolidation ratio (
OCR) of these soils generally ranged from 1 to 3 across most of the subsoil profile. Groundwater levels are generally high in organic soils (organic muds, peat, and gyttja), usually at the depth of 0.2 to 2 or 3 m.
The scope of soil laboratory tests (physical properties of samples) in the analyzed sites included: grain-size analysis (sieve and areometric methods) and determination of soil unit weight (soil density for undisturbed samples, unit weight of soil skeleton, and soil skeleton specific density). The results of the laboratory tests of soil physical properties are presented in
Table 2. The laboratory tests were carried out in accordance with the PN-88/B-04481 standard for building soils. The soil samples, types, and geotechnical conditions were determined in accordance with the PN-86/B-02480 [
38] standard for building soils. The terms, symbols, subdivision, and description of the soils were made in accordance with ASTM D 2487-93 [
39].
7. New Ways of Determining the Unit Weight of Mineral and Organic Soils Using the Marchetti Dilatometer (DMT)
The next task was to search for a direct correlation between the results of laboratory tests of soil unit weight and DMT test results for mineral (sand, silt, and clay) and organic soils (peat, organic mud, and gyttja) in the range of stresses from normally consolidated (NC) to heavy preconsolidated (HOC). The basic impulse of searching for a new form of dependence to determine soil unit weight based on DMT readings was to extend the range of soil types, including organic soils. Therefore, a comprehensive series of multiple regression analyses was performed, using both arithmetic and logarithmic scaling. A full set of regression attempts was not included here, because they were too large for the discussion. Analysis of dilatometer pressure readings showed that parameters p0 (kPa), p1 (kPa), and u0 (kPa), and atmospheric pressure σatm = 100 kPa are sufficient to obtain a reasonable estimate of γ; thus, they do not need to be based on DMT indexes such as ID, KD, or ED, without loss of statistical significance. The obtained statistical parameters are (n = 1021, R2 = 0.69, S.E.Y. (Standard Error of the dependent variable) = 0.1011).
Analysis of the data presented in
Figure 3,
Table 2 showed that for soils such as peat, gyttja, silty clay, and Pliocene clay, some soil unit weight characteristics of the tested soils may differ from linear equations. On the other hand, with virgin subsoil, soil unit weight values did not differ between sites, and can be predicted by a generalized non-linear equation. Based on the analysis of the soil unit weight characteristics presented in
Figure 3 and
Table 2, to describe non-linear changes in coefficients (
ki),
i = 1, 2, and 3 (
Table 3) for a suitable soil as a function of dilatometer pressure
p0,
p1, water unit weight (
γw), pore water pressure (
u0), and atmospheric pressure
σatm = 100 kPa, a non-linear model was adopted, i.e., a power equation (Equation (13)).
Linking dilatometer pressures
p0 (kPa) and
p1 (kPa), and the calculated values of pore water pressure
u0 (kPa) and atmospheric pressure
σatm = 100 (kPa), as well as multiple regression analysis combined with the results of unit weight
γ correlate well with data obtained from laboratory tests based on the following formula (
Table 2):
where:
p0,
p1, and γ
w are expressed in kN/m
3,
u0 is expressed in kPa, and
σatm = 100 kPa.
8. Bayes’ Approach in the Interpretation of Test Results from the Proposed Formula
Statistical analysis has been applied on the measurement results obtained from the DMT field tests [
40,
41]. Additionally,
p0 and
p1 pressures were measured. For each of the indicators, there were 338 measurement results (in 30 screenings) in the peat, gyttja, and organic mud layers, and 683 results (in 65 tests) in the sand, clayey silt, and Pliocene clay layers. The measurement results can be treated as observations of continuous random variables with specific probability distributions. For each profile, there were from 8 to 22 DMT test results in the peat, gyttja, and organic mud layers, and from 45 to 65 DMT test results in the sand, clayey silt, and Pliocene clay layers.
The investigator is obliged to check if the profiles of every layer can be examined together—in other words, if the layers have been distinguished correctly. If new measurement results are included to the calculations according to Bayes’ law and full data about previously examined samples are not available (thus, the standard statistical approach is not applicable), the only thing that can be done is to test each new sample independently. The type of probability distribution has been checked by the Shapiro–Wilk tests, which are applicable to small samples. For the majority of the tests, the null hypothesis that the samples come from a normally distributed population has not been rejected [
5]. No other type of probability distribution has been found. On the other hand, the assumption of the normal distribution of all random variables under investigation is reasonable in accordance with the central limit theorem. Therefore, the formulas (Equations (1)–(3)) for every six (
p0,
p1 and
γ) group of tests have been applied. Since the population standard deviation
σ0 is unknown, it has been decided to use its estimator from the samples in the consecutive steps of formula application (Equations (1)–(3)).
The results of calculations are presented in
Table 4,
Table 5,
Table 6 and
Figure 4. Credible sets for the mean indicator
p0, calculated for the assumed probability 0.95 in the peat, gyttja, organic mud, clayey silt, Pliocene clay, and sand layers are as follows: (176.04; 179.16 MPa), (561.94; 568.46 MPa), and (299.54; 313.06 MPa), respectively. Additionally, for comparison, estimators of confidence intervals are presented in
Table 4,
Table 5 and
Table 6. In turn, the mean values of indicator
p1, calculated for the assumed probability 0.95 in the peat, gyttja, organic mud, clayey silt, Pliocene clay, and sand layers are as follows: (212.58; 217.02 MPa), (1479.58; 1498.42 MPa), and (1654.85; 1715.15 MPa), respectively. Additionally, for comparison, estimators of confidence intervals are presented in
Table 4,
Table 5 and
Table 6. The mean values of indicator
γ, calculated for the assumed probability 0.95 in the peat, gyttja, organic mud, clayey silt, Pliocene clay, and sand layers, are as follows: (13.43; 13.47 kN/m
3), (20.43; 20.45 kN/m
3), and (17.91; 17.99 kN/m
3), respectively.
Additionally, for comparison, estimators of confidence intervals are presented in
Table 4,
Table 5 and
Table 6. Normally, they cannot be calculated because of the lack of full information about previously tested samples. In our case, the calculations are feasible, because we only present one of the possible applications of Bayes’ law, and thus full data are available. Visible discrepancies between credible sets and confidence intervals probably derive from the incomplete fulfillment of the assumption of normality and also from the lack of full knowledge of standard deviation for the populations (it has been estimated on the basis of the samples).
Not all the parameters presented in
Table 2 have a normal distribution. For this purpose, a series of analyses of the normality test were carried out for
p0 (kPa),
p1 (kPa), and
u0 (kPa). The analysis consists of a two-step calculation [
42,
43,
44,
45,
46,
47]. The first stage is to check the normality test together for data from the Stegny and SGGW campus sites. The second stage is to make a separate statistical analysis for each site. The results of these analyses are presented in
Table 6 and in the correlation matrix drawing (
Figure 5 and
Figure 6). After the transformation of (stage 1:
p0 → log (
p0),
p1 → log (
p1),
u0 → log(
u0); stage 2:
p0 →
,
p1 →
,
u0 →
; stage 3:
p0 →
,
p1 →
) parameters, a normal distribution was obtained only in the case of log (
p0) and
(
Table 6,
Figure 5). The correlation for selected variables is presented in
Table 7 and
Figure 5, and
Figure 6 contains the matrix of extended charts for selected variables. The correlation coefficient determined is significant with
p < 0.05, N = 15
Unit weight, as a basic physical feature of soil, is an elementary quantity, and knowledge of this parameter is necessary in each geotechnical and geoengineering task. Estimation of this quantity can be made both with laboratory and field techniques. Particular care should be taken when determining the characteristics, in which the value of unit weight is of particular importance for the quantity to be determined. This is especially applicable to e.g., the dynamic shear modulus Gmax (or Go, Mo). In such cases, unit weight should be determined directly or from local correlations.
Before obtaining Equation (13), a number of statistical analyses were performed with individual factors. Finally, a series of calculations were carried out in the form:
A separate analysis (
) was carried out for each soil peat, gyttja (Gy), organic mud, mud, clayey sand (Sicl), boulder clay (Cl), and sand (Sa, CSa, MSa, FSa). Then, the normality of the Shapiro–Wilk method was checked for each type of soil. The results of this analysis are presented in
Figure 6. The results of the final stage are presented below:
This article does not assume that all variables are normal in the multiple regression analysis. The least squares method was used in Equation (13), which does not require the use of a normal distribution, but normality of the rest of the model is worth checking to verify the stability of the equation’s parameters. The purpose of this paper is not to give up, substitute, or criticize the best practice used in geotechnics; rather, it is only to supplement these tests where possible using the dilatometer of Marchetti (DMT).
Next, we continue the transformation process for formula (
). The following modification was introduced for:
p0 → log (p
0),
p1 → log (p
1),
u0 → log(u
0),
σatm → log(σ
atm) parameters. A separate analysis was carried out for each soil peat, gyttja (Gy), organic mud, mud, clayey sand (Sicl), for boulder clay (Cl),
u0 = 0 kPa, sand (Sa, CSa, MSa, FSa)). Then, the normality of the Shapiro–Wilk method was checked for each type of soil. A normal distribution was obtained after the transformation. The results of the analysis are presented in
Figure 7 and
Table 8 below.
Previous statistical methods using mostly the least squares estimation took data from field and laboratory studies as a closed number of random variables to determine the expected values, variances, and correlations for a given expression as a function of a random variable. The main disadvantage of the least squares method used to estimate the parameters is the difficulty in the representation of knowledge about the expected values of parameters, which should result from the estimation process. A significant progress in parameter estimation, as shown by increasingly numerous examples of applications in various fields, is the Bayesian analysis, in which a set of test results may be increased by new data, and on this basis, the probability of occurrence is determined. In order to determine the values of characteristic geotechnical parameters (
Xk), Schneider (1997) [
48] proposed a formula based on comparative calculations, proposing to use the following formula to select the characteristic value of geotechnical parameters (
Table 9):
, where:
Xm—mean value;
Sd—standard deviation.
Unit weight parameters were calculated for the soil found in each site. The calculation was based on the use of Marchetti’s patterns existing in the literature and on Marchetti’s nomogram, which has not changed since 1980. Based on the nomogram chart for soils with
ED < 1.2 MPa, soil unit weight less than 15.0 kN/m
3 was not determined. However, other formulas gave the possibility to determine this parameter (
γ) with a different result. The results obtained were compared with those from laboratory tests that may be considered as reference. Since the obtained results do not show adequate results consistent with the results of laboratory tests, both on the basis of Marchetti’s nomogram and literature models, there is a need for a new design. Very promising results have been obtained using the unit weight values proposed in this article (Equation (13)) for all soils (mineral and organic soils). The obtained results are presented in
Table 10.
The collected research material allowed the analysis of laboratory characteristics of soil unit weight and the development of non-linear empirical models, enabling forecasting its changes in the function of water unit weight (γw), pore water pressure (u0), and atmospheric pressure σatm = 100 kPa. In the non-linear model, an important parameter determining the shape of this relationship were dilatometer pressures p0, p1.
The non-linear model was developed in the paper. The basic premise that determined the construction of this model for soil unit weight (γ) was not a very precise determination of the value of the free expression by linear multiple regression models. The second reason for the development of non-linear changes in soil unit weight (γ) as a function of dilatometer pressure p0, p1, water unit weight (γw), pore water pressure (u0), and atmospheric pressure σatm = 100 kPa is the analysis of soil unit weight correlation for peat, gyttja, mud, organic mud, silty clay, and Pliocene clay, originating from the same soil profile, but taken from different sites.
The process of the presented measurement characteristics are illustrated against the background of the general linear trend equation resulting from the alignment of all measurement data of soil unit weight characteristics presented in
Figure 8 and the average value of soil unit weight determined by means of the dilatometer test. Linear alignment for both presented measurement relationships does not lead to the determination of the soil unit weight value with an appropriate level of accuracy.
The results obtained herein are satisfactory because when using the proposed equation (Equation (13)) to determine the soil unit weight of mineral and organic soils based on Marchetti’s dilatometer (DMT) from the analyzed sites, the performed analyses prove that 69% of results ((a): Antoniny; (b): Koszyce; (c): Nielisz; (d): Stegny; (e): SGGW Campus) of the soil unit weight are within the limit of the accepted error (mean square relative deviation: MRSD ≤ 6.0%). In addition, the percentage difference between the soil unit weight obtained in the laboratory and calculated from the proposed equation (Equation (13) was analyzed. In the case of the soil unit weight of peat, gyttja, and organic mud, the difference obtained in all the results was averagely only MRSD = 4.9%. In the case of the unit weight of Pliocene clay and clay, it was at MRSD = 5.6%, and of the sand, it was at MRSD = 6.0% (
Figure 8).