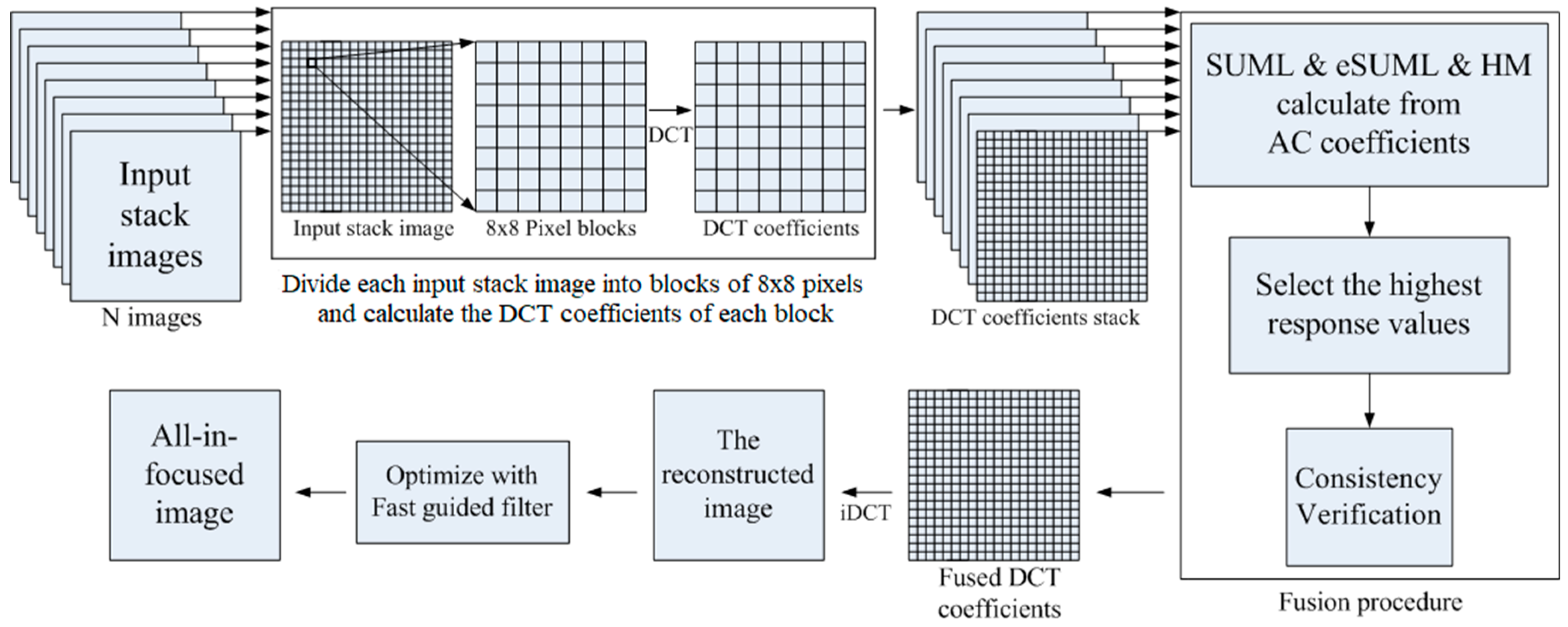
Figure 1.
The procedure of the proposed method.
Figure 1.
The procedure of the proposed method.
Figure 2.
Input images: (a–h) of different focal lengths.
Figure 2.
Input images: (a–h) of different focal lengths.
Figure 3.
The initial MAP(x, y) process.
Figure 3.
The initial MAP(x, y) process.
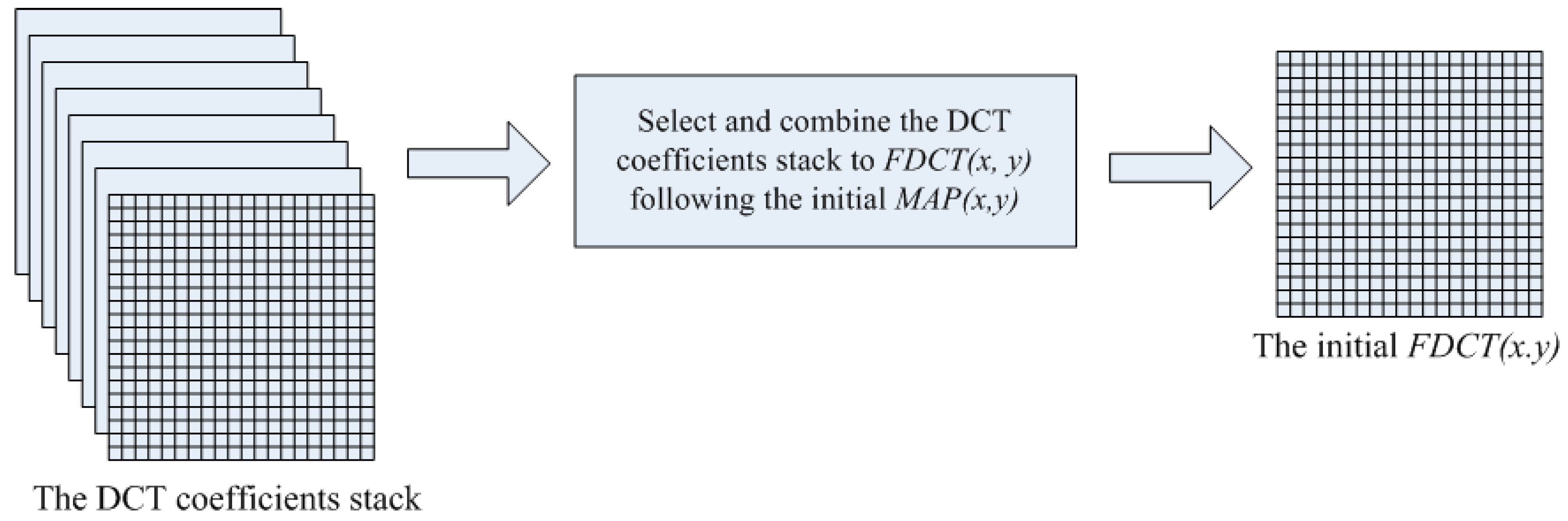
Figure 4.
The initial FDCT(x, y) process.
Figure 4.
The initial FDCT(x, y) process.
Figure 5.
Majority filter in consistency verification to improve MAP(x, y).
Figure 5.
Majority filter in consistency verification to improve MAP(x, y).
Figure 6.
The improved FDCT(x, y).
Figure 6.
The improved FDCT(x, y).
Figure 7.
In-focused regions of the different focal stack images using sum of modified Laplacian (SML) and SUML: ‘Bag’ dataset; (a) The input images of different focal lengths; (b) SML of stack images; and (c) SUML of stack images.
Figure 7.
In-focused regions of the different focal stack images using sum of modified Laplacian (SML) and SUML: ‘Bag’ dataset; (a) The input images of different focal lengths; (b) SML of stack images; and (c) SUML of stack images.
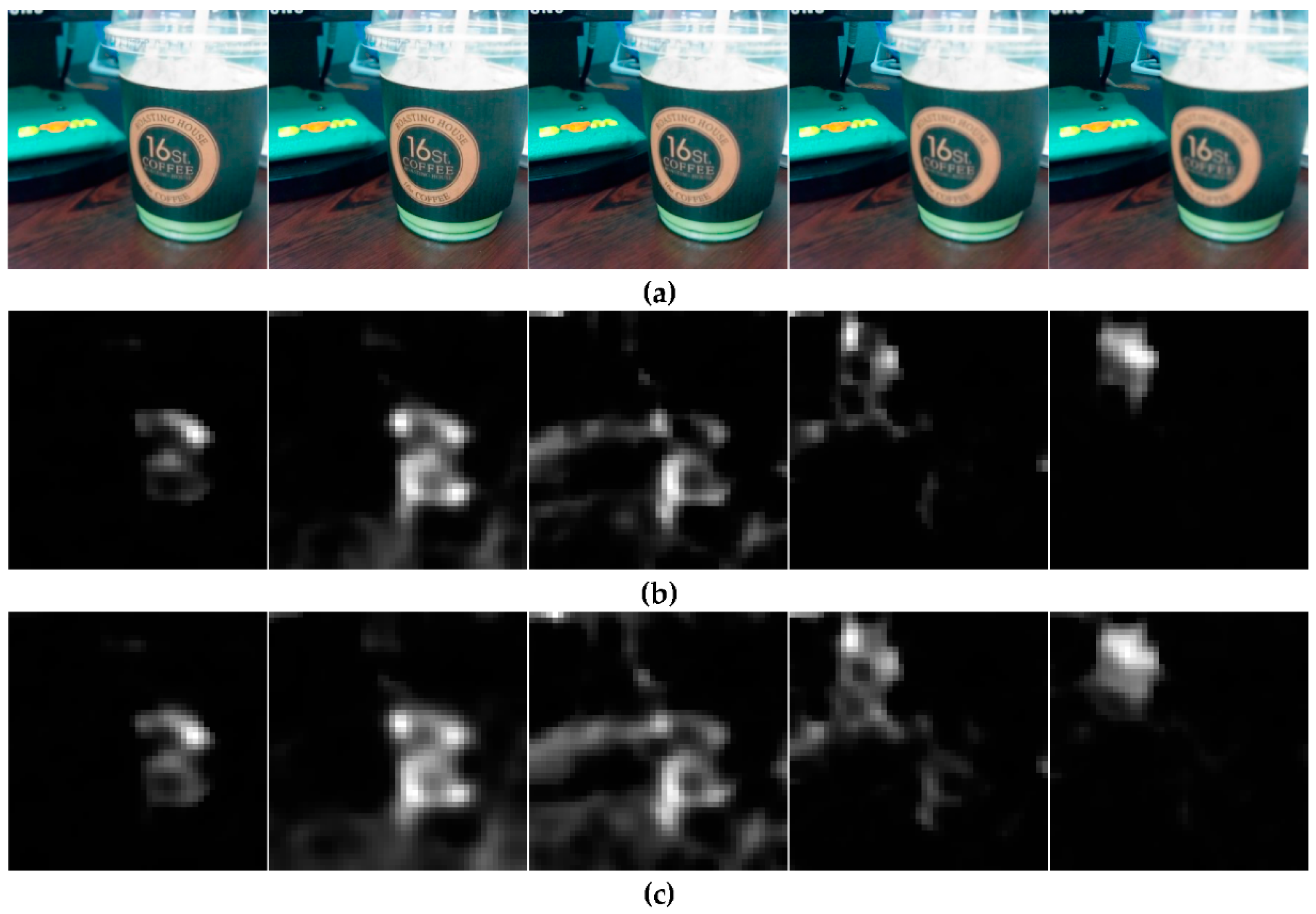
Figure 8.
In-focused regions of the different focal stack images using SML and SUML: ‘Cup’ dataset; (a) The input images of different focal lengths; (b) SML of stack images; and (c) SUML of stack images.
Figure 8.
In-focused regions of the different focal stack images using SML and SUML: ‘Cup’ dataset; (a) The input images of different focal lengths; (b) SML of stack images; and (c) SUML of stack images.
Figure 9.
In-focused regions of the different focal stack images using SML and SUML: ‘Bike’ dataset; (a) The input images of different focal lengths; (b) SML of stack images; and (c) SUML of stack images.
Figure 9.
In-focused regions of the different focal stack images using SML and SUML: ‘Bike’ dataset; (a) The input images of different focal lengths; (b) SML of stack images; and (c) SUML of stack images.
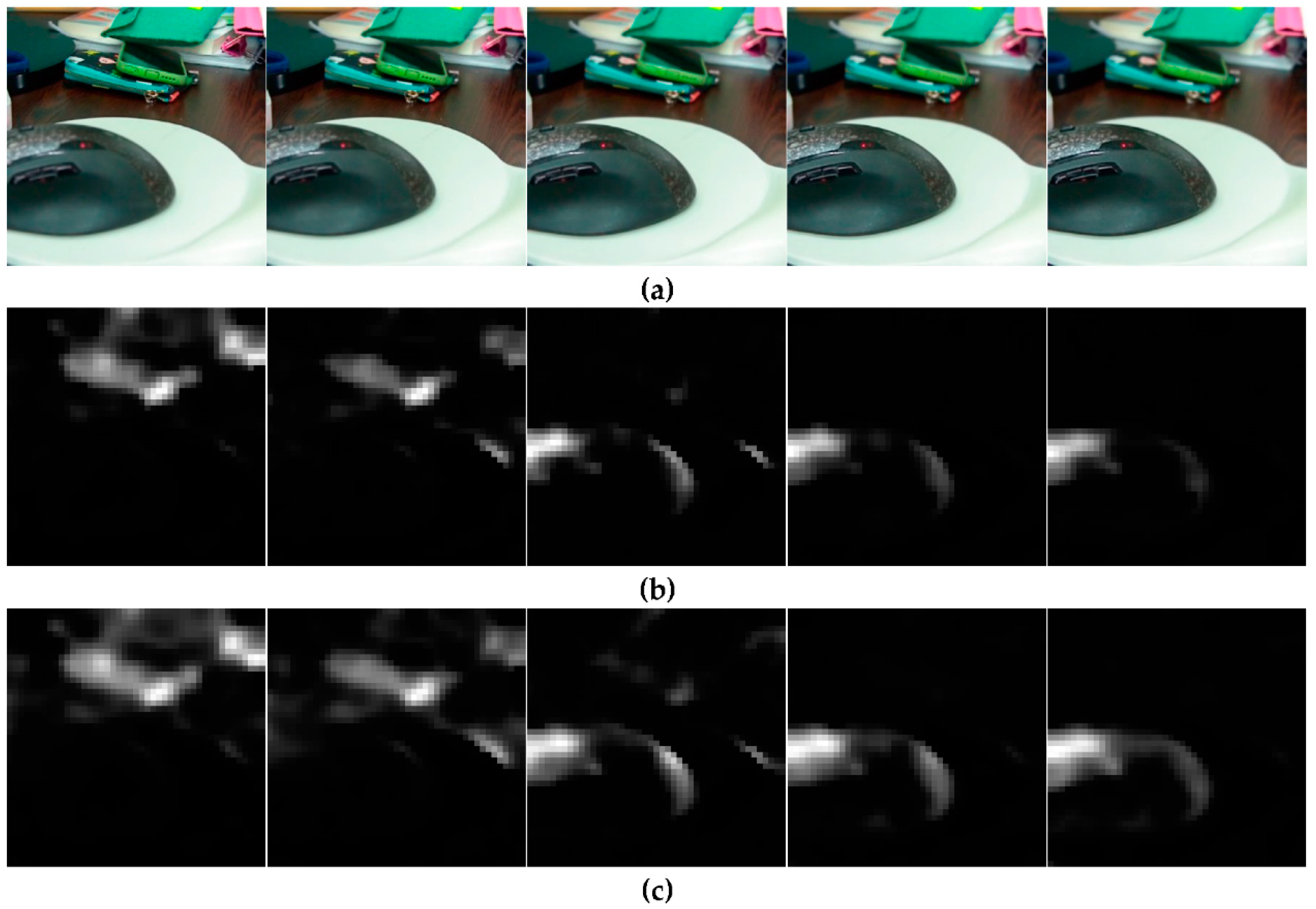
Figure 10.
In-focused regions of the different focal stack images using SML and SUML: ‘Mouse’ dataset; (a) The different focal stack images of ‘Mouse’ dataset; (b) SML of stack images; and (c) SUML of stack images.
Figure 10.
In-focused regions of the different focal stack images using SML and SUML: ‘Mouse’ dataset; (a) The different focal stack images of ‘Mouse’ dataset; (b) SML of stack images; and (c) SUML of stack images.
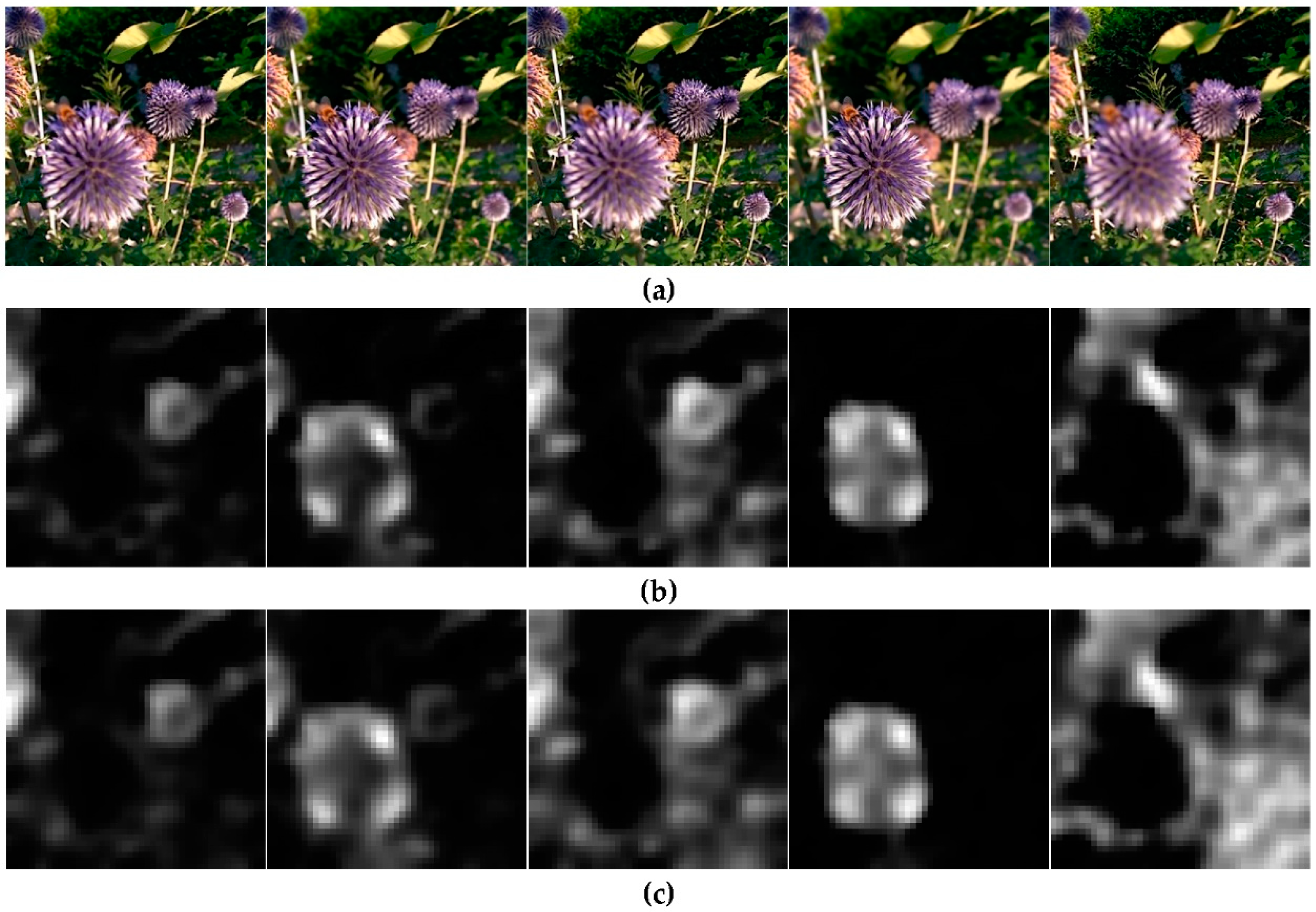
Figure 11.
In-focused regions of the different focal stack images using SML and SUML—‘Flower’ dataset: (a) The input images of different focal lengths; (b) SML of stack images; and (c) SUML of stack images.
Figure 11.
In-focused regions of the different focal stack images using SML and SUML—‘Flower’ dataset: (a) The input images of different focal lengths; (b) SML of stack images; and (c) SUML of stack images.
Figure 12.
Comparison of ‘Bag’ image results: (a) Light Field Software, (b) SML, (c) DCT-STD, (d) DCT-VAR-CV, (e) SML-WHV, (f) Agarwala’s method, (g) DCT-Sharp-CV, (h) DCT-CORR-CV, (i) DCT-SVD-CV, (j) The Proposed Method.
Figure 12.
Comparison of ‘Bag’ image results: (a) Light Field Software, (b) SML, (c) DCT-STD, (d) DCT-VAR-CV, (e) SML-WHV, (f) Agarwala’s method, (g) DCT-Sharp-CV, (h) DCT-CORR-CV, (i) DCT-SVD-CV, (j) The Proposed Method.
Figure 13.
Comparison of ‘Cup’ image results: (a) Light Field Software, (b) SML, (c) DCT-STD, (d) DCT-VAR-CV, (e) SML-WHV, (f) Agarwala’s method, (g) DCT-Sharp-CV, (h) DCT-CORR-CV, (i) DCT-SVD-CV, (j) The Proposed Method.
Figure 13.
Comparison of ‘Cup’ image results: (a) Light Field Software, (b) SML, (c) DCT-STD, (d) DCT-VAR-CV, (e) SML-WHV, (f) Agarwala’s method, (g) DCT-Sharp-CV, (h) DCT-CORR-CV, (i) DCT-SVD-CV, (j) The Proposed Method.
Figure 14.
Comparison of ‘Bike’ image results: (a) Light Field Software, (b) SML, (c) DCT-STD, (d) DCT-VAR-CV, (e) SML-WHV, (f) Agarwala’s method, (g) DCT-Sharp-CV, (h) DCT-CORR-CV, (i) DCT-SVD-CV, (j) The Proposed Method.
Figure 14.
Comparison of ‘Bike’ image results: (a) Light Field Software, (b) SML, (c) DCT-STD, (d) DCT-VAR-CV, (e) SML-WHV, (f) Agarwala’s method, (g) DCT-Sharp-CV, (h) DCT-CORR-CV, (i) DCT-SVD-CV, (j) The Proposed Method.
Figure 15.
Comparison of ‘Mouse’ image results: (a) Light Field Software, (b) SML, (c) DCT-STD, (d) DCT-VAR-CV, (e) SML-WHV, (f) Agarwala’s method, (g) DCT-Sharp-CV, (h) DCT-CORR-CV, (i) DCT-SVD-CV, (j) The Proposed Method.
Figure 15.
Comparison of ‘Mouse’ image results: (a) Light Field Software, (b) SML, (c) DCT-STD, (d) DCT-VAR-CV, (e) SML-WHV, (f) Agarwala’s method, (g) DCT-Sharp-CV, (h) DCT-CORR-CV, (i) DCT-SVD-CV, (j) The Proposed Method.
Figure 16.
Comparison of ‘Flower’ image results: (a) Light Field Software, (b) SML, (c) DCT-STD, (d) DCT-VAR-CV, (e) SML-WHV, (f) Agarwala’s method, (g) DCT-Sharp-CV, (h) DCT-CORR-CV, (i) DCT-SVD-CV, (j) The Proposed Method.
Figure 16.
Comparison of ‘Flower’ image results: (a) Light Field Software, (b) SML, (c) DCT-STD, (d) DCT-VAR-CV, (e) SML-WHV, (f) Agarwala’s method, (g) DCT-Sharp-CV, (h) DCT-CORR-CV, (i) DCT-SVD-CV, (j) The Proposed Method.
Figure 17.
The expanded image ‘Cup’ image results: (a) Light Field Software, (b) SML, (c) DCT-STD, (d) DCT-VAR-CV, (e) SML-WHV, (f) Agarwala’s method, (g) DCT-Sharp-CV, (h) DCT-CORR-CV, (i) DCT-SVD-CV, (j) The Proposed Method.
Figure 17.
The expanded image ‘Cup’ image results: (a) Light Field Software, (b) SML, (c) DCT-STD, (d) DCT-VAR-CV, (e) SML-WHV, (f) Agarwala’s method, (g) DCT-Sharp-CV, (h) DCT-CORR-CV, (i) DCT-SVD-CV, (j) The Proposed Method.
Table 1.
Objective evaluation of the image results (non-reference fusion metrics) for ‘Bag’ image.
Table 1.
Objective evaluation of the image results (non-reference fusion metrics) for ‘Bag’ image.
| Methods | Criteria |
|---|
| FMI | QAB/F |
|---|
| Light Field Software | 0.9612 | 0.7965 |
| SML | 0.9666 | 0.8015 |
| DCT-STD | 0.9619 | 0.8171 |
| DCT-VAR-CV | 0.9673 | 0.8498 |
| SML-WHV | 0.9650 | 0.7994 |
| Agarwala’s Method | 0.9679 | 0.8542 |
| DCT-Sharp-CV | 0.9687 | 0.8626 |
| DCT-CORR-CV | 0.9684 | 0.8637 |
| DCT-SVD-CV | 0.9687 | 0.8635 |
| The Proposed Method | 0.9785 | 0.8729 |
Table 2.
Objective evaluation of the image results (non-reference fusion metrics) for ‘Cup’ image.
Table 2.
Objective evaluation of the image results (non-reference fusion metrics) for ‘Cup’ image.
| Methods | Criteria |
|---|
| FMI | QAB/F |
|---|
| Light Field Software | 0.9286 | 0.7413 |
| SML | 0.9485 | 0.8088 |
| DCT-STD | 0.9419 | 0.8252 |
| DCT-VAR-CV | 0.9502 | 0.8535 |
| SML-WHV | 0.9484 | 0.8176 |
| Agarwala’s Method | 0.9504 | 0.8570 |
| DCT-Sharp-CV | 0.9532 | 0.8706 |
| DCT-CORR-CV | 0.9532 | 0.8709 |
| DCT-SVD-CV | 0.9533 | 0.8708 |
| The Proposed Method | 0.9627 | 0.8788 |
Table 3.
Objective evaluation of the image results (non-reference fusion metrics) for ‘Bike’ image.
Table 3.
Objective evaluation of the image results (non-reference fusion metrics) for ‘Bike’ image.
| Methods | Criteria |
|---|
| FMI | QAB/F |
|---|
| Light Field Software | 0.9384 | 0.7394 |
| SML | 0.9518 | 0.7799 |
| DCT-STD | 0.9476 | 0.7897 |
| DCT-VAR-CV | 0.9538 | 0.8230 |
| SML-WHV | 0.9493 | 0.7734 |
| Agarwala’s Method | 0.9547 | 0.8373 |
| DCT-Sharp-CV | 0.9580 | 0.8443 |
| DCT-CORR-CV | 0.9580 | 0.8512 |
| DCT-SVD-CV | 0.9582 | 0.8505 |
| The Proposed Method | 0.9672 | 0.8574 |
Table 4.
Objective evaluation of the image results (non-reference fusion metrics) for ‘Mouse’ image.
Table 4.
Objective evaluation of the image results (non-reference fusion metrics) for ‘Mouse’ image.
| Methods | Criteria |
|---|
| FMI | QAB/F |
|---|
| Light Field Software | 0.9153 | 0.6917 |
| SML | 0.9293 | 0.7451 |
| DCT-STD | 0.9218 | 0.7626 |
| DCT-VAR-CV | 0.9294 | 0.7819 |
| SML-WHV | 0.9299 | 0.7548 |
| Agarwala’s Method | 0.9310 | 0.7863 |
| DCT-Sharp-CV | 0.9337 | 0.7917 |
| DCT-CORR-CV | 0.9340 | 0.7964 |
| DCT-SVD-CV | 0.9341 | 0.7971 |
| The Proposed Method | 0.9439 | 0.8077 |
Table 5.
Objective evaluation of the image results (non-reference fusion metrics) for ‘Flower’ image.
Table 5.
Objective evaluation of the image results (non-reference fusion metrics) for ‘Flower’ image.
| Methods | Criteria |
|---|
| FMI | QAB/F |
|---|
| Light Field Software | 0.8279 | 0.5945 |
| SML | 0.9255 | 0.8706 |
| DCT-STD | 0.9237 | 0.8655 |
| DCT-VAR-CV | 0.9268 | 0.8684 |
| SML-WHV | 0.9223 | 0.8577 |
| Agarwala’s Method | 0.9273 | 0.8756 |
| DCT-Sharp-CV | 0.9424 | 0.9097 |
| DCT-CORR-CV | 0.9427 | 0.9096 |
| DCT-SVD-CV | 0.9429 | 0.9098 |
| The Proposed Method | 0.9518 | 0.9143 |
Table 6.
The performance summary of different methods on the five image datasets, using QAB/F.
Table 6.
The performance summary of different methods on the five image datasets, using QAB/F.
| Image | Methods |
|---|
| [6] | [9] | [5] | [4] | [16] | [17] | [18] | [19] | [20] | Proposed |
|---|
| Bag | 0.7965 | 0.8015 | 0.8171 | 0.8498 | 0.7994 | 0.8542 | 0.8626 | 0.8637 | 0.8635 | 0.8729 |
| Cup | 0.7413 | 0.8088 | 0.8252 | 0.8535 | 0.8176 | 0.8570 | 0.8706 | 0.8709 | 0.8708 | 0.8788 |
| Bike | 0.7394 | 0.7799 | 0.7897 | 0.8230 | 0.7734 | 0.8373 | 0.8443 | 0.8512 | 0.8505 | 0.8574 |
| Mouse | 0.6917 | 0.7451 | 0.7626 | 0.7819 | 0.7548 | 0.7863 | 0.7917 | 0.7964 | 0.7971 | 0.8077 |
| Flower | 0.5945 | 0.8706 | 0.8655 | 0.8684 | 0.8577 | 0.8756 | 0.9097 | 0.9096 | 0.9098 | 0.9143 |
| Average | 0.7127 | 0.8012 | 0.8120 | 0.8353 | 0.8006 | 0.8421 | 0.8558 | 0.8584 | 0.8583 | 0.8662 |
Table 7.
The performance summary of different methods on the five image datasets, using FMI.
Table 7.
The performance summary of different methods on the five image datasets, using FMI.
| Image | Methods |
|---|
| [6] | [9] | [5] | [4] | [16] | [17] | [18] | [19] | [20] | Proposed |
|---|
| Bag | 0.9612 | 0.9666 | 0.9619 | 0.9673 | 0.9650 | 0.9679 | 0.9687 | 0.9684 | 0.9687 | 0.9785 |
| Cup | 0.9286 | 0.9485 | 0.9419 | 0.9502 | 0.9484 | 0.9504 | 0.9532 | 0.9532 | 0.9533 | 0.9627 |
| Bike | 0.9384 | 0.9518 | 0.9476 | 0.9538 | 0.9493 | 0.9547 | 0.9580 | 0.9580 | 0.9582 | 0.9672 |
| Mouse | 0.9153 | 0.9293 | 0.9218 | 0.9294 | 0.9299 | 0.9310 | 0.9337 | 0.9340 | 0.9341 | 0.9439 |
| Flower | 0.8279 | 0.9255 | 0.9237 | 0.9268 | 0.9223 | 0.9273 | 0.9424 | 0.9427 | 0.9429 | 0.9518 |
| Average | 0.9143 | 0.9443 | 0.9394 | 0.9455 | 0.9430 | 0.9463 | 0.9512 | 0.9513 | 0.9514 | 0.9608 |