A Statistical Performance Analysis of Named Data Ultra Dense Networks
Abstract
:1. Introduction
- We present a four-way factorial design method, which is applied to generate the dataset, including various network parameters, in the ndnSIM simulator.
- We provide a background and overview of the different statistical analysis methods that can be used to evaluate or enhance the interest satisfaction rate (ISR).
- We evaluate various network parameters based on mean plots and interaction plots and use multiple comparison tests to analyze how the main effects and interaction effects influence the ISR.
- We select an adequate multiple linear regression (MLR) model to fit the ISR based on both the Akaike information criterion (AIC) [19] and the coefficient of determination . A network may achieve a higher ISR in the final model.
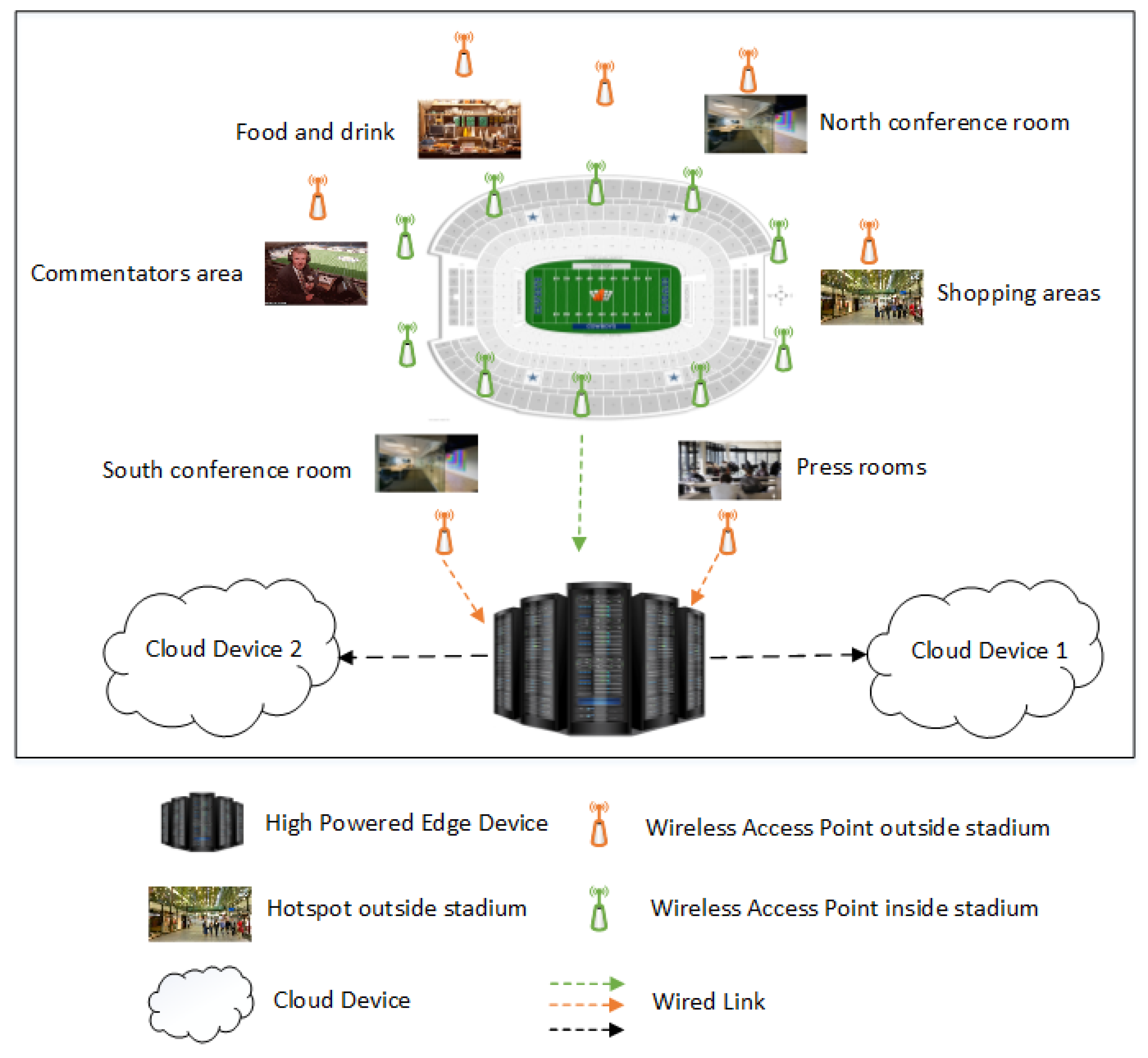
2. Motivation: Ultra-Dense Network
- (1)
- Radio frequency (RF) coverage: The RF coverage must be the same throughout the stadium so that the users are not affected by signal fading due to signal attenuation and obstacles.
- (2)
- Multimedia support: The stadium network must support all service types, such as audio or video streaming [20].
- (3)
- Real-time and reliable connection: The stadium network should support a real-time and extremely reliable connection so that a cooperative and intelligent communication system can handle emergency scenarios in such a crowded area.
- (4)
- Hands-off management: Users in the stadium may be mobile and may change their position very often, mainly if they are outside the bowl area. Therefore, reliable hands-off strategies should be established in these areas to avoid intermittent connectivity.
- (5)
- Interference management: Interference may occur in the stadium due to the deployment of multiple wireless access points (WAP) inside and outside the stadium. Minimizing interference may increase network capacity and throughput.
- (6)
- Edge computing: A stadium network must be facilitated with the emerging technology of edge computing. Edge computing offers cloud resources closer to the end-users, thereby improving the latency requirements and reducing the backhaul traffic on cloud devices [21].
- (7)
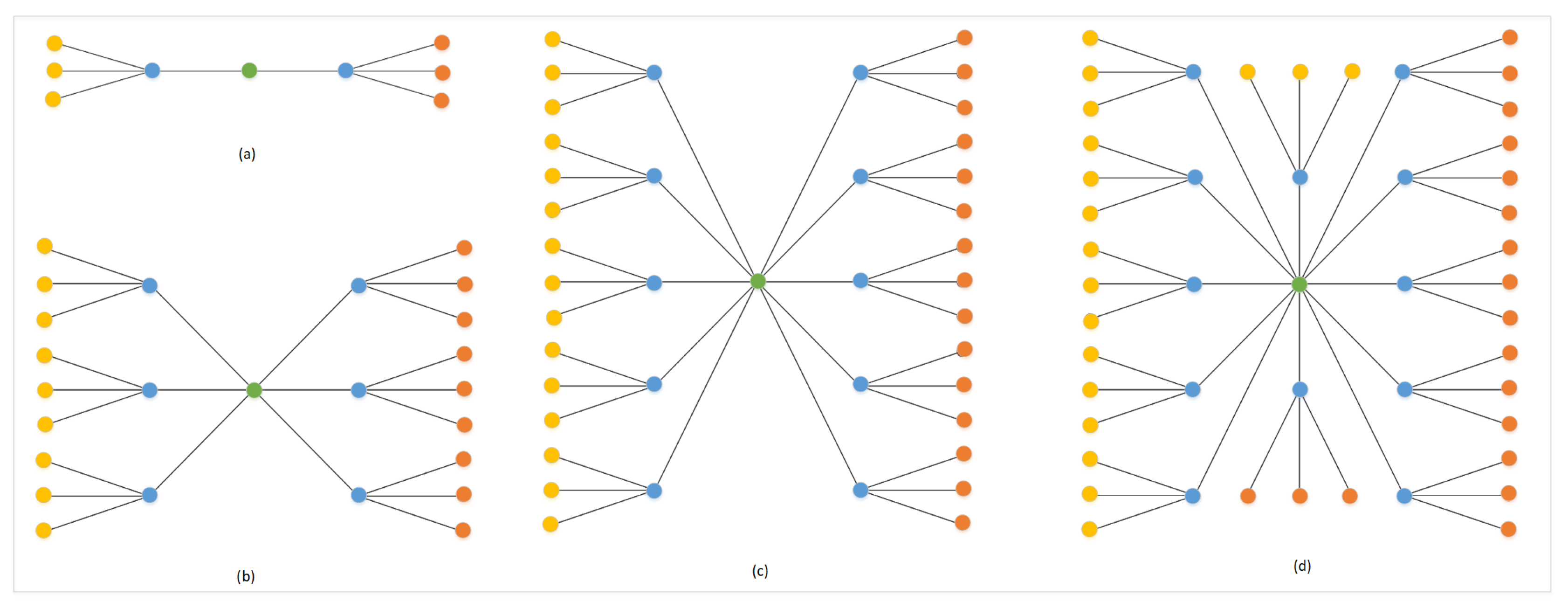
- Bottleneck mitigation: Ultra-dense networks with single edge computing devices are cost efficient. However, bottleneck or congestion may occur [22], since many WAPs may frequently and directly access the information from the edge node, as shown in Figure 2. Therefore, a stadium network must be capable of coping with such situations to give better services to its end users.
3. Simulations and Dataset Generation
3.1. Simulation Environment
3.1.1. Phase 1: Predictors Selection
3.1.2. Phase 2: Dataset Generation
3.2. Four-Way Factorial Design
4. Statistical Methods
4.1. Multiple Linear Regression
4.2. Akaike Information Criterion
4.3. Main and Interaction Effects
4.4. Multiple Comparison Test
5. Results
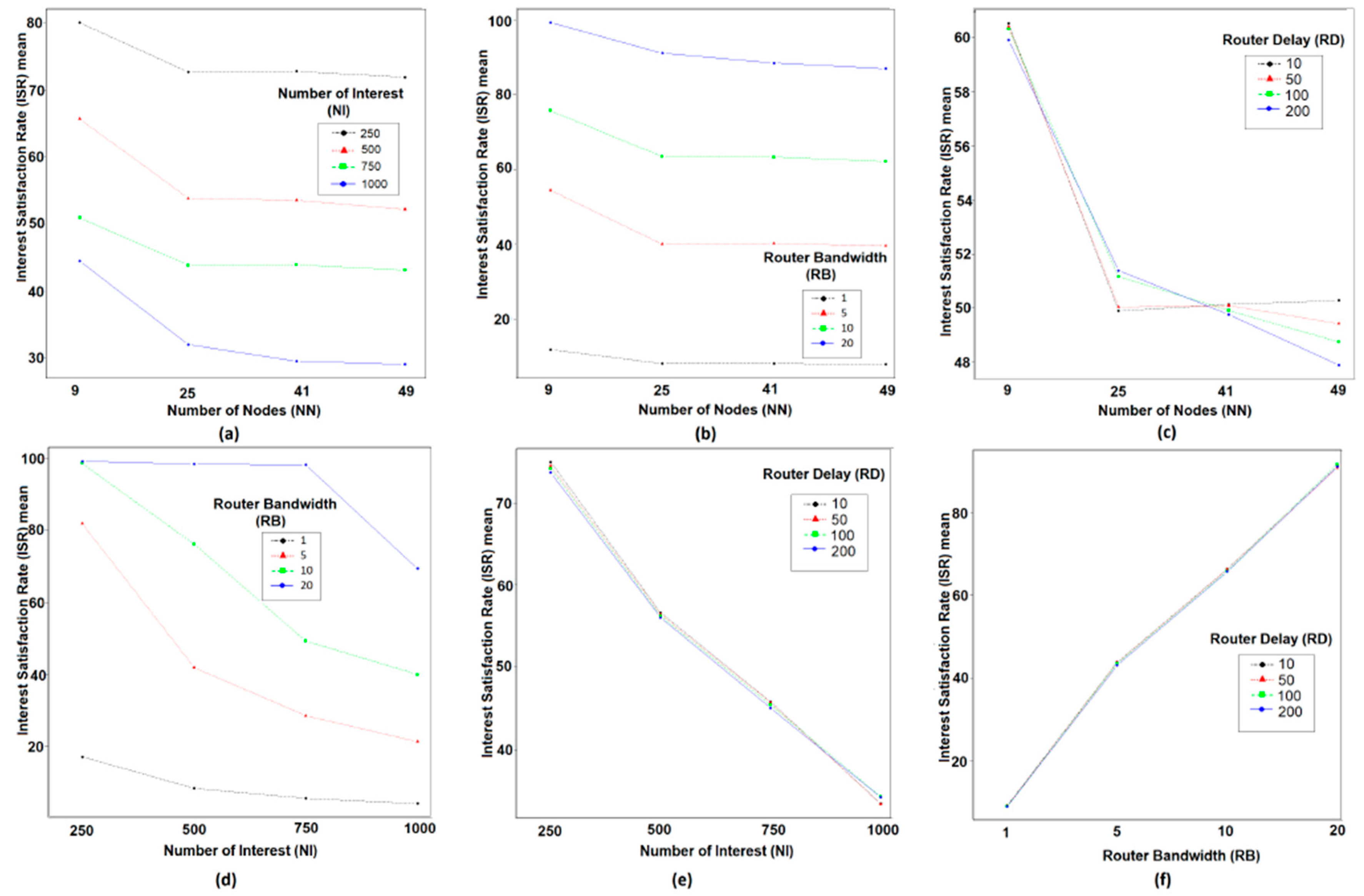
5.1. Main Effect
5.2. Interaction Effects
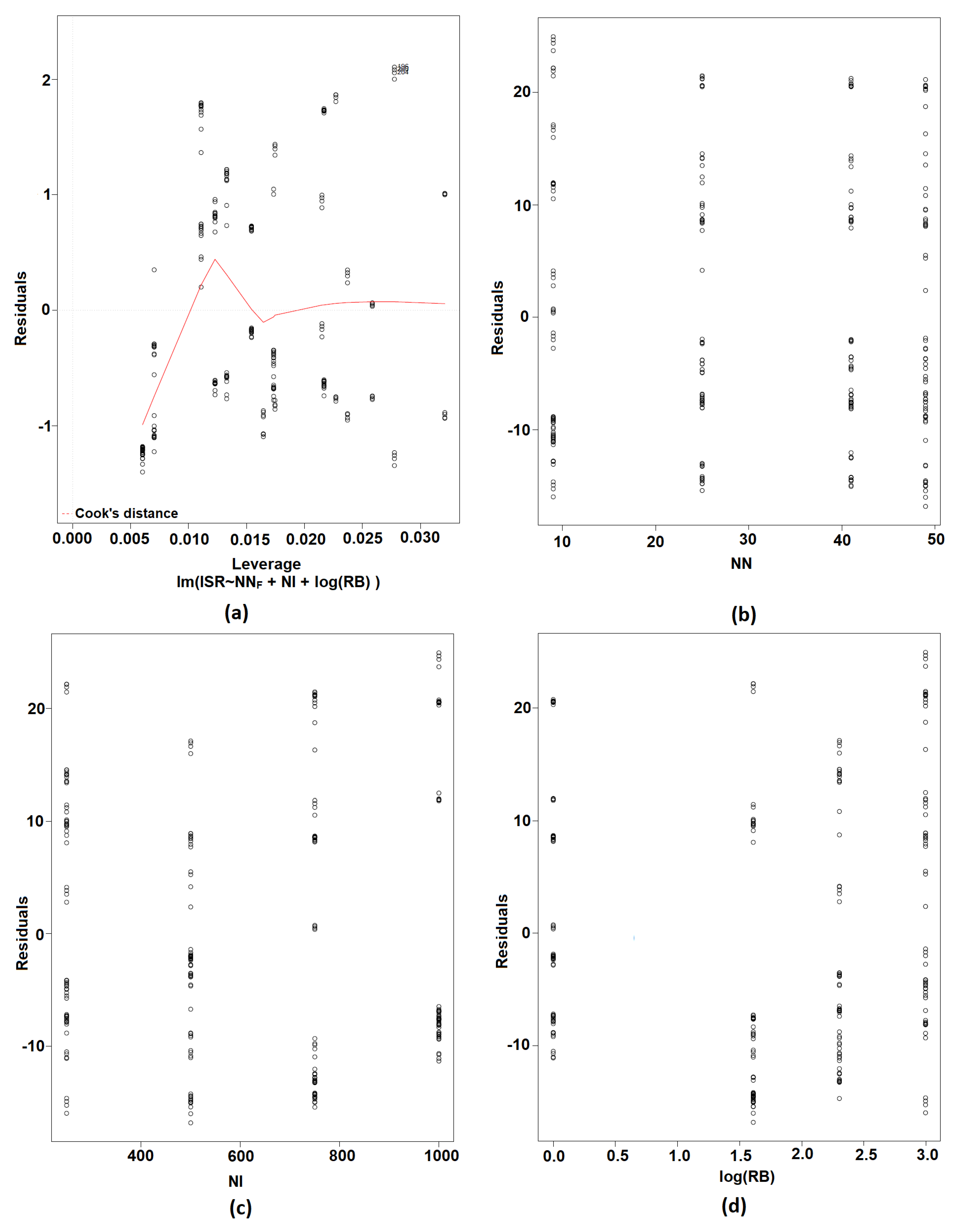
5.3. Model Selection
5.3.1. Initial Model
5.3.2. Step AIC
5.3.3. Model with Categorical NN
5.3.4. Final Model
6. Discussion
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Ullah, R.; Ahmed, S.H.; Kim, B. Information-Centric Networking with Edge Computing for IoT: Research Challenges and Future Directions. IEEE Access 2018, 6, 73465–73488. [Google Scholar] [CrossRef]
- Busari, S.A.; Huq, K.M.S.; Mumtaz, S.; Dai, L.; Rodriguez, J. Millimeter-Wave Massive MIMO Communication for Future Wireless Systems: A Survey. IEEE Commun. Surv. Tutor. 2018, 20, 836–869. [Google Scholar] [CrossRef]
- Wang, X.; Kong, L.; Kong, F.; Qiu, F.; Xia, M.; Arnon, S.; Chen, G. Millimeter Wave Communication: A Comprehensive Survey. IEEE Commun. Surv. Tutor. 2018, 20, 1616–1653. [Google Scholar] [CrossRef]
- Ullah, R.; Faheem, Y.; Kim, B. Energy and Congestion-Aware Routing Metric for Smart Grid AMI Networks in Smart City. IEEE Access 2017, 5, 13799–13810. [Google Scholar] [CrossRef]
- Parane, K.A.; Patil, N.C.; Poojara, S.R.; Kamble, T.S. Cloud based Intelligent Healthcare Monitoring System. In Proceedings of the 2014 International Conference on Issues and Challenges in Intelligent Computing Techniques (ICICT), Ghaziabad, India, 7–8 February 2014; pp. 697–701. [Google Scholar] [CrossRef]
- Rajasekhar, M.V.; Jaswal, A.K. Autonomous vehicles: The future of automobiles. In Proceedings of the 2015 IEEE International Transportation Electrification Conference (ITEC), Chennai, India, 27–29 August 2015; pp. 1–6. [Google Scholar] [CrossRef]
- Sisinni, E.; Saifullah, A.; Han, S.; Jennehag, U.; Gidlund, M. Industrial Internet of Things: Challenges, Opportunities, and Directions. IEEE Trans. Ind. Inform. 2018, 14, 4724–4734. [Google Scholar] [CrossRef]
- Cristina, G.N.; Gheorghita, G.V.; Ioan, U. Gradual Development of an IoT Architecture for Real-World Things. In Proceedings of the 2015 IEEE European Modelling Symposium (EMS), Madrid, Spain, 6–8 October 2015; pp. 344–349. [Google Scholar] [CrossRef]
- Cisco Visual Networking Index Predicts Near-Tripling of IP Traffic by 2020. Cisco, San Jose, CA, USA. 2017. Available online: https://newsroom.cisco.com/press-release-content?type=press-release&articleId=1771211 (accessed on 24 March 2019).
- Shang, W.; Yu, Y.; Droms, R.; Zhang, L. Challenges in IoT Networking via TCP/IP Architecture. NDN Project, Tech. Rep. NDN0038, February 2016. Available online: https://named-data.net/wp-content/uploads/2016/02/ndn-0038-1-challenges-iot.pdf (accessed on 13 March 2019).
- Jacobson, V.; Smetters, D.K.; Thornton, J.D.; Plass, M.F.; Briggs, N.H.; Braynard, R.L. Networking named content. In Proceedings of the 5th International Conference on Emerging Networking Experiments and Technologies (CoNEXT ’09), Rome, Italy, 1–4 December 2009; ACM: New York, NY, USA, 2009; pp. 1–12. [Google Scholar]
- Ahlgren, B.; Dannewitz, C.; Imbrenda, C.; Kutscher, D.; Ohlman, B. A survey of information-centric networking. IEEE Commun. Mag. 2012, 50, 26–36. [Google Scholar] [CrossRef]
- Afanasyev, A.; Shi, J.; Zhang, B.; Zhang, L.; Moiseenko, I.; Yu, Y.; Shang, W.; Li, Y.; Mastorakis, S.; Huang, Y.; et al. NFD Developer’s Guide; Technical Report, NDN-0021, NDN; University of California: Los Angeles, CA, USA, 2018. [Google Scholar]
- Ullah, R.; Rehman, M.A.U.; Kim, B. Design and Implementation of an Open Source Framework and Prototype For Named Data Networking-Based Edge Cloud Computing System. IEEE Access 2019, 7, 57741–57759. [Google Scholar] [CrossRef]
- Ahmed, S.H.; Bouk, S.H.; Yaqub, M.A.; Kim, D.; Song, H.; Lloret, J. CODIE: Controlled Data and Interest Evaluation in Vehicular Named Data Networks. IEEE Trans. Veh. Technol. 2016, 65, 3954–3963. [Google Scholar] [CrossRef]
- Ullah, R.; Rehman, M.A.U.; Kim, B.S. Hierarchical Name-Based Mechanism for Push-Data Broadcast Control in Information-Centric Multihop Wireless Networks. Sensors 2019, 19, 3034. [Google Scholar] [CrossRef]
- Din, I.U.; Hassan, S.; Khan, M.K.; Guizani, M.; Ghazali, O.; Habbal, A. Caching in Information-Centric Networking: Strategies, Challenges, and Future Research Directions. IEEE Commun. Surv. Tutor. 2018, 20, 1443–1474. [Google Scholar] [CrossRef]
- Osseiran, A.; Boccardi, F.; Braun, V.; Kusume, K.; Marsch, P.; Maternia, M.; Queseth, O.; Schellmann, M.; Schotten, H.; Taoka, H.; et al. Scenarios for 5G mobile and wireless communications: The vision of the METIS project. IEEE Commun. Mag. 2014, 52, 26–35. [Google Scholar] [CrossRef]
- Sakamoto, Y.; Ishiguro, M.; Kitagawa, G. Akaike Information Criterion Statistics; KTK Scientific Publishers: Tokyo, Japan; D. Reidel Publishing: Dodrecht, The Netherlands, 1986. [Google Scholar]
- How to Design Better Wireless Networks for Stadiums. Case Study, September 2015. Available online: https://www.cei-das.com/wp-content/uploads/iBwave-Case-Study-Stadiums.pdf (accessed on 8 March 2019).
- Guo, H.; Liu, J.; Zhang, J. Computation Offloading for Multi-Access Mobile Edge Computing in Ultra-Dense Networks. IEEE Commun. Mag. 2018, 56, 14–19. [Google Scholar] [CrossRef]
- Kamel, M.; Hamouda, W.; Youssef, A. Ultra-dense networks: A survey. IEEE Commun. Surveys Tutor. 2016, 18, 2522–2545. [Google Scholar] [CrossRef]
- Shreesha, S.; Routray, S.K. Statistical modeling for communication networks. In Proceedings of the 2016 2nd International Conference on Applied and Theoretical Computing and Communication Technology (iCATccT), Bangalore, India, 21–23 July 2016; pp. 831–834. [Google Scholar] [CrossRef]
- Routray, S.K. Statistical Analysis and Modeling of Optical Transport Networks. Ph.D. Thesis, University of Aveiro, Aveiro, Portugal, 2015. [Google Scholar]
- Korotky, S.K. Network global expectation model: A statistical formalism for quickly quantifying network needs and costs. IEEE/OSA J. Light. Technol. 2004, 22, 703–722. [Google Scholar] [CrossRef]
- Mastorakis, S.; Afanasyev, A.; Zhang, L. On the evolution of ndnSIM: An open-source simulator for NDN experimentation. ACM SIGCOMM Comput. Commun. Rev. 2017, 47, 19–33. [Google Scholar] [CrossRef]
- Arshad, S.; Shahzaad, B.; Azam, M.A.; Loo, J.; Ahmed, S.H.; Aslam, S. Hierarchical and Flat-Based Hybrid Naming Scheme in Content-Centric Networks of Things. IEEE Internet Things J. 2018, 5, 1070–1080. [Google Scholar] [CrossRef]
- Collins, L.M.; Dziak, J.J.; Li, R. Design of experiments with multiple independent variables: a resource management perspective on complete and reduced factorial designs. Psychol. Methods 2009, 14, 202–224. [Google Scholar] [CrossRef] [PubMed]
- Rice, J.A. Mathematical Statistics and Data Analysis, 3rd ed.; Cengage Learning: Boston, MA, USA, 2007. [Google Scholar]
- Weinberg, S.; Abramowitz, S. Statistics Using SPSS; Cambridge University Press: New York, NY, USA, 2008. [Google Scholar]
- McHugh, M.L. Multiple comparison analysis testing in ANOVA. Biochem. Med. 2011, 21, 203–209. [Google Scholar] [CrossRef]
- Tukey, J. Comparing Individual Means in the Analysis of Variance. Biometrics 1949, 5, 99–114. [Google Scholar] [CrossRef] [PubMed]
- CRAN: Manuals—The R Project for Statistical Computing. Available online: https://cran.r-project.org/manuals.html (accessed on 4 February 2019).
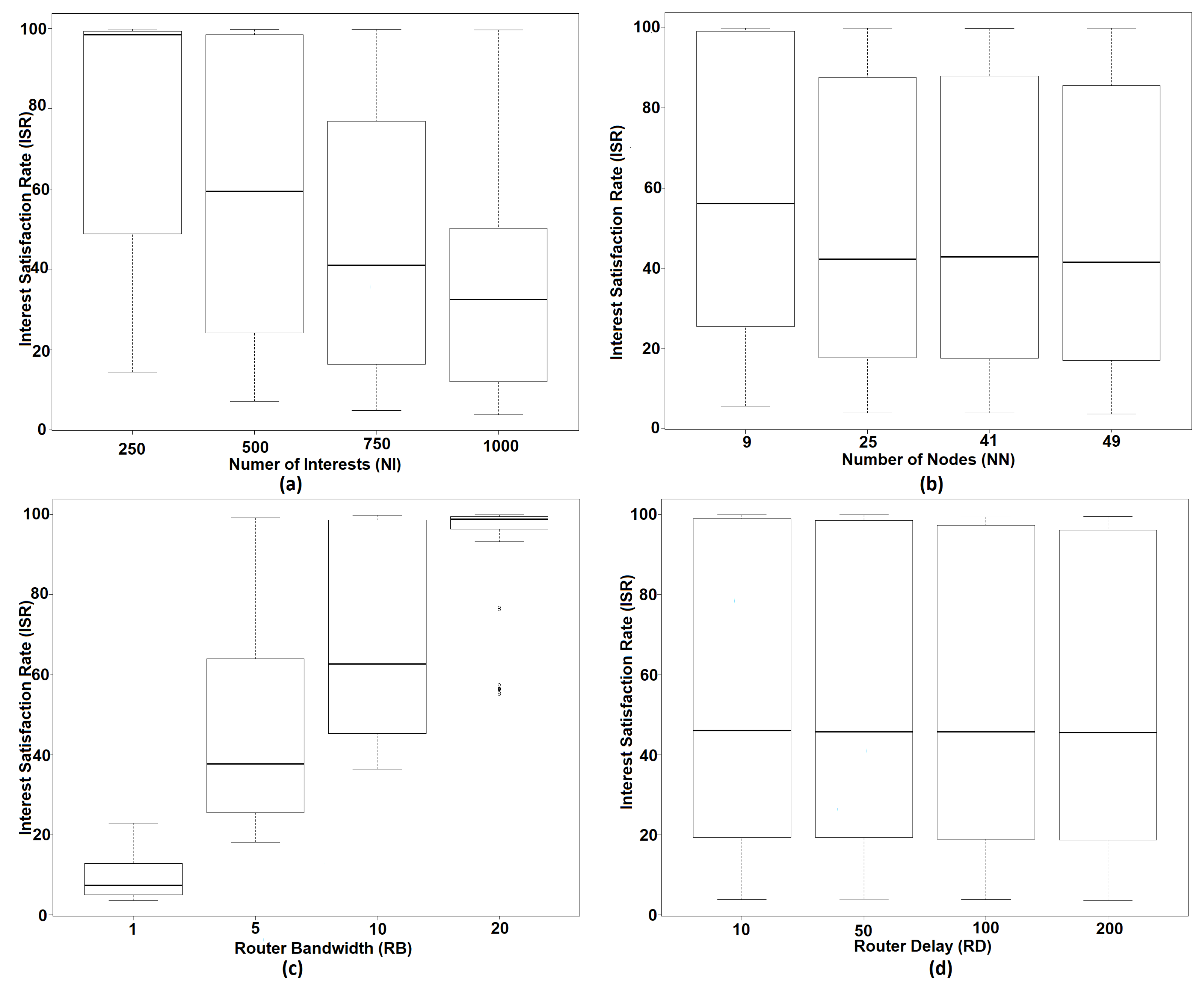
| Factors | Levels |
|---|---|
| Number of Interests (NI) | 250, 500, 750, 1000 |
| Number of Nodes (NN) | 9, 25, 41, 49 |
| Router Bandwidth in Mbps (RB) | 1, 5, 10, 20 |
| Router Delay in ms (RD) | 10, 50, 100, 200 |
| Levels | 250–500 | 250–750 | 250–1000 | 500–750 | 500–1000 | 750–1000 | |
| NI | p-values | 0 | 0 | 0 | 8 × 10 | 0 | 1 × 10 |
| estimates | −18.01813 | −28.85063 | −40.51750 | −10.83250 | −22.49938 | −11.66688 | |
| Levels | 9–25 | 9–41 | 9–49 | 25–41 | 25–49 | 41–49 | |
| NN | p-values | 0.0000134 | 0.0000029 | 0.0000003 | 0.9881607 | 0.8683795 | 0.9706484 |
| estimates | −9.6742188 | −10.3223438 | −11.2096875 | −0.6481250 | −1.5354687 | −0.8873437 | |
| Levels | 1–5 | 1–10 | 1–20 | 5–10 | 5–20 | 10–20 | |
| RB | p-values | 0 | 0 | 0 | 0 | 0 | 0 |
| estimates | 34.59859 | 57.21875 | 82.51203 | 22.62016 | 47.91344 | 25.29328 | |
| Levels | 10–50 | 10–100 | 10–200 | 50–100 | 50–200 | 100–200 | |
| RD | p-values | 0.9995204 | 0.9997671 | 0.9952438 | 0.9999952 | 0.9992516 | 0.9987582 |
| estimates | −0.2200000 | −0.1728125 | −0.4753125 | 0.0471875 | −0.2553125 | −0.3025000 |
| Estimate | Std. Error | t-Value | Pr (>| t |) | |
|---|---|---|---|---|
| (Intercept) | 5.104 × 10 | 7.348 × 10 | 6.946 | 3.36 × 10 *** |
| NN | −6.763 × 10 | 1.796 × 10 | −0.377 | 0.707 |
| NI | −4.744 × 10 | 9.360 × 10 | −5.068 | 7.93 × 10 *** |
| RD | −4.195 × 10 | 4.372 × 10 | −0.096 | 0.924 |
| RB | 4.402 × 10 | 4.372 × 10 | 10.069 | <2 × 10 *** |
| NN:NI | −1.716 × 10 | 2.117 × 10 | −0.810 | 0.419 |
| NN:RD | −2.298 × 10 | 8.328 × 10 | −0.276 | 0.783 |
| NN:RB | −7.338 × 10 | 8.328 × 10 | −0.881 | 0.379 |
| NI:RD | 1.281 × 10 | 4.577 × 10 | 0.280 | 0.780 |
| NI:RB | −1.501 × 10 | 4.577 × 10 | −0.328 | 0.743 |
| RD:RB | 1.194 × 10 | 1.800 × 10 | 0.066 | 0.947 |
| Estimate | Std. Error | t-Value | Pr (>| t |) | |
|---|---|---|---|---|
| (Intercept) | 56.879840 | 3.074145 | 18.503 | <2 × 10 *** |
| NN | −0.261602 | 0.058563 | −4.467 | 1.2 × 10 *** |
| NI | −0.052954 | 0.003219 | −16.452 | <2 × 10 *** |
| RB | 4.091370 | 0.126599 | 32.317 | <2 × 10 *** |
| Estimate | Std. Error | t-value | Pr (>| t |) | |
|---|---|---|---|---|
| (Intercept) | 46.677446 | 2.535294 | 18.411 | <2 × 10 *** |
| factor(newNN)1 | −10.402083 | 1.732878 | −6.003 | 6.72 × 10 *** |
| NI | −0.052954 | 0.002685 | −19.725 | <2 × 10 *** |
| log(RB) | 27.051692 | 0.675387 | 40.054 | <2 × 10 *** |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rehman, M.A.U.; Kim, D.; Choi, K.; Ullah, R.; Kim, B.S. A Statistical Performance Analysis of Named Data Ultra Dense Networks. Appl. Sci. 2019, 9, 3714. https://doi.org/10.3390/app9183714
Rehman MAU, Kim D, Choi K, Ullah R, Kim BS. A Statistical Performance Analysis of Named Data Ultra Dense Networks. Applied Sciences. 2019; 9(18):3714. https://doi.org/10.3390/app9183714
Chicago/Turabian StyleRehman, Muhammad Atif Ur, Donghak Kim, Kyungmee Choi, Rehmat Ullah, and Byung Seo Kim. 2019. "A Statistical Performance Analysis of Named Data Ultra Dense Networks" Applied Sciences 9, no. 18: 3714. https://doi.org/10.3390/app9183714
APA StyleRehman, M. A. U., Kim, D., Choi, K., Ullah, R., & Kim, B. S. (2019). A Statistical Performance Analysis of Named Data Ultra Dense Networks. Applied Sciences, 9(18), 3714. https://doi.org/10.3390/app9183714







