Abstract
Landslides are one type of serious geological hazard which cause immense losses of local life and property. Landslide susceptibility prediction (LSP) can be used to determine the spatial probability of landslide occurrence in a certain area. It is important to implement LSP for landslide hazard prevention and reduction. This study developed a particle-swarm-optimized multilayer perceptron (PSO-MLP) model for LSP implementation to overcome the drawbacks of the conventional gradient descent algorithm and to determine the optimal structural parameters of MLP. Shicheng County in Jiangxi Province of China was used as the study area. In total, 369 landslides, randomly selected non-landslides, and 14 landslide-related predisposing factors were used to train and test the present PSO-MLP model and three other comparative models (an MLP-only model with the gradient descent algorithm, a back-propagation neural network (BPNN), and an information value (IV) model). The results showed that the PSO-MLP model had the most accurate prediction performance (area under the receiver operating characteristic curve (AUC) of 0.822 and frequency ratio (FR) accuracy of 0.856) compared with the MLP-only (0.791 and 0.829), BPNN (0.800 and 0.840), and IV (0.788 and 0.824) models. It can be concluded that the proposed PSO-MLP model addresses the drawbacks of the MLP-only model well and performs better than conventional artificial neural networks (ANNs) and statistical models. The spatial probability distribution law of landslide occurrence in Shicheng County was well revealed by the landslide susceptibility map produced using the PSO-MLP model. Furthermore, the present PSO-MLP model may have higher prediction and classification performances in some other fields compared with conventional ANNs and statistical models.
1. Introduction
A landslide is a type of very serious natural hazard that occurs worldwide and results in immense losses in human life and property [1,2,3]. Much attention has been paid by geological engineers to determine the susceptible areas where landslides are likely to occur, and landslide susceptibility prediction (LSP) and susceptibility mapping are significant technologies used to this end [4,5].
Along with the development of information technologies, remote sensing and the geographic information system (GIS) have gradually become data sources and spatial analysis platforms for LSP [6,7]. Based on remote sensing and GIS, many mathematical models have been proposed to calculate landslide susceptibility indices (LSI), such as the analytic hierarchy process [8,9,10], weight evidence method [11], information value (IV) theory [5,12], frequency ratio (FR) method [13,14], logistic regression model [7,15,16], logistic tree model [17], random tree [18,19], boosted tree [20], multi-criteria evaluation model [21], artificial neural networks (ANNs) [22,23,24], support vector machine (SVM) [25,26,27], and neuro-fuzzy method [28]. Although many models have been proposed for LSP, there is no model that is universally accepted and there is much room for improvement for these models.
It is important and difficult to choose an appropriate model for LSP. Generally speaking, the related literature shows that machine learning models (e.g., ANNs and SVM) have higher prediction performances than other LSP models because machine learning models can more effectively fit and predict the nonlinear mapping relationships between landslides and predisposing factors [14,23,29,30,31]. Among these machine learning models, ANNs have been commonly and successfully introduced into the area of LSP. ANNs are robust when data noise interferes with the LSP modeling processes and their modeling processes are relatively simple, as they are based only on input–output variables. The multilayer perceptron (MLP) model, which has a feed-forward neural network structure, is one of the most popular ANNs [32]. The MLP model has been proposed for LSP by several researchers, and related LSP results have proved the validity of this model [33,34,35].
However, there are still some drawbacks in the MLP model that may reduce LSP performance, which can be summarized as follows: (1) the gradient descent algorithm commonly used in the MLP model is prone to local optimization and low training speed [36,37]; (2) several closely related structural parameters of MLP, such as the learning rate, learning decay rate, momentum, and the number of neurons in the hidden layer, are difficult to appropriately determine [38,39]. To overcome these drawbacks, a particle-swarm-optimized MLP (PSO-MLP) model with mini-batch gradient descent has been proposed to address LSP. The mini-batch gradient descent, which can better avoid the local optimal value and reach a higher training speed compared with the conventional gradient descent algorithm, is used as the sample training algorithm of MLP [40]. The PSO algorithm, which has the advantages of excellent search capability, a global optimum, and high computational efficiency, has been successfully used in many fields [39,41]. In this study, PSO was used to select the appropriate structural parameters of MLP.
To sum up, a novel PSO-MLP model was developed to implement LSP in this study. Shicheng County, China was used as the study area due to the frequent occurrence of landslides in this area. Landslides result in serious socioeconomic and natural problems in Shicheng County. Hence, it is significant to map landslide susceptibility there. In addition, to verify the prediction performance of the PSO-MLP model, an MLP-only model with the conventional gradient descent algorithm, a back-propagation neural network (BPNN), and an IV model were also tested for comparison.
2. Materials and Methods
2.1. Materials
The materials include introduction of study area, landslide inventory information, and related predisposing factors.
2.1.1. Study Area and Landslide Inventory Information
Shicheng County is located in the southeastern part of Jiangxi Province and has a longitude of 116°05′46″ E, 116°38′03″ E and a latitude of 25°57′47″ N, 26°36′13″ N (Figure 1). Its total area is about 1581.5 km2 with a length of 71.8 km and a width of 53.7 km. The total population is about 3.33 × 105. Shicheng County belongs to the subtropical monsoon humid climate zone and has abundant sunshine, four distinctive seasons, and rich rainfall. Its average annual precipitation was about 1748.6 mm between 1970 and 2015, and the total precipitation of the main flood season (April–June) accounts for 50.1% of the total annual precipitation. Both precipitation and temperature are non-uniformly distributed in Shicheng County due to the complex terrain characteristics and the relationship between land and sea locations.
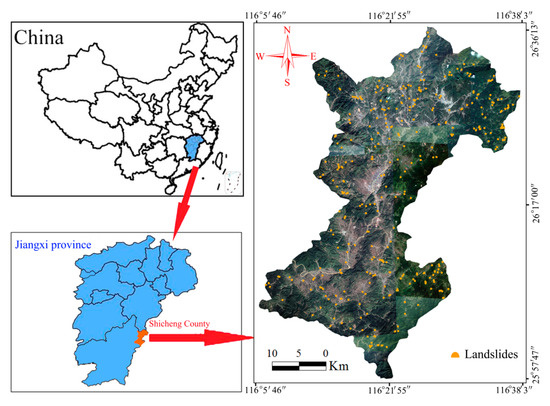
Figure 1.
Geographic location and landslide distribution of Shicheng County.
Shicheng County belongs to a mountainous area with a developed river system and a dense river network (0.6 km of each km2). The Qin River flows through the whole area from northeast to southwest and finally flows into the Ganjiang River. The groundwater type of Shicheng County is mainly shallow groundwater of shallow depth, good recharge conditions, rapid regeneration speed, and easy extraction. Furthermore, Shicheng County is in a mountain basin surrounded by the Wuyi Mountains. These mountains are mainly composed of pre-Devonian metamorphic rocks, Devonian quartz sandstone, sandy conglomerate, and sandy shale. In general, Shicheng County is in a typical southeast hilly region, with many mountains in the northeast area, rolling hills in the southwest area, and flat terrain in the central area.
Based on investigations by the Land and Resources Department of Jiangxi Province, the landslide inventory map shown in Figure 1 suggests that 369 landslides occurred in the study area from 1970 to 2012. The sliding masses of these landslides are mainly composed of quaternary silty clay intercalated with crushed stones that have a thickness ranging from 2 to 8 m. These landslides can be mainly classified as shallow soil landslides with a movement type of clay/silt slide [42]. The main features of these shallow soil landslides are their small scale, high frequency, group occurrence, and wide distribution. The total cover area of the recorded landslides in Shicheng County is about 2.44 × 106 m2, and the area of these landslides ranges from about 1.0 × 103 to 1.6 × 104 m2. Furthermore, the main direct trigger factors of these landslides are seasonal heavy rainfall and frequent unreasonable human engineering activities, such as slope toe cutting and road excavation.
2.1.2. Landslide-Related Predisposing Factors
In this study, we selected 14 landslide-related predisposing factors as input variables of the PSO-MLP, MLP-only, BPNN, and IV models. These predisposing factors were topography factors (digital elevation modeling (DEM), slope, aspect, relief amplitude, plan curvature, and profile curvature); hydrological factors (distance to river, topographic wetness index (TWI), and modified normalization difference water index (MNDWI)); lithological factors (rock types); land cover factors (normalized difference building index (NDBI), normalized difference vegetation index (NDVI), total surface radiation, and population density index). The DEM was obtained from the Global Digital Elevation Model of the Advanced Spaceborne Thermal Emission and Reflection Radiometer (ASTER GDEM), and the MNDWI, NDBI, and NDVI factors were calculated from Landsat 8 TM images (obtained on 5 October 2013, path/row 121/42, 30 m resolution). These 14 predisposing factors were selected according to the related literature and studies in areas with similar physical geography and geological environments [11,43,44].
In this study, the data format of DEM and original remote sensing images was grid cells with a spatial resolution of 30 × 30 m. Moreover, the raster format has the advantages of fast subdivision, simple expression, and high computational efficiency. Hence, the raster format with grid cells was applied to express all 14 predisposing factors in Shicheng County. The recorded landslides were subdivided into 2709 landslide grid cells.
- (1)
- Topography factors in Shicheng County
DEM (Figure 2a), which indicates the altitude above sea level in the study area, was the data source of the five other topographic factors. These six topographic factors have important effects on the probability of landslide occurrence [45]. Slope (Figure 2b) has a direct influence on the landslide stability coefficient, and it is one of the basic elements of landslide evaluation [46]. Aspect (Figure 2c) influences landslide occurrence by affecting moisture movement, soil properties, and so forth [47]. Relief amplitude (Figure 2d) directly reflects terrain complexity through the variations of DEM in a certain area [48]. Plan curvature (Figure 2e) and profile curvature (Figure 2f), respectively defined as the slope of the aspect and the slope of the slope, can also effectively reflect the terrain complexity of the study area [49]. Terrain complexity affects landslide evolution by influencing soil erosion, slope structure, sediment transportation, and so forth.
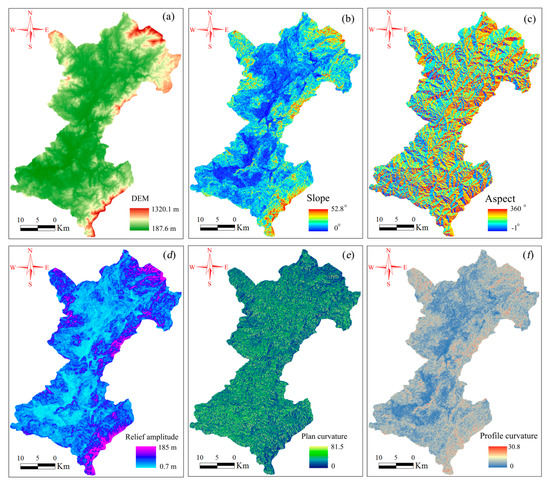
Figure 2.
Topography factors in Shicheng County: (a) DEM, (b) Slope, (c) Aspect, (d) Relief amplitude, (e) Plan curvature, (f) Profile curvature.
- (2)
- Hydrological, lithological, and land cover factors
Hydrological factors are very important factors of landslide evolution which influence the surface water distribution, water and soil saturation, water sources, runoff generation, and so forth [50]. The distance to river and TWI calculated from DEM and the MNDWI were used in this study as hydrological factors (Figure 3a–c). Distance to river reflects the water scour and soil erosion effects of surface runoff on landslide evolution [49], and TWI reflects the influence of terrain on soil saturation, rainfall infiltration, and runoff [50,51]. MNDWI suggests the surface humidity features, which indirectly present the moisture content in the slope mass [13].
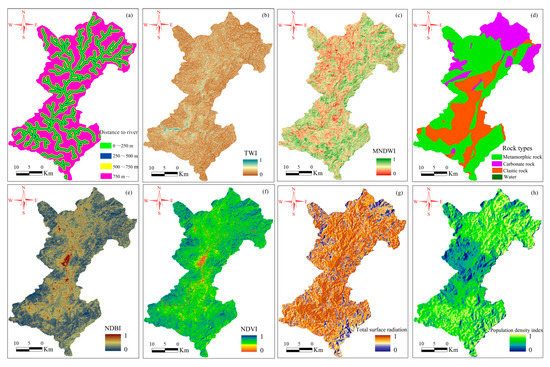
Figure 3.
Hydrological, lithological, and land cover factors in Shicheng County, (a) Distance to river, (b) TWI, (c) MNDWI, (d) Rock types, (e) NDBI, (f) NDVI, (g) Total surface radiation, (h) Population density index.
The lithological factor in Shicheng County was expressed using rock types in this study, which remarkably affect the slope soil types, slope structure, and soil shear strength [11,43]. The rock types in Shicheng County are mainly defined as metamorphic, carbonate, and clastic rocks (Figure 3d).
Land cover is also a key factor for LSP. The NDBI, NDVI, total surface radiation, and population density index were adopted in this study to express the land cover factors (Figure 3e–h). NDBI suggests the building distribution features, and it indirectly affects the hydrological and mechanical strength of slope soil [52,53]. NDVI suggests the vegetation growth features, and it mainly changes the hydrological and soil shear strength features of slope soil [11]. Furthermore, total surface radiation is the sum of direct solar radiation and diffuse solar radiation, and it indirectly influences the probability of landslide occurrence by affecting the aboveground vegetation and soil moisture [54]. The population density index affects landslide evolution indirectly by calculating human engineering activity [55].
2.1.3. FR and Correlation Analysis of Predisposing Factors
The FR values of the 14 predisposing factors were calculated to build connections between the recorded landslide grid cells and the predisposing factors [26,49,50,56]. Two discrete predisposing factors, namely, distance to river and rock types, were directly used, while the other continuous predisposing factors were first divided into several subclasses, which were then used to calculate the FR values. In this study, the continuous predisposing factors were generally divided into eight subclasses using the Jenks natural break classification method [45,49,56].
The calculated FR values are shown in Table 1, which demonstrates that these factors play important roles in landslide occurrence in Shicheng County. Generally, a higher FR value indicates the more significant influence of a subclass of a predisposing factor on landslide occurrence. Therefore, Table 1 shows that, for example, slope values between 7.5° and 14.9° have a greater effect on landslide occurrence than other values; the closer to the river, the greater the influence on landslide occurrence. Further, metamorphic rock is more conducive to landslide occurrence comparing to other rocks.

Table 1.
Frequency ratios of landslide-related predisposing factors.
2.2. Methods
The spatial data of landslide inventory information and related Predisposing are obtained, then the FRs are calculated. Based on these data, a novel PSO-MLP model is proposed to deal with the LSP in Shicheng County.
2.2.1. Multilayer Perceptron
MLP is a multilayer feed-forward network model with one-way error propagation, and it is one of the most widely used ANNs. MLP can solve the problems of pattern recognition, time series prediction, and so forth [34,57]. The evolution of a landslide, which is a complex physical process, is also a nonlinear system affected by the natural environment and human engineering activities [58,59]. Therefore, compared with deterministic models or general linear statistical methods, the MLP model has excellent nonlinear mapping ability for performing LSP [33].
The MLP model is composed of input, hidden, and output layers, all of which are composed of similar neurons (Figure 4). The connections between the input and hidden layers and between the hidden and output layers are all processed by the weight values. By training and testing these weight values, neural networks form an orderly and stable structure with decision-making ability. Since an MLP with a single hidden layer can approximate a nonlinear system with arbitrary accuracy, this paper mainly studied the single-hidden-layer MLP model [60]. For MLP model with multi-input variables and multi-output variables, the number of neurons in input layer , hidden layer and output layer is respectively set as , and , so that the inputs and outputs of hidden layer neurons are:
where , and are respectively the input, the threshold and the output of the th neuron in hidden layer of MLP; is the weight value between the th input neuron and the th neuron in the hidden layer; is the activation function. Then the input and output of neurons in the output layer are:
where, , and are the input, the threshold and the output of the neuron in the th output layer; is the weight value between the neuron in the th hidden layer and the neuron in the th output layer. In general, the error back-propagation method with conventional gradient descent algorithm, which is used as the training rule of MLP, can adjust the weight values between the neurons based on the estimated errors between the actual values and the MLP predicting values for training samples. The minimum value of the objective function and the optimal weight values of machine learning can be calculated step by step with an iterative solution of the conventional gradient descent algorithm. However, conventional gradient descent has the disadvantages of generating difficulties when searching along a straight line, a local optimum, and a slow convergence rate. To overcome these problems, mini-batch gradient descent, a compromise algorithm based on batch gradient descent and stochastic gradient descent was used to train and test the MLP model. Mini-batch gradient descent has advantages of a global optimum and a high convergence rate.
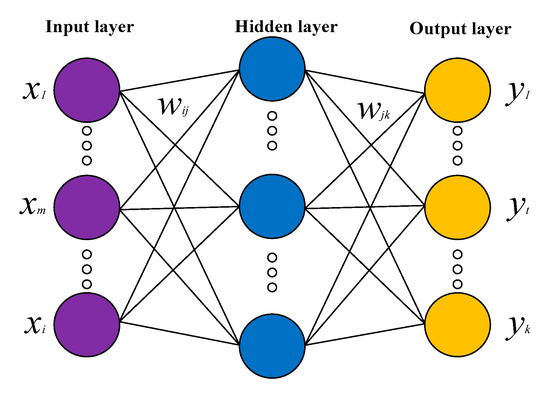
Figure 4.
Perceptron network.
2.2.2. Theory of PSO-MLP Model
PSO is a global optimization algorithm that simulates the foraging behavior of birds in groups [61]. The position and velocity of each particle can be updated based on the globally optimal solution and the current optimal solution; as a result, all the particles move in the direction guided by the objective function. Then, the final global optimal solution can be calculated. The PSO algorithm has better global optimization capability and higher calculation performance than other optimization algorithms (e.g., the genetic algorithm and the ant colony algorithm) [62].
The mini-batch gradient descent algorithm is mainly used to determine the appropriate connection weights between the neurons of MLP. However, several structural parameters, such as the learning rate, learning delay rate, and the learning momentum, are needed for appropriate determination [39]. The learning rate indicates the change range of the weight values between the neurons for each training iteration, and the learning momentum is applied to ensure that the change direction of the weight value is stable. In addition, the number of neurons in the hidden layer has an important effect on the prediction performance of MLP. Thus, it is necessary to select a proper number of neurons in the hidden layer [41]. In this study, the PSO was proposed to determine these four structural parameters of MLP.
The calculation processes of the proposed PSO-MLP are shown in Figure 5. Firstly, the initial parameters of PSO itself were selected, including the number of particles, maximum iterations, and so forth. Secondly, the MLP model with the mini-batch gradient descent algorithm was trained and tested based on landslide and non-landslide samples. Then, the prediction accuracy index of the area under the receiver operating characteristic (ROC) curve (AUC) was selected as the fitness function of the MLP, and this fitness function was also the objective function of PSO. Fourthly, by comparing the AUC value of each particle to the global and local best AUC values, the position and velocity of each particle were updated gradually. Finally, the update process continued until the end of the setting maximum iteration of PSO was reached.
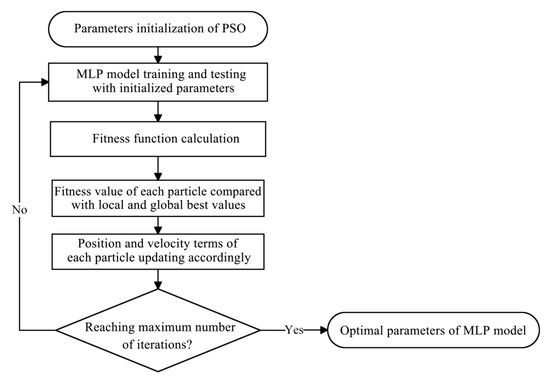
Figure 5.
Flow chart of the PSO-MLP model.
3. Results
3.1. Training and Testing Variables of the Four Models
The model-building processes of LSP can be considered as a 0/1 classification problem. In general, input and output variables are needed to build these binary classification models. In this study, we stored and managed 369 recorded landslide polygons as 2709 landslide grid cells (assigned to 1) in GIS software. Further, 2709 non-landslide grid cells (assigned to 0) were randomly selected from the landslide-free areas [11,13,43]. The recorded landslide grid cells and selected non-landslide grid cells were used as output variables, while the landslide-related predisposing factors were used as input variables of these models. A spatial database containing input and output variables was divided into two parts: a training dataset (70% of the landslide and non-landslide grid cells) for model construction and a testing dataset (the remaining 30% of the landslide and non-landslide grid cells) for model validation. Finally, the FR values of the 14 predisposing factors were used as numeric input variables of these LSP models.
3.2. PSO-MLP Model for LSP
The PSO algorithm was applied to optimize the parameter selection of the MLP model with the mini-batch gradient descent algorithm. First, the PSO algorithm was initialized; for example, the particle population was set to 100, the maximum number of iterations was set to 35, the initial velocity and position of each particle were randomly determined, and the other related parameters were set to default values. Meanwhile, the dimensions of both velocity and position were set to four because there were four parameters (learning rate, learning delay rate, the momentum of the mini-batch gradient descent algorithm, and the number of neurons in the hidden layer of the MLP model) that needed to be determined.
Secondly, several initial parameters of the MLP model were assigned: the number of the hidden layer was set to 1; the learning rate, learning delay rate, and momentum of mini-batch gradient descent were respectively set to 0.001–0.2, 0.001–0.5, and 0.05–0.95; and the number of neurons in the hidden layer ranged from 5 to 35. In addition, some other parameters of MLP were set to default values. Thirdly, the PSO-MLP model was trained and tested based on the datasets introduced in Section 4.3. The PSO-MLP model-building process showed that its optimal parameters were a learning rate of 0.006, a learning decay rate of 0.004, a learning momentum of 0.78, and a hidden-layer neuron number of 23.
Finally, a landslide susceptibility map was produced based on the LSI values calculated by the PSO-MLP model, as shown in Figure 6a. This landslide susceptibility map was divided into five levels using the natural interval point method [63]: very high (10.2%), high (15.7%), moderate (25.7%), low (24.8%), and very low (23.6%) susceptibility levels (Table 2). In general, the high and very high landslide susceptibility levels were mainly distributed in areas within a close distance to river networks and having a relatively low DEM, moderate slope, high population density, and active human engineering building. On the contrary, the low and very low landslide susceptibility levels were mainly located in zones far from river networks and having a high DEM, gentle or steep slopes, high vegetation cover rate, and few human activities.
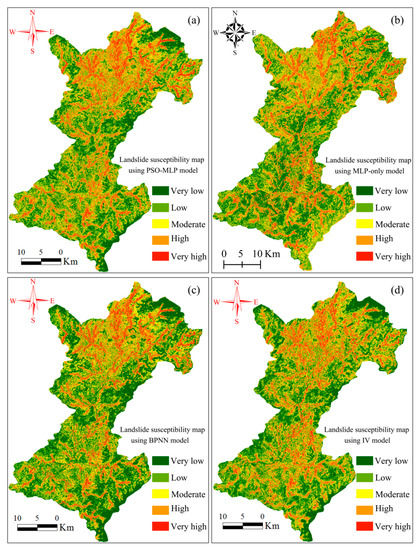
Figure 6.
Landslide susceptibility maps respectively produced by PSO-MLP (a), MLP-only (b), BPNN (c), and IV (d) models.

Table 2.
FR values of landslide susceptibility levels classified by the four models.
3.3. MLP-Only Model for LSP
The MLP-only model with the conventional gradient descent algorithm was used to carry out LSP for comparison. The optimal number of neurons in the hidden layer was determined to be 21 according to the minimum prediction error method [62]. All the other parameters of the MLP-only model were set to default values and/or determined using default methods. The landslide susceptibility map produced by the MLP-only model is shown in Figure 6b and was also divided into very low (27.7%), low (22.9%), moderate (22.7%), high (16.9%), and very high (9.9%) susceptibility levels using the natural interval point method (Table 2).
3.4. BPNN Model
The commonly used BPNN model for LSP is mainly composed of input, hidden, and output layers. Related studies have shown that this model structure can fit any nonlinear function and predict many kinds of complex time series and pattern recognition problem [62]. Therefore, this study also adopted a single-hidden-layer BPNN model to carry out LSP in Shicheng County. Each layer of the BPNN model was composed of a certain number of neurons which connected the input, hidden, and output layers by weight values. Generally, the error back-propagation algorithm was applied to determine these weight values.
In this study, the input–output variables used for PSO-MLP were used again for BPNN model training and testing, and the optimal number of neurons in the hidden layer was set to 20 based on the minimum prediction error method [64]. The other parameters of the BPNN model were set to default values. Finally, the landslide susceptibility map produced by the BPNN model is shown in Figure 6c, which had very low (25.7%), low (22.4%), moderate (24.9%), high (16.1%), and very high (10.9%) susceptibility levels (Table 2).
3.5. IV Model for LSP
The IV model is an indirect conventional statistical model that is often used in LSP [5,65]. According to these researches, the information value of the predisposing factor can be formulated as:
where indicates the number of landslide grid cells with the presence of predisposing factor, indicates the grid cells number with predisposing factor, indicates the sum number of landslide grid cells, indicates the total number of grid cells in Shicheng County. In principle, the presence of predisposing factor does not contribute to landslide evolution when the value of is negative; and the presence of predisposing factor contributes to landslide evolution when the value of is positive. A higher value of suggests a greater correlations between predisposing factor and landslide occurrence. Hence, the total information value , which reflects the landslide susceptible index of each grid cell, can be calculated as:
In this study, the landslide susceptibility map generated by the IV model is shown in Figure 6d, for which the landslide susceptibility levels were divided into very low (23.7%), low (22.8%), moderate (26.7%), high (17.2%), and very high (9.2%) levels (Table 2). The raw distribution of landslide susceptibility indices in Shicheng County was very similar to that generated by the PSO-MLP, MLP-only, and BPNN models.
4. Discussion
4.1. Frequency Ratio Accuracy Analysis
It can be seen from Table 2 that the FR values of the very high susceptibility levels of the PSO-MLP, MLP-only, BPNN, and IV models were 4.546, 4.344, 4.229, and 4.184, respectively, suggesting that a small area with a very high susceptibility level can interpret many landslide locations. Furthermore, the FR values of the landslide susceptibility levels of all four models increased rapidly from the very low to the very high levels, suggesting that the landslide susceptibility maps generated by the four models were all good and reliable. In addition, the FR accuracy of the prediction model was defined as the ratio of the sum of the high and very high susceptibility levels to the sum of all the susceptibility levels [13]. A higher FR accuracy value indicated the greater prediction performance of the model. Table 2 shows that the FR accuracies of the PSO-MLP, MLP-only, BPNN, and IV models were 0.856, 0.829, 0.840, and 0.824, respectively. Hence, the prediction performance of the PSO-MLP model was higher compared with those of the other three models.
4.2. ROC Accuracies of These Models
The prediction performance of the four models was also assessed by the ROC curve method. The y-axis of an ROC curve indicates the sensitivity values of true positive rates, while the x-axis suggests the values of “1-specificity”, which are known as false positive rates. Hence, an ROC curve can be set up as a function of “1-specificity” and can further reflect the prediction accuracy of a 0/1 classification system because of its various cut-off threshold evaluations [7,8,10].
The ROC method has been commonly and successfully applied to landslide susceptibility prediction model evaluation [16,25,26]. An AUC ranging from 0.5 to 1 is the standard index of model prediction performance. The greater the value of the AUC, the better the model prediction performance. Figure 7 shows that the AUC values of the PSO-MLP, MLP-only, BPNN, and IV models were 0.822, 0.791, 0.800, and 0.786, respectively. This precision index once again reflects that the PSO-MLP model had the best prediction performance among these four models.
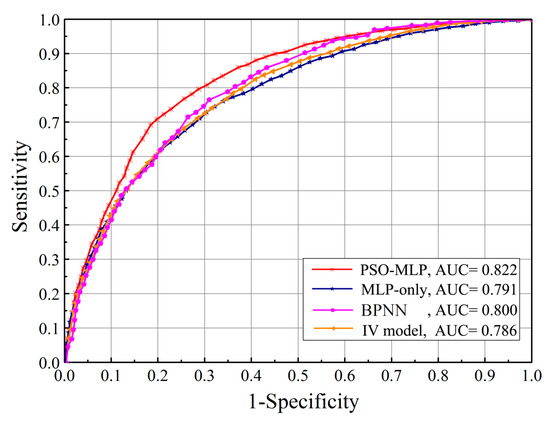
Figure 7.
ROC curves of the four models for LSP.
4.3. PSO-MLP Model-Building Analysis
The PSO-MLP model proposed in this study firstly used FR analysis to build the correlations between recorded landslides and related predisposing factors. FR values are commonly used to obtain the input variables of prediction models and have been acknowledged as an efficient tool. Then, the correlation analysis was used to eliminate the collinear predisposing factors. As a result, the avoidance of redundant information contained in the input variables effectively guaranteed the validity of the prediction models.
Next, the mini-batch gradient descent algorithm was applied to overcome the drawbacks of the conventional gradient descent and stochastic gradient descent algorithms in terms of the non-global optimum, low training speed, reduced accuracy, and lack of parallel computing. In addition, the PSO algorithm was introduced to appropriately screen the optimal structural parameters of MLP, including the learning rate, learning decay rate, learning momentum, and the number of neurons in the hidden layer. The comparative results showed that the proposed PSO-MLP model had significantly better prediction performance than the conventional MLP-only model, suggesting that the PSO-MLP model does address the drawbacks of the MLP model of local optimum and efficient parameter selection. Moreover, it also obtained a more reasonable landslide susceptibility map than the conventional ANN model (i.e., BPNN) and the statistical model (i.e., IV), indicating that the PSO-MLP model is an excellent alternative model and can be extended to other areas for LSP.
5. Conclusions
Based on the PSO and mini-batch gradient descent algorithms, an improved MLP model, namely, the PSO-MLP, was developed to carry out LSP for Shicheng County, China. The FR values of 14 predisposing factors were used as the input variables, while 2709 recorded landslide grid cells and 2709 randomly selected non-landslide grid cells were combined as the output variables of the prediction models. The MLP-only, BPNN, and IV models were also applied to perform LSP for comparison. The results showed that the landslide susceptibility maps produced by all four models were reasonable and reliable. However, the PSO-MLP model had higher prediction capability than the other three models, as assessed by the FR and ROC accuracies.
In summary, the PSO algorithm can effectively optimize the structure parameters of the MLP model with the mini-batch gradient descent algorithm compared with conventional MLP. The proposed PSO-MLP model has the advantage of being able to more globally and accurately predict landslide susceptibility compared with the commonly used BPNN and IV models. This novel PSO-MLP model can be used in other study areas for LSP. Moreover, the produced landslide susceptibility map of Shicheng County is necessary and valuable for the local government to carry out landslide hazard prevention and land use planning.
Author Contributions
Formal analysis: D.L.; investigation: D.L., L.Y. and F.H.; project administration: D.L.; writing—review and editing: D.L., F.H., L.Y., Z.C., J.C., and Z.Y.
Funding
This research is funded by the Natural Science Foundation of China (no. 41807285 and no. 41772370), the Youth National Science Foundation of Jiangxi Province, China (no. 20192BAB216034), and the China Postdoctoral Science Foundation (no. 2019M652287).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Assilzadeh, H.; Levy, J.K.; Wang, X. Landslide catastrophes and disaster risk reduction: A GIS framework for landslide prevention and management. Remote Sens. 2010, 2, 2259–2273. [Google Scholar] [CrossRef]
- Huang, F.; Chen, L.; Yin, K.; Huang, J.; Gui, L. Object-oriented change detection and damage assessment using high-resolution remote sensing images, Tangjiao Landslide, Three Gorges Reservoir, China. Environ. Earth Sci. 2018, 77, 183. [Google Scholar] [CrossRef]
- Guo, Z.; Yin, K.; Gui, L.; Liu, Q.; Huang, F.; Wang, T. Regional rainfall warning system for landslides with creep deformation in three gorges using a statistical black box model. Sci. Rep. 2019, 9, 8962. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, P.T.; Tuyen, T.T.; Shirzadi, A.; Pham, B.T.; Shahabi, H.; Omidvar, E.; Amini, A.; Entezami, H.; Prakash, I.; Phong, T.V.; et al. Development of a novel hybrid intelligence approach for landslide spatial prediction. Appl. Sci. 2019, 9, 2824. [Google Scholar] [CrossRef]
- Chen, T.; Niu, R.; Jia, X. A comparison of information value and logistic regression models in landslide susceptibility mapping by using GIS. Environ. Earth Sci. 2016, 75, 867. [Google Scholar] [CrossRef]
- Park, N.W.; Chi, K.H. Quantitative assessment of landslide susceptibility using high-resolution remote sensing data and a generalized additive model. Int. J. Remote Sens. 2008, 29, 247–264. [Google Scholar] [CrossRef]
- Chen, W.; Shahabi, H.; Zhang, S.; Khosravi, K.; Shirzadi, A.; Chapi, K.; Pham, B.T.; Zhang, T.; Zhang, L.; Chai, H.; et al. Landslide susceptibility modeling based on GIS and novel bagging-based kernel logistic regression. Appl. Sci. 2018, 8, 2540. [Google Scholar] [CrossRef]
- Pourghasemi, H.R.; Beheshtirad, M.; Pradhan, B. A comparative assessment of prediction capabilities of modified analytical hierarchy process (M-AHP) and Mamdani fuzzy logic models using Netcad-GIS for forest fire susceptibility mapping. Geomat. Nat. Hazards Risk 2016, 7, 861–885. [Google Scholar] [CrossRef]
- Althuwaynee, O.F.; Pradhan, B.; Park, H.-J.; Lee, J.H. A novel ensemble bivariate statistical evidential belief function with knowledge-based analytical hierarchy process and multivariate statistical logistic regression for landslide susceptibility mapping. Catena 2014, 114, 21–36. [Google Scholar] [CrossRef]
- Nguyen, T.T.N.; Liu, C.-C. A new approach using ahp to generate landslide susceptibility maps in the chen-yu-lan watershed, taiwan. Sensors 2019, 19, 505. [Google Scholar] [CrossRef]
- Hong, H.; Ilia, I.; Tsangaratos, P.; Chen, W.; Xu, C. A hybrid fuzzy weight of evidence method in landslide susceptibility analysis on the Wuyuan area, China. Geomorphology 2017, 290, 1–16. [Google Scholar] [CrossRef]
- Wang, Q.; Wang, Y.; Niu, R.; Peng, L. Integration of information theory, K-means cluster analysis and the logistic regression model for landslide susceptibility mapping in the Three Gorges Area, China. Remote Sens. 2017, 9, 938. [Google Scholar] [CrossRef]
- Huang, F.; Yao, C.; Liu, W.; Li, Y.; Liu, X. Landslide susceptibility assessment in the Nantian area of china: A comparison of frequency ratio model and support vector machine. Geomat. Nat. Hazards Risk 2018, 9, 919–938. [Google Scholar] [CrossRef]
- Pradhan, B.; Lee, S. Landslide susceptibility assessment and factor effect analysis: Backpropagation artificial neural networks and their comparison with frequency ratio and bivariate logistic regression modelling. Environ. Model. Softw. 2010, 25, 747–759. [Google Scholar] [CrossRef]
- Djeddaoui, F.; Chadli, M.; Gloaguen, R. Desertification susceptibility mapping using logistic regression analysis in the Djelfa Area, Algeria. Remote Sens. 2017, 9, 1031. [Google Scholar] [CrossRef]
- Long, N.T.; De Smedt, F. Analysis and mapping of rainfall-induced landslide susceptibility in a Luoi District, Thua Thien Hue province, Vietnam. Water 2018, 11, 51. [Google Scholar] [CrossRef]
- Truong, X.L.; Mitamura, M.; Kono, Y.; Raghavan, V.; Yonezawa, G.; Truong, X.Q.; Do, T.H.; Tien Bui, D.; Lee, S. Enhancing prediction performance of landslide susceptibility model using hybrid machine learning approach of bagging ensemble and logistic model tree. Appl. Sci. 2018, 8, 1046. [Google Scholar] [CrossRef]
- Park, S.; Kim, J. Landslide susceptibility mapping based on random forest and boosted regression tree models, and a comparison of their performance. Appl. Sci. 2019, 9, 942. [Google Scholar] [CrossRef]
- Park, S.-J.; Lee, C.-W.; Lee, S.; Lee, M.-J. Landslide susceptibility mapping and comparison using decision tree models: A case study of Jumunjin Area, Korea. Remote Sens. 2018, 10, 1545. [Google Scholar] [CrossRef]
- Oh, H.-J.; Lee, S. Shallow landslide susceptibility modeling using the data mining models artificial neural network and boosted tree. Appl. Sci. 2017, 7, 1000. [Google Scholar] [CrossRef]
- Nsengiyumva, J.B.; Luo, G.; Nahayo, L.; Huang, X.; Cai, P. Landslide susceptibility assessment using spatial multi-criteria evaluation model in Rwanda. Int. J. Environ. Res. Public Health 2018, 15, 243. [Google Scholar] [CrossRef] [PubMed]
- Xiao, L.; Zhang, Y.; Peng, G. Landslide susceptibility assessment using integrated deep learning algorithm along the China-Nepal Highway. Sensors 2018, 18, 4436. [Google Scholar] [CrossRef] [PubMed]
- Huang, F.; Zhang, J.; Zhou, C.; Wang, Y.; Huang, J.; Zhu, L. A deep learning algorithm using a fully connected sparse autoencoder neural network for landslide susceptibility prediction. Landslides 2019. [Google Scholar] [CrossRef]
- Huang, F.; Yin, K.; Zhang, G.; Gui, L.; Yang, B.; Liu, L. Landslide displacement prediction using discrete wavelet transform and extreme learning machine based on chaos theory. Environ. Earth Sci. 2016, 75, 1376. [Google Scholar] [CrossRef]
- Shao, X.; Ma, S.; Xu, C.; Zhang, P.; Wen, B.; Tian, Y.; Zhou, Q.; Cui, Y. Planet image-based inventorying and machine learning-based susceptibility mapping for the landslides triggered by the 2018 Mw6.6 Tomakomai, Japan Earthquake. Remote Sens. 2019, 11, 978. [Google Scholar] [CrossRef]
- Tien Bui, D.; Shahabi, H.; Shirzadi, A.; Chapi, K.; Alizadeh, M.; Chen, W.; Mohammadi, A.; Ahmad, B.B.; Panahi, M.; Hong, H.; et al. Landslide detection and susceptibility mapping by airsar data using support vector machine and index of entropy models in Cameron Highlands, Malaysia. Remote Sens. 2018, 10, 1527. [Google Scholar] [CrossRef]
- Huang, F.; Yin, K.; He, T.; Zhou, C.; Zhang, J. Influencing factor analysis and displacement prediction in reservoir landslides—A case study of Three Gorges Reservoir (China). Teh. Vjesn. 2016, 23, 617–626. [Google Scholar]
- Bui, D.T.; Pradhan, B.; Lofman, O.; Revhaug, I.; Dick, O.B. Landslide susceptibility mapping at Hoa Binh province (Vietnam) using an adaptive neuro-fuzzy inference system and GIS. Comput. Geosci. 2012, 45, 199–211. [Google Scholar]
- Tien Bui, D.; Shahabi, H.; Shirzadi, A.; Chapi, K.; Hoang, N.-D.; Pham, B.T.; Bui, Q.-T.; Tran, C.-T.; Panahi, M.; Bin Ahmad, B.; et al. A novel integrated approach of relevance vector machine optimized by imperialist competitive algorithm for spatial modeling of shallow landslides. Remote Sens. 2018, 10, 1538. [Google Scholar] [CrossRef]
- Nourani, V.; Pradhan, B.; Ghaffari, H.; Sharifi, S.S. Landslide susceptibility mapping at zonouz plain, iran using genetic programming and comparison with frequency ratio, logistic regression, and artificial neural network models. Nat. Hazards 2014, 71, 523–547. [Google Scholar] [CrossRef]
- Wang, P.; Bai, X.; Wu, X.; Yu, H.; Hao, Y.; Hu, B.X. GIS-based random forest weight for rainfall-induced landslide susceptibility assessment at a humid region in Southern China. Water 2018, 10, 1019. [Google Scholar] [CrossRef]
- Esteves, J.T.; Rolim, G.D.S.; Ferraudo, A.S. Rainfall prediction methodology with binary multilayer perceptron neural networks. Clim. Dyn. 2019, 52, 2319–2331. [Google Scholar] [CrossRef]
- Pham, B.T.; Bui, D.T.; Prakash, I.; Dholakia, M.B. Hybrid integration of multilayer perceptron neural networks and machine learning ensembles for landslide susceptibility assessment at Himalayan Area (India) using GIS. Catena 2017, 149, 52–63. [Google Scholar] [CrossRef]
- Wang, Z.; Zhuowei, H.U.; Zhao, W.; Guo, Q.; Wan, S. Research on regional landslide susceptibility assessment based on multiple layer perceptron—Taking the hilly area in Sichuan as example. J. Disaster Prev. Mitig. Eng. 2015, 35, 691–698. (in Chinese). [Google Scholar]
- Zare, M.; Pourghasemi, H.R.; Vafakhah, M.; Pradhan, B. Landslide susceptibility mapping at VAZ Watershed (Iran) using an artificial neural network model: A comparison between multilayer perceptron (MLP) and radial basic function (RBF) algorithms. Arab. J. Geosci. 2013, 6, 2873–2888. [Google Scholar] [CrossRef]
- Wang, J.; Chang, Q.; Chang, Q.; Liu, Y.; Pal, N.R. Weight noise injection-based MLPS with group lasso penalty: Asymptotic convergence and application to node pruning. IEEE Trans. Cybern. 2018, 1–19. [Google Scholar] [CrossRef]
- Shan, S.L.; Khalil-Hani, M.; Bakhteri, R. An optimized second order stochastic learning algorithm for neural network training. Neurocomputing 2016, 186, 74–89. [Google Scholar]
- Hordri, N.F.; Yuhaniz, S.S.; Shamsuddin, S.M.; Ali, A. Hybrid biogeography based optimization—multilayer perceptron for application in intelligent medical diagnosis. J. Comput. Theor. Nanosci. 2017, 23, 5304–5308. [Google Scholar] [CrossRef]
- Rivera, E.C.; Da, C.A.; Maciel, M.R.; Maciel, F.R. Ethyl alcohol production optimization by coupling genetic algorithm and multilayer perceptron neural network. Appl. Biochem. Biotechnol. 2006, 132, 969–984. [Google Scholar] [CrossRef]
- Yang, Z.; Cheng, W.; Yu, Z.; Jonathan, L. Mini-batch algorithms with Barzilai-Borwein update step. Neurocomputing 2018, 314, 177–185. [Google Scholar] [CrossRef]
- Babanouri, N.; Nasab, S.K.; Sarafrazi, S. A hybrid particle swarm optimization and multi-layer perceptron;algorithm for bivariate fractal analysis of rock fractures roughness. Int. J. Rock Mech. Min. Sci. 2013, 60, 66–74. [Google Scholar] [CrossRef]
- Hungr, O.; Leroueil, S.; Picarelli, L. The Varnes classification of landslide types, an update. Landslides 2014, 11, 167–194. [Google Scholar] [CrossRef]
- Chen, W.; Peng, J.; Hong, H.; Shahabi, H.; Pradhan, B.; Liu, J.; Zhu, A.X.; Pei, X.; Duan, Z. Landslide susceptibility modelling using GIS-based machine learning techniques for Chongren County, Jiangxi province, China. Sci. Total Environ. 2018, 626, 230. [Google Scholar] [CrossRef] [PubMed]
- Hong, H.; Naghibi, S.A.; Pourghasemi, H.R.; Pradhan, B. GIS-based landslide spatial modeling in Ganzhou City, China. Arab. J. Geosci. 2016, 9, 112. [Google Scholar] [CrossRef]
- Marjanović, M.; Kovačević, M.; Bajat, B.; Voženílek, V. Landslide susceptibility assessment using SVM machine learning algorithm. Eng. Geol. 2011, 123, 225–234. [Google Scholar] [CrossRef]
- Nandi, A.; Shakoor, A. A GIS-based landslide susceptibility evaluation using bivariate and multivariate statistical analyses. Eng. Geol. 2010, 110, 11–20. [Google Scholar] [CrossRef]
- Tsangaratos, P.; Benardos, A. Estimating landslide susceptibility through a artificial neural network classifier. Nat. Hazards 2014, 74, 1489–1516. [Google Scholar] [CrossRef]
- Bui, D.T.; Pradhan, B.; Lofman, O.; Revhaug, I.; Dick, O.B. Spatial prediction of landslide hazards in Hoa Binh province (Vietnam): A comparative assessment of the efficacy of evidential belief functions and fuzzy logic models. Catena 2012, 96, 28–40. [Google Scholar]
- He, S.; Pan, P.; Dai, L.; Wanga, H. Application of kernel-based fisher discriminant analysis to map landslide susceptibility in the Qinggan River Delta, Three Gorges, China. Geomorphology 2012, 171, 30–41. [Google Scholar] [CrossRef]
- Chen, W.; Pourghasemi, H.R.; Panahi, M.; Kornejady, A.; Wang, J.L.; Xie, X.S.; Cao, S.B. Spatial prediction of landslide susceptibility using an adaptive neuro-fuzzy inference system combined with frequency ratio, generalized additive model, and support vector machine techniques. Geomorphology 2017, 297, 69–85. [Google Scholar] [CrossRef]
- Li, Y.; Huang, J.; Jiang, S.-H.; Huang, F.; Chang, Z. A web-based GPS system for displacement monitoring and failure mechanism analysis of reservoir landslide. Sci. Rep. 2017, 7, 17171. [Google Scholar] [CrossRef]
- Jiang, S.-H.; Huang, J.; Huang, F.; Yang, J.; Yao, C.; Zhou, C.-B. Modelling of spatial variability of soil undrained shear strength by conditional random fields for slope reliability analysis. Appl. Math. Model. 2018, 63, 374–389. [Google Scholar] [CrossRef]
- Liu, W.; Luo, X.; Huang, F.; Fu, M. Uncertainty of the soil–water characteristic curve and its effects on slope seepage and stability analysis under conditions of rainfall using the Markov Chain Monte Carlo Method. Water 2017, 9, 758. [Google Scholar] [CrossRef]
- Dixon, N.; Brook, E. Impact of predicted climate change on landslide reactivation: Case study of Mam Tor, UK. Landslides 2007, 4, 137–147. [Google Scholar] [CrossRef]
- Duc, D.M. Rainfall-triggered large landslides on 15 December 2005 in Van Canh district, Binh Dinh province, Vietnam. Landslides 2013, 10, 219–230. [Google Scholar] [CrossRef]
- Chen, W.; Xie, X.; Wang, J.; Pradhan, B.; Hong, H.; Bui, D.T.; Duan, Z.; Ma, J. A comparative study of logistic model tree, random forest, and classification and regression tree models for spatial prediction of landslide susceptibility. Catena 2017, 151, 147–160. [Google Scholar] [CrossRef]
- Fortin, J.G.; Anctil, F.; Parent, L.E. Comparison of multiple-layer perceptrons and least squares support vector machines for remote-sensed characterization of in-field Lai patterns—A case study with potato. Can. J. Remote Sens. 2014, 40, 75–84. [Google Scholar] [CrossRef]
- Huang, F.; Huang, J.; Jiang, S.; Zhou, C. Landslide displacement prediction based on multivariate chaotic model and extreme learning machine. Eng. Geol. 2017, 218, 173–186. [Google Scholar] [CrossRef]
- Huang, F.; Luo, X.; Liu, W. Stability analysis of hydrodynamic pressure landslides with different permeability coefficients affected by reservoir water level fluctuations and rainstorms. Water 2017, 9, 450. [Google Scholar] [CrossRef]
- Guo, W.; Wei, H.; Zhao, J.; Zhang, K. Theoretical and numerical analysis of learning dynamics near singularity in multilayer perceptrons. Neurocomputing 2015, 151, 390–400. [Google Scholar] [CrossRef]
- Eberhart, R.C.; Kennedy, J. A new optimizer using particle swarm theory. In Proceedings of the Sixth International Symposium on Micro Machine and Human Science, Nagoya, Japan, 4–6 October 1995; pp. 39–43. [Google Scholar] [CrossRef]
- Huang, F.; Huang, J.; Jiang, S.-H.; Zhou, C. Prediction of groundwater levels using evidence of chaos and support vector machine. J. Hydroinf. 2017, 19, 586–606. [Google Scholar] [CrossRef]
- Huang, F.; Yin, K.; Huang, J.; Lei, G.; Peng, W. Landslide susceptibility mapping based on self-organizing-map network and extreme learning machine. Eng. Geol. 2017, 223, 11–22. [Google Scholar] [CrossRef]
- Pradhan, B.; Lee, S. Regional landslide susceptibility analysis using back-propagation neural network model at Cameron Highland, Malaysia. Landslides 2010, 7, 13–30. [Google Scholar] [CrossRef]
- Sharma, L.P.; Patel, N.; Ghose, M.K.; Debnath, P. Development and application of Shannon’s entropy integrated information value model for landslide susceptibility assessment and zonation in Sikkim Himalayas in India. Nat. Hazards 2015, 75, 1555–1576. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).