Efficient Conjunctive Keywords Search over Encrypted E-Mail Data in Public Key Setting

Abstract

Searchable public key encryption supporting conjunctive keywords search (SPE-CKS) enables data users to retrieve the encrypted data of interest from an untrusted server. Based on SPE-CKS, one can realize a multi-keywords search over the encrypted e-mails. In this paper, we propose an efficient SPE-CKS scheme by utilizing a keyword conversion method and the bilinear map technique. Our scheme is proven to be secure against chosen keyword attack under a standard security definition and can also withstand the keywords guessing attack. Furthermore, we design an experiment over a real world e-mail dataset to illustrate that our scheme has a better performance on time and space complexities than the previous schemes. A detailed analysis shows that our scheme is very practical for the encrypted e-mail system in the mobile cloud environment.

1. Introduction

Nowadays, with the rapid development of cloud computing technology, enterprises and individuals can obtain good e-mail services at lower costs. However, the events of leakage of sensitive e-mail data from the cloud server have occurred occasionally since e-mail data stored in the server is in plaintext. How to safely and effectively retrieve e-mail data from the cloud server is one of the concerns in the e-mail system. A straightforward solution is encrypting e-mails before outsourcing it to the cloud server. But the traditional encryption schemes disrupt the structure of the original data and then hinder users querying e-mails stored in the cloud server. To solve this problem, searchable encryption (SE) [1,2]—which can realize information retrieval over the encrypted data—is regarded as one of suitable techniques.

SE supporting keyword search can be built in symmetric key setting or public key setting. In symmetric key setting, authorized users sends encrypted documents and encrypted indexes to a server and retrieve documents containing certain keywords which they query by using a trapdoor without loss of data confidentiality. In this setting, the index and the trapdoor are constructed by using the same secret key. However, if one of the authorized users leaks the secret key, all authorized users’ data will be revealed. Thus, it is impractical in some applications, such as encrypted e-mail system (EES) [2] and wireless sensor networks (WSNs) [3]. For the EES system, there are three roles in an EES system, that is, data senders, data receiver and service provider. Under this scenario, any data senders use the searchable public key encryption (SPE) scheme to encrypt e-mails and send these encrypted e-mails to service provider. After that, data receiver performs a secure query to the e-mail service provider and the service provider executes query operations over the encrypted e-mails and returns e-mails associated to this query. The interactive process among these three roles is described in Figure 1. In this application scenario, the security requirements is summarized as follows: (1) any data senders can generate the encrypted e-mails; (2) only data receiver can perform data query and decrypt the encrypted e-mails; (3) anyone except the data receiver cannot obtain the contents of encrypted e-mails. According to these security requirements, we can find that SPE is very suitable for constructing a secure EES than searchable symmetric key encryption (SSE).

The first SPE scheme supporting keyword search was introduced by Boneh et al. [2]. But, this scheme only supports single keyword search. For supporting multi-keywords search, Part et al. first proposed a SPE supporting conjunctive keywords search scheme [4], which is called the public key encryption with conjunctive keywords search (PECK). After that, an efficient PECK scheme [5] was proposed to reduce the time and space cost. Note that these schemes all need keyword fields as compulsory information, which is not practical for many applications. For example, if documents which senders send to the server are scientific papers, each paper has its keyword list and the keywords in the list are arranged in the alphabetical order. So, the same keyword might occur in different positions of the keyword list for different papers. In this situation, schemes with fixed-position keyword fields are not suitable for a keywords search. To overcome this problem, Boneh and Waters introduced a public key encryption scheme called hidden vector encryption (HVE) which can support conjunctive keyword search without keyword field [6]. To achieve a better efficiency, a PECK scheme without keyword field was proposed in Reference [7]. In order to achieve advanced keywords search function, many SPE schemes which can support conjunctive or disjunctive keywords search have been proposed in recent years [8,9,10]. For the security concern, in order to withstand the keyword guessing attack launched by the outsider attacker and the malicious insider, the SPE scheme against the keyword guessing attack was given in Reference [11].

Our Work. Considering that SPE scheme supporting conjunctive keywords search (SPE-CKS) without keyword field has a good application in many scenarios, especially, for example, encrypted e-mail system, this paper is to construct an efficient and secure SPE-CKS scheme without the keyword field. More precisely, we make two types of contributions, improving both the efficiency and the security of the recent schemes of SPE-SMKS introduced in References [7,8,10]. These contributions are listed as follows.

(1)

Based on the keyword conversion method introduced in Reference [10], we create a novel keyword conversion method which can change the index and query keyword set into an attribute and a predicate vector, respectively. The dimension of vector generated by using our method is much less than that generated by adopting the previous method. Through applying the existing technique called bilinear map to encrypt the attribute and predicate vectors, our scheme achieves a better performance in time and space complexities than the previous schemes.

(2)

For security concern, we give a detailed proof to demonstrate that our scheme is secure against chosen keyword attack. Moreover, inspired by the idea introduced in Reference [11], through sharing a secret number between the senders and the receiver, our scheme can limit the capability of index building for adversaries. If the adversaries fail to generate the index, the adversaries cannot launch the keyword guessing attack. Compared with the previous schemes, our scheme can both defend against chosen keyword attack and keyword guessing attack.

Besides, we also design a detailed experiment based on a real-world e-mail dataset to show the advantage of our scheme.

Organization. This paper is organized as follows. Related work is discussed in Section 2. In Section 3, we define model of SPE-CKS and security model of SPE-CKS and also introduce some background related to our work. In Section 4, we introduce the keyword conversion method and the concrete SPE-CKS scheme. The security proof of our scheme is also given. In Section 5, we analyze the time and space complexities of our scheme and give a detailed experiment to verify the efficiency of our scheme. This paper concludes in Section 6.

2. Related Work

Searchable encryption supporting keyword search has been researched widely in recent years, which are grouped into two categories. One is searchable symmetric key encryption (SSE); the other is searchable public key encryption (SPE).

In symmetric key setting, Song et al. introduced the concept of search over encrypt data and gave an approach about it [1]. Goh defined the notion of security for searchable encryption and presented an effective scheme by using Bloom filter [12]. However, these works only provide a single keyword search. The concept of conjunctive keyword search on encrypted data in symmetric key setting was first proposed by Golle et al. [13]. In their paper, they also gave two constructions which are based on this concept. In comparing with Golle’s work, subsequent works [14,15] were trying to construct schemes which had much better performance in computational and communication cost. Considering that the practical scheme requires supporting multi-keyword search and returning the top-k search results, Cao et al. [16] constructed a multi-keyword rank search scheme over encrypted cloud data. After that, many SSE schemes supporting rank search were given in References [17,18], which achieve a better search performance.

In public key setting, Boneh et al. defined the concept of public key encryption with keyword search and gave one construction of importance which were related to the Identity-Based Encryption scheme proposed by Boneh and Frannklin [19]. Abdalla et al. defined the computational and statistical notion of PEKS and presented a new scheme that is statistically consistent [20]. However, their works only support a single keyword search in public key setting. The concept and security model of conjunctive keyword search over encrypted data in public key system were proposed in Reference [4] in which they also gave two PECK schemes. The first scheme needs lots of bilinear pairing computations and the second scheme needs private keys in proportion to the number of keywords. Then, Hwang and Lee designed a more efficient scheme on time and space complexities than the previous works and introduced a new concept called a multi-user PECK scheme which can effectively manage the encrypted documents in a server for a group of users [5]. The above PECK schemes all use keyword fields as an addition of information. In order to eliminate the keyword field, Boneh and Waters proposed a public key system that supports comparison queries(such as $x\ge a$) and conjunctive keywords queries [6]. To achieve a better performance on time and space complexities, Zhang and Zhang addressed this issue and proposed a more efficient PECK scheme without using keyword field [7]. For supporting disjunctions and polynomial equations, Katz et al. proposed a predicate encryption supporting inner product scheme (IPE) [21]. In their work, they also give a method for applying IPE scheme to realize conjunctive or disjunctive keywords search. To achieve a fully secure level, fully secure IPE scheme was proposed by Lewko et al. in Reference [22]. After this, an IPE scheme with less time and space cost was introduced in Reference [8]. In the past of few years, numerous efforts have been devoted to constructing a SPE scheme with advanced keywords search. Wang et al. described a new SPE scheme to support range search [23]. Zhang et al. achieved disjunctive and conjunctive keywords search over encrypted data [9,10]. Zhu et al. proposed a SPE scheme supporting fuzzy keyword search [24]. Byun et al. [15] firstly defined offline keyword guessing attack and showed that SPE schemes are insecure against keyword guessing attack. Jeong et al. [25] pointed that the consistency implies insecurity of a PEKS scheme against keyword guessing attack. Addressing this problem, two works [26,27] were constructed to defeat the offline keyword guessing attack. The first work using the method of registered keyword was given by Tang and Chen [27]. The second work given by Hyun et al. [26] can defeat keyword guessing attack since only the designated server can test which index is related with a given trapdoor by using the server’s private key. However, their schemes only against offline keyword guessing attacks by outsider attackers. After that, based on the scheme [28], Lu et al. proposed a SPE scheme which is secure against KG attacks by either outsider attackers or malicious insider servers [11].

3. Preliminaries

In this section, we give the model and security definition of SPE-CKS. In addition, we will briefly introduce some tools adopted in our scheme, including the bilinear map and the complexity assumptions.

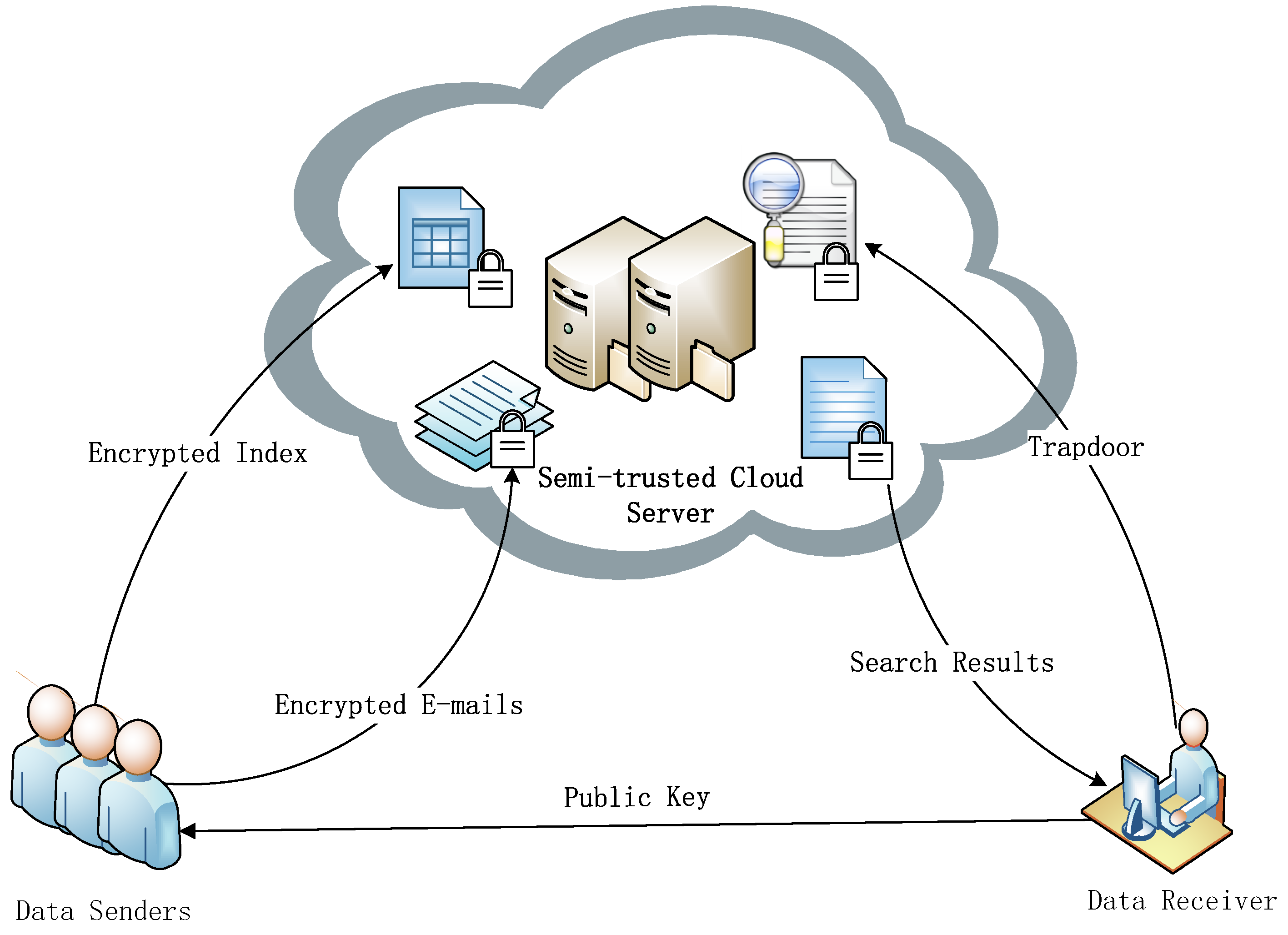
3.1. Model of Spe-Cks

In SPE-CKS, there are three roles: e-mail sender, receiver and service provider (server). Let $p{k}_R$ and $s{k}_R$ be e-mail receiver’s public key and secret key and $p{k}_S$ and $s{k}_S$ be e-mail senders’ public key and secret key. An e-mail sender can send an encrypted e-mail M to a server with an encrypted index generated by using the keywords $w_1,w_2,\dots ,w_n$ of M and the keys $p{k}_R$, $p{k}_S$, $s{k}_S$. When an e-mail receiver wants to query e-mails with keywords $q_1,q_2,\dots ,q_m$ where $m\le n$, the receiver generates a trapdoor by using these keywords and the keys $p{k}_R$, $p{k}_S$, $s{k}_R$ and then sends this trapdoor to the e-mail service provider. When the server receives the trapdoor, the server tests each secure index against the trapdoor and returns the matched e-mails to the receiver. From the above, we give the definition of the SPE-CKS model, which is regared as a variant of PECK model proposed in Reference [4].

Definition 1.

SPE-CKS consists of 5 probabilistic polynomial time (PPT) algorithms: $KeyGe{n}_R$, $KeyGe{n}_S$, IndexBuild, Trapdoor, Test. There are:

1.

$KeyGe{n}_R$($1^n$): Given a security parameter $1^n$, the algorithm is executed by the receiver and generates the a pair of key $(p{k}_R,s{k}_R)$, where $p{k}_R$ and $s{k}_R$ are the public and private key for the receiver, respectively.

2.

$KeyGe{n}_S$($1^n$): This is a key generation algorithm for the data sender. The algorithm creates a pair of key $(p{k}_S,s{k}_S)$, where $p{k}_S$ and $s{k}_S$ are the public and private key for the sender, respectively.

3.

IndexBuild($p{k}_S$, $s{k}_S$, $p{k}_R$, W): The algorithm is executed by the sender to encrypt a keyword set $W=\{w_1,w_2,\dots ,w_n\}$ without keyword field. It produces a searchable index $I_W$ of W by using the keys $p{k}_S$, $s{k}_S$ and $p{k}_R$.

4.

Trapdoor($p{k}_R$, $s{k}_R$, $p{k}_S$, Q): The algorithm is executed by the receiver to construct a trapdoor. Given the keys $p{k}_R$, $s{k}_R$, $p{k}_S$ and the keyword query $Q=\{q_1,q_2,\dots ,q_m\}$ where $m\le n$, the algorithm generates a trapdoor $T_Q$.

5.

Test($p{k}_R$, $p{k}_S$, $T_Q$, $I_W$): The algorithm is executed by the server to test the trapdoor $T_Q$ whether matches the index $I_W$ or not. It takes a trapdoor $T_Q$, a secure index $I_W$ and the public keys $p{k}_S,p{k}_R$ as input, then outputs 1 if $Q\subseteq W$ or 0 otherwise.

Correctness of SPE-CKS. Let W and Q be two keywords sets. $(p{k}_R,s{k}_R)$, $(p{k}_S,s{k}_S)$, $I_W$ and $T_Q$ are generated correctly by algorithms $KeyGe{n}_R\left(1^n\right)$, $KeyGe{n}_S\left(1^n\right)$, $IndexBuild$($p{k}_S$, $s{k}_S$, $p{k}_R$, W) and $Trapdoor$($p{k}_R$, $s{k}_R$, $p{k}_S$, Q), respectively. If $Q\subseteq W$, the $Test$($p{k}_R$, $p{k}_S$, $T_Q$, $I_W$) outputs 1. Otherwise, it outputs 1 with negligible probability.

3.2. Security Definition of Spe-Cks

To prove the security of the SPE-CKS scheme, we introduce a security game called indistinguishability of ciphertext from random against chosen keyword attacks (IND-CR-CKA) defined by Hwang and Lee [5]. IND-CR-CKA is a variant of security game called indistinguishability of ciphertext from ciphertext (ICC) defined by Golle et al. [13] for a symmetric key system. The essential of IND-CR-CKA of SPE-CKS is that the scheme should ensure that the encrypted indices of two challenge keyword sets cannot be distinguished by any adversaries.

The IND-CR-CKA game is as follows:

• Setup: the challenger $\mathbb{C}$ runs the $KeyGe{n}_R$($1^n$) and $KeyGe{n}_S$($1^n$) algorithms to generate $p{k}_R$, $s{k}_R$, $p{k}_S$ and $s{k}_S$ and gives $p{k}_R$ and $p{k}_S$ to the attacker $\mathbb{A}$.
• Phase 1: the attacker $\mathbb{A}$ can adaptively ask the challenger $\mathbb{C}$ for the trapdoor $T_Q$ for any query Q of his choice. Moreover, $\mathbb{A}$ can adaptively ask $\mathbb{C}$ for the encrypted index for any keyword set of his choice.
• Challenge: $\mathbb{A}$ selects a target keyword set $W^{*}$ and sends it to the $\mathbb{C}$. $\mathbb{C}$ selects a random keyword set R. The restrictions are that the secure indices of $W^{*}$ and R have not been obtained in the previous phase and the trapdoor queried in previous phase can not distinguish $W^{*}$ from R. Then, $\mathbb{C}$ picks a random bit $\beta \in \{0,1\}$. Suppose that $W_0=W^{*}$ and $W_1=R$, $\mathbb{C}$ produces $I_{\beta }=IndexBuild(p{k}_R,s{k}_S,p{k}_S,W_{\beta })$ and sends $\{I_{\beta },W_0,W_1\}$ to $\mathbb{A}$.
• Phase 2: $\mathbb{A}$ can continue asking for trapdoor $T_Q$ and index $I_W$ for any query Q and keyword set W of his choice. The restrictions in this phase are the same as that in the challenge phase.
• Response:the attacker $\mathbb{A}$ outputs ${\beta }^{{}^{\prime }}\in \{0,1\}$ and wins the game if ${\beta }^{{}^{\prime }}=\beta$.

So, $\mathbb{A}$’s advantage can be expressed as a function of the security parameter ($1^n$):

$$Ad{v}_{\mathbb{A}}^{IND-CR-CKA}\left(1^n\right)=|Pr[{\beta }^{{}^{\prime }}=\beta ]-\frac{1}{2}|$$

Based on the game above, the security definition is described as follows:

Definition 2.

We say that a SPE-CKS is IND-CR-CKA secure if for any PPT attacker $\mathbb{A}$ according to the game IND-CR-CKA, the function $Ad{v}_{\mathbb{A}}^{IND-CR-CKA}\left(1^n\right)$ is negligible.

Jeong et al. [25] pointed that the consistency implies insecurity of a SPE scheme against keyword guessing attacks, since the public key in the tradition SPE scheme can be accessed by anyone and anyone can create the secure index. When trapdoors are obtained by attackers, attackers can run keyword guessing attack to guess the keywords contained in the indices and trapdoors. Inspired by the idea in Reference [11], by limiting the adversary’s ability to generate the index, our scheme can defend against the offline guessing attack.

3.3. Bilinear Map

The definition of the bilinear map was introduced in Reference [2]. Let $G_1$, $G_2$ be two cyclic groups of lager prime order q. A bilinear pairings map $\widehat{e}:G_1\times G_1\to G_2$ can be defined, satisfying the following properties:

• Bilinear: $\widehat{e}(u^a,v^b)=\widehat{e}{(u,v)}^{ab}$, where $u,v\in G_1$ and $a,b\in Z_q^{*}$ ;
• Non-degenerate: $\widehat{e}$ does not send all pairs of points in $G_1\times G_1$ to the identity in $G_2$. If g is a generator of $G_1$ then $\widehat{e}(g,g)$ is a generator of $G_2$;
• Computable: There is an efficient algorithm to compute $\widehat{e}(u,v)$, for any $u,v\in G_1$.

A bilinear pairing map satisfying three properties above is reckoned as an admissible bilinear map. An efficient admissible bilinear map can be constructed by using the Weil pairing or the Tate pairing proposed in Reference [29] .

3.4. Complexity Assumption

We review two complexity assumptions related to bilinear map named Decision n-Bilinear Diffie-Hellman Inversion (D-n-BDHI) assumption proposed in Reference [30] and computational Diffie-Hellman (CDH) assumption introduced in Reference [31]. The security proof of our scheme is based on these two assumptions.

Decision n-Bilinear Diffie-Hellman Inversion Assumption [30]: An algorithm $\mathbb{C}$ which outputs $b\in \{0,1\}$ has advantage $\epsilon$ in solving the D-n-BDHI assumption in $G_1$ if:

$$Ad{v}_{\mathbb{C}}^{D-n-BDHI}=|Pr[\mathbb{C}(P,xP,x^{2}P,\dots ,x^{n}P,\widehat{e}{(p,p)}^{\frac{1}{x}})=1]-Pr[\mathbb{C}(P,xP,x^{2}P,\dots ,x^{n}P,R)=1]|\ge \epsilon$$

where the probability is over the random choice of $x\in Z_q^{*}$, the random choice of a generator $P\in G_1^{*}$, the random choice $R\in G_2^{*}$ and random bits used by $\mathbb{C}$.

Definition 3.

It can be said that the decision(t,n,ϵ) n-Bilinear Diffie-Hellman Inversion assumption holds in $G_1$, if no t-time algorithm has advantage at least ϵ in solving the decision n-Bilinear Diffie-Hellman Inversion problem in $G_1$.

Computational Diffie-Hellman (CDH) Assumption [31]: Consider a cyclic group G of a prime order q. The $CDH$ assumption states that, for a randomly chosen generator g and the random integers $a,b\in Z_q^{*}$, given a tuple $(g,g^a,g^b)$, it is computationally intractable to compute the value $g^{\left(ab\right)}$.

4. Proposed Spe-Cks Scheme

In this section, we first introduce a keyword conversion method which transforms the index and query keyword sets into the index and query vectors, respectively. Then, through encrypting these vector by adopting the bilinear pairs over a prime order group, a concrete SPE-CKS scheme will be proposed. Finally, a rigorous security proof is given to verify the security of the proposed SPE-CKS scheme.

4.1. Keyword Conversion Method

The keyword conversion method is similar with the one proposed by Zhang et al. [10]. Let $\varphi$ be a random string, $\varphi \in {\{0,1\}}^{*}$. Let a hash function $H_1$ be ${\{0,1\}}^{*}\to Z_q^{*}$, which can map a keyword $w\in {\{0,1\}}^{*}$ to a integer. Let q be a large prime which is larger than the size of the dictionary. So, $H_1$ can be collision-resistance, which means that, if $i\ne j$, then $H_1\left(w_i\right|\varphi )\ne H_1\left(w_j\right|\varphi )$, where $w_i$ and $w_j$ are two distinct keywords and $w_i|\varphi$ means a concatenation operation over $w_i$ and $\varphi$. The details of this method is described as follows.

(1)

For an index keyword set $W=\{w_1,w_2,\dots ,w_n\}$, the following function is given.

$$\begin{array}{cc}\hfill f\left(x\right)& =(x-H_1\left(w_1\right|\varphi ))(x-H_1\left(w_2\right|\varphi ))\dots (x-H_1\left(w_n\right|\varphi ))\hfill \\ \hfill & =a_n{x}^n+a_{n-1}{x}^{n-1}+\dots +a_0{x}^0\hfill \end{array}$$

The coefficients of the $f\left(x\right)$ can be built as an index vector $\overrightarrow{a}=\{a_0,a_1,\dots ,a_n\}$.

(2)

For an query keyword set $Q=\{q_1,q_2,\dots ,q_m\}$, a vector $\overrightarrow{x}=\{x_0,x_1,\dots ,x_n\}$ can be obtained, where $x_i=H_1{\left(q_1\right|\varphi )}^i+H_1{\left(q_2\right|\varphi )}^i+\dots +H_1{\left(q_m\right|\varphi )}^i$ and $i\in [0,n]$.

Note that if there is $Q\subseteq W$, it is easy to find that $\overrightarrow{a}·\overrightarrow{x}=0$. This property can be used for the keywords search. The concrete SPE-CKS scheme is given in the next subsection.

4.2. Construction

Based on the method described in Section 4.1, the index vector $\overrightarrow{a}$ and the query vector $\overrightarrow{x}$ are obtained by converting W and Q, respectively. Then, through encrypting $\overrightarrow{a}$ and $\overrightarrow{x}$ under two cyclic groups over a prime order, the encrypted index for W and the trapdoor for Q are built. By utilizing the bilinear pairing technique, the test algorithm tests whether Q is a subset of W. The concrete construction of SPE-CKS scheme is given as follows.

-

$KeyGe{n}_R$($1^n$): Given a security parameter $1^n$, the algorithm generates three cyclic groups G, $G_1$, $G_2$ of prime order q and an admissible bilinear pairing $\widehat{e}:G_1\times G_1\to G_2$ and picks a random generator $g_0$ of G, a random generator g of $G_1$ and two hash functions $H_1:{\{0,1\}}^{*}\to Z_q^{*}$ and $H_2:G_2\to {\{0,1\}}^{lo{g}_2^q}$. $\widehat{e},H_1,H_2$ and g are open to the public. Choosing $n+3$ random numbers ${\alpha }_0,{\alpha }_1,\dots ,{\alpha }_n,\beta ,t\in Z_q^{*}$, it outputs the public key $p{k}_R=\{X_0=g^{{\alpha }_0},X_1=g^{{\alpha }_1},\dots ,X_n=g^{{\alpha }_n},Y=g^{\beta },\mu =\widehat{e}(g,g),g_0,T=g_0^t\}$ and the secret key $s{k}_R=\{{\alpha }_0,{\alpha }_1,\dots ,{\alpha }_n,\beta ,t\}$.

-

$KeyGe{n}_S$($1^n$, $p{k}_R$): Given a security parameter $1^n$, the algorithm generates a hash function $H_3:G\to {\{0,1\}}^{*}$. Randomly choosing a number $s\in Z_q^{*}$, it outputs $p{k}_S=\{S=g_0^s,H_3\}$ and $s{k}_S=\left\{s\right\}$.

-

$IndexBuild$($p{k}_R$, $p{k}_S$, $s{k}_S$, W): The algorithm first computes $\varphi =H_3\left(T^s\right)=H_3\left(g^{\left(ts\right)}\right)$. Then, given a keyword set $W=\{w_1,w_2,\dots ,w_n\}$, the algorithm constructs a n-degree polynomial $f\left(x\right)=a_n{x}^n+a_{n-1}{x}^{n-1}+\dots +a_{1}x+a_0=(x-H_1\left(w_1\right|\varphi ))(x-H_1\left(w_2\right|\varphi ))\dots (x-H_1\left(w_n\right|\varphi ))$ by using the keyword conversion method mentioned in Section 4.1, where $H_1\left(w_1\right|\varphi ),H_1\left(w_2\right|\varphi ),\dots ,H_1\left(w_n\right|\varphi )$ are n roots of the equation $f\left(x\right)=0$. Given a random numbers r and the coefficient of $f\left(x\right)$ that is $a_n,a_{n-1},\dots ,a_0$, it computes $C_i=X_i^r\times g^{r{a}_i}=g^{r(a_i+{\alpha }_i)}$ for each $i\in [0,n]$ by using $p{k}_R$. Let $C_W=Y^r=g^{r\beta }$ and $D_W=H_2\left({\mu }^r\right)$, the index of the keyword set W is: $I_W=(C_0,C_1,\dots ,C_n,C_W,D_W)$.

-

$Trapdoor$($p{k}_R$, $p{k}_S$, $s{k}_R$, Q): The algorithm computes $\varphi =H_3\left(S^t\right)=H_3\left(g^{\left(ts\right)}\right)$. Given a keyword set $Q=\{q_1,q_2,\dots ,q_m\}$, it selects a random number $u\in Z_q$ and computes $T_i=g^{\frac{H_1{\left(q_1\right|\varphi )}^i+H_1{\left(q_2\right|\varphi )}^i+\dots +H_1{\left(q_m\right|\varphi )}^i}{u\beta +{\sum }_{j=0}^n{\alpha }_j(H_1{\left(q_1\right|\varphi )}^j+H_1{\left(q_2\right|\varphi )}^j+\dots +H_1{\left(q_m\right|\varphi )}^j)}}$ for each $i\in [0,n]$ by using $s{k}_R$. Let $T=g^{\frac{u}{u\beta +{\sum }_{j=0}^n{\alpha }_j(H_1{\left(q_1\right|\varphi )}^j+H_1{\left(q_2\right|\varphi )}^j+\dots +H_1{\left(q_m\right|\varphi )}^j)}}$, the trapdoor for the keyword query Q is $T_Q=(T_0,T_1\dots ,T_n,T)$.

-

$Test$($p{k}_R$, $p{k}_S$, $T_Q$, $I_W$): Given a trapdoor $T_Q=(T_0,T_1,\dots ,T_n,T)$ and a secure index $I_W=(C_0,C_1,\dots ,C_n,C_W,D_W)$, the algorithm computes ${\theta }_1={\prod }_{i=0}^n\widehat{e}(C_i,T_i)$, ${\theta }_2=\widehat{e}(C_W,T)$ and tests if $H_2({\theta }_1\times {\theta }_2)=D_W$. If so, outputs 1; otherwise, outputs 0.

Correctness. For an index $I_W=(C_0,C_1,\dots ,C_n,C_W,D_W)$ and a trapdoor $T_Q=(T_0,T_1\dots ,T_n,T)$, the computation process of $\widehat{e}(C_i,T_i)$ is as follows:

$$\begin{array}{cc}\hfill \widehat{e}(C_i,T_i)& =\widehat{e}(g^{r(a_i+{\alpha }_i)},g^{\frac{H_1{\left(q_1\right|\varphi )}^i+H_1{\left(q_2\right|\varphi )}^i+\dots +H_1{\left(q_m\right|\varphi )}^i}{u\beta +{\sum }_{j=0}^n{\alpha }_j(H_1{\left(q_1\right|\varphi )}^j+H_1{\left(q_2\right|\varphi )}^j+\dots +H_1{\left(q_m\right|\varphi )}^j)}})\hfill \\ \hfill & =\widehat{e}{(g,g)}^{\frac{r{a}_i(H_1{\left(q_1\right|\varphi )}^i+H_1{\left(q_2\right|\varphi )}^i+\dots +H_1{\left(q_m\right|\varphi )}^i)+r{\alpha }_i(H_1{\left(q_1\right|\varphi )}^i+H_1{\left(q_2\right|\varphi )}^i+\dots +H_1{\left(q_m\right|\varphi )}^i)}{u\beta +{\sum }_{j=0}^n{\alpha }_j(H_1{\left(q_1\right|\varphi )}^j+H_1{\left(q_2\right|\varphi )}^j+\dots +H_1{\left(q_m\right|\varphi )}^j)}}\hfill \end{array}$$

According to the above, the result of ${\theta }_1$ is:

$$\begin{array}{cc}\hfill {\theta }_1& =\prod _{i=0}^n\widehat{e}(C_i,T_i)\hfill \\ \hfill & =\prod _{i=0}^n\widehat{e}{(g,g)}^{\frac{r{a}_i(H_1{\left(q_1\right|\varphi )}^i+H_1{\left(q_2\right|\varphi )}^i+\dots +H_1{\left(q_m\right|\varphi )}^i)+r{\alpha }_i(H_1{\left(q_1\right|\varphi )}^i+H_1{\left(q_2\right|\varphi )}^i+\dots +H_1{\left(q_m\right|\varphi )}^i)}{u\beta +{\sum }_{j=0}^n{\alpha }_j(H_1{\left(q_1\right|\varphi )}^j+H_1{\left(q_2\right|\varphi )}^j+\dots +H_1{\left(q_m\right|\varphi )}^j)}}\hfill \\ \hfill & =\widehat{e}{(g,g)}^{\frac{r{\sum }_{i=0}^n{a}_i(H_1{\left(q_1\right|\varphi )}^i+H_1{\left(q_2\right|\varphi )}^i+\dots +H_1{\left(q_m\right|\varphi )}^i)+r{\sum }_{i=0}^n{\alpha }_i(H_1{\left(q_1\right|\varphi )}^i+H_1{\left(q_2\right|\varphi )}^i+\dots +H_1{\left(q_m\right|\varphi )}^i)}{u\beta +{\sum }_{j=0}^n{\alpha }_j(H_1{\left(q_1\right|\varphi )}^j+H_1{\left(q_2\right|\varphi )}^j+\dots +H_1{\left(q_m\right|\varphi )}^j)}}\hfill \end{array}$$

Moreover, the result of ${\theta }_2$ is:

$$\begin{array}{cc}\hfill {\theta }_2& =\widehat{e}(C_W,T)=\widehat{e}(g^{r\beta },g^{\frac{u}{u\beta +{\sum }_{j=0}^n{\alpha }_j(H_1{\left(q_1\right|\varphi )}^j+H_1{\left(q_2\right|\varphi )}^j+\dots +H_1{\left(q_m\right|\varphi )}^j)}})\hfill \\ \hfill & =\widehat{e}{(g,g)}^{\frac{ru\beta }{u\beta +{\sum }_{j=0}^n{\alpha }_j(H_1{\left(q_1\right|\varphi )}^j+H_1{\left(q_2\right|\varphi )}^j+\dots +H_1{\left(q_m\right|\varphi )}^j)}}\hfill \end{array}$$

Then, the result of $H_2({\theta }_1\times {\theta }_2)$ is:

$$\begin{array}{cc}\hfill H_2({\theta }_1\times {\theta }_2)& =H_2\left(\widehat{e}{(g,g)}^{\frac{r{\sum }_{i=0}^n{a}_i(H_1{\left(q_1\right|\varphi )}^i+H_1{\left(q_2\right|\varphi )}^i+\dots +H_1{\left(q_m\right|\varphi )}^i)+r{\sum }_{i=0}^n{\alpha }_i(H_1{\left(q_1\right|\varphi )}^i+H_1{\left(q_2\right|\varphi )}^i+\dots +H_1{\left(q_m\right|\varphi )}^i)+ru\beta }{u\beta +{\sum }_{j=0}^n{\alpha }_j(H_1{\left(q_1\right|\varphi )}^j+H_1{\left(q_2\right|\varphi )}^j+\dots +H_1{\left(q_m\right|\varphi )}^j)}}\right)\hfill \\ & =\widehat{e}{(g,g)}^{\frac{r{\sum }_{i=0}^n{a}_i(H_1{\left(q_1\right|\varphi )}^i+H_1{\left(q_2\right|\varphi )}^i+\dots +H_1{\left(q_m\right|\varphi )}^i)}{u\beta +{\sum }_{j=0}^n{\alpha }_j(H_1{\left(q_1\right|\varphi )}^j+H_1{\left(q_2\right|\varphi )}^j+\dots +H_1{\left(q_m\right|\varphi )}^j)}+r}\hfill \end{array}$$

Note that, according to the keyword conversion method introduced in Section 4.1, if $Q\subseteq W$, it must be ${\sum }_{i=0}^n{a}_i(H_1{\left(q_1\right|\varphi )}^i+H_1{\left(q_2\right|\varphi )}^i+\dots +H_1{\left(q_m\right|\varphi )}^i)=0$, which means that $H_2({\theta }_1\times {\theta }_2)=H_2\left(\widehat{e}{(g,g)}^r\right)=D_W$. Therefore, according the equations above, we can argue that our scheme is correct.

4.3. Security Proof

In this subsection, we will give a rigorous proof to show the security of the proposed scheme. The essential of the proof is that we will show the difficulty of breaking our scheme is the same as that of solving the assumption of $(q_T+1)$-BDHI, according to the security game described in Section 3.2. The concrete proof is given as follows.

Theorem 1.

The scheme of SPE-CKS is secure according to IND-CR-CKA game if the decision $(q_T+1)$-BDHI assumption is hard.

Proof. 

Suppose that an algorithm $\mathbb{A}$ has advantage $ϵ$ in breaking the SPE-CKS under the security game IND-CR-CKA. Suppose that $\mathbb{A}$ makes at most $q_{H_2}$ hash function queries to $H_2$, at most $q_I$ secure index queries and at most $q_T$ trapdoor queries, we can build an algorithm $\mathbb{C}$ that solves the decision $(q_T+1)$-BDHI assumption with probability at least ${ϵ}^{{}^{\prime }}=\frac{ϵ}{e^{n+m}{q}_T^n}$, where e is base of natural logarithm, n and m are the number of keywords contained in an index and a trapdoor, respectively. Algorithm $\mathbb{C}$’s running time is approximately the same as $\mathbb{A}$’s. Let g be a generator of $G_1$, given $g,g^x,g^{x^2},\dots ,g^{x^{q_T+1}}$ and R, the goal of algorithm $\mathbb{C}$ is to output 1 if $R=\widehat{e}{(g,g)}^{\frac{1}{x}}$ and 0 otherwise. Algorithm $\mathbb{C}$ simulating the challenger interacts with algorithm $\mathbb{A}$ simulating attacker as follows:

-

Setup: Algorithm $\mathbb{C}$ works as follows:

• Algorithm $\mathbb{C}$ randomly chooses $q_T$ random numbers ${\rho }_1,{\rho }_2,\dots ,{\rho }_{q_T}\in Z_q^{*}$ and computes $f\left(z\right)={\prod }_{i=1}^{q_T}(z+{\rho }_i)={\sum }_{j=0}^{q_T}{c}_j{z}^j$.
• $\mathbb{C}$ computes $U=g^{f\left(x\right)}=g^{{\sum }_{j=0}^{q_T}{c}_j{x}^j}$ and $V=g^{xf\left(x\right)}=g^{{\sum }_{j=0}^{q_T}{c}_j{x}^{j+1}}$. Since $f_i\left(z\right)=\frac{1}{z+{\rho }_i}f\left(z\right)={\sum }_{j=0}^{q_T-1}{d}_j{z}^j$ , $\mathbb{C}$ gets $U^{\frac{1}{x+{\rho }_i}}=g^{f_i\left(x\right)}=g^{{\sum }_{j=0}^{q_T-1}{d}_j{x}^j}$ where $i\in [1,q_T]$. Then $\mathbb{C}$ stores the pairs $\{{\rho }_i,g^{f_i\left(x\right)}\}$ in a list named S-list where $i\in [1,q_T]$.
• $\mathbb{C}$ computes $\frac{f\left(z\right)-c_0}{z}={\sum }_{j=1}^{q_T}{c}_j{z}^{j-1}$ and sets $R_U=\widehat{e}(g^{{\sum }_{j=1}^{q_T}{c}_j{x}^{j-1}},g^{{\sum }_{j=0}^{q_T}{c}_j{x}^j+c_0})\times R^{c_0^2}$. Obviously, if $R=\widehat{e}{(g,g)}^{\frac{1}{x}}$, then it has $R_U=\widehat{e}(g^{{\sum }_{j=1}^{q_T}{c}_j{x}^{j-1}},g^{{\sum }_{j=0}^{q_T}{c}_j{x}^j+c_0})\times R^{c_0^2}=\widehat{e}(g^{\frac{f\left(x\right)-c_0}{x}},g^{f\left(x\right)+c_0})\times \widehat{e}{(g,g)}^{\frac{c_0^2}{x}}=\widehat{e}{(g,g)}^{\frac{f^2\left(x\right)-c_0^2}{x}}\times \widehat{e}{(g,g)}^{\frac{c_0^2}{x}}=\widehat{e}{(g,g)}^{\frac{f^2\left(x\right)}{x}}=\widehat{e}{(U,U)}^{\frac{1}{x}}$.
• $\mathbb{C}$ randomly chooses $2n+3$ numbers $s_0,s_1,\dots ,s_n,t_1,\dots ,t_n,\eta \in Z_q^{*}$ and computes $f\left(z\right)={\prod }_{i=1}^n(z-t_i)={\sum }_{j=0}^n{b}_j{z}^j$. Let $Z=V^{\eta }$, $\mathbb{C}$ constructs $X_j=V^{s_j}-U^{b_j}$ for each $j\in [0,n]$. $\mathbb{C}$ randomly chooses a $g_0\in G$ and a number $t\in Z_q^{*}$ and then computes $T=g_0^t$. After that, $\mathbb{C}$ gives the public key $p{k}_R=\{X_0,X_1,\dots ,X_n,Z,\mu =\widehat{e}(U,U),g_0,T\}$ to $\mathbb{A}$. The corresponding private key $s{k}_R$ unknown to $\mathbb{C}$ is $\{s_{0}x-b_0,s_{1}x-b_1,\dots ,s_{n}x-b_n,\eta x,t\}$.
• $\mathbb{C}$ randomly chooses a number $s\in Z_q^{*}$ and sets $S=g_0^s$. $\mathbb{C}$ generates a hash function $H_3:G\to {\{0,1\}}^{*}$. After that, $\mathbb{C}$ outputs $p{k}_S=\{S,H_3\}$ and keeps $s{k}_S=\left\{s\right\}$ secret.

-

$H_1,H_2-$queries: Algorithm $\mathbb{A}$ can query the random oracles $H_1$ or $H_2$ at any time. To respond to $H_1$ queries, algorithm $\mathbb{C}$ maintains a list of tuples $(w_j,h_j,{\sigma }_j)$ called $H_1-$list which is initially empty. $\mathbb{C}$ generates $\varphi =H_3\left(T^s\right)=H_3\left(g^{\left(ts\right)}\right)$ by using the keys $p{k}_S,p{k}_R,s{k}_S$. When $\mathbb{A}$ queries the random oracle $H_1$ at a point $w_i\in {\{0,1\}}^{*}$, algorithm $\mathbb{C}$ responds as follows:

$H_1-$queries:

• If the query $w_i$ already appears on the $H_1$-list in a tuple $(w_i,h_i,{\sigma }_i)$, algorithm $\mathbb{C}$ responds with $H_1\left(w_i\right|\varphi )=h_i$, where $h_i\in {\{0,1\}}^{{log}_2^q}$.
• Otherwise, $\mathbb{C}$ generates a random coin ${\sigma }_i\in [1,n{q}_T]$ so that $Pr[1\le {\sigma }_i\le n]=\frac{1}{q_T}$.
• If $1\le {\sigma }_i\le n$, $\mathbb{C}$ set $h_i=t_{{\sigma }_i}$. Otherwise, $\mathbb{C}$ picks a random $a_i\in {\{0,1\}}^{{log}_2^q}$ and sets $h_i=a_i$.
• $\mathbb{C}$ adds the tuple $(w_i,h_i,{\sigma }_i)$ to the $H_1$-list. $\mathbb{C}$ responds $\mathbb{A}$ with $H_1\left(w_i\right|\varphi )=h_i$.

The $H_2-$queries is similar to $H_1-$queries. To respond to $H_2$ queries from $\mathbb{A}$, algorithm $\mathbb{C}$ maintains a list of tuples $({\phi }_j,{\psi }_j)$ called $H_2-$list which initially empty. When $\mathbb{A}$ queries the random oracle $H_2$ at a point ${\phi }_i\in G_2$, algorithm $\mathbb{C}$ responds as follows:

$H_2-$queries:

• If the query ${\phi }_i$ already appears on the $H_2$-list in a tuple $({\phi }_i,{\psi }_i)$, then algorithm $\mathbb{C}$ responds with $H_2\left({\phi }_i\right)={\psi }_i$, where ${\psi }_i\in {\{0,1\}}^{{log}_2^q}$.
• Otherwise, $\mathbb{C}$ picks a random $b_i\in {\{0,1\}}^{{log}_2^q}$ and sets ${\psi }_i=b_i$.
• $\mathbb{C}$ adds the tuple $({\phi }_i,{\psi }_i)$ to the $H_2$-list and responds $\mathbb{A}$ with $H_2\left({\phi }_i\right)={\psi }_i$.

-

Index queries: For any keyword set $W_i=\{w_{i1},w_{i2},\dots ,w_{in}\}$ in which $i\in [1,q_I]$, when $\mathbb{A}$ asks for the secure index of $W_i$, $\mathbb{C}$ responds as follows:

• $\mathbb{C}$ runs $H_1-$queries algorithm to obtain $h_{ij}$ such that $h_{ij}=H_1\left(w_{ij}\right|\varphi )$ where $j\in [1,n]$. Let $(w_{ij},h_{ij},{\sigma }_{ij})$ be the corresponding tuples on the $H_1$-list. If ${\sigma }_{ij}\le n$ for all $j\in [1,n]$, then $\mathbb{C}$ reports failure and terminates.
• Otherwise, by using $(h_{i1},h_{i2},\dots ,h_{in})$, $\mathbb{C}$ adopts the keyword conversion method in Section 4.1 to generate a vector $\overrightarrow{a}$. Following the algorithm $IndexBuild$ in Section 4.2, $\mathbb{C}$ generates the secure index $I_W$ by using $p{k}_R$.

-

Trapdoor queries: When $\mathbb{A}$ issues a query for the trapdoor corresponding to the keyword query $Q_i=\{q_{i1},q_{i2},\dots ,q_{im}\}$ where $i\in [1,q_T]$, algorithm $\mathbb{C}$ responds as follows:

• Algorithm $\mathbb{C}$ runs $H_1-$queries algorithm to obtain $h_{ij}$ such that $h_{ij}=H_1\left(q_{ij}\right|\varphi )$ where $j\in [1,m]$. Let $(q_{ij},h_{ij},{\sigma }_{ij})$ be the corresponding tuples on the $H_1$-list. If ${\sigma }_{ij}\le n$ for all $j\in [1,m]$, then $\mathbb{C}$ reports failure and terminates.
• Otherwise, by using $(h_{i1},h_{i2},\dots ,h_{im})$ and $s{k}_R$, $\mathbb{C}$ constructs the trapdoor for query $Q_i$. $\mathbb{C}$ computes: $l_i=\frac{1}{\eta }+\frac{{\rho }_i{\sum }_{y=0}^n{s}_y(h_{i1}^y+h_{i2}^y+\dots +h_{im}^y)}{\eta {\sum }_{y=0}^n{b}_y(h_{i1}^y+h_{i2}^y+\dots +h_{im}^y)}$ and $u_i=-\frac{{\sum }_{y=0}^n{b}_y(h_{i1}^y+h_{i2}^y+\dots +h_{im}^y)+{\rho }_i{\sum }_{y=0}^n{s}_y(h_{i1}^y+h_{i2}^y+\dots +h_{im}^y)}{{\rho }_i\eta }$, which are satisfied with the equality $\frac{u_i}{u_i\eta x+{\sum }_{y=0}^n(s_{y}x-b_y)(h_{i1}^y+h_{i2}^y+\dots +h_{im}^y)}=\frac{l_i}{x+{\rho }_i}$. Moreover, $\mathbb{C}$ constructs $l_{ik}=-\frac{(h_{i1}^k+h_{i2}^k+\dots +h_{im}^k){\rho }_i}{{\sum }_{y=0}^n{b}_y(h_{i1}^y+h_{i2}^y+\dots +h_{im}^y)}$ which is satisfied with the equality $\frac{h_{i1}^k+h_{i2}^k+\dots +h_{im}^k}{u_i\eta x+{\sum }_{y=0}^n(s_{y}x-b_y)(h_{i1}^y+h_{i2}^y+\dots +h_{im}^y)}=\frac{l_{ik}}{x+{\rho }_i}$ for each $k\in [0,n]$. Obviously, $(U^{\frac{l_{i1}}{x+{\rho }_i}},U^{\frac{l_{i2}}{x+{\rho }_i}},\dots ,U^{\frac{l_{in}}{x+{\rho }_i}},U^{\frac{l_i}{x+{\rho }_i}})$ is a trapdoor for keyword query $Q_i$.
• Through searching the S-list to obtain the tuple $\{{\rho }_i,g^{f_i\left(x\right)}\}$, $\mathbb{C}$ sends $(g^{f_i\left(x\right)l_{i0}},g^{f_i\left(x\right)l_{i1}},\dots ,g^{f_i\left(x\right)l_{in}},g^{f_i\left(x\right)l_i})$ to $\mathbb{A}$ as the correct trapdoor for the query $Q_i$.

-

Challenge: Algorithm $\mathbb{A}$ produces a target keyword set $W^{*}$ which it wants to challenge on and sends $W^{*}$ to $\mathbb{C}$. Algorithm $\mathbb{C}$ chooses a random keyword set R and sets $W_0=W^{*}=\{w_{01},w_{02},\dots ,w_{0n}\}$, $W_1=R=\{w_{11},w_{12},\dots ,w_{1n}\}$. The only restriction is that the trapdoor queried in previous phase can not distinguish $W_0$ from $W_1$. Let $(w_{0i},h_{0i},{\sigma }_{0i})$ be the corresponding tuples on the $H_1-$list, for each $i\in [1,n]$, if ${\sigma }_{0i}>n$, then $\mathbb{C}$ reports failure and terminates. After that, $\mathbb{C}$ selects a random bit $\beta \in \{0,1\}$ and runs the above algorithm for responding to $H_1-$queries to obtain the values $h_{\beta 1},h_{\beta 2},\dots ,h_{\beta n}$ where $H_1\left(w_{\beta i}\right|\varphi )=h_{\beta i},w_{\beta i}\in W_{\beta },i\in [1,n]$. Then, $\mathbb{C}$ generates the challenge SPE-CKS index $I_{\beta }$ as follows:

(1)

$\mathbb{C}$ constructs $f\left(z\right)={\prod }_{i=1}^n(z-h_{\beta i})={\sum }_{j=0}^n{a}_j{z}^j$. Then $\mathbb{C}$ computes $C_{\beta j}={X_j}^{\frac{r_{\beta }}{x}}\times U^{\frac{r_{\beta }}{x}{a}_j}=U^{s_j{r}_{\beta }-b_j\frac{r_{\beta }}{x}+a_j\frac{r_{\beta }}{x}}=U^{s_j{r}_{\beta }}$ for each $j\in [0,n]$ and $C_{W_{\beta }}=Z^{\frac{r_{\beta }}{x}}=V^{\frac{r_{\beta }}{x}}=U^{r_{\beta }}$. Let $D_{W_{\beta }}=H_2\left(R_U^{r_{\beta }}\right)$, observe that if $R=\widehat{e}{(g,g)}^{\frac{1}{x}}$, then $R_U=\widehat{e}{(U,U)}^{\frac{1}{x}}$. This means that $(C_{\beta 0},C_{\beta 1},\dots ,C_{\beta n},C_{W_{\beta }},D_{W_{\beta }})$ is a valid SPE-CKS index of keyword set $W_{\beta }$ when $R=\widehat{e}{(g,g)}^{\frac{1}{x}}$.

(2)

$\mathbb{C}$ sends $I_{\beta }=(C_{\beta 0},C_{\beta 1},\dots ,C_{\beta n},C_{W_{\beta }},D_{W_{\beta }})$ and two keyword sets $W_0$ and $W_1$ to $\mathbb{A}$.

-

More queries: $\mathbb{A}$ continues to issue index and trapdoor queries. The only restriction is that no index and trapdoor query can distinguish $W_0$ from $W_1$.

-

Response: $\mathbb{A}$ outputs a guess ${\beta }^{{}^{\prime }}\in \{0,1\}$ . If ${\beta }^{{}^{\prime }}=\beta$, then $\mathbb{C}$ outputs 1 which means $R={\widehat{e}(g,g)}^{\frac{1}{x}}$. Otherwise, $\mathbb{C}$ outputs 0 which means R is a random number where $R\in G_2^{*}$.

We analyze the probability that $\mathbb{C}$ does not abort in trapdoor queries phase and challenge phase. We define three events:

${\omega }_1$: $\mathbb{C}$ does not abort in index quries phase for generating the $I_W$.

${\omega }_2$: $\mathbb{C}$ does not abort as a result of any of $\mathbb{A}$’s trapdoor queries.

${\omega }_3$: $\mathbb{C}$ does not abort in challenge phase for generating the $I_{\beta }$.

If $q_I$ is sufficiently large, then the probability of event ${\omega }_1$ is at least ${(1-\frac{1}{q_I})}^{n{q}_I}=\frac{1}{e^n}$. Suppose that $q_T$ is sufficiently large. Therefore, the probability of event ${\omega }_2$ is at least ${(1-\frac{1}{q_T})}^{m{q}_T}=\frac{1}{e^m}$. The probability of event ${\omega }_3=\frac{1}{q_T^n}$.

If $R={\widehat{e}(g,g)}^{\frac{1}{x}}$, $\mathbb{A}$’s view is identical to its view in a real attack game and it must satisfy $|Pr[{\beta }^{{}^{\prime }}=\beta ]-\frac{1}{2}|\ge ϵ$. If R is a random number and $R\in G_2^{*}$, then it must have $|Pr[{\beta }^{{}^{\prime }}=\beta ]|=\frac{1}{2}$.

Therefore, we have that:

$$|Pr[\mathbb{C}(P,xP,x^{2}P,\dots ,x^{q_T+1}P,{\widehat{e}(p,p)}^{\frac{1}{x}})=1]-Pr[\mathbb{C}(P,xP,x^{2}P,\dots ,x^{q_T+1}P,R)=1]|\ge \frac{ϵ}{e^n{e}^m{q}_T^n}$$

This means that $\mathbb{C}$ can solve the decision $(q_T+1)$-BDHI assumption with probability at least ${ϵ}^{{}^{\prime }}=\frac{ϵ}{e^n{e}^m{q}_T^n}$. We complete the proof of the theorem. □

The above security proof demonstrates that our scheme is secure against chosen keywords attack. The following paragraph is showing that our scheme can defend against the keyword guessing attack. As figured out by Shao and Yang in Reference [28], the reason SPE schemes inherently suffer from the keyword guessing attacks by adversaries is that they have abilities to execute the $IndexBuild$ and $Test$ algorithms simultaneously. If the capability of index building for adversaries is limited, the adversaries fail to launch the keyword guessing attack. In the proposed scheme, for the $IndexBuild$ and $Trapdoor$ algorithms, the adversaries only can obtain $g_0$, $g_0^s$ and $g_0^t$. If the adversaries can calculate the value of $\varphi =g_0^{st}$, then it means that the adversaries can solve the CDH problem [31] in a polynomial probabilistic time. Considering that the CDH problem is hard for any polynomial probabilistic time adversaries, the secret $\varphi$ is unknown to anyone except the senders and the receiver. Based on this, neither the outsider attacker nor the malicious insider server is able to produce a correct ciphertext for any keyword set of theirs interest. Thus, we argue that our scheme can defend against the keyword guessing attack.

5. Performance Evaluation

This section gives the performance evaluation of the proposed scheme through theoretical and experimental analysis.

5.1. Theoretical Analysis

To reveal the performance of the proposed scheme, we compared it with the existing SPE-CKS schemes. For simplicity, we denote these schemes introduced in References [7,8,10] by ZZ11, OT15 and ZLW19, respectively. Concretely, ZZ11 is a standard SPE-CKS scheme; OT15 is an efficient IPE scheme, which can be changed to a SPE-CKS scheme by using a method mentioned in Reference [21]; ZLW19 is a SPE scheme that supports disjunctive and conjunctive keywords search simultaneously. Moreover, for simplicity, we combine the $KeyGe{n}_R$ algorithm to the $KeyGe{n}_S$ algorithm and denote these two algorithms by $KeyGen$.

Table 1. Comparison with previous searchable public key encryption supporting conjunctive keywords search (SPE-CKS) schemes on time complexity.

Algorithm	ZZ11 [7]	OT15 [8]	ZLW19 [10]	Our Scheme
KeyGen	$P_1$	$O\left(n^2\right)P_1$	$(2n+3)P_1+P_2$	$(n+2)P_1+P_2+2P$
IndexBuild	$(n+1)P_1+(n+2)P_2+e$	$(12n+10)P_1$	$(3n^2+4n)P_1+P_2+P$	$(n+2)P_1+P_2$
Trapdoor	$3(n+2)P_1+P_2$	$(12n+10)P_1$	$(2m+2)P_1$	$(n+2)P_1+P$
Test	$(2n+3)e$	$11e+5(n-1)P_1$	$2n(m+1)e$	$(n+2)e$
Denotation	P, $P_1$, $P_2$: The time cost of one exponentiation computation in G, $G_1$ and $G_2$, respectively.
	e: The time cost of one pairing operation.

and

Table 2. Comparison with previous SPE-CKS schemes on space complexity.

Parameters	ZZ11 [7]	OT15 [8]	ZLW19 [10]	Our Scheme
pk	$(n+2)L_1+2L_2$	$(12n+16)L_1+L_2$	$(2n+3)L_1+L_2$	$(n+2)L_1+L_2+3L$
sk	$|Z_q|$	$(12n+16)L_1$	$(2n+3)|Z_q|$	$(n+4)|Z_q|$
Index	$(n+1)L_1+(n+2)L_2+\left|Z_q\right|$	$(5n+1)L_1+L_2$	$(2n^2+4n)L_1+L_2$	$(n+2)L_1+\left|Z_q\right|$
Trapdoor	$(n+2)L_1+L_2$	$11L_1$	$(2m+2)L_1+\left|Z_q\right|$	$(n+2)L_1$
Denotation	L, $L_1$, $L_2$ and $|Z_q|$: the size of an element of G, $G_1$, $G_2$ and $Z_q$, respectively.
	n, m: the number of keywords in an index keyword set and a query, respectively.

show the comparison between our scheme and the previous schemes in terms of the storage and time overhead.

Because the time cost of exponentiation computation and pairing is much higher than that of other operations, such as addition and multiplication operations, the comparison only considers these two operations. Table 1 shows that the time cost of index building, trapdoor generation and test in our scheme are all less than that in other three schemes. Although the time cost of “KeyGen” algorithm in our scheme is not as good as that in ZZ11, our scheme is also practical since this algorithm only runs when system initialization and key pair replacement. In addition, because the pairing operation and exponentiation computation are big computation burden in the test process, we can argue that the test efficiency is improved a lot in our scheme.

For simplicity, we denote $p{k}_S$ and $p{k}_R$ by $pk$ and $s{k}_S$ and $s{k}_R$ by $sk$. From Table 2, we can find that the storage cost of index in our scheme is much less than that in the other schemes. Moreover, the storage cost of $pk$ is also the smallest of all. Since n is not large and the storage cost of $|Z_q|$ is small, the storage cost of $sk$ and trapdoor in our scheme is still as practical as the other schemes.

5.2. Experimental Results

Our experiment is run on Intel(R) Core(TM) i7 CPU at 3.40 Ghz processor with 16 GB memory size. The experiment is based on Java language because Java is a cross platform development language and the bilinear pairing technique is realized by adopting the Java Pairing Based Cryptography (JPBC) library [32]. The experiment is based on a real-world e-mail dataset called Enron e-mail dataset [33]. We randomly select 1000 e-mail messages from the dataset and extract 5∼25 words from each document as its keyword list. By utilizing these e-mails and its associated keywords, we implement the schemes introduced in References [7,8,10] and our scheme in the same environment to demonstrate the advantages of the proposed scheme in term of time and space overhead (The source code can be accessed through the website http://www.inforstation.com/webservers/SPE-CKS/).

5.2.1. Time Overhead

The time overhead is tested in term of key generation, index building, trapdoor generation and testing. The experiment results are shown in Figure 2.

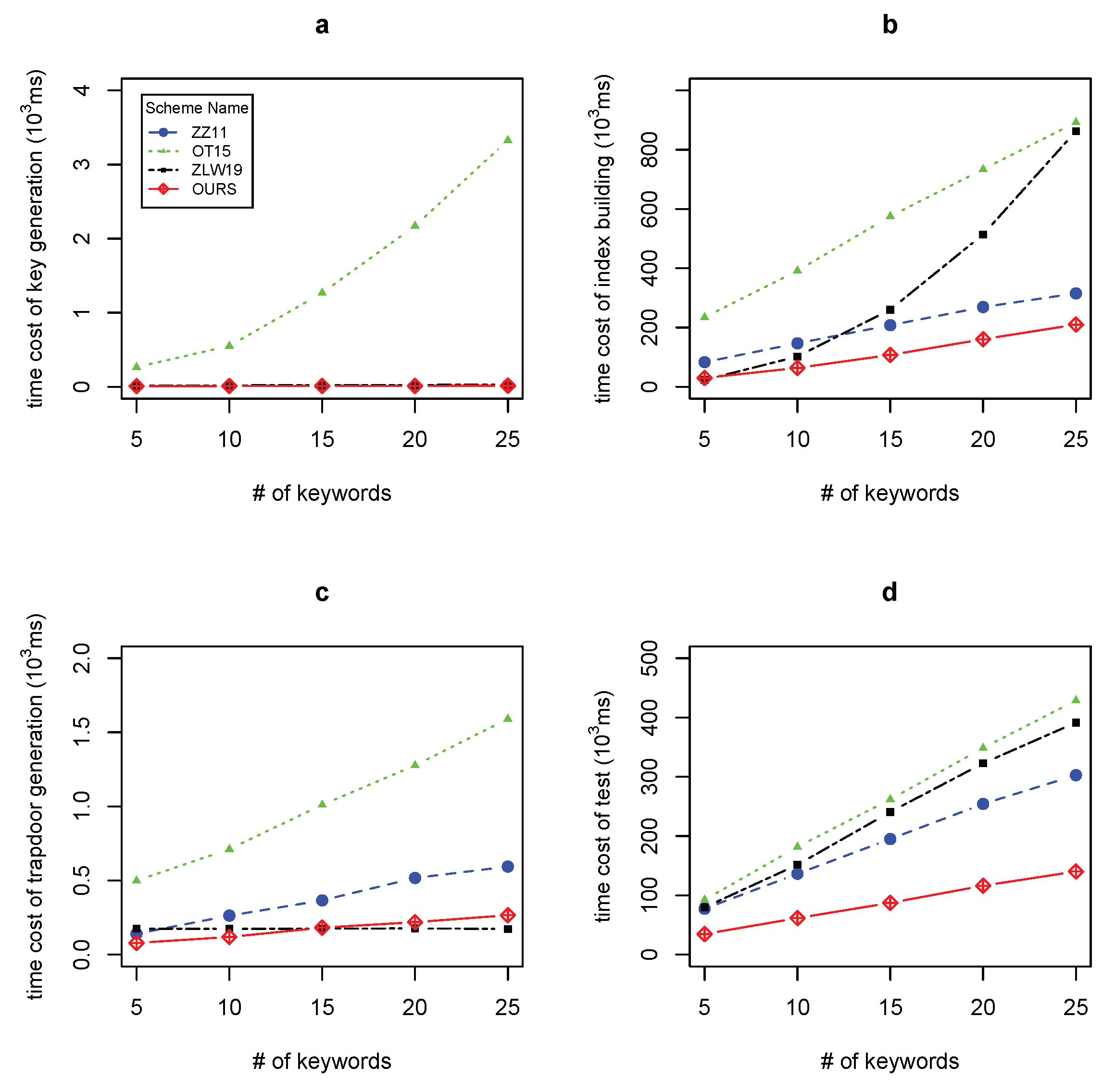
1.

Key generation. Because of adopting the technique called dual pairing vector space (DPVS)[8], the time complexity of key generation in OT15 is $O\left(n^2\right)$. The time cost of key generation in other three schemes are all linear with n.

2.

Index building. The time cost of index building in ZZ11, OT15 and ours are all linearly with n. The time cost of index building in our scheme is still much less than that in ZZ11 and OT15. Furthermore, as n grows, for example, $n>10$, the time cost of index building in ZLW19 is more than that in our scheme since it is linear with $n^2$.

3.

Trapdoor generation. Although the time cost of trapdoor generation in ZZ11, OT15 and ours are all linear with n, our scheme needs less time cost than ZZ11 and OT15 due to needing less exponentiation computation operations. The time cost of trapdoor generation in ZLW19 is linear with m. Because m is less than n, the time cost of trapdoor generation in our scheme is slightly more than that in ZLW19.

4.

Testing. The time cost of test in these four schemes are all linear with n. Compared with ZZ11 and ZLW19, our scheme needs less pairing operations. Compared with OT15, our scheme needs less exponentiation operations on group elements. Since the time cost of exponentiation operation is only one fourth of that of pairing operation, our solution requires less test time.

5.2.2. Space Overhead

This experiment evaluates the space cost of $pk$, $sk$, index and trapdoor. The experiment results are illustrated in Figure 3.

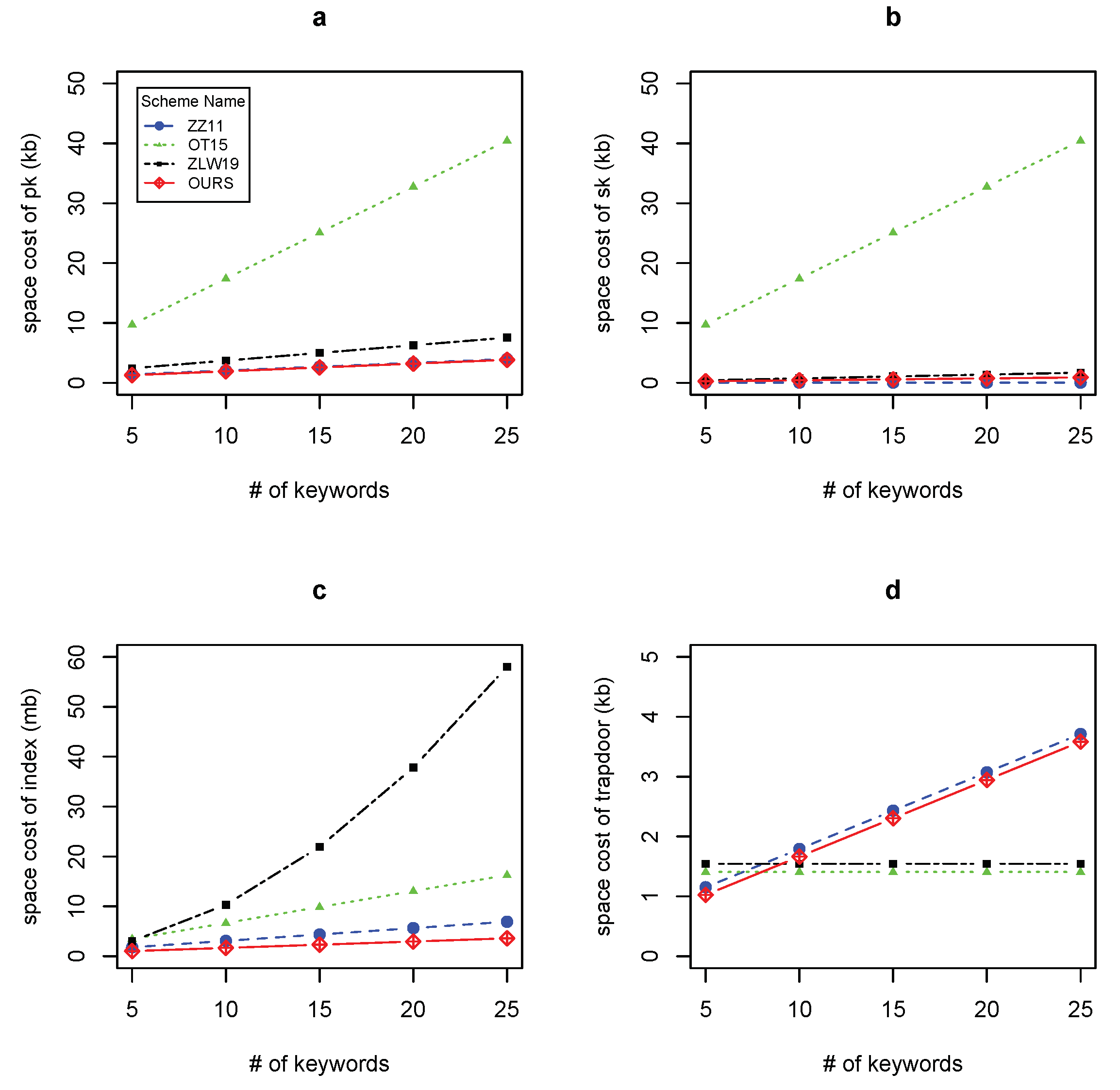
1.

$pk$ size. The $pk$ size in these four schemes are all linear with n. Our scheme is the best of these four schemes since it needs less elements in group $G_1$.

2.

$sk$ size. ZZ11 only needs one integer in $Z_q$. Although $sk$ size in OT15, ZLW19 and ours are all linear with n, both ZLW19 and our scheme need less space cost since the space cost of $Z_q$ is less than that of $G_1$. In addition, the $sk$ size in our scheme is only a half of that in ZLW19.

3.

Index size. Our scheme needs less space cost than OT15 and ZLW19, although the index size of OT15, ZLW19 and our scheme are all linear with n. This is fit to the theoretical analysis. The index size of ZLW19 is linear with $n^2$, so it is not as efficient as our scheme.

4.

Trapdoor size. The space complexity of trapdoor in OT15 and ZLW19 are $O\left(1\right)$ and $O\left(m\right)$, respectively. Thus, these two schemes need less storage cost. The space cost of trapdoor in ZZ11 and our scheme are both linear with n. Our scheme needs less storage consumption than ZZ11 for trapdoor since our scheme needs less group element in trapdoor.

5.2.3. Comments

Based on the theoretical analysis and experimental results, we find that our scheme is better than ZZ11 except the time cost of key generation and the storage cost of $sk$. Note that the key generation algorithm does not run often and $sk$ is stored only several copies. So, we can argue that our scheme has a better performance than ZZ11. Compared with OT15, our scheme is better than it except the space cost of trapdoor. Considering that n is not very large, we can argue that our scheme is much practical than OT15. Compared with ZLW19, our scheme is better than this scheme except the time cost of trapdoor generation and the storage cost of trapdoor. The reason is that the time and space cost of trapdoor are both linear with m, not n. However, since n and m are commonly small, we can argue that our scheme is still much more practical than ZLW19.

For our scheme, when $n=10$, the average time costs of index building and testing of one document are 63 ms and 62 ms, respectively. The average time costs of key and trapdoor generation are 10 ms and 119 ms, respectively. Thus, we can argue that our scheme is very practical in the mobile setting in which data receiver has limited computation capacity. Note that the index structure for our scheme is that each document has its own index. We can accelerate the process of the index building and testing by using the parallel computation mechanism. What is more, our scheme can efficiently support dynamic operation, that is, documents deletion and insertion, on the account of the property of the index structure. According to these analysis, we can argue that our scheme is very suitable for the actual e-mail system.

6. Conclusions

In this paper, we propose a secure and efficient SPE-CKS scheme for realizing multi-keywords search over the encrypted e-mail data. The rigorous theoretical analysis shows that our scheme has better performance on the time and space complexities than the previous SPE-CKS schemes. Furthermore, an experiment over a real world e-mail dataset illustrates that our scheme is practical in the mobile cloud setting. Considering that advanced search functions, for example, disjunctive, Boolean and fuzzy keywords search, are very useful for the encrypted e-mail system, we will construct a secure and efficient SPE scheme supporting various advanced search functions in the future work.