GA Optimization Method for a Multi-Vector Energy System Incorporating Wind, Hydrogen, and Fuel Cells for Rural Village Applications
Abstract
1. Introduction
2. State-of-the-Art Technologies
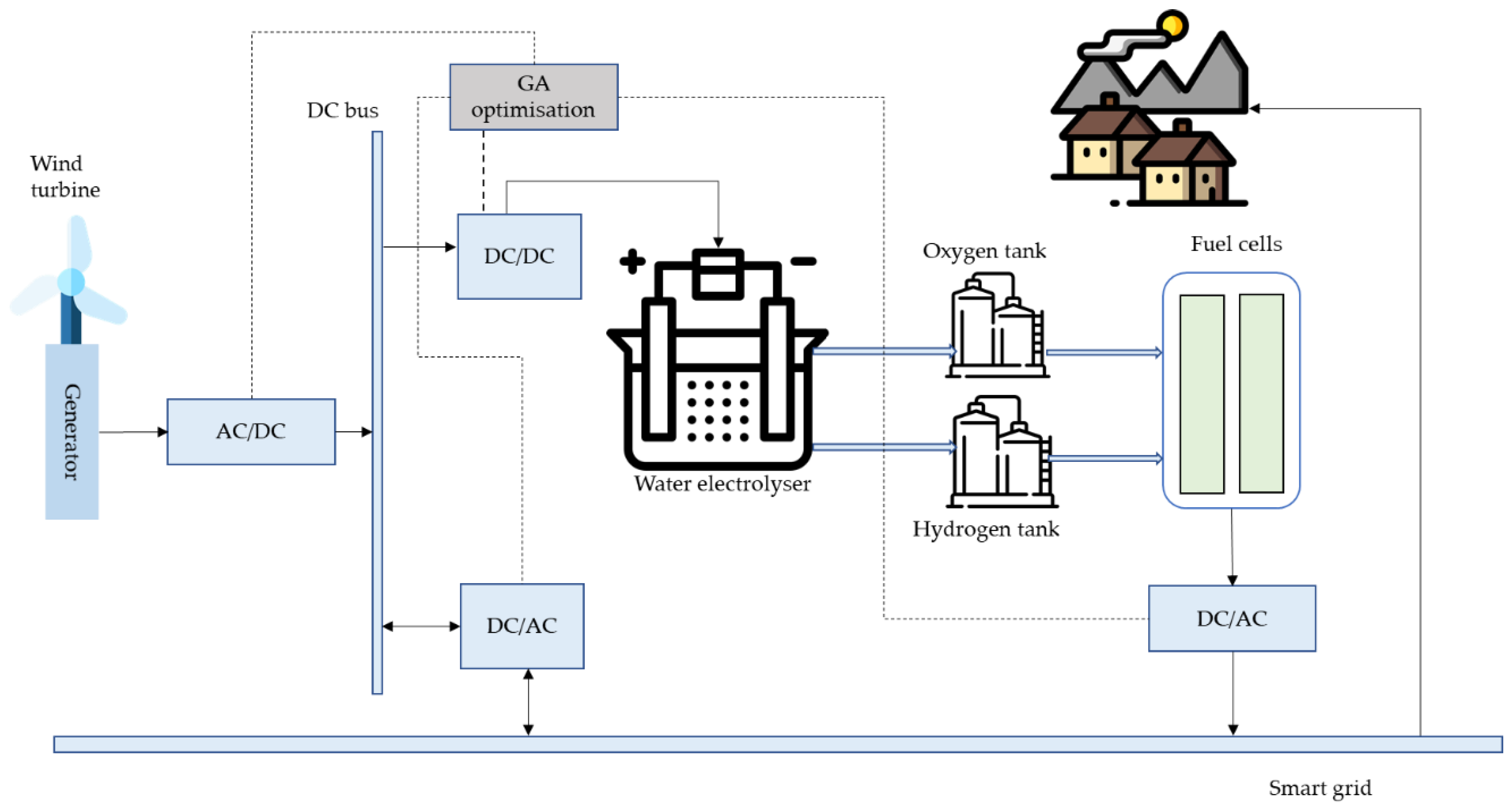
3. Principles of Operation
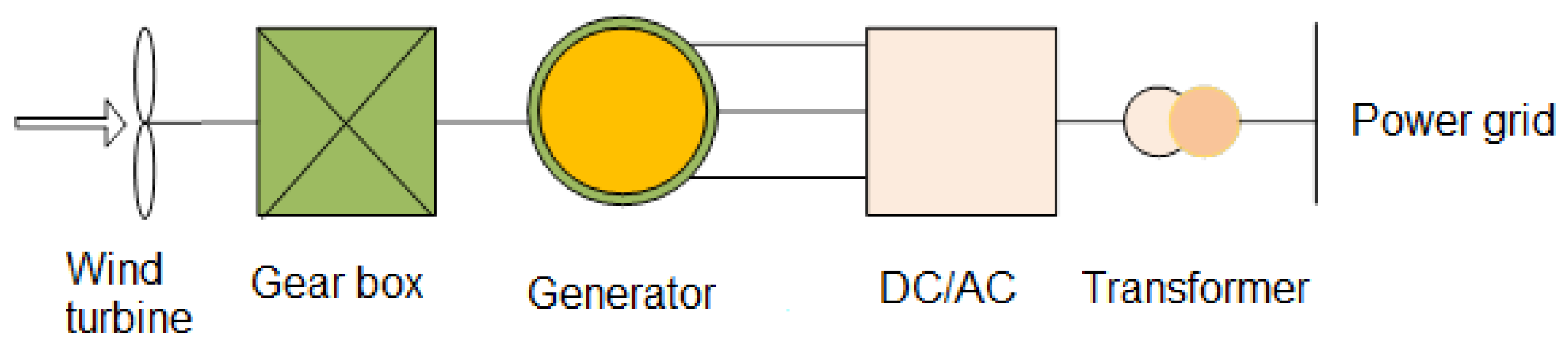
3.1. Wind Energy Conversion
3.2. Hydrogen and Oxygen Production
3.3. Fuel Cells
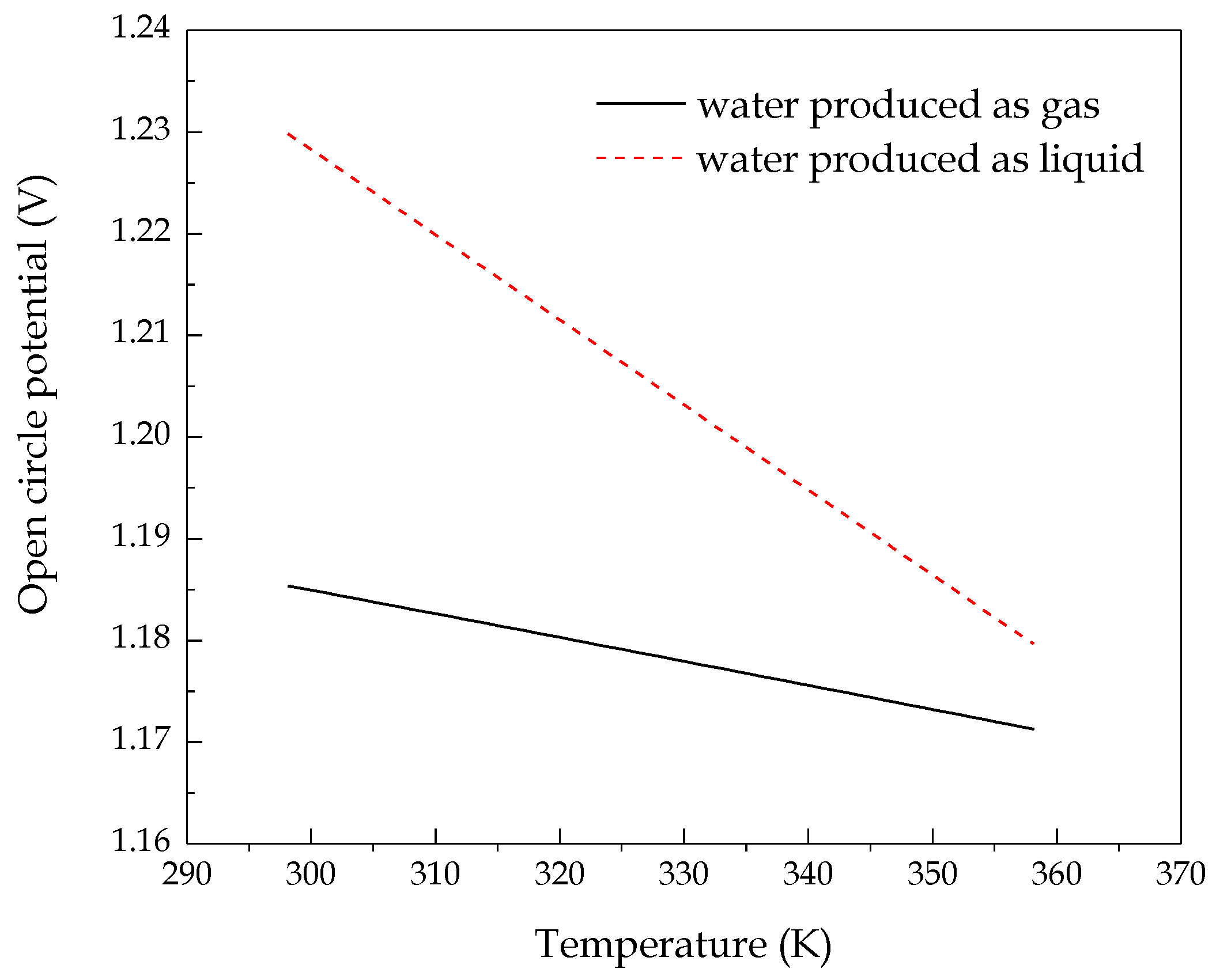
3.3.1. Open-Circuit Potential
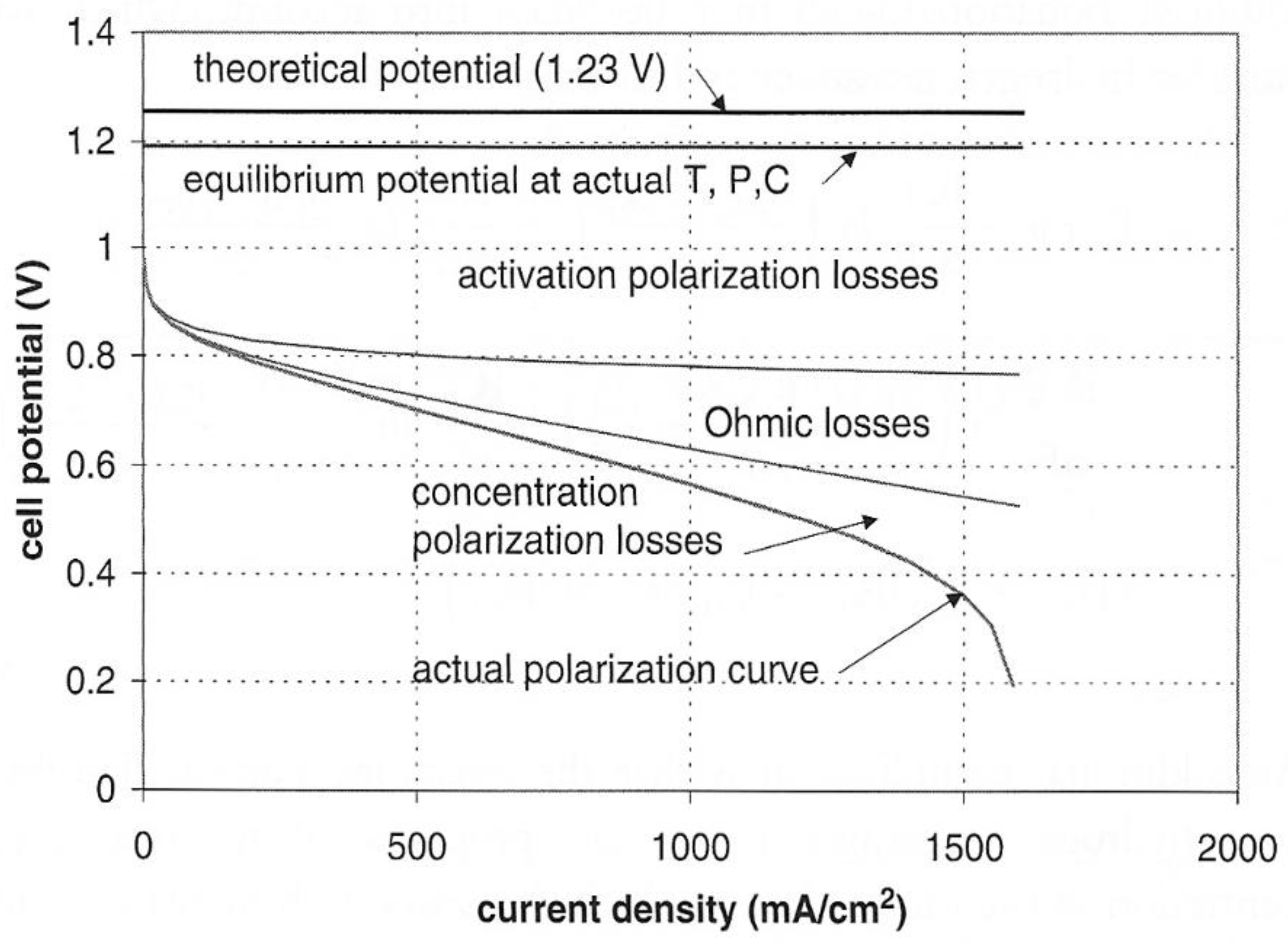
3.3.2. Activation Loss
3.3.3. Ohmic Loss
3.3.4. Concentration Loss
3.3.5. Fuel Cell Efficiency
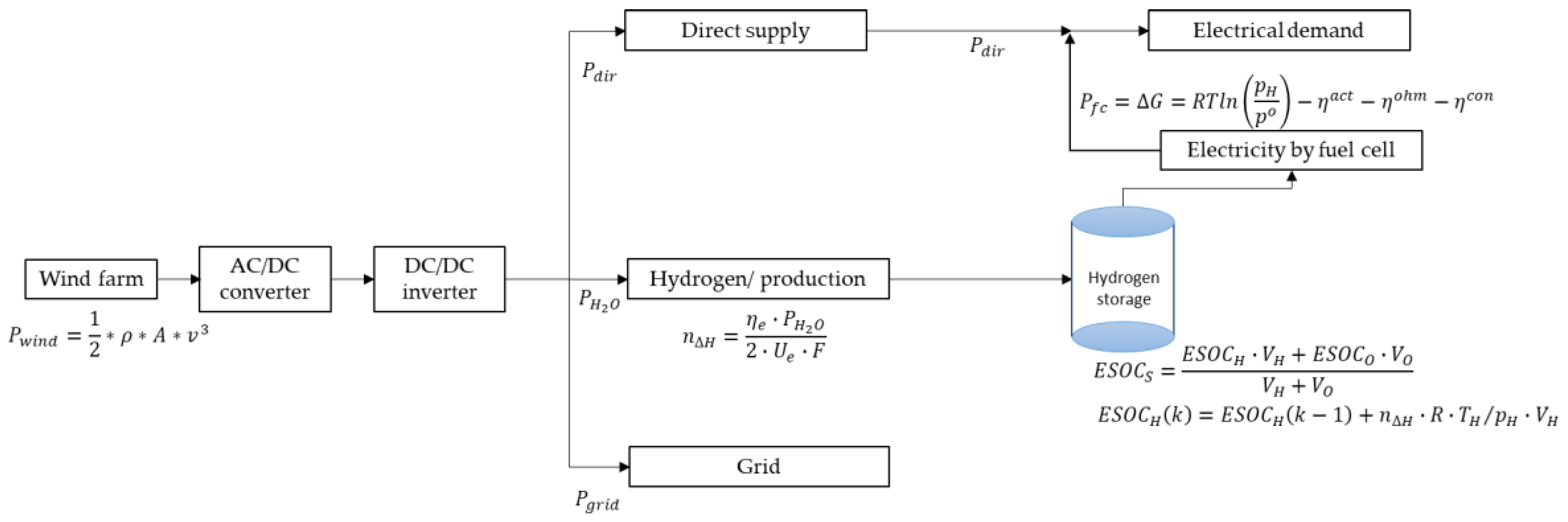
3.4. Energy Flow in the System
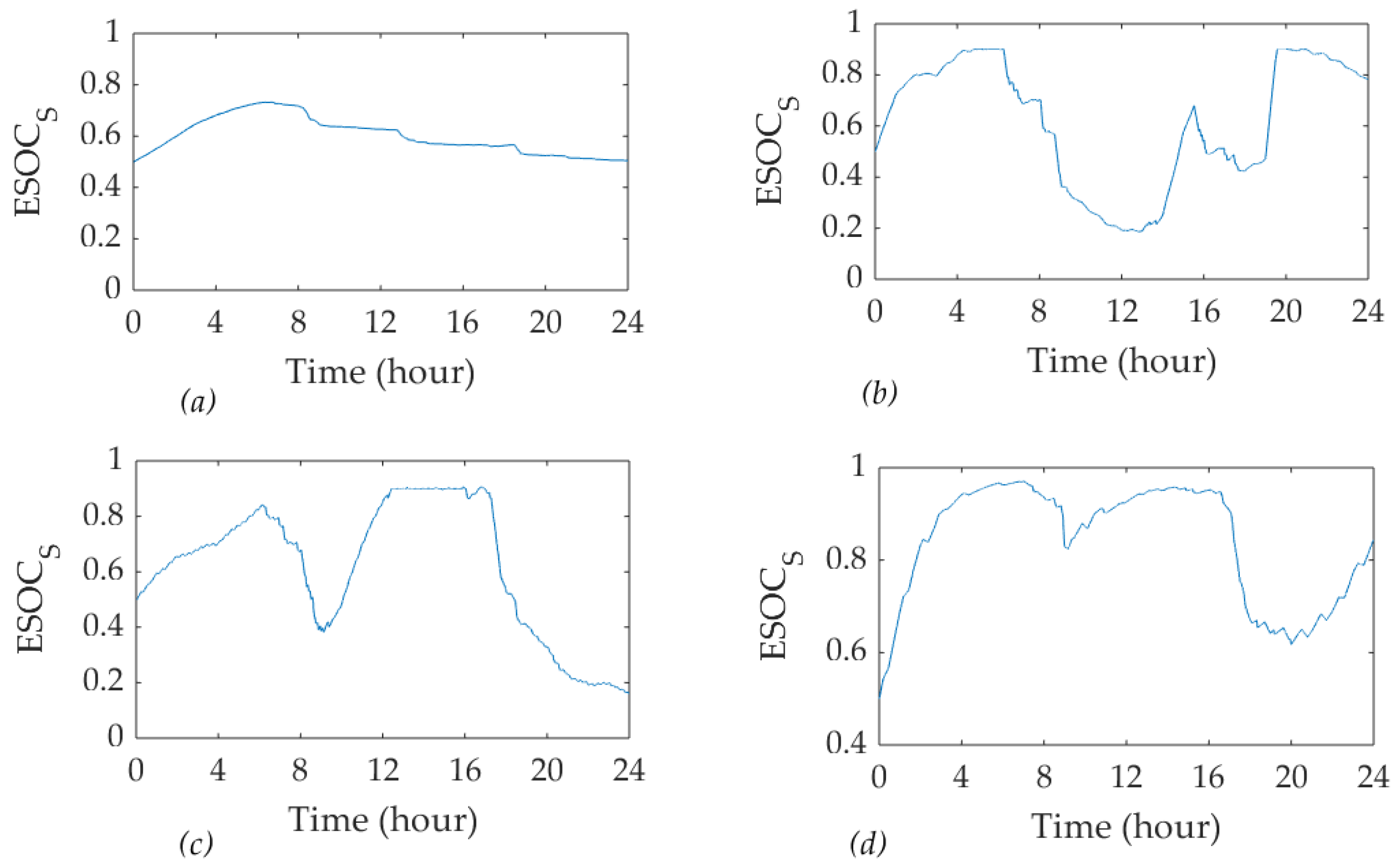
3.4.1. Equivalent State of the Charge of the Energy Storage System
3.4.2. Energy Flow Chart
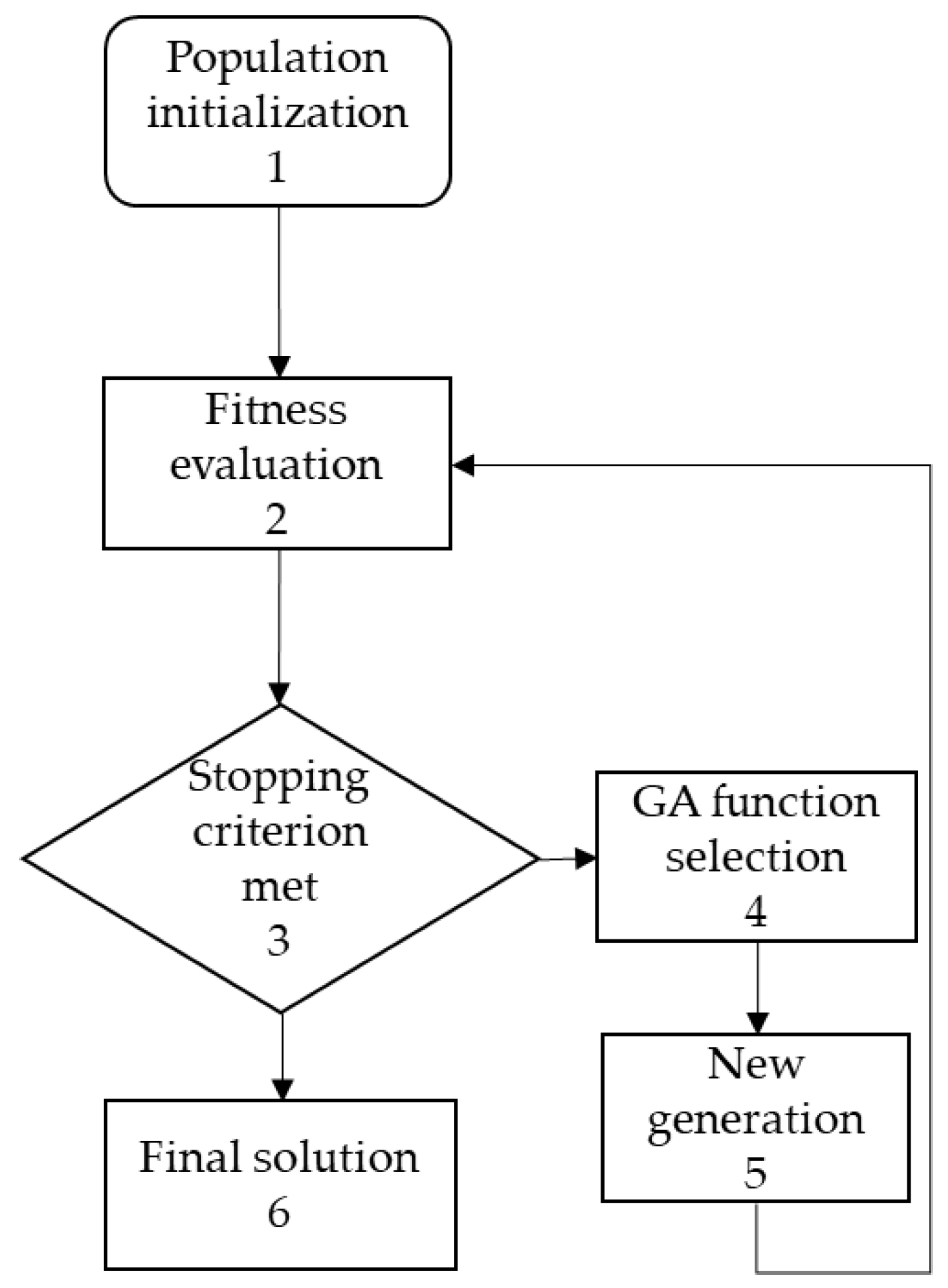
4. SSM-GA Optimization for Energy Management
- An initial solution is randomly selected between 0.2 and 0.9. For instance, the state variable in the SSM could be ;
- A new generation of solution candidate is applied to the fitness function. The fitness function in this study consists of the SSM function and a series of constraints. An SSM function represents the correlation between the variables , and while the constraints are defined;
- If the solution candidate satisfies the stopping criterion and the objective function is met;
- Crossover and mutation methods are used to generate a new solution candidate;
- Under the operation of the GA function, a new generation is created;
- A final solution is found when the GA optimization ends.
4.1. SSM and Fitness Function
4.2. GA Optimization Process
5. Results and Analysis
5.1. Consumption Characteristics of the Household Application
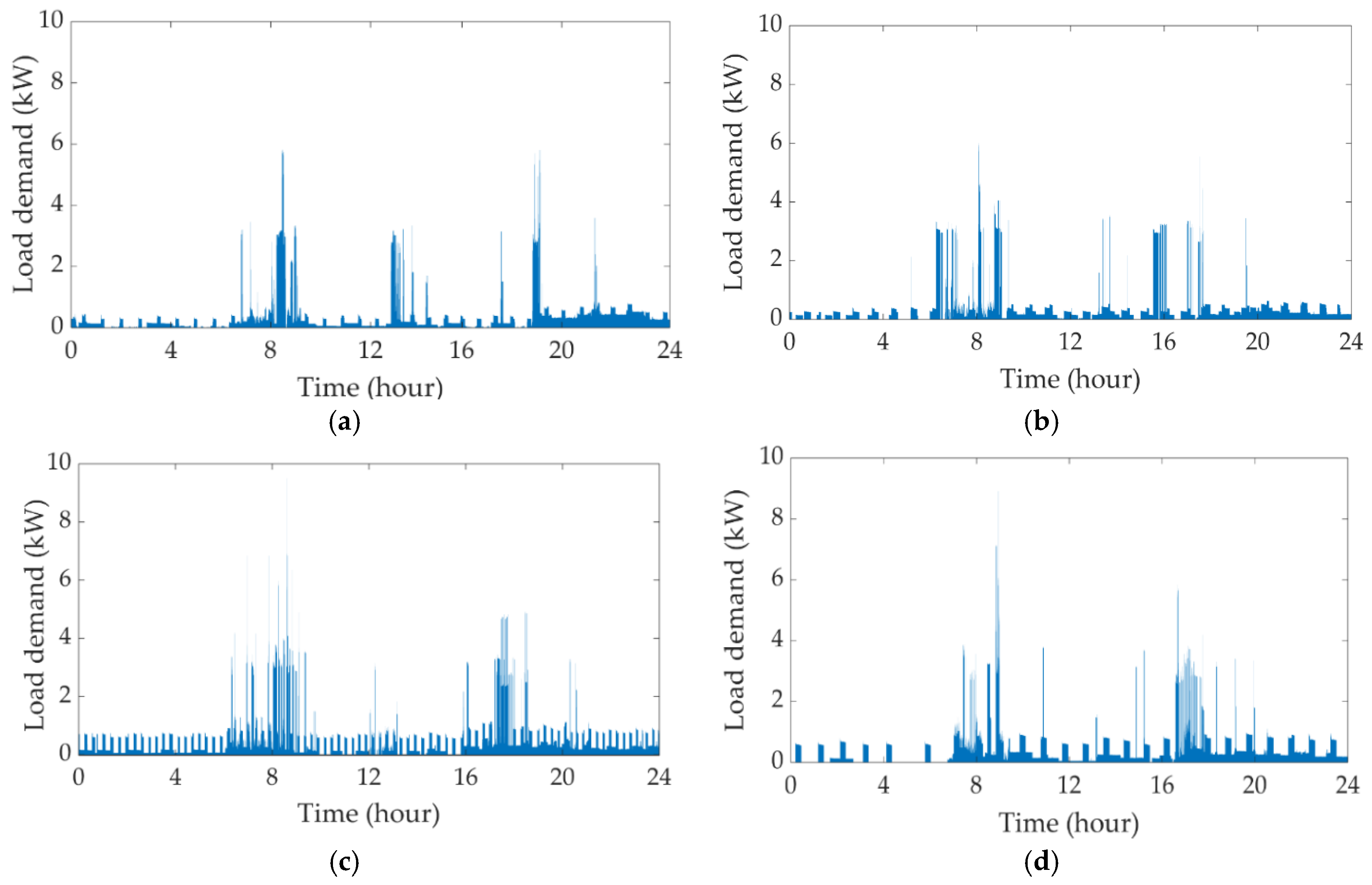
5.2. Demand Profiles in Case Studies
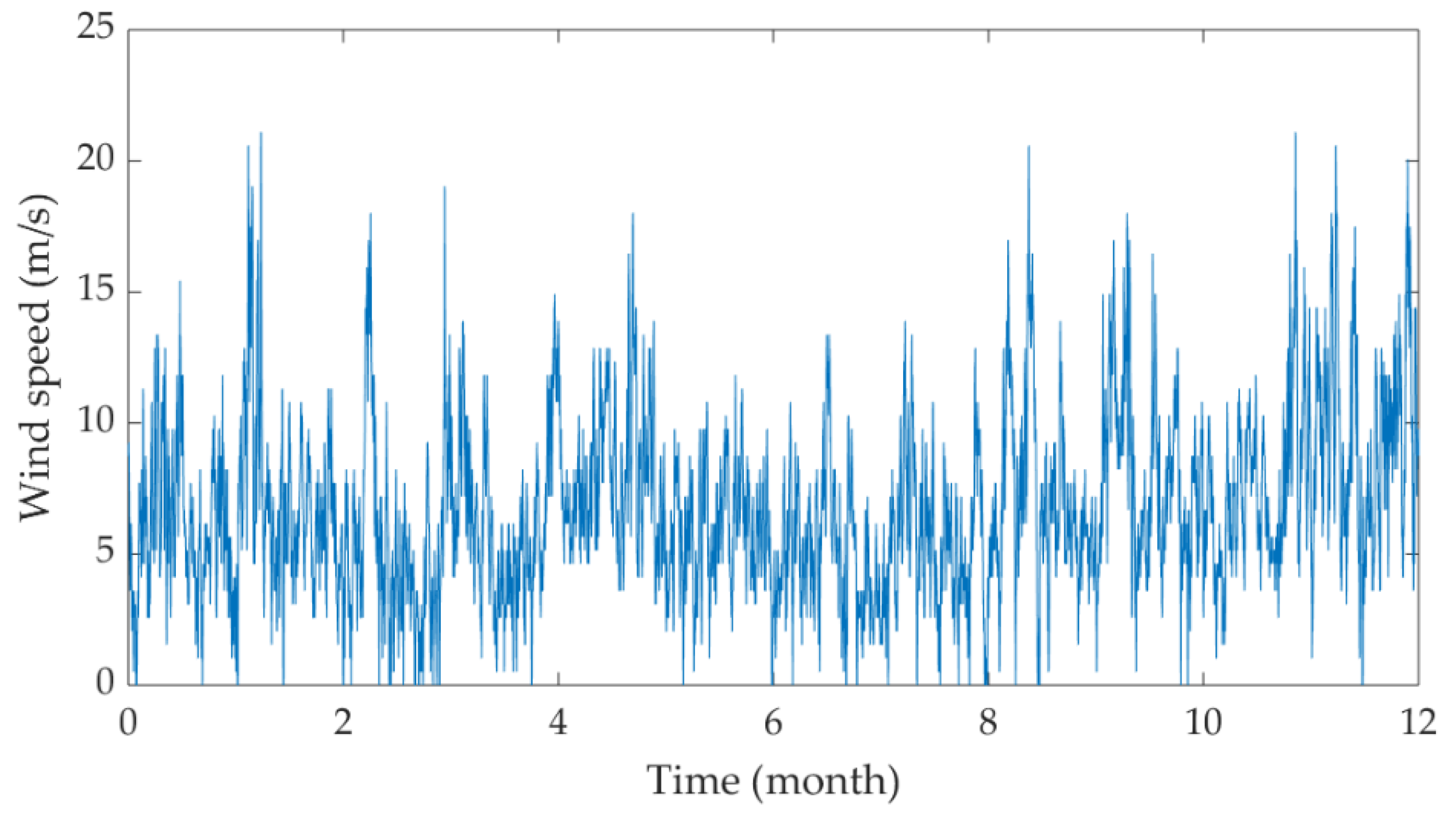
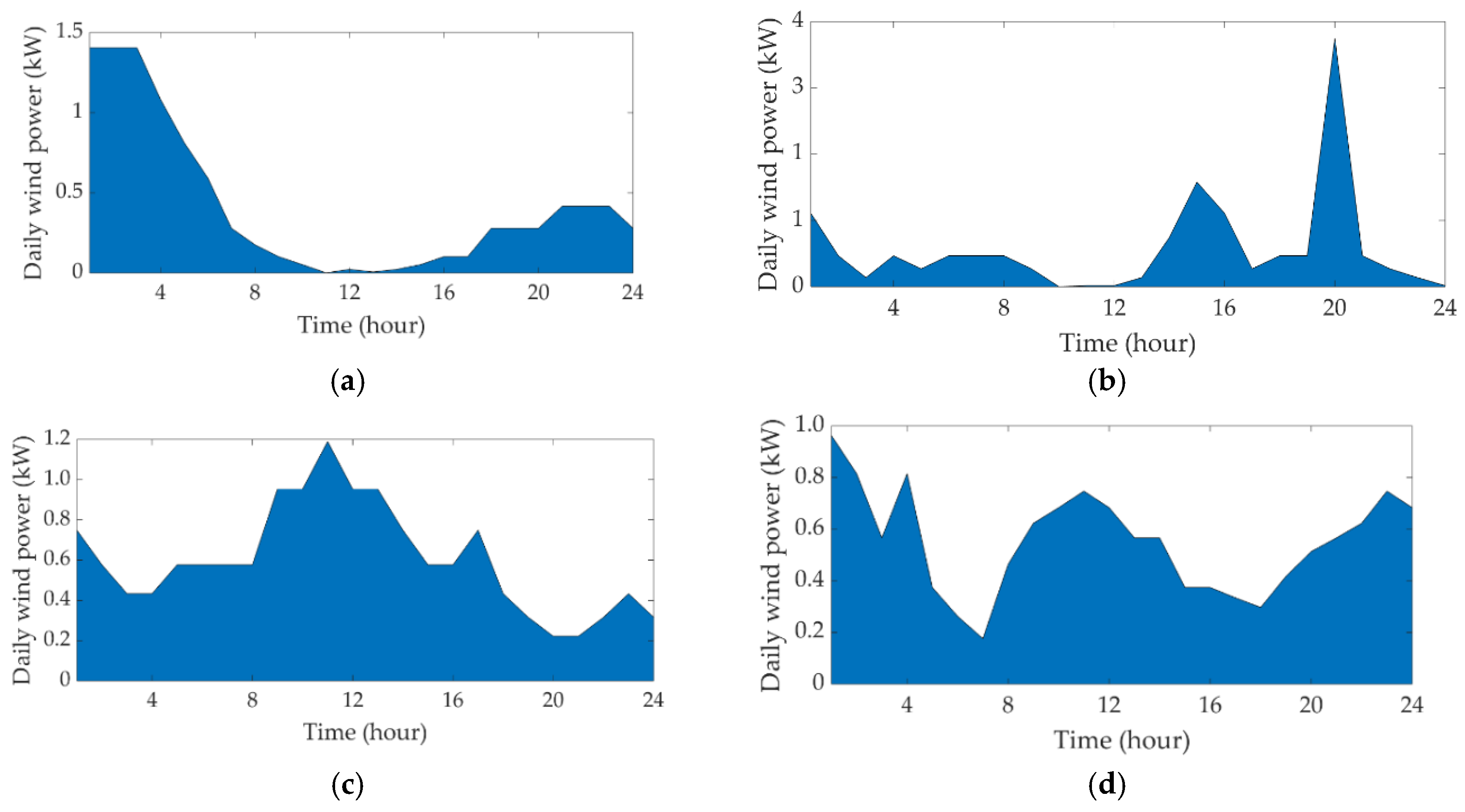
5.3. Wind Speed and Power Profiles
5.4. Analysis and Discussion
- The peak demand is over 4 kW but it only lasts for a couple of minutes. The demand is 4 kW in summer days and below 1 kW on winter days;
- The energy demand has 3 peaks over selected days while the wind power is random on these days.
- The peak demand and the peak supply do not occur in the same time on any selected days.
- In general, the wind power is higher than the energy demand over the night time on any chosen days.
5.4.1. Variations
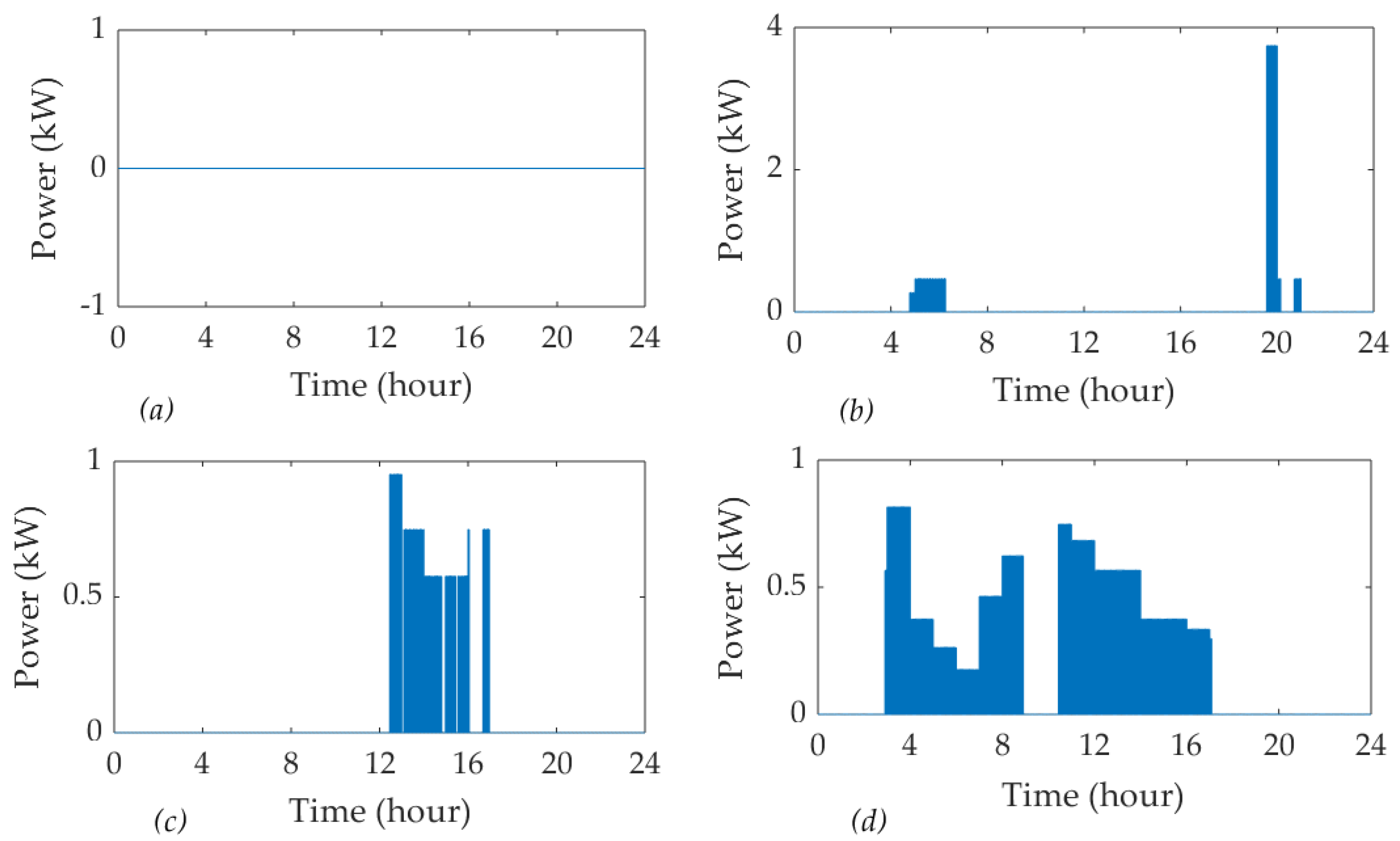
5.4.2. Fed-in Power to the Grid
5.5. Key Performance Indicators
5.5.1. Energy Indicator
5.5.2. Power Indicator
5.5.3. Time Indicator
5.5.4. Other Indicators
6. Conclusions
- (1)
- In this study, actual demands fluctuated over the four days and the wind power was also intermittent. By using the energy storage system with hydrogen fuel cells, the demand was balanced.
- (2)
- During the operating period, the loads were levelled by the energy storage system to consume wind power locally.
- (3)
- By the GA optimization scheme, the wind energy is converted into either chemical (in hydrogen) or electrical forms with relatively high conversion efficiency.
- (4)
- The developed technologies provide a new methods to operate a grid-tied power network where intermittent renewables can be effectively used. This will encourage the uptake of wind, hydrogen, and fuel cells in power generation.
Author Contributions
Funding
Conflicts of Interest
References
- Loh, P.C.; Li, D.; Chai, Y.K.; Blaabjerg, F. Autonomous control of interlinking converter with energy storage in hybrid AC–DC microgrid. IEEE Trans. Ind. Appl. 2013, 49, 1374–1382. [Google Scholar] [CrossRef]
- Mojtahedzadeh, S.; Ravadanegh, S.N.; Haghifam, M.R. Optimal multiple microgrids based forming of greenfield distribution network under uncertainty. IET Renew. Power Gener. 2017, 11, 1059–1068. [Google Scholar] [CrossRef]
- Department for Business, Energy & Industrial Strategy. Energy Trends: Renewables. 2017. Available online: https://www.gov.uk/government/uploads/system/uploads/attachment_data/file/604105/Renewables.pdf (accessed on 4 May 2017).
- Tan, Y.; Meegahapola, L.; Muttaqi, K.M. A review of technical challenges in planning and operation of remote area power supply systems. Renew. Sustain. Energy Rev. 2014, 38, 876–889. [Google Scholar] [CrossRef]
- Kharlamova, G.; Nate, S.; Chernyak, O. Renewable energy and security for Ukraine: Challenge or smart way. J. Int. Stud. 2016, 9, 88–115. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Kasperowicz, R.; Pinczynski, M.; Khabdullin, A. Modeling the power of renewable energy sources in the context of classical electricity system transformation. J. Int. Stud. 2017, 10, 264–272. [Google Scholar] [CrossRef]
- Tvaronaviciene, M.; Prakapiene, D.; Garskaite-Milvydiene, K.; Prakapas, R.; Nawrot, L. Energy efficiency in the long run in the selected European countries. Econ. Sociol. 2018, 11, 245–254. [Google Scholar] [CrossRef]
- Shindina, T.; Streimikis, J.; Sukhareva, Y.; Nawrot, L. Social and economic properties of the energy markets. Econ. Sociol. 2018, 11, 334–344. [Google Scholar] [CrossRef]
- Stavytskyy, A.; Kharlamova, G.; Giedraitis, V.; Sumskis, V. Estimating the interrelation between energy security and macroeconomic factors in European countries. J. Int. Stud. 2018, 11, 217–238. [Google Scholar] [CrossRef]
- Simionescu, M.; Bilan, Y.; Krajnakova, E.; Streimikiene, D.; Gedek, S. Renewable energy in the electricity sector and GDP per capita in the European Union. Energies 2019, 12, 2520. [Google Scholar] [CrossRef]
- Pérez-Navarro, A.; Alfonso, D.; Ariza, H.E.; Cárcel, J.; Correcher, A.; Escrivá-Escrivá, G.; Roldán, C. Experimental verification of hybrid renewable systems as feasible energy sources. Renew. Energy 2016, 86, 384–391. [Google Scholar] [CrossRef]
- Kohsri, S.; Meechai, A.; Prapainainar, C.; Narataruksa, P.; Hunpinyo, P.; Sin, G. Design and preliminary operation of a hybrid syngas/solar PV/battery power system for off-grid applications: A case study in Thailand. Chem. Eng. Res. Des. 2018, 131, 346–361. [Google Scholar] [CrossRef]
- Seeling-Hochmuth, G.C. A combined optimisation concet for the design and operation strategy of hybrid-PV energy systems. Sol. Energy 1997, 61, 77–87. [Google Scholar] [CrossRef]
- Krausen, E.; Mertig, D. Sewage plant powered by combination of photovoltaic, wind and biogas on the Island of Fehmarn, Germany. Renew. Energy 1991, 1, 745–748. [Google Scholar] [CrossRef]
- Xing, L.; Liu, X.; Alaje, T.; Kumar, R.; Mamlouk, M.; Scott, K. A two-phase flow and non-isothermal agglomerate model for a proton exchange membrane (PEM) fuel cell. Energy 2014, 73, 618–634. [Google Scholar] [CrossRef]
- Xing, L.; Das, P.K.; Song, X.; Mamlouk, M.; Scott, K. Numerical analysis of the optimum membrane/ionomer water content of PEMFCs: The interaction of Nafion? ionomer content and cathode relative humidity. Appl. Energy 2015, 138, 242–257. [Google Scholar] [CrossRef]
- Xing, L.; Du, S.; Chen, R.; Mamlouk, M.; Scott, K. Anode partial flooding modelling of proton exchange membrane fuel cells: Optimisation of electrode properties and channel geometries. Chem. Eng. Sci. 2016, 146, 88–103. [Google Scholar] [CrossRef]
- Xing, L. An agglomerate model for PEM fuel cells operated with non-precious carbon-based ORR catalysts. Chem. Eng. Sci. 2018, 179, 198–213. [Google Scholar] [CrossRef]
- Xing, L.; Shi, W.; Su, H.; Xu, Q.; Das, P.K.; Mao, B.; Scott, K. Membrane electrode assemblies for PEM fuel cells: A review of functional graded design and optimization. Energy 2019, 177, 445–464. [Google Scholar] [CrossRef]
- Noroozian, R. On-grid and Off-grid Operation of Multi-Input Single-Output DC/DC Converter based Fuel Cell Generation System. In Proceedings of the 2010 18th Iranian Conference on Electrical Engineering (ICEE), Isfahan, Iran, 11–13 May 2010. [Google Scholar]
- Carla, B. Hydrogen fuel cell scooter with plug-out features for combined transport and residential power generation. Int. J. Hydrog. Energy 2019. [Google Scholar] [CrossRef]
- Sathyaprabakaran, B.; Paul, S. Modeling and Simulation of PEM Fuel Cell Based Power Supply and its Control. In Proceedings of the Institution of Engineering and Technology IET Chennai 3rd International Conference on Sustainable Energy and Intelligent Systems (SEISCON 2012), Tiruchengode, India, 27–29 December 2012; pp. 311–316. [Google Scholar]
- Bukar, A.; Tan, C. A review on stand-alone photovoltaic-wind energy system with fuel cell: System optimization and energy management strategy. Clean. Prod. 2019, 221, 73–88. [Google Scholar] [CrossRef]
- Eriksson, E.L.V.; Gray, E.M. Optimization and integration of hybrid renewable energy hydrogen fuel cell energy systems—A critical review. Appl. Energy 2017, 202, 348–364. [Google Scholar] [CrossRef]
- Dobo, Z.; Palotas, A.B. Impact of the voltage fluctuation of the power supply on the efficiency of alkaline water electrolysis. Int. J. Hydrog. Energy 2016, 41, 11849–11856. [Google Scholar] [CrossRef]
- Ning, N. Study on adaptability of wide power fluctuation in water electrolysis hydrogen production plant. Ship Sci. Technol. 2017, 39, 133–136. [Google Scholar]
- Li, Z.; Guo, P.; Han, R.; Sun, H. Current status and development trend of wind power generation-based hydrogen production technology. Energy Explor. Exploit. 2019, 37, 5–25. [Google Scholar] [CrossRef]
- Ma, W.; Xue, X.; Liu, G. Techno-economic evaluation for hybrid renewable energy system: Application and merits. Energy 2018, 159, 385–409. [Google Scholar] [CrossRef]
- Prakash, P.; Khatod, D.K. Optimal sizing and siting techniques for distributed generation in distribution systems: A review. Renew. Sustain. Energy Rev. 2016, 57, 111–130. [Google Scholar] [CrossRef]
- Theo, W.L.; Lim, J.S.; Ho, W.S.; Hashim, H.; Lee, C.T. Review of distributed generation (DG) system planning and optimisation techniques: Comparison of numerical and mathematical modelling methods. Renew. Sustain. Energy Rev. 2017, 67, 531–573. [Google Scholar] [CrossRef]
- Chen, X.; Wang, Y.; Wu, Q. A bio-fuel power generation system with hybrid energy storage under a dynamic programming operation strategy. IEEE Access 2019, 7, 64966–64977. [Google Scholar] [CrossRef]
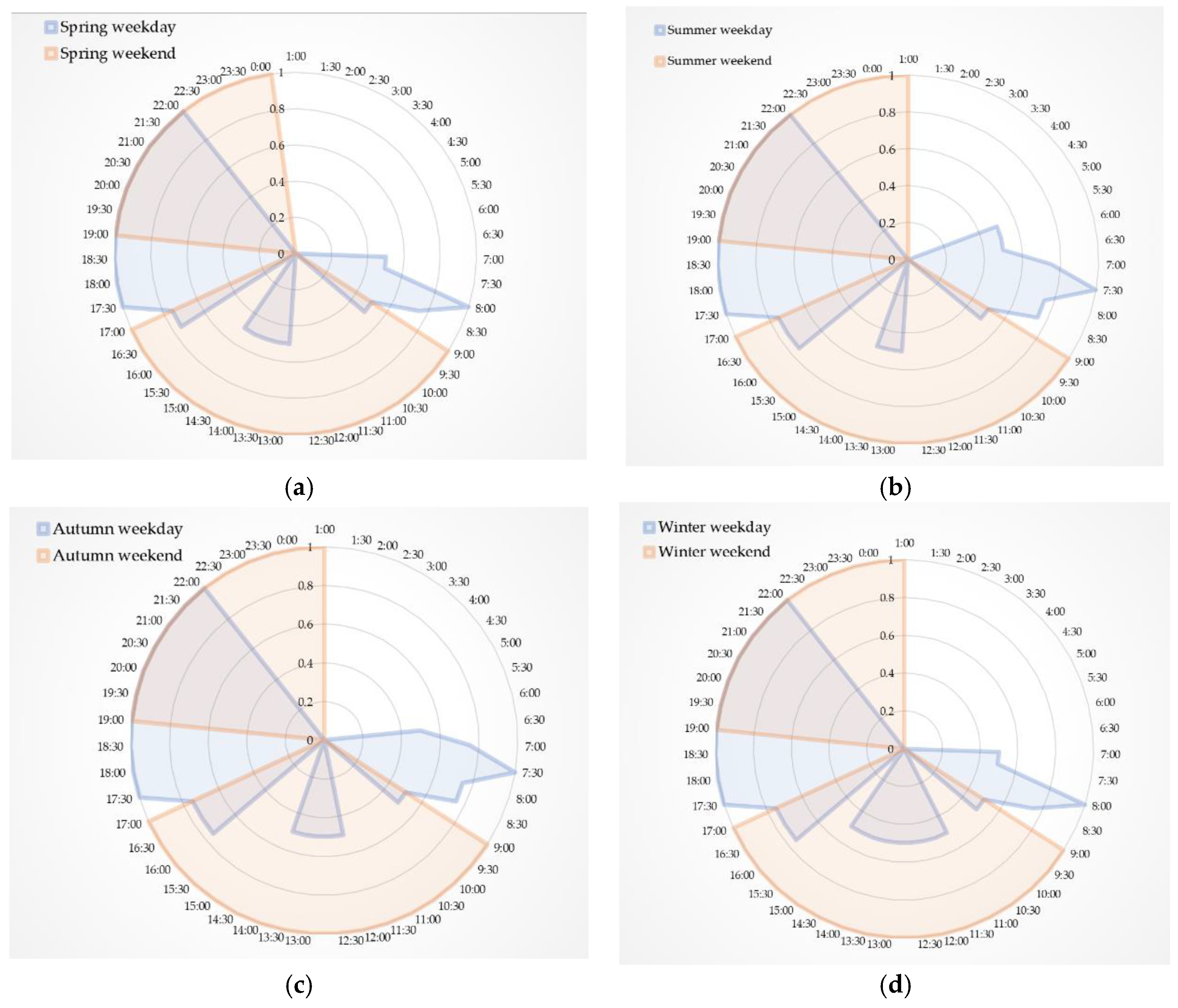
| Key Indicator | Spring Day | Summer Day | Autumn Day | Winter Day |
|---|---|---|---|---|
| Power range of the demand (kW) | 0–5.8 | 0–6.1 | 0–9.7 | 0–8.9 |
| Daily electrical consumption (kWh) | 12.0 | 11.1 | 16.1 | 12.5 |
| Period of demand lower than 1 kW (h) | 22.4 | 22.2 | 21.4 | 21.4 |
| Period of demand over 4 kW (h) | 0.12 | 0.12 | 0.23 | 0.23 |
| Percentage of low demand (%) | 93.3 | 92.5 | 89.2 | 89.2 |
| Percentage of high demand (%) | 0.5 | 0.5 | 0.96 | 0.96 |
| Performance Indicator | Spring Day | Summer Day | Autumn Day | Winter Day | |
|---|---|---|---|---|---|
| Energy (kWh) | Electricity from wind energy | 9.99 | 13.6 | 14.4 | 13.2 |
| Electricity from fuel cells | 6.25 | 5.66 | 6.65 | 5.11 | |
| Electricity for hydrogen generation | 6.36 | 7.87 | 5.58 | 6.60 | |
| Load consumption | 9.86 | 10.40 | 14.65 | 11.75 | |
| Fed-in energy to the grid | 0 | 1.26 | 1.53 | 6.06 | |
| Power (kW) | Load power | 0–5.81 | 0–6.1 | 0–9.63 | 0–8.91 |
| Power from wind | 0–1.4 | 0–4 | 0–1.2 | 0–0.9 | |
| Power from fuel cells | 0–5.71 | 0–5.82 | 0–8.68 | 0–8.29 | |
| Fed-in power to the grid | 0 | 0–3.75 | 0–0.95 | 0.82 | |
| Duration (h) | Fuel cell duty time | 14.6 | 10.3 | 9.2 | 7.3 |
| Hydrogen production | 9.4 | 12.5 | 13.6 | 16.7 | |
| Peak hours | 0.09 | 0.03 | 0.05 | 0.25 | |
| Percentage (%) | 50–73.2 | 18.6–90 | 16–90 | 50–90 | |
| Local consumption of the wind energy | 100 | 90.7 | 89.4 | 51.7 | |
| Fed-in energy to the grid | 0 | 9.3 | 10.6 | 48.3 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, X.; Cao, W.; Xing, L. GA Optimization Method for a Multi-Vector Energy System Incorporating Wind, Hydrogen, and Fuel Cells for Rural Village Applications. Appl. Sci. 2019, 9, 3554. https://doi.org/10.3390/app9173554
Chen X, Cao W, Xing L. GA Optimization Method for a Multi-Vector Energy System Incorporating Wind, Hydrogen, and Fuel Cells for Rural Village Applications. Applied Sciences. 2019; 9(17):3554. https://doi.org/10.3390/app9173554
Chicago/Turabian StyleChen, Xiangping, Wenping Cao, and Lei Xing. 2019. "GA Optimization Method for a Multi-Vector Energy System Incorporating Wind, Hydrogen, and Fuel Cells for Rural Village Applications" Applied Sciences 9, no. 17: 3554. https://doi.org/10.3390/app9173554
APA StyleChen, X., Cao, W., & Xing, L. (2019). GA Optimization Method for a Multi-Vector Energy System Incorporating Wind, Hydrogen, and Fuel Cells for Rural Village Applications. Applied Sciences, 9(17), 3554. https://doi.org/10.3390/app9173554






