Abstract
The fluid gear pump-based system has repetitive disturbances, such as flow ripples, due to the mechanical characteristics of the gear system. The periodic disturbances have negative effects on the precise flowrate control, which is essential for consistent coating quality in the painting process. This study proposes a precise flowrate control method of the fluid gear pump-based painting system to compensate for the periodic disturbances. The compensation value of the controller output can be obtained by a repetitive controller. A compensation lookup table corresponding to the reference speed and the rotation angle can be generated through the repetitive controller. In order to secure robustness against various situations, a closed-loop system consists of the conventional proportional-derivative (PD) controller and a compensation lookup table in the form of the feedforward controller. The lookup table-based feedforward controller was compared with the open-loop controller and PD controller. Experimental results show that the proposed method is more effective than existing controllers in terms of periodic disturbance compensation. By using the results of this study, it is possible to improve the performance of the fluid gear pump-based painting system and precisely control the paint spray amount.
1. Introduction
A painting system using a six-axis articulated robot has been developed to paint complex-shaped objects uniformly and efficiently. Particularly, the automobile painting process requires high quality, and methods of spraying paint quickly and precisely have been developed. For the precise fluid transfer, the fluid gear pump is widely used. As shown in Figure 1, the fluid gear pump operates to control the flowrate using the electronic actuator and the rotational gear.
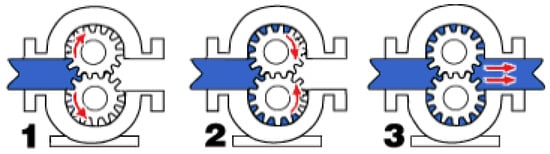
Figure 1.
Fluid gear pump mechanism.
The fluid gear pump has repetitive disturbances, such as flow ripples, that decrease the precision of the fluid transfer. To compensate for the repetitive disturbances, previous studies have suggested a mathematical model of the repetitive flow ripples. The characteristics of the flow ripple are expressed by the theoretical method according to the number of gear teeth [1]. The characteristics of the trapped volume between the gear teeth, which cause the flow ripple, can be calculated by a geometric formula [2]. To express the fluctuation of the flowrate as a mathematical model, a flowrate formula uses an analytical method that considers the shape of the fluid gear pump [3]. A numerical method has been proposed for analyzing the kinematic flow ripple of a fluid gear pump, which allows more precise mathematical modeling than conventional analytical methods [4,5,6].
The zero phase error tracking controller (ZPETC) and the repetitive controller based on the internal model principle have been applied to various applications for the repetitive disturbance rejection [7,8]. The repetitive controller is very effective in servo systems with repetitive disturbances [9]. For more stable control in systems with periodic disturbances, the repetitive controller can be combined with a low-pass filter [10]. The discrete wavelet transform-based repetitive controller minimizes the memory used in the repetitive controller and minimizes the tracking error [11]. To track the desired trajectory while eliminating repetitive disturbances, the repetitive controller can be plugged into a conventional controller such as a proportional-derivative (PD) controller. This plug-in repetitive controller has been applied to the pulse-width modulation (PWM) rectifier and has shown effective performance [12]. The repetitive controller with a disturbance observer can effectively compensate for the disturbances with non-repetitive frequency components [13].
Previous studies have proposed control methods to eliminate system disturbances, and the disturbance observer and the repetitive controller are representative examples [7,8,9,10,11,12,13,14,15,16,17]. To eliminate multiple disturbances as well as single disturbances, a composite hierarchical anti-disturbance control was proposed [18]. Active disturbance rejection control was proposed in order to compensate for disturbances that are difficult to model, by automatically updating the parameters of the controller [19]. Many disturbance rejection methods have been developed, but repetitive controllers can effectively remove periodic disturbances [20,21]. As an example of the implementation of repetitive control, repetitive disturbances are effectively removed for servo systems such as optical disk drives and hard disk drives [22,23]. In addition, a repetitive controller applied to the rotor of a wind turbine minimized periodic wind disturbance [24].
For the precise flowrate control of the fluid gear pump-based painting system used in automotive painting processes, this study attempts to eliminate various periods of disturbance for a wide range of flowrate commands. The disturbances in various periods can be expressed by the rotational speed and rotation angle of the motor, relative to the flowrate command. Therefore, a lookup table-based controller can be designed to effectively compensate for periodic disturbances. In this study, the compensation lookup table-based controller corresponding to the flowrate and the rotation angle is experimentally generated through the repetitive controller. To secure robustness against various situations, a closed-loop system consists of the conventional PD controller and a compensation lookup table, in the form of the feedforward controller. The proposed method is evaluated by comparison with the open-loop controller and the conventional PD controller, which are widely used in the industry.
This paper is organized as follows. Section 2 introduces the robot arm and the fluid gear pump system used in vehicle painting in this study, and it identifies the problems that occur in the precise flowrate control. The Section 2 presents a repetitive control-based feedback controller that compensates for the repetitive disturbance of the fluid gear pump system. In Section 3, experimental results are presented for the verification of the proposed control method. Section 4 presents conclusions and a future direction of study.
2. Materials and Methods
To ensure a high level of painting quality in the automotive painting process, a robotic arm with a fluid gear pump-based painting system is used. Figure 2a shows the outline of the robotic arm for vehicle painting, and Figure 2b shows the vehicle painting system based on the fluid gear pump to be controlled in this study. As shown in Figure 2b(1), the color change valve unit can be used to change the paint color. The servo motor in Figure 2b(2) is connected to the reducer in Figure 2b(3) for proper torque. Then, the fluid gear pump in Figure 2b(4) is used to discharge the paint in the correct amount. The atomizer in Figure 2b(5) rotates the paint at a high speed and atomizes it before spraying it onto the substrate. The flow/pressure sensor in Figure 2b(6) can measure the amount of paint dispensed.
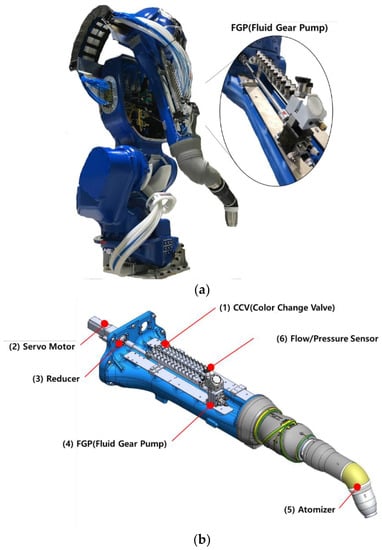
Figure 2.
Configuration of the painting system; (a) the robotic arm of the automated automotive painting system; (b) the details of the painting system using the fluid gear pump.
In the system of Figure 2b, the servo motor has a rated power of 200 W and a rated rotational speed of 3000 rpm, and the reducer has a gear ratio of 10:1. The fluid gear pump (DGP 6SAD01) is capable of delivering 6 cc of fluid per revolution, and has 14 teeth. The flow sensor (G250HR, Graco) is capable of measuring fluids with an accuracy of 0.061 cc/pulse at flow rates ranging from 38 to 1900 cc/min. The fluid gear pump-based painting system in Figure 2a has an output range of 0 to 500 cc/min, so the flow sensor can sufficiently measure the flowrate output. In this study, a fluid with a viscosity of 31.5 cSt at 40 °C (FM AW Hydraulic ISO 32, Guardsman) is used to control the fluid gear pump system.
As shown in Figure 3, the fluid gear pump-based painting system (Figure 2b) is defined as a transfer function () in which the input signal is the flowrate command and the output signal is the flowrate output. When a constant flowrate command is an input to the painting system, the servo motor rotates at the speed corresponding to the reference, and the flowrate output of the fluid transferred through the fluid gear pump is measured from the flow sensor. The rotational angle of the motor can be measured by an encoder. Figure 4 shows the measurement result of the steady-state flowrate output of for the constant flowrate command. In Figure 4a and Figure 4b, the flowrate commands are 400 cc/min and 100 cc/min, respectively. The results of the open-loop control for the constant flowrate command show that the steady-state flowrate output contains periodic disturbances.
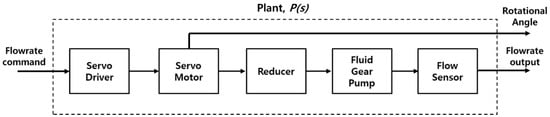
Figure 3.
Block diagram of the fluid gear pump-based painting system.
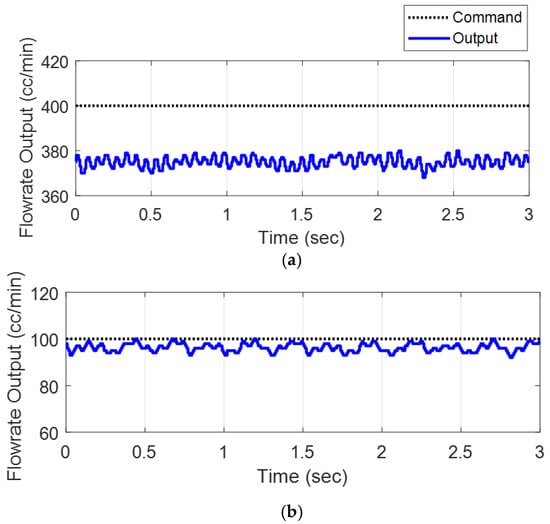
Figure 4.
Time trend of flow feedback; (a) 400 cc/min flowrate command; (b) 100 cc/min flowrate command.
Fast Fourier transform (FFT) is applied for the frequency analysis of the periodic disturbances. Figure 5a is the result of applying the FFT to the flowrate output of Figure 4a, and Figure 5b is the result of its application to the output of Figure 4b. The peak frequency due to periodic disturbance is 15.556 Hz for the constant flowrate command of 400 cc/min, and 3.972 Hz for 100 cc/min. Since the flowrate command is a fixed value, the peak frequency of the flowrate output is considered as the frequency of the periodic disturbance.
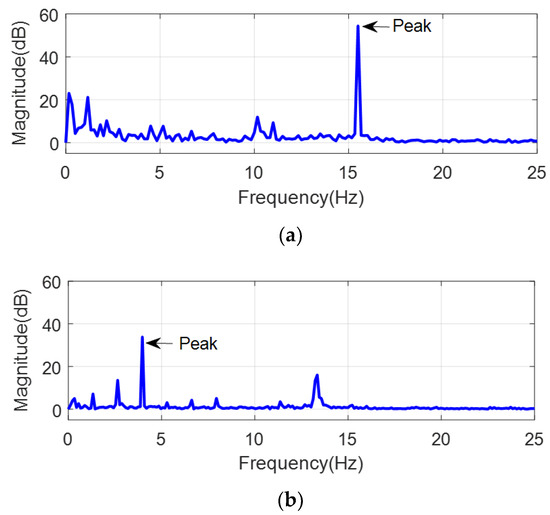
Figure 5.
Fast Fourier transform (FFT) of flowrate; (a) 400 cc/min flowrate command; (b) 100 cc/min flowrate command.
The constant flowrate commands of 100, 200, 300, 400, and 500 cc/min were used to obtain the frequency of the disturbance. Table 1 shows the peak frequency of the measured flowrate output. Experimental results show that the peak frequency of the flowrate output is as large as the amplitude of the flowrate command. Since the rotational speed of the motor increases as the flowrate command increases, the frequency of the periodic disturbance is proportional to the rotational speed of the motor. Periodic disturbances can also be affected by the angle and the rotational speed of the motor. The periodic disturbances related to the rotational speed and the angle of the servomotor must be compensated for, in order to achieve the precise spraying of the fluid gear pump-based painting system.

Table 1.
Peak frequency of measured flowrate output.
For a closed-loop system in the discrete-time domain given a flowrate command and a plant model, the repetitive controller can be implemented as a block diagram, as shown in Figure 6. In Figure 6, , , and denote the reference, output, and disturbance, respectively, and , , and are the plant model, the repetitive controller, the dynamic compensator, and the low-pass filter, respectively. If is a period of the repetitive disturbance, and satisfy as delay counts. If the plant model satisfies and all of the poles of the are in the unit circle, and are established.
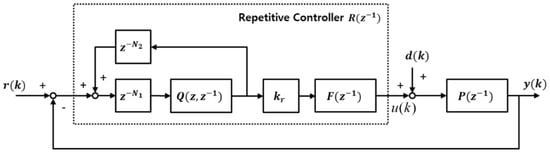
Figure 6.
Repetitive control system with a low-pass filter in the discrete-time domain.
To design a repetitive controller for periodic disturbances, the nominal model of the plant () in Figure 3 was experimentally obtained, and expressed in the second-order system in the continuous-time domain as follows:
The poles of P(s) are in the left-half of the plane, and the stability of the nominal plant model is guaranteed. is the discrete-time transfer function obtained by using the zero-order hold equivalent in P(s) of Equation (1) at the sampling period of 1 msec, and it is expressed as follows:
Since the poles of are and the zero of is , all of the poles and zeros of exist inside of the unit circle.
To verify the similarity between the actual plant model and the nominal plant model in Equation (2), the step response for the flowrate command of 100 cc/min is analyzed, as shown in Figure 7. MATLAB (2018b, Mathworks) was used for the simulation of the nominal plant model. After 2 s in Figure 7, the mean square error (MSE) between the simulation and experimental results is 2.134 cc/min, and the correlation between the results from 0 to 4 s is = 0.9384. For the flowrate commands of 100, 200, 300, 400, and 500 cc/min, the simulation results using the nominal plant model are compared with the experimental results in Table 1, and listed in Table 2. For the five flowrate commands, all of the MSEs were less than 2.5, and all were above 0.9. In Table 2, the MSE was relatively large in the low-frequency range of 100 and 200 cc/min due to the influence of the gear shape and frictions. In conclusion, the nominal plant model of Equation (2) is a transfer function expressing the actual plant model and that can be used for designing repetitive controllers.
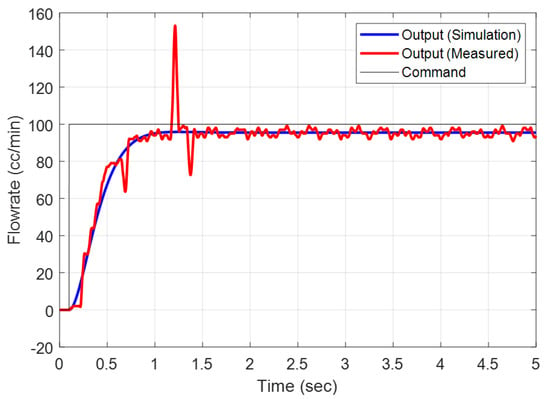
Figure 7.
The measured flowrate output of the actual plant model, and the simulated flowrate output of the nominal plant model for the flowrate command of 100 cc/min.

Table 2.
Comparison of the measured flowrate output and simulation result using the nominal plant model.
To design the repetitive controller, the nominal plant model of Equation (1) can be represented as = , and and are asymptotically stable polynomial (i.e., all of the poles are located in the unit circle). Note that a closed-loop system including the and the repetitive controller () is asymptotically stable if satisfies the following conditions [10]:
where N is the period of periodical disturbance. The closed-loop system containing the repetitive controller of Equation (3) is always asymptotically stable in [10]. In this study, the repetitive controller factor ( was set to 0.8 in order to ensure the stability. The transfer function in the form of a low-pass filter is defined as follows:
The bandwidth of the is 181.7 Hz, including the output range, so the can act as a moving average filter, which effectively removes the measurement noise without reducing the system bandwidth.
When the repetitive controller of Equation (3) is applied to the plant of Equation (2), Figure 8 shows the repetitive controller output (u(k)) at the steady state for flowrate commands of 100, 200, 300, and 400 cc/min. Figure 8 shows two characteristics of the controller output: (1) The controller output changes according to the motor’s flowrate command, and (2) the controller output is synchronized according to the rotational angle of the motor. This means that periodic disturbance occurs depending on the angle and rotational speed of the motor. It is difficult to remove the disturbance only by the repetitive controller if the disturbance of various periods occurs for a wide range of flowrate commands. Therefore, this study proposes a compensation lookup table that removes disturbance according to the rotation angle and rotation speed of the motor.
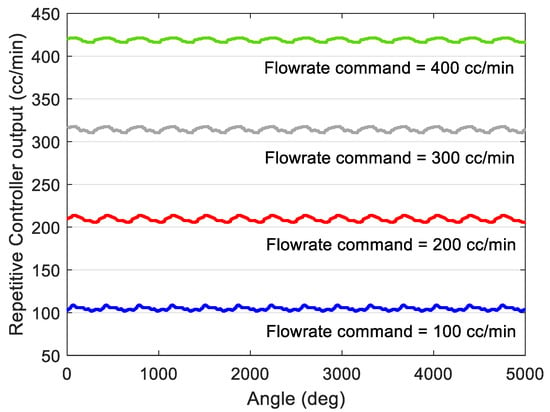
Figure 8.
Repetitive controller output at the steady state for various references.
In this study, the compensation value of the controller output according to each flowrate command is defined as the mean value of the controller output during N samples in the steady state:
where index i is the kind of constant flowrate i.e., (). For example, in Figure 8, M = 4, . Thus, Equation (5) gives the average of the controller outputs for N samples at each flowrate command. The sampling period of this study was 1 ms, and N = 10,000 was set to average the controller output for 10 s in the steady state. From Equation (5), the compensation values for the flowrate commands of 100, 200, 300, 400, and 500 cc/min were experimentally obtained, and the linear equation obtained by linear interpolation is expressed as follows:
where is the compensation value for the flowrate command, and is the constant flowrate command. Figure 9 shows the experimental data and Equation (6). The compensation value according to the rotation angle of the motor is obtained by the following equation:
where is the mean value during N samples of the controller output for the i-th flowrate command, as shown in Equation (5). Equation (7) first obtains the zero mean value signal () from the controller output for each constant flowrate command. Secondly, Equation (7) obtains an average value of M zero mean value signals at every angle. Figure 8 shows the compensation value according to the condition of M = 4, and the rotation angle of the motor obtained from Equation (7) is shown in Figure 10.
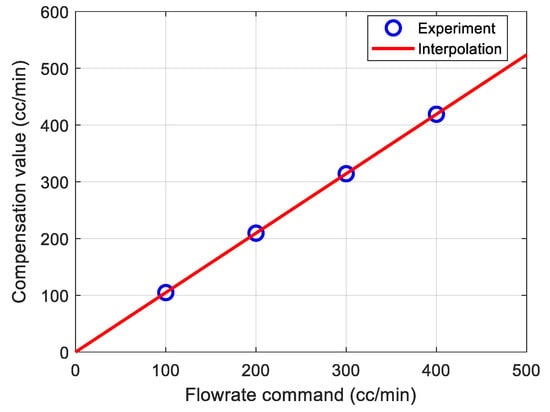
Figure 9.
Flowrate command dependent compensation value.
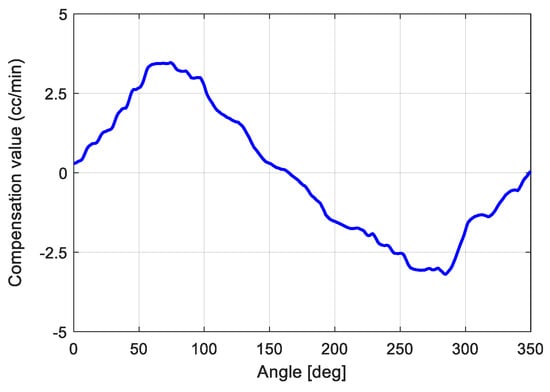
Figure 10.
Rotational angle of the motor-dependent compensation.
The flowrate command dependent compensation value and the angle-dependent compensation value obtained experimentally in Figure 9 and Figure 10, respectively, can be expressed as a lookup table, as shown in Figure 11. The input data of the compensation lookup table is the flowrate command and the current rotation position. Compensation lookup tables can obtain optimal compensation values that can remove periodic disturbances from input data.
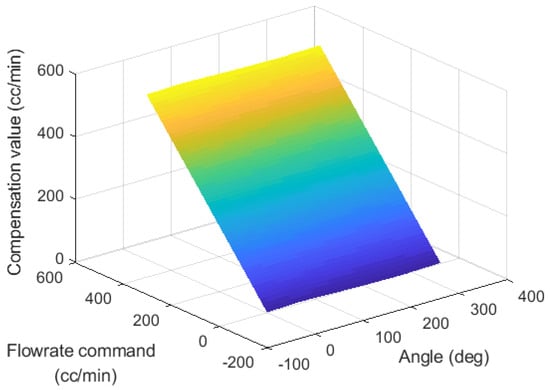
Figure 11.
Compensation lookup table based on flowrate command and rotational angle of the motor.
A closed-loop system with feedforward control based on a compensation lookup table in a conventional feedback controller is proposed as shown in Figure 12. The symbols , , and denote the flowrate command, flowrate output, disturbance, and rotational angle of the motor, respectively. and are the plant model and feedback controller, respectively. The feedback controller—such as a PD controller—secures robustness, tracking performance, and the stability of a closed-loop system. The feedforward controller using a compensation lookup table effectively compensates for periodic disturbances.
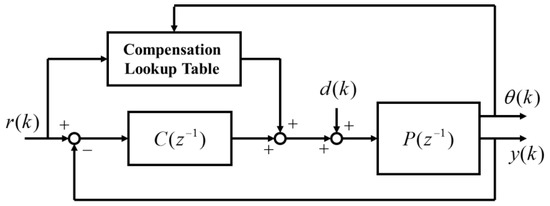
Figure 12.
Conventional feedback controller with a compensation lookup table.
3. Results
The proposed method in Figure 12 is experimentally evaluated. For the efficient tracking control, the PD controller is used as the feedback controller in Figure 12. Since the integral action can amplify the sensor noise and degrade the stability of the closed-loop, the proportional integral derivative (PID) controller is not used. The feedback controller follows the flowrate command () of 100, 150, and 400 cc/min, respectively. The experimental results of the measured flowrate output in the steady state are shown in Figure 13 and Table 3. The Figure 13a–c shows the experimentally measured flowrate outputs of 100, 150, and 400 cc/min, respectively. As shown in Figure 13, the blue line is the measured output of the open-loop system (Open-loop), the green line is the closed-loop system only using the PD controller (PD), and the red line is the closed-loop system using the compensation lookup table-based feedforward controller and the PD controller (Lookup).

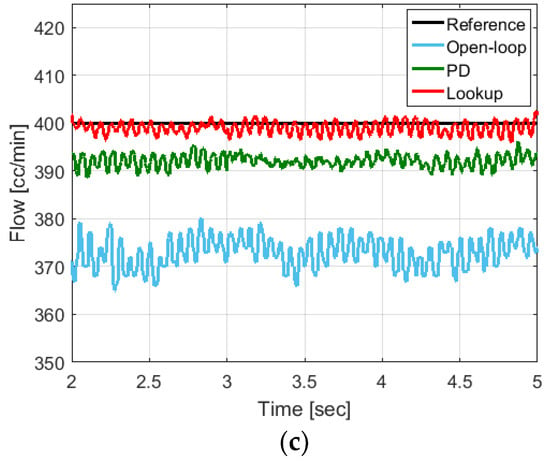
Figure 13.
Comparison of experimental results with flow feedback at the steady state; (a) 100 cc/min flowrate command; (b) 150 cc/min flowrate command; (c) 400 cc/min flowrate command.

Table 3.
The experimental results of the steady-state feedback error.
As shown in Figure 13a–c, the open-loop control system showed that the root mean square (RMS) values of the steady-state error were 3.9604, 7.1526, and 27.2863, respectively. In the closed-loop system only using the PD controller, the RMS errors between the flowrate command and the measured output were 2.3493, 3.6986, and 8.0320, respectively. The two control systems could not effectively remove the periodic disturbances. On the other hand, in the case of the proposed control method, the RMS values of tracking error were 0.7275, 1.1953, and 1.6392, respectively. The RMS values of the proposed method are much less than the RMS values of the open-loop system and the PD controller. In the case of the open-loop control system and the PD controller, the flow feedback at the steady state did not reach the flow command in the biased form. On the other hand, the proposed controller compensated the flowrate dependent value in the compensation lookup table as the feedforward type, so that the biased characteristics at the steady state were improved remarkably. Non-biased flow feedback that follows the flowrate command precisely in the painting process is essential. If the flow feedback does not reach the flowrate command sufficiently, there may be a lack of coating. In contrast, defects such as sagging may occur if the flow feedback is higher than the flowrate command. The experimental results show that the proposed controller can reduce the steady-state error significantly for the low-frequency flowrate commands, as well as for the high-frequency flowrate commands compared to the open-loop control system.
From the experimental results, the proposed control method can reduce the fluctuation amplitude, which is the minimum peak to the maximum peak difference in the steady-state error. The compensation lookup table-based feedforward controller showed that the mean values of fluctuation amplitude were 1.8790, 2.1891, and 3.3696, respectively, when the flowrate commands were 100 cc/min, 150 cc/min, and 400 cc/min. In the closed-loop system only using the PD controller, the mean values of fluctuation amplitude were 3.3110, 3.3740, and 3.5198.
In the low-speed flowrate command, the fluctuation amplitude of the proposed controller is low, whereas the fluctuation amplitude is as high as much as the conventional PD controller at high-speed flowrate command. The influence of the flowrate dependent compensation value is relatively greater than in the rotational angle-dependent compensation value at a high-speed flow rate command. Therefore, there is a limitation to remove periodic disturbances at high-speed flowrate commands effectively. However, the proposed controller can be effectively used because most of the flowrate commands are operated in the low-speed range of 100 to 150 cc/min in the painting process.
4. Discussion
This study proposes a closed-loop system combining the conventional feedback controller and the feedforward controller based on a compensation lookup table, in order to eliminate the periodic disturbances of the fluid gear pump. For the design of the compensation lookup table, the compensation value according to the rotational angle and speed were experimentally obtained using the repetitive controller in the fluid gear pump. Experimental results have shown that the feedback controller based on the compensation lookup table improves the control performance, compared to the conventional feedback controllers such as the open-loop control system and the PD controller. For the low-speed flowrate command between 100–150 cc/min, which is widely used in the painting process, the proposed controller reduces the tracking error and fluctuation amplitude better than the conventional feedback controllers. From the result of this study, it is possible to improve the performance of the fluid gear pump-based painting system that controls the amount of paint sprayed in the automobile painting process. Based on this study, we will analyze the correlation with the compensation value according to the characteristics of the paint, such as the viscosity of the paint used in the fluid gear pump, and add it to the compensation lookup table so as to control the flowrate more precisely.
Author Contributions
Conceptualization and methodology, K.P. and D.J.; software, data curation, validation, formal analysis and writing, K.P. and M.C.; review and supervision, D.J.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Manring, N.D.; Kasaragadda, S.B. The theoretical flow ripple of an external gear pump. J. Dyn. Syst. Meas. Control 2003, 125, 396–404. [Google Scholar] [CrossRef]
- Foster, K.; Taylor, R.; Bidhendi, I.M. Computer prediction of cyclic excitation sources for an external gear pump. Proc. Inst. Mech. Eng. Part B Manag. Eng. Manuf. 1985, 199, 175–180. [Google Scholar] [CrossRef]
- Huang, K.J.; Lian, W.C. Kinematic flowrate characteristics of external spur gear pumps using an exact closed solution. Mech. Mach. Theory 2009, 44, 1121–1131. [Google Scholar] [CrossRef]
- Zhao, X.; Vacca, A. Numerical analysis of theoretical flow in external gear machines. Mech. Mach. Theory 2017, 108, 41–56. [Google Scholar] [CrossRef]
- Zhao, X.; Vacca, A. Analysis of continuous-contact helical gear pumps through numerical modeling and experimental validation. Mech. Syst. Signal Process. 2018, 109, 352–378. [Google Scholar] [CrossRef]
- Rituraj, F.; Vacca, A. External gear pumps operating with non-Newtonian fluids: Modelling and experimental validation. Mech. Syst. Signal Process. 2018, 106, 284–302. [Google Scholar] [CrossRef]
- Francis, B.A.; Wonham, W.M. The internal model principle for linear multivariable regulators. Appl. Math. Optim. 1975, 2, 170–194. [Google Scholar] [CrossRef]
- Tomizuka, M. Zero Phase Error Tracking Algorithm for Digital Control. ASME J. Dyn. Syst. Meas. Control 1987, 65, 65–68. [Google Scholar] [CrossRef]
- Hara, S.; Yamamoto, Y.; Omata, T.; Nakano, M. Repetitive control system: A new type servo system for periodic exogenous signals. IEEE Trans. Autom. Control 1988, 33, 659–668. [Google Scholar] [CrossRef]
- Tomizuka, M. Dealing with periodic disturbances in controls of mechanical systems. Annu. Rev. Control 2008, 32, 193–199. [Google Scholar] [CrossRef]
- Mondal, U.; Sengupta, A.; Pathak, R.R. Servomechanism for periodic reference input: Discrete wavelet transform-based repetitive controller. Trans. Inst. Meas. Control 2016, 38, 14–22. [Google Scholar] [CrossRef]
- Zhou, K.; Wang, D. Digital repetitive controlled three-phase PWM rectifier. IEEE Trans. Power Electron. 2003, 18, 309–316. [Google Scholar] [CrossRef]
- Chen, X.; Tomizuka, M. New repetitive control with improved steady-state performance and accelerated transient. IEEE Trans. Control Syst. Technol. 2013, 22, 664–675. [Google Scholar] [CrossRef]
- Chen, W.H.; Balance, D.J.; Gawthrop, P.J.; O’Reilly, J. A nonlinear disturbance observer for robotic manipulators. IEEE Trans. Ind. Electron. 2000, 47, 932–938. [Google Scholar] [CrossRef]
- Chen, W.H.; Guo, L. Analysis of disturbance observer based control for nonlinear systems under disturbances with bounded variation. In Proceedings of the International Conference on Control, University of Bath, UK, 6–9 September 2004; pp. 1–5. [Google Scholar]
- Sariyildiz, E.; Ohnishi, K. A guide to design disturbance observer. J. Dyn. Syst. Meas. Control 2014, 136, 021011. [Google Scholar] [CrossRef]
- Li, S.; Yang, J.; Chen, W.H.; Chen, X. Disturbance Observer-Based Control: Methods and Applications; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Guo, L.; Cao, S. Anti-disturbance control theory for systems with multiple disturbances: A survey. ISA Trans. 2014, 53, 846–849. [Google Scholar] [CrossRef] [PubMed]
- Han, J. From PID to active disturbance rejection control. IEEE Trans. Ind. Electron. 2009, 56, 900–906. [Google Scholar] [CrossRef]
- Houtzager, I.; van Wingerden, J.W.; Verhaegen, M. Rejection of periodic wind disturbances on a smart rotor test section using lifted repetitive control. IEEE Trans. Control Syst. Technol. 2012, 21, 347–359. [Google Scholar] [CrossRef]
- Kempf, C.J.; Kobayashi, S. Disturbance observer and feedforward design for a high-speed direct-drive positioning table. IEEE Trans. Control Syst. Technol. 1999, 7, 513–526. [Google Scholar] [CrossRef]
- Moon, J.H.; Lee, M.N.; Chung, M.J. Repetitive control for the track-following servo system of an optical disk drive. IEEE Trans. Control Syst. Technol. 1998, 6, 663–670. [Google Scholar] [CrossRef]
- Guo, L. Reducing the manufacturing costs associated with hard disk drives—A new disturbance rejection control scheme. IEEE/ASME Trans. Mechatron. 1997, 2, 77–85. [Google Scholar]
- Eom, K.S.; Suh, I.H.; Chung, W.K. Disturbance observer based path tracking control of robot manipulator considering torque saturation. Mechatronics 2001, 11, 325–343. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).