Adaptive Backstepping Fractional Fuzzy Sliding Mode Control of Active Power Filter
Abstract
:1. Introduction
- (1)
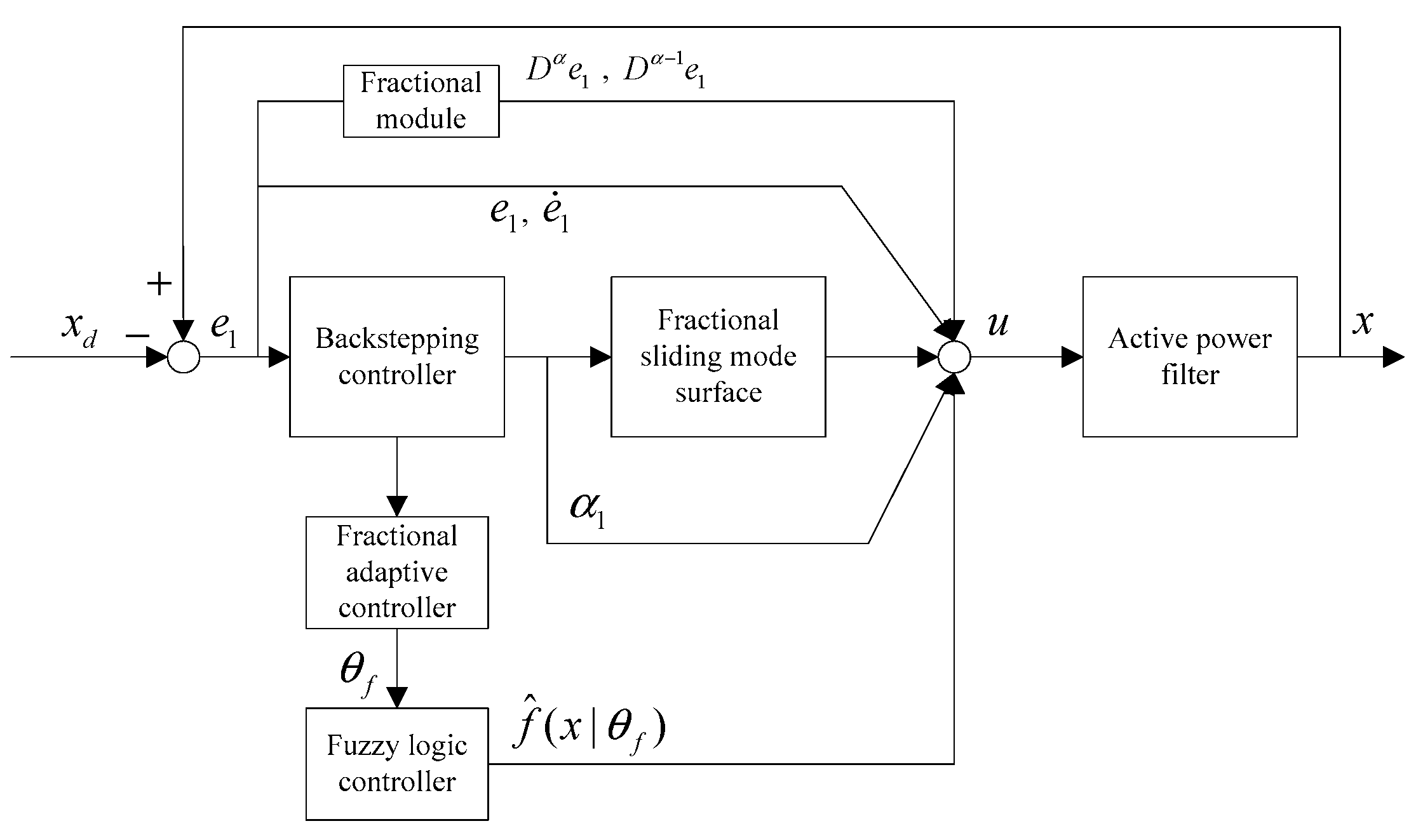
- A backstepping control strategy is applied to the design of a fractional sliding mode adaptive fuzzy controller. We avoid establishing a precise mathematical model of active power filter by transforming the general circuit equation into an analogical cascade system where the backstepping approach can be implemented.
- (2)
- Based on the backstepping control design, this paper extends the conventional integer-order sliding surface to fractional ones for three-phase active power filter. That means the system can achieve an extra degree of freedom and there would be more parameters to be adjusted to improve total harmonic distortion (THD).
- (3)
- A fractional sliding mode controller ensures that the control system reaches the sliding surface while the adaptive control strategy and fuzzy controller are also combined together to approximate the unknown dynamic model term and identify adaptive parameters online.
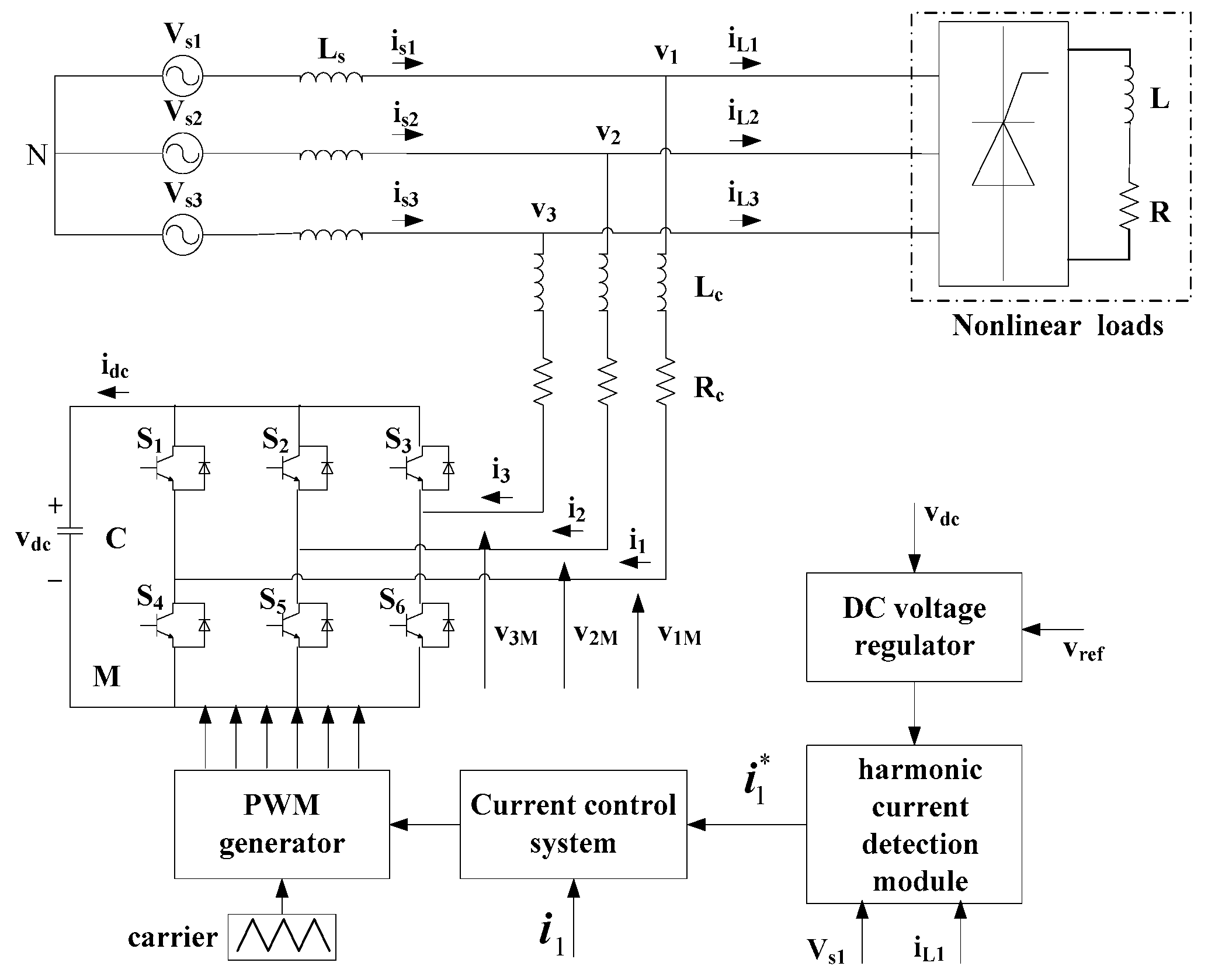
2. System Description
3. Design of Fractional Backstepping Sliding Mode Controller
3.1. Fractional Calculus Preliminaries
3.2. Fractional Backstepping Sliding Mode Controller
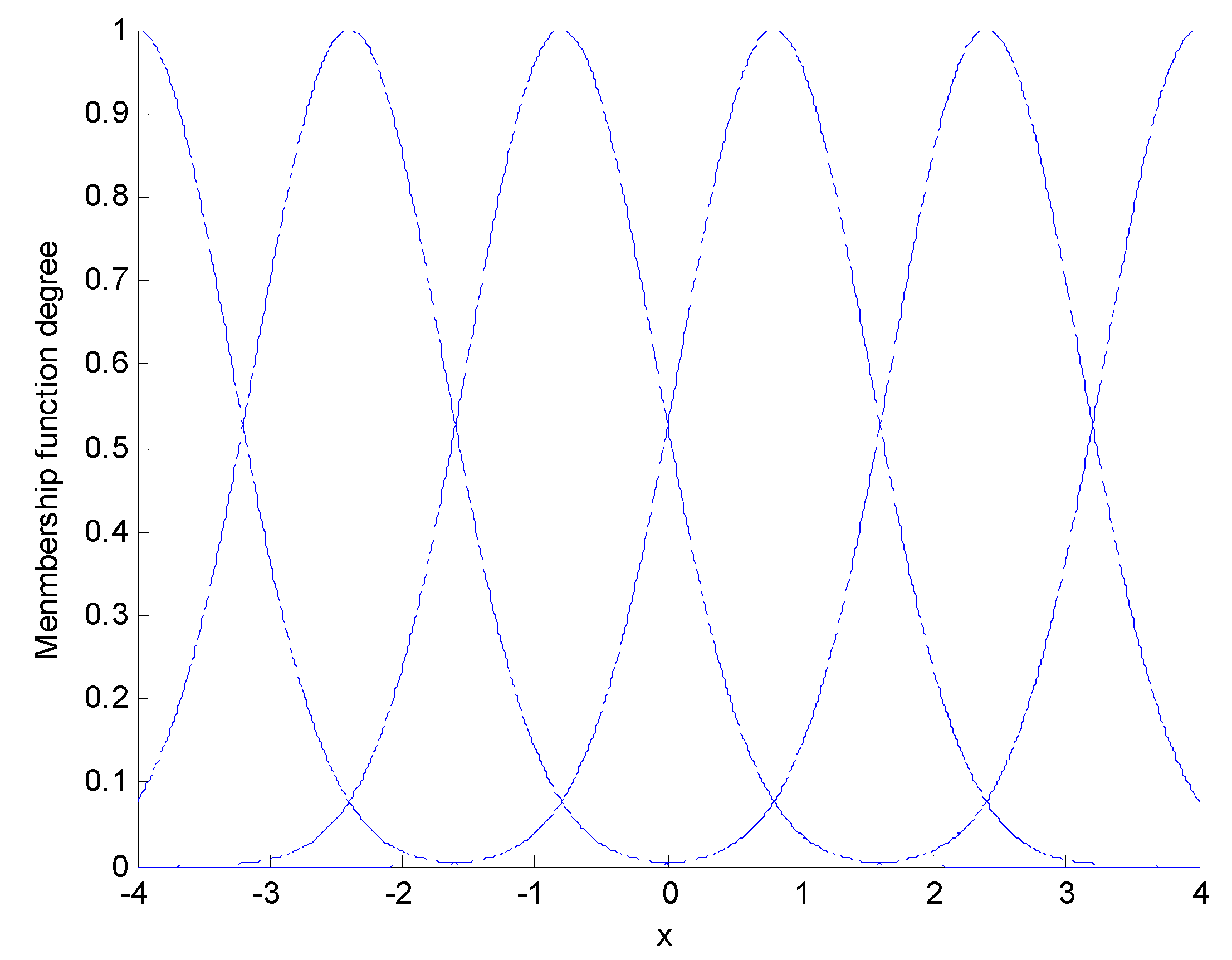
4. Design of Fractional Backstepping Sliding Mode Adaptive Fuzzy Controller
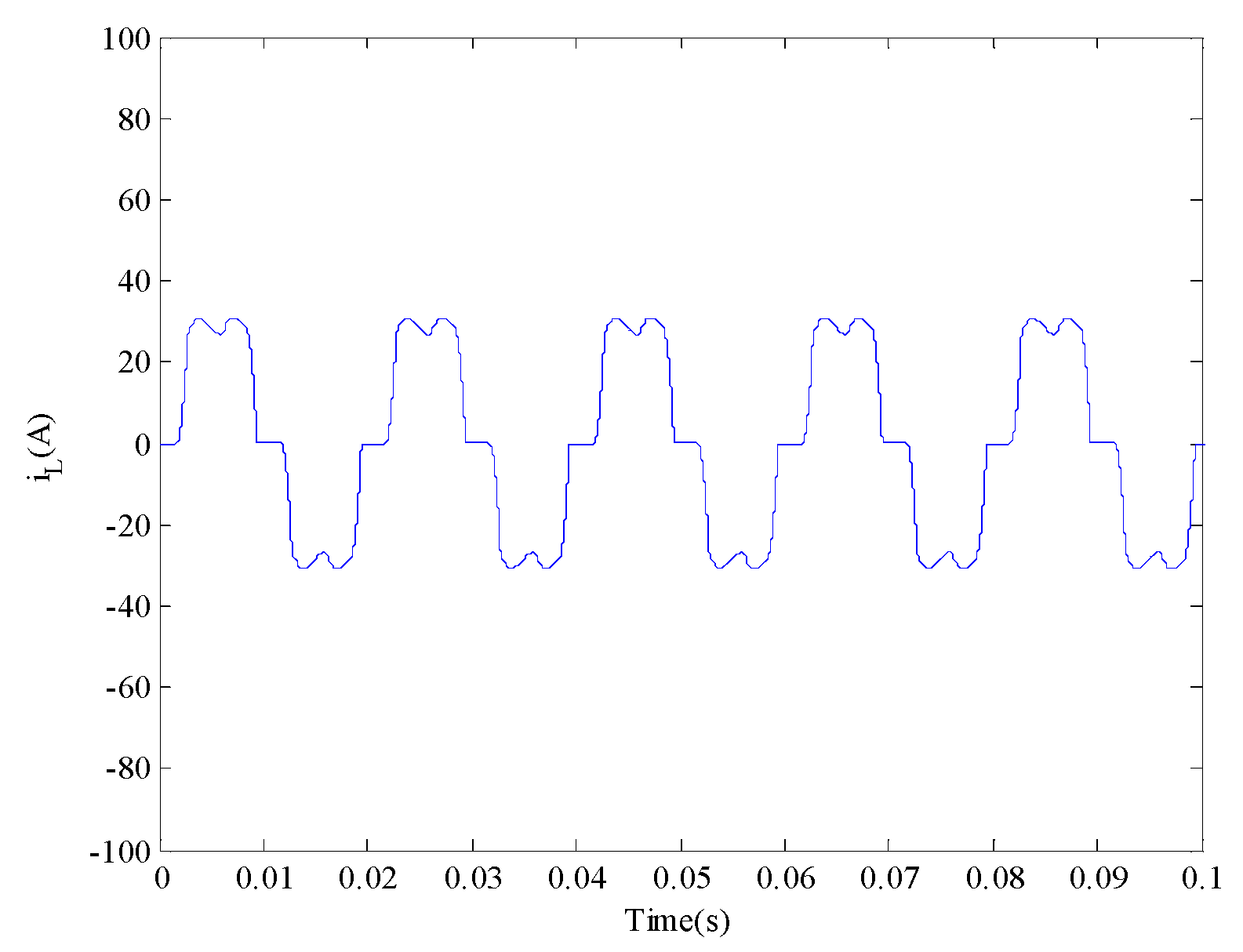
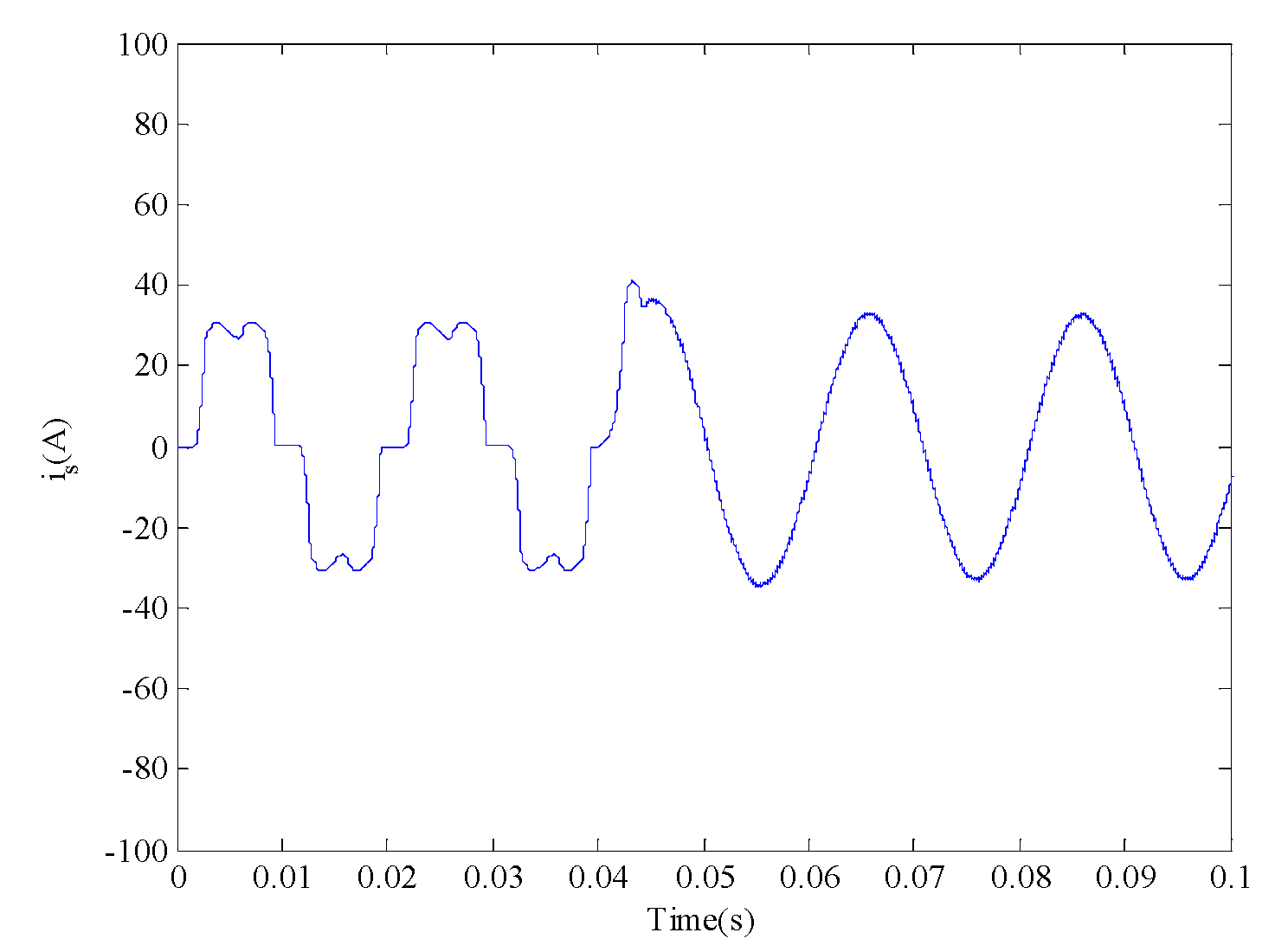
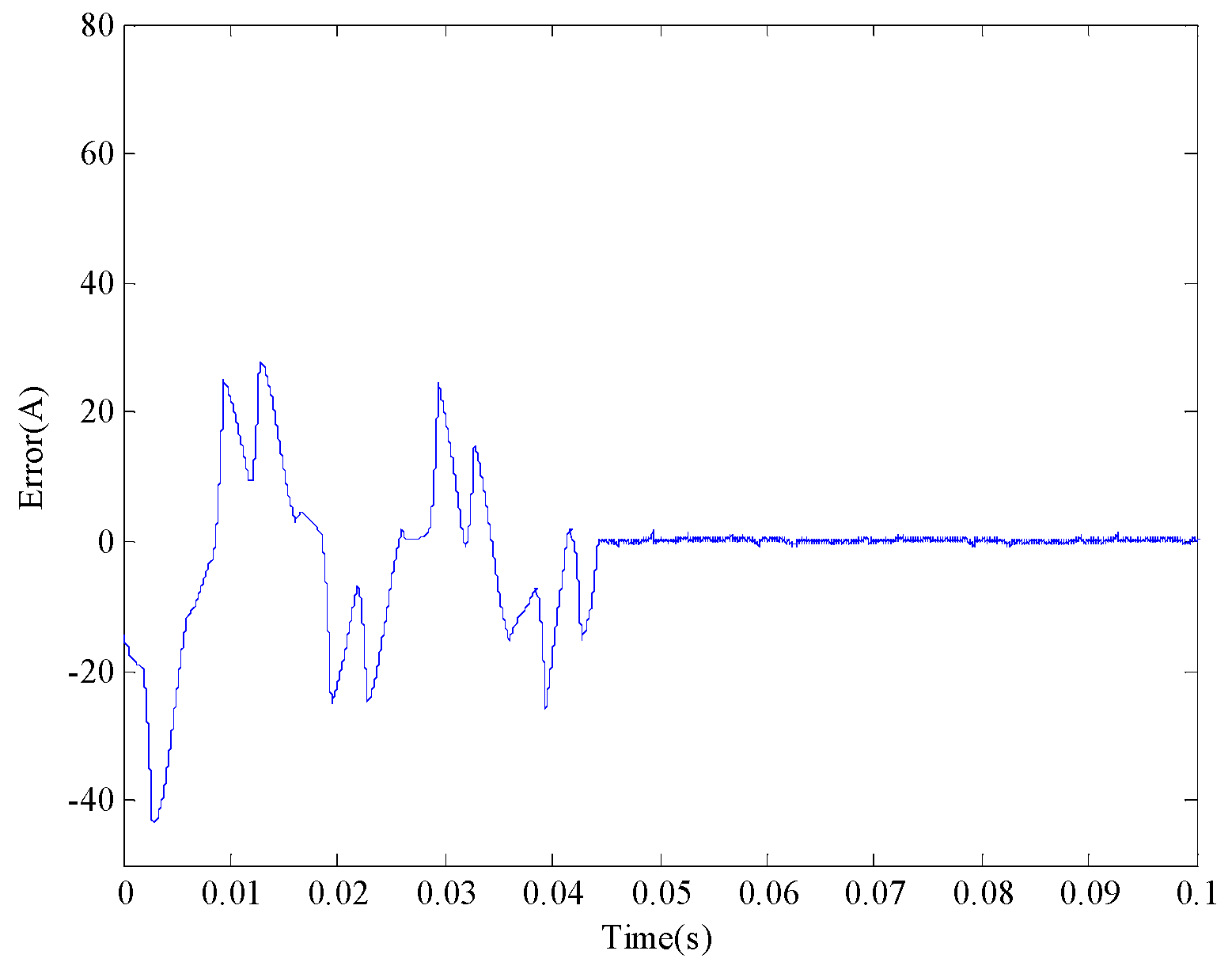
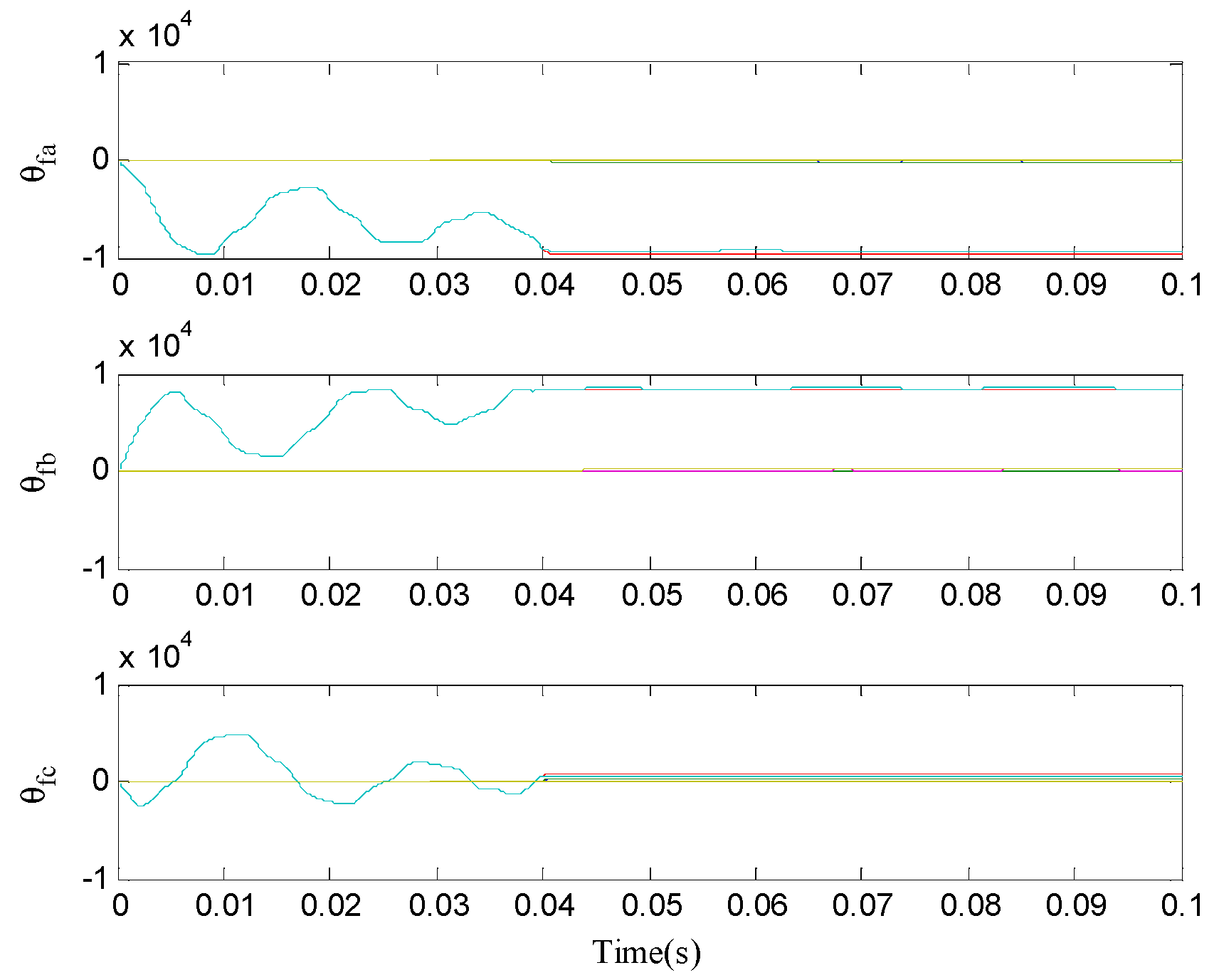
5. Simulation and Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Ouadi, H.; Chihab, A.; Giri, F. Adaptive nonlinear control of three-phase shunt active power filters with magnetic saturation. Electr. Power Energy Syst. 2015, 69, 104–115. [Google Scholar] [CrossRef]
- Kale, M.; Karabacak, M. Chattering free robust control of LCL filter based shunt active power filter using adaptive second order sliding mode and resonant controllers. Electr. Power Energy Syst. 2016, 76, 174–184. [Google Scholar] [CrossRef]
- Fei, J.; Chu, Y. Double Hidden Layer Recurrent Neural Adaptive Global Sliding Mode Control of Active Power Filter. IEEE Trans Power Electr. 2019. [Google Scholar] [CrossRef]
- Chu, Y.; Fei, J. Dynamic global PID sliding mode control using RBF neural compensator for three-phase active power filter. Trans. Inst. Meas. Control 2018, 40, 3549–3559. [Google Scholar] [CrossRef]
- Fang, Y.; Fei, J.; Ma, K. Model Reference Adaptive Sliding Mode Control using RBF Neural Network for Active Power Filter. Int. J. Electr. Power Energy Syst. 2015, 73, 249–258. [Google Scholar] [CrossRef]
- Fei, J.; Wang, T. Adaptive Fuzzy-Neural-Network Based on RBFNN Control for Active Power Filter. Int. J. Mach. Learn. Cybern. 2019, 10, 1139–1150. [Google Scholar] [CrossRef]
- Gregory, A.; Cursino, B. Shunt active power filter with open-end winding transformer and series-connected converters. IEEE Trans. Ind. Appl. 2015, 51, 3273–3283. [Google Scholar]
- Dey, P.; Mekhilef, S. Current harmonics compensation with three-phase four-wire shunt hybrid active power filter based on modified D-Q theory. IET Power Electron. 2015, 8, 2265–2280. [Google Scholar] [CrossRef]
- Sondhi, S.; Hote, Y. Fractional order PID controller for perturbed load frequency control using Kharitono’s theorem. Int. J. Electr. Power Energy Syst. 2016, 78, 884–896. [Google Scholar] [CrossRef]
- Yin, C.; Zhong, S. Design of sliding mode controller for a class of fractional-order chaotic systems. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 356–366. [Google Scholar] [CrossRef]
- Jakovljevic, B.; Pisano, A. On the sliding-mode control of fractional-order nonlinear uncertain dynamics. Int. J. Robust Nonlinear Control 2016, 26, 782–798. [Google Scholar] [CrossRef]
- Vinagre, B.; Podlubny, I. Using fractional order adjustment rules and fractional order reference models in model-reference adaptive control. Nonlinear Dyn. 2002, 29, 269–279. [Google Scholar] [CrossRef]
- Fei, J.; Lu, C. Adaptive fractional order sliding mode controller with neural estimator. J. Frankl. Inst. 2018, 355, 2369–2391. [Google Scholar] [CrossRef]
- Sun, G.; Zhu, Z. Fractional order tension control for stable and fast tethered satellite retrieval. Acta Astronaut. 2014, 104, 304–312. [Google Scholar] [CrossRef]
- Fang, Y.; Fei, J.; Yang, Y. Adaptive Backstepping Design of a Microgyroscope. Micromachines 2018, 9, 338. [Google Scholar] [CrossRef]
- Fei, J.; Liang, X. Adaptive backstepping fuzzy-neural-network fractional order control of microgyroscope using nonsingular terminal sliding mode controller. Complexity 2018, 2018, 5246074. [Google Scholar] [CrossRef]
- Sun, W.; Kaynak, O. Adaptive backstepping control for active suspension systems with hard constraints. IEEE/ASME Trans. Mech. 2013, 18, 1072–1079. [Google Scholar] [CrossRef]
- Davila, J. Exact tracking using backstepping control design and high-order sliding modes. IEEE Trans. Autom. Control 2013, 58, 2077–2081. [Google Scholar] [CrossRef]
- Cao, D.; Fei, J. Adaptive fractional fuzzy sliding mode control for three-phase active power filter. IEEE Access 2016, 4, 6645–6651. [Google Scholar] [CrossRef]
- Fang, Y.; Fei, J.; Cao, D. Adaptive Fuzzy-Neural Fractional-Order Current Control of Active Power Filter with Finite-Time Sliding Controller. Int. J. Fuzzy Syst. 2019. [Google Scholar] [CrossRef]
- Hou, S.; Fei, J.; Chen, C. Finite-Time Adaptive Fuzzy-Neural-Network Control of Active Power Filter. IEEE Trans. Power Electron. 2019, 34, 10298–10313. [Google Scholar] [CrossRef]
- Liu, Y.; Gong, M.; Tong, S. Adaptive Fuzzy Output Feedback Control for a Class of Nonlinear Systems with Full State Constraints. IEEE Trans. Fuzzy Syst. 2018. [Google Scholar] [CrossRef]
- Li, Y.; Tong, S. Adaptive fuzzy control with prescribed performance for block-triangular-structured nonlinear systems. IEEE Trans. Fuzzy Syst. 2017. [Google Scholar] [CrossRef]
- Fei, J.; Feng, Z. Adaptive Fuzzy Super-Twisting Sliding Mode Control for Microgyroscope. Complexity 2019, 2019, 6942642. [Google Scholar] [CrossRef]
- Wang, H.; Liu, P.; Niu, B. Robust Fuzzy Adaptive Tracking Control for Nonaffine Stochastic Nonlinear Switching Systems. IEEE Trans. Cybern. 2018, 48, 2462–2471. [Google Scholar]
- Fei, J.; Zhou, J. Robust adaptive control of MEMS triaxial gyroscope using fuzzy compensator. IEEE Trans. Syst. Man Cybern. Part B Cybern. 2012, 42, 1599–1607. [Google Scholar]
- Wu, H.N.; Feng, S. Mixed Fuzzy/Boundary Control Design for Nonlinear Coupled Systems of ODE and Boundary-Disturbed Uncertain Beam. IEEE Trans. Fuzzy Syst. 2018. [Google Scholar] [CrossRef]
- Zhu, Y.; Fei, J. Disturbance Observer Based Fuzzy Sliding Mode Control of PV Grid Connected Inverter. IEEE Access 2018, 6, 21202–21211. [Google Scholar] [CrossRef]
- Wu, H.N.; Wang, Z. Observer-Based Hinfty Sampled-Data Fuzzy Control for a Class of Nonlinear Parabolic PDE Systems. IEEE Trans. Fuzzy Syst. 2018, 26, 454–473. [Google Scholar] [CrossRef]
- Chu, Y.; Fei, J.; Hou, S. Adaptive Global Sliding Mode Control for Dynamic Systems Using Double Hidden Layer Recurrent Neural Network Structure. IEEE Trans. Neural Netw. Learn. Syst. 2019. [Google Scholar] [CrossRef]
- Liu, Y.; Li, S.; Tong, S. Neural Approximation-Based Adaptive Control for a Class of Nonlinear Nonstrict Feedback Discrete-Time Systems. IEEE Trans. Neural Netw. Learn. Syst. 2017, 28, 1531–1541. [Google Scholar] [CrossRef]
- Fei, J.; Lu, C. Adaptive Sliding Mode Control of Dynamic Systems Using Double Loop Recurrent Neural Network Structure. IEEE Trans. Neural Netw. Learn. Syst. 2017, 29, 1275–1286. [Google Scholar] [CrossRef]
- Fei, J.; Ding, H. Adaptive sliding mode control of dynamic system using RBF neural network. Nonlinear Dyn. 2012, 70, 1563–1573. [Google Scholar] [CrossRef]
- Wang, H.; Liu, P.; Li, S. Adaptive Neural Output-Feedback Control for a Class of Nonlower Triangular Nonlinear Systems with Unmodeled Dynamics. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 3658–3668. [Google Scholar]
- Xu, B.; Yang, D.; Shi, Z.; Pan, Y.; Chen, B.; Sun, F. Online Recorded Data Based Composite Neural Control of Strict-feedback Systems with Application to Hypersonic Flight Dynamics. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 3839–3849. [Google Scholar]
- Hammond, P.W. A harmonic filter installation to reduce voltage distortion from static power converters. IEEE Trans. Ind. Appl. 1988, 24, 53–58. [Google Scholar] [CrossRef]
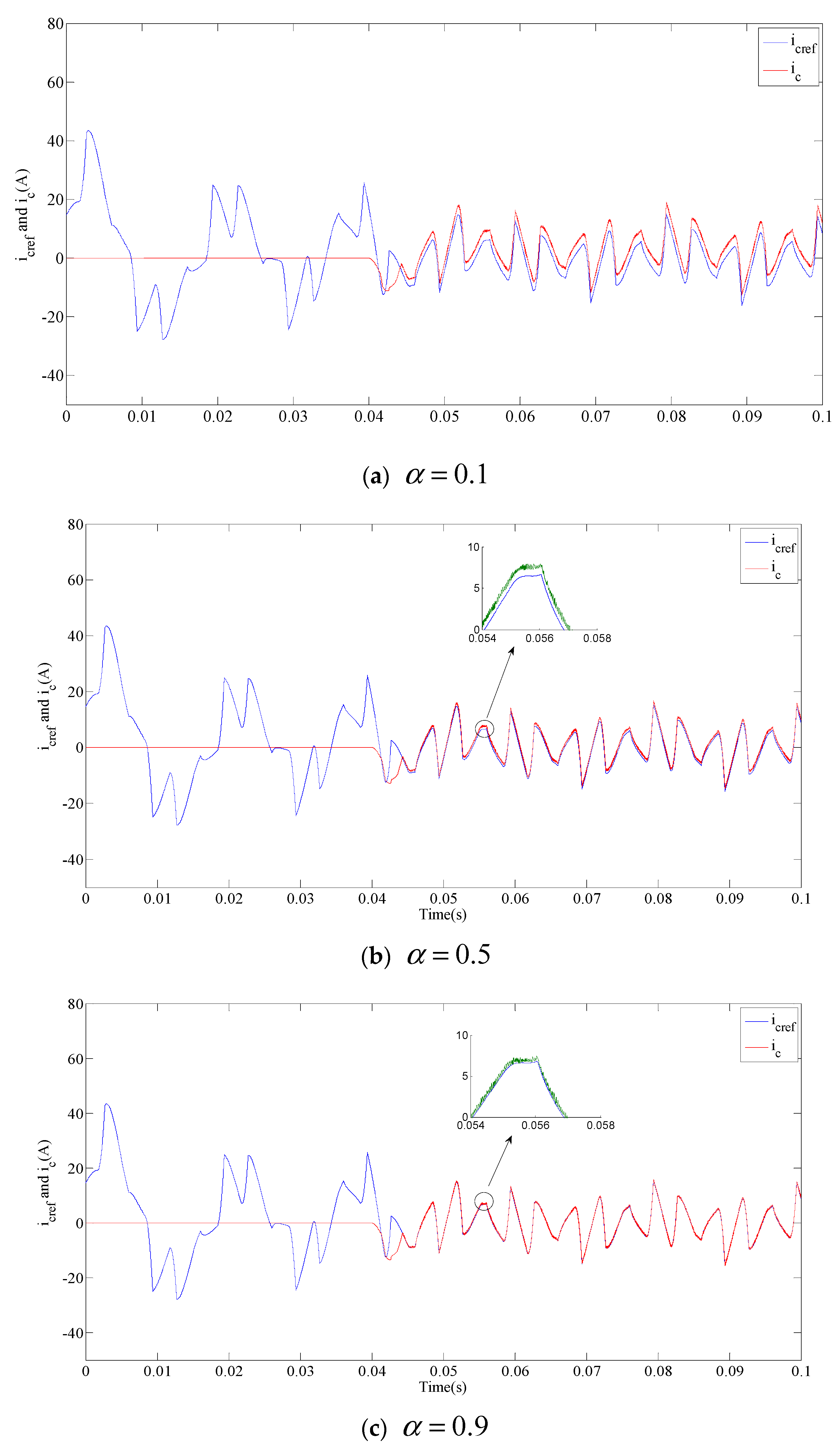
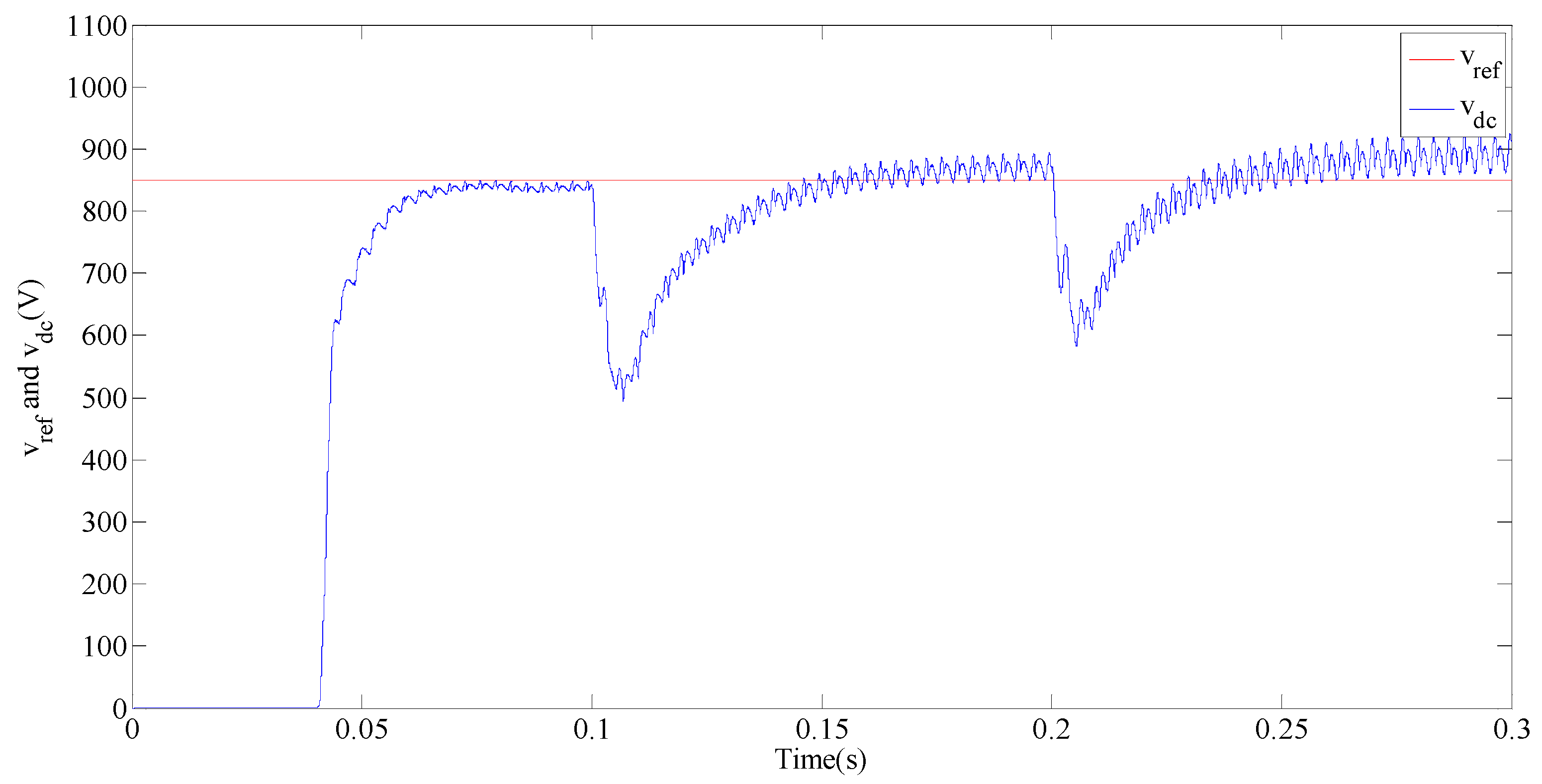
| Supply voltage and frequency | |
| Switching frequency | |
| The non-linear load | , |
| Active power filter parameters | , , , |
| PI controller | , |
| Time | THD (%) | |
|---|---|---|
| Fractional Backstepping Sliding Mode Adaptive Fuzzy Control | Backstepping Sliding Mode Adaptive Fuzzy Control with Integer Order | |
| 0 | 24.71% | 24.71% |
| 0.06 s | 1.50% | 2.33% |
| 0.16 s | 1.39% | 2.30% |
| 0.26 s | 1.83% | 2.37% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fei, J.; Wang, H.; Cao, D. Adaptive Backstepping Fractional Fuzzy Sliding Mode Control of Active Power Filter. Appl. Sci. 2019, 9, 3383. https://doi.org/10.3390/app9163383
Fei J, Wang H, Cao D. Adaptive Backstepping Fractional Fuzzy Sliding Mode Control of Active Power Filter. Applied Sciences. 2019; 9(16):3383. https://doi.org/10.3390/app9163383
Chicago/Turabian StyleFei, Juntao, Huan Wang, and Di Cao. 2019. "Adaptive Backstepping Fractional Fuzzy Sliding Mode Control of Active Power Filter" Applied Sciences 9, no. 16: 3383. https://doi.org/10.3390/app9163383
APA StyleFei, J., Wang, H., & Cao, D. (2019). Adaptive Backstepping Fractional Fuzzy Sliding Mode Control of Active Power Filter. Applied Sciences, 9(16), 3383. https://doi.org/10.3390/app9163383





