Sensorless Air Flow Control in an HVAC System through Deep Learning
Abstract
:1. Introduction
- This paper demonstrates that a Long Short-Term Memory (LSTM)-based predictor can replace a static pressure sensor component using a real AHU. This approach can reduce costs in many ways: the hardware cost ($500–600 per sensor) for each AHU, the installation and operational cost, and the maintenance cost.
- This paper explores the impacts of various input parameters and processing steps on the performance of the LSTM-based multivariate time-series prediction. It provides insight into optimization that can be applied to similar systems.
- This paper shows that the developed prediction model can be applied to HVAC systems with different capacities and in different seasonal conditions.
2. Related Work
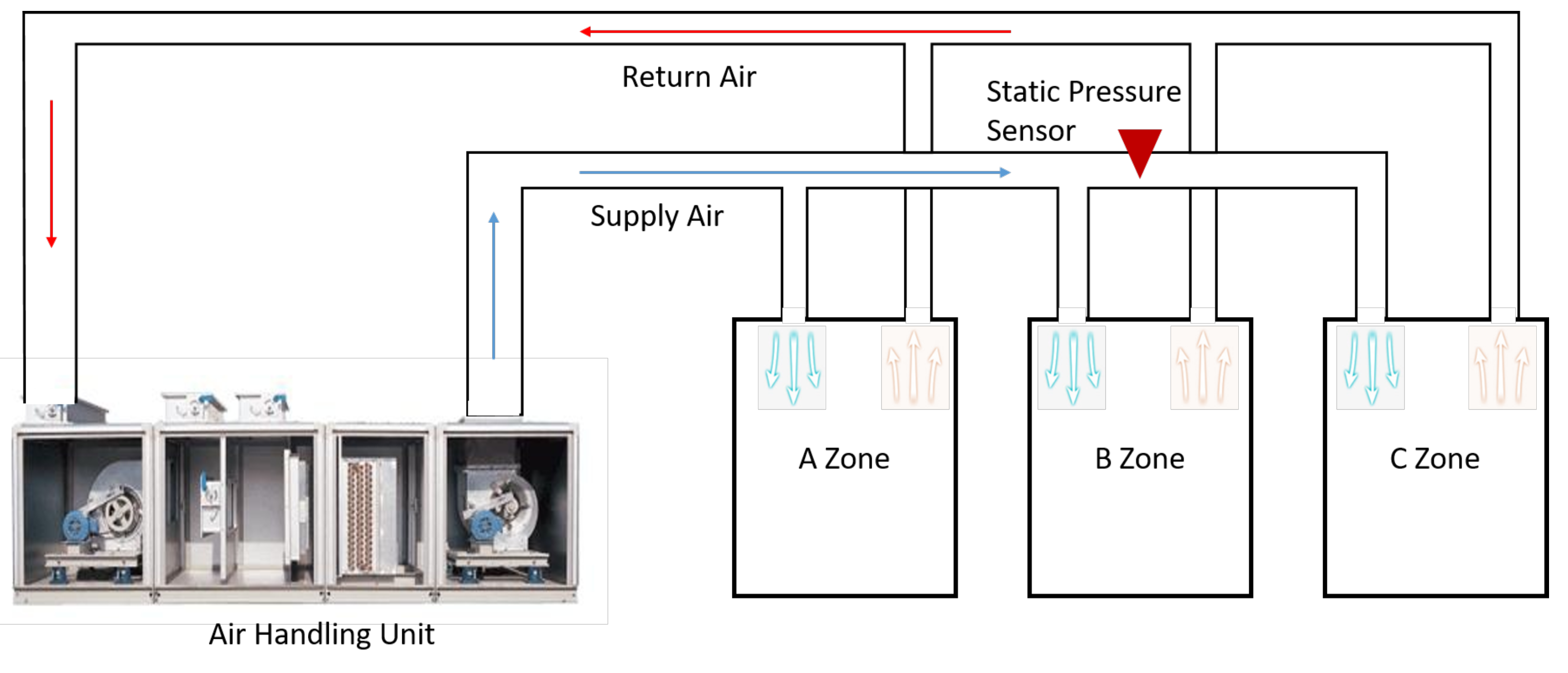
3. Predicting Static Pressure Using Deep Learning
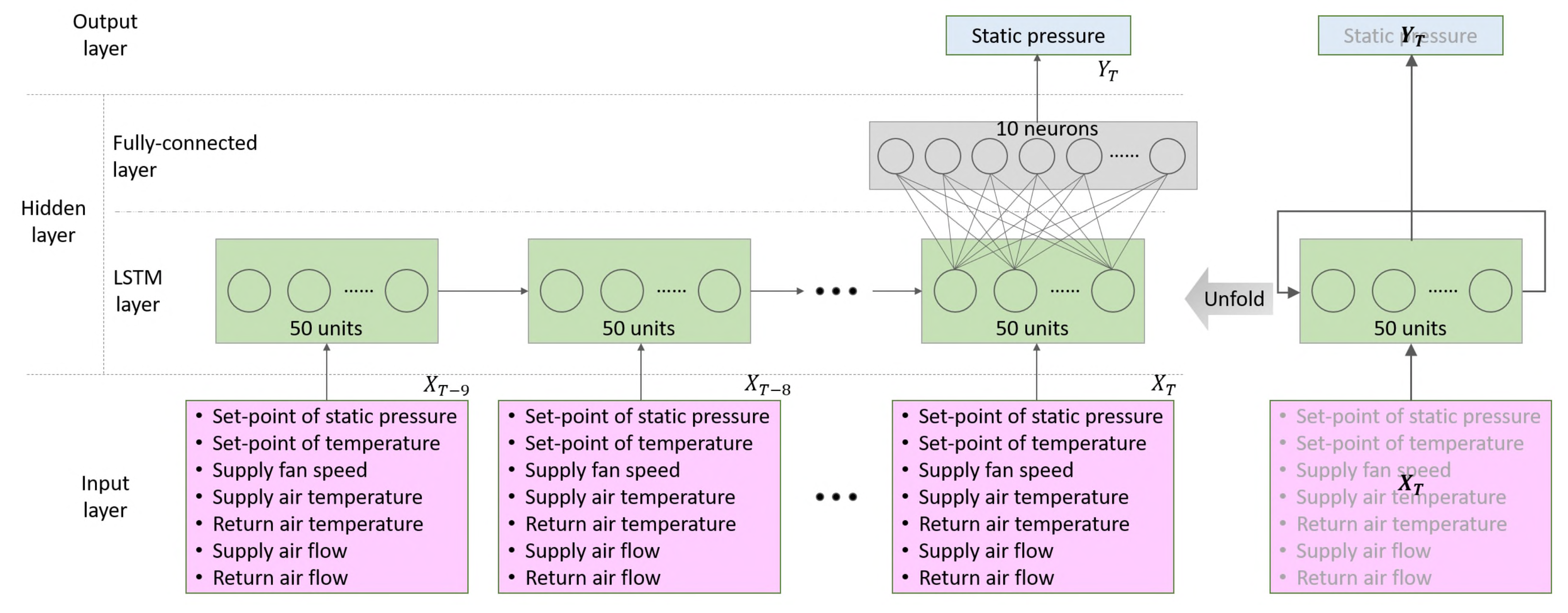
3.1. Input Data Characteristics
- Set-point of the static pressure (Millimeter Aqua; mmAq),
- Set-point of the temperature (C),
- Volume of the supply air (Cubic Feet per Minute; CFM),
- Volume of the return air (CFM),
- Temperature of the supply air (C),
- Temperature of the return air (C),
- Speed of the inverter fan (Hz).
- All data sets are for a four-month period, from May through August, and were collected at 1-min intervals from 12:00 a.m. to 11:59 p.m.
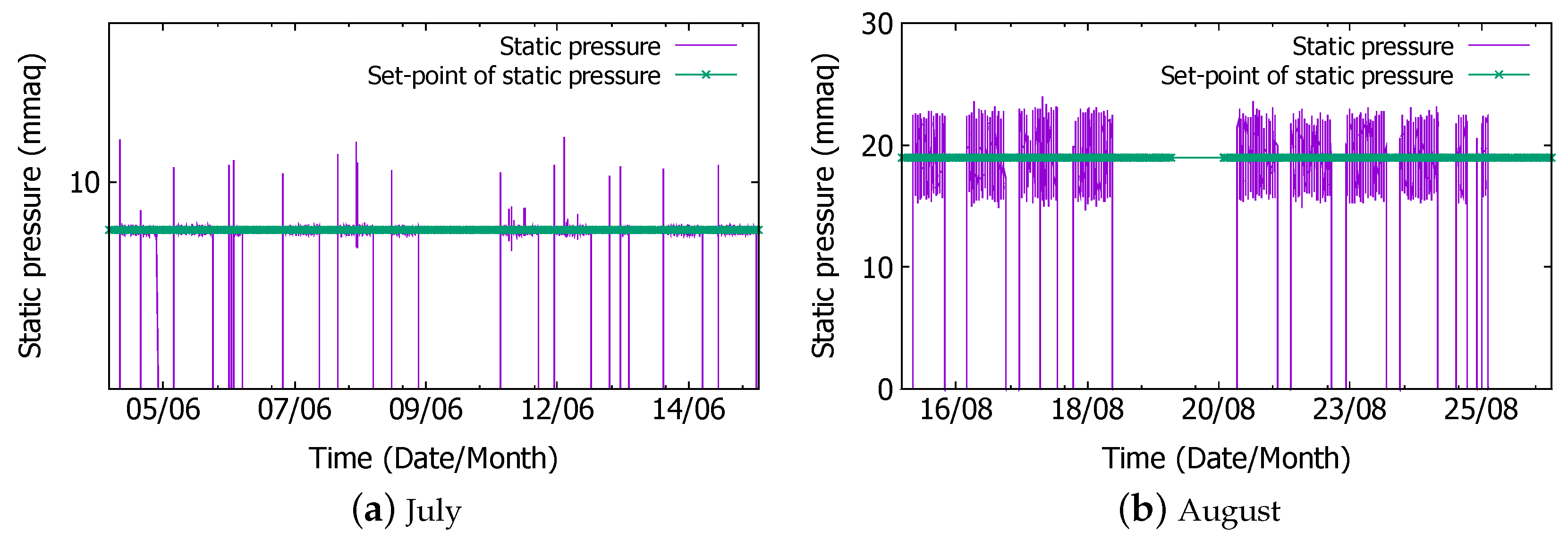
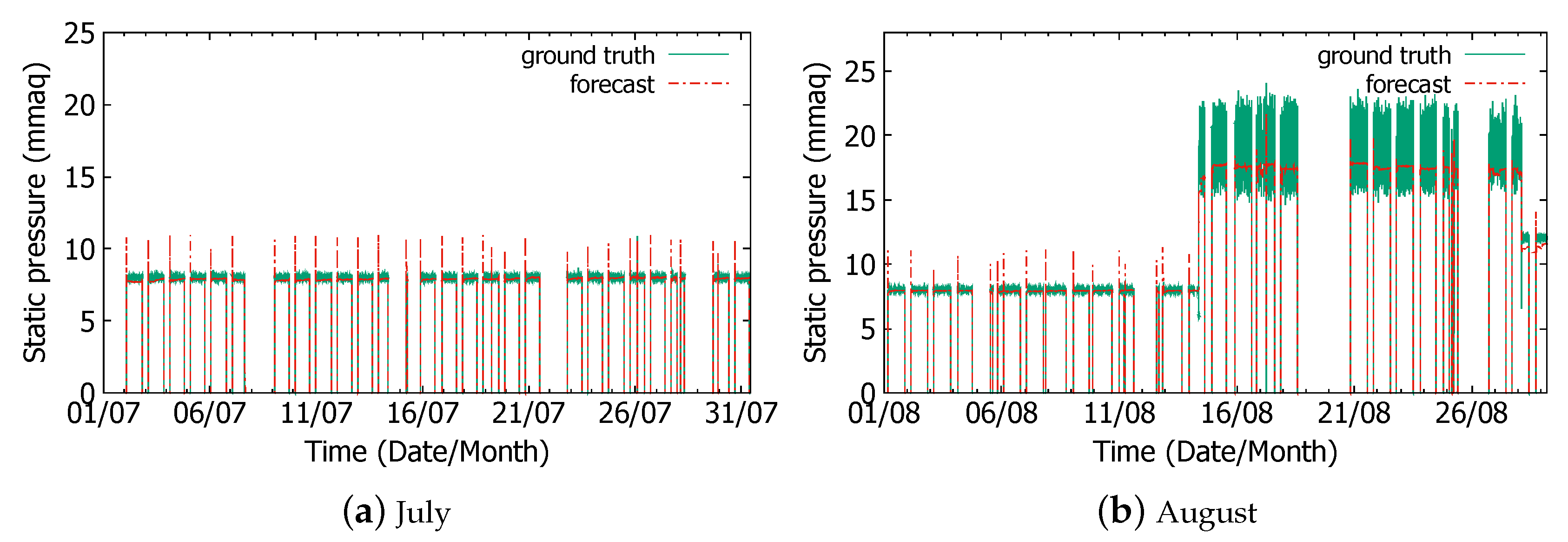
- All data sets consist of operational data from spring (from May to June) and summer (from July to August). These two periods have different operational targets because the HVAC system only blows air in spring, but it supplies cold air in summer.
- All data sets were subjected to the HVAC system test at varying static pressures from 10 August to the end of August.
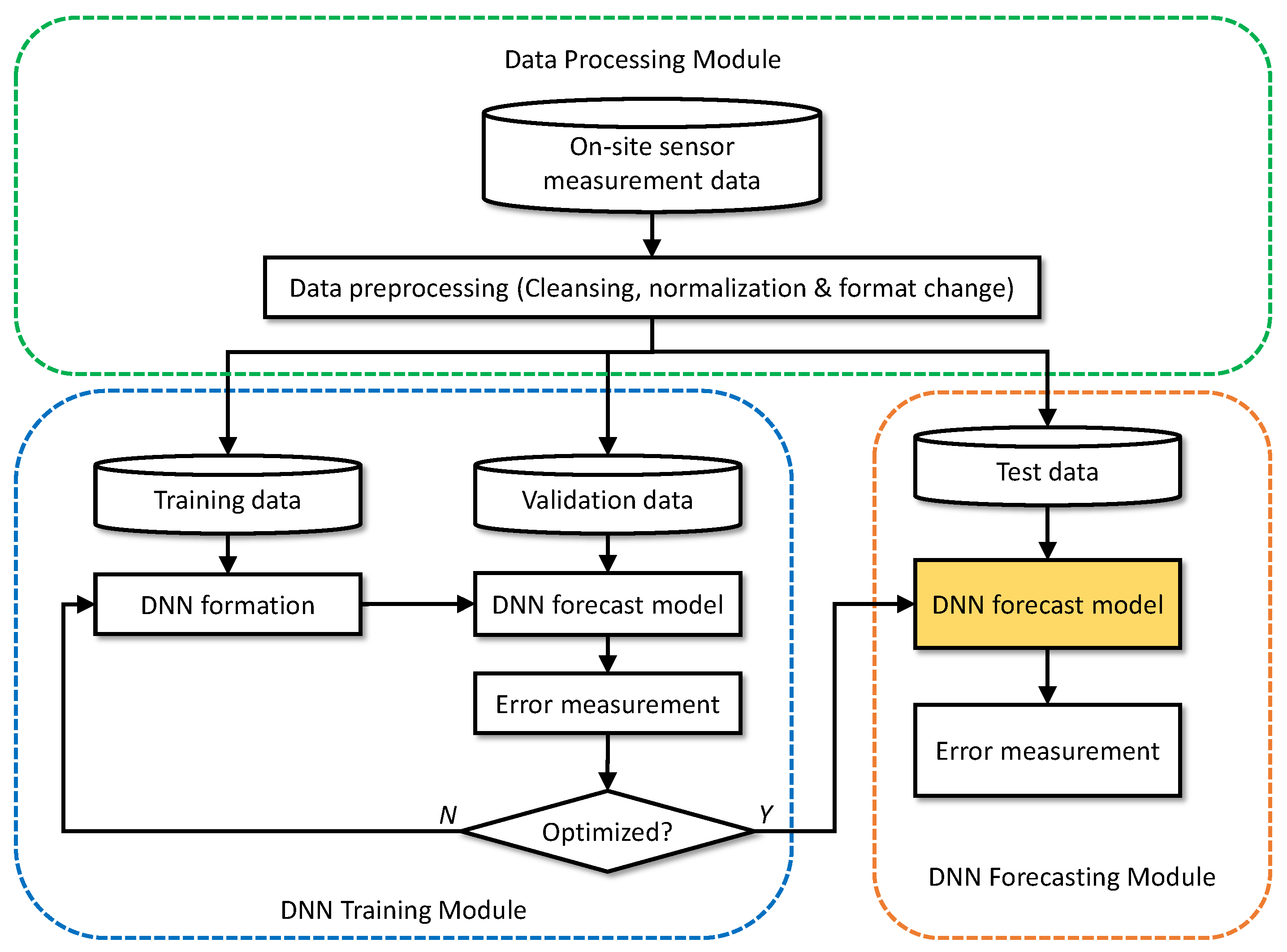
3.2. Proposed Deep Learning Model
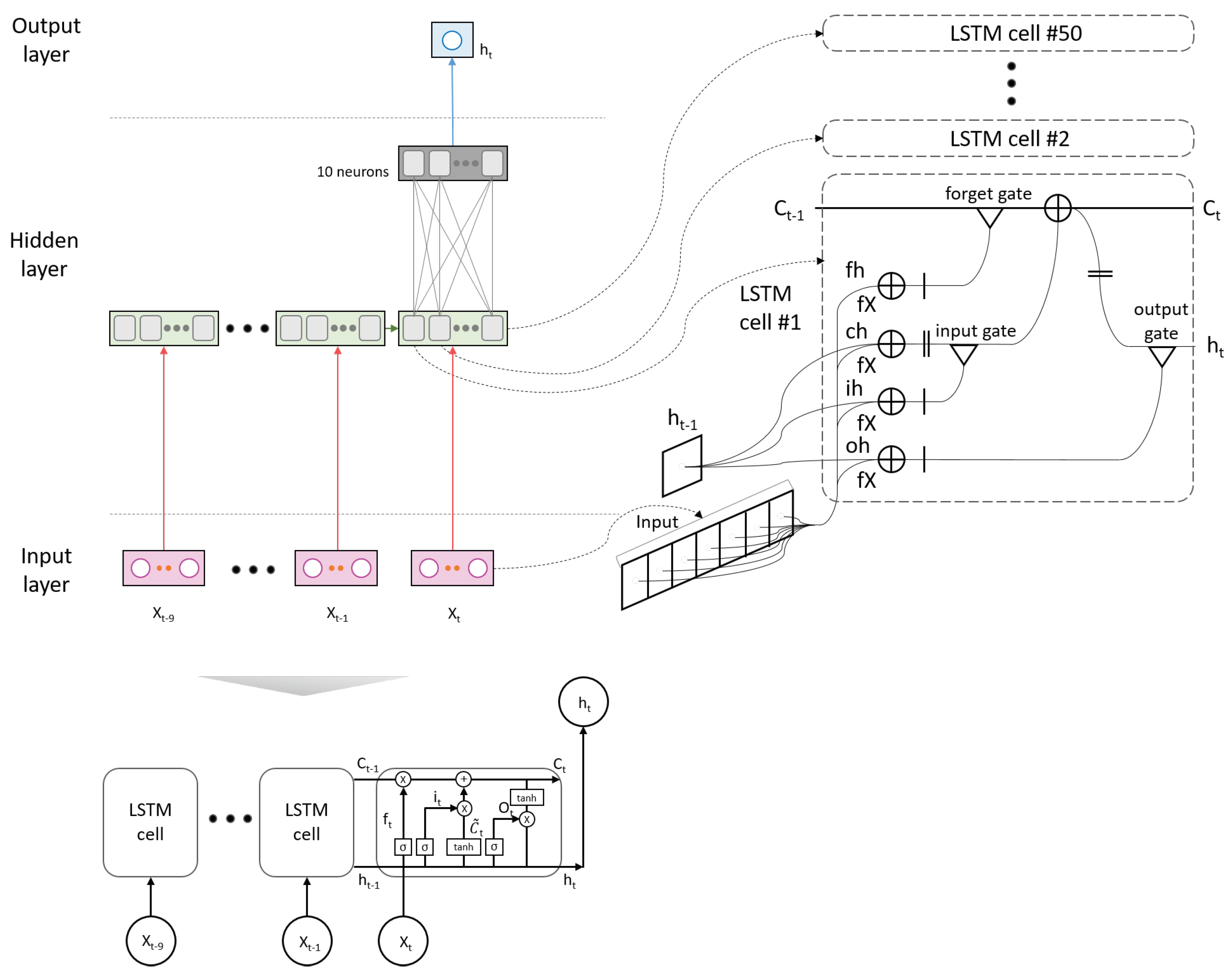
3.2.1. LSTM Network
3.2.2. Hyperparameters
4. Experimental Evaluation
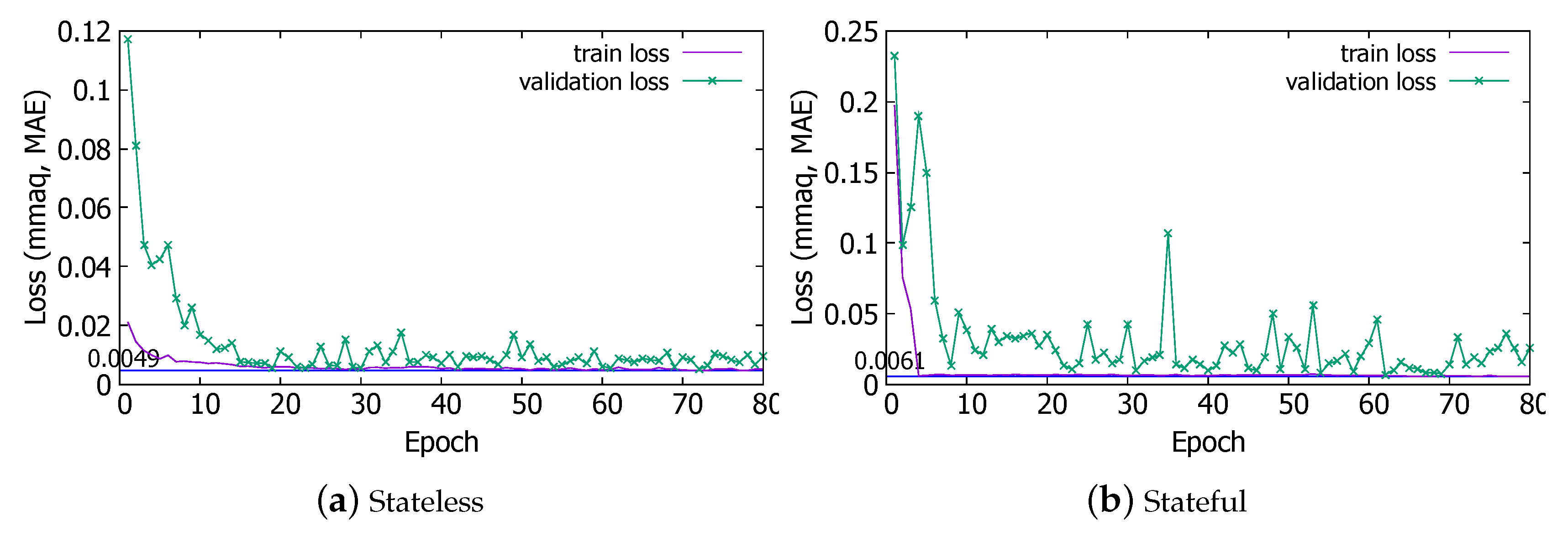
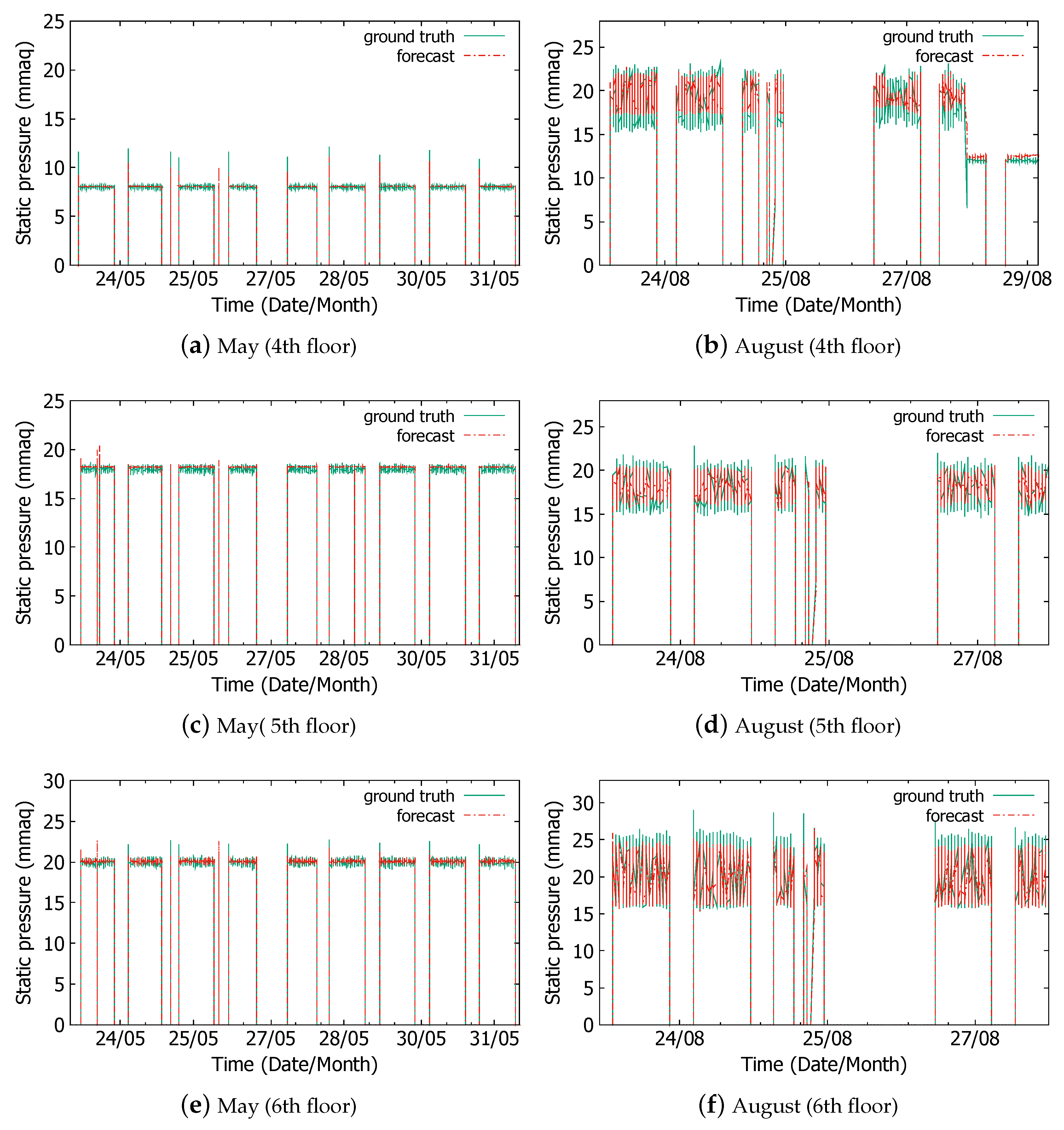
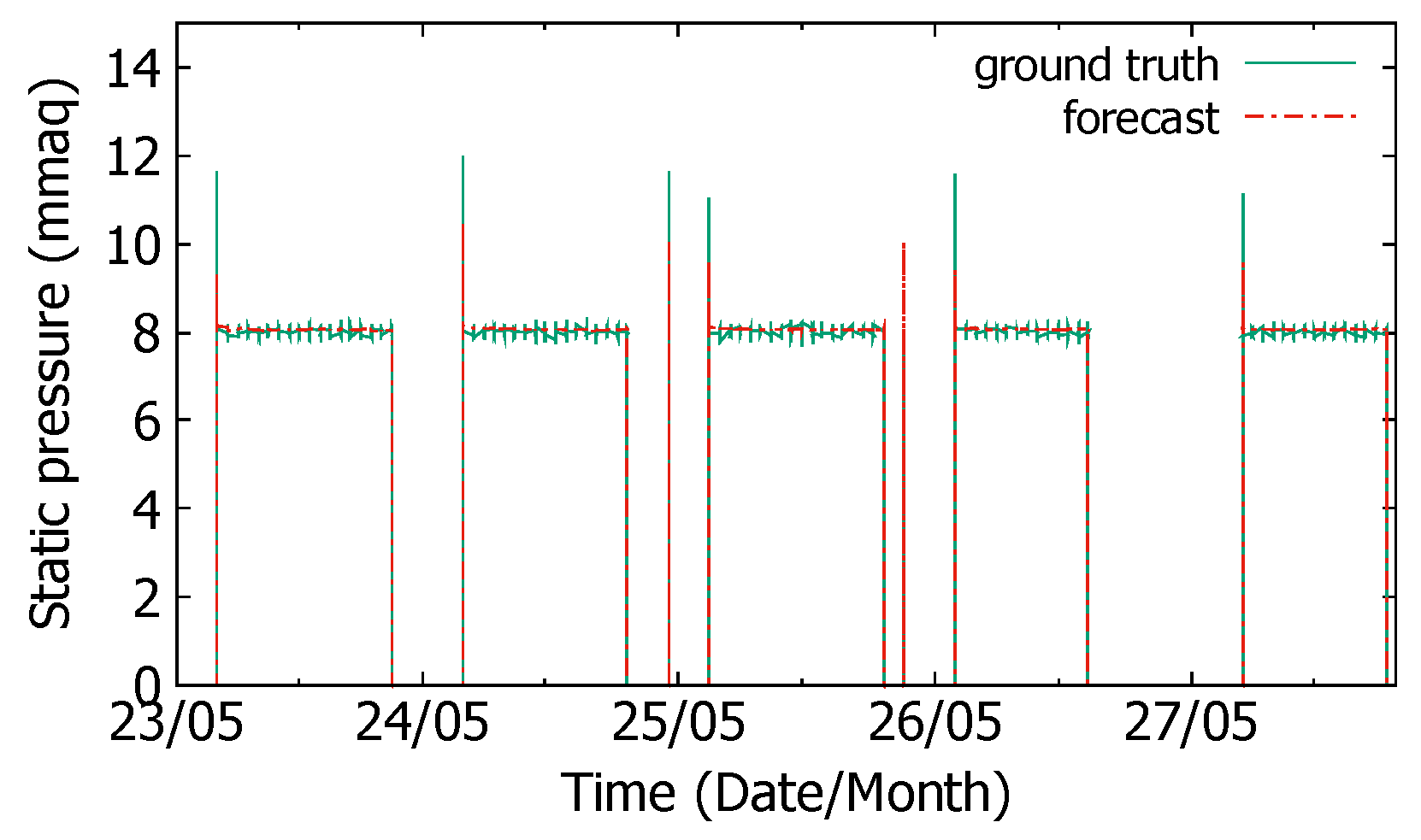
4.1. Static Pressure Prediction in Normal and Test Operations
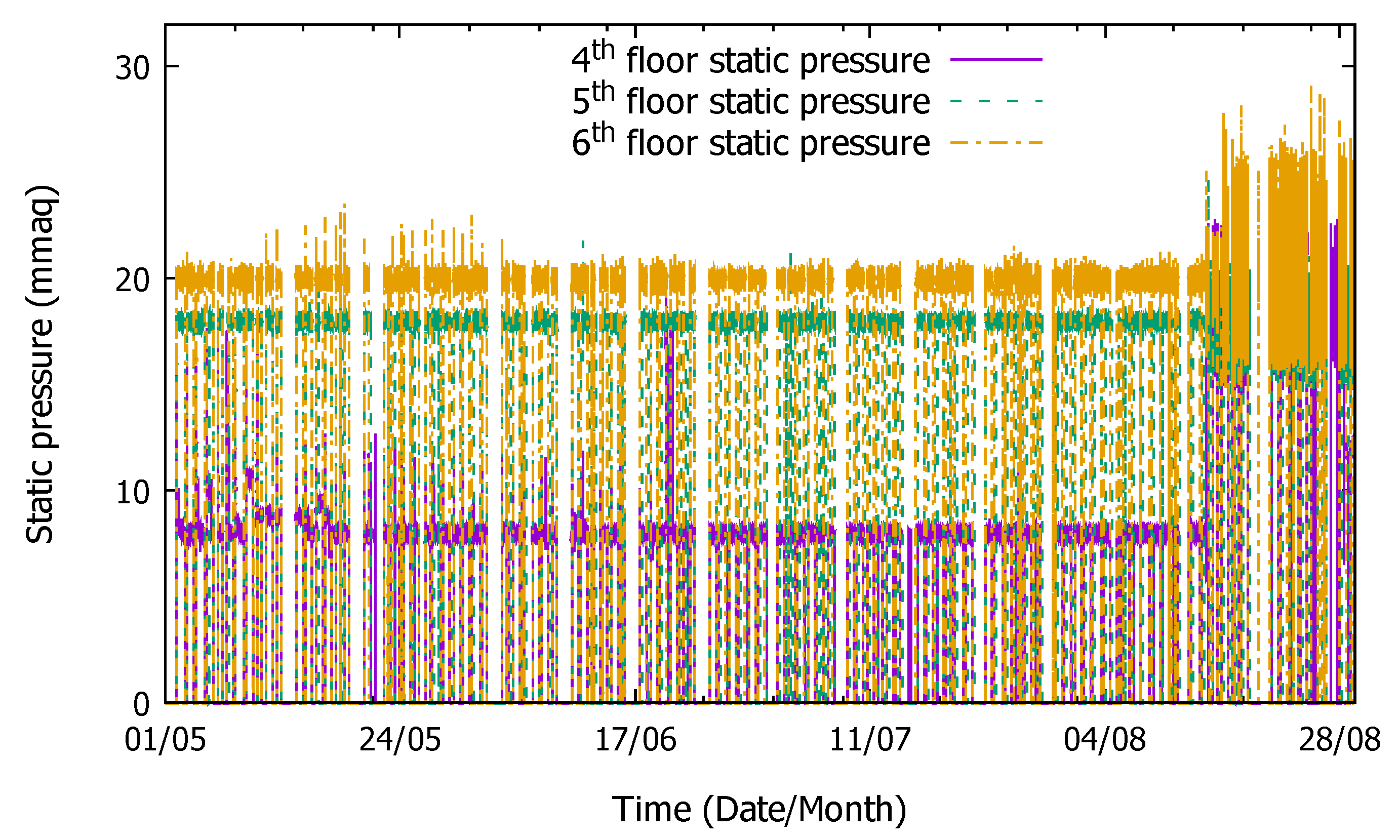
4.2. Static Pressure Prediction for Untrained Seasons
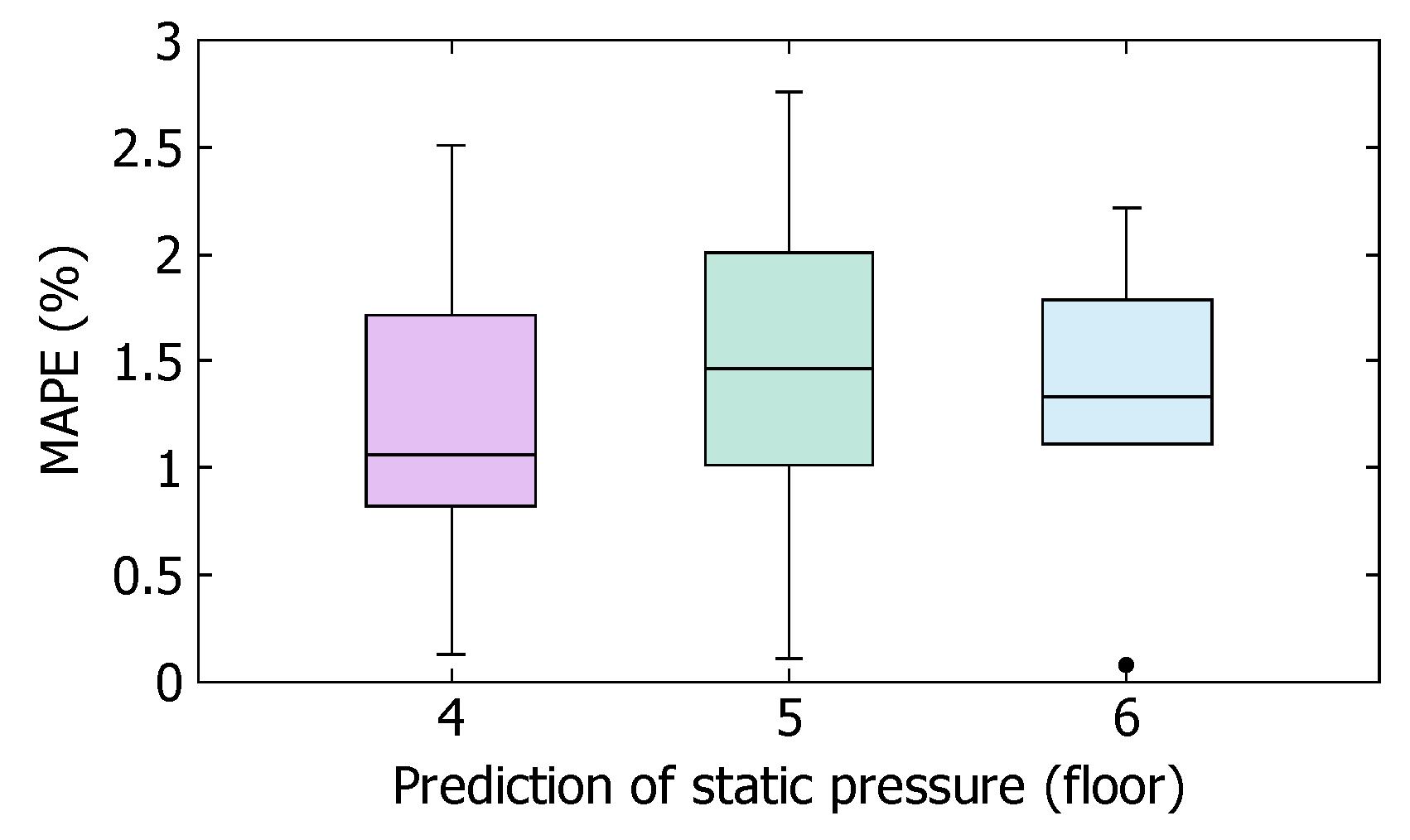
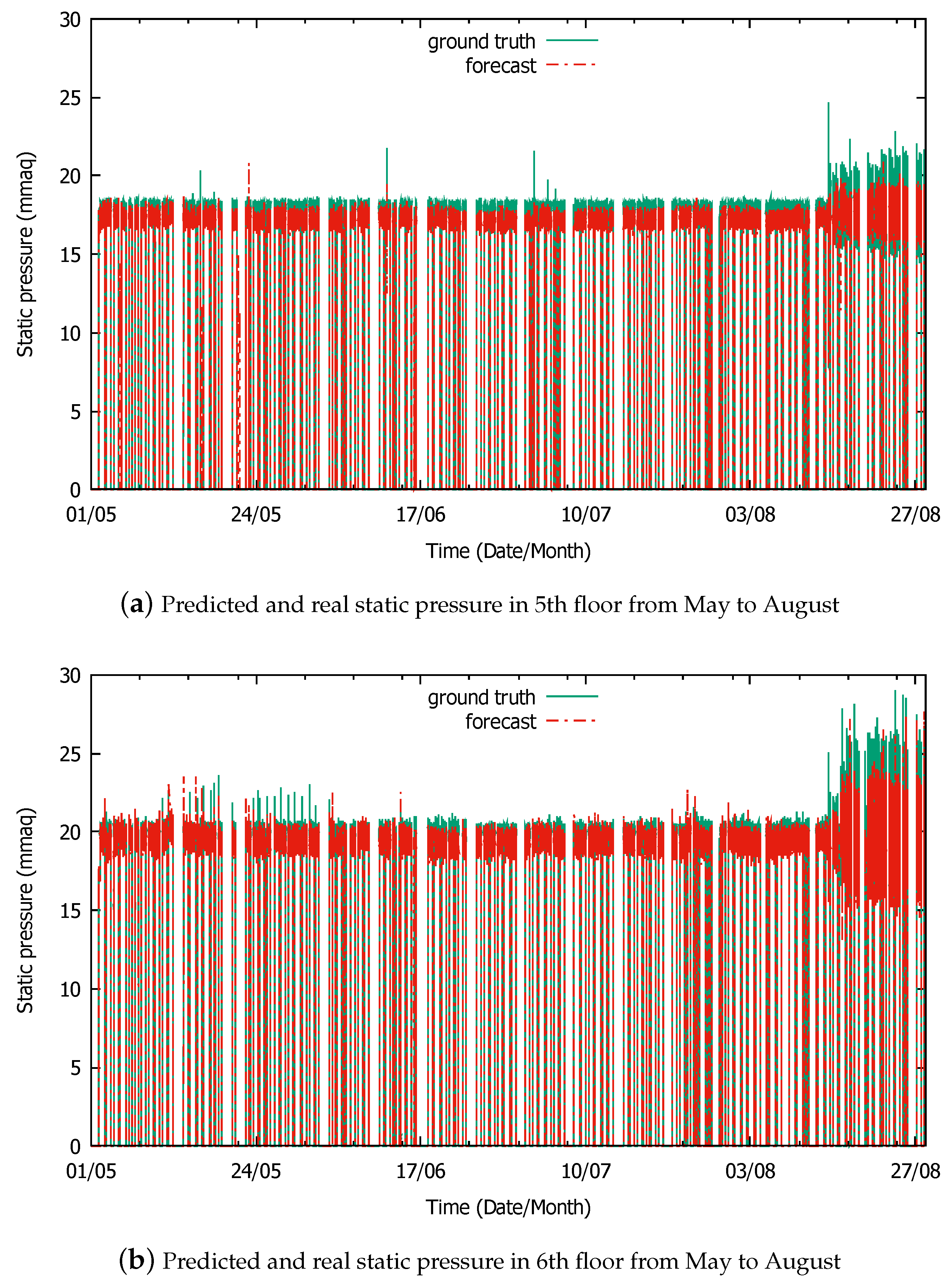
4.3. Static Pressure Prediction in Operations with Different Capacity
4.4. Prediction of Data with Different Time Intervals
5. Conclusions and Future Work
Author Contributions
Funding
Conflicts of Interest
References
- IBM Research Editorial Staff. IoT and Machine Learning to Reduce Energy Use in Cooling Systems. Available online: https://www.ibm.com/blogs/research/2018/07/reduce-energy-cooling/ (accessed on 10 January 2018).
- Ahmad, M.W.; Mourshed, M.; Yuce, B.; Rezgui, Y. Computational intelligence techniques for HVAC systems: A review. Build. Simul. 2016, 9, 359–398. [Google Scholar] [CrossRef] [Green Version]
- Li, X.; Zhao, T.; Fan, P.; Zhang, J. Rule-based fuzzy control method for static pressure reset using improved Mamdani model in VAV systems. J. Build. Eng. 2019, 22, 192–199. [Google Scholar] [CrossRef]
- Ethan, P.; Seshadhri, S.; Korkut, B.; Jiang, C.; Rong, S.; Kameshwar, P. An internet of things upgrade for smart and scalable heating, ventilation and air-conditioning control in commercial buildings. Appl. Energy 2019, 239, 408–424. [Google Scholar]
- Shahnazari, H.; Mhaskar, P.; House, J.M.; Salsbury, T.I. Modeling and fault diagnosis design for HVAC systems using recurrent neural networks. Comput. Chem. Eng. 2019, 126, 189–203. [Google Scholar] [CrossRef]
- Reynolds, J.; Ahmad, M.W.; Rezgui, Y.; Hippolyte, J.L. Operational supply and demand optimisation of a multi-vector district energy system using artificial neural networks and a genetic algorithm. Appl. Energy 2019, 235, 699–713. [Google Scholar] [CrossRef]
- Iqbal, R.; Maniak, T.; Doctor, F.; Karyotis, C. Fault Detection and Isolation in Industrial Processes Using Deep Learning Approaches. IEEE Trans. Ind. Inform. 2019, 9, 359–398. [Google Scholar] [CrossRef]
- Jantscher, P. AI in Sensors for IoT. Available online: https://siliconsemiconductor.net/article/106227/AI_In_Sensors_For_IoT (accessed on 28 January 2019).
- Carrier Design Manual Part 2: Air Distribution, 10th ed.; Carrier Corporation: Farmington, CT, USA, 1960.
- Kato, K.; Sakawa, M.; Ishimaru, K.; Ushiro, S.; Shibano, T. Heat load prediction through recurrent neural network in district heating and cooling systems. In Proceedings of the 2008 IEEE International Conference on Systems, Man and Cybernetics, Singapore, 12–15 October 2008; pp. 1401–1406. [Google Scholar]
- Vázquez-Canteli, J.R.; Ulyanin, S.; Kämpf, J.; Nagy, Z. Fusing TensorFlow with building energy simulation for intelligent energy management in smart cities. Sustain. Cities Soc. 2019, 45, 243–257. [Google Scholar] [CrossRef]
- Park, J.Y.; Dougherty, T.; Fritz, H.; Nagy, Z. LightLearn: An adaptive and occupant centered controller for lighting based on reinforcement learning. Build. Environ. 2019, 147, 397–414. [Google Scholar] [CrossRef]
- Papadopoulos, S.; Kontokosta, C.E.; Vlachokostas, A.; Azar, E. Rethinking HVAC temperature set-points in commercial buildings: The potential for zero-cost energy savings and comfort improvement in different climates. Build. Environ. 2019, 155, 350–359. [Google Scholar] [CrossRef]
- Valladares, W.; Galindo, M.; Gutierrez, J.; Wu, W.-C.; Liao, K.-K.; Liao, J.-C.; Liu, K.-C.; Wang, C.-C. Energy optimization associated with thermal comfort and indoor air control via a deep reinforcement learning algorithm. Build. Environ. 2019, 155, 105–117. [Google Scholar] [CrossRef]
- Jackson, D.A. Stopping rules in principal components analysis: A comparison of heuristical and statistical approaches. Ecology 1993, 74, 2204–2214. [Google Scholar] [CrossRef]
- Lee, K.P.; Wu, B.H.; Peng, S.L. Deep-learning-based fault detection and diagnosis of air-handling units. Build. Environ. 2019, 157, 24–33. [Google Scholar] [CrossRef]
- Guo, Y.; Tan, Z.; Chen, H.; Li, G.; Wang, J.; Huang, R.; Liu, J.; Ahmad, T. Deep learning-based fault diagnosis of variable refrigerant flow air-conditioning system for building energy saving. Appl. Energy 2018, 225, 732–745. [Google Scholar] [CrossRef]
- Consoli, A.; Scarcella, G.; Testa, A. Industry application of zero-speed sensorless control techniques for PM synchronous motors. IEEE Trans. Ind. Appl. 2001, 37, 513–521. [Google Scholar] [CrossRef]
- Maes, J.; Melkebeek, J.A. Speed-sensorless direct torque control of induction motors using an adaptive flux observer. IEEE Trans. Ind. Appl. 2000, 36, 778–785. [Google Scholar] [CrossRef]
- Kim, T.H.; Ehsani, M. Sensorless control of the BLDC motors from near-zero to high speeds. IEEE Trans. Power Electron. 2004, 19, 1635–1645. [Google Scholar] [CrossRef]
- Yilmaz, M.; Tuncay, R.N.; Ustun, O.; Krein, T.P. Sensorless Control of Brushless DC Motor Based on Wavelet Theory. Electr. Power Compon. Syst. 2009, 37, 1063–1080. [Google Scholar] [CrossRef]
- Hirose, N.; Tajima, R. Modeling of rolling friction by recurrent neural network using LSTM. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; pp. 6471–6478. [Google Scholar] [CrossRef]
- Shamshirband, S.; Petković, D.; Anuar, N.B.; Kiah, M.L.M.; Akib, S.; Gani, A.; Ćojbašićb, Ž.; Nikolić, V. Sensorless estimation of wind speed by adaptive neuro-fuzzy methodology. Int. J. Electr. Power Energy Syst. 2014, 62, 490–495. [Google Scholar] [CrossRef]
- Nikolić, V.; Motamedi, S.; Shamshirband, S.; Petković, D.; Ch, S.; Arif, M. Extreme learning machine approach for sensorless wind speed estimation. Mechatronics 2016, 34, 78–83. [Google Scholar] [CrossRef]
- Kumar, R.; Sivashanmugam, P. Neuro and Fuzzy Computing Approach for the Flow Sensorless Measurement. Sens. Transducers 2009, 109, 21. [Google Scholar]
- Measurement, Testing, Adjusting, and Balancing of Building HVAC Systems. In ANSI/ASHRAE Standard 111-2008; ASHRAE: New York, NY, USA, 2008.



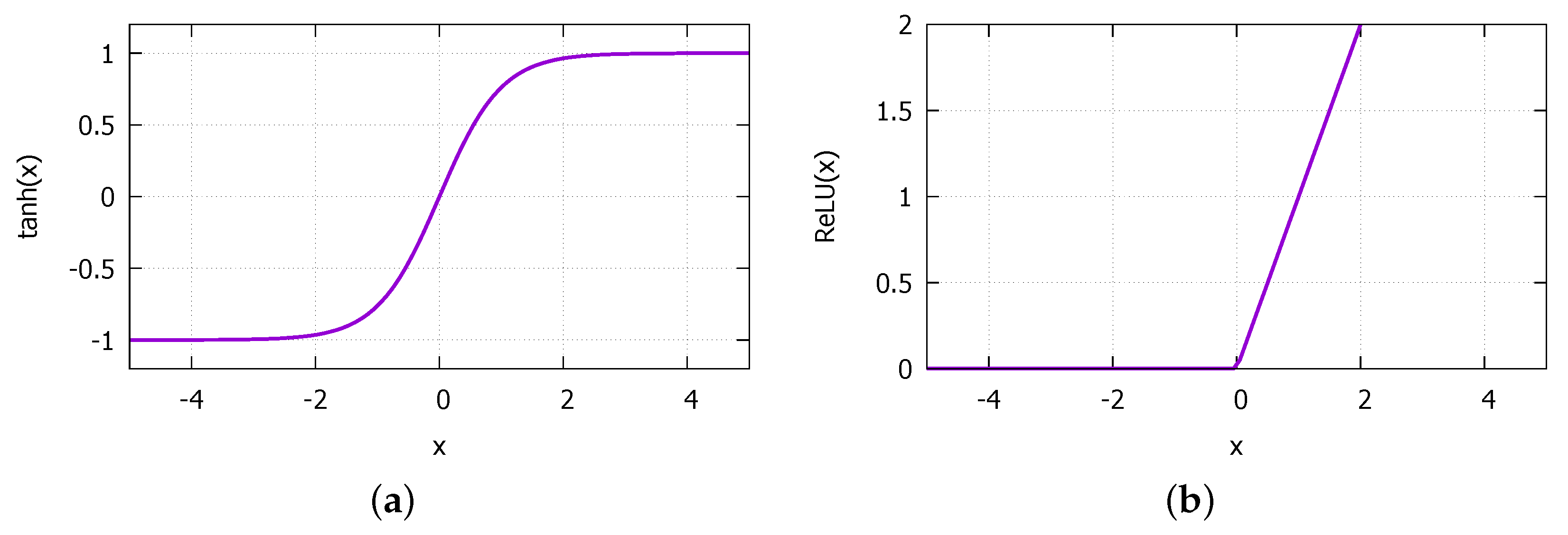
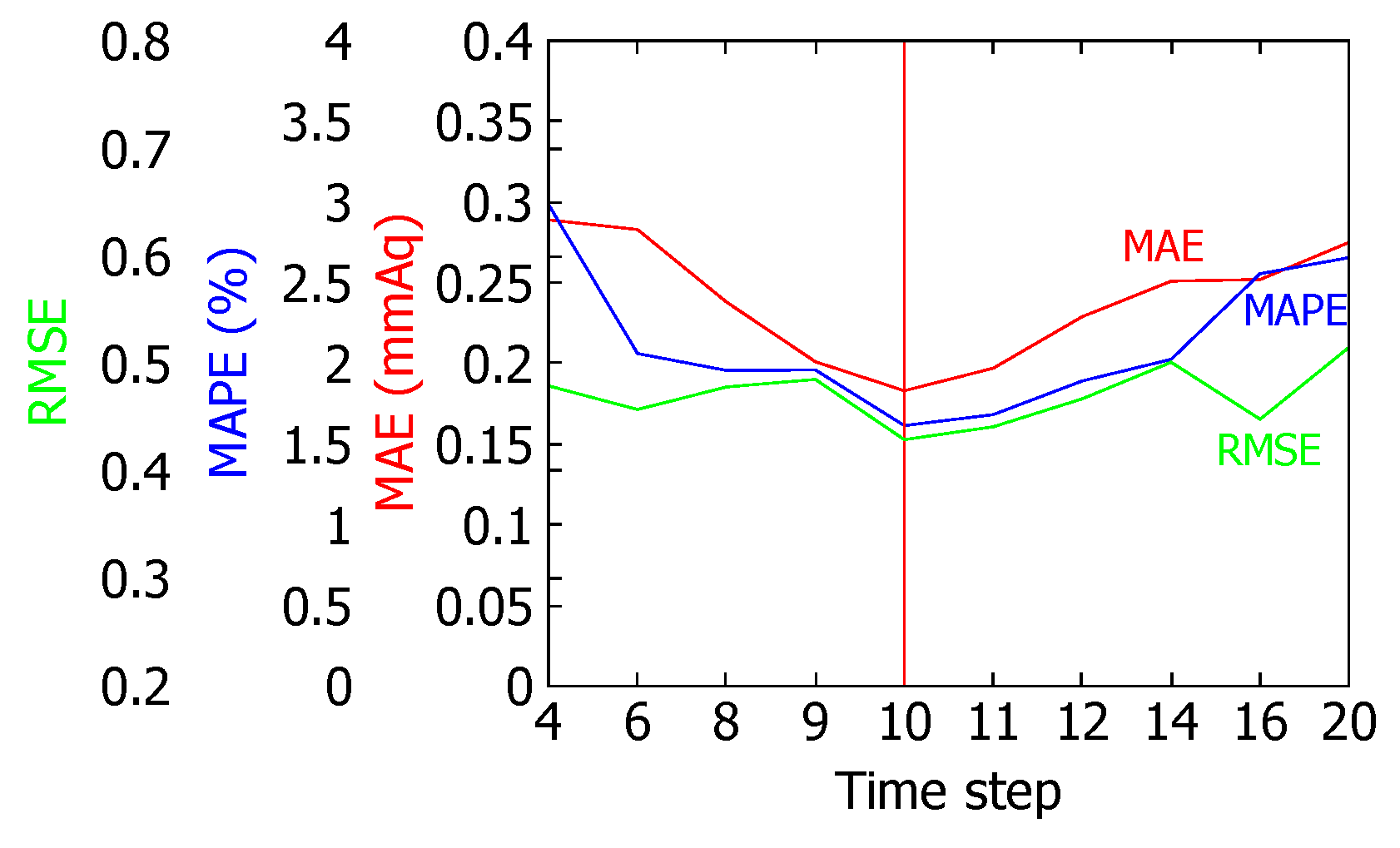

| Time Step | Units of LSTM | Batch Size | MAE | MAPE | RMSE |
|---|---|---|---|---|---|
| 10 | 50 | 36 | 0.197 | 1.715 | 0.451 |
| 72 | 0.194 | 1.698 | 0.433 | ||
| 128 | 0.218 | 1.962 | 0.487 | ||
| 100 | 72 | 0.195 | 1.711 | 0.425 | |
| 50 × 24 | 72 | 0.182 | 1.608 | 0.421 |
| Option | Parameter Setting |
|---|---|
| Batch size | 72 |
| Time step | 10 |
| Training stop strategy | Early stopping |
| Loss function | MAE (Mean Absolute Error) |
| Training method | Adam optimizer |
| Experiment | Training Data | Validation Data | Test Data |
|---|---|---|---|
| 4.1 (4F, 5F, 6F) | 01/05–17/05 (17 days) | 18/05–22/05 (5 days) | 23/05–31/05 (9 days) |
| 01/06–18/06 (18 days) | 19/06–22/06 (4 days) | 23/06–30/06 (8 days) | |
| 01/07–17/07 (18 days) | 18/07–22/07 (5 days) | 23/07–31/07 (9 days) | |
| 01/08–17/08 (17 days) | 18/08–20/08 (3 days) | 21/08–29/08 (9 days): 4F | |
| 21/08–28/08 (8 days): 5F, 6F | |||
| 4.2 (4F) | 01/05–25/05 (25 days) | 26/05–31/05 (6 days) | 01/07–29/08 (60 days) |
| 4.3 | 01/05–25/05 (25 days) | 26/05–31/05 (6 days) | 01/05–28/08 (120 days): 5F, 6F |
| 01/06–24/06 (24 days) | 25/06–30/06 (6 days) | ||
| 01/07–25/07 (25 days) | 26/07–31/07 (6 days) | ||
| 01/08–24/08 (24 days) | 25/08–29/08 (5 days) |
| Time Step | Unit | MAE | MAPE | RMSE |
|---|---|---|---|---|
| 1 | 50 | 1.289 | 8.241 | 2.628 |
| 2 | 50 | 0.801 | 5.651 | 1.958 |
| 100 | 0.791 | 5.312 | 1.799 | |
| 3 | 50 | 0.318 | 1.965 | 0.782 |
| 4 | 50 | 0.275 | 1.327 | 0.574 |
| 100 | 0.259 | 1.575 | 0.580 | |
| 5 | 50 | 0.302 | 1.679 | 0.694 |
| 7 | 50 | 0.494 | 3.065 | 1.221 |
| 10 | 50 | 1.007 | 7.115 | 2.571 |
| 12 | 50 | 1.025 | 7.526 | 2.598 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Son, J.; Kim, H. Sensorless Air Flow Control in an HVAC System through Deep Learning. Appl. Sci. 2019, 9, 3293. https://doi.org/10.3390/app9163293
Son J, Kim H. Sensorless Air Flow Control in an HVAC System through Deep Learning. Applied Sciences. 2019; 9(16):3293. https://doi.org/10.3390/app9163293
Chicago/Turabian StyleSon, Junseo, and Hyogon Kim. 2019. "Sensorless Air Flow Control in an HVAC System through Deep Learning" Applied Sciences 9, no. 16: 3293. https://doi.org/10.3390/app9163293
APA StyleSon, J., & Kim, H. (2019). Sensorless Air Flow Control in an HVAC System through Deep Learning. Applied Sciences, 9(16), 3293. https://doi.org/10.3390/app9163293





