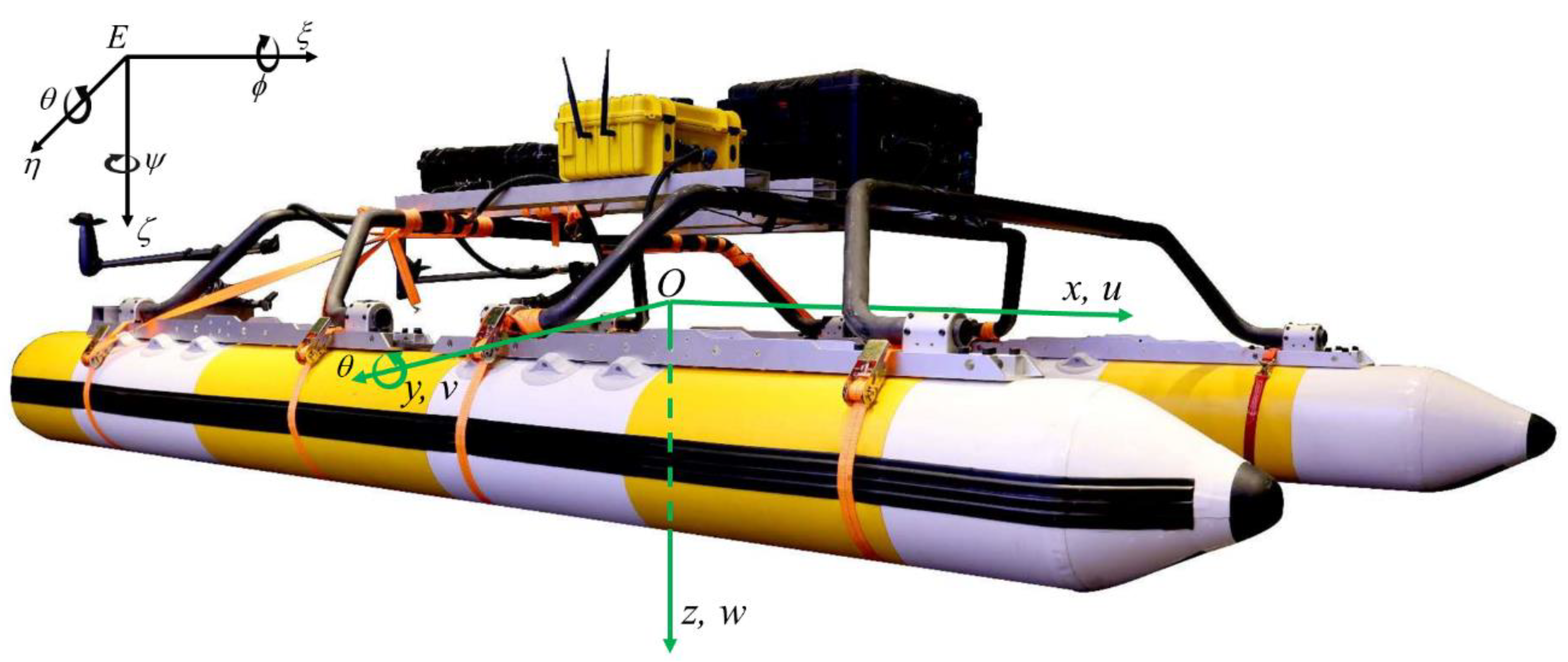
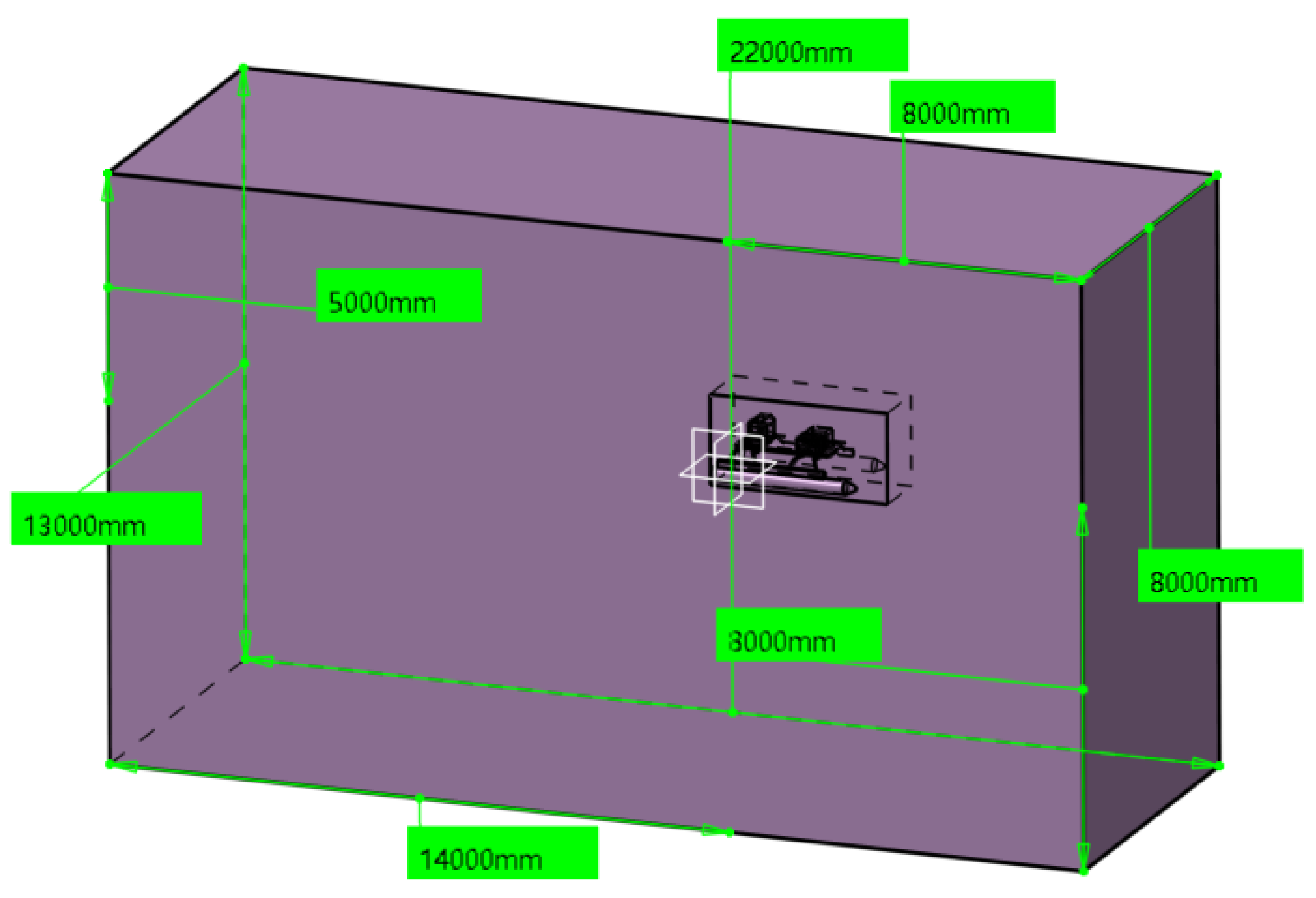
1. Introduction
As a sort of autonomous ocean vehicles, USV (unmanned surface vehicles) can autonomously perform tasks in various environments without human intervention [
1]. USV with non-linear dynamic characteristics have better endurance ability and payload ability than other unmanned vehicles, which makes them to be essential tools in the area of marine scientific research, marine resources development, marine environment monitoring and national marine security [
2,
3,
4]. Autonomy and intellectualization are the crucial manifestations of the development of USV. Research on intelligent planning and controlling can improve the working performance of USV [
5].
In the area of intelligent planning and control, path planning of single objectives, such as shortest distance, time optimality, energy consumption optimality, smoothness optimality and minimal risk, has gradually been studied furtherly [
6]. Multi-objective motion planning and intelligent decision-making [
7,
8] considering dynamic constraints of mobile robots is the difficulty of current research, where it is necessary to obtain more comprehensive and accurate environmental information by using environmental comprehensive perception methods, such as maps to optimize the path planning results. In this context, it is of great significance to study the path planning algorithm based on ENC (electronic navigation chart) considering the hydrodynamic characteristics of USVs for improving the USV’s autonomous environmental awareness, optimizing the path planning results and improving the autonomy and intelligence level of USVs.
A star algorithm, (A* algorithm) is a deterministic algorithm with outstanding consistency and completeness which is widely applied in the research of path planning. It was firstly proposed by Hart P. et al. [
9] and usually combined with grid method [
10]. The minimum cost function is used to search the minimum cost path from the starting node to the end node. The grid-based A* path search methods are mainly based on the center point of the grid [
11,
12,
13,
14,
15,
16] and grid vertexes [
7,
10,
17,
18,
19]. Grid method can be divided into a uniform grid and non-uniform grid with diverse shapes and sizes of the grid. Aiming at the deficiencies of the grid-based A* algorithm, such as huge memory expenditure, large path turning angle and unsmooth path, studies have been done to improve it.
Larson et al. [
20] found the optimal path with the least nodes in limited time by using A*. Svec et al. [
21] combined the A* and locally bounded plan, Naeem et al. [
22] proved A* by direction priority sequential selection (DPSS), Improving path quality and computational capacity. Svec et al. [
23] introduced a model prediction algorithm and combined it with A* algorithm. The above work concentrates on improving the computational performance and path quality of traditional A* algorithm.
Daniel, K [
16] and Soulignac, M [
24] carried out the Theta* which released the limited that the center points of the grid can only moves along the center points within A*. Kim et al. [
13] solved the problem of unlimited direction with the theory of limit-cycle circle set. Nash, A et al. [
15] carried out Lazy Theta*, it was found that vertexes visibility check decreases by using this method. Improved dynamic search D* was put forward by Yang, J.M. et al. [
17] based on A*, it was demonstrated that this algorithm fits the dynamic map very well.
Wu, P.P et al. [
7] carried out a multi-objective A*, it improves the real-time performance of A*. Naus et al. [
25] applied A* to search the shortest and safest trajectory in electronic chart. Kim et al. [
26] carried out a curvature path planning algorithm which considering the turning ability of USV through perfecting A*. Liu, C.G. et al. [
18] established the surface obstacles risk model considering current, traffic separation and maneuverability and improved the practicability of A* algorithm, but ignored the effect of water depth on navigation safety. In the above work, the A* algorithm is applied to the area of path planning for USVs.
Previous researches perfected the calculating quality of A* and expanded the range where A* could be involved in, and they focused on the estimation of the criticality of surface obstacles in the research concerning safest path planning of USVs, rarely discussed the hazard, due to the shallow depth. Depth is a crucial factor affecting navigation safety and performance for unmanned surface vehicles operation in shallow waters, which is more vulnerable to ocean disturbances, such as wind, waves and currents, [
27]. On the other hand, the hydrodynamic characteristics can well reveal the navigation stability of small USVs in shallow waters [
28,
29], and then evaluate the safe depth of navigation.
In this paper, a method of safe path planning is carried out to improve the depth safety of the shortest path of USV, which guarantees navigation safety in different conditions. In this paper, the navigation stability of USVs in various situations is studied, and the minimum safe water depth is calculated according to the results of hydrodynamics simulation. On this basis, the safer path of USVs is calculated by considering the risk of water depth. The depth safety of USV, which followed the shortest path, could be improved by using the information of depth in ENC, the water depth risk level (WDRL) of shortest path could be reduced as well.
4. Discussions
The spline function interpolation method with obstacles is performed to get the raster depth area with the water depth point selected as input point feature and the smoothing coefficient chosen as 0 and the grid size set as 25 m. The feasible space is updated according to the calculated minimum depth of safe navigation (1.29 m). Related parameters are shown in
Table 6. The simulation is also based on the following assumptions: Assuming the unmanned vehicle as a mass point, unmanned vehicles can safely cross the junction vertex of the blocked grid and free gird between the obstacle area and the non-obstacle area, and unmanned vehicles can complete the turnaround operation in the grid. The proposed approach is simulated using Matlab R2018b. All simulations are performed on a PC with Microsoft Windows 10 as OS with Intel i5 2.712 GHz quad core CPU and 8 GB RAM.
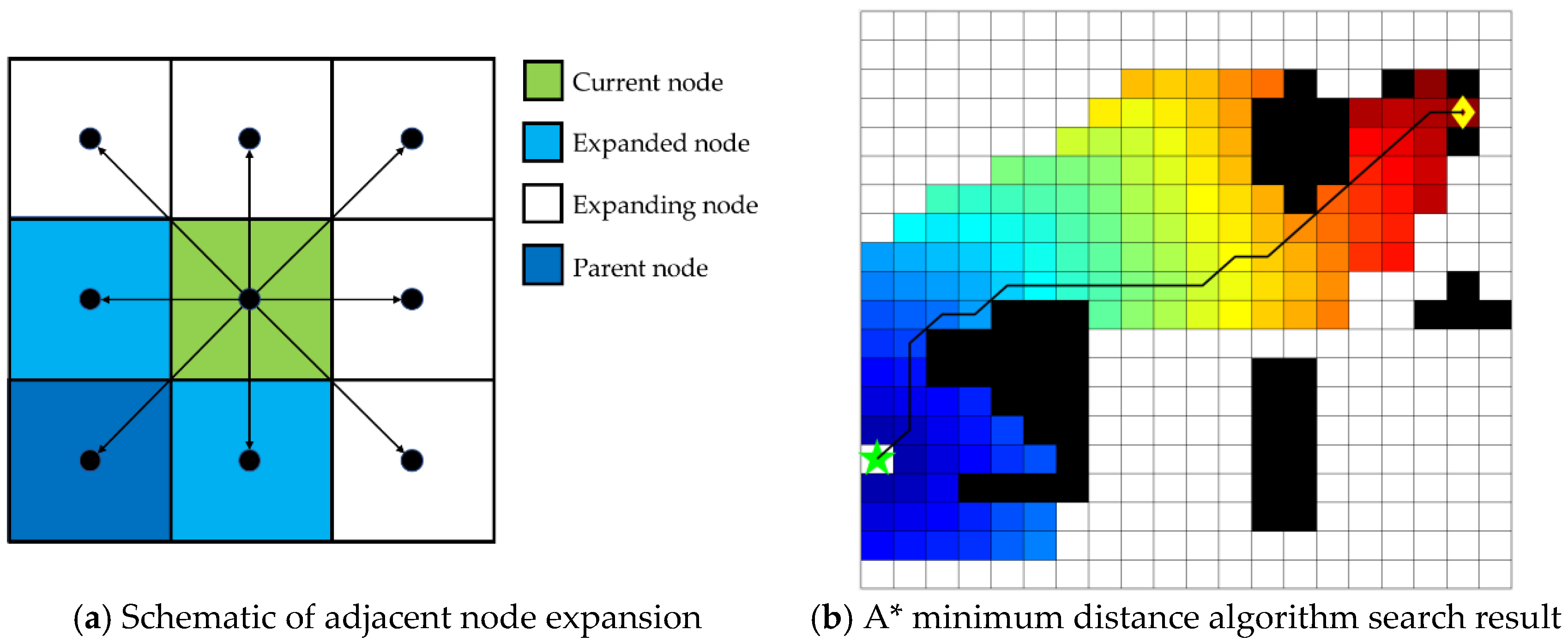
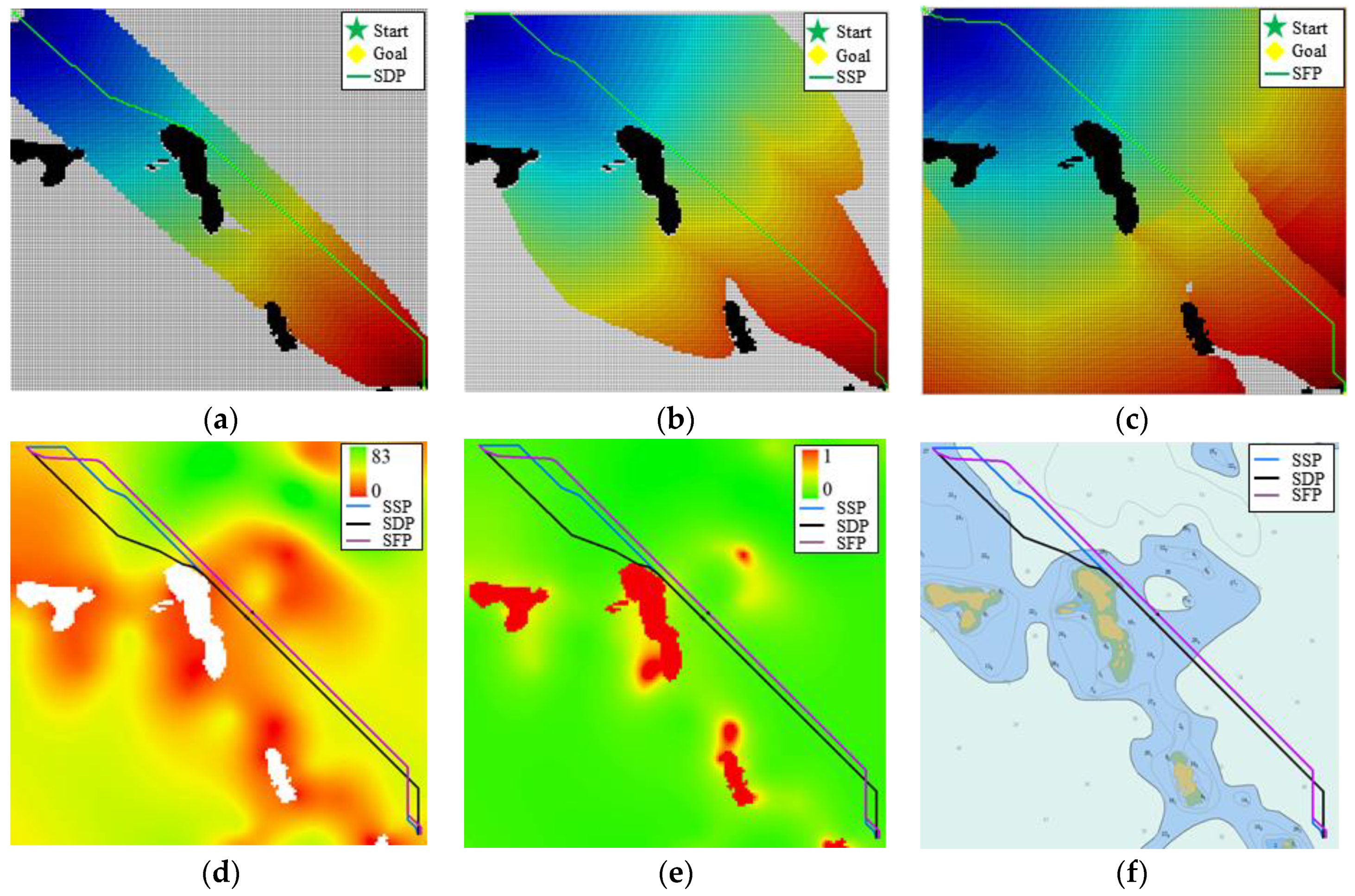
The positions of USV are represented by the grid index value of row and column where the point is located. S(500, 500) is chosen as the starting node and G(650, 650) as the goal node. Three kinds of cost function, including only distance, cost seeing Equation (15), only risk level cost seeing Equation (13), cost of combining seeing equation (16), were used to calculate the paths of shortest distance path (SDP), the shorter and safer path (SSP), the safest path (SFP) The results are shown in
Figure 12. Compared with
Figure 12a–c, it can be seen that the path planning algorithm considering water depth risk level will lead to more expanded nodes, so the search speed will be slower than A* and the expanded nodes of WDRLA* is less than those of SFP seeing
Figure 12b,c.
Figure 12d,e indicate that there is little difference between SSP and SFP, which means approximate depth risk level, but SDP is closer to the obstacle, so the risk level is much higher. Water depth risk level A* algorithm (WDRLA*) can reduce the depth risk and improve the safety of path, but sacrificing a certain calculation time.
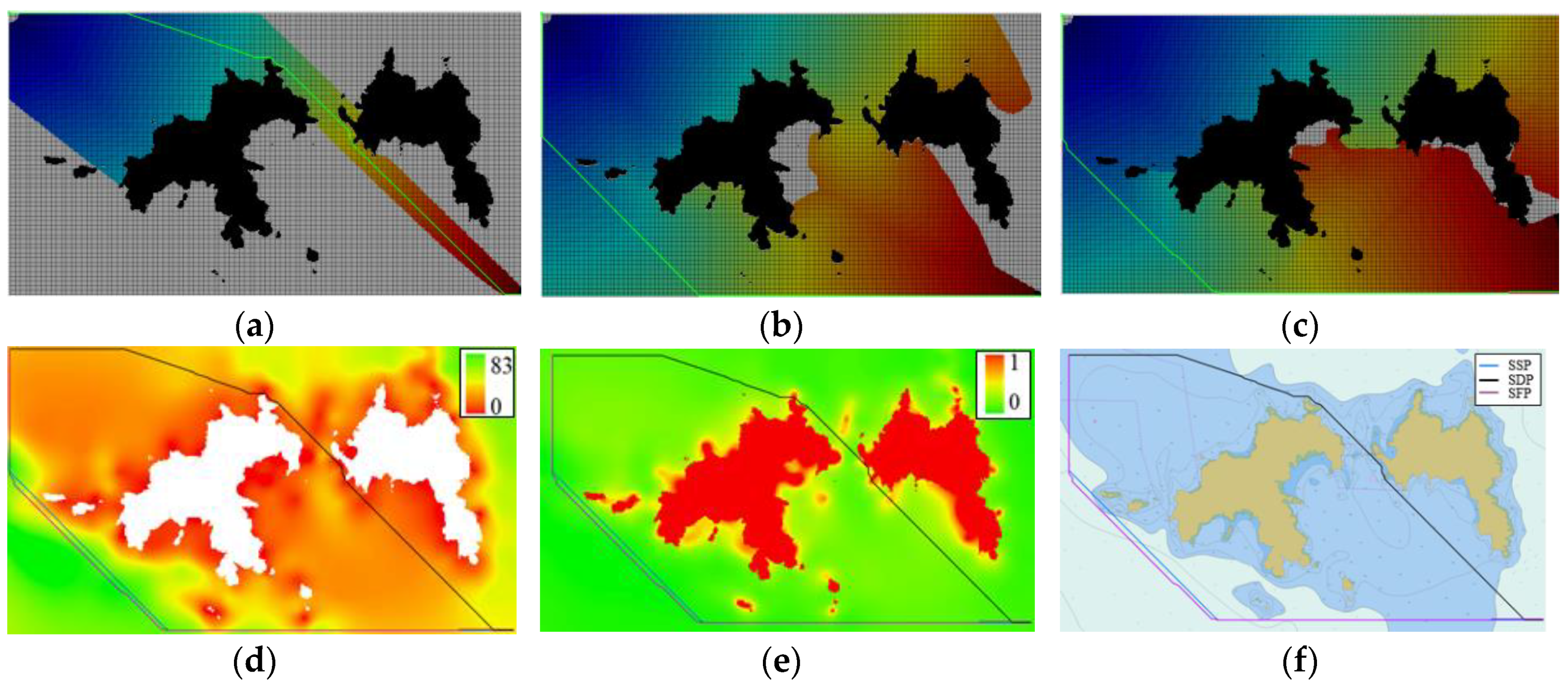
Take S(710, 902) as the starting node, and G(990, 1408) as the goal node, Results of three kinds of paths are shown in
Figure 13. From
Figure 13, it can be drawn that there are marked differences between SDP and SSP in shallow coastal waters. SDP passes through a narrow channel with shallow water depth which is more dangerous, while SSP and SFP avoid narrow channel by choosing deeper water area, where SSP reduces the risk of the path by 39.61% (see
Table 7). At the same time, the number of extended nodes increases greatly, so WDLRA* path search process is slower than A*. SSP increases 1652m and 10.54% in length compared with SDP. The length of SSP and SFP is approximate, but SSP with less expanded nodes.
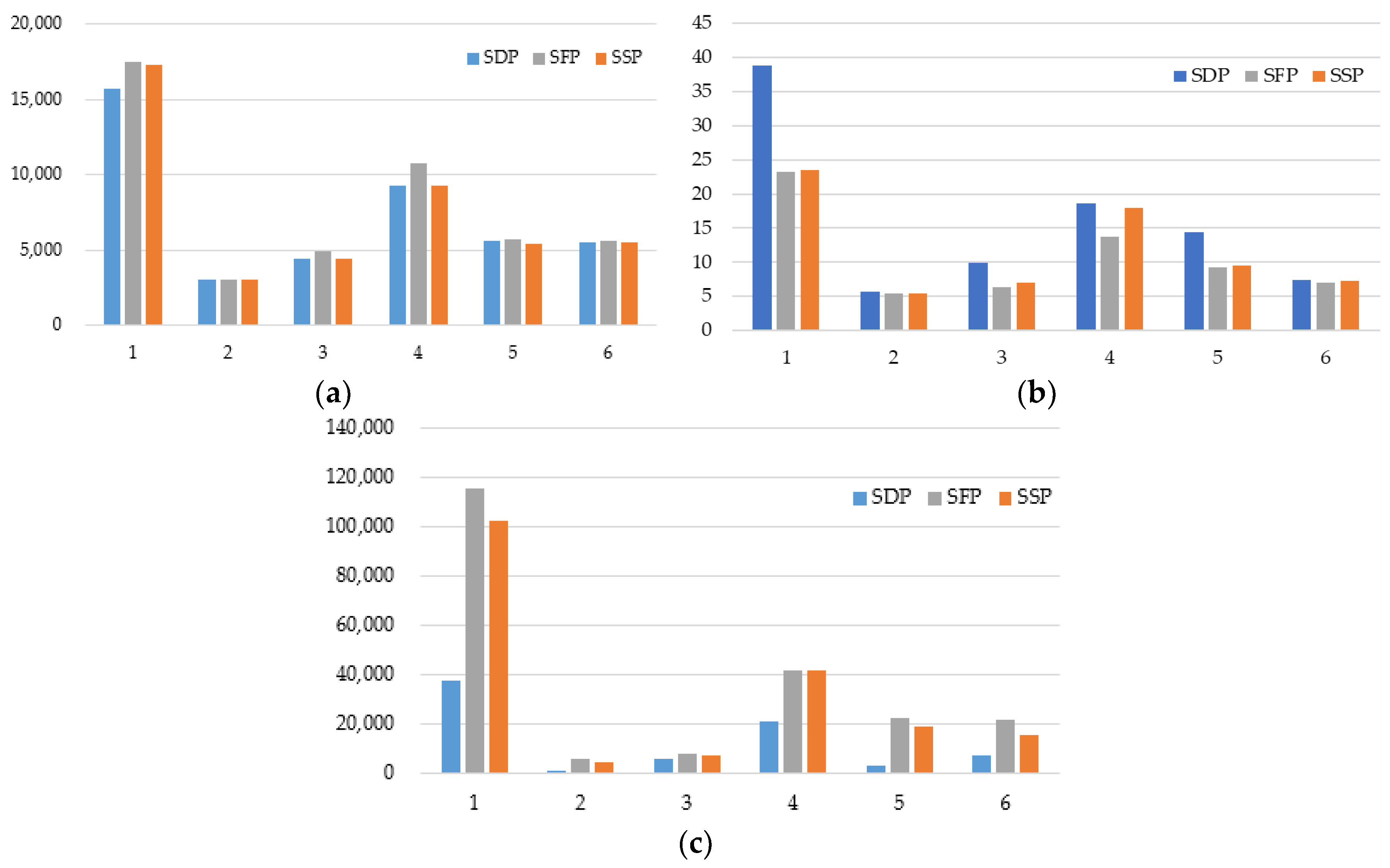
In order to determine the reliability and consistency of the algorithm furtherly, disparate starting nodes and end nodes cases are simulated, and several parameters, such as the path length, the number of expanded nodes, and the risk level of the path, are compared simultaneously, in which the depth risk level is calculated by Equations (11)–(13). All of the results are shown in
Table 7. From
Table 7 combined with
Figure 12,
Figure 13 and
Figure 14, it can be seen that the depth risk level of the path can be reduced, and the path is relatively short, especially in the area with complicated underwater topography, such as
Figure 13 with WDLRA* algorithm, but in the cost of decreasing computational efficiency with redundant expanded nodes (see
Figure 12c and
Figure 13c). This method can ensure the safety of small USV navigating in complicated sea areas.
5. Conclusions
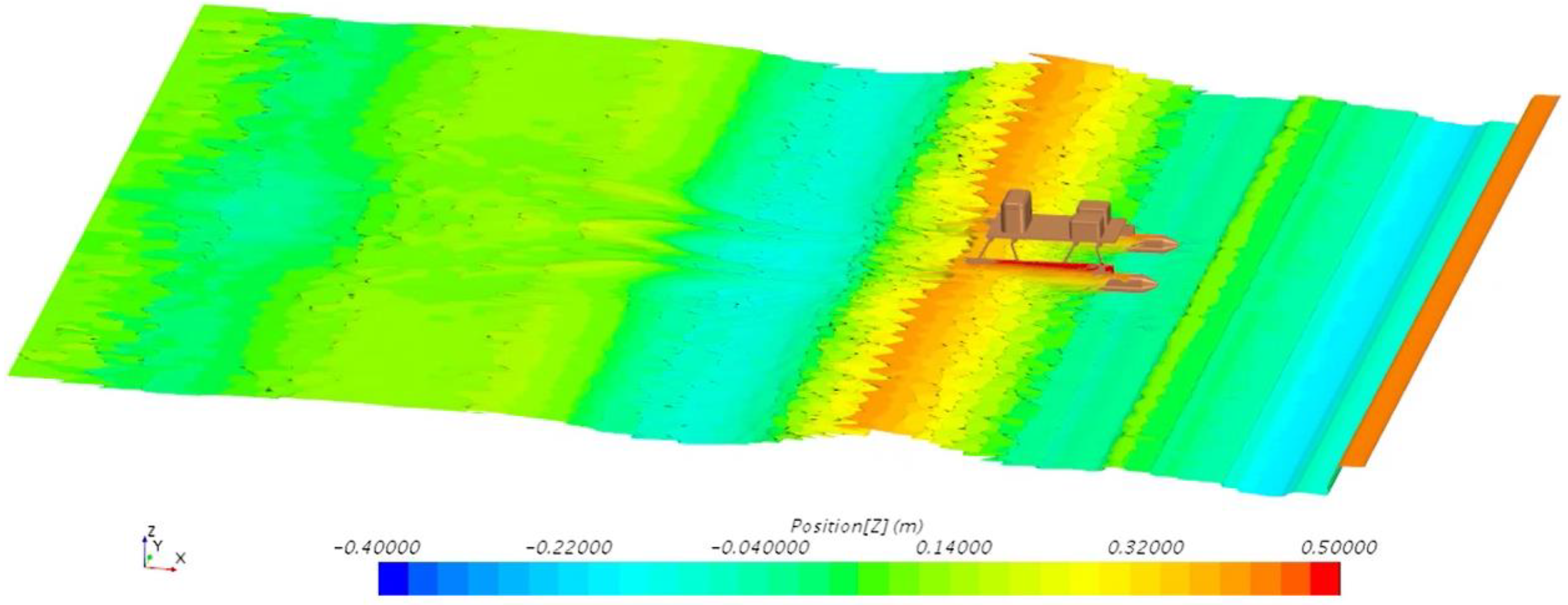
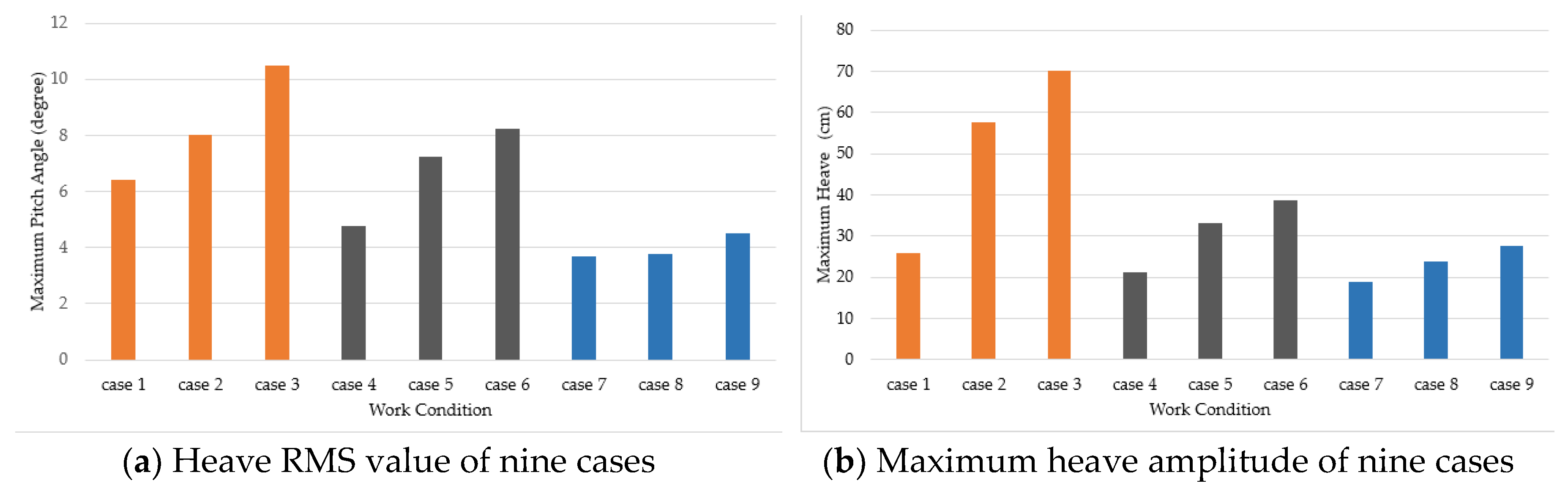
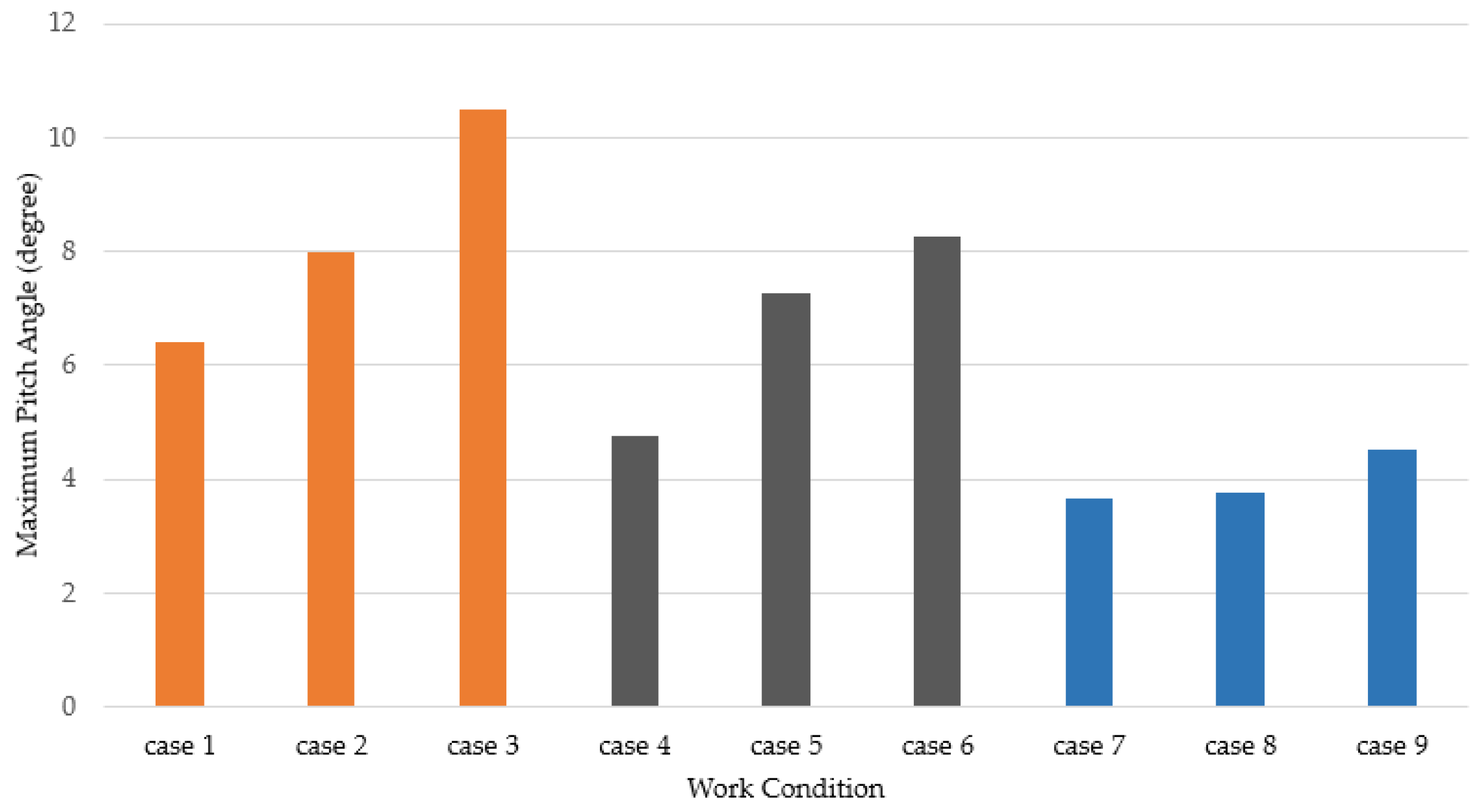
In this paper, hydrodynamic numerical simulation of a new marine surveying and mapping USV platform developed by the author’s research group is performed to evaluate its navigation status in irregular waves. It is found that the heave and pitch of the USV decrease with the increase of velocity and increase with the increase of significant wave height. The heave and pitch navigation status of the unmanned surface vehicle is evaluated through the analysis of 9 working conditions to ascertain minimum safe depth for navigation.
A grid environment modeling method considering water depth is carried out, in which the spline function interpolation algorithm with obstacles is employed to acquire the gridding prediction depth according to the discrete sparse depth points of ENC. The grid modeling method considering water depth can make the utmost of the water depth information provided by ENC to evaluate the depth risk level of path of unmanned surface vehicles.
The quantitative evaluation method of the depth risk level of the path is proposed, and the simulation of path planning is carried out based on A* algorithm using depth hazard degree as an index, named the water depth risk level A* algorithm (WDRLA*). The results show that WDRLA* can hit a safer and shorter path taking into account of the mean draft, the hydrodynamic property, including the maximum heave value and the maximum pitch angle of a USV sailing in an irregular wave, position errors, including ENC positioning errors, positioning system errors and chart depth errors. WDRLA* algorithm can reduce the risk of planned paths in shallow offshore waters to ensure the navigation safety of a USV. The method of path depth risk assessment is not only appropriate to USV path planning, but also can provide guidance for manned ship path planning.
The works are still not completed for the limitations existing. For example, we neglected the influence of tide to water depth, which determines dynamic depth, since the depth on ENC is defined as the vertical distance between the theoretically lowest tide level and seabed. In the future, dynamic water depth will be involved in to acquire bathymetric in better accuracy. The search efficiency of the safe path planning algorithm is expected to be improved in the future.