Deep Learning Resolves Representative Movement Patterns in a Marine Predator Species
Abstract
1. Introduction
2. Related Work
3. Approach
3.1. Data Preprocessing
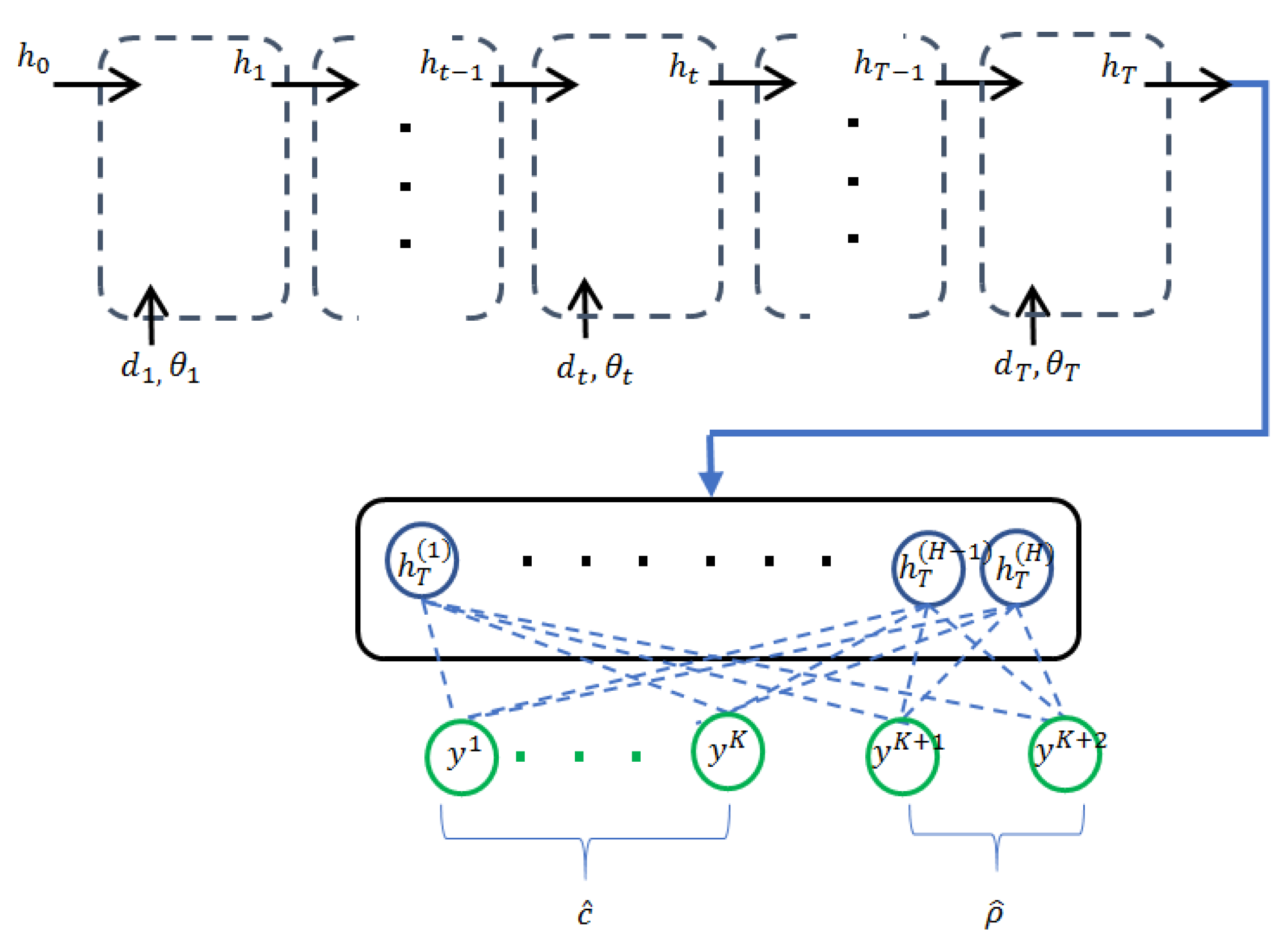
3.2. Recurrent Neural Networks with Confidence Measure
3.3. Multi-Scale Recurrent Neural Networks
3.4. Data Set
4. Results
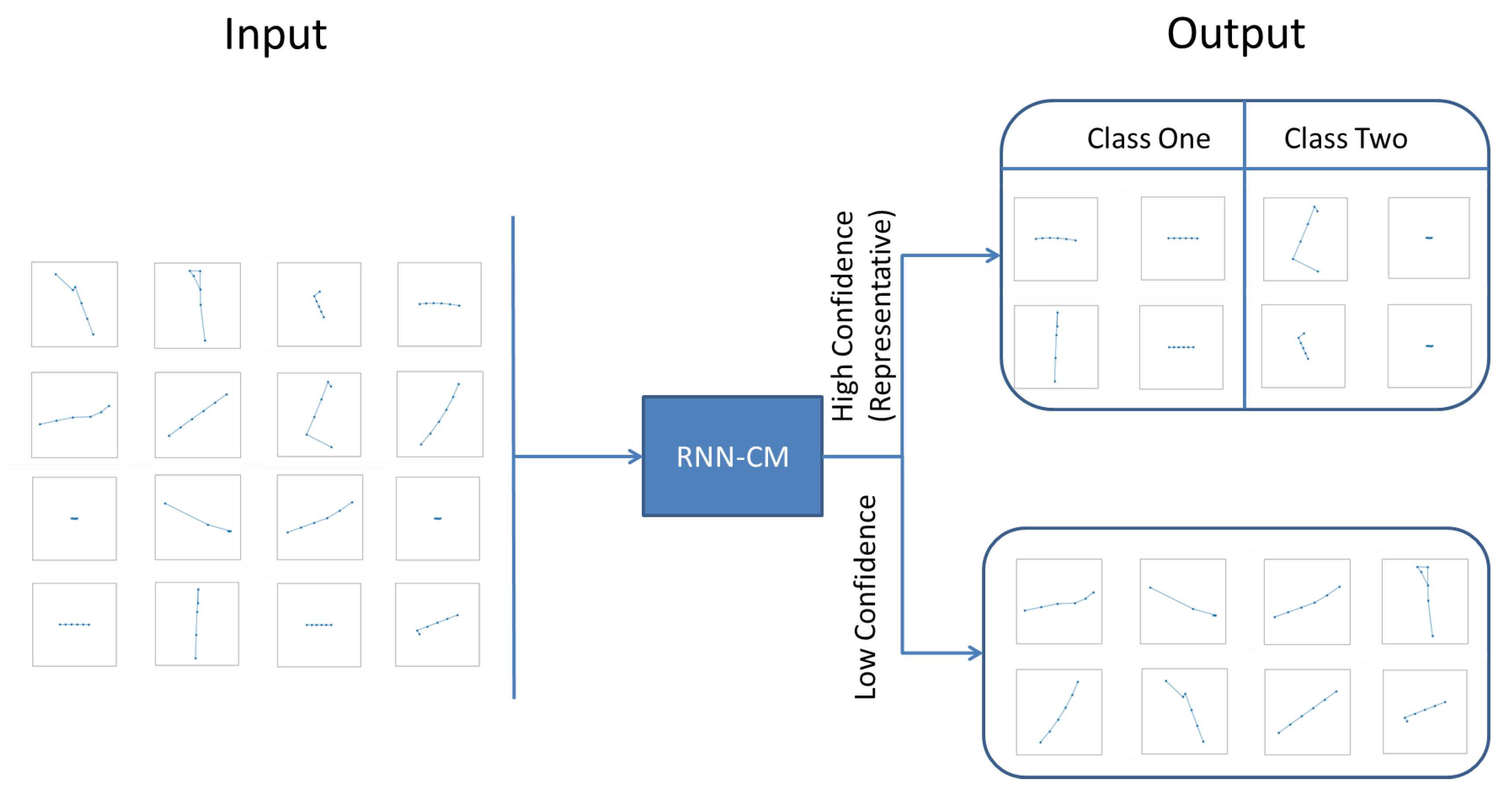
4.1. Representative Trajectory Segments
4.2. Effectiveness of the Proposed RNN-CM Model
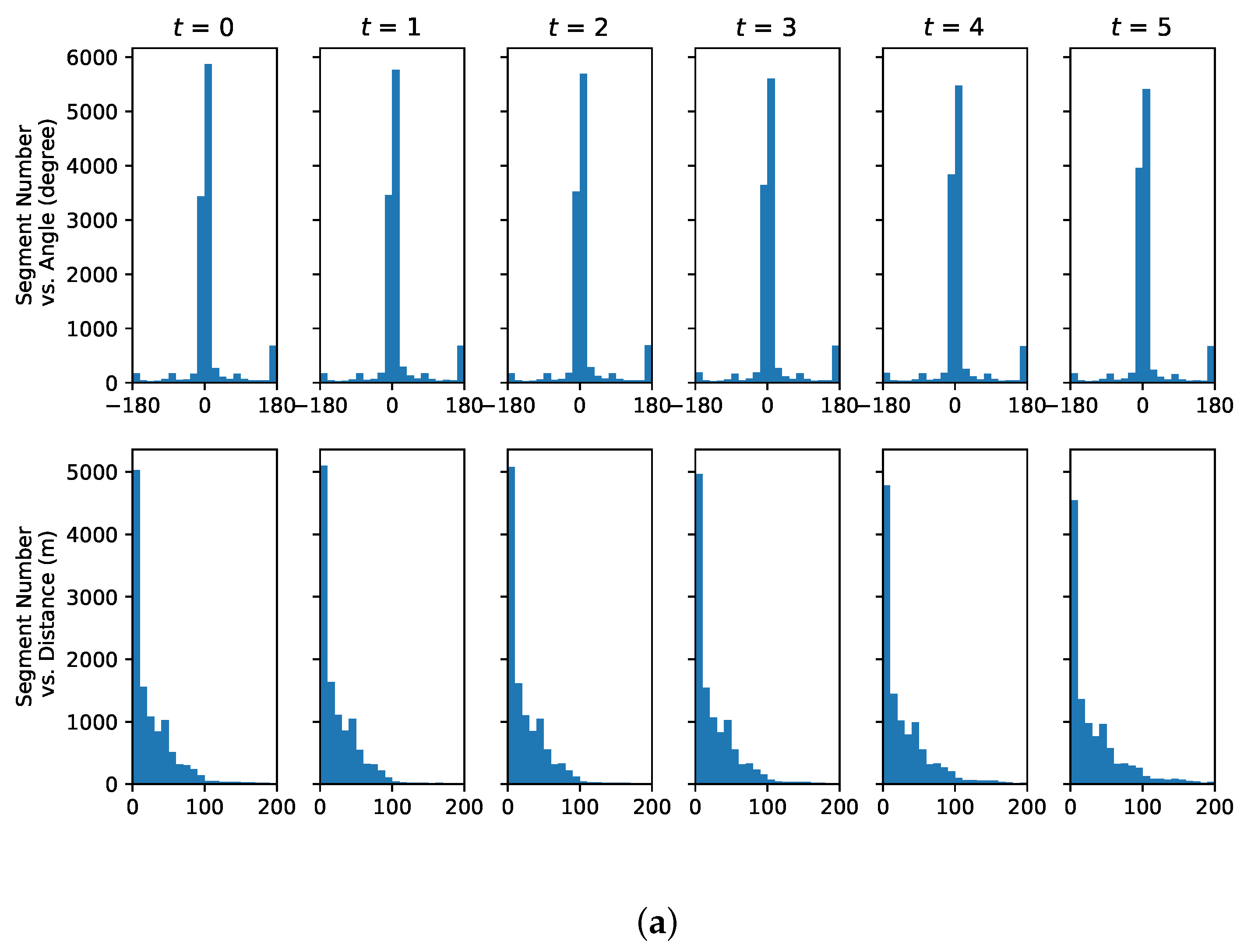
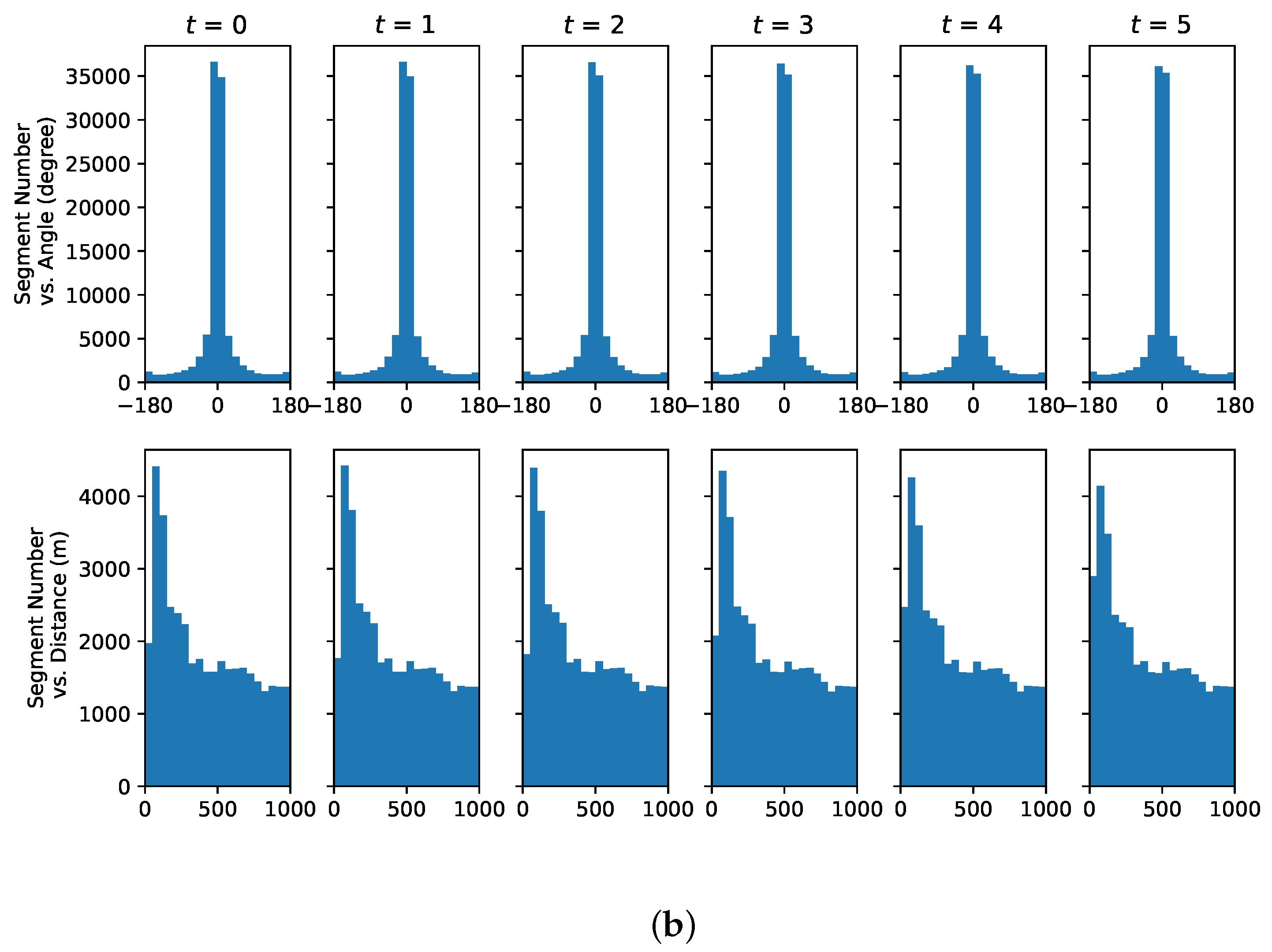
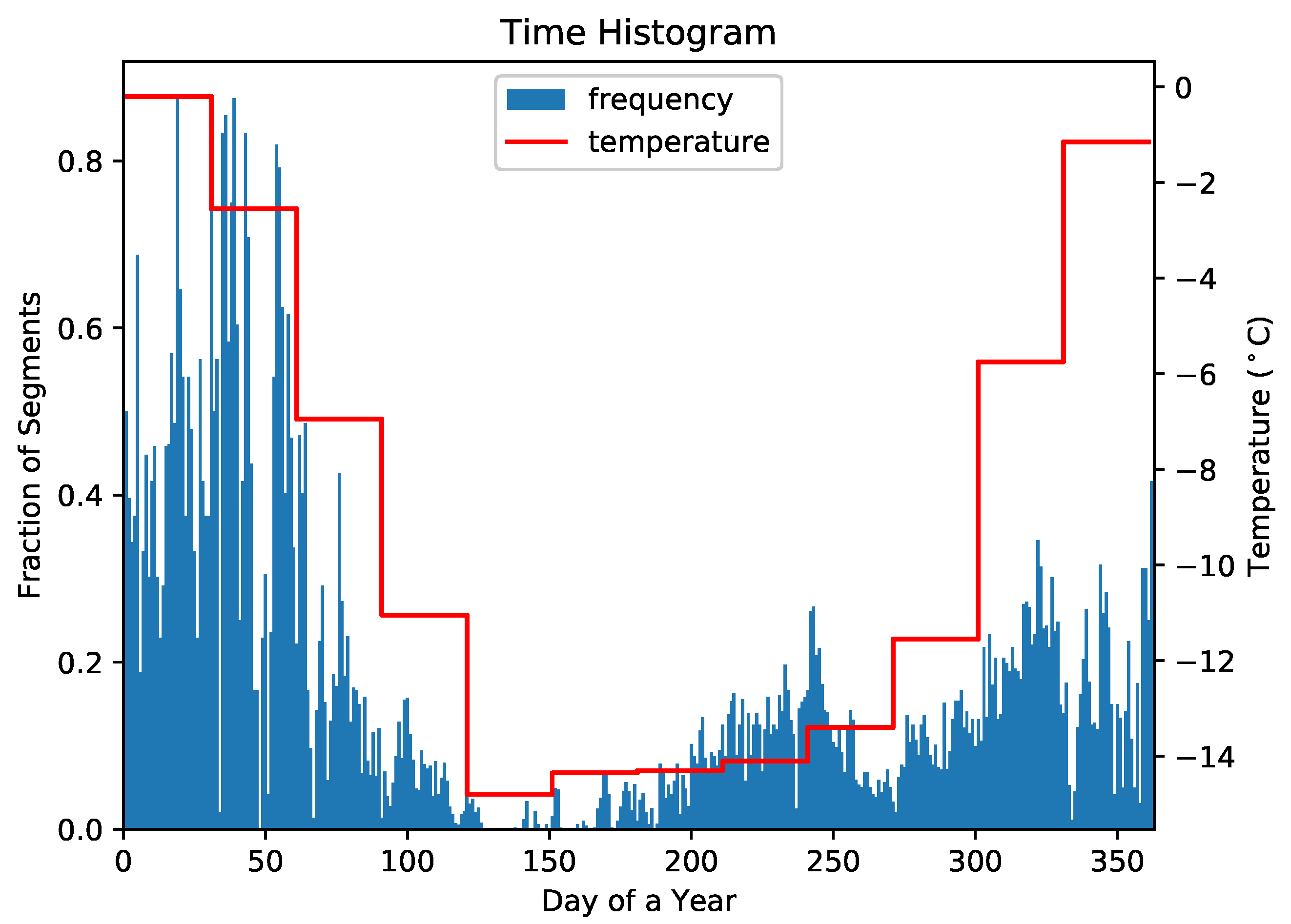
4.3. Understanding Representative Trajectory Segments
4.4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Block, B.A.; Jonsen, I.D.; Jorgensen, S.J.; Winship, A.J.; Shaffer, S.A.; Bograd, S.J.; Hazen, E.L.; Foley, D.G.; Breed, G.; Harrison, A.L.; et al. Tracking apex marine predator movements in a dynamic ocean. Nature 2011, 475, 86–90. [Google Scholar] [CrossRef] [PubMed]
- Burton, A.; Groenewegen, D.; Love, C.; Treloar, A.; Wilkinson, R. Making research data available in Australia. IEEE Intell. Syst. 2012, 27, 40–43. [Google Scholar] [CrossRef]
- Giuggioli, L.; Bartumeus, F. Animal movement, search strategies and behavioural ecology: A cross-disciplinary way forward. J. Anim. Ecol. 2010, 79, 906–909. [Google Scholar] [CrossRef] [PubMed]
- Hays, G.C.; Ferreira, L.C.; Sequeira, A.M.; Meekan, M.G.; Duarte, C.M.; Bailey, H.; Bailleul, F.; Bowen, W.D.; Caley, M.J.; Costa, D.P.; et al. Key questions in marine megafauna movement ecology. Trends Ecol. Evol. 2016, 31, 463–475. [Google Scholar] [CrossRef] [PubMed]
- Kays, R.; Crofoot, M.C.; Jetz, W.; Wikelski, M. Terrestrial animal tracking as an eye on life and planet. Science 2015, 348. [Google Scholar] [CrossRef] [PubMed]
- Cotté, C.; d’Ovidio, F.; Dragon, A.C.; Guinet, C.; Lévy, M. Flexible preference of southern elephant seals for distinct mesoscale features within the Antarctic Circumpolar Current. Prog. Oceanogr. 2015, 131, 46–58. [Google Scholar] [CrossRef]
- Gaspar, P.; Georges, J.Y.; Fossette, S.; Lenoble, A.; Ferraroli, S.; Le Maho, Y. Marine animal behaviour: Neglecting ocean currents can lead us up the wrong track. Proc. R. Soc. Lond. B Biol. Sci. 2006, 273, 2697–2702. [Google Scholar] [CrossRef]
- Campagna, C.; Piola, A.R.; Marin, M.R.; Lewis, M.; Fernández, T. Southern elephant seal trajectories, fronts and eddies in the Brazil/Malvinas Confluence. Deep Sea Res. Part I Oceanogr. Res. Pap. 2006, 53, 1907–1924. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436. [Google Scholar] [CrossRef]
- Chen, Y.; Lin, Z.; Zhao, X.; Wang, G.; Gu, Y. Deep learning-based classification of hyperspectral data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 2094–2107. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. Adv. Neural Inf. Proc. Syst. 2012, 1097–1105. [Google Scholar] [CrossRef]
- Cai, Z.; Vasconcelos, N. Cascade r-cnn: Delving into high quality object detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 6154–6162. [Google Scholar]
- Chambon, S.; Galtier, M.N.; Arnal, P.J.; Wainrib, G.; Gramfort, A. A deep learning architecture for temporal sleep stage classification using multivariate and multimodal time series. IEEE Trans. Neural Syst. Rehabil. Eng. 2018, 26, 758–769. [Google Scholar] [CrossRef] [PubMed]
- Pedersen, M.; Bruslund Haurum, J.; Gade, R.; Moeslund, T.B. Detection of Marine Animals in a New Underwater Dataset with Varying Visibility. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Long Beach, CA, USA, 15–21 June 2019; pp. 18–26. [Google Scholar]
- Sun, R.; Giles, C.L. Sequence learning: From recognition and prediction to sequential decision making. IEEE Intell. Syst. 2001, 16, 67–70. [Google Scholar] [CrossRef]
- Grossman, G.D.; Nickerson, D.M.; Freeman, M.C. Principal component analyses of assemblage structure data: Utility of tests based on eigenvalues. Ecology 1991, 72, 341–347. [Google Scholar] [CrossRef]
- Smouse, P.E.; Focardi, S.; Moorcroft, P.R.; Kie, J.G.; Forester, J.D.; Morales, J.M. Stochastic modelling of animal movement. Philos. Trans. R. Soc. Lond. B: Biol. Sci. 2010, 365, 2201–2211. [Google Scholar] [CrossRef] [PubMed]
- Patterson, T.A.; Thomas, L.; Wilcox, C.; Ovaskainen, O.; Matthiopoulos, J. State-space models of individual animal movement. Trends Ecol. Evol. 2008, 23, 87–94. [Google Scholar] [CrossRef] [PubMed]
- Langrock, R.; King, R.; Matthiopoulos, J.; Thomas, L.; Fortin, D.; Morales, J.M. Flexible and practical modeling of animal telemetry data: hidden Markov models and extensions. Ecology 2012, 93, 2336–2342. [Google Scholar] [CrossRef] [PubMed]
- Dalziel, B.D.; Morales, J.M.; Fryxell, J.M. Fitting probability distributions to animal movement trajectories: using artificial neural networks to link distance, resources, and memory. Am. Nat. 2008, 172, 248–258. [Google Scholar] [CrossRef] [PubMed]
- Wu, F.; Lei, T.K.H.; Li, Z.; Han, J. Movemine 2.0: Mining object relationships from movement data. Proc. VLDB Endow. 2014, 7, 1613–1616. [Google Scholar] [CrossRef]
- Yuan, G.; Sun, P.; Zhao, J.; Li, D.; Wang, C. A review of moving object trajectory clustering algorithms. Artif. Intell. Rev. 2017, 47, 123–144. [Google Scholar] [CrossRef]
- Shamoun-Baranes, J.; Dokter, A.M.; van Gasteren, H.; van Loon, E.E.; Leijnse, H.; Bouten, W. Birds flee en mass from New Year’s Eve fireworks. Behav. Ecol. 2011, 22, 1173–1177. [Google Scholar] [CrossRef] [PubMed]
- Zheng, Y. Trajectory data mining: an overview. ACM Trans. Intell. Syst. Technol. 2015, 6, 29. [Google Scholar] [CrossRef]
- More, A. Survey of resampling techniques for improving classification performance in unbalanced datasets. arXiv 2016, arXiv:1608.06048. [Google Scholar]
- Crone, S.F.; Finlay, S. Instance sampling in credit scoring: An empirical study of sample size and balancing. Int. J. Forecast. 2012, 28, 224–238. [Google Scholar] [CrossRef]
- Gers, F.A.; Schmidhuber, J.; Cummins, F. Learning to Forget: Continual Prediction with LSTM. Neural Comput. 2000, 12, 2451–2471. [Google Scholar] [CrossRef] [PubMed]
- Zaremba, W.; Sutskever, I.; Vinyals, O. Recurrent neural network regularization. arXiv 2014, arXiv:1409.2329. [Google Scholar]
- Abadi, M.; Agarwal, A.; Barham, P.; Brevdo, E.; Chen, Z.; Citro, C.; Corrado, G.S.; Davis, A.; Dean, J.; Devin, M.; et al. TensorFlow: Large-Scale Machine Learning on Heterogeneous Systems. 2015. Available online: www.tensorflow.org (accessed on 1 July 2019).
- Fan, R.E.; Chang, K.W.; Hsieh, C.J.; Wang, X.R.; Lin, C.J. LIBLINEAR: A library for large linear classification. J. Mach. Learn. Res. 2008, 9, 1871–1874. [Google Scholar]
- Hsia, C.Y.; Zhu, Y.; Lin, C.J. A study on trust region update rules in Newton methods for large-scale linear classification. In Proceedings of the Asian Conference on Machine Learning (ACML), Seoul, Korea, 15–17 November 2017. [Google Scholar]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Zhang, C.; Liu, C.; Zhang, X.; Almpanidis, G. An up-to-date comparison of state-of-the-art classification algorithms. Exp. Syst. Appl. 2017, 82, 128–150. [Google Scholar] [CrossRef]
- Labrousse, S.; Williams, G.; Tamura, T.; Bestley, S.; Sallée, J.B.; Fraser, A.D.; Sumner, M.; Roquet, F.; Heerah, K.; Picard, B.; et al. Coastal polynyas: Winter oases for subadult southern elephant seals in East Antarctica. Sci. Rep. 2018, 8, 3183. [Google Scholar] [CrossRef]
- Rodríguez, J.P.; Fernández-Gracia, J.; Thums, M.; Hindell, M.A.; Sequeira, A.M.; Meekan, M.G.; Costa, D.P.; Guinet, C.; Harcourt, R.G.; McMahon, C.R.; et al. Big data analyses reveal patterns and drivers of the movements of southern elephant seals. Sci. Rep. 2017, 7, 112. [Google Scholar] [CrossRef] [PubMed]

| Confidence Level | Top 10% | Top 20% | Top 30% | All |
|---|---|---|---|---|
| RNN-CM | 91.1% [100%] | 85.2% [100%] | 79.4% [99.5%] | 54.6% [59.0%] |
| Random Forest | 83.5% [99.5%] | 78.4% [94.4%] | 72.1% [85.8%] | 57.0% [65.4%] |
| Linear SVM | 85.6% [100.0%] | 78.8% [100.0%] | 75.2% [100.0%] | 49.8% [48.3%] |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peng, C.; Duarte, C.M.; Costa, D.P.; Guinet, C.; Harcourt, R.G.; Hindell, M.A.; McMahon, C.R.; Muelbert, M.; Thums, M.; Wong, K.-C.; et al. Deep Learning Resolves Representative Movement Patterns in a Marine Predator Species. Appl. Sci. 2019, 9, 2935. https://doi.org/10.3390/app9142935
Peng C, Duarte CM, Costa DP, Guinet C, Harcourt RG, Hindell MA, McMahon CR, Muelbert M, Thums M, Wong K-C, et al. Deep Learning Resolves Representative Movement Patterns in a Marine Predator Species. Applied Sciences. 2019; 9(14):2935. https://doi.org/10.3390/app9142935
Chicago/Turabian StylePeng, Chengbin, Carlos M. Duarte, Daniel P. Costa, Christophe Guinet, Robert G. Harcourt, Mark A. Hindell, Clive R. McMahon, Monica Muelbert, Michele Thums, Ka-Chun Wong, and et al. 2019. "Deep Learning Resolves Representative Movement Patterns in a Marine Predator Species" Applied Sciences 9, no. 14: 2935. https://doi.org/10.3390/app9142935
APA StylePeng, C., Duarte, C. M., Costa, D. P., Guinet, C., Harcourt, R. G., Hindell, M. A., McMahon, C. R., Muelbert, M., Thums, M., Wong, K.-C., & Zhang, X. (2019). Deep Learning Resolves Representative Movement Patterns in a Marine Predator Species. Applied Sciences, 9(14), 2935. https://doi.org/10.3390/app9142935






