A Hybrid Approach Using Fuzzy AHP-TOPSIS Assessing Environmental Conflicts in the Titan Mining Industry along Central Coast Vietnam
Abstract
1. Introduction
2. Methodology
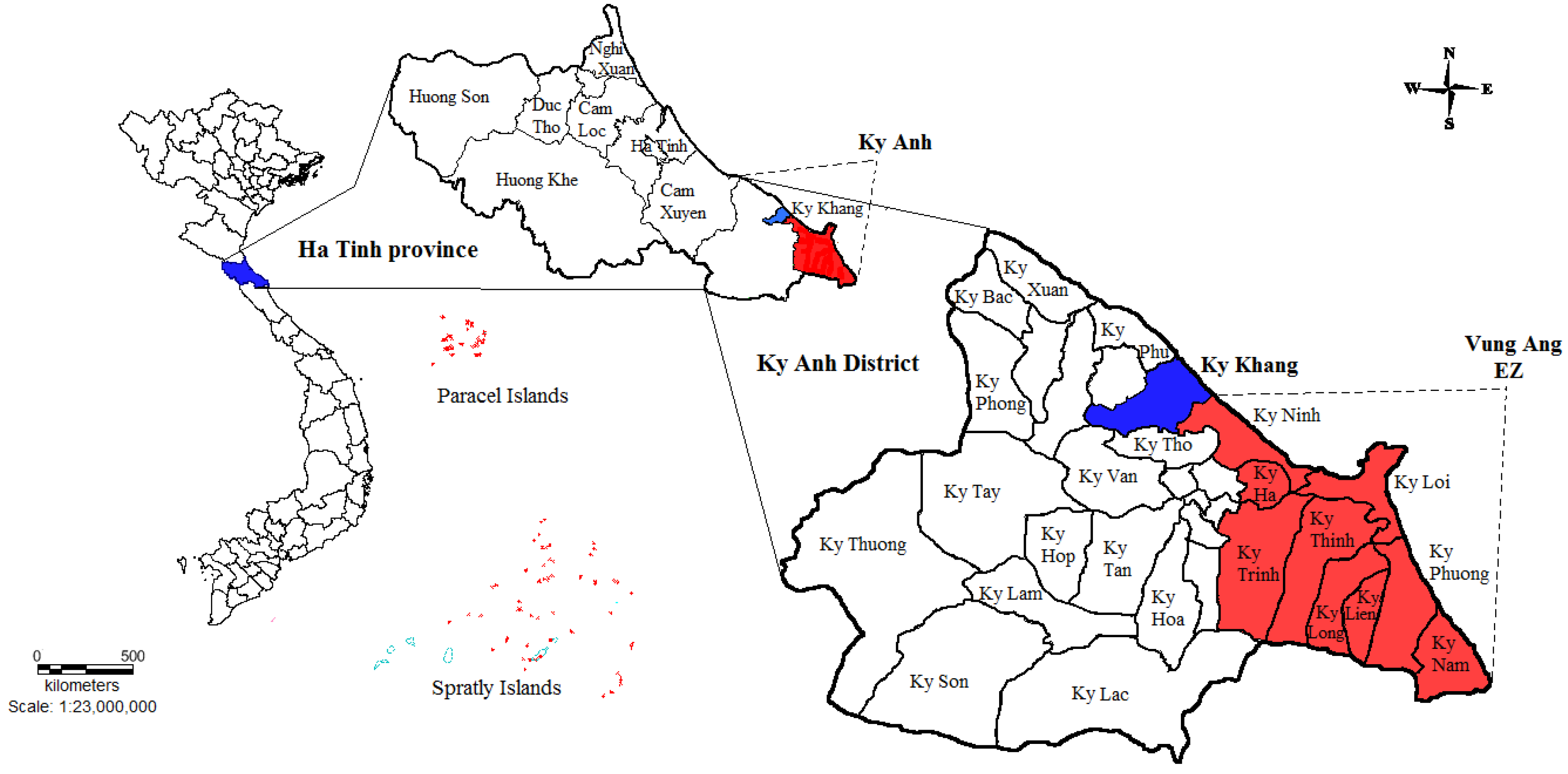
2.1. Study Area
2.2. A Combination of Fuzzy AHP and Fuzzy TOPSIS
2.2.1. Fuzzy AHP
2.2.2. Fuzzy TOPSIS
2.2.3. Data Collection
3. Results
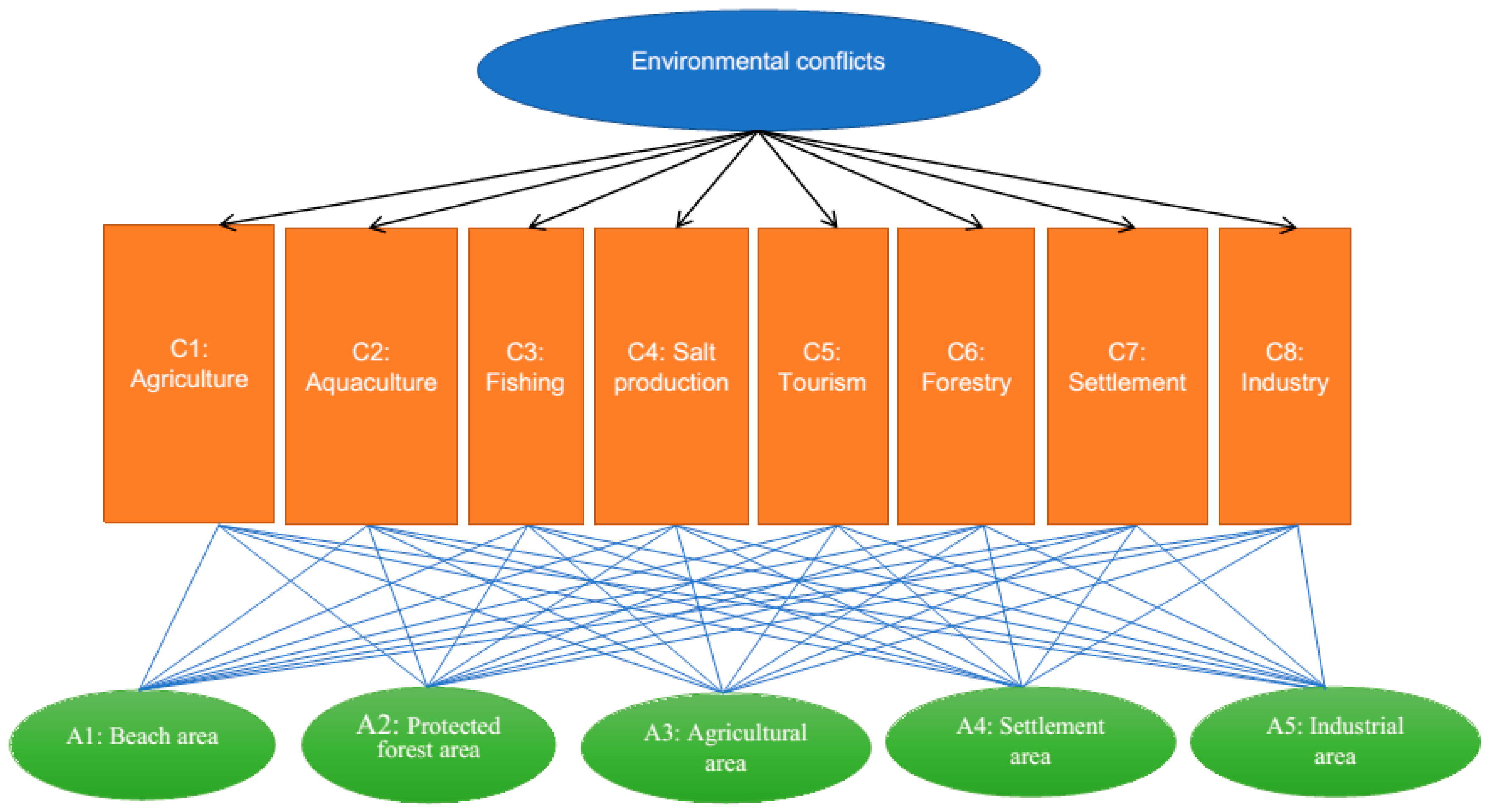
3.1. Determining Criteria of Sectors and Alternative Sites
3.2. Levels of Environmental Conflict and Priority Alternative Sites to Implement Conflict Prevention Solutions
3.2.1. Weighting Criteria
3.2.2. Final Ranking of the Alternatives
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Lu, Y.; Fu, B.; Chen, L.; Ouyang, Z.; Xu, J. Resolving the conflicts between biodiversity conservation and socioeconomic development in China: Fuzzy clustering approach. Biodivers. Conserv. 2006, 15, 2813–2827. [Google Scholar] [CrossRef]
- Young, J.C.; Marzano, M.; White, R.M.; McCracken, I.; Redpath, S.M.; Carss, D.N.; Quine, C.P.; Watt, A.D. The emergence of biodiversity conflicts from biodiversity impacts: Characteristics and management strategies. Biodivers. Conserv. 2010, 19, 3973–3990. [Google Scholar] [CrossRef]
- Meng, H.H.; Zhou, S.S.; Li, L.; Tan, Y.H.; Li, J.W.; Li, J. Conflict between biodiversity conservation and economic growth: Insight into rare plants in tropical China. Biodivers. Conserv. 2019, 28, 523–537. [Google Scholar] [CrossRef]
- Cadoret, A. Conflict dynamics in coastal zones: A perspective using the example of Languedoc-Rousillon (France). Coast. Conserv. 2009, 13, 151. [Google Scholar] [CrossRef]
- Bramatia, M.C.; Musellab, F.; Allevaa, G. What drives environmental conflicts in coastal areas? An econometric approach. Ocean Coast. Manag. 2014, 101, 63–78. [Google Scholar] [CrossRef]
- Stepanova, O. Conflict resolution in coastal resource management: Comparative analysis of case studies from four European countries. Ocean Coast. Manag. 2015, 103, 109–122. [Google Scholar] [CrossRef]
- Rempis, N.; Alexandrakis, G.; Tsilimigkas, G.; Kampanis, N. Coastal use synergies and conflicts evaluation in the framework of spatial, development and sectoral policies. Ocean Coast. Manag. 2018, 166, 40–51. [Google Scholar] [CrossRef]
- Solomon, N.; Birhane, E.; Gordon, C.; Haile, M.; Taheri, F.; Azadi, H.; Scheffran, J. Environmental impacts and causes of conflict in the Horn of Africa: A review. Earth-Sci. Rev. 2018, 177, 284–290. [Google Scholar] [CrossRef]
- Barry, M.B.; Dewar, D.; Whittal, J.F.; Muzondo, I.F. Land Conflicts in Informal Settlements: Wallacedene in Cape Town, South Africa. Urban Forum 2007, 18, 171–189. [Google Scholar] [CrossRef]
- Pape, R.; Löffler, J. Climate change, land use conflicts, predation and ecological degradation as challenges for reindeer husbandry in Northern Europe: What do we really know after half a century of research? AMBIO 2012, 41, 421–434. [Google Scholar] [CrossRef]
- Zeitoun, M.; Mirumachi, N. Transboundary water interaction I: Reconsidering conflict and cooperation. Int. Environ. Agreem. Politics Law Econ. 2008, 8, 297. [Google Scholar] [CrossRef]
- Strauß, S. Water conflicts among different user groups in South Bali, Indonesia. Hum. Ecol. 2011, 39, 69–79. [Google Scholar] [CrossRef]
- Gunasekara, N.K.; Kazama, S.; Yamazaki, D.; Oki, T. Water conflict risk due to water resource availability and unequal distribution. Water Resour. Manag. 2014, 28, 169–184. [Google Scholar] [CrossRef]
- Yuling, S.; Lein, H.; Chen, X. Water conflicts in Hetian District, Xinjiang, during the Republic of China period. Water Hist. 2016, 8, 77–94. [Google Scholar] [CrossRef]
- Abrahams, D.; Carr, E.R. Understanding the connections between climate change and conflict: Contributions from geography and political ecology. Curr. Clim. Chang. Rep. 2017, 3, 233–242. [Google Scholar] [CrossRef]
- Pearson, D.; Newman, P. Climate security and a vulnerability model for conflict prevention: A systematic literature review focusing on African agriculture. Sustain. Earth 2019, 2, 2. [Google Scholar] [CrossRef]
- Brock, L. Environmental Conflict Research—Paradigms and Perspectives. In Environmental Change and Security: International and European Environmental Policy Series; Carius, A., Lietzmann, K.M., Eds.; Springer: Berlin/Heidelberg, Germany, 1999; pp. 37–53. [Google Scholar]
- Klaus, R. Agrarian development and conflicts of land utilization in the coastal plains of Calabria (South Italy). GeoJournal 1986, 13, 27–35. [Google Scholar]
- Sebastiani, M.; González, S.E.; Castillo, M.M.; Alvizu, P.; Oliveira, M.A.; Pérez, J.; Quilici, A.; Rada, M.; Yáber, M.C.; Lentino, M. Large-scale shrimp farming in coastal wetlands of Venezuela, South America: Causes and consequences of land-use conflicts. Environ. Manag. 1994, 18, 647–661. [Google Scholar] [CrossRef]
- Pérez-Rincón, M.; Vargas-Morales, J.; Crespo-Marín, Z. Trends in social metabolism and environmental conflicts in four Andean countries from 1970 to 2013. Sustain. Sci. 2018, 13, 635–648. [Google Scholar] [CrossRef]
- Carpenter, S.L.; Kennedy, W.J.D. Environmental conflicts in mineral development. Miner. Environ. 1980, 2, 159–164. [Google Scholar] [CrossRef]
- McKenna, J.; Cooper, J.A.G.; O’Hagan, A.M. Coastal erosion management and the European principles of ICZM: Local versus strategic perspectives. Coast. Conserv. 2009, 13, 165–173. [Google Scholar] [CrossRef]
- Tuda, A.O.; Stevens, T.F.; Rodwell, L.D. Resolving coastal conflicts using marine spatial planning. Environ. Manag. 2014, 133, 59–68. [Google Scholar] [CrossRef] [PubMed]
- Zhao, X.; Jia, P. Multi-planning integration advancing coastal zone management: A case study from Hainan Island, China. Coast. Conserv. 2018, 1–7. Available online: https://link.springer.com/article/10.1007/s11852-018-0667-0 (accessed on 30 June 2019). [CrossRef]
- Rudianto Tantu, A.G. An analysis of coastal land conflict in the North of Jakarta coastal area: (A general algebraic modelling system approach). Coast. Conserv. 2014, 18, 69–74. [Google Scholar] [CrossRef]
- Chuang, Y.H.; Yu, R.F.; Chen, W.Y.; Chen, H.W.; Su, Y.T. Sustainable planning for a coastal wetland system with an integrated ANP and DPSIR model for conflict resolution. Wetl. Ecol. Manag. 2018, 26, 1015–1036. [Google Scholar] [CrossRef]
- Bascetin, A. A decision support system using analytical hierarchy process (AHP) for the optimal environmental reclamation of an open-pit mine. Environ. Geol. 2007, 52, 663–672. [Google Scholar] [CrossRef]
- Sadiq, R.; Tesfamariam, S. Environmental decision-making under uncertainty using intuitionistic fuzzy analytic hierarchy process (IF-AHP). Stoch. Environ. Res. Risk Assess. 2009, 23, 75–91. [Google Scholar] [CrossRef]
- Afshar, A.; Mariño, M.A.; Saadatpour, M.; Afshar, A. Fuzzy TOPSIS Multi-Criteria Decision Analysis applied to Karun Reservoirs System. Water Resour. Manag. 2011, 25, 545–563. [Google Scholar] [CrossRef]
- Pourebrahim, S.; Mokhtar, M.B. Conservation priority assessment of the coastal area in the Kuala Lumpur mega-urban region using extent analysis and TOPSIS. Environ. Earth Sci. 2016, 75, 348. [Google Scholar] [CrossRef]
- Asghari, M.; Nassiri, P.; Monazzam, M.R.; Golbabaei, F.; Arabalibeik, H.; Shamsipour, A.; Allahverdy, A. Weighting criteria and prioritizing of heat stress indices in surface mining using a Delphi Technique and Fuzzy AHP-TOPSIS Method. Environ. Health Sci. Eng. 2017, 15, 1. [Google Scholar] [CrossRef]
- MONRE (Ministry of Natural Resources and Environment). Basic Contents of Survey on Geology, Environmental Geology and Disasters of Geology in Coastline of Vietnam; General Department of Geology and Minerals of Vietnam: Hanoi, Vietnam, 2001; 463p. (In Vietnamese)
- DGM (Department of Geology and Minerals of Vietnam). Report on Mineral Resources in Coastal Provinces; Department of Geology and Minerals of Vietnam: Hanoi, Vietnam, 2016; 365p. (In Vietnamese) [Google Scholar]
- KAG (Ky Anh Government). Socio-Economic Development of Ky Anh; Official Report; KAG: Ky Anh, Vietnam, 2019; 78p. (In Vietnamese)
- Nguyen, A.T.; Vu, D.A.; Vu, P.V.; Nguyen, T.N.; Pham, T.M.; Nguyen, H.T.T.; Le, H.T.; Nguyen, T.V.; Hoang, L.K.; Duc Vu, T.; et al. Human ecological effects of tropical storms in the coastal area of Ky Anh (Ha Tinh, Vietnam). Environ. Dev. Sustain. 2017, 19, 745–767. [Google Scholar] [CrossRef]
- PMV (Prime Minister of Vietnam). “Decision 1880/Q-TTg on the Compensation to the Provinces of Ha Tinh, Quang Binh, Quang Tri, and Thue Thien-Hue Following the Marine Environmental Incident”; PMV: Ha Noi, Vietnam, 2016. (In Vietnamese) [Google Scholar]
- PMV (Prime Minister of Vietnam). “Decision 309/Q-TTg on the revision of Decision 1880/Q-TTg on September 29 2016 Regarding the Compensation for the Provinces of Ha Tinh, Quang Binh, Quang Tri, and Thue Thien-Hue following the Marine Environmental Incident”; PMV: Ha Noi, Vietnam, 2017. (In Vietnamese) [Google Scholar]
- Saaty, R.W. The analytic hierarchy process—What it is and how it is used. Math. Model. 1987, 9, 161–176. [Google Scholar] [CrossRef]
- Vargas, L.G. An overview of the analytical hierarchy process and its applications. Eur. J. Oper. Res. 1990, 48, 2–8. [Google Scholar] [CrossRef]
- Carnero, M.C. Multicriteria model for maintenance benchmarking. Manuf. Syst. 2014, 33, 303–321. [Google Scholar] [CrossRef]
- Chang, D.Y. Applications of the extent analysis method on fuzzy AHP. Eur. J. Oper. Res. 1996, 95, 649–655. [Google Scholar] [CrossRef]
- Pourjavad, E.; Mayorga, R.V. A hybrid approach integrating AHP and TOPSIS for sustainable end-of-life vehicle strategy evaluation under fuzzy environment. Wseas Trans. Circuits Syst. 2016, 15, 216–223. [Google Scholar]
- Hwang, C.L.; Yoon, K. Multiple Attribute Decision Making: Methods and Applications; Springer: Berlin/Heidelberg, Germany, 1981; 225p, ISBN 978-3-642-48318-9. [Google Scholar]
- Yasmi, Y.; Schanz, H.; Salim, A. Manifestation of conflict escalation in natural resource management. Environ. Sci. Policy 2006, 9, 538–546. [Google Scholar] [CrossRef]
- Taylan, O.; Bafail, A.O.; Abdulaal, R.M.S.; Kabli, M.R. Construction projects selection and risk assessment by fuzzy AHP and fuzzy TOPSIS methodologies. Appl. Soft Comput. 2014, 17, 105–116. [Google Scholar] [CrossRef]
- Sirisawat, P.; Kiatcharoenpol, T. Fuzzy AHP-TOPSIS approaches to prioritizing solutions for reverse logistics barriers. Comput. Ind. Eng. 2018, 117, 303–318. [Google Scholar] [CrossRef]
- Tyagi, M.; Kumar, P.; Kumar, D. A hybrid approach using AHP-TOPSIS for analyzing e-SCM performance. Procedia Eng. 2014, 97, 2195–2203. [Google Scholar] [CrossRef]
- Sun, L.; Zhu, D.; Chan, E.H.W. Public participation impact on environment NIMBY conflict and environmental conflict management: Comparative analysis in Shanghai and Hong Kong. Land Use Policy 2016, 58, 208–217. [Google Scholar] [CrossRef]
- Rincón-Ruiz, A.; Rojas-Padilla, J.; Agudelo-Rico, C.; Perez-Rincon, M.; Vieira-Samper, S.; Rubiano-Paez, J. Ecosystem services as an inclusive social metaphor for the analysis and management of environmental conflicts in Colombia. Ecosyst. Serv. 2019, 37, 100924. [Google Scholar] [CrossRef]
- Koornneef, J.; Faaij, A.; Turkenburg, W. The screening and scoping of environmental impact assessment and strategic environmental assessment of carbon capture and storage in the Netherlands. Environ. Impact Assess. Rev. 2008, 28, 392–414. [Google Scholar] [CrossRef]
- Nguyen, A.T.; Vu, A.D.; Dang, G.T.H.; Hoang, A.H.; Hens, L. How do local communities adapt to climate changes along heavily damaged coasts? A Stakeholder Delphi study in Ky Anh (Central Vietnam). Environ. Dev. Sustain. 2018, 20, 749–767. [Google Scholar] [CrossRef]
| Linguistic Variables | Fuzzy Numbers |
|---|---|
| Extreme importance (EXI) | (7; 9; 9) |
| Very strong importance (VSI) | (5; 7; 9) |
| Strong importance (SI) | (3; 5; 7) |
| Moderate importance (MI) | (1; 3; 5) |
| Equal importance (EI) | (1; 1; 1) |
| Criteria of Sectors | Decision Matrices | C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 |
|---|---|---|---|---|---|---|---|---|---|
| C1 (Agriculture) | DM1 | EI | VSI | EI | MI | MI | SI | EXI | SI |
| DM2 | EI | SI | MI | VSI | VSI | (MI) | (SI) | SI | |
| DM3 | EI | SI | EI | SI | EXI | SI | SI | VSI | |
| DM4 | EI | (MI) | MI | SI | SI | (SI) | (SI) | (MI) | |
| DM5 | EI | MI | EI | SI | VSI | (SI) | (MI) | (MI) | |
| C2 (Aquaculture) | DM1 | (VSI) | EI | (SI) | (MI) | EI | EI | VSI | MI |
| DM2 | (SI) | EI | (MI) | SI | SI | (SI) | (VSI) | MI | |
| DM3 | (SI) | EI | (MI) | MI | EXI | EI | SI | VSI | |
| DM4 | MI | EI | SI | VSI | SI | (SI) | (SI) | (MI) | |
| DM5 | (MI) | EI | (MI) | MI | MI | (VSI) | (VSI) | (SI) | |
| C3 (Fishing) | DM1 | SI | EI | EI | EI | MI | SI | EXI | VSI |
| DM2 | MI | (MI) | EI | SI | VSI | (SI) | (SI) | SI | |
| DM3 | MI | EI | EI | SI | SI | MI | SI | VSI | |
| DM4 | (SI) | (MI) | EI | MI | EI | (VSI) | (SI) | (SI) | |
| DM5 | MI | EI | EI | MI | SI | (SI) | (SI) | (MI) | |
| C4 (Salt production) | DM1 | MI | (MI) | EI | EI | MI | SI | EXI | VSI |
| DM2 | (SI) | (VSI) | (SI) | EI | MI | (VSI) | (EXI) | (MI) | |
| DM3 | (MI) | (SI) | (SI) | EI | SI | (SI) | EI | MI | |
| DM4 | (VSI) | (SI) | (MI) | EI | (MI) | (EXI) | (VSI) | (SI) | |
| DM5 | (MI) | (SI) | (MI) | EI | MI | (EXI) | (VSI) | (SI) | |
| C5 (Tourism) | DM1 | EI | (MI) | (MI) | (MI) | EI | MI | VSI | SI |
| DM2 | (SI) | (VSI) | (VSI) | (MI) | EI | (EXI) | (EXI) | (SI) | |
| DM3 | (EXI) | (EXI) | (SI) | (SI) | EI | (VSI) | (SI) | (MI) | |
| DM4 | (SI) | (SI) | EI | MI | EI | (EXI) | (VSI) | (SI) | |
| DM5 | (MI) | (VSI) | (SI) | (MI) | EI | (EXI) | (EXI) | (VSI) | |
| C6 (Forestry) | DM1 | EI | (SI) | (SI) | (SI) | (MI) | EI | SI | MI |
| DM2 | SI | MI | SI | VSI | EXI | EI | (MI) | VSI | |
| DM3 | EI | (SI) | (MI) | SI | VSI | EI | SI | SI | |
| DM4 | SI | SI | VSI | EXI | EXI | EI | MI | MI | |
| DM5 | VSI | SI | SI | EXI | EXI | EI | MI | SI | |
| C7 (Settlement) | DM1 | (VSI) | (EXI) | (EXI) | (EXI) | (VSI) | (SI) | EI | (MI) |
| DM2 | VSI | SI | SI | EXI | EXI | MI | EI | EXI | |
| DM3 | (SI) | (SI) | (SI) | EI | SI | (SI) | EI | EI | |
| DM4 | SI | SI | SI | VSI | VSI | (MI) | EI | EI | |
| DM5 | VSI | MI | SI | VSI | EXI | (MI) | EI | EI | |
| C8 (Industry) | DM1 | (MI) | (SI) | (VSI) | (VSI) | (SI) | (MI) | MI | EI |
| DM2 | (MI) | (SI) | (SI) | MI | SI | (VSI) | (EXI) | EI | |
| DM3 | (VSI) | (VSI) | (VSI) | (MI) | MI | (SI) | EI | EI | |
| DM4 | MI | MI | SI | SI | SI | (MI) | EI | EI | |
| DM5 | SI | MI | MI | SI | VSI | (SI) | EI | EI |
| V | S(C1) | S(C2) | S(C3) | S(C4) | S(C5) | S(C6) | S(C7) | S(C8) | d’ | Weight (w) | Ranking |
|---|---|---|---|---|---|---|---|---|---|---|---|
| S(C1)≥ | - | 0.97 | 0.99 | 1.00 | 1.00 | 0.96 | 0.98 | 1.00 | 0.96 | 0.129 | 2 |
| S(C2)≥ | 1.00 | - | 1.00 | 1.00 | 1.00 | 0.99 | 1.00 | 1.00 | 0.99 | 0.125 | 5 |
| S(C3)≥ | 1.00 | 0.98 | - | 1.00 | 1.00 | 0.97 | 0.99 | 1.00 | 0.97 | 0.127 | 4 |
| S(C4)≥ | 0.98 | 0.94 | 0.96 | - | 1.00 | 0.93 | 0.95 | 0.99 | 0.93 | 0.121 | 7 |
| S(C5)≥ | 0.95 | 0.91 | 0.93 | 0.98 | - | 0.89 | 0.92 | 0.96 | 0.89 | 0.116 | 8 |
| S(C6)≥ | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | - | 1.00 | 1.00 | 1.00 | 0.131 | 1 |
| S(C7)≥ | 1.00 | 0.99 | 1.00 | 1.00 | 1.00 | 0.98 | - | 1.00 | 0.98 | 0.128 | 3 |
| S(C8)≥ | 0.99 | 0.96 | 0.98 | 1.00 | 1.00 | 0.94 | 0.96 | - | 0.94 | 0.123 | 6 |
| Alternative Sites | Decision Matrices | C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 |
|---|---|---|---|---|---|---|---|---|---|
| A1 (Beach area) | DM1 | L | VH | H | H | M | M | L | VL |
| DM2 | VL | VH | VH | VH | H | M | VL | L | |
| DM3 | VL | VH | VH | H | M | VH | VL | L | |
| DM4 | VL | L | L | M | VL | M | M | VL | |
| DM5 | M | VH | VH | VH | VH | H | M | H | |
| A2 (Protected forest area) | DM1 | L | M | H | L | L | M | VL | VL |
| DM2 | L | H | L | VL | H | VH | L | VL | |
| DM3 | L | VL | VL | L | M | VH | M | M | |
| DM4 | L | M | L | M | VL | VH | M | L | |
| DM5 | L | M | M | VL | H | VH | VL | VL | |
| A3 (Agricultural area) | DM1 | M | M | L | M | VL | L | VL | L |
| DM2 | VH | M | L | M | M | M | VH | L | |
| DM3 | VH | M | VL | L | VL | L | H | M | |
| DM4 | VH | M | M | H | L | M | L | L | |
| DM5 | VH | H | H | VL | M | L | L | L | |
| A4 (Settlement area) | DM1 | VL | L | M | VL | L | L | H | L |
| DM2 | M | VL | VL | M | M | H | VH | M | |
| DM3 | M | L | L | M | L | M | VH | M | |
| DM4 | M | L | M | L | L | L | VH | M | |
| DM5 | H | VL | VL | M | L | M | VH | M | |
| A5 (Industrial area) | DM1 | M | M | VH | M | M | VH | VL | VL |
| DM2 | VL | VL | VL | VL | VL | L | VH | VH | |
| DM3 | VL | VL | M | L | L | M | VH | VH | |
| DM4 | L | VL | M | M | L | VL | M | VH | |
| DM5 | VL | L | L | H | VL | VL | H | VH |
| Criteria of Sectors | A1 (Beach Area) | A2 (Protected Forest Area) | A3 (Agricultural Area) | A4 (Settlement Area) | A5 (Industrial Area) | Weight (w) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C1 | 0.04 | 0.13 | 0.35 | 0.00 | 0.22 | 0.43 | 0.57 | 0.78 | 1.00 | 0.22 | 0.39 | 0.61 | 0.04 | 0.13 | 0.35 | 0.129 |
| C2 | 0.55 | 0.77 | 1.00 | 0.23 | 0.41 | 0.64 | 0.27 | 0.50 | 0.73 | 0.00 | 0.14 | 0.36 | 0.05 | 0.14 | 0.36 | 0.125 |
| C3 | 0.52 | 0.76 | 1.00 | 0.14 | 0.33 | 0.57 | 0.14 | 0.33 | 0.57 | 0.10 | 0.24 | 0.48 | 0.24 | 0.43 | 0.67 | 0.127 |
| C4 | 0.52 | 0.76 | 1.00 | 0.05 | 0.19 | 0.43 | 0.19 | 0.38 | 0.62 | 0.14 | 0.33 | 0.57 | 0.19 | 0.38 | 0.62 | 0.121 |
| C5 | 0.44 | 0.69 | 1.00 | 0.31 | 0.56 | 0.88 | 0.13 | 0.31 | 0.63 | 0.06 | 0.38 | 0.69 | 0.06 | 0.25 | 0.56 | 0.116 |
| C6 | 0.35 | 0.57 | 0.78 | 0.57 | 0.78 | 1.00 | 0.09 | 0.30 | 0.52 | 0.17 | 0.39 | 0.61 | 0.17 | 0.30 | 0.52 | 0.131 |
| C7 | 0.08 | 0.21 | 0.42 | 0.08 | 0.21 | 0.42 | 0.21 | 0.38 | 0.58 | 0.58 | 0.79 | 1.00 | 0.38 | 0.54 | 0.75 | 0.128 |
| C8 | 0.09 | 0.22 | 0.43 | 0.04 | 0.13 | 0.35 | 0.04 | 0.26 | 0.48 | 0.17 | 0.39 | 0.61 | 0.52 | 0.70 | 0.91 | 0.123 |
| (a) Separation from Positive Ideal Solution (d+) | |||||||||
| Alternative Sites | Criteria of Sectors | d+ | |||||||
| C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 | ||
| A1 (Beach area) | 0.98 | 0.90 | 0.90 | 0.90 | 0.92 | 0.93 | 0.97 | 0.97 | 7.47 |
| A2 (Protected forest area) | 0.97 | 0.95 | 0.96 | 0.97 | 0.93 | 0.90 | 0.97 | 0.98 | 7.62 |
| A3 (Agricultural area) | 0.90 | 0.94 | 0.96 | 0.95 | 0.96 | 0.96 | 0.95 | 0.97 | 7.58 |
| A4 (Settlement area) | 0.95 | 0.98 | 0.97 | 0.96 | 0.96 | 0.95 | 0.90 | 0.95 | 7.60 |
| A5 (Industrial area) | 0.98 | 0.98 | 0.94 | 0.95 | 0.97 | 0.96 | 0.93 | 0.91 | 7.61 |
| (b) Separation from Negative Ideal Solution (d−) | |||||||||
| Alternative Sites | Criteria of Sectors | d− | |||||||
| C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 | ||
| A1 (Beach area) | 0.03 | 0.10 | 0.10 | 0.10 | 0.09 | 0.08 | 0.04 | 0.04 | 0.56 |
| A2 (Protected forest area) | 0.04 | 0.06 | 0.05 | 0.03 | 0.07 | 0.10 | 0.04 | 0.03 | 0.42 |
| A3 (Agricultural area) | 0.10 | 0.07 | 0.05 | 0.05 | 0.05 | 0.05 | 0.05 | 0.04 | 0.46 |
| A4 (Settlement area) | 0.05 | 0.03 | 0.04 | 0.05 | 0.05 | 0.06 | 0.10 | 0.06 | 0.44 |
| A5 (Industrial area) | 0.03 | 0.03 | 0.06 | 0.05 | 0.04 | 0.05 | 0.07 | 0.10 | 0.43 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dao, M.T.; Nguyen, A.T.; Nguyen, T.K.; Pham, H.T.T.; Nguyen, D.T.; Tran, Q.T.; Dao, H.G.; Nguyen, D.T.; Dang, H.T.; Hens, L. A Hybrid Approach Using Fuzzy AHP-TOPSIS Assessing Environmental Conflicts in the Titan Mining Industry along Central Coast Vietnam. Appl. Sci. 2019, 9, 2930. https://doi.org/10.3390/app9142930
Dao MT, Nguyen AT, Nguyen TK, Pham HTT, Nguyen DT, Tran QT, Dao HG, Nguyen DT, Dang HT, Hens L. A Hybrid Approach Using Fuzzy AHP-TOPSIS Assessing Environmental Conflicts in the Titan Mining Industry along Central Coast Vietnam. Applied Sciences. 2019; 9(14):2930. https://doi.org/10.3390/app9142930
Chicago/Turabian StyleDao, Manh Tien, An Thinh Nguyen, The Kien Nguyen, Ha T.T. Pham, Dinh Tien Nguyen, Quoc Toan Tran, Huong Giang Dao, Duyen T. Nguyen, Huong T. Dang, and Luc Hens. 2019. "A Hybrid Approach Using Fuzzy AHP-TOPSIS Assessing Environmental Conflicts in the Titan Mining Industry along Central Coast Vietnam" Applied Sciences 9, no. 14: 2930. https://doi.org/10.3390/app9142930
APA StyleDao, M. T., Nguyen, A. T., Nguyen, T. K., Pham, H. T. T., Nguyen, D. T., Tran, Q. T., Dao, H. G., Nguyen, D. T., Dang, H. T., & Hens, L. (2019). A Hybrid Approach Using Fuzzy AHP-TOPSIS Assessing Environmental Conflicts in the Titan Mining Industry along Central Coast Vietnam. Applied Sciences, 9(14), 2930. https://doi.org/10.3390/app9142930






