Automated Rediscovery of the Maxwell Equations
Abstract
:Featured Application
Abstract
1. Introduction
…it may be within current computing and algorithmic technology to infer the Maxwell Equations directly from data given knowledge of vector calculus.
2. Preliminaries
2.1. Rapid Enumeration of Candidate Theories Over a Language
2.2. Theory Validation: Fitting Constants
3. Results: Electrodynamics and Light
3.1. The Maxwell Equations
3.2. Observations and the Virtual Experiment
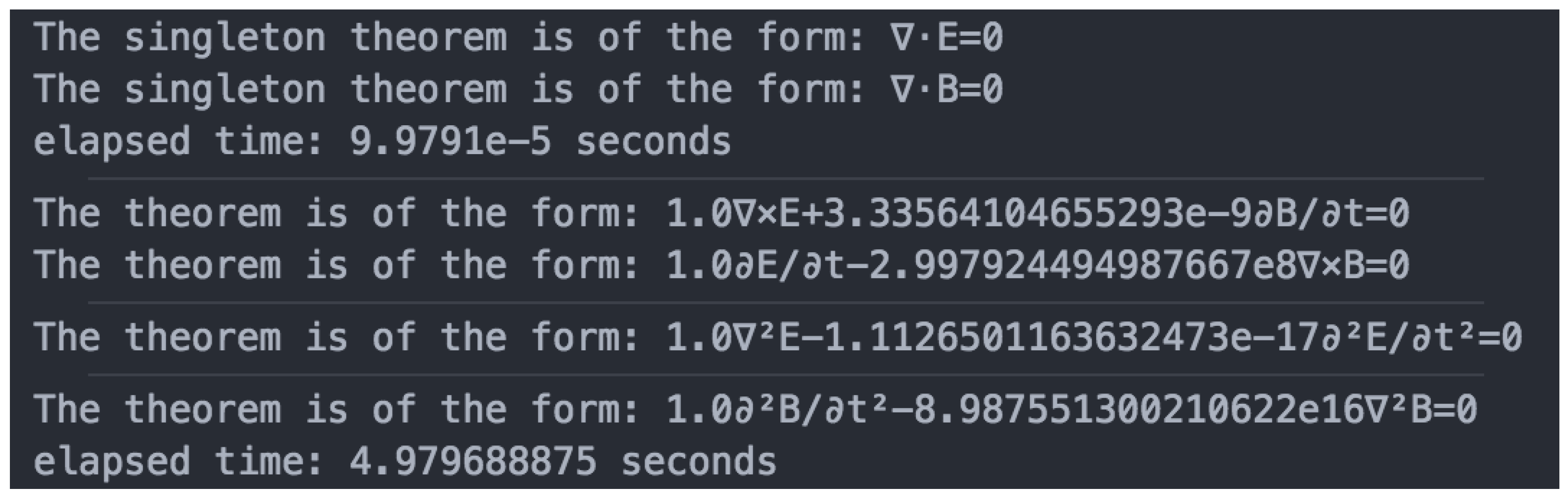
3.3. Rediscovery
4. Concluding Remarks and Future Work
- Expand the enumeration language to allow more expressive theories. Right now TheoSea is limited to theories of the form where the A’s are operators over fields like The Xu ideal gas law code works with scalar fields and exponents. Somehow these should be merged;
- Bigger data and parallelism. The dataset used was very small but semantically very rich. Other datasets, such as for macro-economics, will be far larger. Here Julia’s on-the-fly compilation (of candidate theories) and support for parallel processing will be very helpful, and this is one of the reasons the language was chosen (the author encourages the Julia developers to continue work on threads as the model is natural for multicore processors. For example, the main thread could enumerate candidate theories and then send them to several worker threads for validation. At any instant, several theories would be under consideration);
- Develop methods to work with more noisy data. The current approach works with numerical noise but not measurement noise (Equation (1));
- The fully general Maxwell Equations can be rediscovered just by adding a current and source region The changes to the virtual experiment and language are straightforward;
- Field discovery. The fields are treated as observables. It would be nice if TheoSea could discover the fields from the forces, e.g., . One step is to use a relativistic moving charge q with velocity where the magnetic field can be written in terms of the electric field [13]: Then, the field discovery problem is reduced to finding the electric field and then the magnetic field will fall out from the search.
[Einstein] knew in advance what the theory should look like, and he explored the theories with mathematical tools, not actual experiments.
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Stalzer, M.; Mentzel, C. A Preliminary Review of Influential Works in Data-Driven Discovery; SpringerPlus: Berlin, Germany, 2016. [Google Scholar]
- Stalzer, M. On the enumeration of sentences by compactness. arXiv 2017, arXiv:1706.06975. [Google Scholar]
- Stalzer, M.; Ju, C. TheoSea: Marching theory to light. arXiv 2017, arXiv:1708.04927. [Google Scholar]
- Maxwell, J.C. A dynamical theory of the electromagnetic field. Philo. Trans. R. Soc. Lond. 1865, 155, 459–512. [Google Scholar]
- Langley, P. Rediscovering physics with BACON.3. Proc. Int. Jt. Conf. Artif. Intell. 1979, 152, 505–507. [Google Scholar]
- Xu, W.; Stalzer, M. Deriving compact laws based on algebraic formulation of data set. arXiv 2017, arXiv:1706.05123. [Google Scholar] [CrossRef]
- Schmidt, M.; Lipson, H. Distilling free-form natural laws from experimental data. Science 2009, 324, 81–85. [Google Scholar] [CrossRef] [PubMed]
- Bezanson, J.; Edelman, A.; Karpinski, S.; Shah, V.B. Julia: A fresh approach to numerical computing. SIAM Rev. 2017, 59, 65–98. [Google Scholar] [CrossRef]
- Denning, P.J.; Dennis, J.B.; Qualitz, J.E. Machines, Languages, and Computation; Prentice-Hall: Upper Saddle River, NJ, USA, 1978. [Google Scholar]
- Borel, E. Mécanique statistique et irréversibiliité. J. Phys. 1913, 53, 189–196. [Google Scholar]
- Korf, R.E. Depth-First Iterative-Deepening: An optimal admissible tree search. Artif. Intell. 1985, 27, 97–109. [Google Scholar] [CrossRef]
- Griffiths, D.J. Introduction to Electrodynamics, 4th ed.; Pearson Education: London, UK, 2015. [Google Scholar]
- Fitzpatrick, R. Maxwell’s Equations and the Principles of Electromagnetism; Firewall Media: New York, NY, USA, 2008. [Google Scholar]
- Ju, C.; Stalzer, M. Finding exact forms on thermodynamic manifolds. arXiv 2018, arXiv:1808.03863v2. [Google Scholar]
- Dirac, P.A.M. The Principles of Quantum Mechanics; Oxford University Press: Oxford, UK, 1967. [Google Scholar]
- Hamming, R.W. The unreasonable effectiveness of mathematics. Am. Math. Mon. 1980, 87, 81–90. [Google Scholar] [CrossRef]
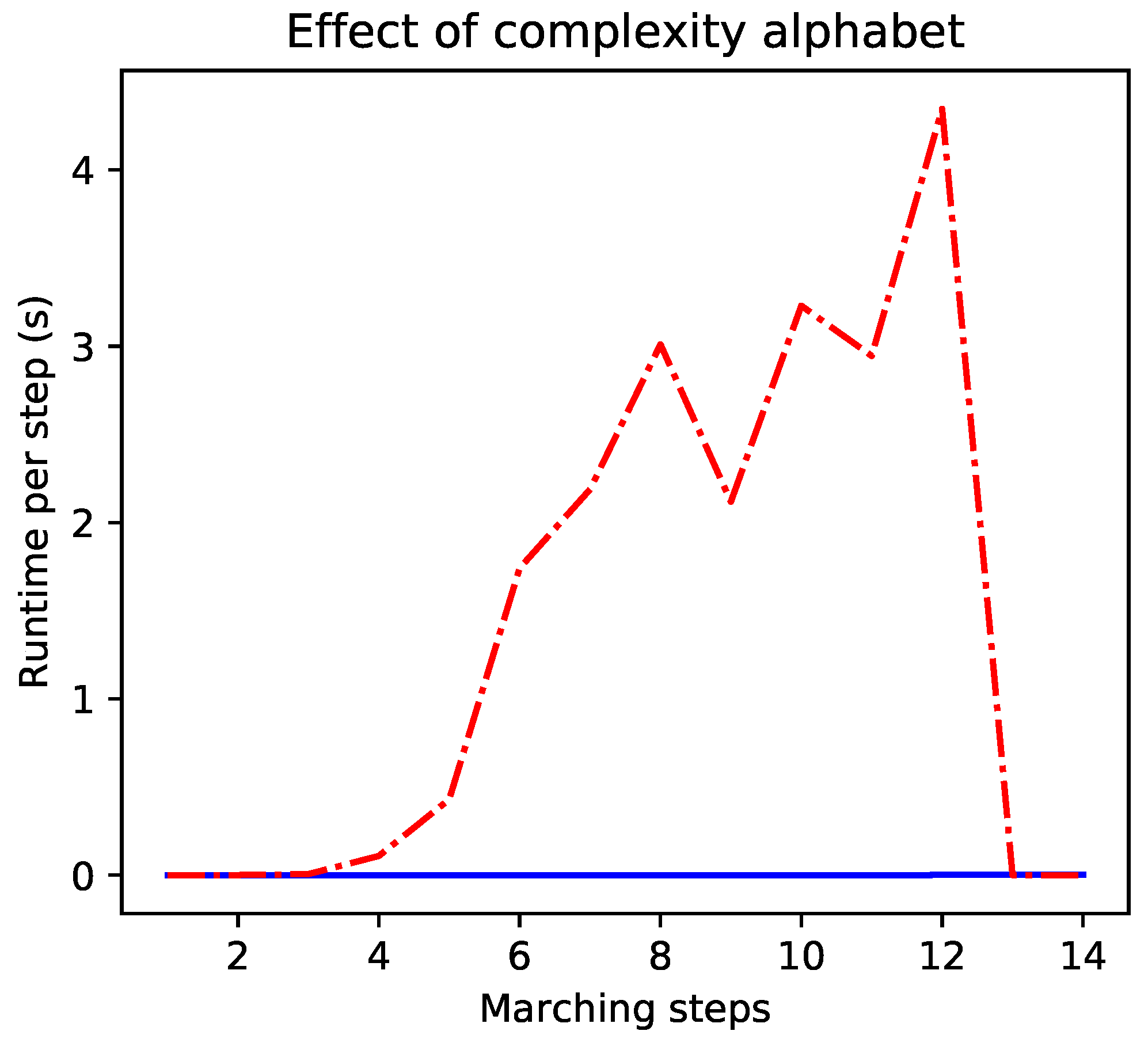


| Operator | Term Cost | Alphabet |
|---|---|---|
| 1 | A, B | |
| 4 | C, D | |
| 4 | E, F | |
| 7 | G, H | |
| 19 | I, J | |
| 19 | K, L |
| 1 | 0.905 | 0.997 | (2.713, 3.455, −6.793) | (−6.363, 4.996, 0) |
| 1 | 2.767 | 2.908 | (2.018, −0.794, −0.516) | (−0.816, −2.074, 0) |
| 1 | 4.631 | 0.291 | (−0.214, −2.639, −0.793) | (2.754, −0.224, 0) |
| 1 | 5.597 | 3.051 | (−0.666, 0.546, −0.078) | (0.548, 0.669, 0) |
| 1 | 0.468 | 2.369 | (−4.299, −2.170, −4.690) | (−3.029, 6.001, 0) |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stalzer, M.; Ju, C. Automated Rediscovery of the Maxwell Equations. Appl. Sci. 2019, 9, 2899. https://doi.org/10.3390/app9142899
Stalzer M, Ju C. Automated Rediscovery of the Maxwell Equations. Applied Sciences. 2019; 9(14):2899. https://doi.org/10.3390/app9142899
Chicago/Turabian StyleStalzer, Mark, and Chao Ju. 2019. "Automated Rediscovery of the Maxwell Equations" Applied Sciences 9, no. 14: 2899. https://doi.org/10.3390/app9142899
APA StyleStalzer, M., & Ju, C. (2019). Automated Rediscovery of the Maxwell Equations. Applied Sciences, 9(14), 2899. https://doi.org/10.3390/app9142899





