1. Introduction
Electric power distribution system with multifarious topologies, configurations, and characteristics is one of the salient components of a power system. In most developing countries, increasing demand for electrical energy enforces distribution systems for an increasingly expansion and broadening. For any expansion, power energy quality and efficiency require special attention of control, improvement, and management. One of the most effective factors in an electric power energy quality is voltage deviation and stability. Extension of a network length and expansion of topology can be associated with the risk of statutory and standard limit [
1]. Kabul is a densely populated and capital city of Afghanistan that distribution networks suffer unstable-rated operation. These networks are extended without length limitation consideration, which demonstrates unstable voltage beyond the statutory range with huge technical and economic losses. In recent years, the government of Afghanistan bounded to retain environmental protection and sustainable development in accordance with the Paris Agreement 2015 (combat climate change), and Sustainable Development Goals (SDGs) 2030. Reform of the energy sector has been part of this endeavor. Afghanistan’s distribution networks are the least developed and old-fashioned part of the power system. In addition to the technical and financial losses, shortage of access to electric energy has led to increased utilization of primary energy resources and fossil fuel with high environmental impact. Meanwhile, distribution systems to remote areas are extended without expandability capacity (in local and regional networks) consideration. In priority, it must seriously consider and adopt appropriate solutions. The effective delivery of power to the end users can be achieved by improving reliability, efficiency, cost-effectiveness, and sustainability measures of production and distribution [
2].
Various investigations using different optimization techniques, methods, and solutions are conducted to regulate voltage and reduce energy losses in a distribution system. In [
3], multiobjective optimization of auto-tap-changer pole transformer with respect to minimizing the voltage deviation of a 16-bus distribution network was tested. In [
4], a coordinated control of distributed energy storage system (ESS) with traditional voltage regulators including on-load tap changer transformers (OLTC) and step voltage regulators (SVR) was applied. Authors of [
5] proposed data fusion theory to develop a comparative diagnostic method to determine the operation status of on-load tap changers mechanism. A study was carried out in [
6] to enhance power quality with automatic tap change in transformer in a smart grid distribution system. In [
7], an implementation of a prototype electronic tap-changer instead of mechanical tap-changer was proposed. This method was demonstrated with some shortcomings, such as low operating speed, short lifetime, and heavy size. In [
8], the authors employed a nonlinear dynamic model of OLTC, impedance loads, and decoupled reactive power voltage relations to reconstruct the voltage collapse phenomenon. This method aims to determine operation status of on-load tap changers mechanism. Likewise, in [
9], a network reconfiguration was carried out over two domains simultaneously: Re-switching strategies and transformer tap-changer adjustments. Similarly, several techniques and strategies for voltage stability enhancement and regulation have been applied, using several case studies under different conditions [
10,
11,
12,
13,
14,
15]. This study aims to present a fully solid-state tap-changer solution with a new control strategy and optimal configuration.
Over the past decades, power system blackouts due to voltage instability were repeatedly reported; namely, Tokyo blackout on 23 July 1987 and United Kingdom, Sweden, Canada, Denmark, Italy, and the United States blackouts in 2003 [
16]. Power system voltage stability has been discussed enough over the past decades. In [
17], a control strategy for reactive power compensation using storage system was studied. This study aimed to improve system stability by a proper prediction of reactive behavior and demand for different operation conditions. In [
18], the authors presented the stability analysis using the load and generation levels as a direction vector for the base system through continuation power flow (CPF) under normal condition and contingency. The authors of [
19] proposed a wavelet transform (WT) based on data analysis to extract the features from real-time active power and RMS (root mean square) voltage of the power grid. This study applied a hybrid classification technique based on particle swarm optimization (PSO) and support vector machines (SVM) to classify the features and diagnose different types of faults in a smart grid system.
Previous studies investigated the use of control devices in a variety of ways based on different optimization methods. Most of these studies were focused on required number of control device without considering the optimum placement and number of these devices. The proposed methods can technically be feasible, but economically they are not acceptable. Therefore, reducing number of control devices in a system is another important objective. To solve the trade-off problem, the multiobjective optimization is an excellent tool. Additionally, the increase in tap position changing can reduce contacts lifespan and accelerate deterioration of transformer oil in the switching process [
20]. This paper provides a method of multiobjective optimization of auto-tap-changer pole transformer (ATCTr), in term of optimum number and placement of tap position changes. Meanwhile, a multiobjective optimization using genetic algorithm [
21,
22,
23,
24,
25] is applied to minimize voltage deviation. In
Section 2, characteristics of system model and problem description are discussed.
Section 3 presents the methodology, follows by the simulation result and comparison in
Section 4. At last,
Section 5 concludes simulations findings and briefs novelty and effectiveness of the study.
2. Characteristics of the System Model and Problem Description
The targeted model in this study was located in Kabul city (capital of Afghanistan). Triple energy sectors, generation, transmission, and distribution systems, suffer technical and economic losses. After a long-term political instability and lack of maintenances, Kabul city distribution networks demonstrate many problems; namely, transformer no-load loss, imbalance between primary and secondary distribution systems in terms of power transfer, scattered distribution transformer from gravity center of load, unbalance reactive power and distributed three phase supply, lack of protection devices, long length of customers cables, use of nonstandard equipment, etc. [
26]. Reports pertain 25–40% losses to distribution systems that require a viable solution and proper management of technical and economic losses [
27]. Meanwhile, an increasing population growth forces distribution networks to operate close to their stability limit within maximum expandability [
28]. Definitely, system expansion under stressed voltage control condition has a direct impact on voltage profile and power losses [
29]. For this case study, voltage deviation at distribution level is out of acceptable range; whereas, at the time of peak load demand, it reaches 15% voltage deviation.
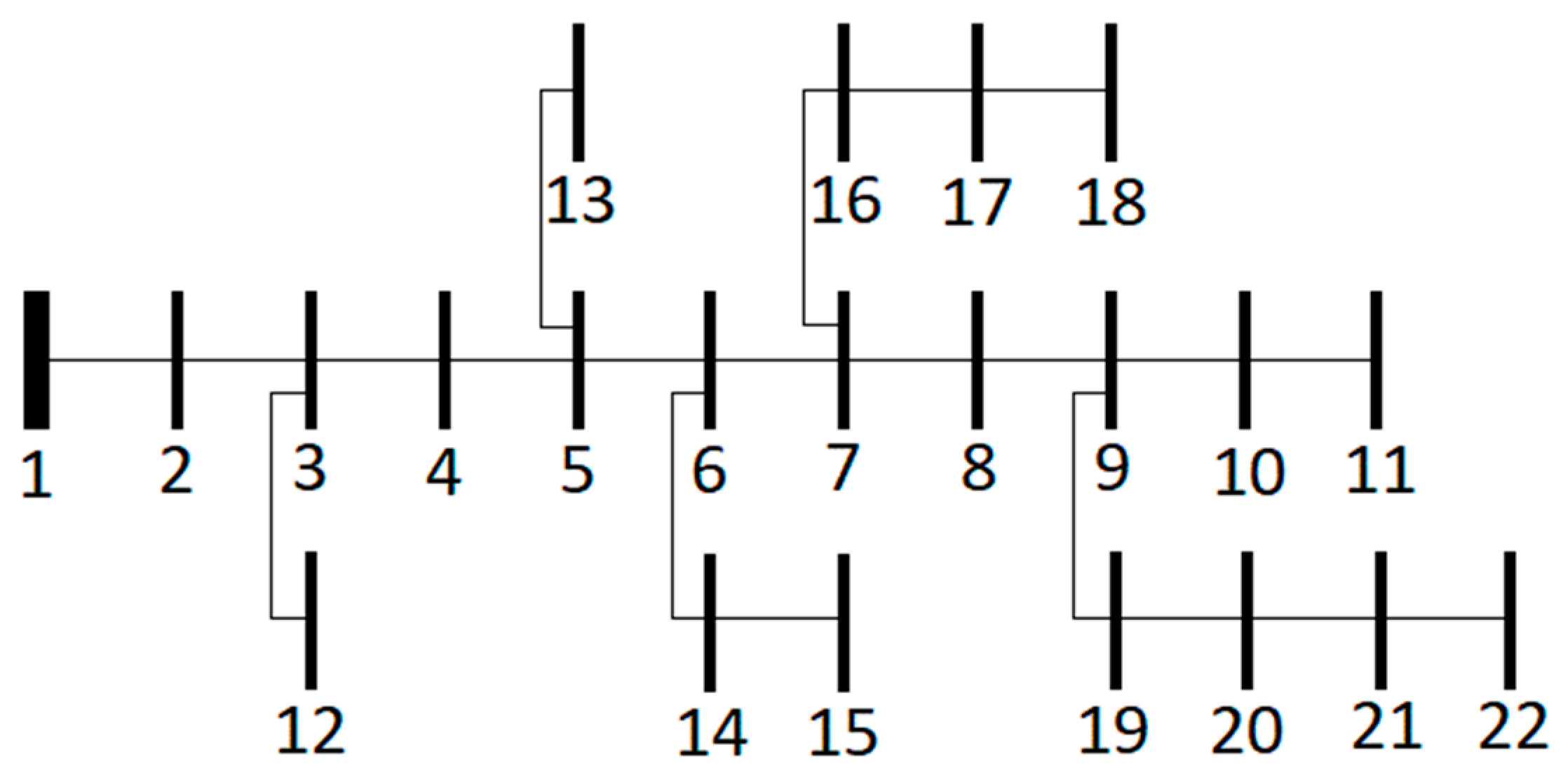
Figure 1 shows the proposed 20 kV distribution system consisting of 22 buses and 21 lines that are considered a real model of simulation.
Table 1 illustrates the mentioned distribution system transmission lines parameters. The proposed model supplies residential, commercial, and industrial consumers. This system consists of transformer stations (TSs) and junction station (JS-6) that feeds from the (110/20 KV, 50 MVA Breshna Kot substation).
4. Simulation Result and Comparison
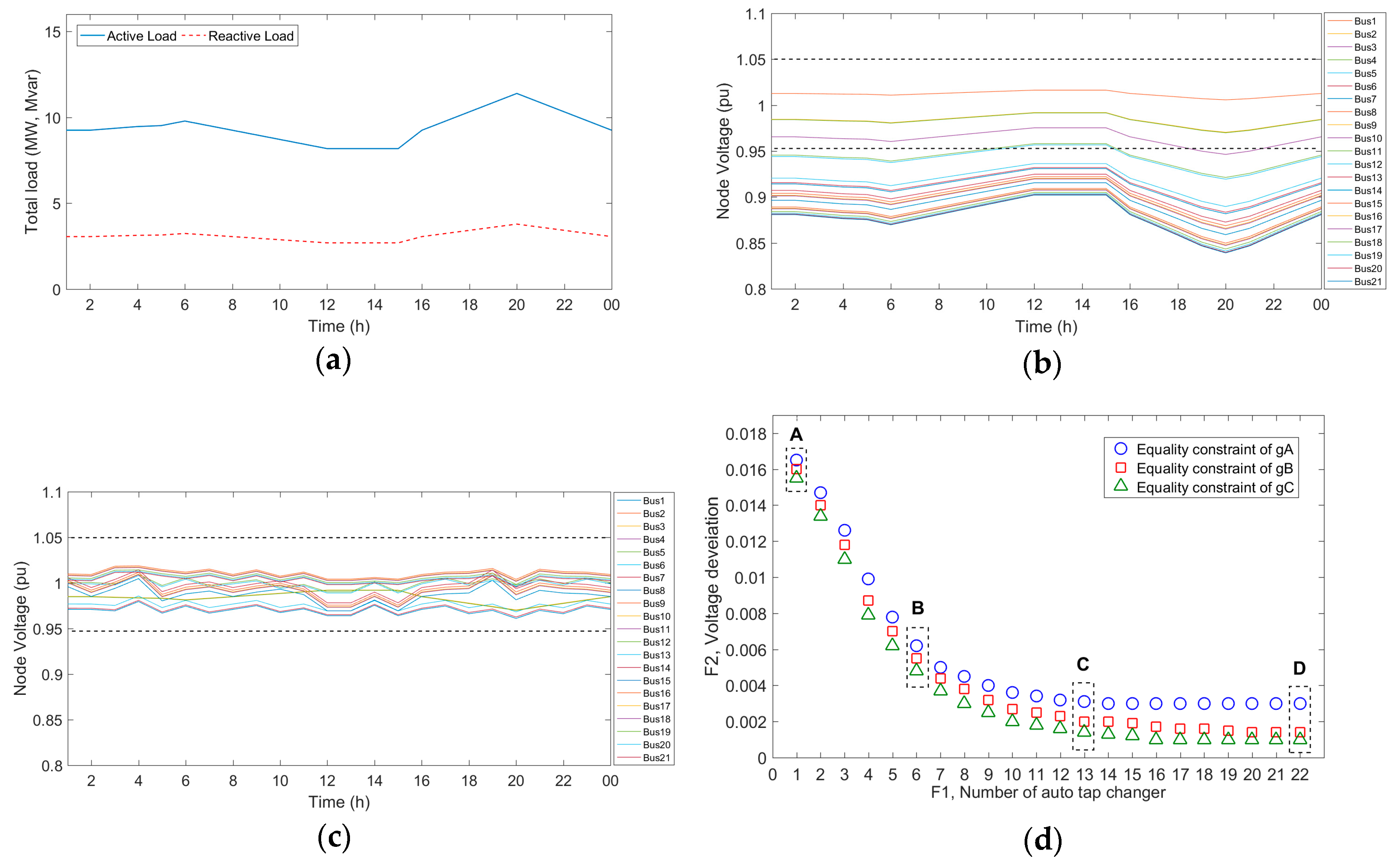
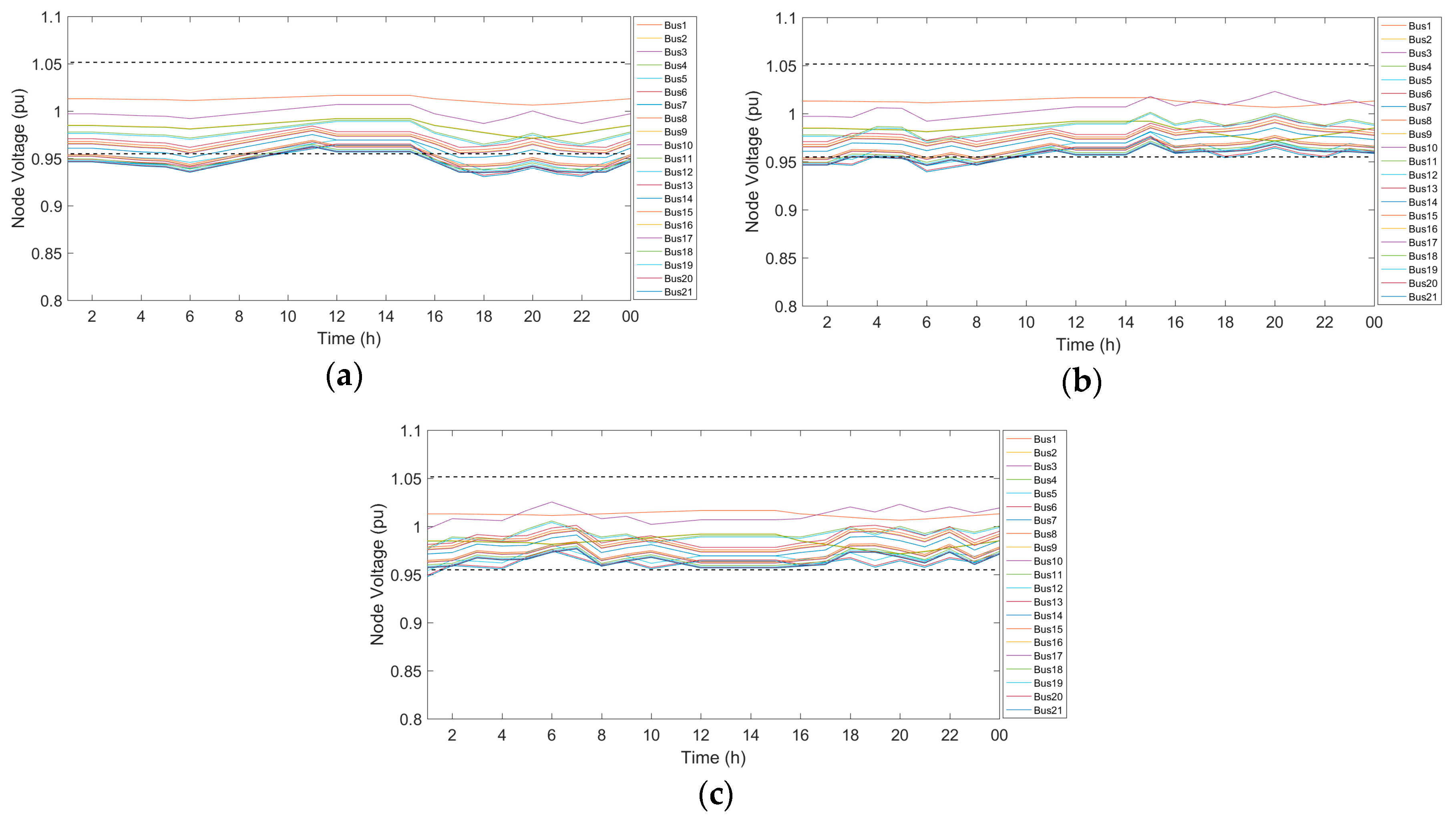
To confirm the effectiveness of introducing ATCTr (with a provision of ±10% change in voltage at 1.25% additional voltage per tap), simulation results based on the physical structure of the current distribution system is shown in
Figure 1.
Proper range for voltage deviation as defined by standard is
pu. The proposed distribution network parameters considering daily load profile and real-time voltage profile of the entire system are plotted in
Figure 4a,b, respectively. This is followed by the distribution voltage magnitude using ATCTrs in
Figure 4c. The number of tap position changes in a 24-h period (
) is 15 times. Moreover, the Pareto optimum solution for minimizing the number of introduced ATCTrs and minimizing of the voltage deviation considering tap position changes is shown in
Figure 4d.
Genetic algorithm (GA) as a multiobjective optimization technique is used to obtain study objectives. Since the number of tap position changes is representative of a rough equipment lifetime, multiobjective optimization was solved for tap position using the number of tap position changes as a parameter (
).
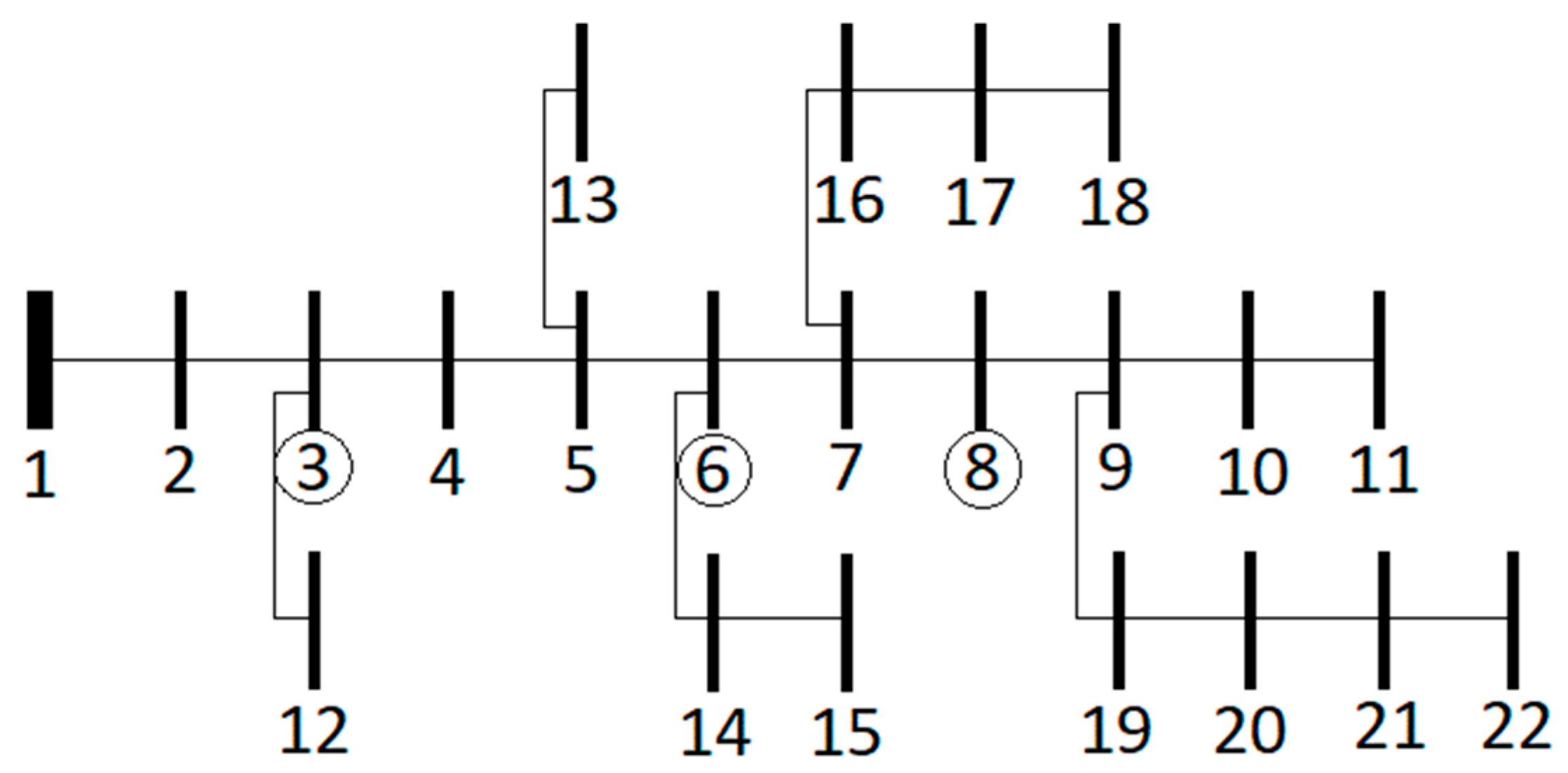
Table 3,
Table 4,
Table 5 and
Table 6 show the location of ATCTrs for the solutions A–D. Pareto optimal solutions are shown in
Figure 4d.
Simulation findings manifest a decisive improvement of voltage profile with stability indicator. Comparison of
Figure 4b, c shows an entire system of stable operation and voltage profile transition from lower than 0.85 pu to more than 0.98 pu. Previous studies relied on optimal placement of control devices; while, this study in addition to optimal placement of control devices (
Table 3,
Table 4,
Table 5 and
Table 6), focused on optimum number of control devices to ensure technical and economic dimensions within a single solution.
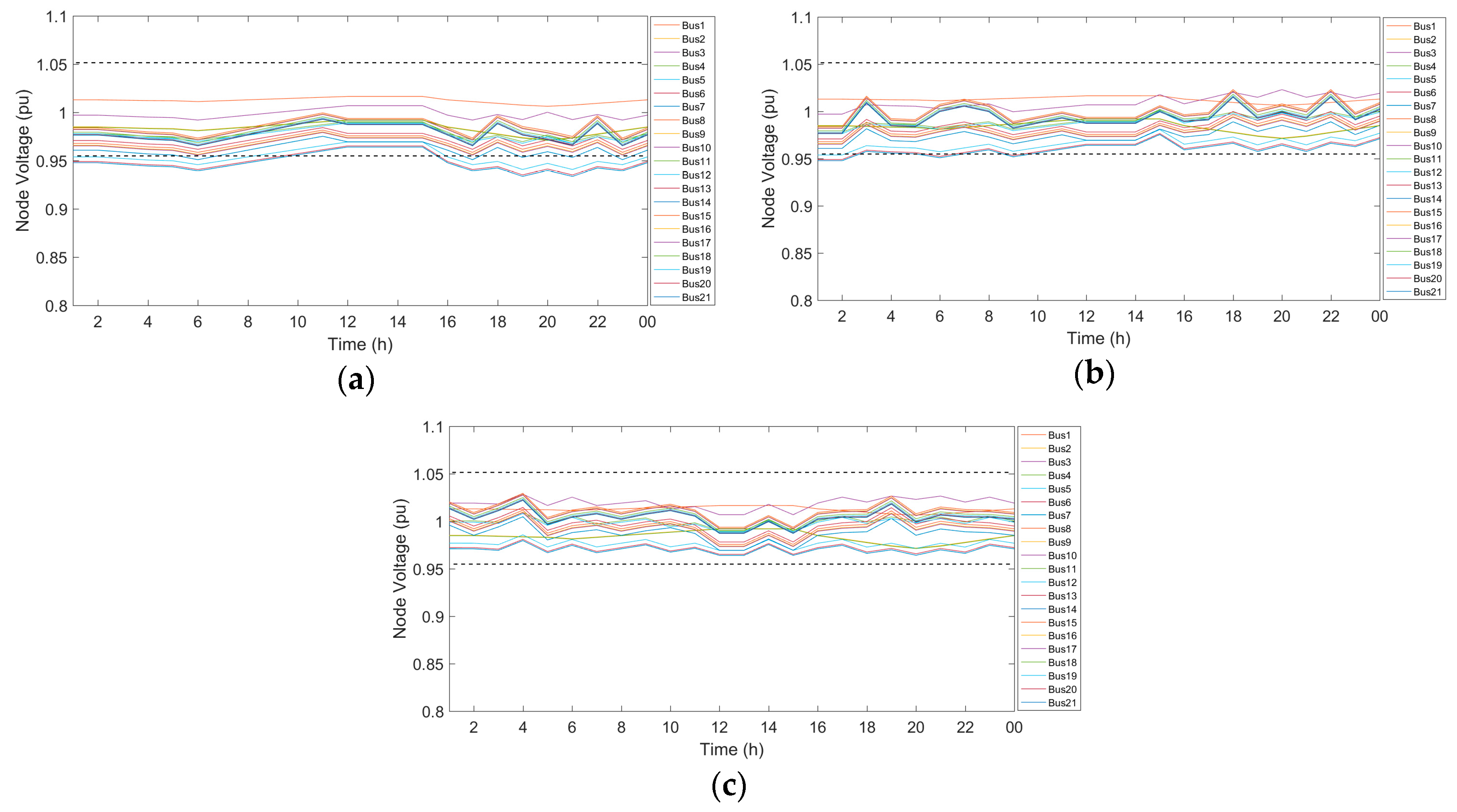
Figure 4d shows the Pareto optimum solution, which indicates the relationship between the number of ATCTrs and voltage deviation. Besides, number of tap position changes have also been considered as an important factor in a rough equipment life time of an ATCTr depreciation. Increasing changing tap position can significantly reduce a contact lifespan, and accelerates deterioration of transformer oil in switching process. Therefore, the control of changing tap potions is a known exigence. As shown in
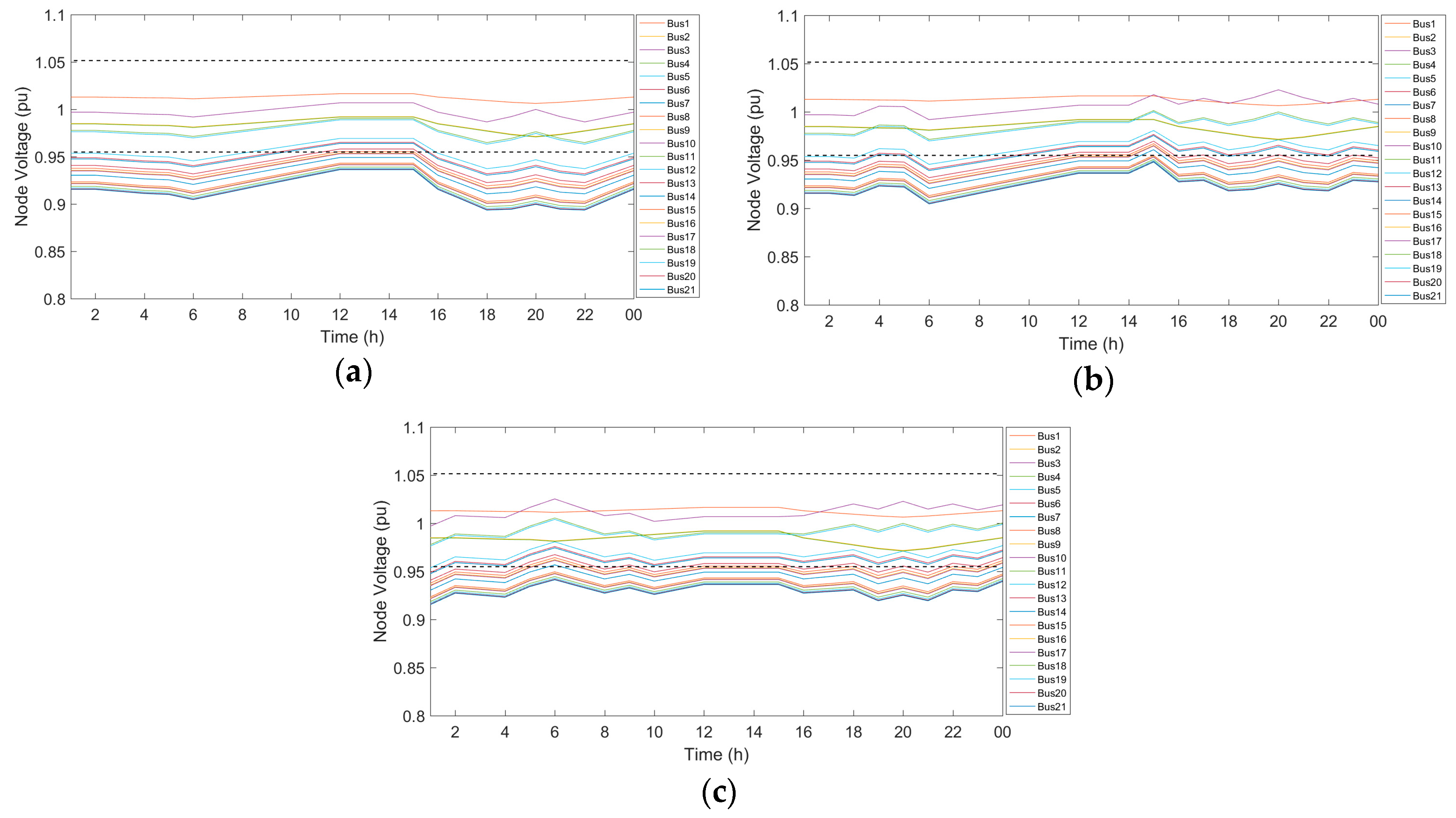
Figure 5,
Figure 6,
Figure 7 and
Figure 8, depending on the equality constraints (
), reducing voltage deviation for constants (
) is very close (almost equal). With automatic control and using
instead of
(in addition to setting voltage) enhances the lifespan of ATCTr.
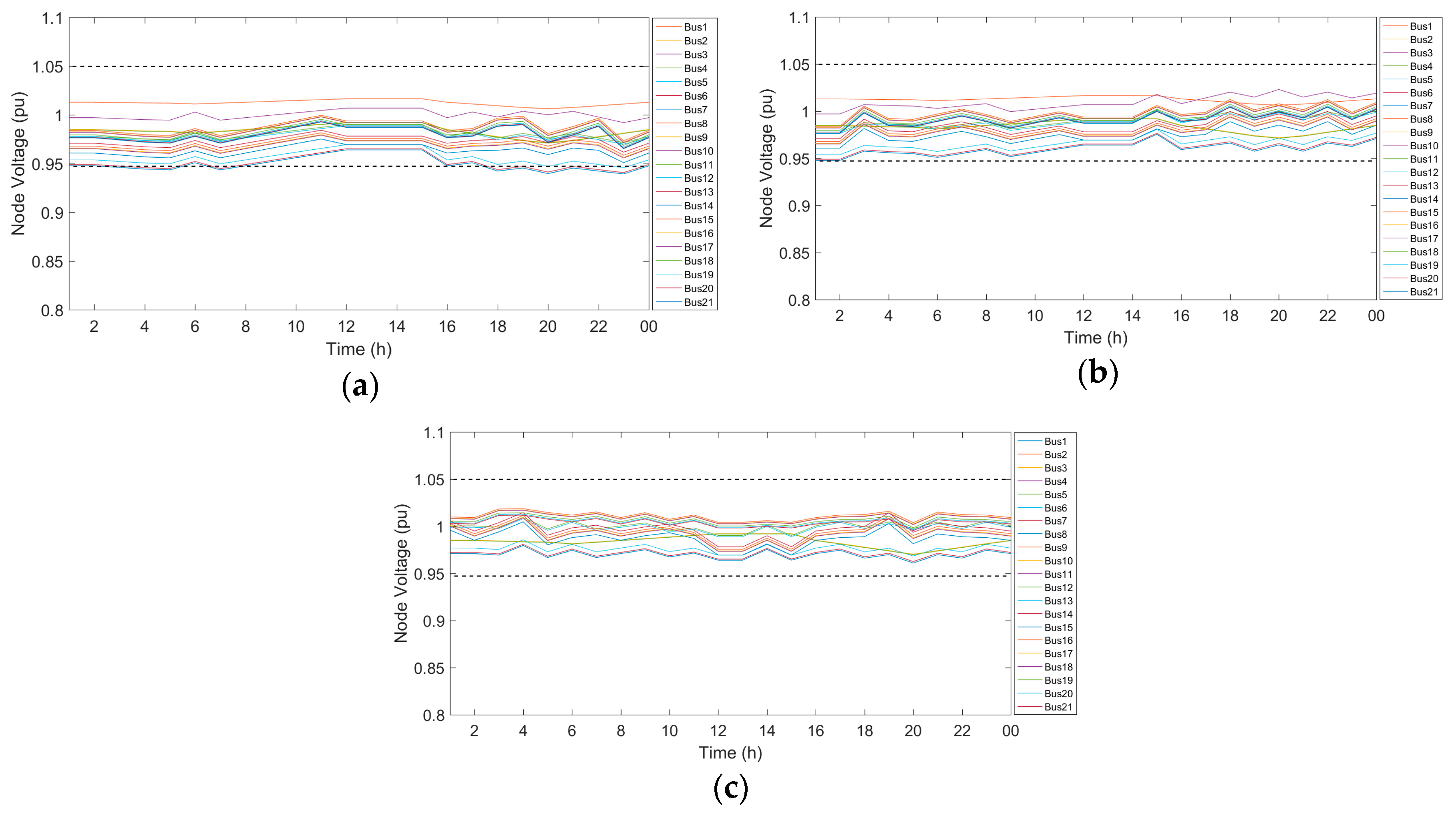
The first column of
Table 7 shows voltage magnitudes for solution A, which shows an increase in accordance with equality constraints (
), respectively. In the second column, by adding the number of ATCTrs in solution B, voltage magnitudes are maintained at statutory limits (
pu). For constant
, voltage is at an acceptable range. In the third column of
Table 7, in addition to maintaining voltage in an appropriate range, a comparison of
and
indicate that voltage values are very close and almost equal (
Figure 7). Furthermore, the fourth column shows the similarity of the voltage magnitudes for constants
and
as well (
Figure 8). Hence, using
is preferred compared to
for ATCTr’s better performances.
For the entire system, the proposed method can improve reinstates busses voltage to rated level and maintain unity behavior among all buses in term of voltage profile. Results indicate that in the presence of the ATCTrs, voltage stability and profile for entire distribution system can be improved. Meanwhile, it can maintain voltage at a proper and statutory range by installing ATCTrs in less than half nodes.