Trajectory Planning and Optimization for a Par4 Parallel Robot Based on Energy Consumption
Abstract
1. Introduction
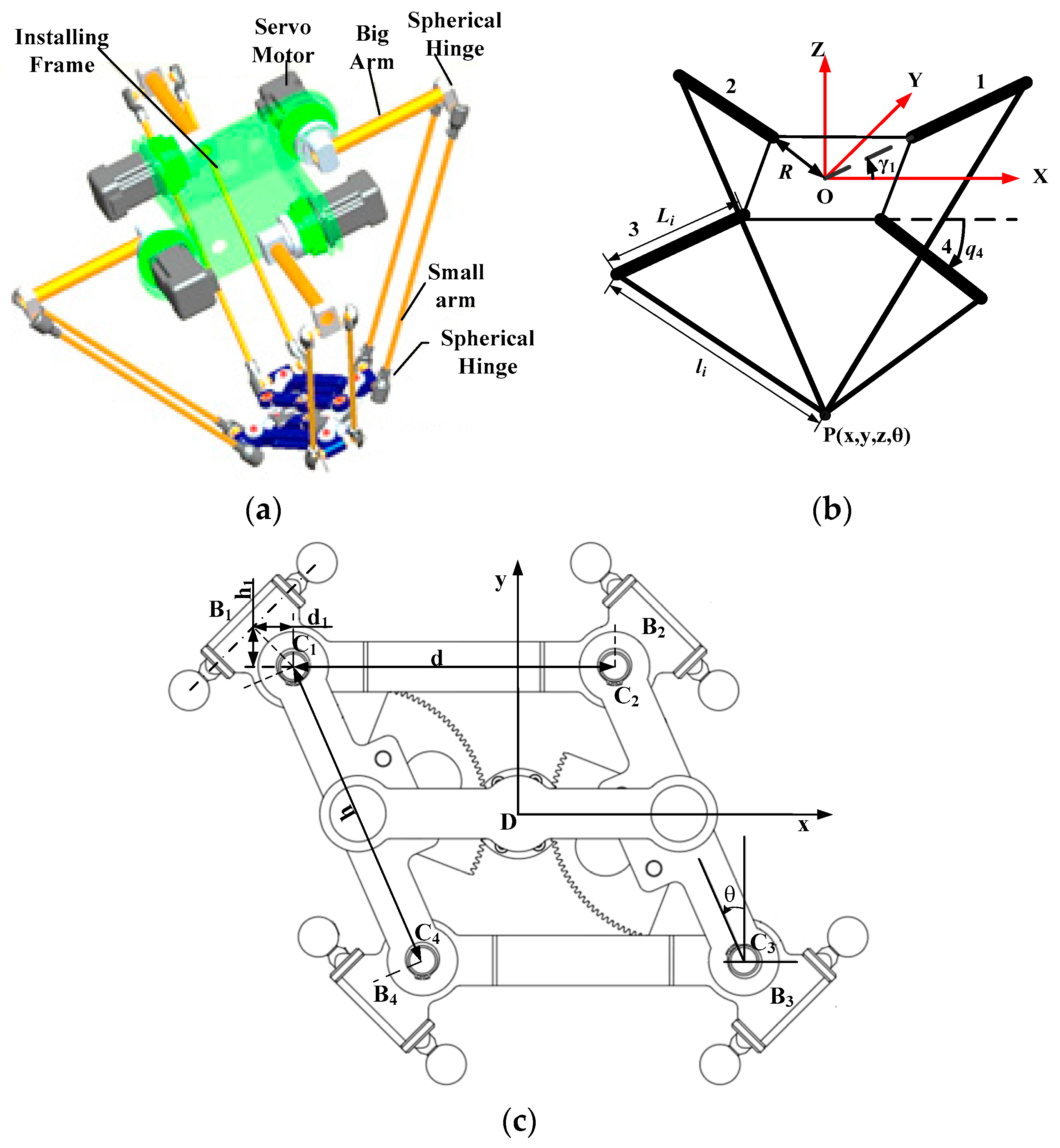
2. Par4 Parallel Robot
2.1. Inverse Kinematics of the Par4 Parallel Robot
2.2. Dynamic Equation of the Par4 Parallel Robot
3. Trajectory Planning of the Par4 Parallel Robot
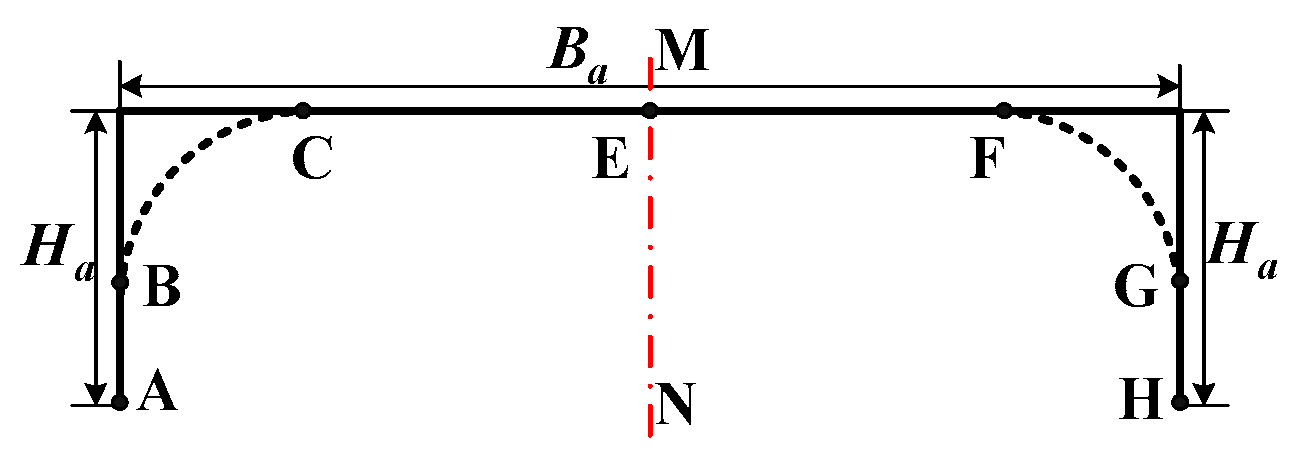
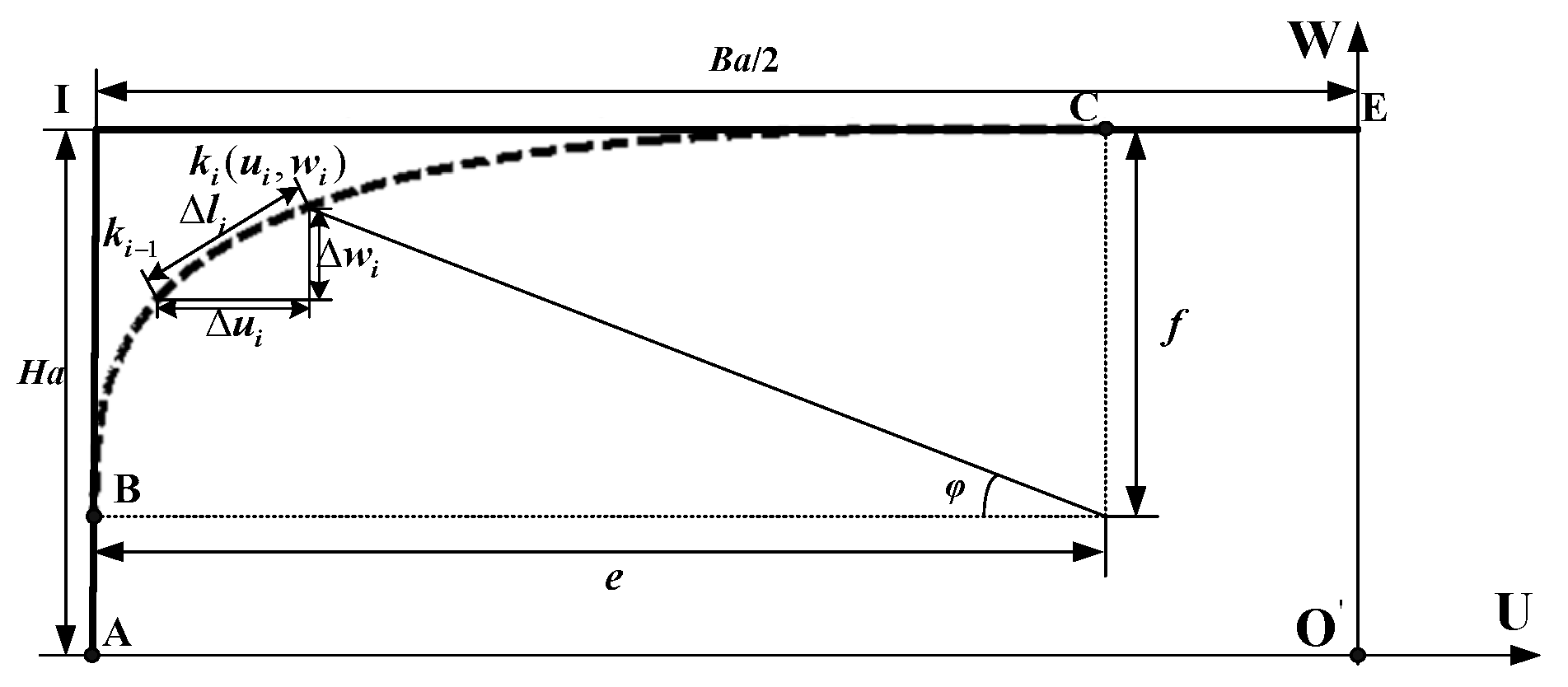
3.1. Trajectory Planning Based on Lamé Curve
3.2. Space-Path Coordinate Transform
3.3. Motion Law Planning
3.3.1. Polynomial Displacement Planning
- Quintic Polynomial Displacement Planning
- Sextic Polynomial Displacement Planning
3.3.2. Piecewise Motion Planning Based on the Lamé Curve
- AB Segment Motion Planning
- 2.
- BC Segment Motion Planning
- Displacement Planning
- Speed Planning
- Acceleration Planning
- 3.
- CF Segment Motion Planning
- 4.
- Other Segment Motion Planning
4. Trajectory Optimization Based on GWO
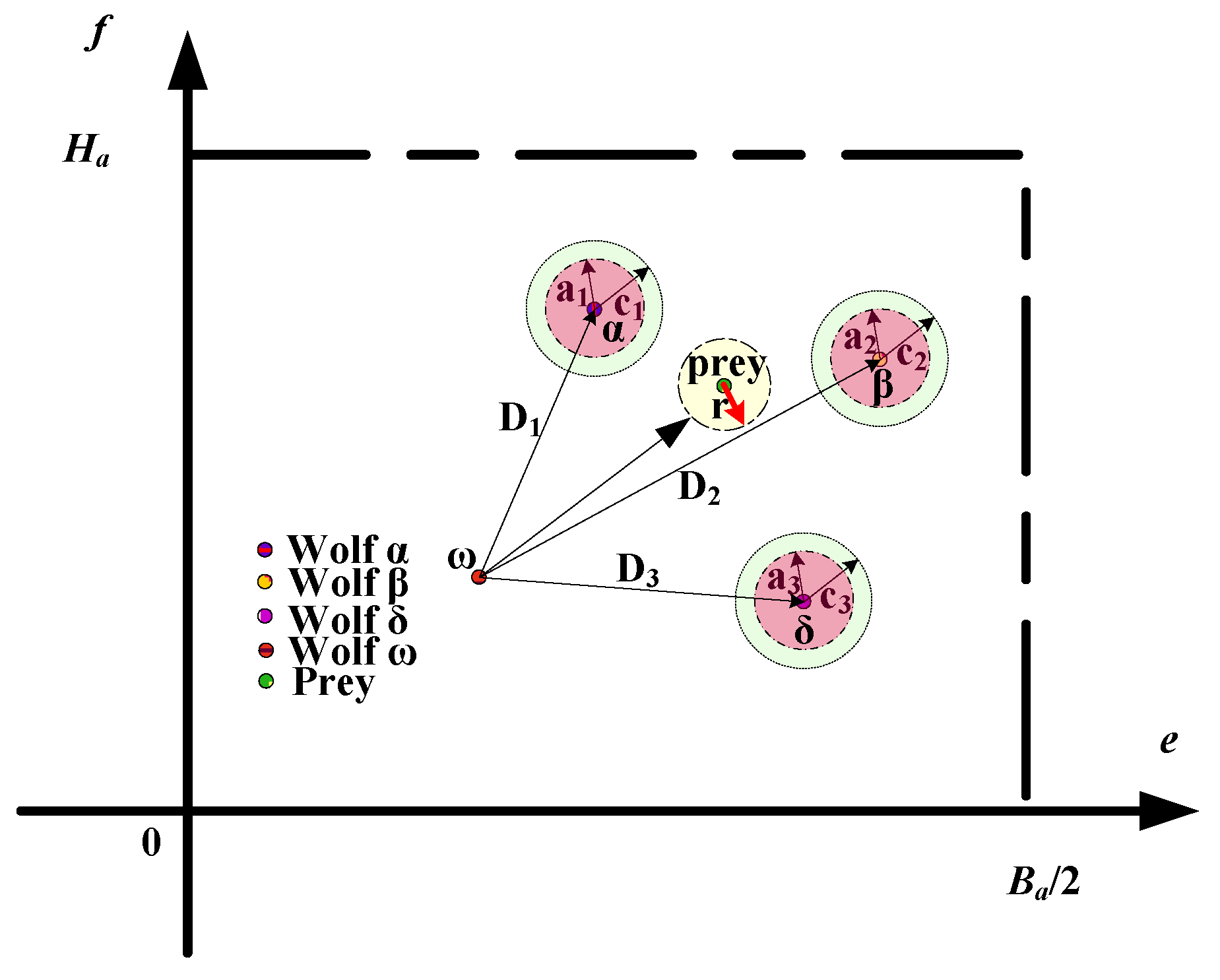
4.1. Grey Wolf Optimizer
4.2. Trajectory Optimization
4.2.1. Mechanical Energy Consumption of the Par4 Parallel Robot
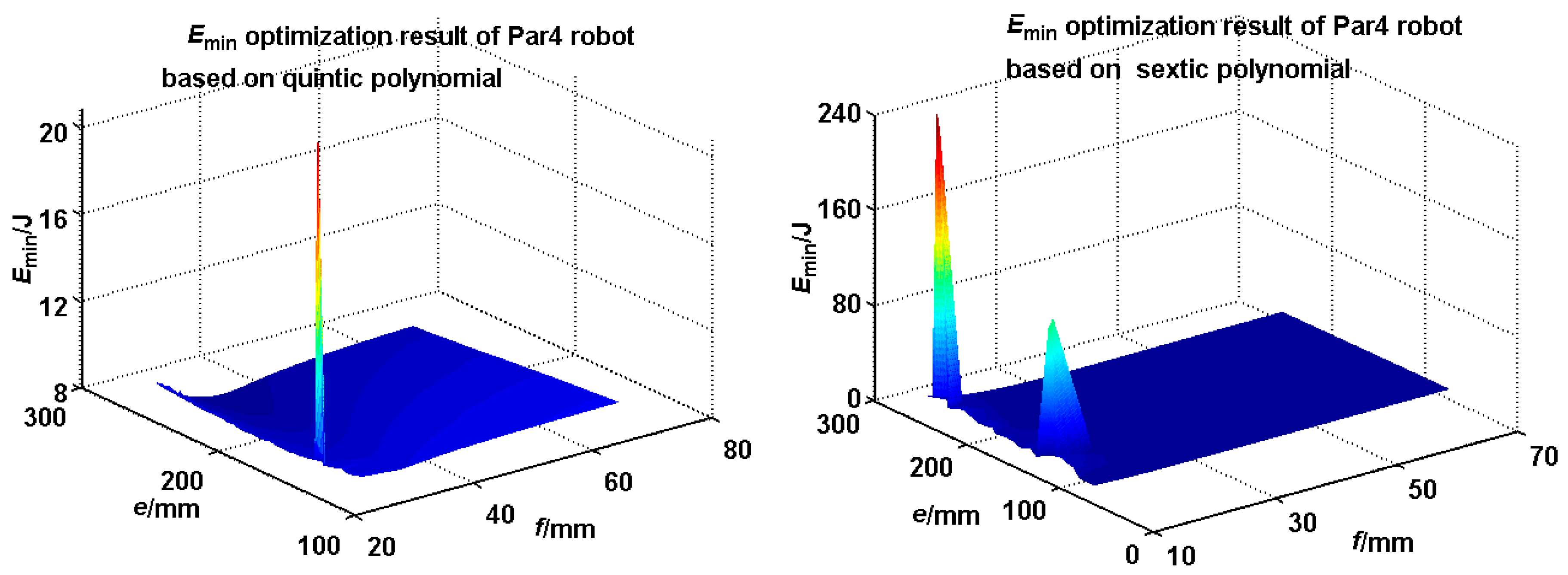
4.2.2. Trajectory Optimization Based on the GWO Algorithm
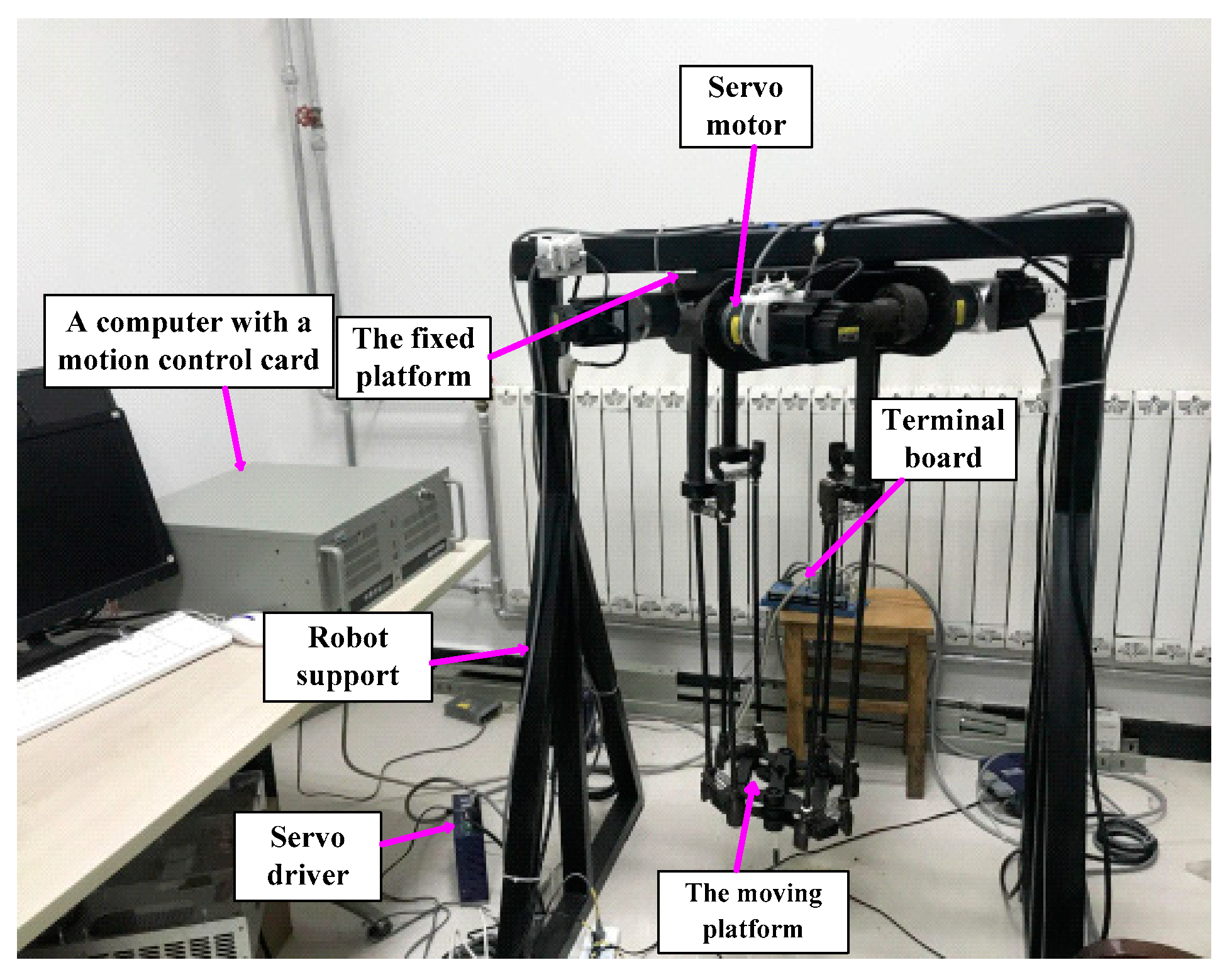
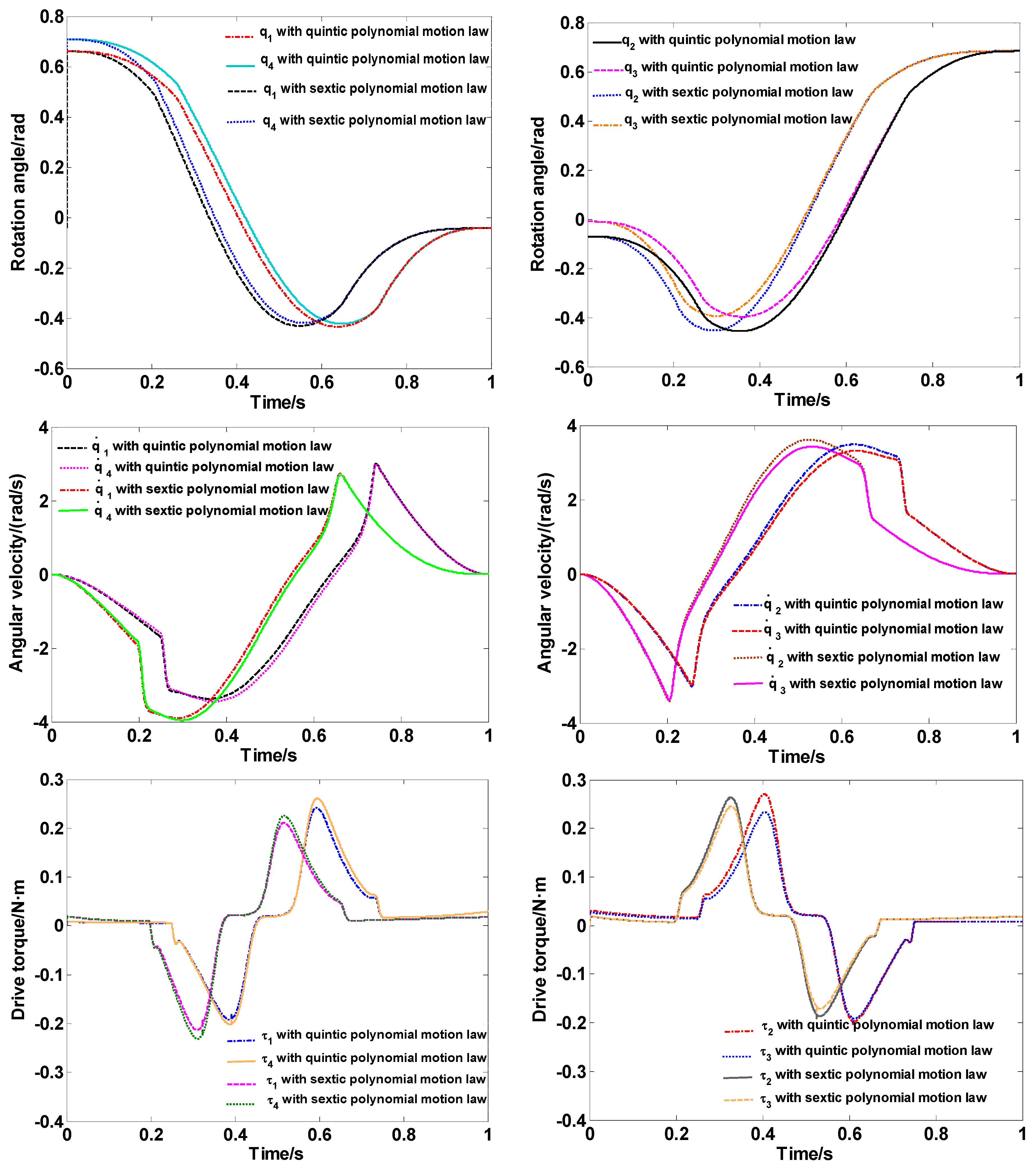
5. Experimental Verification of Trajectory Optimization
5.1. Basic Experiment
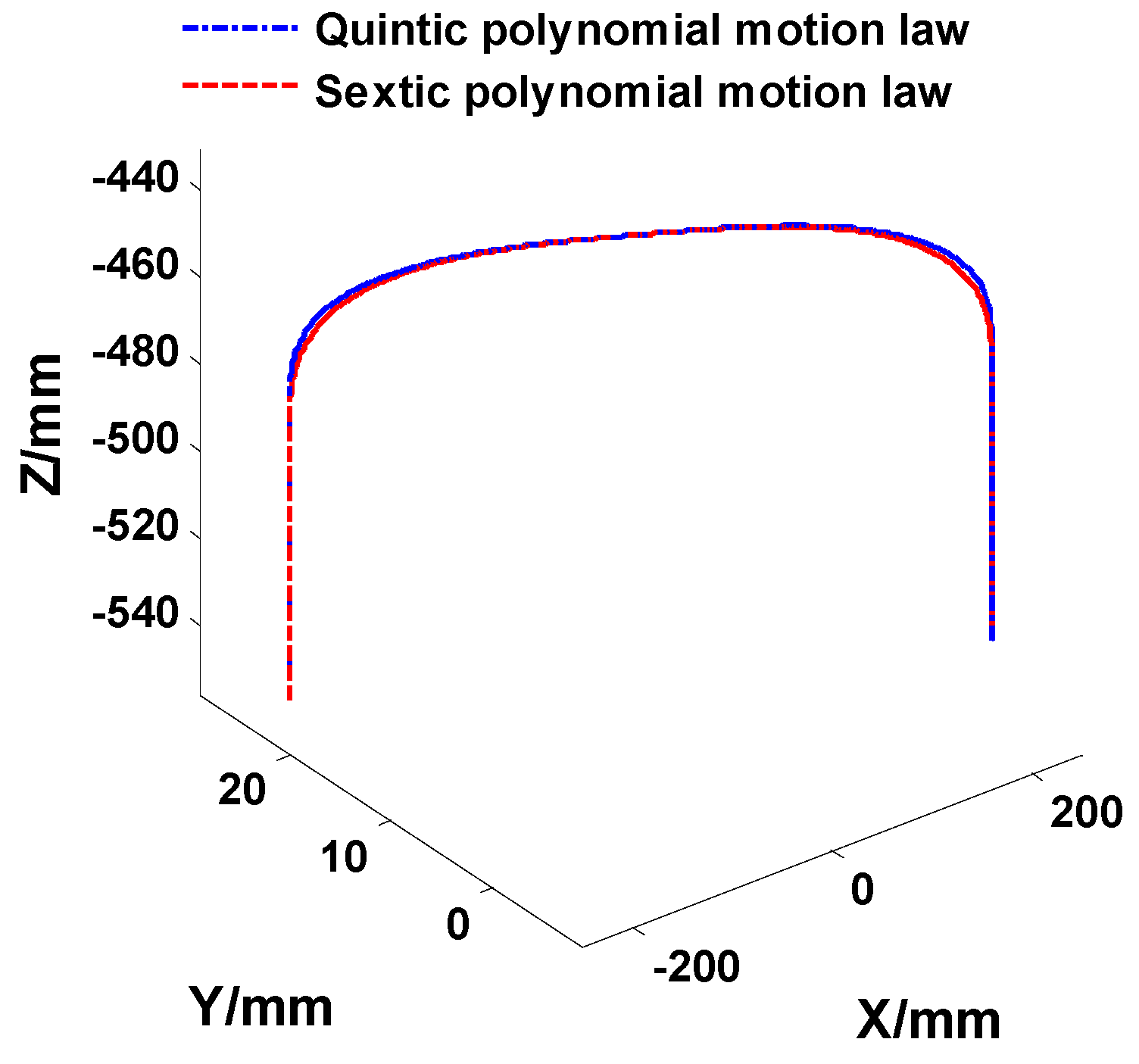
5.2. Experiments with the Same Pick-and-Place Endpoints and Different Pick-Up Heights
5.3. Experiments with Different Pick-and-Place Endpoints and the Same Pick-Up Height and Span
5.4. Experiments with Different Pick-Up Spans, Different Pick-and-Place Endpoints and the Same Pick-Up Height
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Song, X.G.; Zhao, Y.J.; Jin, L.; Zhang, P.; Chen, C.W. Dynamic feedforward control in decoupling space for a four-degree-of-freedom parallel robot. Int. J. Adv. Robot. Syst. 2019, 2, 1–10. [Google Scholar] [CrossRef]
- Sohn, J.W.; Kim, G.W.; Choi, S.B. A State-of-the-Art Review on Robots and Medical Devices Using Smart Fluids and Shape Memory Alloys. Appl. Sci. 2018, 8, 1928. [Google Scholar] [CrossRef]
- Nabat, V.; François, P.; Poignet, P. Dynamic Modeling and Identification of Par4, A Very High Speed Parallel Manipulator. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots & Systems, Beijing, China, 9–15 October 2006. [Google Scholar]
- Staicu, S.; Shao, Z.F.; Zhang, Z.K.; Tang, X.Q.; Wang, L.P. Kinematic analysis of the X4 translational–rotational parallel robot. Int. J. Adv. Robot Syst. 2018, 10, 1–12. [Google Scholar] [CrossRef]
- Sun, T.; Liang, D.; Song, Y.M. Singular-Perturbatio-Based Nonlinear Hybrid Control of Redundant Parallel Robot. IEEE T. Ind. Electron. 2018, 65, 3326–3336. [Google Scholar] [CrossRef]
- Francisco, G.S.; Jorge, O.S.; Raymundo, J.T.; Ricardo, P.P. A stable proportional–proportional integral tracking controller with self-organizing fuzzy-tuned gains for parallel robots. Int. J. Adv. Robot. Syst. 2019, 2, 1–16. [Google Scholar]
- Mohan, S.; Corves, B. Inverse dynamics and trajectory tracking control of a new six degrees of freedom spatial 3-RPRS parallel manipulator. Mech. Sci. 2017, 8, 235–248. [Google Scholar] [CrossRef][Green Version]
- Vincent, R.; Mohammed, T.; Gilles, L. Fast genetic algorithm path planner for fixed-wing military UAV using GPU. IEEE Trans. Aero. Electron. Syst. 2018, 54, 2105–2117. [Google Scholar]
- Farajtabar, M.; Daniali, H.M.; Varedi, S.M. Pick and place trajectory planning of planar 3-RRR parallel manipulator in the presence of joint clearance. Robotica 2017, 35, 241–253. [Google Scholar] [CrossRef]
- Lin, C.J.; Chen, C.T. Reconfiguration for the Maximum Dynamic Wrench Capability of a Parallel Robot. Appl. Sci. 2016, 6, 80. [Google Scholar] [CrossRef]
- Kucuk, S. Optimal trajectory generation algorithm for serial and parallel manipulators. Robot. Cim. Int. Manuf. 2017, 48, 219–232. [Google Scholar] [CrossRef]
- Jiang, X.L.; Barnett, E.; Gosselin, C. Dynamic point-to-point trajectory planning beyond the static workspace for six-dof cable-suspended parallel robots. IEEE Trans. Robot. 2018, 34, 781–793. [Google Scholar] [CrossRef]
- Jiang, X.L.; Gosselin, C. Dynamic point-to-point trajectory planning of a three-dof cable-suspended parallel robot. IEEE Trans. Robot. 2016, 32, 1550–1557. [Google Scholar] [CrossRef]
- Zhang, N.; Shang, W.W.; Cong, S. Geometry-based trajectory planning of a 3-3 cable-suspended parallel robot. IEEE Trans. Robot. 2017, 33, 484–491. [Google Scholar] [CrossRef]
- Chen, Y.D.; Li, L. Predictable trajectory planning of industrial robots with constraints. Appl. Sci. 2018, 8, 2648. [Google Scholar] [CrossRef]
- Jahanpour, J.; Motallebi, M.; Porghoveh, M. A novel trajectory planning scheme for parallel machining Robots enhanced with NURBS curves. J. Intell. Robot. Syst. 2016, 82, 257–275. [Google Scholar] [CrossRef]
- Nan, W.H.; Tang, X.Q.; Song, B. A new automatic motion planning algorithm for a 4-degree-of-freedom parallel kinematic manipulator based on the centre sphere method. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2015, 229, 64–77. [Google Scholar] [CrossRef]
- Chen, Z.H.; Wang, Y.; Ouyang, P.; Huang, J.; Zhang, W.J. A novel iteration-based controller for hybrid machine systems for trajectory tracking at the end-effector level. Robotica 2011, 29, 317–324. [Google Scholar] [CrossRef]
- Mei, J.P.; Zang, J.W.; Qiao, Z.Y.; Liu, S.T.; Song, T. Trajectory planning of 3-DOF Delta parallel manipulator. J. Mech. Eng. 2016, 52, 9–17. [Google Scholar] [CrossRef]
- Bourbonnais, F.; Bigras, P.; Bonev, I.A. Minimum- time trajectory planning and control of a pick-and-place five-bar parallel robot. IEEE/ASME Trans. Mech. 2015, 20, 740–749. [Google Scholar] [CrossRef]
- Bonami, P.; Olivares, A.; Staffetti, E. Energy-optimal multi-goal motion planning for planar robot manipulators. J. Optimiz. Theory App. 2014, 163, 80–104. [Google Scholar] [CrossRef]
- Petrinec, K.; Kovačić, Z. Trajectory planning algorithm based on the continuity of jerk. In Proceedings of the 15th Mediterranean Conference on Control and Automation, Athens, Greece, 27–29 June 2007. [Google Scholar]
- Chen, C.T.; Liao, T.T. Trajectory planning of parallel kinematic manipulators for the maximum dynamic load-carrying capacity. Meccanica 2016, 51, 1653–1674. [Google Scholar] [CrossRef]
- Fares, J.A.; Iyad, F.A.; Rasha, M.A.; Mohamed, A. Statistical evaluation of an evolutionary algorithm for minimum time trajectory planning problem for industrial robots. Int. J. Adv. Manuf. Technol. 2017, 89, 389–406. [Google Scholar]
- Su, T.T.; Cheng, L.; Wang, Y.K.; Liang, X.; Zheng, J.; Zhang, H.J. Time-optimal trajectory planning for Delta robot based on quintic Pythagorean-hodograph curves. IEEE Access. 2018, 6, 28530–28539. [Google Scholar] [CrossRef]
- Abe, A. Minimum energy trajectory planning method for robot manipulator mounted on flexible base. In Proceedings of the 9th Asian Control Conference (ASCC), Istanbul, Turkey, 23–26 June 2013. [Google Scholar]
- Sun, Z.H.; Zhang, B.; Cheng, L.; Zhang, W.J. Application of the redundant servomotor approach to design of path generator with dynamic performance improvement. Mech. Mach. Theory 2011, 46, 1784–1795. [Google Scholar] [CrossRef]
- Zhang, T.; Zhang, W.J.; Gupta, M.M. An underactuated self-reconfigurable robot and the reconfiguration evolution. Mech. Mach. Theory 2018, 124, 248–258. [Google Scholar] [CrossRef]
- Shintaku, E. Minimum energy trajectory for an underwater manipulator and its simple planning method by using a genetic algorithm. Adv. Robot. 1999, 13, 115–138. [Google Scholar] [CrossRef]
- Mo, J.; Shao, Z.F.; Guan, L.W.; Xie, F.G. Dynamic performance analysis of the X4 high-speed pick-and-place parallel robot. Robot. Cim. Int. Manuf. 2017, 46, 48–57. [Google Scholar] [CrossRef]
- Li, Y.H.; Huang, T.; Chetwynd, D.G. An approach for smooth trajectory planning of high-speed pick-and-place parallel robots using quintic B-splines. Mech. Mach. Theory 2018, 126, 479–490. [Google Scholar] [CrossRef]
- Zhang, N.; Shang, W.W.; Cong, S. Dynamic trajectory planning for a spatial 3-DoF cable-suspended parallel robot. Mech. Mach. Theory 2018, 122, 177–196. [Google Scholar] [CrossRef]
- Machmudah, A.; Parman, S.; Zainuddin, A.; Chacko, S. Polynomial joint angle arm robot motion planning in complex geometrical obstacles. Appl. Soft. Comput. 2013, 13, 1099–1109. [Google Scholar] [CrossRef]
- Barnard, C.J.; Briot, S.; Caro, S. Trajectory generation for high speed pick and place robots. In Proceedings of the ASME 2012 11th Biennial Conference on Engineering Systems Design, Nantes, France, 2–4 July 2012. [Google Scholar]
- Six, D.; Briot, S.; Chriette, A.; Martinet, P. The kinematics, dynamics and control of a flying parallel robot with three quadrotors. IEEE Robot. Autom. Lett. 2018, 3, 559–566. [Google Scholar] [CrossRef]
- Gauthier, J.F.; Angeles, J.; Nokleby, S. Optimization of a Test Trajectory for Scara Systems; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Xie, Z.X.; Li, B.; Ren, P. Energy-Based optimization and experimental validation of the pick-and-place trajectories for the delta parallel robot. Comput. Integr. Manuf. 2018, 24, 3073–3081. [Google Scholar]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Zhang, X.Q.; Ming, Z.F. An optimized grey wolf optimizer based on a mutation operator and eliminating-reconstructing mechanism and its application. Front. Inform. Technol. Electron. Eng. 2017, 18, 1705–1719. [Google Scholar] [CrossRef]
- Ali, M.E.; Hassan, M.H. Dynamic global maximum power point tracking of the PV systems under variant partial shading using hybrid GWO-FLC. Sol. Energy 2019, 177, 306–316. [Google Scholar]
- Rao, A.M.; Ramji, K.; Kumar, T.N. Intelligent navigation of mobile robot using grey wolf colony optimization. Mater. Today Proc. 2018, 5, 19116–19125. [Google Scholar]
| Parameter Name | Value |
|---|---|
| Length of big arm Li | 273 mm |
| Length of small arm li | 600 mm |
| Radius of big arm revolute R | 190 mm |
| Length of moving platform along x axis d | 160 mm |
| Length of moving platform along y axis h | 160 mm |
| Distance between Bi and Ci along y axis hi | 20 mm |
| Distance between Bi and Ci along x axis di | 20 mm |
| Load mass of moving platform mc | 0 kg |
| Mass of big arm mb | 0.08 kg |
| Mass of small arm ms | 0.07 kg |
| Mass of moving platform md | 2.6 kg |
| Mass of big arm end connections mend | 0.59 kg |
| Motion Law | e/mm | f/mm | |
|---|---|---|---|
| Quintic polynomial | 250.2 | 32.3 | 8.209 |
| Sextic polynomial | 250.2 | 38.2 | 8.500 |
| Quintic Polynomial | Sextic Polynomial | |||||
|---|---|---|---|---|---|---|
| e/mm | f/mm | e/mm | f/mm | |||
| 100 mm | 250.2 | 32.3 | 8.209 | 250.2 | 38.2 | 8.500 |
| 110 mm | 250.2 | 33.7 | 8.757 | 250.2 | 40.2 | 9.054 |
| 120 mm | 250.2 | 35.4 | 9.323 | 250.2 | 42.3 | 9.628 |
| 130 mm | 250.2 | 37.1 | 9.912 | 250.2 | 44.6 | 10.224 |
| 140 mm | 250.2 | 38.7 | 10.528 | 250.2 | 47.1 | 10.847 |
| 150 mm | 250.2 | 40.5 | 11.178 | 250.2 | 50.0 | 11.503 |
| Motion Law/Pick-and-Place Points | Quintic Polynomial | Sextic Polynomial | |||||
|---|---|---|---|---|---|---|---|
| e/mm | f/mm | e/mm | f/mm | ||||
| [−200,237.6] | [150,−120] | 250.2 | 39.2 | 9.445 | 250.2 | 50.3 | 9.566 |
| [−250,20] | [250,0] | 250.2 | 35.4 | 9.323 | 250.2 | 42.3 | 9.628 |
| [20,20] | [360,387.2] | 250.2 | 120.0 | 11.266 | 250.2 | 120 | 12.515 |
| [−10,−20] | [−260,−453.5] | 250.2 | 120.0 | 15.142 | 250.0 | 120 | 15.167 |
| [0,200] | [−400,−100.7] | 250.2 | 120.0 | 10.954 | 250.2 | 120 | 10.963 |
| Motion Law/Pick-and-Place Points | Quintic Polynomial | Sextic Polynomial | ||||||
|---|---|---|---|---|---|---|---|---|
| Ba/2/mm | e/mm | f/mm | e/mm | f/mm | ||||
| [80,30] | [30,−20] | 35.4 | 35.4 | 81.5 | 7.283 | 35.3 | 76.8 | 7.287 |
| [75,55] | [−35,150] | 72.7 | 72.7 | 120 | 7.746 | 72.7 | 120 | 7.744 |
| [150,50] | [−50,20] | 101.1 | 101.1 | 120 | 7.883 | 101.1 | 120 | 7.878 |
| [300,0] | [−10,75] | 159.5 | 159.5 | 120.0 | 7.721 | 159.5 | 120 | 7.711 |
| [−210,50] | [150,235] | 202.4 | 202.4 | 37.0 | 8.852 | 202.4 | 40.8 | 8.890 |
| [0,−305] | [0,396.7] | 350.9 | 350.9 | 63.3 | 11.048 | 350.9 | 76.5 | 11.124 |
| average | 8.422 | 8.439 | ||||||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Ming, Z. Trajectory Planning and Optimization for a Par4 Parallel Robot Based on Energy Consumption. Appl. Sci. 2019, 9, 2770. https://doi.org/10.3390/app9132770
Zhang X, Ming Z. Trajectory Planning and Optimization for a Par4 Parallel Robot Based on Energy Consumption. Applied Sciences. 2019; 9(13):2770. https://doi.org/10.3390/app9132770
Chicago/Turabian StyleZhang, Xiaoqing, and Zhengfeng Ming. 2019. "Trajectory Planning and Optimization for a Par4 Parallel Robot Based on Energy Consumption" Applied Sciences 9, no. 13: 2770. https://doi.org/10.3390/app9132770
APA StyleZhang, X., & Ming, Z. (2019). Trajectory Planning and Optimization for a Par4 Parallel Robot Based on Energy Consumption. Applied Sciences, 9(13), 2770. https://doi.org/10.3390/app9132770





