1. Introduction
For many years, composites have been used for a variety of applications, such as mechanical, aerospace, and civil engineering structures [
1,
2,
3]. However, the dynamic behavior of composite structures has not been widely investigated: composite structures are slender and light compared with steel and concrete structures, and their dynamic behavior may be entirely different. Understanding this behavior is crucial to the effective application of composite materials in structural engineering [
1,
4,
5,
6]. Thus, it is very important to study the dynamic behavior of composite structures in response to changes in material-specific factors (e.g., lamination fiber angles). The structural design process, demand, and the reliability of numerical analysis usually require the optimization of the shape, size, and/or placement of fibers within the material. However, this approach increases the difficulty and complexity of the design process [
7] since the design of optimized composite laminate is combined with the search for the best fiber orientation in each layer of composite material. The optimization procedure of laminated composite structures is usually more complex than the one associated with isotropic material structures because of the large number of variables involved and the intrinsic anisotropic behavior of individual layers [
8,
9].
In optimization problems associated with the design of a composite structure, two scenarios are possible [
7,
10]: (i) a constant–stiffness design in which the lamination parameters are constant over the whole domain; (ii) a variable–stiffness design in which the lamination parameters may vary in a continuous manner over the domain. The constant–stiffness design scenario is simpler than the variable–stiffness design since there are generally fewer design variables involved [
7]. In this study, a constant–stiffness design is applied for a one-segment shell structure, in which the same stacking layup is used over the whole structure, and a variable–stiffness design is applied for a three-segment shell, in which a different stacking layup is used in segments.
In many engineering problems involving dynamic phenomena, the optimization of selected parameters is necessary. Such optimization is usually performed through the minimization or maximization of a carefully selected
objective function that describes the distance of particular structure parameters from their desired values (e.g., overall mass, strength, or fundamental natural frequency). The objective function is usually repeatedly solved during the optimization procedure. Moreover, the application of first-order optimization algorithms also involves derivatives of the objective function. In composite laminate design, the precise calculation or even approximation of objective function derivatives is often computationally costly or, in some cases, even impossible. One of the advantages of direct search algorithms (or zero-order optimization algorithms, e.g., Genetic Algorithms, GAs) is that they require only objective function values; no information about the gradient of the objective function is necessary. The single calculation of the objective function is neither difficult nor time-consuming. However, it is extremely computationally demanding when it has to be repeated thousands of times (e.g., when a zero-order search algorithm is applied). Artificial Neural Networks (ANNs) are employed to reduce this demand [
11,
12]. The task of objective function calculation is herein improved and accelerated by using ANN as a tool to replace the Finite Element Method (FEM) for the prediction of dynamic parameters. The authors of [
13] considered a reliability problem for laminated four-ply composite plates in free vibration. The design variables were the material properties, stacking sequence, and thickness of the plies, and the goal of the procedure was to obtain a fundamental natural frequency that was higher than the assumed excitation frequency. The application of neural networks shortened the computation time in the considered problem by more than 40%. Neural networks, trained and tested in advance with FE data almost instantly provide their precise prediction from a big set of candidate solutions, and a GA optimization procedure involving ANNs is thus highly efficient and robust.
In the proposed technique, GA was included to solve the optimization task because functions that describe the dynamic parameters to be optimized have several variables and usually a great number of minima. GA ignores potential local minima and leads to the best solution. This paper presents the maximization of the fundamental natural frequency by determining the optimal fiber orientation in a cylindrical shell’s layers of composite material. The lamination fiber angles are treated as constrained variables that are either continuous or discrete. In the context of improving anti-resonance performance, the maximization of the natural frequency of a structure is a primary task in engineering dynamics because it provides the optimal solution to the resonance problem for all external excitation frequencies between zero and the particular optimum fundamental eigenfrequency. Optimization with respect to higher-order eigenfrequencies produces a considerable gap between the specified excitation frequency and the adjacent lower and upper eigenfrequencies. In the offshore oil and gas exploitation industry, risers are indispensable components that are vulnerable to vortex-induced vibration. Vortex-induced vibration strictly depends on the natural frequencies of the risers, so there is a need for optimizing the design of fiber reinforced polymer composite risers by considering different laminate stacking sequences and different lamina thicknesses [
14,
15]. This approach grants the possibility of avoiding resonance if external excitation frequencies are confined to a large interval with finite lower and upper limits [
16].
The optimization of the layer stacking sequence of composite structures (plates, panels, cylinders, beams) for the maximization of their fundamental frequency has been analyzed by many authors. Using the weighted summation method, the authors in [
11] presented a multi-objective optimization strategy for the optimal stacking sequence of laminated cylindrical panels with respect to the first natural frequency and critical buckling load. In order to improve the speed of the optimization process, ANNs were used to reproduce the behavior of the structure in both free vibration and buckling conditions. In [
17], the authors reported the optimization of laminated cylindrical panels based on the fundamental natural frequency.
In [
18], a study of layer optimization was carried out for the maximum fundamental frequency of laminated composite plates under a combination of three classical edge conditions. The optimal stacking sequences of laminated composite plates were found by means of a GA and ANN procedure. The procedure successfully predicted the natural frequencies of the composite plates, and the predicted frequencies and optimal layered sequences corresponded with those of the Ritz-based layerwise optimization method.
The usual goal in the design of vibrating structures is to avoid resonance of the structure in a given interval of external excitation frequencies. This was discussed in [
16], in which the design objective was the maximization of specific eigenfrequencies and distances (gaps) between two consecutive eigenfrequencies of the structures. The results demonstrated that the creation of structures with multiple optimum eigenfrequencies is the rule rather than the exception in topology optimization of vibrating structures. The study emphasized that this feature needs special attention.
The structural optimization problem of laminated composite materials with a reliability constraint was addressed in [
19] by using GA and two types of ANNs. The optimization process was performed using GA, and a Multilayer Perceptron or Radial Basis ANNs were applied to overcome high computational costs. This methodology can be used without loss of accuracy and with large computational time-savings (even when dealing with nonlinear behavior).
As a new concept, a Layerwise Optimization Approach (LOA) to optimizing vibration behavior for the maximum natural frequency of laminated composite plates was proposed in [
20]. As design variables, the fiber orientation angles in all layers were selected, and the search for the optimum solution in N-dimensional space was replaced by N repetitions of the optimization, with each repetition in one-dimensional space. This idea is based on the physical consideration of bending plates, during which the outer layer has a greater influence on the structure stiffness than the inner layer and is more important in the determination of the natural frequency. The Layerwise Optimization (LO) scheme was also used in [
21] to determine the optimum fiber orientation angles for the maximum fundamental frequency of cylindrically curved laminated panels under general edge conditions.
In [
22], differential evolution optimization was used to find stacking sequences for the maximization of the natural frequency of symmetric and asymmetric laminates. Optimized stacking sequences for eight-ply asymmetric laminates were presented.
The authors in [
23] dealt with the maximization of the fundamental frequency of laminated plates and cylinders by finding the optimal stacking sequence for symmetric and balanced laminates with neglected bending–twisting and torsion–curvature couplings. Vosoughi et al. [
24] introduce a combined method to obtain the maximum fundamental frequency of thick laminated composite plates by finding the optimum fiber orientation. To find the optimum fiber orientation of a thick plate, a mixed implementable evolutionary algorithm was used, and the particle swarm optimization (PSO) method was added to improve the specified percent of the GA population. Excellent reviews of techniques applied to the optimization of stacking sequence are given in [
7,
25].
The use of ANNs in optimization problems in civil engineering have been documented in several other publications. In the vast majority of them, ANNs were applied to reduce the time-consuming evaluations of objective functions that occur in iterative global search algorithms, such as GAs or other evolution strategies [
26,
27,
28]. The authors in [
27] examined the application of ANNs to reliability-based structural optimization of large-scale structural systems.
In [
26], a critical assessment of three metaheuristic optimization algorithms—differential evolution, harmony search, and particle swarm optimization—was used to find the optimum design of real-world structures. Furthermore, a neural network-based prediction scheme of the structural response, which is required to assess the quality of each candidate design during the optimization procedure, was introduced. In [
28], ANN approximation of the limit–state function was proposed in order to find the most efficient methodology for performing reliability analysis in conjunction with the performance-based optimum design under seismic loading. The non-uniqueness of the optimum design of cylindrical shells for vibration requirements was presented in [
29], and its implications were discussed in depth. Authors have shown that the design optimization of cylindrical shells for modal characteristics is often non-unique. In the above-mentioned paper, some selected issues, such as the new mode sequence, mode crossing, repeated natural frequencies, and stationary modes, were demonstrated and discussed. The numerical results were compared with the analytically obtained ones.
This paper presents a novel method for the maximization of eigenfrequency gaps around external excitation frequencies through stacking sequence optimization in laminated structures. The proposed procedure makes it possible to create an array of suggested lamination angles to avoid resonance for each excitation force frequency within the considered range. The main task (the maximization of frequency gaps) is preceded by an auxiliary task, namely, the maximization of the first natural frequency of considered structures. The aim of the initial step is to test the proposed procedure by comparing the obtained results with the results of the classical optimization approach, which involves FEM, and the results of an optimization example from the literature that used a different evolutionary optimization algorithm. The results of the comparison verified the proposed procedure. The results obtained using the proposed method are more accurate and significantly less time-consuming—which should be emphasized—because so-called “deep networks” were applied, enabling the use of very large sets, with the number of patterns reaching at least 10,000.
4. Verification Example
The optimization procedure described above, with GA as a tool to solve the optimization problem and ANN as a tool that substitutes time-consuming FE calculations, was verified using an example described in [
41]. All of the following assumptions (regarding the FE model, material parameters, lamination angles, and so on) are based on this article.
The structure (see
Figure 4a) is a cantilever tube. Its model is a thin-walled cylindrical shell with a circular cross-section, and the diameter of the middle-surface of the cross-section is
m. The thickness of the shell is
m, and the length of the cantilever is
m. The shell web consists of 64 layers of composite material of equal thickness but with different fiber orientations. The boundary conditions are defined on the cylinder axis and correspond to the support conditions of a simply supported beam. The material properties are
GPa,
GPa,
,
GPa, and
kg/m
.
The lamination angles considered are 0, ±45, and 90. The laminates are considered symmetric, and neighboring layers are grouped into pairs, with lamination angles equal to (herein called ‘0’), (called ’’), or (called ‘90’). For example, the stacking sequence described as should be read as four pairs of layers , eight pairs of layers , and four pairs of layers . Assuming that the stacking sequence is symmetric, the overall number of layers is equal to 64, while the number of varying lamination angles equals 16.
The fundamental natural frequency reported herein was obtained by using the commercial FE code ADINA [
40]. The FE model (called MODEL3) was built using multi-layered shell 4-node MITC4 elements (first-order shear theory), the number of which equals 72 along the circumferential direction and 20 in the axial direction. The overall number of FE elements, nodes, and degrees of freedom equals 1440, 1514, and 9084, respectively.
In order to verify the compatibility of MODEL3 with the FE model used by Koide and Luersen in [
41], the fundamental natural frequency was calculated for three different stacking sequences described in [
41] and compared with the values in that paper. The results, shown in
Table 1, prove that the proposed FE model and the FE model in [
41] can be considered compatible.
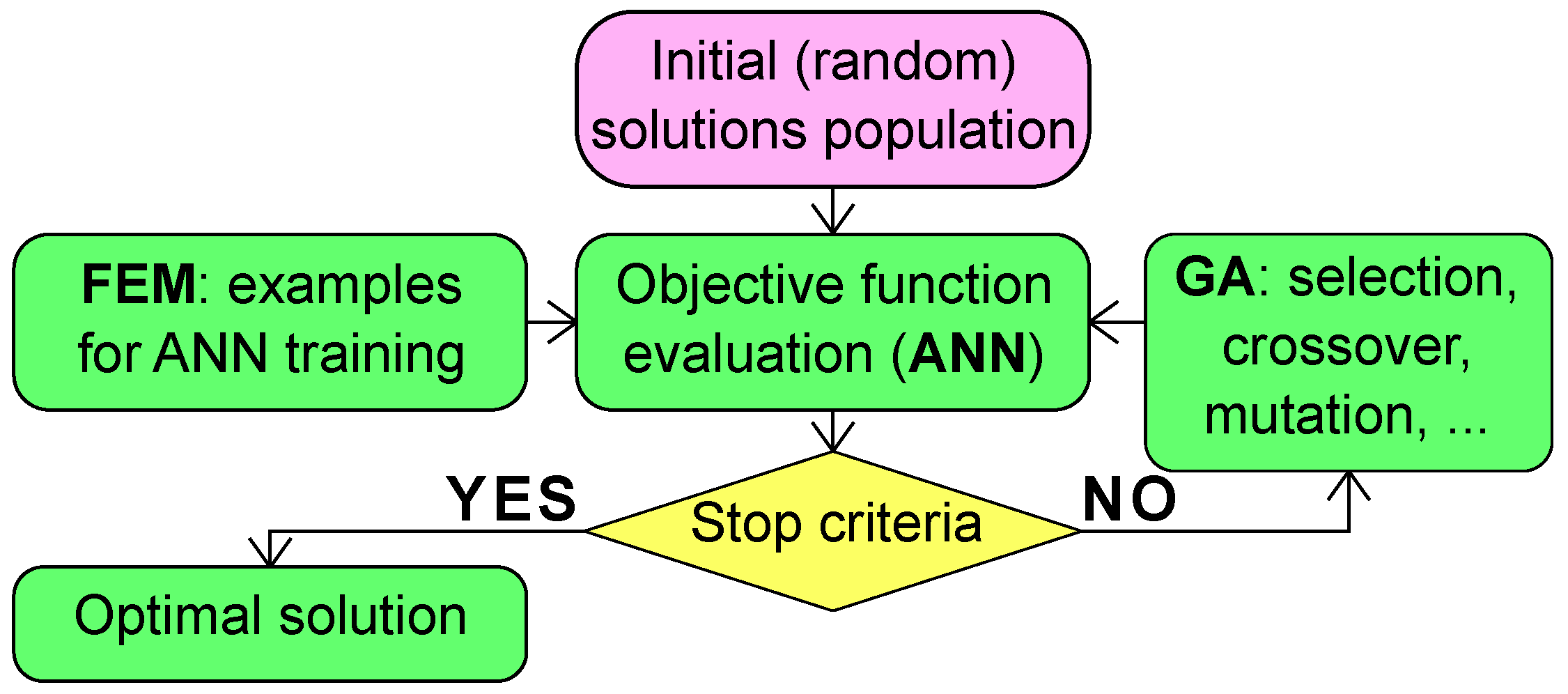
The optimization of the lamination angles in order to obtain the maximum value of the fundamental natural frequency
was performed according to the scheme shown in
Figure 2. Four pattern sets were generated. The first one,
, consists of 5184 patterns, each composed of 16 angles of neighboring laminate pairs (ANN inputs) and one corresponding fundamental frequency (ANN output). The fundamental natural frequency corresponding to the particular set of lamination angles was computed using FEM. The patterns gathered in
were generated according to two scenarios:
For the first three pairs of lamination angles, all three possible cases (, , and ) are considered. Starting from the fourth lamination angle pair to the 16th (the last one), two cases ( and ) are considered for even lamination pairs (the 4th, the 6th, the 8th, and so on), and only one case () is considered for odd lamination angle pairs.
For the first three pairs of lamination angles, all three possible cases (, , and ) are considered. Starting from the fourth lamination angle pairs to the 16th (the last one), one case () is considered for even lamination pairs, and two cases ( and ) are considered for odd lamination angle pairs.
The second, the third, and the fourth pattern sets—, , and —consist of 16 randomly generated angles of neighboring laminate pairs (ANN inputs) and one corresponding fundamental frequency (ANN output). The number of patterns in , , and equal 1500, 3500, and 5000, respectively.
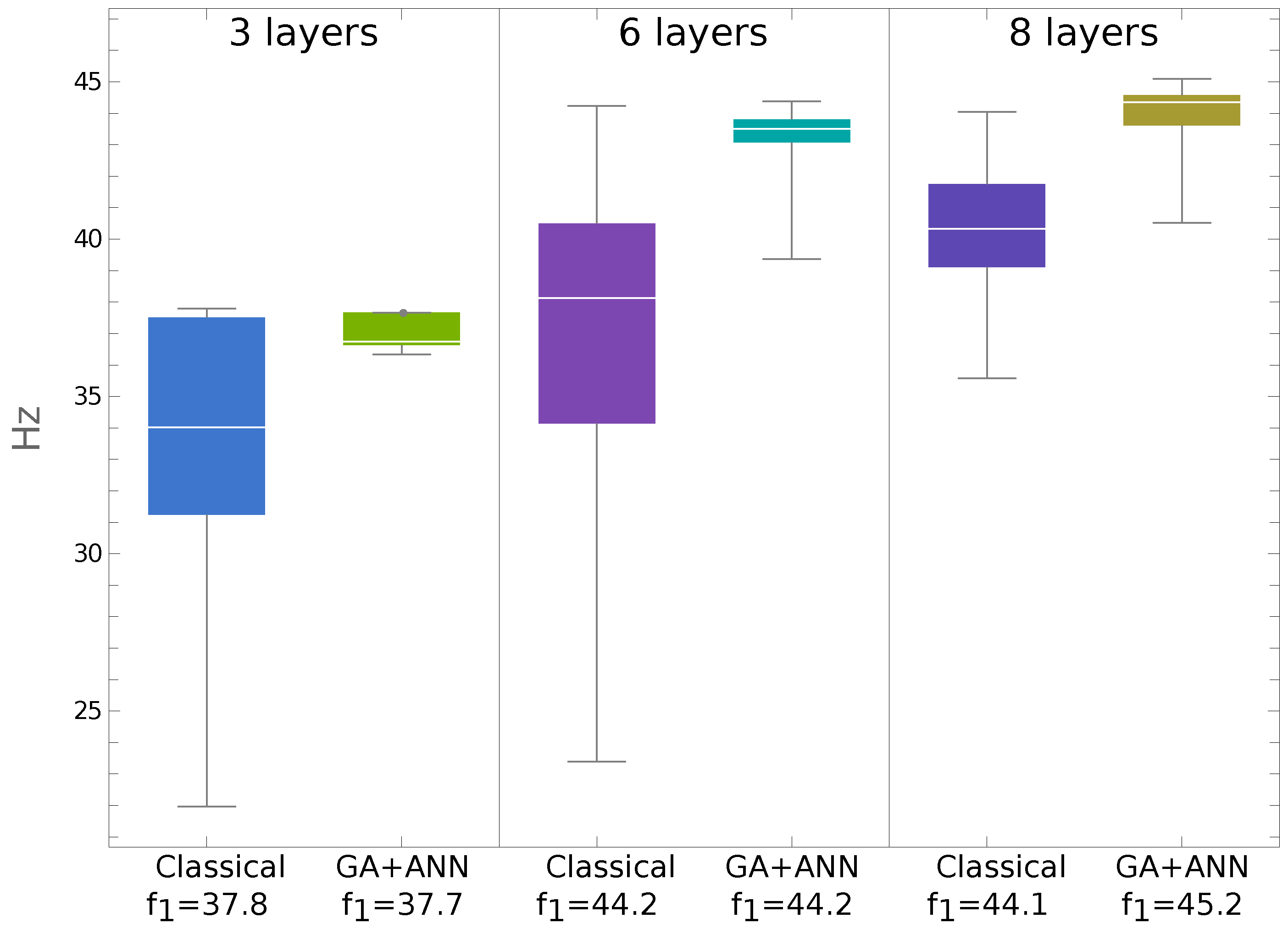
The pattern sets were applied in different combinations to train the deep network (see
Table 2), and the trained network substituted the FE simulations in the GA optimization of the lamination angles. The results reported herein from the GA+ANN optimization procedure, together with the results presented in [
41], are shown in
Table 2.
The results presented in
Table 2 prove that the proposed GA+ANN optimization procedure is capable of solving the optimization problem. Moreover, even when applying a significantly smaller number of time-consuming FE calls, the results obtained by applying the GA+ANN procedure are still better than those presented in [
41]. The proposed procedure is able to solve the optimization problem involving half the number of FE calls, which directly leads to considerable time-savings. Analysis of the results presented in
Table 1 leads to the conclusion that there are multiple local maxima with
equal to or higher than the value found in [
41]. The value of
Hz seems to be a global extreme.
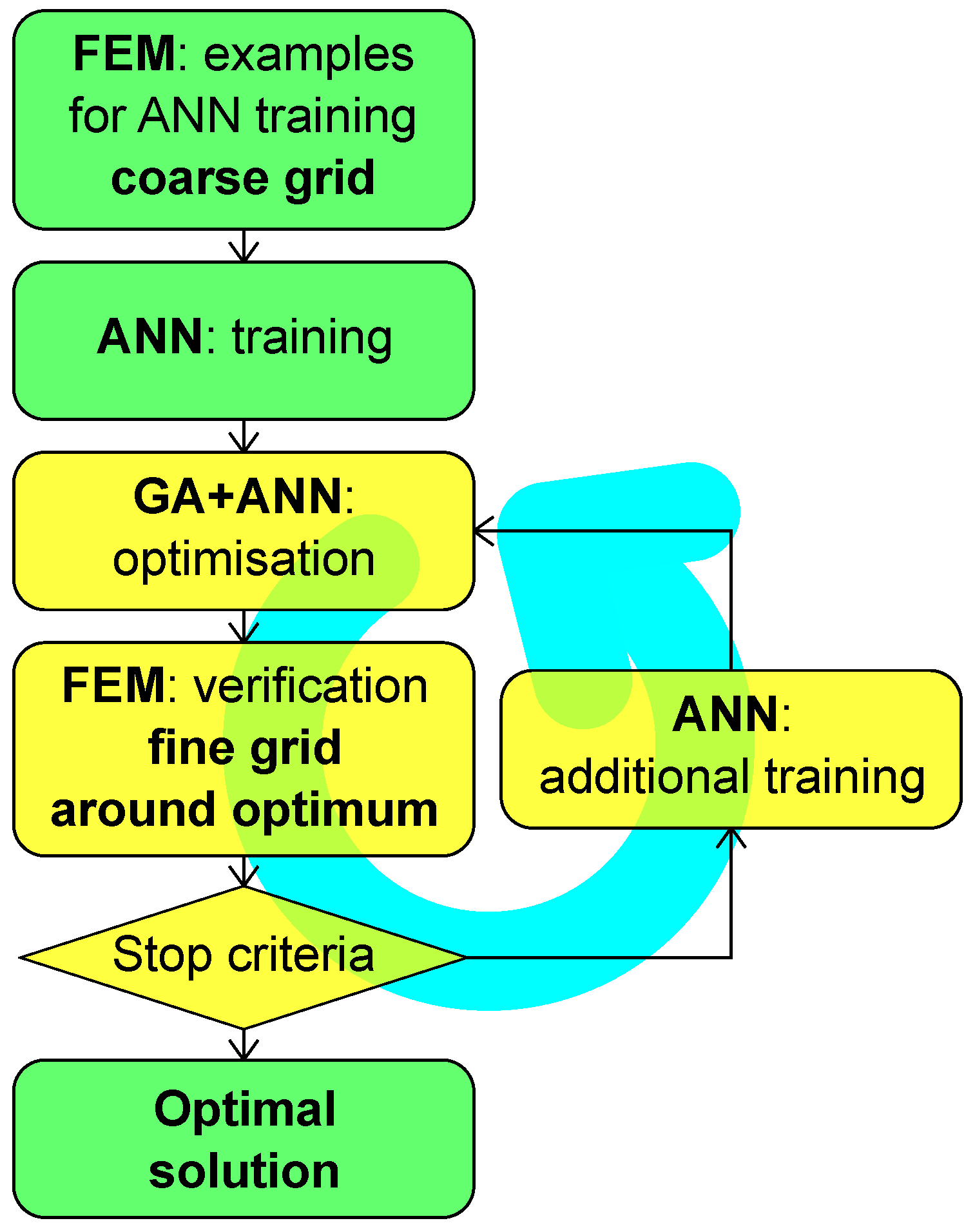
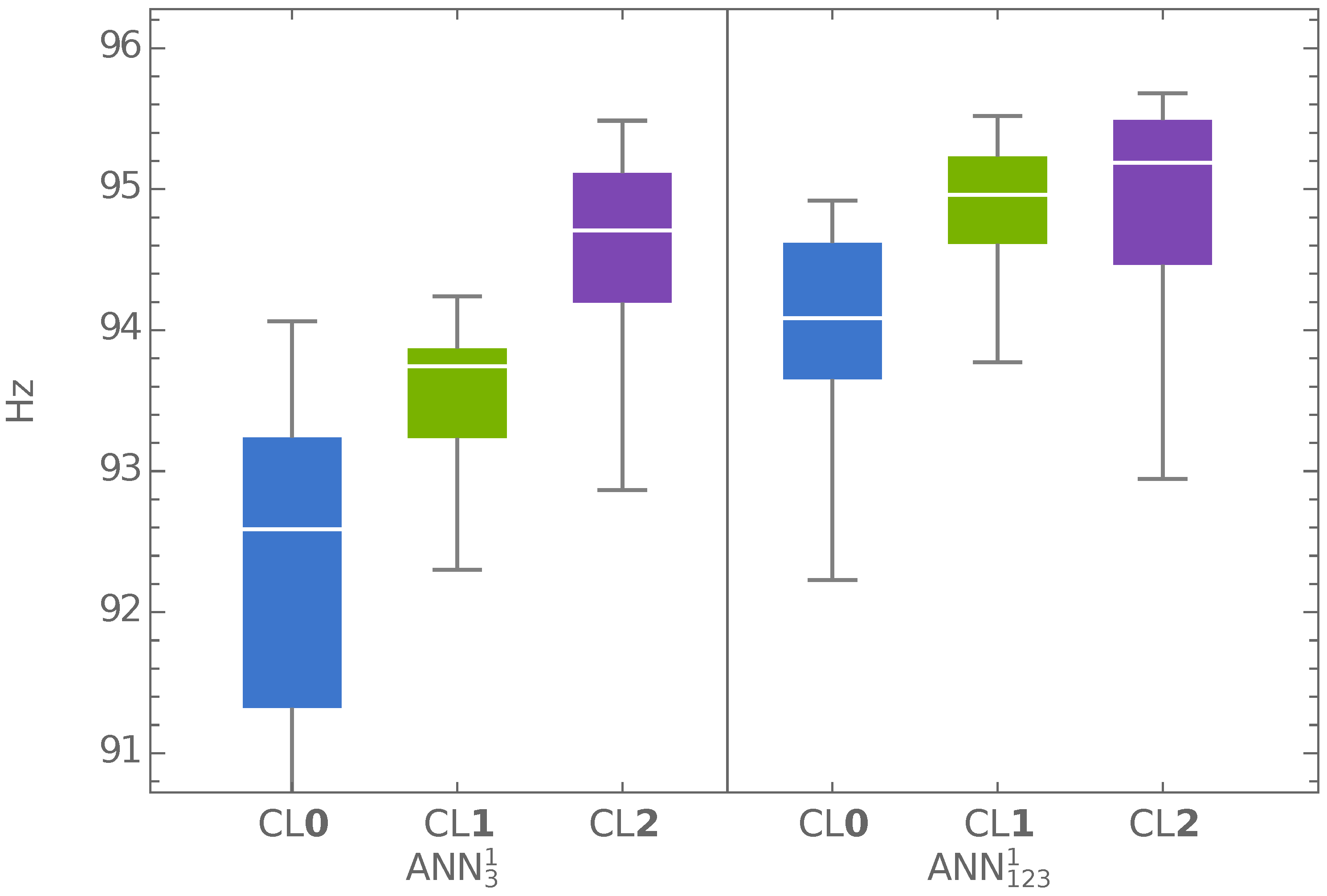
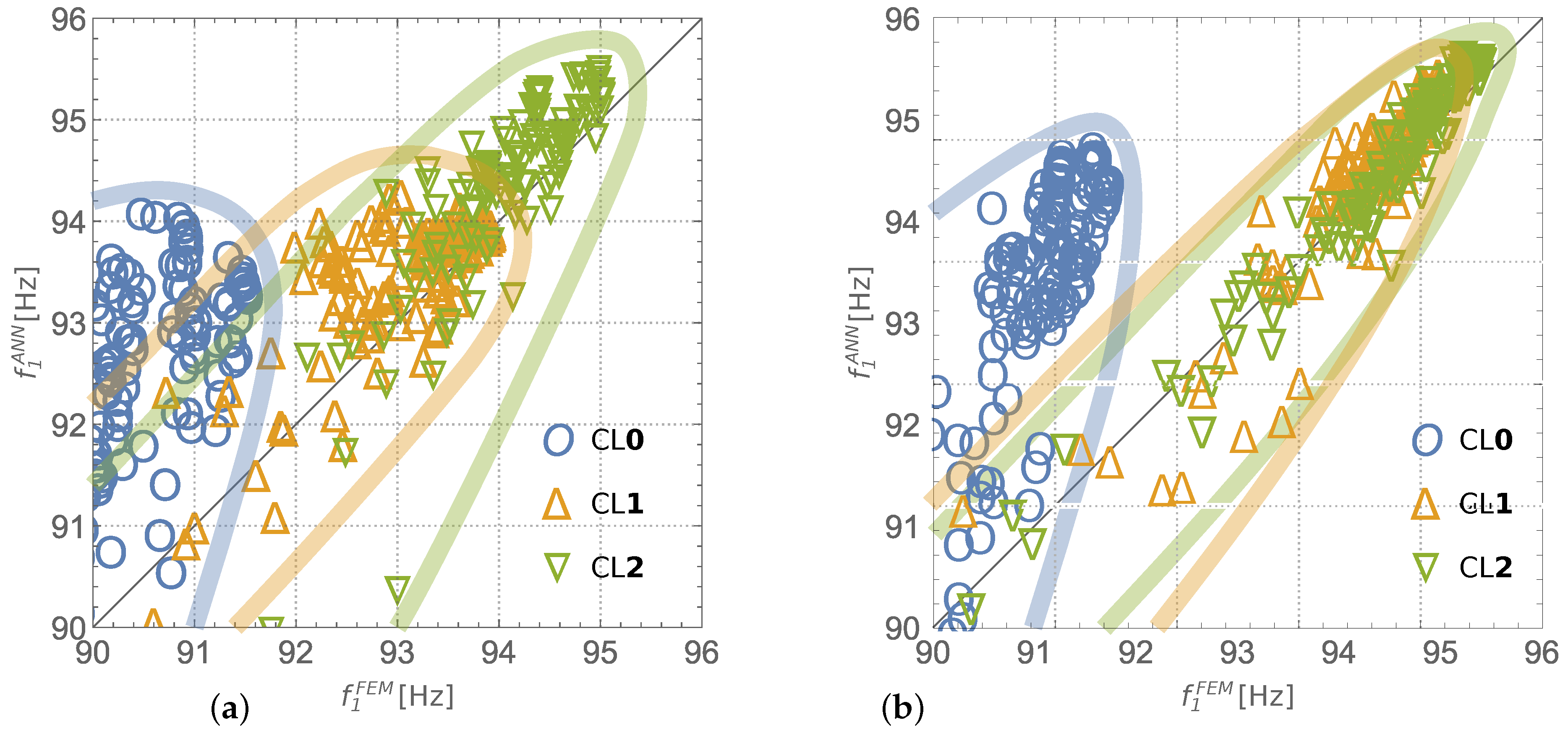
Special attention should be given to the results in the rows labeled “GA+ANN (CL
1)”, which were obtained after one curriculum learning loop (see
Figure 3). The CL approach was tested with all considered pattern set combinations and, in all of them, gave more precise ANN predictions of
fundamental frequency. The cases shown in the rows “GA+ANN (CL
1)” are those in which the CL approach also improved the optimization result. The most important observation is that the maximum of the fundamental frequency, which is higher than the one presented in [
41], was obtained with half the number of FE calls (5100 instead of 11,250).
5. Optimization of the Three-Layer One-Segment Tube
5.1. Case Description
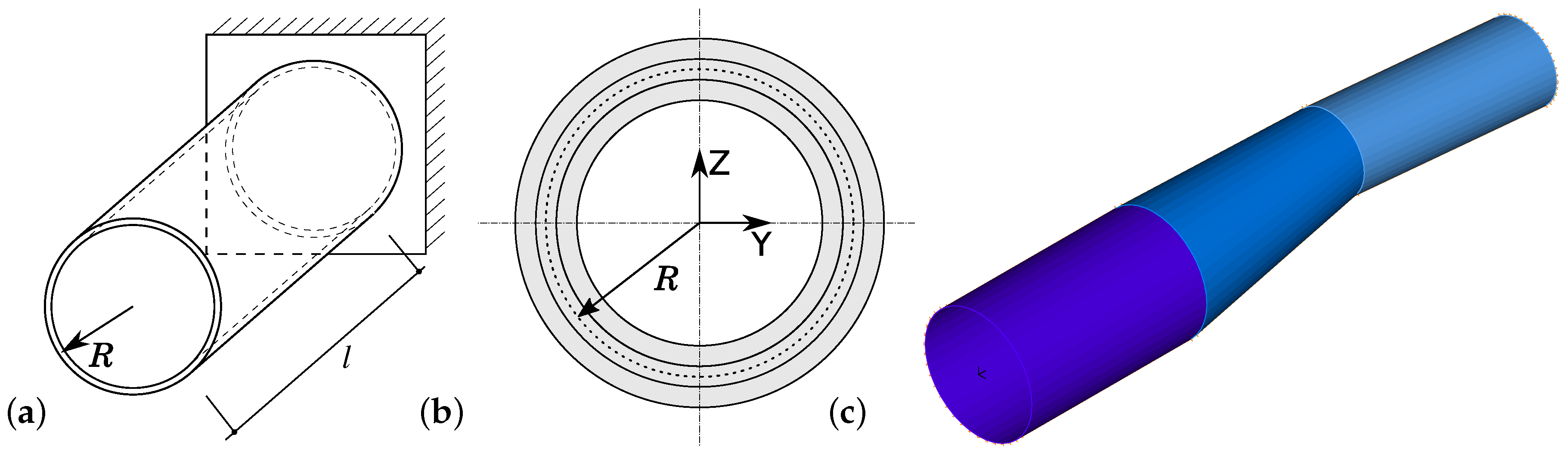
This rather simple problem was chosen to check the method’s accuracy and time consumption. Moreover, the use of three free model parameters makes the analysis of the behavior of the model’s natural frequencies possible. The investigated model, a six-meter-long laminate tube with three layers of composite material, is shown in
Figure 1.
5.2. Classical FEM-Based Optimization Procedure
The average time necessary for FEM computations to find the first ten natural frequencies for a six-meter-long, three-layer non-symmetric laminate tube fixed at one end reaches approximately 13.9 s on a 4-core system with Intel
® Core
® i5-4570 CPU@3.20 GHz and 8 GB RAM. This, of course, depends very much on the adopted FE mesh and the applied numerical procedure. However, it can be accepted as a basis for further consideration. The problem of maximization of the fundamental natural frequency
needs the objective function, that is,
, to be solved about 180 times on average. The parameters of the applied interior-point optimization algorithm (see [
34,
42]) are as follows: no constraints, no gradient nor Hessian supplied, maximum number of iterations equal to 100, 50 repetitions with a unique random starting point, and each calculation of the objective function needs an FE call. The exact number of objective function evaluations varies from 4 to 592, and the time necessary to perform
maximization reaches an average of 25 min. However, for a particular case, it varies from 33 to 85 min (the time covers the entire optimization procedure, including all necessary FE simulations).
Each random initiation of the procedure leads to a different solution (and probably to a different local minimum). For 50 multi-start random initiations, the best-obtained result is Hz for lamination angles . The overall time necessary to repeat the procedure 50 times and the number of FE calls are 21 h and 9061, respectively. The result of calculations involving classical, derivative-based optimization methods and FEM to obtain the objective function value is a reference point for the proposed GA+ANN optimization procedure. The genetic algorithm needs the objective function to be computed thousands of times, and for the maximization of , the time necessary to obtain the results using FEM to calculate the objective function value would be 28 days. Obviously, this is an unacceptable time investment.
In order to make the GA procedure applicable with limited time constraints and typical computer hardware, the evaluation of natural frequencies was not done through FEM. Instead, neural networks were applied since, in contrast to FE simulations, a trained neural network is capable of giving its prediction almost instantly.
5.3. Pattern Generation and ANN Training
The procedure described above was tested on the MODEL1 structure (see
Figure 1), with three layers of composite material and dense FE mesh applied during FEM computations. Patterns for ANN training were calculated using the FE ADINA code [
40]. Each one is composed of three lamination angles
, one for each layer of the tube shell, and the corresponding natural frequencies of the tube
:
where the natural frequencies in pattern number
j were obtained through FEM computations for lamination angles
:
The number of natural frequencies computed amounted to ten in order to make the second optimization task (see Equation (
8)) solvable. The patterns were generated on a regular grid in
space; that is, natural frequencies of the laminate tube were computed for all parameter vectors
, with
varying according to one of the scenarios gathered in
Table 3. Only the last pattern set
was generated with random values of lamination angles. The generation of patterns, together with ANN training, formed the longest part of the simulation (in
Figure 2, it is labeled
FEM: examples for ANN training), which predicts the actual optimization.
The penultimate column in
Table 3 shows the duration of the generation of a particular
pattern set. The average time necessary to compute one pattern (the last column in
Table 3) differs for particular sets since, in some cases, the method applied to solve the generalized eigenproblem (Equation (
3)), namely, the
subspace iteration method (see [
30]), has to calculate a number of natural frequencies that is greater than the desired one (i.e., ten).
Pattern set generation is the most time-consuming part of the proposed GA+ANN procedure. The number of patterns should be large enough to accurately describe the function
and simultaneously small enough to ensure that the time necessary for their generation is acceptable. Obviously, the number of FE calls during pattern set generation should be significantly smaller than the number of FE calls during the classical minimization procedure (here that number is 9061) and the assumed number of FE calls during GA+FEM optimization (50 repetitions of GA optimization with 100 iterations of 100-element generation: 500,000 FE calls in total). In the considered case, the largest acceptable number of patterns was assumed to equal about 3000–4000. Some preliminary calculations showed that, instead of one pattern set generated using a regular grid (e.g.,
,
,
), it is advisable to generate a few small pattern sets, each generated using a different grid and completed by a randomly generated pattern set. The considered pattern sets, described in
Table 3, follow this preliminary conclusion. One of the goals of the following is to find a solution of a given optimization problem using the minimum number of patterns.
In the following experiment, five different learning sets were considered. In each case, the ANN was trained and tested on a different combination of
sets (see
Table 4, the first column). In the last row of the table, the network ANN
is described. All available patterns were used to train this network, so no testing was performed. The overall time consumption shown in the last column in
Table 4 includes the time spent both on the generation of the learning and testing patterns as well as on network training.
The errors shown in
Table 4 are commonly used error measures in ANN training, i.e., standard deviation
, Mean Squared Error (MSE), and
prediction Average Relative Error (ARE
). Assuming that
is the ANN prediction of natural frequencies,
MSE and ARE
are given by the following formulas:
where
P is the number of testing patterns (see Equation (
10)).
The results shown in
Table 4 prove that the applied deep networks are properly trained and can predict the values of the natural frequencies of a laminate tube with very high accuracy. However, the accuracy is significantly lower in two cases, namely, ANN
(trained using random patterns only) and ANN
(trained using a very limited number of patterns).
5.4. Maximization of the Fundamental Natural Frequency
The maximization (optimization) of
was performed by applying the procedure shown in
Figure 2, with the following assumptions:
the lamination angle increment is expressed either in real numbers (in the tables with the results coded as ‘0’), integer numbers (‘1’), or integers divisible by 2, 5, or 15 (‘2’, ‘5’, or ‘15’, respectively);
the usefulness of all networks listed in
Table 4 is verified;
the GA optimization procedure for each lamination angle increment (‘0’, ‘1’, ‘2’, ‘5’, or ‘15’) and for each network (from ANN to ANN) is repeated 50 times with different random initial populations.
Altogether, the optimization procedure was repeated
times. The results obtained are illustrated in
Figure 5.
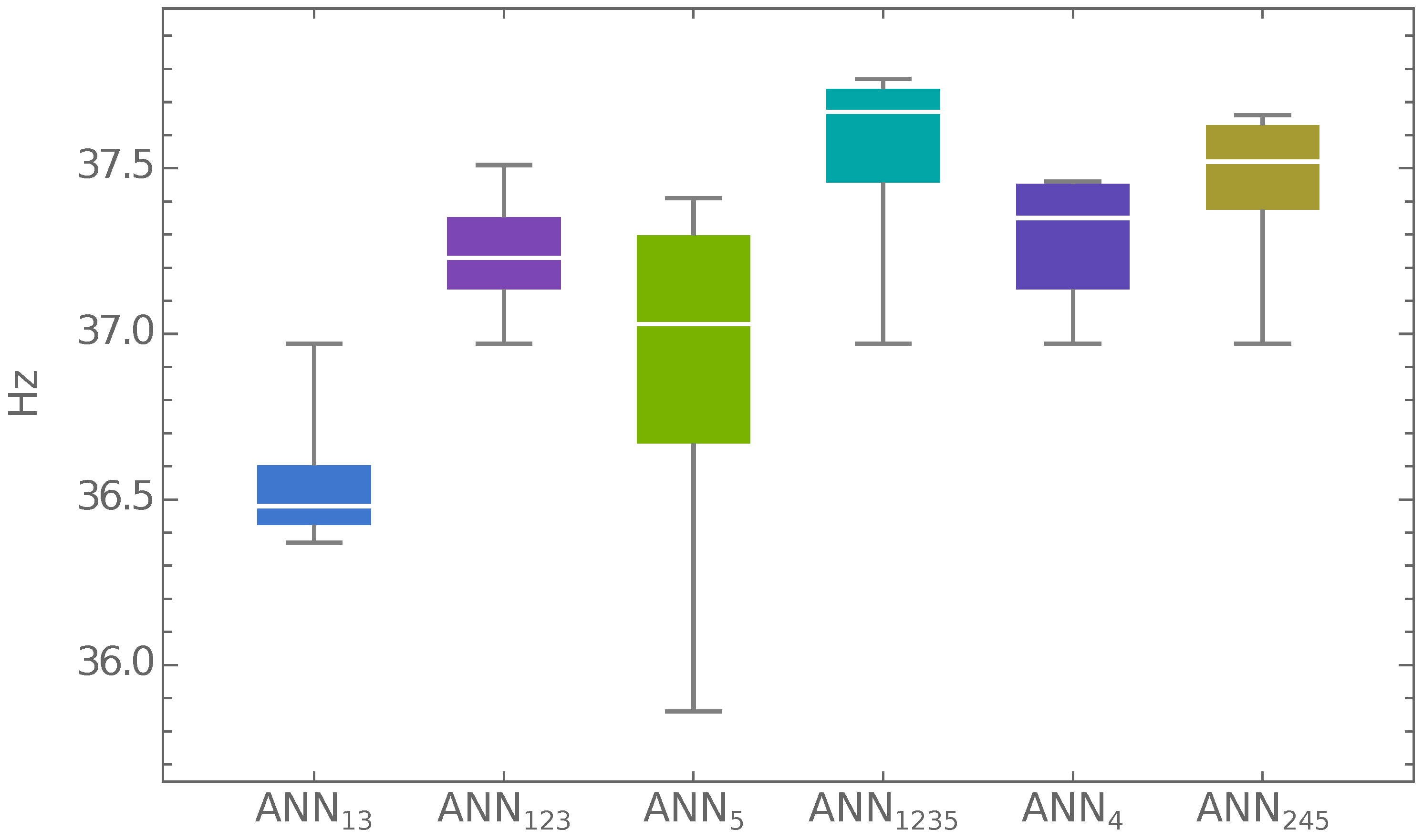
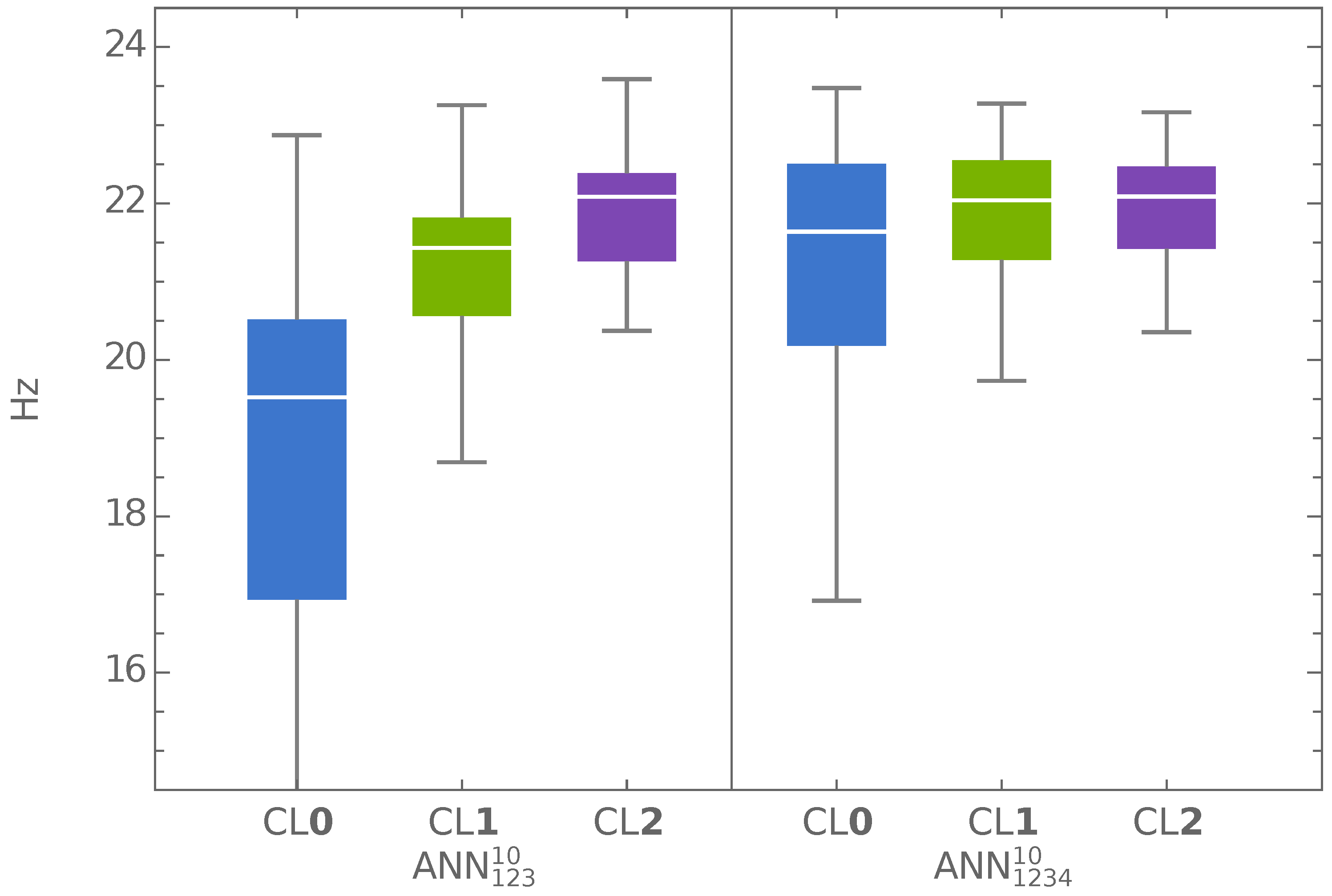
Figure 5 presents the so-called
box-and-whisker diagram with the following metrics used to describe the results of 250 runs (five different lamination angle increments and 50 repetitions in each case) of
maximization for a particular ANN applied: minimum and maximum values of the obtained results (whiskers); the interquartile range, representing the results between the 75th and 25th percentiles (the colored boxes); and the mean (the white lined inside the colored boxes). The box-and-whisker diagram was created using the
results.
Of six verified networks, only one, ANN, gave a mean result of that is lower than 36.97 Hz (the maximum value of available in the data sets). Four of the six networks gave a minimum of of almost 36.97 Hz, with the mean and the maximum clearly higher than 36.97 Hz. The best results are from applying optimization procedure using the ANN network: the value Hz is almost 1 Hz higher than the value that can be found in rather dense sets of patterns.
The proposed optimization approach can be adopted for both real values of lamination angles and integer values with a user-defined angle increment. The rather narrow spread of results, e.g., those from ANN, indicates the robustness of the proposed procedure. The time consumption of one optimization case (for example, using the network ANN, a lamination angle increment of ‘0’, and 50 repetitions was one of the most time-consuming cases investigated) is 802 min for pattern generation, 15 s for GA+ANN optimization, and 22 min for FEM verification of the obtained results for a total time of slightly less than 14 h. The number of FE calls is 3413 during pattern generation and 50 during FE verification of GA+ANN results for a total of 3463 FE calls. For the network ANN, whose application generates the best-obtained results (for the increment ‘0’) of Hz and , the overall time consumption is 9 min less, and the number of FE calls remains constant. In a reference case (classical optimization involving FEM), the best-obtained results are Hz and , and the overall time and the number of FE calls are 21 h and 9061, respectively.
5.5. Maximization of the Distance between Natural Frequencies and a Selected Frequency
The main optimization task in the proposed approach is the maximization of the distance between an arbitrarily selected excitation frequency
p and the neighboring natural frequencies (see Equation (
8)). The considered values of
p are 30, 40, 50, 60, 70, and 80 Hz.
The minimal difference between any natural frequency and any of the arbitrarily selected excitation frequencies is significantly higher than the targeted of the excitation frequency. Actually, in every case, it reaches of the excitation frequency p, whereas the minimum difference for every i should be higher than of p to avoid the resonance phenomenon.
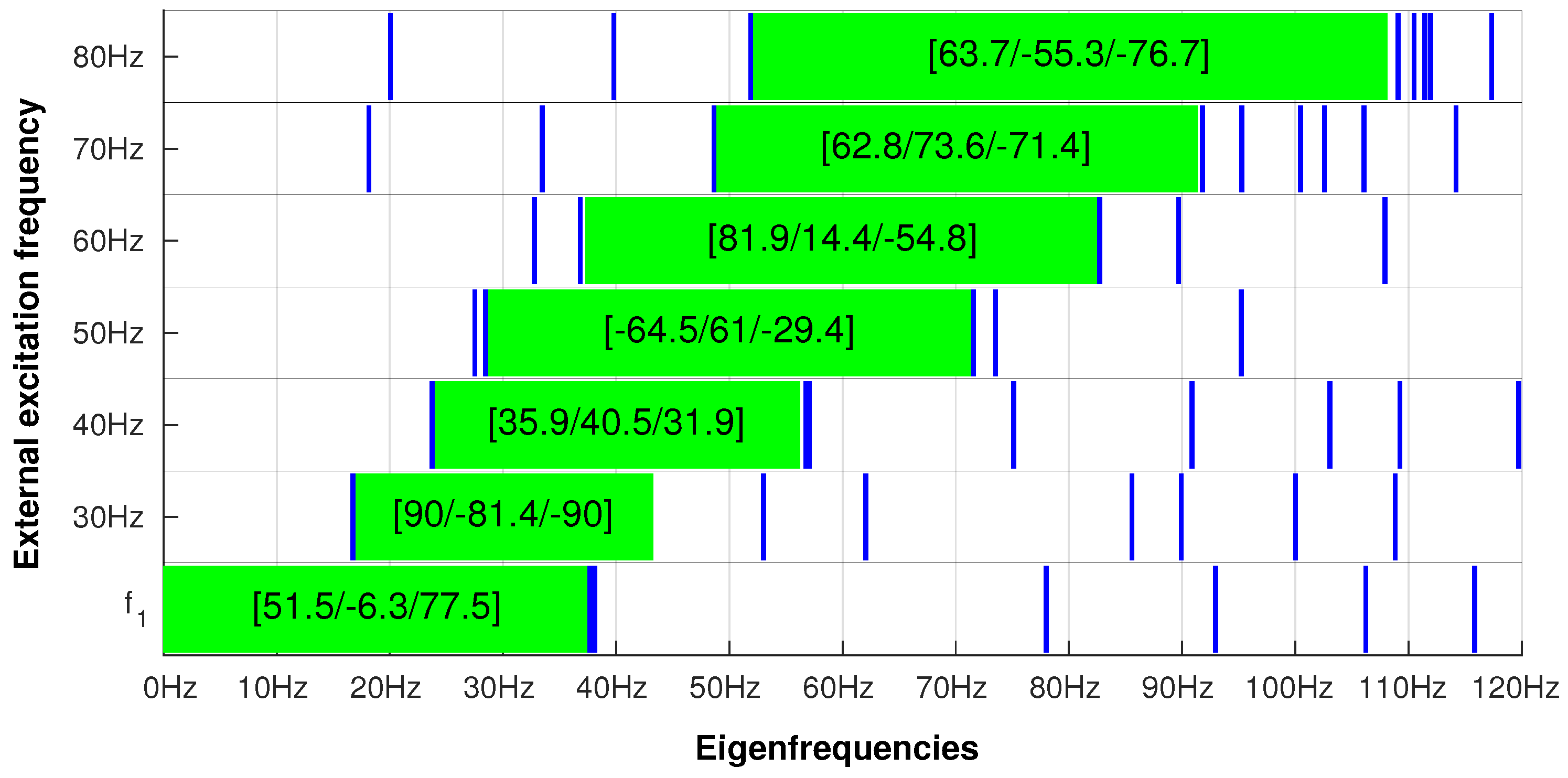
The results obtained from the ANN
network are presented in a graphical form in
Figure 6. Successive rows in
Figure 6 present the results of
maximization (the bottom row) and the maximization of the distance between arbitrarily selected excitation frequencies (30–80 Hz) and natural frequencies calculated for MODEL1.
The green boxes represent the distance in the frequency space around a selected excitation frequency (30–80 Hz) that is free from natural frequencies and obtained when a particular set of lamination angles is applied. The blue vertical lines represent the natural frequencies calculated for the same lamination angles.
It is clearly visible that the ANN
network gives the expected results.
Table 5 shows a kind of lookup table that enables the quick selection of lamination angles that lead to resonance avoidance for any excitation force frequency up to about 72 Hz. For example, for the excitation frequency
Hz, the suggested lamination angle set [−64.5/61/−29.4] leads to a distance from
Hz to the closest natural frequency
of at least 17.4 Hz (or, expressed as a percentage, 32.1%). No calculations are necessary for resonance avoidance once
Table 5 is ready.
Both problems, namely, the maximization of and the maximization of frequency gaps (eight optimization cases in total), were successfully solved using the network. The network was trained and tested using only 3413 FE calls during pattern set generation and 400 FE calls during the verification of obtained results. If it is assumed that the number of FE calls necessary to perform the same tasks using the classical optimization approach exceeds 70,000 (eight optimization cases, each needing about 9000 FE calls), then, in the GA+FEM approach, the number of FE calls reaches 4,000,000. The number of FE calls in the application of the proposed GA+ANN procedures decreases by at least one order of magnitude compared with the classical optimization approach.
8. Conclusions
This paper presents a novel method for the optimization of the stacking sequence in laminated structures. The proposed method is robust and efficient in simple optimization cases as well as in more complicated problems with more design variables. Complex boundary conditions, the complicated shape of the investigated structures, and the type of variable (continuous or discrete) do not hinder the effective use of the method. Moreover, the procedure can be successfully applied to optimization cases in which it is not possible to derive analytical formulae that combine design variables and optimized quantities.
As a result of replacing the finite element method by deep neural networks for the calculation of the optimized structure parameters, the proposed method significantly accelerates the optimization and enables the optimization to be performed in limited time on typical computer hardware. In addition to instantly calculating the objective function, deep neural networks have another important advantage: they facilitate the use of a very large number of patterns describing the optimization space. In the examples described in this paper, the number of available patterns reaches . In other cases, which are not discussed in this paper, deep networks were trained on patterns, and the training time did not exceed 30 min.
The main idea presented in this paper, i.e., the curriculum learning of the applied deep networks, opens the door to new applications of the combined GA+ANN optimization procedure. The procedure can start with a very sparse description of the optimization space, and, in the successive iteration steps, the space description acquires a higher level of accuracy around the global minimum. The increasing accuracy of the objective space description and the possibility of deep network retraining presents the opportunity to create a very precise neural approximation of optimized structure parameters and, therefore, to significantly increase the precision of GA+ANN optimization.
The combined GA+ANN procedure was successfully applied to problems related to the avoidance of vibration resonance, which is a major concern for every structure subjected to periodic external excitations. The presented examples show two approaches to resonance avoidance: the maximization of the fundamental natural frequency (for external excitation frequencies possibly smaller than the fundamental natural frequency) or the maximization of a frequency gap around the external excitation frequencies (in other cases). In all examples presented in this paper, the necessary changes in natural frequencies are the result of appropriate changes in lamination angles only. In other words, no changes in the boundary conditions, geometry, or mass of the structures are introduced.
A further study of the proposed optimization procedure would be of interest. The proposed problems to be discussed include the following:
vibration resonance avoidance in the case of a few periodic excitations with different frequencies;
multi-criteria optimization, e.g., the maximization of the fundamental natural frequency, together with the maximization of the buckling force;
composite material design (e.g., topological constraints, varying thickness and/or stiffness);
a full variable–stiffness approach to lamination parameters that considers continuous changes in lamination parameters over the investigated domain;
multi-dimensional problems with the number of design variables exceeding twenty; and
optimization of a shell with openings.