Analysis of Damage Models for Cortical Bone
Abstract
1. Introduction
2. Damage Models
2.1. Frémond–Nedjar Model
2.2. García et al. Model
3. Numerical Results and Discussion
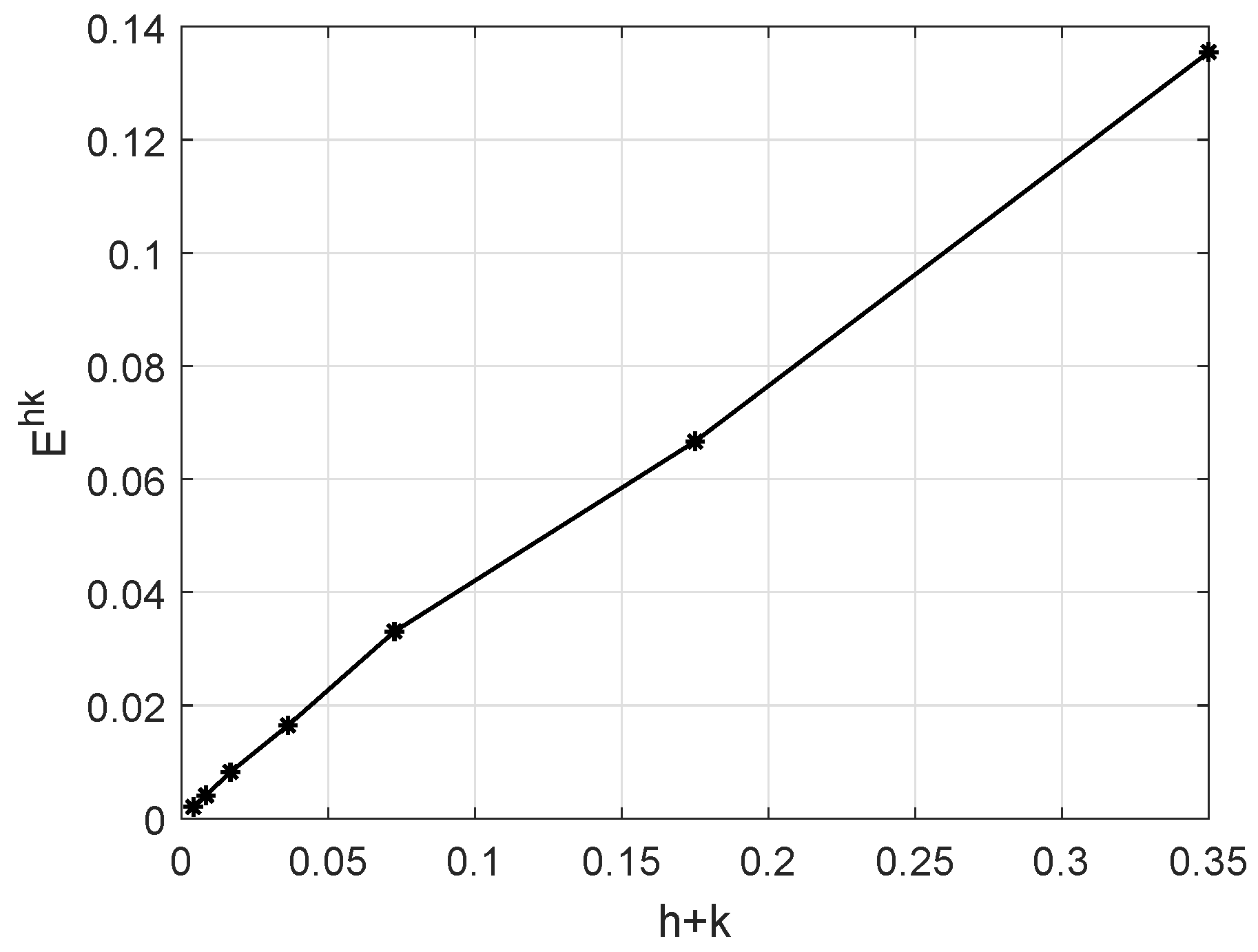
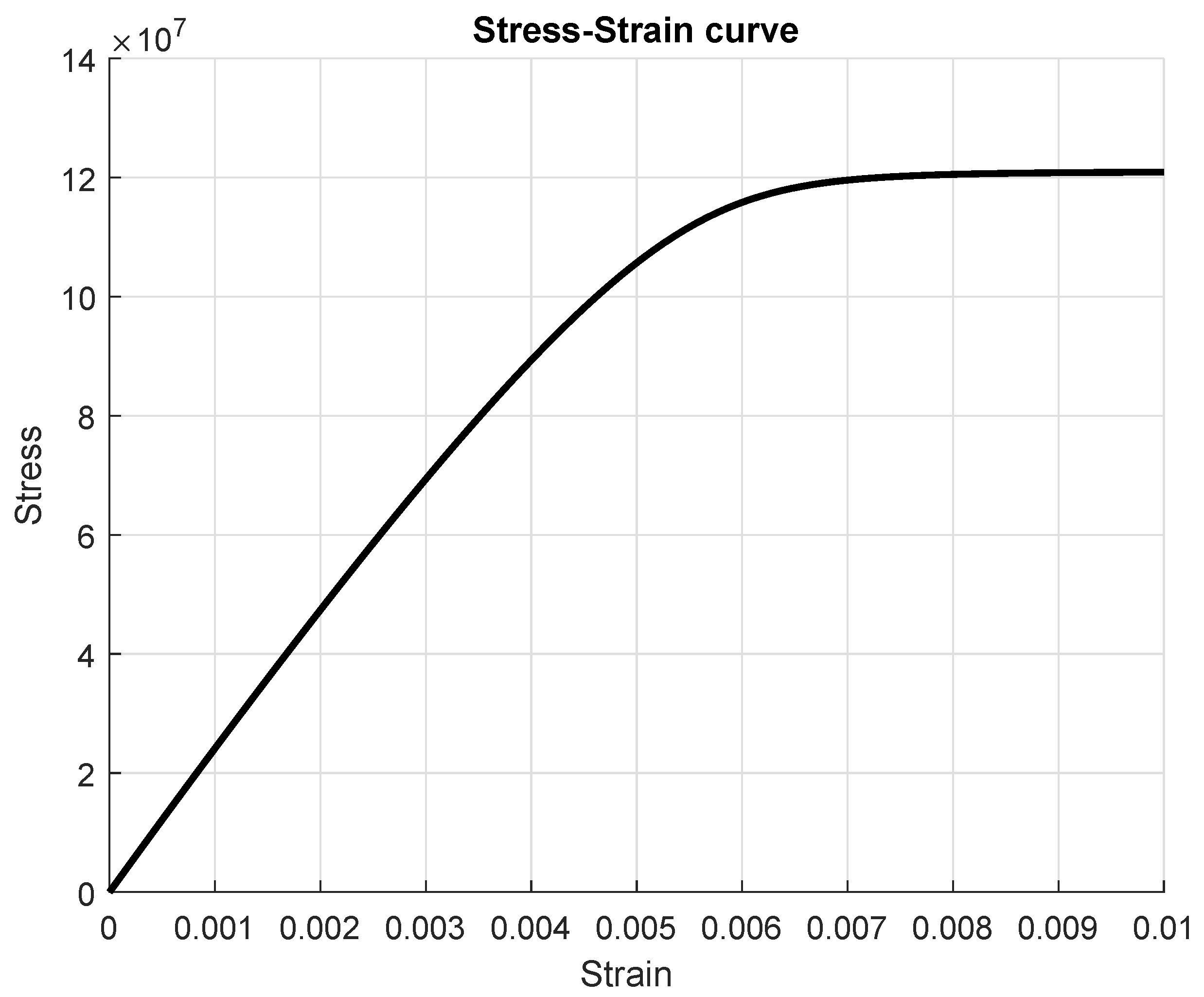
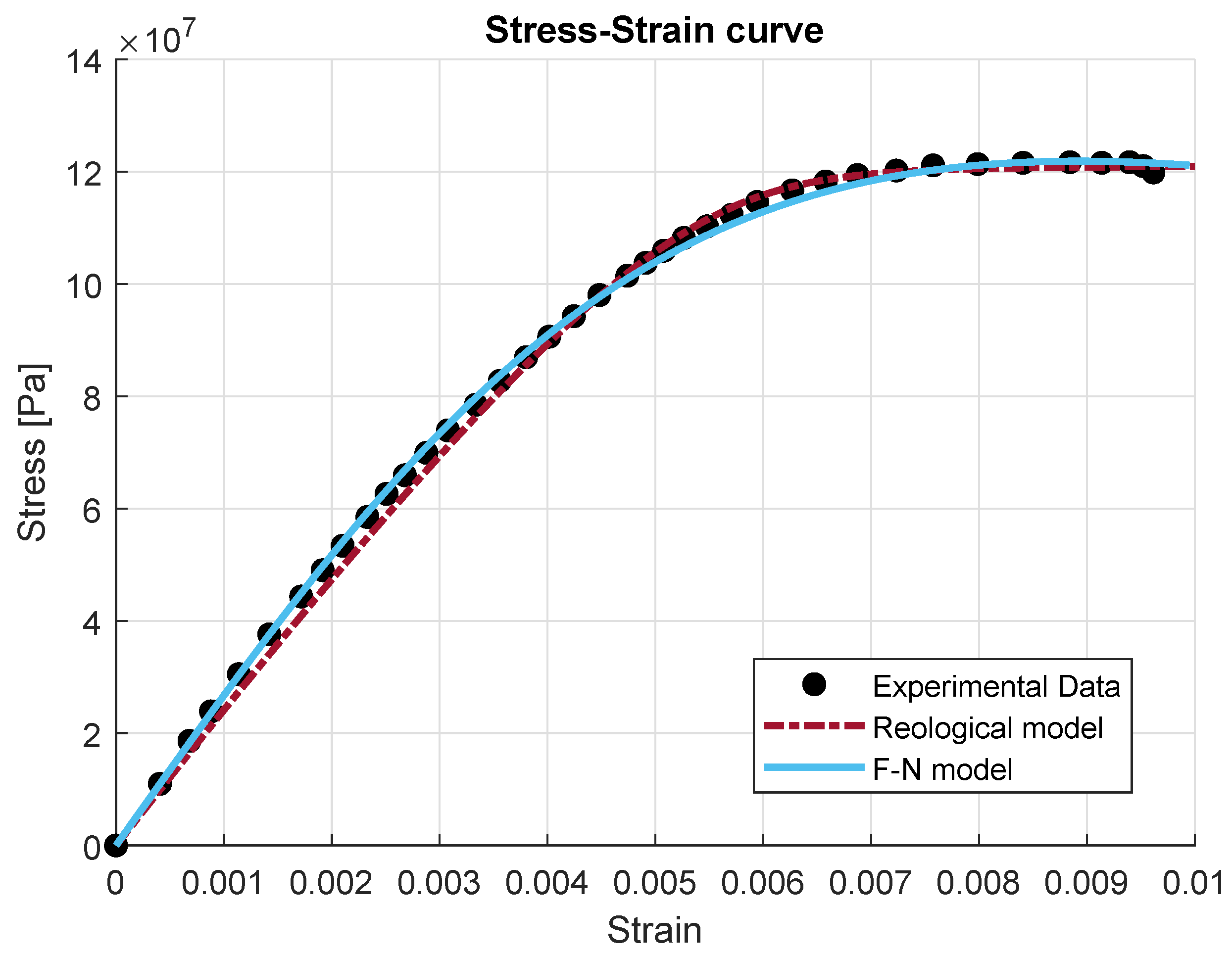
3.1. Comparison in a One-Dimensional Problem
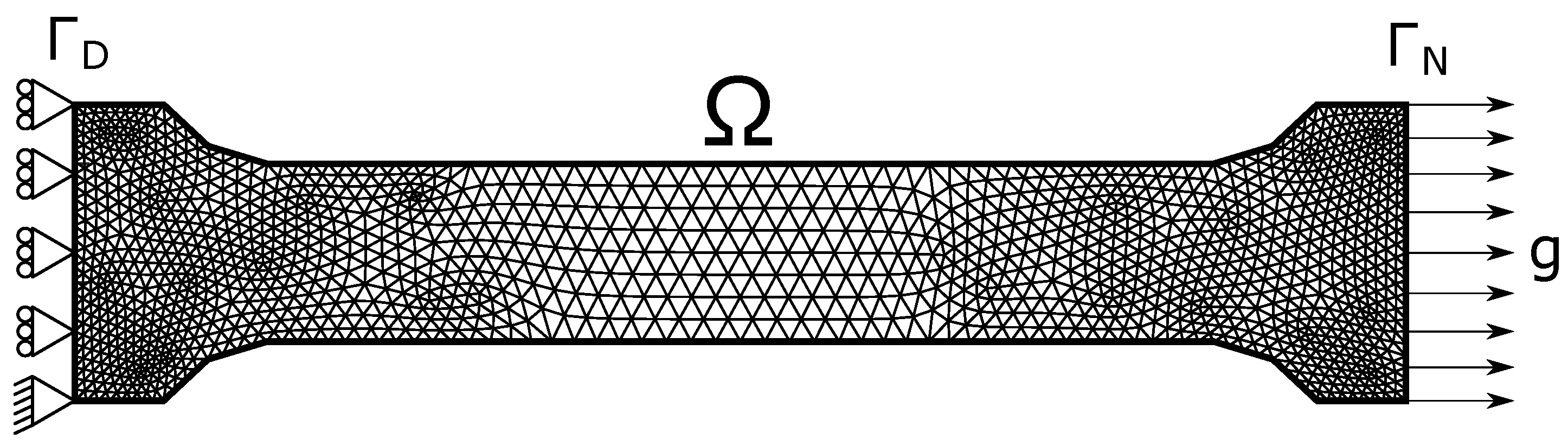
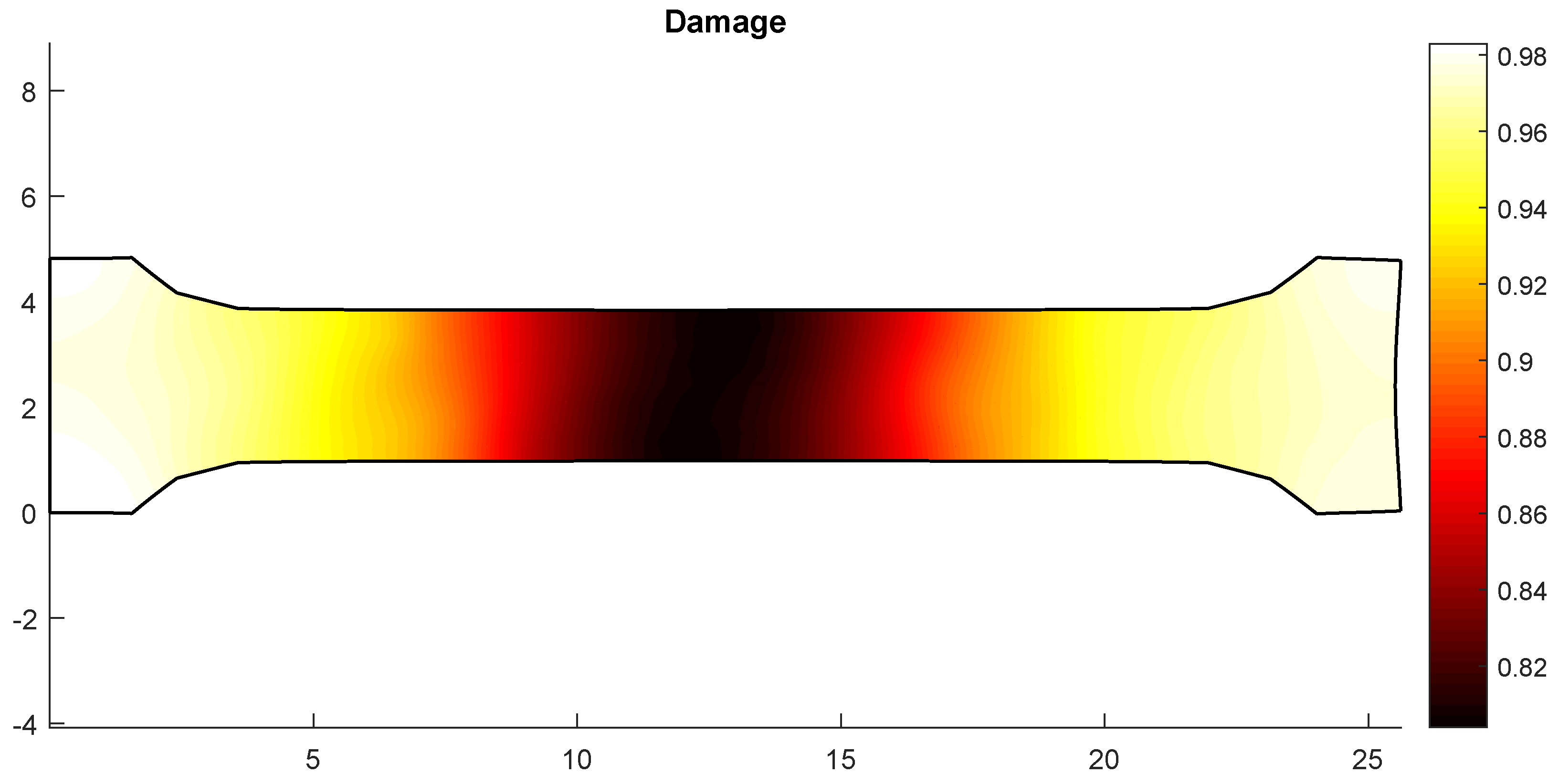
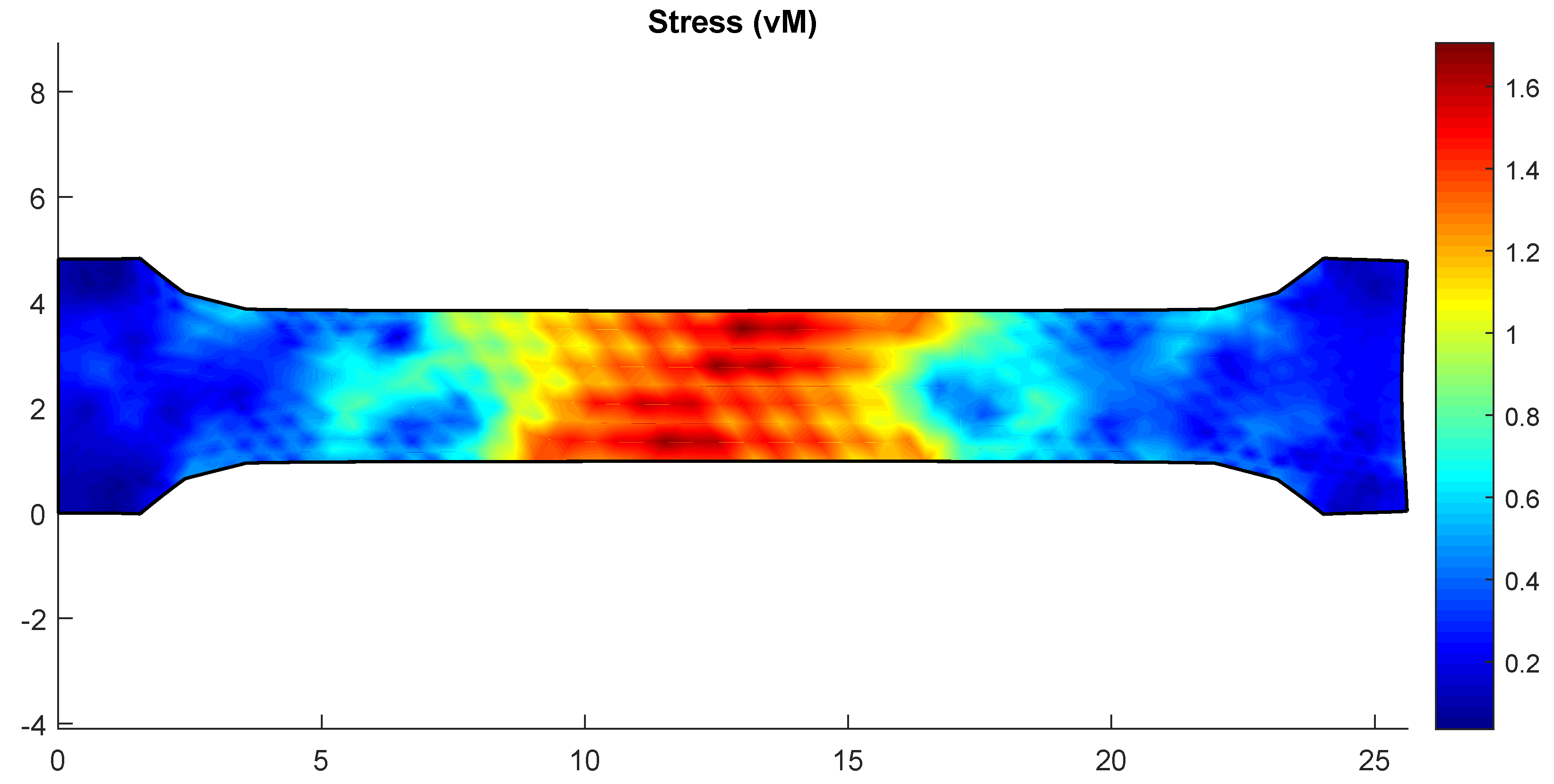
3.2. A Two-Dimensional Problem Solved Using Frémond–Nedjar Model
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Mazars, J. A description of micro- and macroscale damage of concrete structures. Eng. Fract. Mech. 1986, 25, 729–739. [Google Scholar] [CrossRef]
- Frémond, M.; Nedjar, B. Damage, gradient of damage and principle of virtual power. Int. J. Solids Struct. 1996, 33, 1083–1103. [Google Scholar] [CrossRef]
- Nedjar, B. Elastoplastic-damage modelling including the gradient of damage: Formulation and computational aspects. Int. J. Solids Struct. 2001, 38, 5421–5451. [Google Scholar] [CrossRef]
- Wolff, J. The Law of Bone Remodelling; Springer: Berlin/Heidelberg, Germany, 1986. [Google Scholar]
- Weinans, H.; Huiskes, R.; Grootenboer, H.J. The behavior of adaptive bone-remodeling simulation models. J. Biomech. 1992, 25, 1425–1441. [Google Scholar] [CrossRef]
- Fondrk, M.T.; Bahniuk, E.H.; Davy, D.T. Inelastic strain accumulation in cortical bone during rapid transient tensile loading. J. Biomech. Eng. 1999, 121, 616–621. [Google Scholar] [CrossRef] [PubMed]
- Carter, D.R.; Caler, W.E. A cumulative damage model for bone fracture. J. Orthop. Res. 1985, 3, 84–90. [Google Scholar] [CrossRef] [PubMed]
- Pattin, C.A.; Caler, W.E.; Carter, D.R. Cyclic mechanical property degradation during fatigue loading of cortical bone. J. Biomech. 1996, 29, 69–79. [Google Scholar] [CrossRef]
- Fondrk, M.T.; Bahniuk, E.H.; Davy, D.T. A Damage Model for Nonlinear Tensile Behavior of Cortical Bone. J. Biomech. Eng. 1999, 121, 533–541. [Google Scholar] [CrossRef] [PubMed]
- Garcia, D.; Zysset, P.K.; Charlebois, M.; Curnier, A. A 1D elastic plastic damage constitutive law for bone tissue. Arch. Appl. Mech. 2009, 80, 543–555. [Google Scholar] [CrossRef]
- Ramtani, S. Damaged elastic bone-column buckling theory within the context of adaptive elasticity. Mech. Res. Commun. 2018, 88, 1–6. [Google Scholar] [CrossRef]
- Ramtani, S.; Zidi, M. Damaged-bone remodeling theory: Thermodynamical Approach. Mech. Res. Commun. 1999, 26, 701–708. [Google Scholar] [CrossRef]
- Hosseini, H.S.; Horák, M.; Zysset, P.K.; Jirásek, M. An over-nonlocal implicit gradient-enhanced damage-plastic model for trabecular bone under large compressive strains. Int. J. Numer. Methods Biomed. Eng. 2015, 31, e02728. [Google Scholar] [CrossRef] [PubMed]
- Martínez, G.; García-Aznar, J.M.; Doblaré, M.; Cerrolaza, M. External bone remodeling through boundary elements and damage mechanics. Math. Comput. Simul. 2006, 73, 183–199. [Google Scholar] [CrossRef]
- Mengoni, M.; Ponthot, J.P. An enhanced version of a bone-remodelling model based on the continuum damage mechanics theory. Comput. Methods Biomech. Biomed. Eng. 2015, 18, 1367–1376. [Google Scholar] [CrossRef] [PubMed]
- Campo, M.; Fernández, J.R.; Kuttler, K.L.; Shillor, M.; Via no, J.M. Numerical analysis and simulations of a dynamic frictionless contact problem with damage. Comput. Methods Appl. Mech. Eng. 2006, 196, 476–488. [Google Scholar] [CrossRef]
- Ciarlet, P.G. Basic error estimates for elliptic problems. In Handbook of Numerical Analysis; Ciarlet, P.G., Lions, J.L., Eds.; North-Holland: Amsterdam, The Netherlands, 1993; Volume II, pp. 17–351. [Google Scholar]
- García, D. Elastic Plastic Damage Laws for Cortical Bone. Ph.D. Thesis, Lausanne, École Polytechnique Fédérale de Lausanne, Lausanne, Switzerland, 2006. [Google Scholar]

| 0.1 | 0.01 | 0.001 | 0.0001 | |
|---|---|---|---|---|
| 13.5490 | 13.5613 | 13.561268 | 13.561268 | |
| 6.6596 | 6.6679 | 6.667863 | 6.667863 | |
| 3.3080 | 3.3054 | 3.305386 | 3.305386 | |
| 1.6641 | 1.6457 | 1.645661 | 1.645661 | |
| 0.8460 | 0.8210 | 0.821036 | 0.821036 | |
| 0.4370 | 0.4099 | 0.409942 | 0.409942 | |
| 0.2328 | 0.2046 | 0.204565 | 0.204565 | |
| 0.1315 | 0.1017 | 0.101652 | 0.101653 | |
| 0.0822 | 0.0496 | 0.049597 | 0.049596 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Baldonedo, J.; Fernández, J.R.; López-Campos, J.A.; Segade, A. Analysis of Damage Models for Cortical Bone. Appl. Sci. 2019, 9, 2710. https://doi.org/10.3390/app9132710
Baldonedo J, Fernández JR, López-Campos JA, Segade A. Analysis of Damage Models for Cortical Bone. Applied Sciences. 2019; 9(13):2710. https://doi.org/10.3390/app9132710
Chicago/Turabian StyleBaldonedo, Jacobo, José R. Fernández, José A. López-Campos, and Abraham Segade. 2019. "Analysis of Damage Models for Cortical Bone" Applied Sciences 9, no. 13: 2710. https://doi.org/10.3390/app9132710
APA StyleBaldonedo, J., Fernández, J. R., López-Campos, J. A., & Segade, A. (2019). Analysis of Damage Models for Cortical Bone. Applied Sciences, 9(13), 2710. https://doi.org/10.3390/app9132710






