Individualized Interaural Feature Learning and Personalized Binaural Localization Model †
Abstract
1. Introduction
2. Individualized Feature Selection Using Mutual Information
2.1. Mutual Information Computation
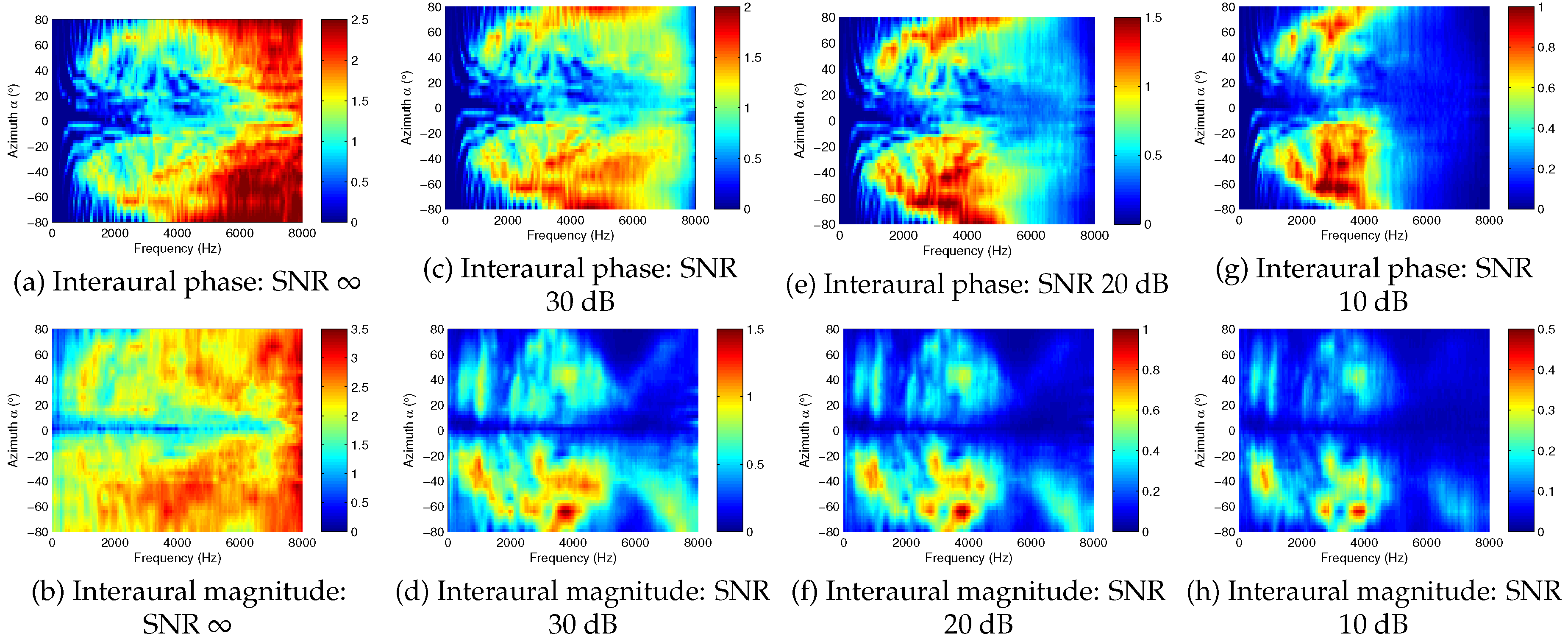
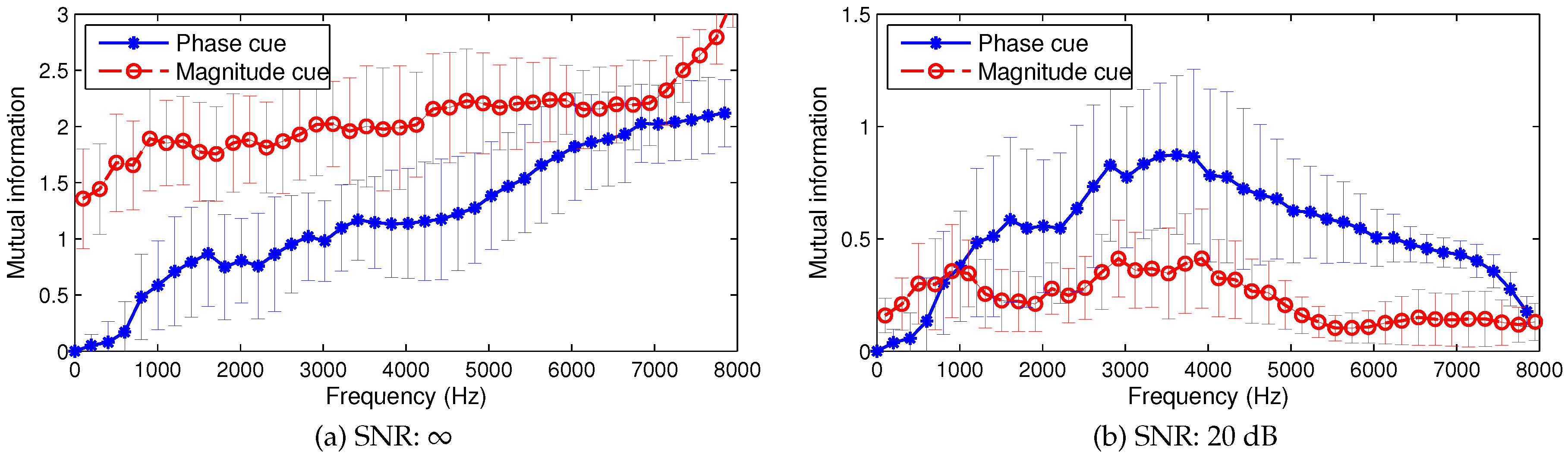
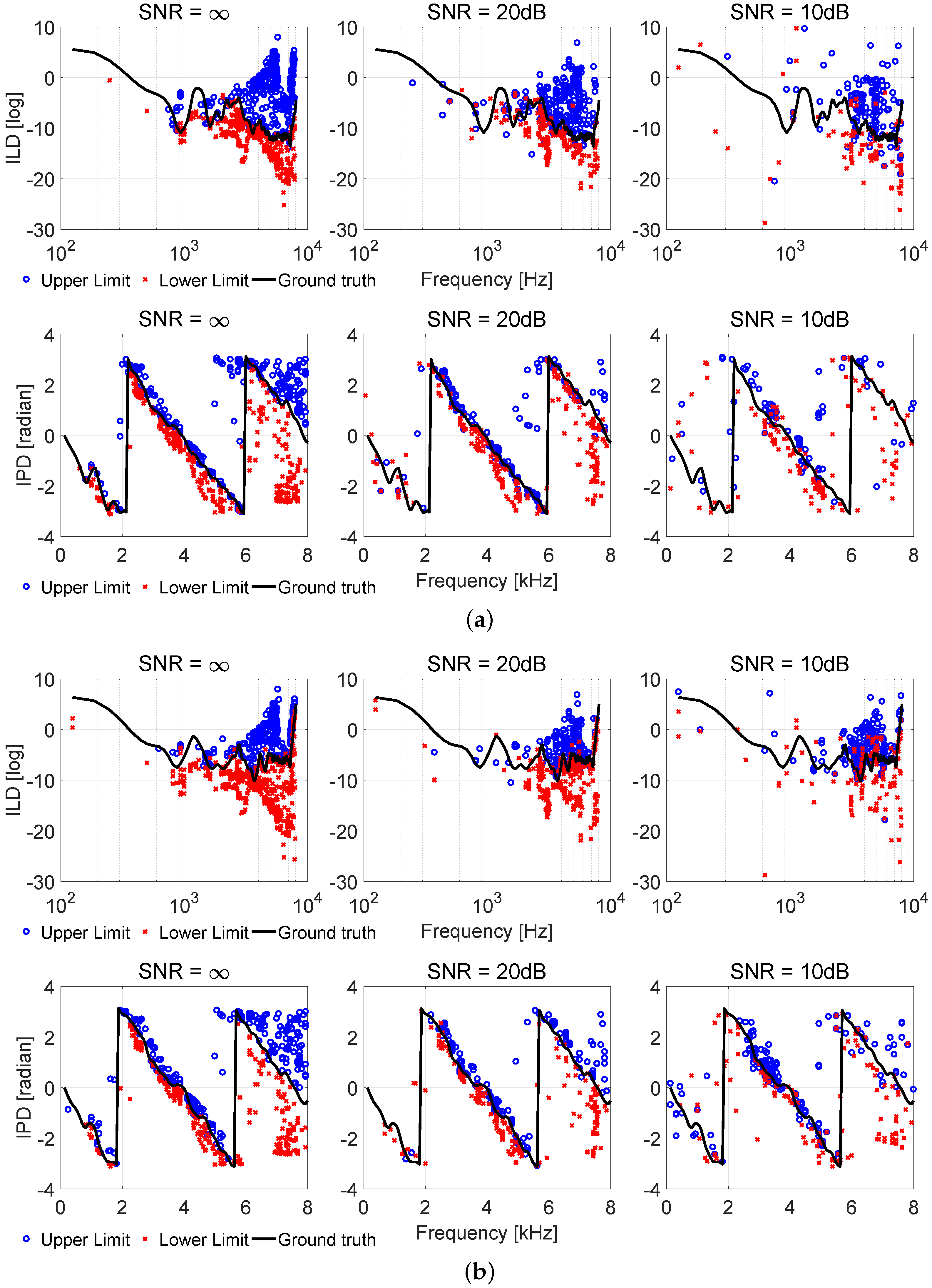
2.2. Analysis of Mutual Information in Interaural Cues
2.3. Spatial Feature Learning and Selected Feature Vector
| Algorithm 1: Spatial feature learning for robust localization |
 |
3. Probabilistic Localization Model and System Design
4. Feature Dependency Analysis and Assembled Data Partition Model
4.1. Data Partition and Tree-Structured Model
4.2. Random Forest Bagging and Unbiased Probability Estimation
5. Model Training and Interpretation
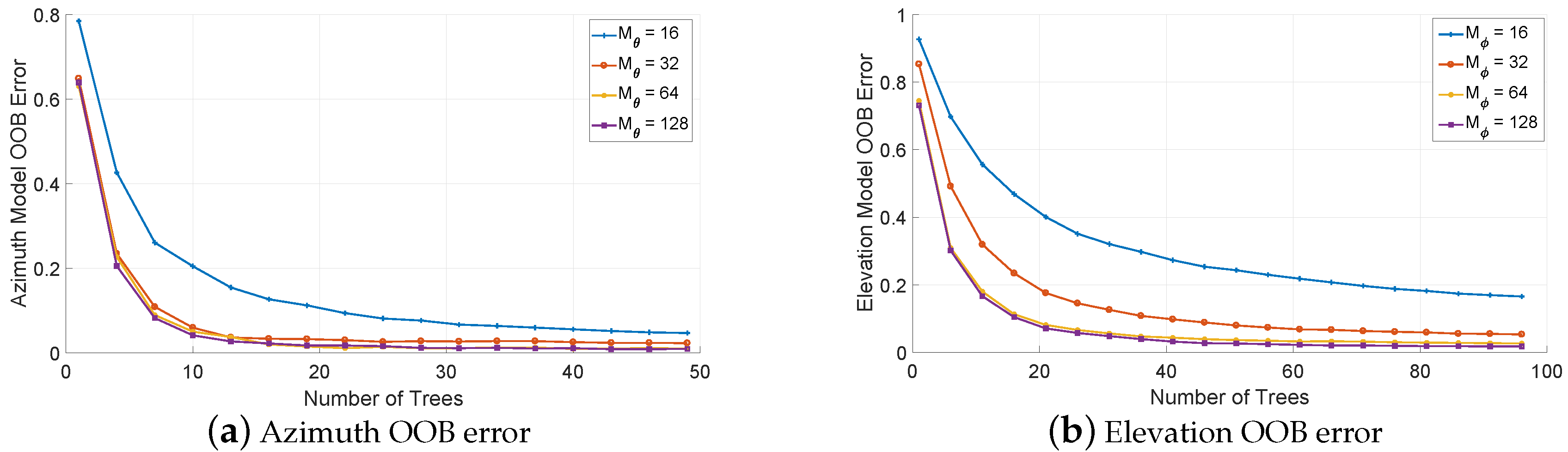
5.1. Model Training and Parameter Selection
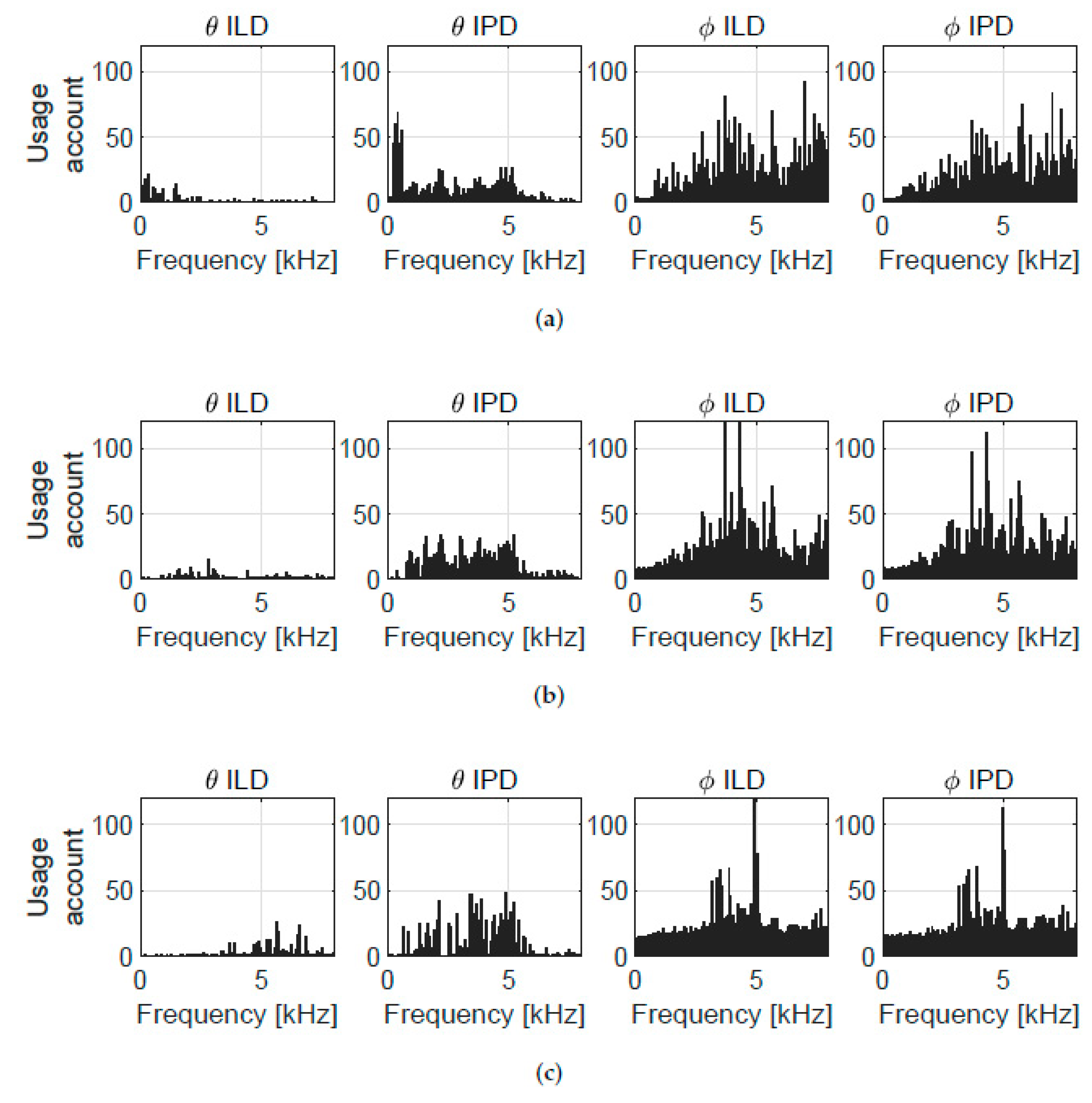
5.2. Trained Model Interpretation
6. Experiments With Simulated Data
6.1. 3-D Space Localization with Mutual Information–Based Feature Selection
6.1.1. Simulation Configuration
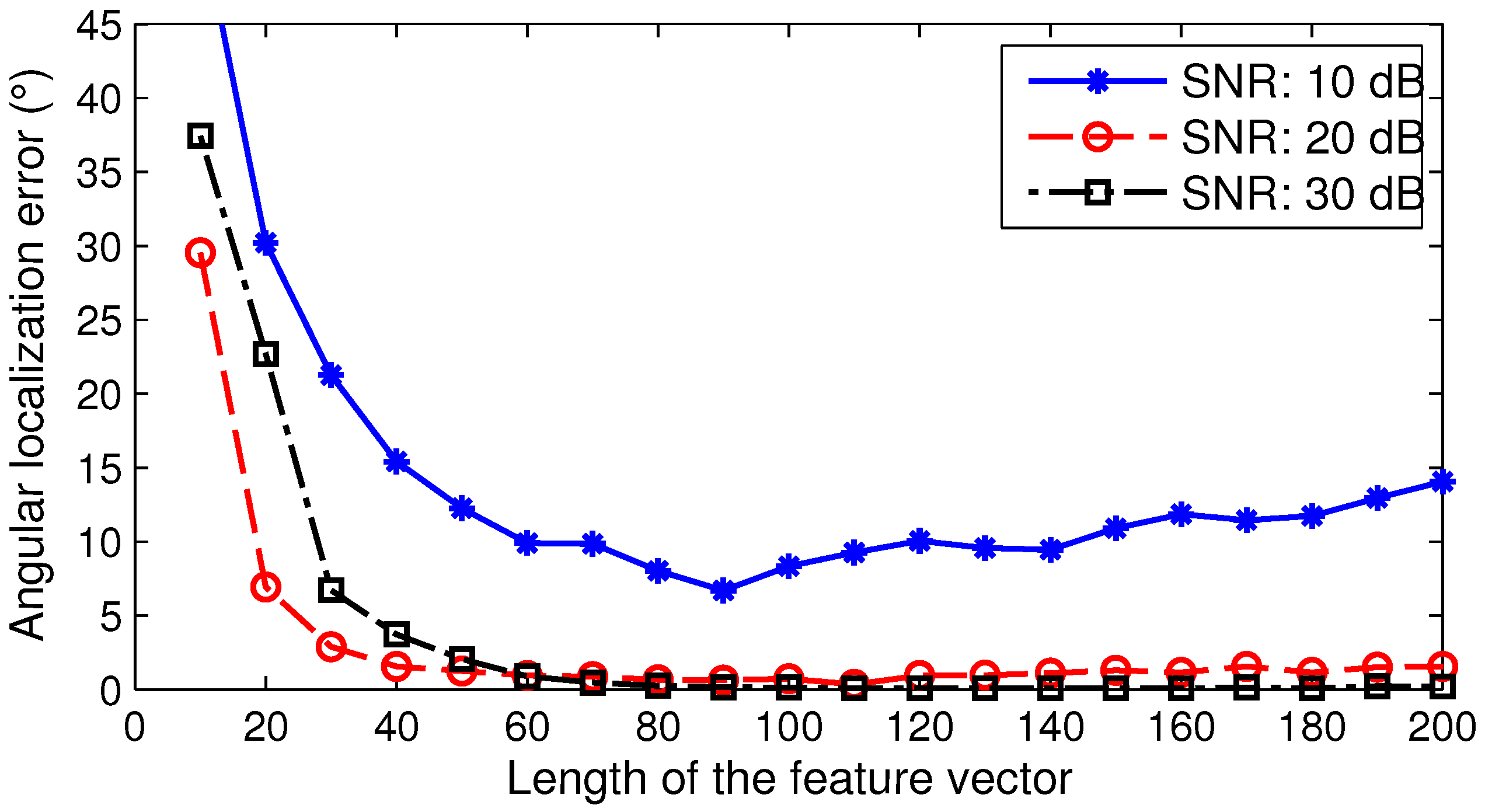
6.1.2. Performance Impact of the Feature Vector Length
6.1.3. Localization Performance
6.2. 3-D Space Localization with Probabilistic Model
6.2.1. Performance Measurements and Simulation Configuration
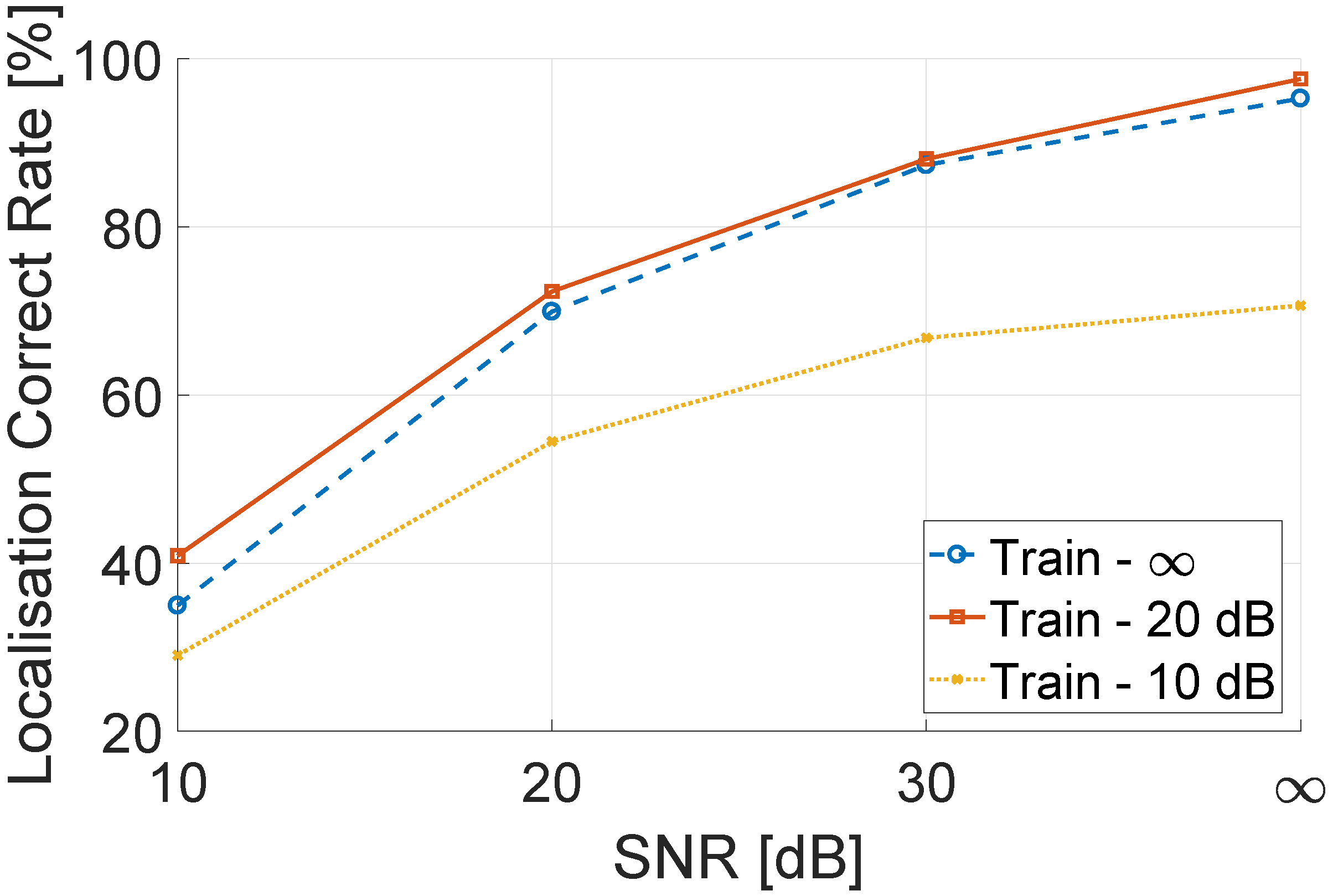
6.2.2. Localization Performance with Different Training Environment
6.2.3. Localization Performance with Additive Noise
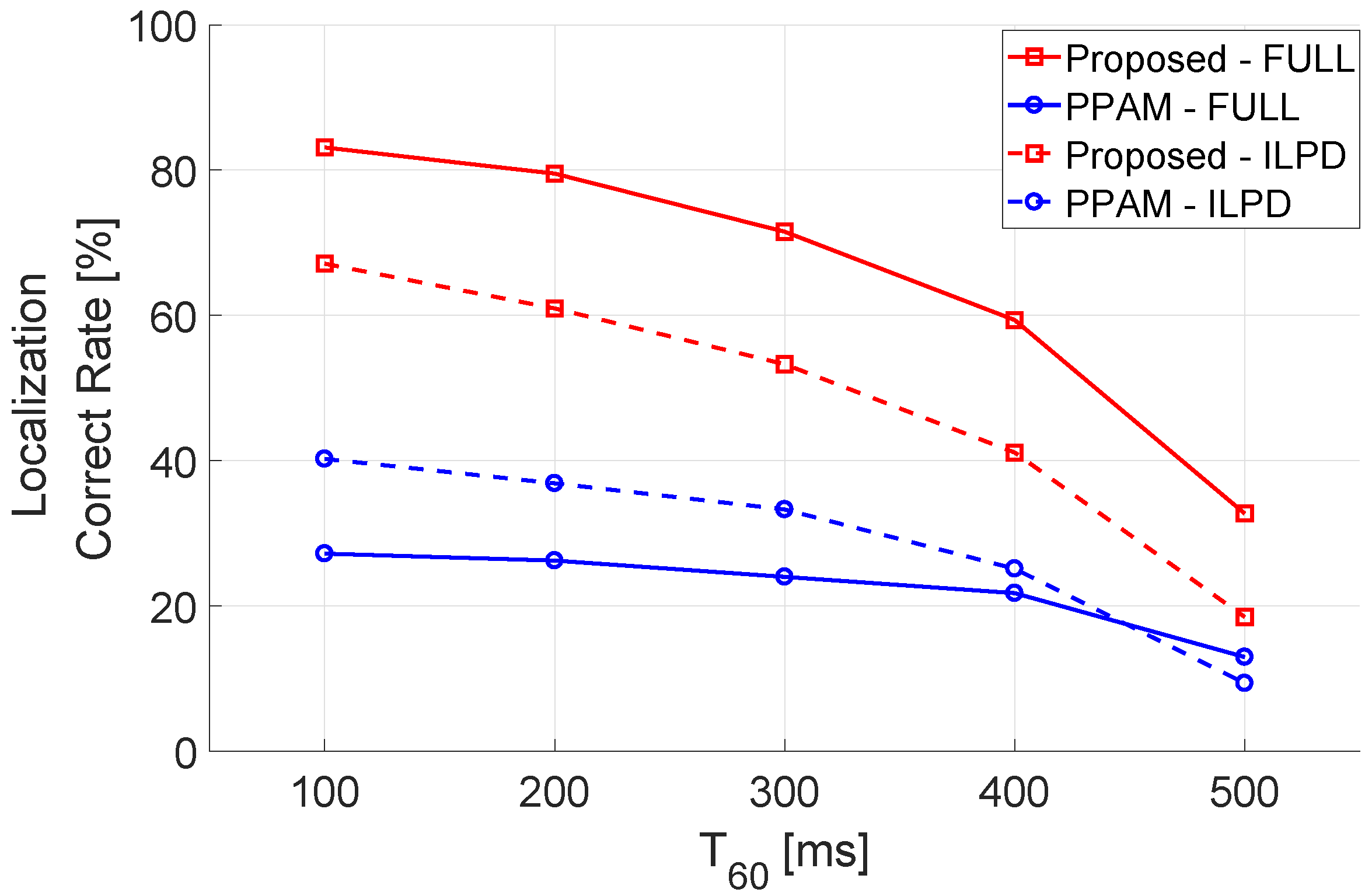
6.2.4. Localization Performance with Reverberations
7. Experiment in Laboratory Environment
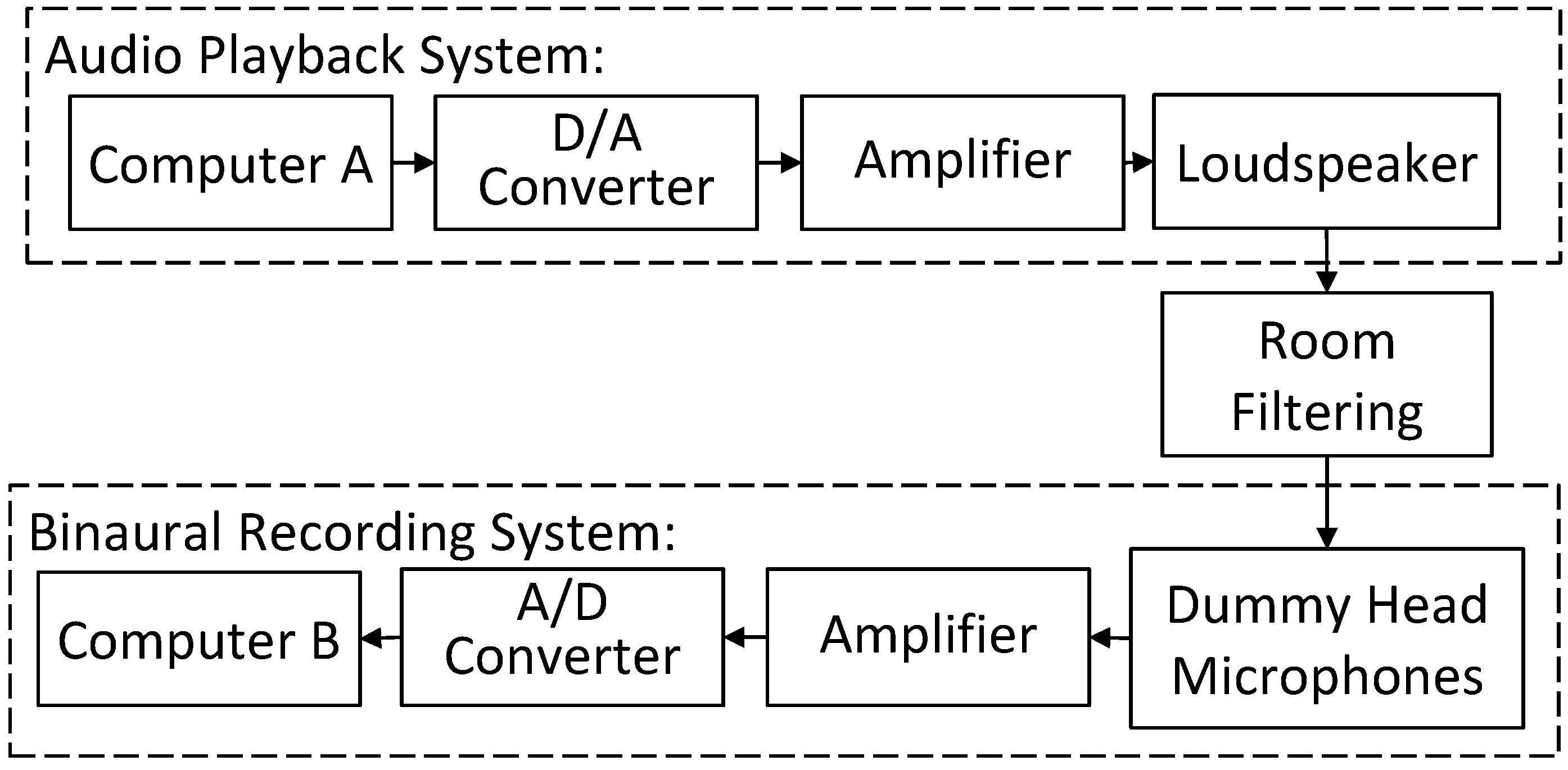
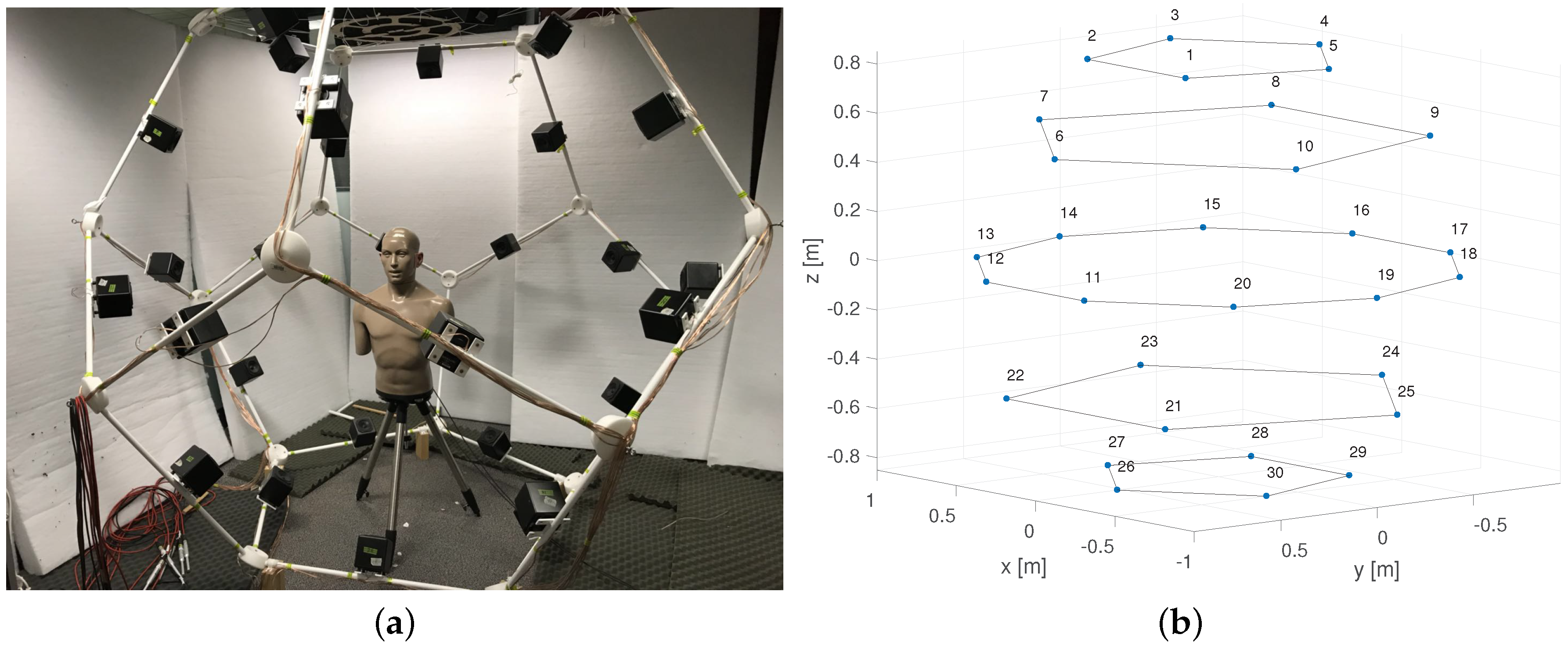
7.1. Experiment Facility and Room Configurations
7.2. Testing Positions and Microphone Data Pre-Processing
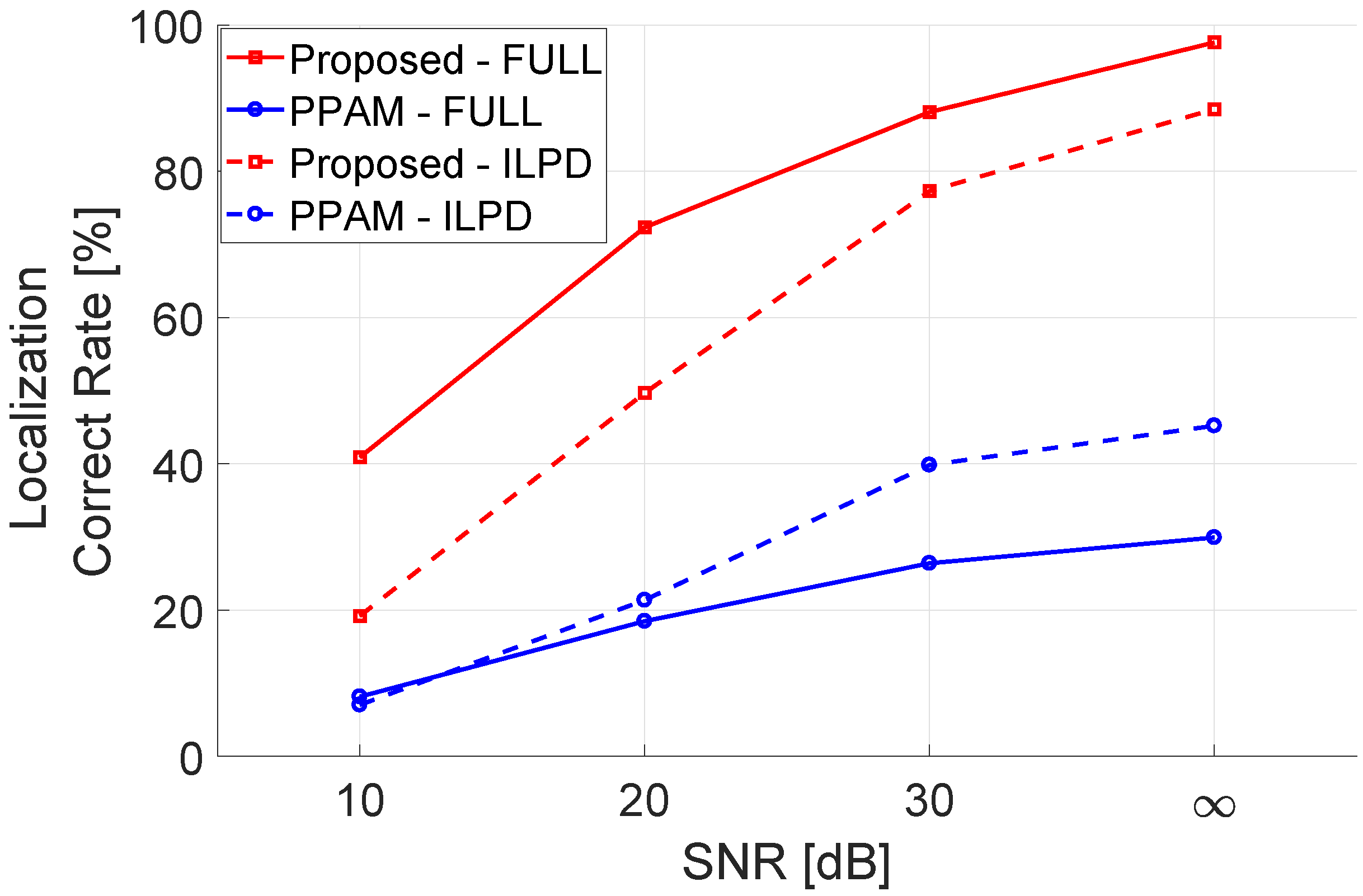
7.3. Experiment Result
8. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Xie, B. Head-Related Transfer Function and Virtual Auditory Display; J. Ross Publishing: Plantation, FL, USA, 2013. [Google Scholar]
- Gan, W.S.; Peksi, S.; He, J.; Ranjan, R.; Hai, N.D.; Chaudhary, N.K. Personalized HRTF Measurement and 3D Audio Rendering for AR/VR Headsets. In Proceedings of the Audio Engineering Society 142nd International Convention Committee Announced, Berlin, Germany, 20–23 May 2017. [Google Scholar]
- Hai, N.D.; Chaudhary, N.K.; Peksi, S.; Ranjan, R.; He, J.; Gan, W. Fast HRFT measurement system with unconstrained head movements for 3D audio in virtual and augmented reality applications. In Proceedings of the 2017 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), New Orleans, LA, USA, 5–9 March 2017; pp. 6576–6577. [Google Scholar]
- Sunder, K.; Gan, W.S. Individualization of Head-Related Transfer Functions in the Median Plane using Frontal Projection Headphones. J. Audio Eng. Soc. 2016, 64, 1026–1041. [Google Scholar] [CrossRef]
- Reijniers, J.; Vanderelst, D.; Jin, C.; Carlile, S.; Peremans, H. An ideal-observer model of human sound localization. Biol. Cybern. 2014, 108, 169–181. [Google Scholar] [CrossRef] [PubMed]
- Pereira, F.; Martens, W.L. Psychophysical Validation of Binaurally Processed Sound Superimposed upon Environmental Sound via an Unobstructed Pinna and an Open-Ear-Canal Earspeaker. In Proceedings of the Audio Engineering Society Conference: 2018 AES International Conference on Spatial Reproduction—Aesthetics and Science, Tokyo, Japan, 7–9 August 2018. [Google Scholar]
- Gamper, H.; Tervo, S.; Lokki, T. Head Orientation Tracking Using Binaural Headset Microphones. In Proceedings of the Audio Engineering Society Convention 131, New York, NY, USA, 20–23 October 2011. [Google Scholar]
- Braasch, J.; Martens, W.L.; Woszczyk, W. Modeling auditory localization in the low-frequency range. J. Acoust. Soc. Am. 2005, 117, 2391. [Google Scholar] [CrossRef]
- Li, D.; Levinson, S.E. A Bayes-rule based hierarchical system for binaural sound source localization. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Hong Kong, China, 6–10 April 2003; Volume 5, pp. 521–524. [Google Scholar]
- Raspaud, M.; Viste, H.; Evangelista, G. Binaural Source Localization by Joint Estimation of ILD and ITD. IEEE Trans. Audio Speech Lang. Process. 2010, 18, 68–77. [Google Scholar] [CrossRef]
- Woodruff, J.; Wang, D. Binaural Localization of Multiple Sources in Reverberant and Noisy Environments. IEEE Trans. Audio Speech Lang. Process. 2012, 20, 1503–1512. [Google Scholar] [CrossRef]
- Duda, R.O. Elevation dependence of the interaural transfer function. In Binaural and Spatial Hearing in Real and Virtual Environments; Psychology Press: New York, NY, USA, 1997; pp. 49–75. [Google Scholar]
- Keyrouz, F. Advanced Binaural Sound Localization in 3-D for Humanoid Robots. IEEE Trans. Instrum. Meas. 2014, 63, 2098–2107. [Google Scholar] [CrossRef]
- Keyrouz, F.; Diepold, K. An enhanced binaural 3D sound localization algorithm. In Proceedings of the 2006 IEEE International Symposium on Signal Processing and Information Technology, Vancouver, BC, Canada, 27–30 August 2006; pp. 663–665. [Google Scholar]
- Zhang, J.; Liu, H. Robust Acoustic Localization Via Time-Delay Compensation and Interaural Matching Filter. IEEE Trans. Signal Process. 2015, 63, 4771–4783. [Google Scholar] [CrossRef]
- Liu, H.; Zhang, J.; Fu, Z. A new hierarchical binaural sound source localization method based on Interaural Matching Filter. In Proceedings of the IEEE International Conference on Robotics and Automation, Hong Kong, China, 31 May–7 June 2014; pp. 1598–1605. [Google Scholar]
- Deleforge, A.; Forbes, F. Acoustic space learning for sound-source separation and localization on binaural manifolds. Int. J. Neural Syst. 2015, 25. [Google Scholar] [CrossRef] [PubMed]
- Deleforge, A.; Horaud, R. 2D sound-source localization on the binaural manifold. In Proceedings of the IEEE International Workshop on Machine Learning for Signal Processing, Santander, Spain, 23–26 September 2012; pp. 1–6. [Google Scholar]
- Weng, J.; Guentchev, K.Y. Three-dimensional sound localization from a compact non-coplanar array of microphones using tree-based learning. J. Acoust. Soc. Am. 2001, 110, 310–323. [Google Scholar] [CrossRef] [PubMed]
- Algazi, V.R.; Avendano, C.; Duba, R.O. Elevation localization and head-related transfer function analysis at low frequencies. J. Acoust. Soc. Am. 2001, 109, 1110–1122. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Girin, L.; Horaud, R.; Gannot, S. Estimation of the Direct-Path Relative Transfer Function for Supervised Sound-Source Localization. IEEE Trans. Audio Speech Lang. Process. 2016, 24, 2171–2186. [Google Scholar] [CrossRef]
- Parisi, R.; Camoes, F.; Scarpiniti, M.; Uncini, A. Cepstrum prefiltering for binaural source localization in reverberant environments. IEEE Signal Process. Lett. 2012, 19, 99–102. [Google Scholar] [CrossRef]
- Westermann, A.; Buchholz, J.M.; Dau, T. Binaural dereverberation based on interaural coherence histograms. J. Acoust. Soc. Am. 2013, 133, 2767–2777. [Google Scholar] [CrossRef] [PubMed]
- Algazi, V.R.; Duda, R.O.; Thompson, D.M.; Avendano, C. The CIPIC HRTF database. In Proceedings of the IEEE ASSP Workshop on Applications of Signal Processing to Audio and Acoustics (WASPAA), New Platz, NY, USA, 24 October 2001; pp. 99–102. [Google Scholar]
- Wu, X.; Talagala, D.S.; Zhang, W.; Abhayapala, T.D. Binaural localization of speech sources in 3-D using a composite feature vector of the HRTF. In Proceedings of the 2015 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Brisbane, QLD, Australia, 19–24 April 2015; pp. 2654–2658. [Google Scholar]
- Hanchuan, P.; Fuhui, L.; Chris, D. Feature Selection Based on Mutual Information: criteria of Max-Dependency, Max-Relevance, and Min-Redundancy. IEEE Trans. Pattern Anal. Mach. Intell. 2005, 27, 1226–1238. [Google Scholar] [CrossRef] [PubMed]
- Vinh, L.T.; Lee, S.; Part, Y.T.; Auriol, B. A novel feature selection mehtod based on normalized mutual information. Springer Appl. Intell. 2012, 37, 100–120. [Google Scholar] [CrossRef]
- Fan, W.; Greengrass, E.; McCloskey, J.; Yu, P.S.; Drammey, K. Effective estimation of posterior probabilities: explaining the accuracy of randomized decision tree approaches. In Proceedings of the IEEE International Conference on Data Mining (ICDM’05), Houston, TX, USA, 27–30 November 2005; p. 8. [Google Scholar]
- Kamkar-Parsi, A.; Bouchard, M. Improved Noise Power Spectrum Density Estimation for Binaural Hearing Aids Operating in a Diffuse Noise Field Environment. IEEE Trans. Audio Speech Lang. Process. 2009, 17, 521–533. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Keyrouz, F.; Naous, Y.; Diepold, K. A new method for binaural 3-D localization based on HRTFs. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Toulouse, France, 14–19 May 2006; Volume 5, pp. 341–344. [Google Scholar]
- Barker, J.; Vincent, E.; Ma, N.; Christensen, H.; Green, P. The PASCAL CHiME speech separation and recognition challenge. Comput. Speech Lang. 2013, 27, 621–633. [Google Scholar] [CrossRef]
- Raykar, V.C.; Duraiswami, R.; Yegnanarayana, B. Extracting the frequencies of the pinna spectral notches in measured head related impulse responses. J. Acoust. Soc. Am 2005, 118, 364–374. [Google Scholar] [CrossRef] [PubMed]
- Campbell, R.D.; Palomki, K.J.; Brown, G. A MATLAB Simulation of “Shoebox” Room Acoustics for Use in Research and Teaching. Comput. Inf. Syst. 2005, 9, 48–51. [Google Scholar]

| Localization Approach | Mean Angular Localization Error | ||
|---|---|---|---|
| 10 dB | 20 dB | 30 dB | |
| Proposed learning | 5.63 | 0.89 | 0.14 |
| Composite feature [25] | 24.30 | 5.11 | 0.85 |
| Cross-Correlation [31] | 67.65 | 58.55 | 51.58 |
| (a) Azimuth Accuracy Comparison | ||||||||
| SNR | No Noise | 30 dB | 20 dB | 10 dB | ||||
| Tolerance | ≤2.5 | ≤5 | ≤2.5 | ≤5 | ≤2.5 | ≤5 | ≤2.5 | ≤5 |
| Proposed - FULL | ||||||||
| PPAM - FULL | 73.84% | |||||||
| Proposed - ILPD | ||||||||
| PPAM - ILPD | 73.84% | |||||||
| (b) Elevation Accuracy Comparison | ||||||||
| SNR | No Noise | 30 dB | 20 dB | 10 dB | ||||
| Tolerance | ≤2.5 | ≤6 | ≤2.5 | ≤6 | ≤2.5 | ≤6 | ≤2.5 | ≤6 |
| Proposed - FULL | ||||||||
| PPAM - FULL | ||||||||
| Proposed - ILPD | ||||||||
| PPAM - ILPD | ||||||||
| (a) Azimuth Accuracy Comparison | ||||||||
| 200 ms | 300 ms | 400 ms | 500 ms | |||||
| Tolerance | ≤2.5 | ≤5 | ≤2.5 | ≤5 | ≤2.5 | ≤5 | ≤2.5 | ≤5 |
| Proposed - FULL | ||||||||
| PPAM - FULL | ||||||||
| Proposed - ILPD | ||||||||
| PPAM - ILPD | 83.92% | |||||||
| (b) Elevation Accuracy Comparison | ||||||||
| 200 ms | 300 ms | 400 ms | 500 ms | |||||
| Tolerance | ≤2.5 | ≤6 | ≤2.5 | ≤6 | ≤2.5 | ≤6 | ≤2.5 | ≤6 |
| Proposed - FULL | ||||||||
| PPAM - FULL | 24.80% | |||||||
| Proposed - ILPD | ||||||||
| PPAM - ILPD | ||||||||
| Loudspeaker No. | True Azimuth | True Elevation | Estimated Azimuth | Estimated Elevation | Estimated Error |
|---|---|---|---|---|---|
| 1 | 63.44 | 81.68 | 35.25 | ||
| 2 | 18.00 | 63.44 | 20.00 | 67.50 | 4.33 |
| 3 | 30.00 | 100.82 | 30.00 | 71.43 | 31.53 |
| 4 | 0.00 | 121.72 | 123.75 | 2.03 | |
| 5 | 100.82 | 84.38 | 14.04 | ||
| 6 | 0.00 | 31.72 | 0.00 | 33.75 | 2.03 |
| 7 | 54.00 | 63.44 | 55.00 | 60.19 | 3.56 |
| 8 | 30.00 | 142.62 | 30.00 | 140.63 | 1.73 |
| 9 | 142.62 | 135.56 | 6.11 | ||
| 10 | 63.44 | 59.06 | 2.82 | ||
| 11 | 0.00 | 0.00 | 2.00 | ||
| 12 | 18.00 | 0.00 | 19.50 | 10.69 | 11.88 |
| 13 | 54.00 | 0.00 | 55.00 | 0.00 | 1.48 |
| 14 | 90.00 | 0.00 | 80.00 | 10.00 | |
| 15 | 54.00 | 180.00 | 55.00 | 194.06 | 9.61 |
| 16 | 18.00 | 180.00 | 20.00 | 177.75 | 3.47 |
| 17 | 180.00 | 157.50 | 24.36 | ||
| 18 | 180.00 | 182.81 | 2.21 | ||
| 19 | 0.00 | 10.00 | |||
| 20 | 0.00 | 1.69 | 2.69 | ||
| 21 | 1.87 | ||||
| 22 | 30.00 | 30.00 | 3.14 | ||
| 23 | 54.00 | 243.43 | 55.00 | 168.75 | 41.26 |
| 24 | 0.00 | 211.74 | 219.38 | 9.14 | |
| 25 | 243.43 | 101.25 | 66.65 | ||
| 26 | 0.00 | 0.00 | 24.54 | ||
| 27 | 30.00 | 30.00 | 73.13 | 114.47 | |
| 28 | 18.00 | 243.43 | 20.00 | 196.88 | 43.93 |
| 29 | 243.43 | 157.50 | 80.27 | ||
| 30 | 39.08 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, X.; Talagala, D.S.; Zhang, W.; Abhayapala, T.D. Individualized Interaural Feature Learning and Personalized Binaural Localization Model. Appl. Sci. 2019, 9, 2682. https://doi.org/10.3390/app9132682
Wu X, Talagala DS, Zhang W, Abhayapala TD. Individualized Interaural Feature Learning and Personalized Binaural Localization Model. Applied Sciences. 2019; 9(13):2682. https://doi.org/10.3390/app9132682
Chicago/Turabian StyleWu, Xiang, Dumidu S. Talagala, Wen Zhang, and Thushara D. Abhayapala. 2019. "Individualized Interaural Feature Learning and Personalized Binaural Localization Model" Applied Sciences 9, no. 13: 2682. https://doi.org/10.3390/app9132682
APA StyleWu, X., Talagala, D. S., Zhang, W., & Abhayapala, T. D. (2019). Individualized Interaural Feature Learning and Personalized Binaural Localization Model. Applied Sciences, 9(13), 2682. https://doi.org/10.3390/app9132682





