Assessment of Crystallinity Development during Fused Filament Fabrication through Fast Scanning Chip Calorimetry
Abstract
1. Introduction
2. Materials and Methods
2.1. Printing of Wall Geometry
2.2. IR Thermography
2.3. Fast Scanning Chip Calorimetry
2.3.1. Device Specifications and Sample Preparation
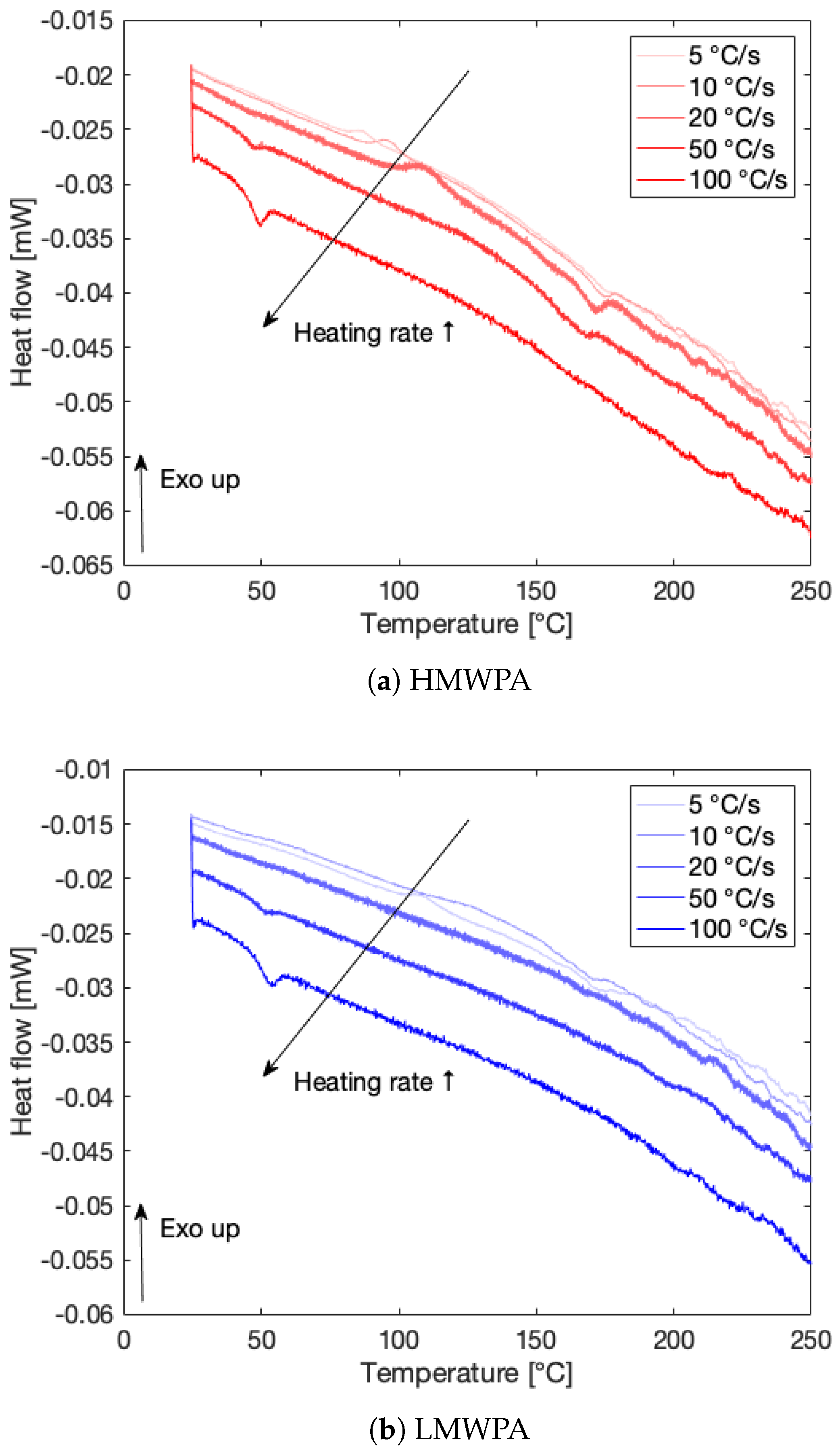
2.3.2. Determination of the Critical Heating and Cooling Rate
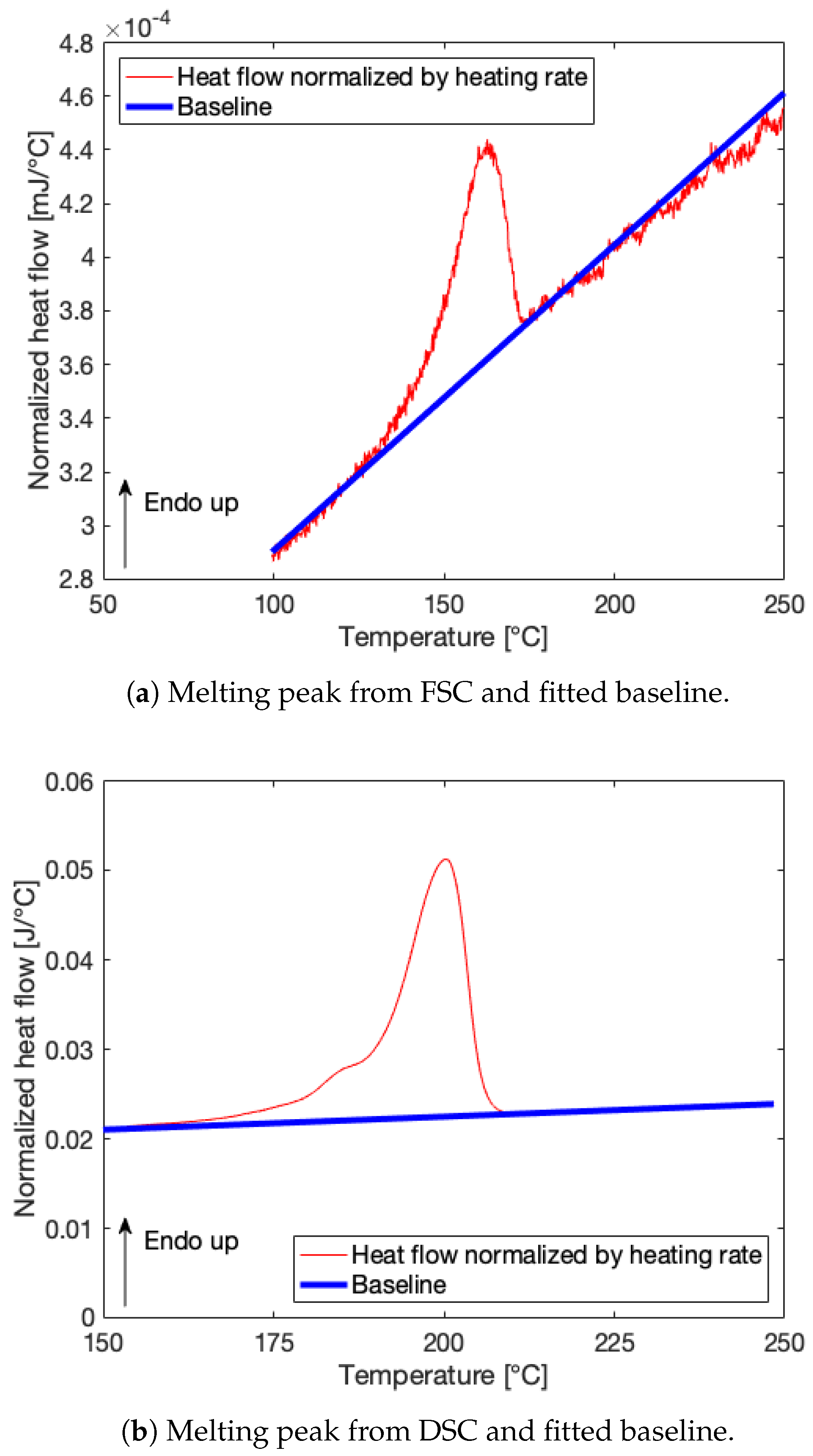
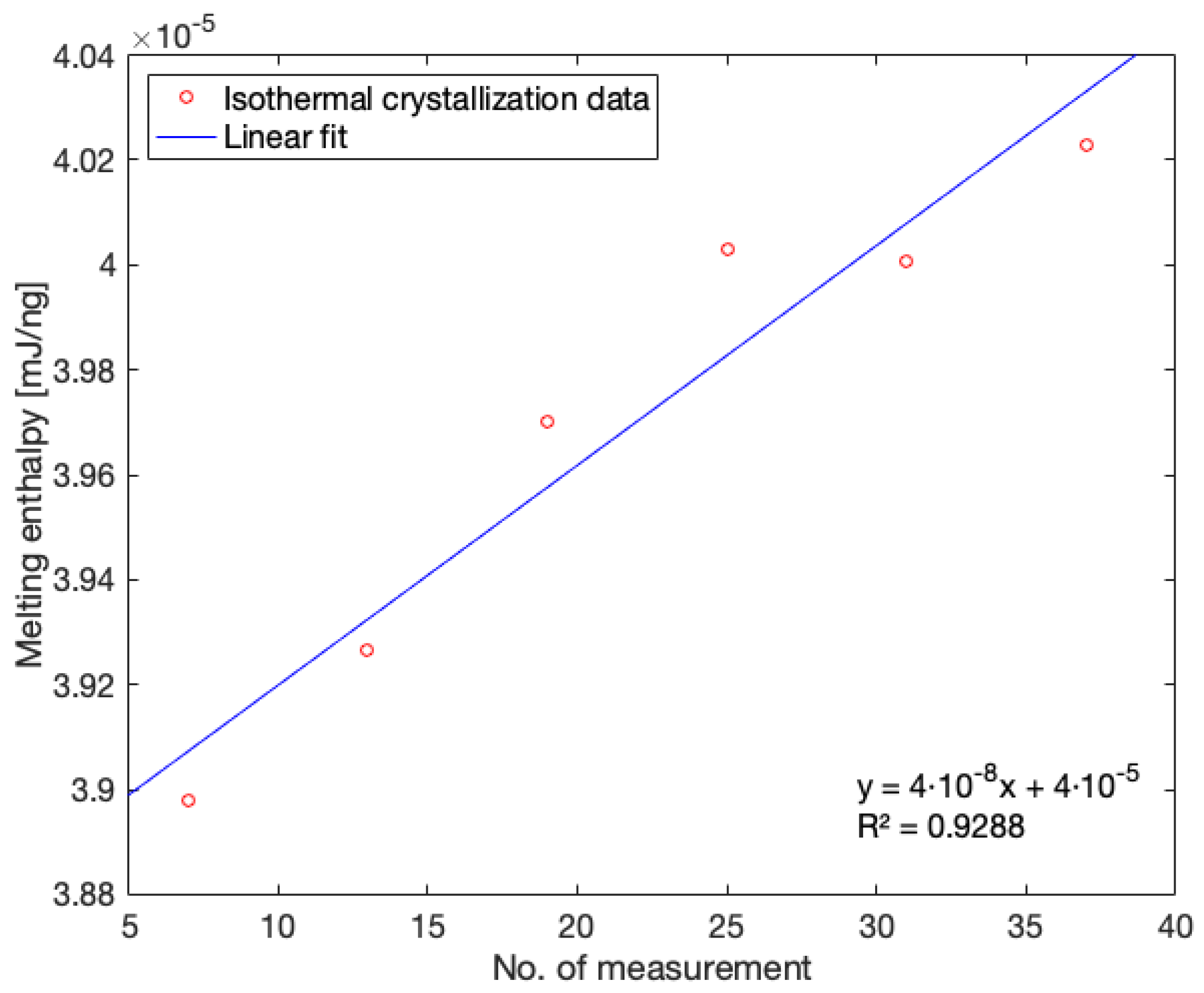
2.3.3. Correction for the Difference in FSC Chip Sample Mass Using DSC
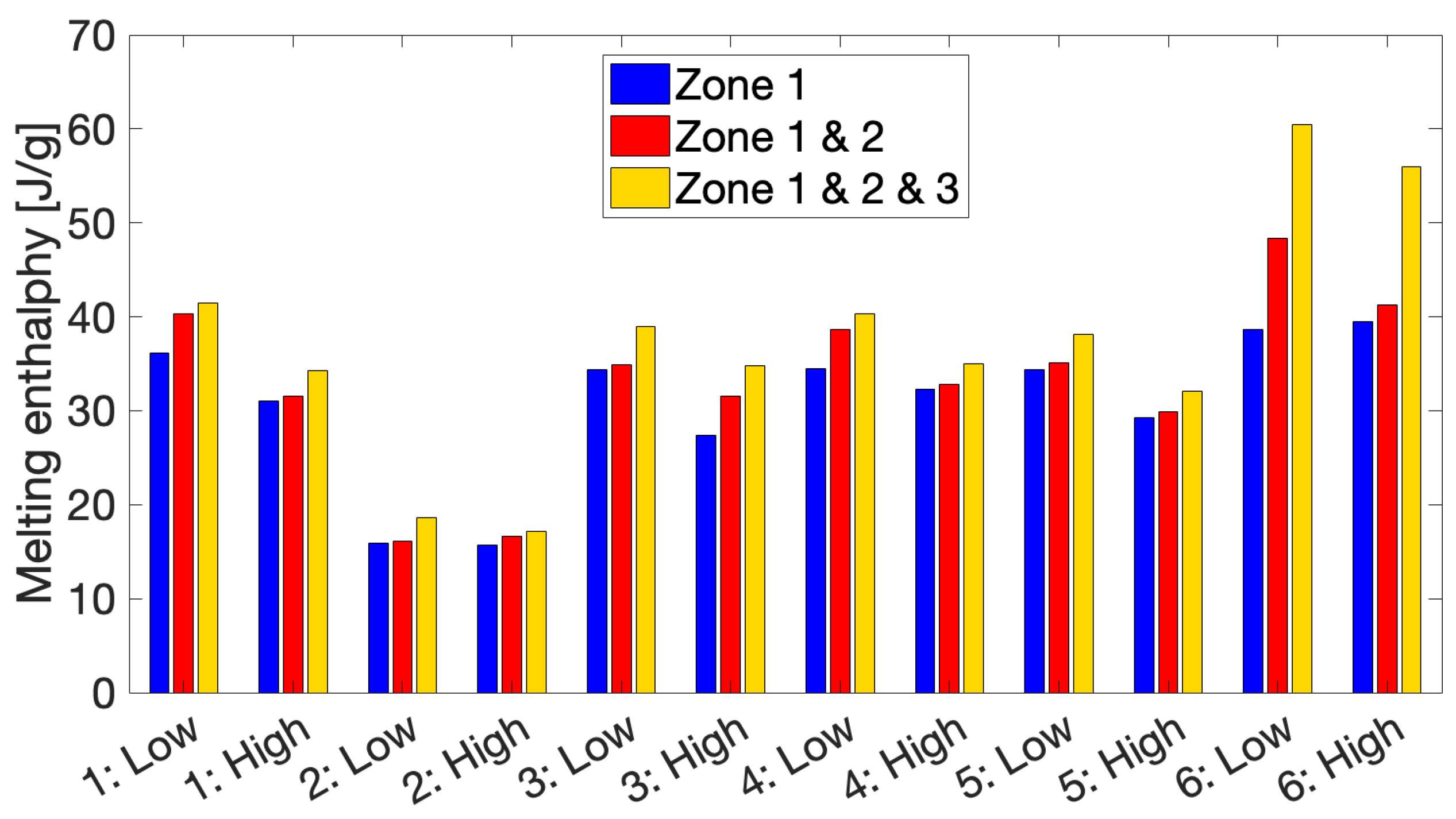
2.3.4. Isothermal Crystallization Measurements as a Reference
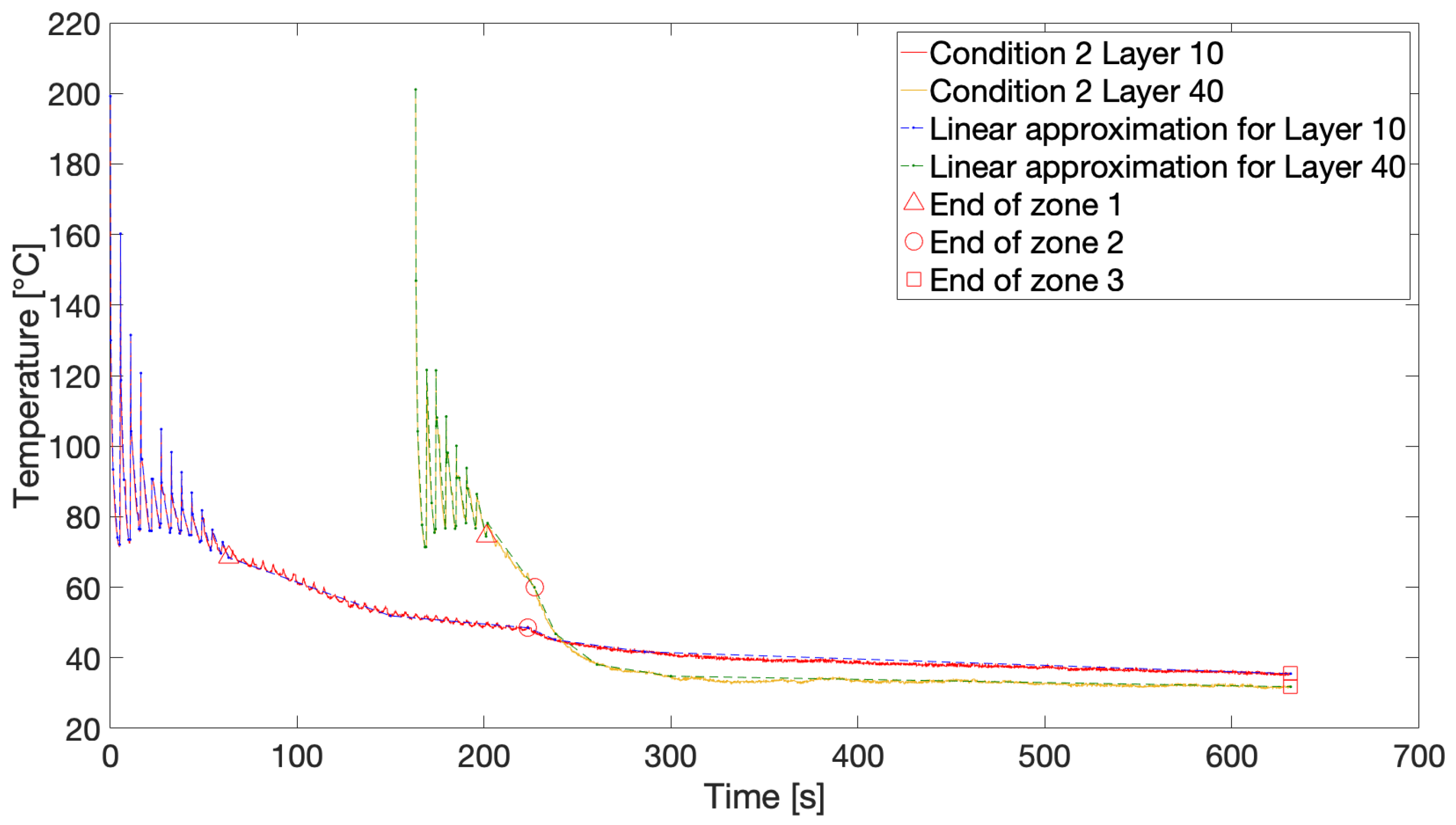
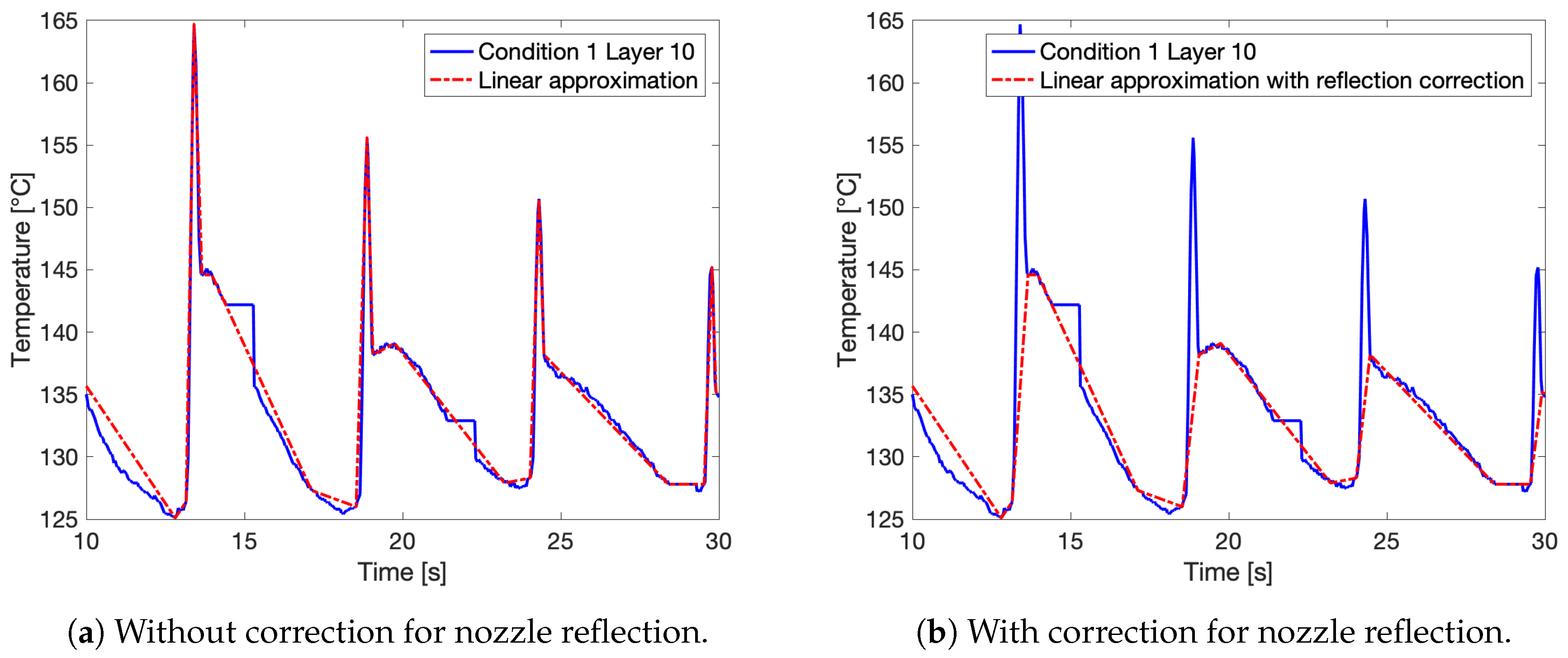
2.3.5. Simulation of IR Thermal Profiles
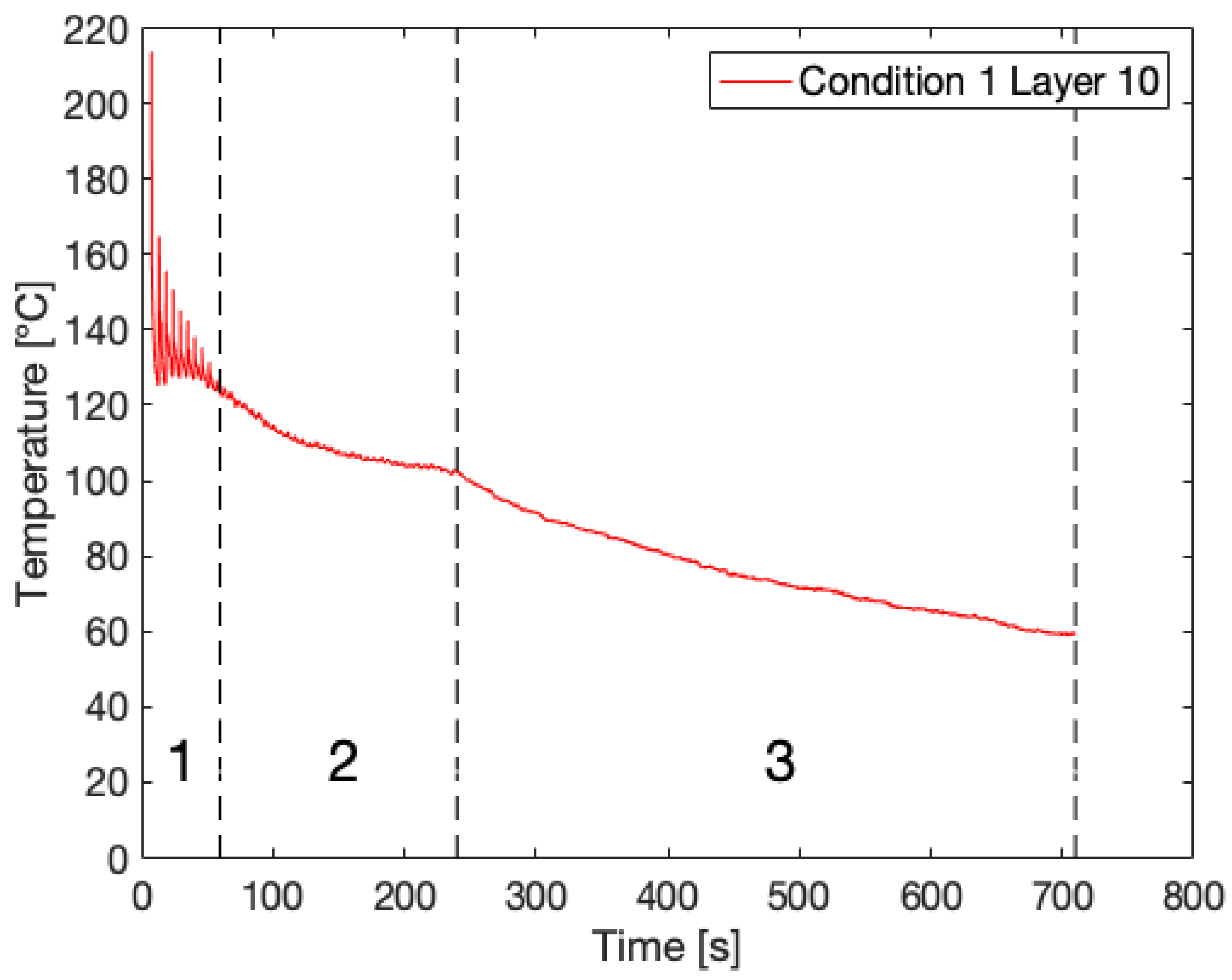
- after the cyclic heating and cooling at the beginning of the temperature profile, resulting from the deposition of new layers;
- after the print finished, i.e., the last layer was deposited; and
- at the end of the recorded temperature profile.
3. Results and Discussion
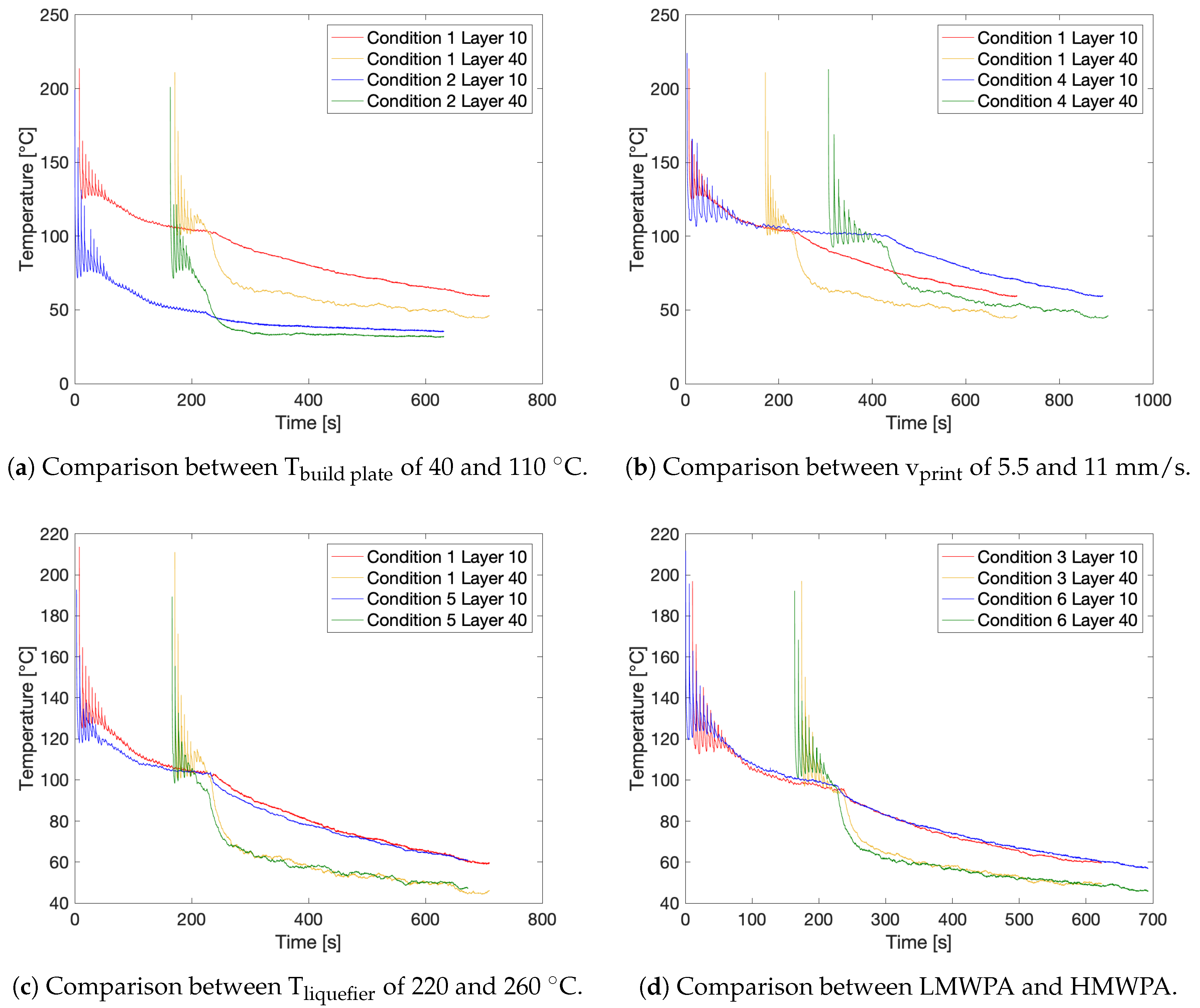
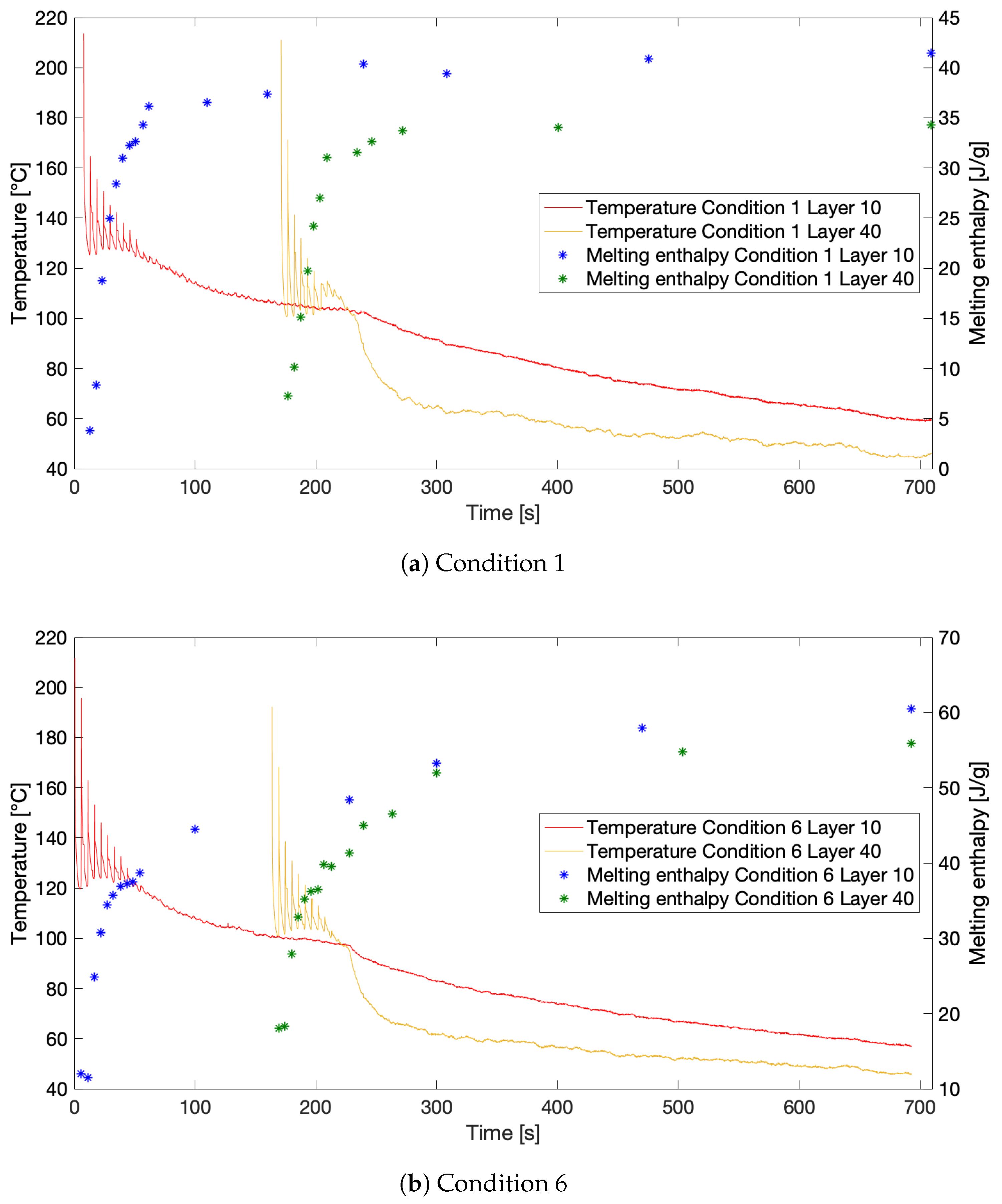
3.1. Thermal Monitoring of the FFF Process
3.2. Simulation of Thermal Profiles Using FSC
3.2.1. Critical Heating and Cooling Rate
3.2.2. Correction for Difference in Sample Mass
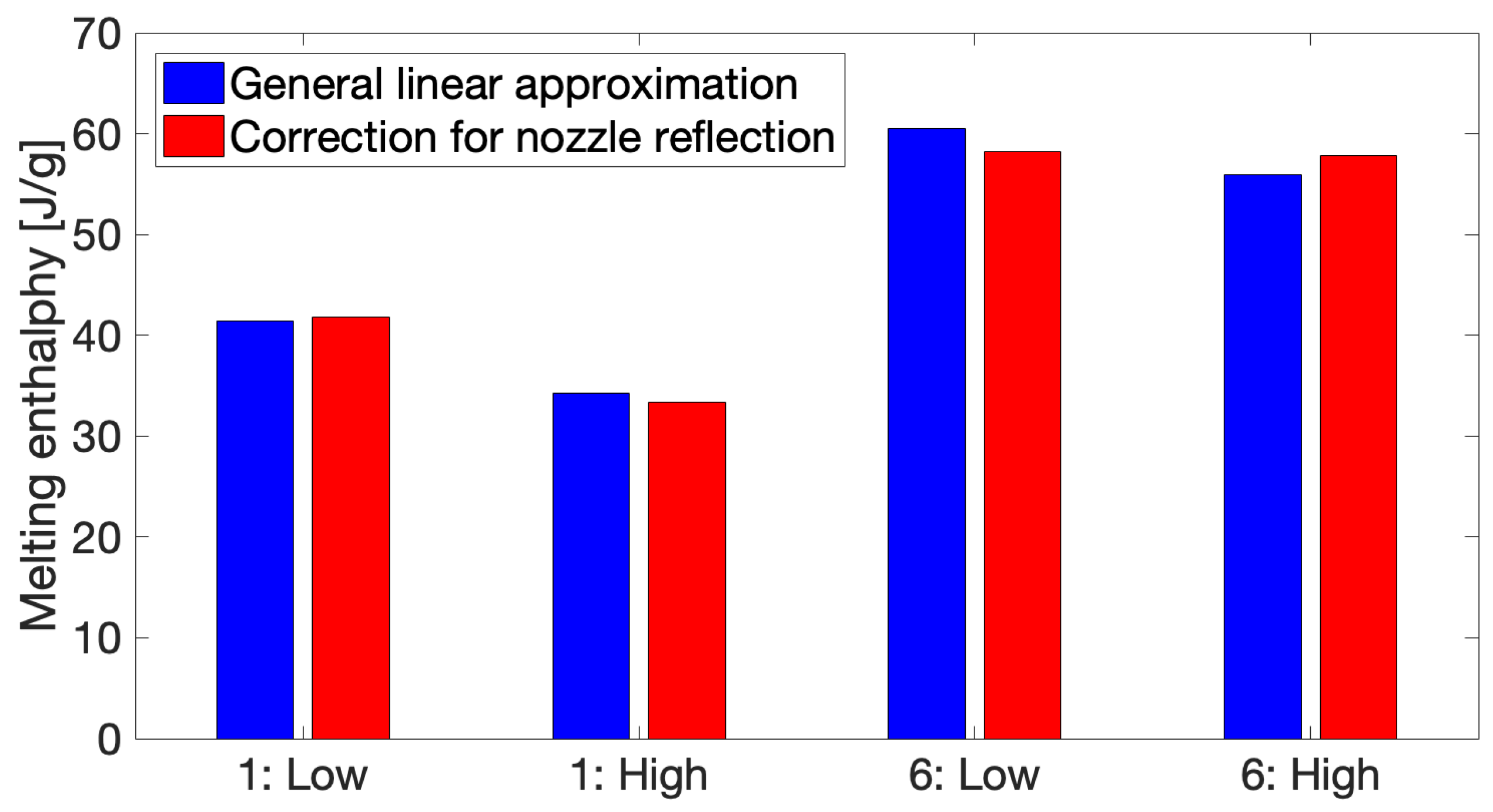
3.2.3. Correction for Drift Due to Sample Changes
3.2.4. Approximation of Thermal Profiles and Simulation in FSC
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| AM | Additive Manufacturing |
| 3D | Three-dimensional |
| CAD | Computer-aided-design |
| FFF | Fused Filament Fabrication |
| FDM | Fused Deposition Modeling |
| SLS | Selective Laser Sintering |
| SLA | Stereolithography |
| IR | Infrared |
| DSC | Differential Scanning Calorimetry |
| XRD | X-ray Diffraction |
| Tg | Glass transition temperature [°C] |
| FSC | Fast Scanning Chip Calorimetry |
| Mw | Weight average molecular weight [kg/mol] |
| Tm | Melting temperature [°C] |
| HMWPA | High molecular weight PA |
| LMWPA | Low molecular weight PA |
| Tliquefier | Liquefier temperature [°C] |
| Tbuild plate | Build plate temperature [°C] |
| vprint | Print speed [mm/s] |
| mFSC | FSC sample mass [ng] |
| mDSC | DSC sample mass [mg] |
| Hm,FSC | FSC melting enthalpy [mJ] |
| Hm,DSC | DSC melting enthalpy [J] |
References
- Ligon, S.C.; Liska, R.; Stampfl, J.; Gurr, M.; Mülhaupt, R. Polymers for 3D Printing and Customized Additive Manufacturing. Chem. Rev. 2017, 117, 10212–10290. [Google Scholar] [CrossRef] [PubMed]
- Gao, W.; Zhang, Y.; Ramanujan, D.; Ramani, K.; Chen, Y.; Williams, C.B.; Wang, C.C.; Shin, Y.C.; Zhang, S.; Zavattieri, P.D. The status, challenges, and future of additive manufacturing in engineering. Comput. Aided Des. 2015, 69, 65–89. [Google Scholar] [CrossRef]
- Wohlers, T. Wohlers Report 2012: Additive Manufacturing and 3D Printing State of Industry; Annual worldwide progress report; Wohlers Associates, Inc.: Fort Collins, CO, USA, 2012. [Google Scholar]
- Scott, J.; Gupta, N.; Wember, C.; Newsom, S.; Wohlers, T.; Caffrey, T. Additive Manufacturing: Status and Opportunities; Technical report; Science and Technology Policy Institute: Alexandria, VA, USA, 2012. [Google Scholar]
- Turner, B.N.; Gold, S.A. A review of melt extrusion additive manufacturing processes: II. Materials, dimensional accuracy, and surface roughness. Rapid Prototyp. J. 2015, 21, 250–261. [Google Scholar] [CrossRef]
- Turner, B.N.; Strong, R.; Gold, S.A. A review of melt extrusion additive manufacturing processes: I. Process design and modeling. Rapid Prototyp. J. 2014, 20, 192–204. [Google Scholar] [CrossRef]
- Luo, M.; Tian, X.; Zhu, W.; Li, D. Controllable interlayer shear strength and crystallinity of PEEK components by laser-assisted material extrusion. J. Mater. Res. 2018, 33, 1632–1641. [Google Scholar] [CrossRef]
- Rubinstein, M.; Colby, R.H. Polymer Physics; Oxford University Press: Oxford, UK, 2003. [Google Scholar]
- Vaezi, M.; Yang, S. Extrusion-based additive manufacturing of PEEK for biomedical applications. Virtual Phys. Prototyp. 2015, 10, 123–135. [Google Scholar] [CrossRef]
- Rahim, T.N.A.T.; Abdullah, A.M.; Akil, H.M.; Mohamad, D.; Rajion, Z.A. Preparation and characterization of a newly developed polyamide composite utilising an affordable 3D printer. J. Reinf. Plast. Compos. 2015, 34, 1628–1638. [Google Scholar] [CrossRef]
- Drummer, D.; Cifuentes-Cuéllar, S.; Rietzel, D. Suitability of PLA/TCP for fused deposition modeling. Rapid Prototyp. J. 2012, 18, 500–507. [Google Scholar] [CrossRef]
- Pires, L.S.O.; Fernandes, M.H.F.V.; de Oliveira, J.M.M. Crystallization kinetics of PCL and PCL–glass composites for additive manufacturing. J. Thermal Anal. Calorim. 2018, 134, 2115–2125. [Google Scholar] [CrossRef]
- Liu, F.; Vyas, C.; Poologasundarampillai, G.; Pape, I.; Hinduja, S.; Mirihanage, W.; Bartolo, P.J. Process-Driven Microstructure Control in Melt-Extrusion-Based 3D Printing for Tailorable Mechanical Properties in a Polycaprolactone Filament. Macromol. Mater. Eng. 2018, 303, 1800173. [Google Scholar] [CrossRef]
- Santis, F.D.; Pantani, R.; Speranza, V.; Titomanlio, G. Analysis of Shrinkage Development of a Semicrystalline Polymer during Injection Molding. Ind. Eng. Chem. Res. 2010, 49, 2469–2476. [Google Scholar] [CrossRef]
- Spoerk, M.; Sapkota, J.; Weingrill, G.; Fischinger, T.; Arbeiter, F.; Holzer, C. Shrinkage and Warpage Optimization of Expanded-Perlite-Filled Polypropylene Composites in Extrusion-Based Additive Manufacturing. Macromol. Mater. Eng. 2017, 302, 1700143. [Google Scholar] [CrossRef]
- Panda, B.N.; Shankhwar, K.; Garg, A.; Jian, Z. Performance evaluation of warping characteristic of fused deposition modelling process. Int. J. Adv. Manuf. Technol. 2017, 88, 1799–1811. [Google Scholar] [CrossRef]
- Fitzharris, E.R.; Watanabe, N.; Rosen, D.W.; Shofner, M.L. Effects of material properties on warpage in fused deposition modeling parts. Int. J. Adv. Manuf. Technol. 2018, 95, 2059–2070. [Google Scholar] [CrossRef]
- McIlroy, C.; Olmsted, P. Disentanglement effects on welding behaviour of polymer melts during the fused-filament-fabrication method for additive manufacturing. Polymer 2017, 123, 376–391. [Google Scholar] [CrossRef]
- Kim, Y.H.; Wool, R.P. A Theory of Healing at a Polymer-Polymer Interface. Macromolecules 1983, 16, 1115–1120. [Google Scholar] [CrossRef]
- Doi, M.; Edwards, S.F. The Theory of Polymer Dynamics; Oxford University Press: Oxford, UK, 1986. [Google Scholar]
- Xue, Y.Q.; Tervoort, T.A.; Lemstra, P.J. Welding Behavior of Semicrystalline Polymers. 1. The Effect of Nonequilibrium Chain Conformations on Autoadhesion of UHMWPE. Macromolecules 1998, 31, 3075–3080. [Google Scholar] [CrossRef]
- Mackay, M. The importance of rheological behavior in the additive manufacturing technique material extrusion. J. Rheol. 2018, 62, 1549–1561. [Google Scholar] [CrossRef]
- McIlroy, C.; Graham, R. Modelling flow-enhanced crystallisation during fused filament fabrication of semi-crystalline polymer melts. Addit. Manuf. 2018, 24, 323–340. [Google Scholar] [CrossRef]
- Jarrousse, G. Self Adhesion of Semi-Crystalline Polymers between Their Glass Transition Temperature and Their Melting Temperature. Ph.D. Thesis, Université Pierre et Marie Curie, Paris, France, 2004. [Google Scholar]
- Xue, Y.Q.; Tervoort, T.A.; Rastogi, S.; Lemstra, J. Welding Behavior of Semicrystalline Polymers. 2. Effect of Cocrystallization on Autoadhesion. Macromolecules 2000, 33, 7084–7087. [Google Scholar] [CrossRef]
- Yang, F.; Pitchumani, R. Healing of Thermoplastic Polymers at an Interface under Nonisothermal Conditions. Macromolecules 2002, 35, 3213–3224. [Google Scholar] [CrossRef]
- Seppala, J.E.; Hoon Han, S.; Hillgartner, K.E.; Davis, C.S.; Migler, K.B. Weld formation during material extrusion additive manufacturing. Soft Matter 2017, 13, 6761–6769. [Google Scholar] [CrossRef] [PubMed]
- Sun, Q.; Rizvi, G.; Bellehumeur, C.; Gu, P. Effect of processing conditions on the bonding quality of FDM polymer filaments. Rapid Prototyp. J. 2008, 14, 72–80. [Google Scholar] [CrossRef]
- Kousiatza, C.; Karalekas, D. In-situ monitoring of strain and temperature distributions during fused deposition modeling process. Mater. Des. 2016, 97, 400–406. [Google Scholar] [CrossRef]
- Srinivas, V.; van Hooy-Corstjens, C.S.; Harings, J.A. Correlating molecular and crystallization dynamics to macroscopic fusion and thermodynamic stability in fused deposition modeling; a model study on polylactides. Polymer 2018, 142, 348–355. [Google Scholar] [CrossRef]
- Compton, B.G.; Post, B.K.; Duty, C.E.; Love, L.; Kunc, V. Thermal analysis of additive manufacturing of large-scale thermoplastic polymer composites. Addit. Manuf. 2017, 17, 77–86. [Google Scholar] [CrossRef]
- Costa, S.; Duarte, F.; Covas, J. Estimation of filament temperature and adhesion development in fused deposition techniques. J. Mater. Process. Technol. 2017, 245, 167–179. [Google Scholar] [CrossRef]
- Dinwiddie, R.; Kunc, V.; Lindal, J.M.; Post, B.; Smith, R.; Love, L.; Duty, C. Infrared imaging of the polymer 3D-printing process. In Thermosense: Thermal Infrared Applications XXXVI; SPIE Press: Bellingham, WA, USA, 2014; Volume 9105, p. 910502. [Google Scholar]
- Lu, Q.Y.; Wong, C.H. Additive manufacturing process monitoring and control by non-destructive testing techniques: Challenges and in-process monitoring. Virtual Phys. Prototyp. 2018, 13, 39–48. [Google Scholar] [CrossRef]
- Seppala, J.; Hillgartner, K.; Davis, C.; Migler, K. Thermography and weld strength characterization of thermoplastic 3D printing. In Proceedings of the 74th Annual Technical Conference and Exhibition of the Society of Plastics Engineers, SPE ANTEC Indianapolis 2016, Indianapolis, IN, USA, 23–25 May 2016; pp. 42–44. [Google Scholar]
- Seppala, J.E.; Migler, K.D. Infrared thermography of welding zones produced by polymer extrusion additive manufacturing. Addit. Manuf. 2016, 12, 71–76. [Google Scholar] [CrossRef]
- Northcutt, L.A.; Orski, S.V.; Migler, K.B.; Kotula, A.P. Effect of processing conditions on crystallization kinetics during materials extrusion additive manufacturing. Polymer 2018, 154, 182–187. [Google Scholar] [CrossRef]
- Wolszczak, P.; Lygas, K.; Paszko, M.; Wach, R.A. Heat distribution in material during fused deposition modelling. Rapid Prototyp. J. 2018, 24, 615–622. [Google Scholar] [CrossRef]
- Bellehumeur, C.; Li, L.; Sun, Q.; Gu, P. Modeling of Bond Formation Between Polymer Filaments in the Fused Deposition Modeling Process. J. Manuf. Process. 2004, 6, 170–178. [Google Scholar] [CrossRef]
- Coogan, T.J.; Kazmer, D.O. Healing simulation for bond strength prediction of FDM. Rapid Prototyp. J. 2017, 23, 551–561. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, X.Z.; Yu, W.W.; Deng, Y.H. Numerical investigation of the influence of process conditions on the temperature variation in fused deposition modeling. Mater. Des. 2017, 130, 59–68. [Google Scholar] [CrossRef]
- Yang, H.; Zhang, S. Numerical simulation of temperature field and stress field in fused deposition modeling. J. Mech. Sci. Technol. 2018, 32, 3337–3344. [Google Scholar] [CrossRef]
- Cuiffo, M.A.; Snyder, J.; Elliott, A.M.; Romero, N.; Kannan, S.; Halada, G.P. Impact of the Fused Deposition (FDM) Printing Process on Polylactic Acid (PLA) Chemistry and Structure. Appl. Sci. 2017, 7, 579. [Google Scholar] [CrossRef]
- Wang, L.; Gramlich, W.M.; Gardner, D.J. Improving the impact strength of Poly(lactic acid) (PLA) in fused layer modeling (FLM). Polymer 2017, 114, 242–248. [Google Scholar] [CrossRef]
- Yang, D.; Wang, G.; Zhang, G. Thermal analysis for single-pass multi-layer GMAW based additive manufacturing using infrared thermography. J. Mater. Process. Technol. 2017, 244, 215–224. [Google Scholar] [CrossRef]
- Benwood, C.; Anstey, A.; Andrzejewski, J.; Misra, M.; Mohanty, A.K. Improving the Impact Strength and Heat Resistance of 3D Printed Models: Structure, Property, and Processing Correlationships during Fused Deposition Modeling (FDM) of Poly(Lactic Acid). ACS Omega 2018, 3, 4400–4411. [Google Scholar] [CrossRef]
- Wach, R.; Wolszczak, P.; Adamus-Włodarczyk, A. Enhancement of Mechanical Properties of FDM-PLA Parts via Thermal Annealing. Macromol. Mater. Eng. 2018, 303. [Google Scholar] [CrossRef]
- Fitzharris, E.R.; Rosen, D.W.; Shofner, M.L. Fast scanning calorimetry for semicrystalline polymers in fused deposition modeling. Polymer 2019, 166, 196–205. [Google Scholar] [CrossRef]
- Mathot, V.; Pyda, M.; Pijpers, T.; Vanden Poel, G.; van de Kerkhof, E.; van Herwaarden, S.; van Herwaarden, F.; Leenaers, A. The Flash DSC 1, a power compensation twin-type, chip-based fast scanning calorimeter (FSC): First findings on polymers. Thermochim. Acta 2011, 522, 36–45. [Google Scholar] [CrossRef]
- Toda, A.; Androsch, R.; Schick, C. Insights into polymer crystallization and melting from fast scanning chip calorimetry. Polymer 2016, 91, 239–263. [Google Scholar] [CrossRef]
- Schick, C.; Mathot, V. (Eds.) Fast Scanning Calorimetry; Springer Nature: Berlin, Germany, 2016. [Google Scholar]
- Kolesov, I.; Mileva, D.; Androsch, R.; Schick, C. Structure formation of polyamide 6 from the glassy state by fast scanning chip calorimetry. Polymer 2011, 52, 5156–5165. [Google Scholar] [CrossRef]
- Wunderlich, B. Macromolecular Physics, Crystal Melting; Academic Press: New York, NY, USA, 1997; Volume 3, Chapter 8. [Google Scholar]
- Harvey, E.D.; Hybart, F.J. Rates of crystallization of copolyamides. II. Random copolymers of nylons 66 and 6. J. Appl. Polym. Sci. 1970, 14, 2133–2143. [Google Scholar] [CrossRef]
- Telen, L.; Van Puyvelde, P.; Goderis, B. Random Copolymers from Polyamide 11 and Polyamide 12 by Reactive Extrusion: Synthesis, Eutectic Phase Behavior, and Polymorphism. Macromolecules 2016, 49, 876–890. [Google Scholar] [CrossRef]
- Watanabe, N.; Shofner, M.; Treat, N.; Rosen, D. A model for residual stress and part warpage prediction in material extrusion with application to polypropylene. In Proceedings of the 2016 Annual International Solid Freeform Fabrication Symposium, Austin, TX, USA, 8–10 August 2016. [Google Scholar]
- Peng, F.; Vogt, B.D.; Cakmak, M. Complex flow and temperature history during melt extrusion in material extrusion additive manufacturing. Addit. Manuf. 2018, 22, 197–206. [Google Scholar] [CrossRef]

| Material | Mw [kg/mol] | Tg [°C] | Tm [°C] |
|---|---|---|---|
| HMWPA | 58 | 49 | 199 |
| LMWPA | 24 | 41 | 198 |
| Condition | Material | Tliquefier [°C] | Tbuild plate [°C] | vprint [mm/s] |
|---|---|---|---|---|
| 1 | HMWPA | 260 | 110 | 11 |
| 2 | HMWPA | 260 | 40 | 11 |
| 3 | HMWPA | 240 | 110 | 11 |
| 4 | HMWPA | 260 | 110 | 5.5 |
| 5 | HMWPA | 220 | 110 | 11 |
| 6 | LMWPA | 240 | 110 | 11 |
| Material | mDSC [mg] | Hm,DSC [J] | Hm,FSC [mJ] | mFSC [ng] |
|---|---|---|---|---|
| HMWPA | 8.39 | 0.37 | 98.86 | |
| LMWPA | 8.28 | 0.34 | 33.88 |
| Valid for Condition(s): | Correction Factor |
|---|---|
| 1 & 4 | |
| 2, 3 & 5 | |
| 6 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vaes, D.; Coppens, M.; Goderis, B.; Zoetelief, W.; Van Puyvelde, P. Assessment of Crystallinity Development during Fused Filament Fabrication through Fast Scanning Chip Calorimetry. Appl. Sci. 2019, 9, 2676. https://doi.org/10.3390/app9132676
Vaes D, Coppens M, Goderis B, Zoetelief W, Van Puyvelde P. Assessment of Crystallinity Development during Fused Filament Fabrication through Fast Scanning Chip Calorimetry. Applied Sciences. 2019; 9(13):2676. https://doi.org/10.3390/app9132676
Chicago/Turabian StyleVaes, Dries, Margot Coppens, Bart Goderis, Wim Zoetelief, and Peter Van Puyvelde. 2019. "Assessment of Crystallinity Development during Fused Filament Fabrication through Fast Scanning Chip Calorimetry" Applied Sciences 9, no. 13: 2676. https://doi.org/10.3390/app9132676
APA StyleVaes, D., Coppens, M., Goderis, B., Zoetelief, W., & Van Puyvelde, P. (2019). Assessment of Crystallinity Development during Fused Filament Fabrication through Fast Scanning Chip Calorimetry. Applied Sciences, 9(13), 2676. https://doi.org/10.3390/app9132676





