Abstract
In this paper, we propose a high accuracy fingerprint-based localization scheme for the Internet of Things (IoT). The proposed scheme employs mathematical concepts based on sparse representation and matrix completion theories. Specifically, the proposed indoor localization scheme is formulated as a simple optimization problem which enables efficient and reliable algorithm implementations. Many approaches, like Nesterov accelerated gradient (Nesterov), Adaptative Moment Estimation (Adam), Adadelta, Root Mean Square Propagation (RMSProp) and Adaptative gradient (Adagrad), have been implemented and compared in terms of localization accuracy and complexity. Simulation results demonstrate that Adam outperforms all other algorithms in terms of localization accuracy and computational complexity.
1. Introduction
The concept of the Internet of Things (IoT), where objects, with their own identifiers, have the ability to transfer data over a network without requiring human interaction, is federating more and more interests nowadays [1,2]. In addition to communication technology, data management and data privacy and security, the development of smart applications is strongly related to the notion of physical location and positions [3,4,5]. Therefore, the infrastructure has to support finding things according to location taking mobility into account. Localization technologies will then play a crucial role for the future of IoT and may be directly embedded into the infrastructure or into “things”.
The Global Positioning System (GPS) is the most popular localization solution allowing positioning, with a high accuracy, when at least four satellites are available [6]. In addition, a high signal quality from those satellites is necessary to perform localization and this is why such a solution cannot easily be deployed in an indoor environment. An alternative solution is to use the communication infrastructure to perform localization. Different methods have been proposed and studied. The radio fingerprinting is a well known localization technique which is organized in two steps [7,8]. In the first step, a radio map is constructed and, in the second step, online measurement is compared to the radio map [9]. The communication signal can also be used to perform the trilateration [10,11,12] where the distances between the target and reference positions can be estimated by using the Received Signal Strength Indicator (RSSI) [13]. The performance of such a localization technique depends on the number of detected reference positions.
In indoor environments, when the propagation conditions are very severe, the RSSI is often too weak to be correctly detected by the target receiver. So, only partial pairwise inter sensor nodes distances can be calculated from the measured RSSI values. To overcome this problem, we propose in this paper, to estimate the complete distance matrix using matrix completion algorithm. This approach aims to approximate the distance between the target and all the reference positions through the spatial correlation structure of the fingerprints. After the matrix completion, the localization can be performed using either matrix decomposition or fingerprinting [14,15,16,17]. In this paper, given a set of reference nodes and the RSSI information between sensors, we process sensor localization using the trilateration technique. To the best of our knowledge, it is the first time that matrix completion algorithms are combined with trilateration. So, we propose to improve the localization accuracy of the trilateration technique using a complete pairwise squared Euclidean distance matrix instead of only using a partial number of pairwise distances calculated from measured RSSI only.
1.1. Related Works
As mentioned in the previous section, it is difficult, from available RSSI measurements, to acquire all the pairwise distances between sensors and to obtain a full connected squared distance matrix so called the Euclidean distance matrix (EDM) [18]. This is due to the limitation of communication range and multipath effects. To provide a reliable distance information to each sensor node, the matrix completion is then proposed and its role is to recover the complete Euclidean distance matrix EDM from an incomplete matrix.
Several algorithms and approaches have been proposed and studied to approximate the missing distances for RSSI measurements based systems. Authors in [14] formulate the matrix completion problem using the least squared minimization. To solve the minimization problem, they introduce a modified iterative Newton’s algorithm [19] to optimize the objective function. This solution can be very fast if the parameters are well chosen. The main drawback is that the result is very sensitive to initialization. It can be considered as a good initial location estimation for other fine localization algorithms. Other existing approaches based on Singular Value Thresholding (SVT) [20], Accelerated Proximal Gradient (APG) [21] and Augmented Lagrange Multiplier (ALM) [22] have been proposed in recent years. SVT method which relies on the Singular Value Decomposition (SVD) of a low rank matrix is associated to poor completion performance and slow convergence rate. Motivated by the above reasons, ALM and APG methods have been proposed. However, these methods depend on the choice of relevant parameters and are sensitive to noise. To overcome this problem, a regularized matrix completion model is proposed in [23] introducing the multivariate function Bregman divergence to solve the EDM problem. The major drawback of such a centralized method is its computational cost. The aforementioned methods are all based on RSSI. As an alternative to RSSI measurements, Nguyen et al. focus on connectivity/distance information setting a routing protocol in place [15,16]. They formulate the matrix completion problem as an unconstrained optimization in Smooth Riemannian manifold. Then, the nonlinear conjugate gradient algorithm is applied on the smooth Riemannian manifold. This approach recovers the EDM in noiseless and noisy environments. However, it focused only on two dimensional position information. Authors in [24] cover the unknown measurements under the existence of noise which is classified into three categories. This approach achieves a good localization accuracy compared to other existing ones. However, it is a centralized localization approach. Motivated by the above reasons, based on RSSI measurements, we solve the minimization problem using advanced algorithms to reduce the running time and the computational complexity while ensuring a good localization accuracy.
After completing the EDM, the second step is to estimate the location of sensors. For this, the completed pairwise distance information can be transformed into the estimated coordinates of sensor nodes by applying a factorization process [14]. This factorization requires that the matrix is Semi Definite Positive (SDP). The SDP problem can be efficiently and accurately solved by CVX toolbox on Matlab [25]. However, if the matrix is not SDP, the problem can also be solved by introducing Semidefinite Relaxations (SDR) [26,27]. The SDR based localization scheme in [26] relaxes the non convex localization into a convex one and marks a good localization accuracy. However, the computational complexity of SDR-based techniques is closely related to the problem size. Therefore, this algorithm is adapted for medium size network only due to the highly required running time. To reduce the running time, a weighted semidefinite relaxation localization method is carried out in [27]. It aims to improve the accuracy of localization, but it is still not suitable for dealing with large networks. A multiple sources localization problem is formulated in [28] as a unimodality constrained matrix factorization (UMF) and two rotation techniques have been developed to solve the problem. In [29], an eigendecomposition is first applied to find the local locations of sensor nodes, then a rotation matrix and a translation vector are used to transform them to true locations. Zhang et al. in [30] proposed to estimate the positions of nodes by the classic multidimensional scaling algorithm (MDS) [31] using a truncated eigendecomposition. However, the MDS method requires high recovery rate of the EDM which is not guaranteed when working in noisy environments. The localization can be also ensured by the fingerprinting technique. The principal drawback is that an offline radio map construction is needed. Furthermore, due to environment changes this radio map has to be frequently updated. In this paper, we propose to use the trilateration method. It can be applied if we have at least three pairwise known distances between the sensors if the localization is performed in 2D space. At each sensor node to be localized, data fusion is conducted by combining measurements from different nodes to estimate its location.
1.2. Contribution
The contribution of our work is threefold:
- Improving the localization accuracy of trilateration technique: We develop high accuracy fingerprint based indoor localization scheme which is based on sparse representation and matrix completion theories. As said before, trilateration technique is based on pairwise distances between the target node and the anchor nodes. Due to the fact that propagation conditions are not optimal in an indoor environment, several pairwise distances cannot be measured. So, our main contribution is to enhance the localization’s accuracy of trilateration by estimating all pairwise distances.
- Matrix completion resolution: We formulate the indoor localization scheme as a simple optimization problem which enables efficient and reliable algorithm implementation.
- Solving the proposed optimization problem: We develop closed-form algorithms, which can be reproduced by simple implementation, to solve the indoor localization problem. Specifically, we adopt recent methods like Nesterov accelerated gradient (Nesterov), adaptative Moment Estimation (Adam), Adadelta, Root Mean Square Propagation (RMSProp) and Adaptative gradient (Adagrad).
The remainder of this paper is organized as follows: In Section 2, we present the system model. In Section 3, details of our contribution and different algorithms are given. Obtained simulation results are presented and discussed in Section 4. The method verification using real measurements is detailed in Section 5. Finally, we conclude the paper in Section 6.
Notations: The following notations are used throughout our paper. is the transpose operation. , and denote the norm, the Frobenius norm and the nuclear norm, respectively. returns a column vector of the diagonal elements of the matrix . is the gradient of function f. is the matrix obtained at iteration t. is the product of matrices. is the Hadamard product of and . Matrices are presented by non italic bold capital letters. Furthermore, variables are presented by italic lowercase characters.
2. System Model
In a system where our approach is adopted, each sensor node uses the following 2 steps to find its position (Figure 1).
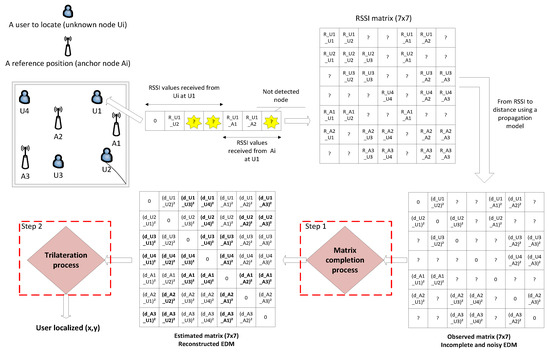
Figure 1.
Algorithm details considering the sensor network consisting of seven sensor nodes from which three are anchors.
- Step 1: Refine and complete the squared distance matrix.
- Step 2: Once the matrix is completed, the coordinates of the node can be retrieved using the classic trilateration process.
RSSI measurements corresponding to different sensor nodes are used to construct an RSSI matrix. From the RSSI values, the Euclidean Distance Matrix containing the distance information between each pair of sensor nodes X is built. Due to the limitation of radio communication range, the matrix of RSSI measurements is partially known. Thus, the matrix is incomplete (only a small number of entries are available) and can be affected by noise. This incomplete matrix can not efficiently serve for localization. It should be completed. Let us define the matrix which is the complete EDM. Therefore, the problem is how to recover the unknown elements of giving a small number of known entries of .
Assume that m is the number of nodes with known positions named ’Anchor nodes’. In contrast, is the number of sensors with unknown positions. n is the total number of sensor nodes (anchor nodes and unknown nodes) placed in the indoor environment. is the ith unknown node where . is the jth anchor node where . is the Euclidean distance matrix. It can be partitioned as follows:
where is the distance sub matrix between each pair of anchor nodes. It is obtained by calculating the exact distance between each pair of anchors. is the pairwise distance between anchor node i () and anchor node j (). are the location coordinates of anchor node i. is the distance sub matrix between each pair of unknown nodes. and , where , are the distance sub matrices between each pair of anchors and unknown nodes. , and are obtained from RSSI measurements using the log normal shadowing propagation model which is used to express the pathloss measurements in dBs [32]:
where is the pathloss value at a reference distance , is the pathloss exponent, f is the used frequency, is the distance between node i and node j. The used propagation parameters are defined later in Section 4. Since pairwise distances are dependant because of the dependency of RSSI in the indoor environments, this matrix should have low rank which motivates the use of matrix completion algorithms.
After completing the Euclidean distance matrix, a trilateration process is adopted by each unknown node in order to estimate its location [10]. A reminder of this method is introduced below. A combination of estimated distances is required. In this combination process, we use only the distance estimated submatrix which contains the distances between the unknown nodes and all anchor nodes. The completion of the total matrix brings more distance information. Distances are estimated from each other due to the fact that columns are dependant (low rank matrix).
Let be the estimated coordinates of an unknown node; . , are the coordinates of the anchor nodes. where and . The estimated coordinates are calculated by the following equation
where And
3. Proposed Matrix Completion Based Localization
In this section, we formulate our proposed approach as a convex optimization problem which is resolved using the developed closed form algorithms via Gradient descent and its variants.
3.1. Problem Formulation
Our goal is to reconstruct the complete distance matrix from incomplete and noisy data. The problem of recovering a low rank matrix from a small number of known entries is known as:
is the set of known entries. Due to the non convexity and non linearity of the rank matrix [33], the problem in Equation (1) cannot be solved numerically. Inspired by the theory of Compressed Sensing (CS), Candes and Recht proposed to replace the rank function in Equation (1) by the nuclear norm [34]. The model in (1) is reformulated into:
is the sum of the singular values of (i.e., . Where ). Considering the assumption of low rank () and taking into account that observations are usually affected by noise, the model of matrix completion can be defined as:
is a tunable parameter and is the Frobenius norm. . is the matrix whose entries are:
We denote the objective function as:
where and . The defined optimization problem can be solved efficiently by using iterative Gradient Descent method and its variants. The developed algorithm is summarized in Table 1. Where is the matrix used to update the distance matrix, index t refers to the number of update iteration. Many approaches, detailed in the next section, have been adopted to find the matrix update .

Table 1.
The problem described in four steps.
3.2. Matrix Completion: Optimization over GD and Its Variants
In the following, we review the different optimization methods that are widely used by the deep learning community to update the localization matrix : Gradient descent (GD), Nesterov accelerated gradient (NAG), Adaptive Gradient (Adagrad), Root Mean Square Propagation (RMSProp), Adadelta and Adaptive Moment Estimation (Adam). We discard the class of algorithms that are computationally very expensive for high dimensional data sets, e.g., the second-order Newton’s method [35].
3.2.1. Gradient Descent (GD)
Gradient descent is an iterative method that aims to find local minimum of differentiable cost functions [36]. It is the most common first-order optimization algorithm in machine learning and deep learning. GD is based on updating each element of matrix in the direction to optimize the objective function . The new parameter can be adjusted as
is the learning rate from range . is the gradient of the cost function with respect to the parameter matrix. It can be computed as follows:
where
is calculated as follows:
We might need some sort of regularization because the inverse of the square root of may not exist, e.g.,
where is a regularization parameter and is the identity matrix. Then
We obtain
Using the classic Gradient descent, the known entries are very well estimated, this is why it will be used in the rest of the paper to estimate . To estimate , we propose to use the following algorithms.
3.2.2. Nesterov Accelerated Gradient (NAG)
A second commonly used variant is the acceleration of Nesterov, that has been published in [37] and fits in the same vein as the idea of the Momentum [38]. It has the same intuition using the gradient history but it calculates the gradient with respect to an approximate future values of our parameters instead of the current parameters. To update with NAG, we use the following equation.
where
and
Suppose that
Then,
We obtain
The main advantage of the NAG method compared to the GD one is related to the fact that an anticipatory update prevents us from going too fast and results in increased responsiveness to the landscape of the loss function [36].
3.2.3. Adaptive Gradient (Adagrad)
Duchi et al. [35] introduced Adagrad algorithm in the context of projected gradient method. Adagrad aims to adapt the learning rate to the updated parameters, performing low learning rate (i.e., smaller updates) when the memory of squared gradients is high and larger updates conversely. Adagrad update rule is as follows:
- We set to be the gradient of the objective function with respect to the parameter
- we compute the memory of squared gradients over time as
- we modify the general learning rate at each time step t for every parameter based on the sum of the squares of the gradients that have been computed for up to time step t.while is a regularizing term used to avoid division by zero. It is worth mentioning that we do not need to adjust the learning rate.
3.2.4. Root Mean Square Propagation (RMSProp)
Tieleman et al. [39] introduced this algorithm in 2012. It is described in the following 2 steps. Instead of using the memory of all squared gradients, RMSProp uses only recent past gradients computed in a restricted time.
- We compute the local average of previous as
- Then, we apply the update
3.2.5. Adadelta
Adadelta was introduced in 2012 by Zeiler [39]. It aims at circumventing Adagrad’s weakness that consists in its aggressive decreasing learning rate caused by accumulating all past squared gradients in the denominator. Adadelta scales learning rate using only recent past gradients computed in a restricted time (i.e., not the whole history). In addition, Adadelta uses an accelerator term by taking into account past updates (as in Momentum). Adadelta update rule is as follows:
- we compute gradient as in Equation (23).
- we compute the local average of previous
- we compute new term accumulating prior updates (Momentum: acceleration term)
- Then, we apply the update
3.2.6. Adaptive Moment Estimation (Adam)
Another optimization method that computes adaptive learning rate for each parameter is introduced by Kingma and Ba in [40]. Adam uses the first and the second moments of the gradients and has strong similarities with Adadelta. Indeed, it uses the second gradient moment in the denominator and a momentum term. Adam update rule consists of the following steps.
- Compute second gradient moment with local accumulation (Adadelta/RMSProp)
- Compute the first gradient moment
- Compute bias-corrected first moment and second moment estimate
- Update parameters
4. Simulation Results and Discussion
In this section, we adjust by simulations different used parameters. The beneficial use of matrix completion in order to improve the localization accuracy is justified empirically. We also study the recovery performance, the localization accuracy and the computational complexity of each cited algorithm.
4.1. Determining the Best Ratio between the Number of Unknown Nodes and the Number of Anchors
It is reasonable to state that the completion of a high dimensional matrix improves the localization accuracy. This is due to the diversity of the information introduced by each sensor node. However, from a finite dimension, the algorithm converges and the use of additional data increases the complexity and the execution time. To ensure the best localization accuracy and decrease the execution time of the algorithm, we set up this ratio. Let
where is the number of unknown nodes and is the number of anchors. To determine the best ratio in terms of localization accuracy, simulations have been done. Using 35 unknown nodes, the number of anchors varies from 5 to 20. The localization error applying Adam respect to the number of anchors is shown in (Figure 2). When the number of anchors reaches 10, the localization error becomes almost stable. Figure 3 illustrates the localization error in meters depending on the number of unknown nodes using 10 anchor nodes. It can be observed that the localization error is almost the same from 35 unknown nodes. The trade-off between accuracy and complexity leads us to use a ratio equal to .
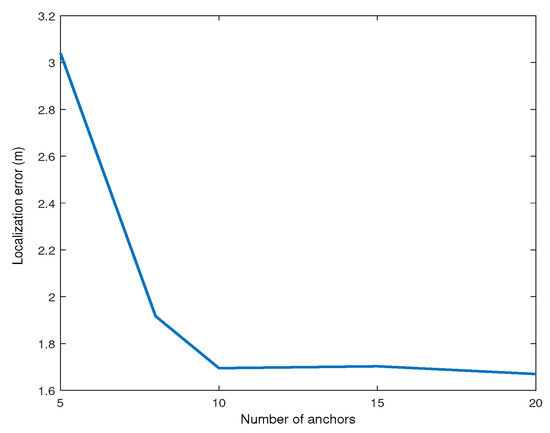
Figure 2.
The localization error using 35 unknown nodes with the varying number of anchors in 400 m applying Adam for sigma shadowing = 2.
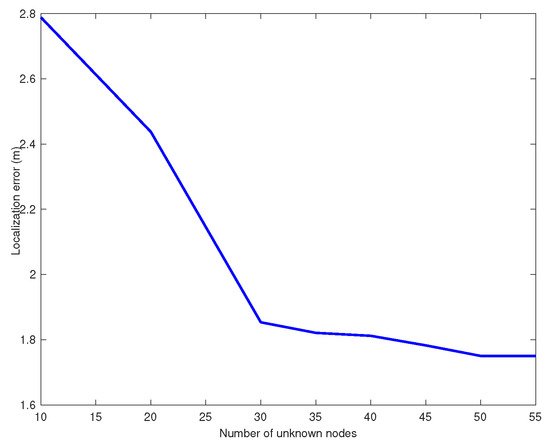
Figure 3.
The localization error using 10 anchors with the varying number of unknown nodes in 400 m applying Adam for sigma shadowing = 2.
We mention that simulations have been done for each optimization algorithm and for each value of sigma shadowing. The ratio guaranteeing the best performance is always . Thus, to simplify presentation and without loss of generality, we present only simulation results corresponding to Adam when working with sigma shadowing equal to 2.
4.2. Simulation Setup
We consider a wireless sensor network of 45 sensor nodes with 10 of them being anchors and 35 being unknown nodes, placed in an area of 400 m (i.e., 20 m × 20 m) and its architecture is illustrated in Figure 4. The sensor nodes (anchors and unknown nodes) are randomly placed in the studied area.
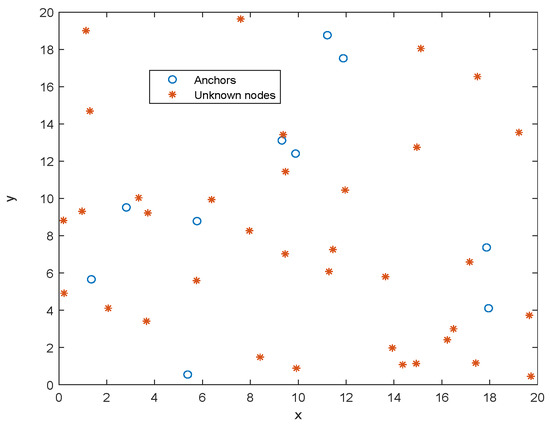
Figure 4.
Configuration of the wireless sensor network.
The accuracy of the studied algorithms is investigated over many environment realizations. In order to simplify the presentation of the paper and without loss of generality, we present results only for one environment test, as illustrated in Figure 4. Simulation results are consistent with other environments. 10 RSSI measurements of received from sensor i are taken at each position j for each sigma shadowing value. This value is calculated in dBs as:
where is the transmission power, is a Gaussian random variable which describes the random shadowing effects, is the pathloss calculated using Equation (2). In this paper, we use parameters related to our laboratory: , dBm, m, GHz. The sigma of the random variable a takes the values 0, 2, 5 to study the effect of its variation on the algorithm recovery performance and localization accuracy.
4.3. Verification of the Low Rank Property
To apply the matrix completion technique to recover the EDM matrix from observed entries, the matrix should have low rank r to ensure that the generated distances have a strong correlation. We can approximate unknown entries from known ones because they are dependant. To check whether the data matrix has a good low-rank approximation, we apply the singular value decomposition [41]. An matrix , can be decomposed as:
where is an unitary matrix, is a unitary matrix and is a diagonal matrix. The diagonal elements of are the singular values of , they are organized in a decreasing order (i.e., ). r is the rank of the matrix , it is equal to the number of its non zero singular values. If is a low rank matrix, its top l singular values occupy the total or nearly the total energy (i.e., ) [42]. The metric used to verify the property of low rank, is the fraction of the nuclear norm caught by the top l singular values. This fraction is defined as:
Figure 5 illustrates the fraction of the nuclear norm captured by the top l singular values. We find that the top 3 singular values capture of the nuclear norm. This indicates that the matrix has a low rank approximation. So, we are able to apply matrix completion.
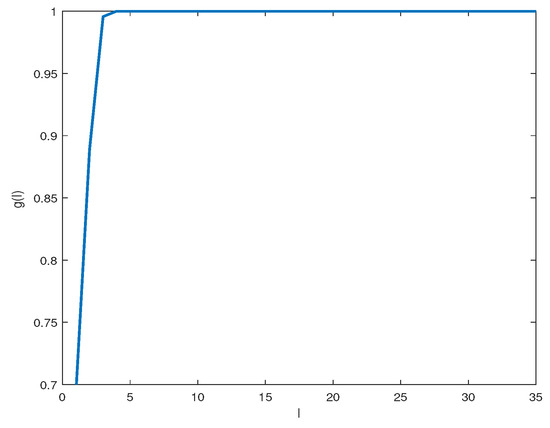
Figure 5.
Energy fraction captured by the top l singular values.
4.4. Recovery Performance and Localization Accuracy
For evaluating the studied solutions based on GD and its variants combined with the trilateration process, we define the following two metrics.
- EDM reconstruction error using the mean square error
- Localization error
As mentioned before, is the matrix of estimated coordinates of unknown nodes and are their real coordinates.
We recall that parameters , , , , , and are adjusted by simulations, selected to ensure the best result in terms of localization mean error on a validation dataset. To find the best set of these parameters, an empirical process is conducted. Thus, several simulations are required to identify the optimal value of each parameter. The parameters used in the rest of the paper are presented in Table 2. The rest of algorithms includes GD, NAG, Adagrad, RMSProp and Adadelta.

Table 2.
Values of different used parameters.
To verify that trilateration guarantees better localization accuracy when more distance information is provided, we firstly apply the trilateration with observed distances only. We can easily notice that it introduces the worse localization accuracy compared to tested combinations in both noisy and noiseless environments (Figure 6b,d,f). The localization accuracy is much better when we use a complete EDM than using only the observed distances. Moreover, to apply the trilateration process, at least three detected anchors are needed. If this is not the case, the sensor node cannot be localized. This problem can be solved when using a compete EDM containing all pairwise distances. Therefore, the combination of matrix completion technique and trilateration is highly recommended.
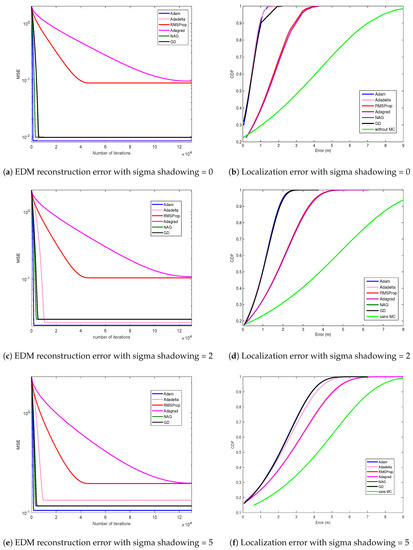
Figure 6.
Algorithms’ performances (EDM: Euclidean distance matrix).
In the first set of simulations, we investigate the performances, in terms of EDM reconstruction and localization error, of different cited algorithms in a noiseless environment as shown in Figure 6a,b. It shows the effectiveness of the location estimation of the proposed schemes for 10 simulations. Figure 6a illustrates the EDM reconstruction error ’MSE’. The error estimation of pairwise known distances is in the order of . The reconstruction error varies between and for different cited algorithms. The best EDM reconstruction rate is obtained by Adadelta which produces a localization mean error of m. This result is close to those obtained by GD, NAG and Adam. The difference is the number of iterations required to reach the convergence of the algorithm. Adam converges at 790 iterations which is about the of required iterations by Adadela. GD converges at 5910 iterations which is about the of required iterations by Adadela and NAG converges at 3100 iterations.
The performances of GD and NAG in terms of localization accuracy are very close. So that, their cumulative distribution functions (CDF) are confused for each sigma shadowing value. However, it accelerates the convergence of GD. Instead of converging at 5910, it converges at 3100 when working in a noiseless indoor environment.
Adagrad exhibits the worst performances in terms of EDM reconstruction error and localization error. This is due to the fact that it accumulates the squared gradients in the denominator. So, the sum of positive terms keeps growing and the learning rate becomes very small, thus making the algorithm no longer able to ensure updates in order to reach a lower minimum. RMSProp, Adadelta and Adam aim to reduce decreasing learning rate.
Instead of accumulating all past squared gradients, RMSProp and Adadelta use a window of size of accumulated past gradients. RMSProp improves a little bit the EDM reconstruction error (Figure 6a) and the localization error compared to those introduced by Adagrad in a noiseless environment. However, the result is still worse than those obtained by GD and NAG. The performances of RMSProp and Adagrad are quite close in a noisy environment. They converge to close minimums (Figure 6c,e) and their CDF are almost confused (Figure 6d,f).
Adadelta performs a bit better than GD and NAG for sigma shadowing = 0 and 2. However, it requires times the number of iterations required by GD to converge and times the number of iterations required by NAG to converge (in a noiseless environment) and it is more complex than GD and NAG, which increases the execution time of the algorithm. We notice that adadelta is more affected by noise than other algorithms. Its performances decrease more quickly than the others. In a noiseless indoor environment, Adadelta introduces the best localization accuracy. For sigma shadowing equal to 2, Adam performs better than it. Furthermore, for sigma shadowing equal to 5, Adam, GD and NAG are better than Adadelta in terms of EDM reconstruction error, localization accuracy and speed of convergence. The advantage of Adadelta is that we do not need to set a default learning rate since has been eliminated from the update rule. However, this can have a negative effect as we cannot control the learning rate. To resolve this flaw, Adam is used.
Adam works well compared to other algorithms considering the compromise between the localization accuracy and the execution time. It requires the smallest number of iterations to converge. This is due to the fact that it uses an accelerator term by taking into account past updates. Furthermore, it achieves to the best localization mean error in a noisy environment. For sigma shadowing equal to 2, its localization mean error is m and it reaches m when sigma shadowing is equal to 5. As mentioned before, these results have been done on 10 simulations and the variance is about m for each value of sigma shadowing. Therefore, Adam is the most adapted algorithm for indoor localization schemes.
4.5. Complexity
4.5.1. Analytical Expressions
This section aims at approximating the theoretical complexity of the different studied algorithms. The complexity will be assessed by counting the number of multiplications per iteration and neglecting additions and subtractions. The square root and the power of elements are also neglected. For matrices multiplication, the used computational formula is the classic one and not Strassen formula [43]. To calculate the square power of a matrix, the binary method is considered [44]. The complexity of the negative square root of a matrix is obtained by calculating the inverse of the square root of this matrix. We calculate the complexity of the inverse of a matrix based on the Gauss method [43]. The complexity of the square root of a matrix is determined through the Denman-Beavers algorithm [45]. We define , , , , and the computational complexity per iteration of GD, NAG, Adagrad, RMSProp, Adadelta and Adam, respectively. Furthermore, as defined before, n is the number of sensor nodes (anchors and unknown nodes).
4.5.2. Analysis
According to the closed-form expressions mentioned in Section 4.5.1, it is possible to numerically calculate the complexity of the different algorithms , since the value of n is known, as given in Table 3. The complexity of each iteration and the complexity of the algorithm are normalized with respect to the complexity of GD, in order to highlight the contribution of other cited algorithms compared to GD. The localization mean error in Table 3 corresponds to the best mean error registered by each algorithm at different values of sigma shadowing.

Table 3.
Algorithms’ complexity normalized with respect to `Gradient descent’ (GD).
The best localization mean errors reached by GD and NAG are close. However, in terms of execution time, the GD wins. In terms of number of iterations required to converge, NAG converges fast compared to GD. However, the complexity taken by each iteration, which represents operations instead of 1 operation registered by GD. The worst localization mean error is introduced by Adagrad. It is also associated with the highest computational complexity. Its required number of operations per iteration is the best one compared to other used algorithms (except GD). However, the number of iterations to converge is too high, which increases significantly the complexity of the algorithm. The complexity of RMSProp to converge is around of the one registered by Adagrad. However, it is still high and cannot be adapted in large networks or in real time localization systems.
The required number of operations per iteration for Adadelta and Adam is around . However, the number of iterations required by Adadelta to converge is significantly higher than the number needed by Adam. For this, the execution time and the computational complexity are higher for Adadelta than Adam. Adam corresponds to the best complexity, it is of the complexity reached by GD. Compared to other cited algorithms, it is associated to the lowest complexity. It does not require a high computational time, so, it can be adapted to real time localization systems. Thus, considering the trade-off between localization accuracy and computational complexity, Adam outperforms other optimization algorithms.
5. Method Verification Using Real Measurements
For method verification, we consider a classroom of our university as an indoor area of 88 m illustrated in Figure 7. The used technology is LoRa which uses 868 MHz as frequency band. We placed eight sensor nodes which can transmit and receive messages. We collect RSSI data during an afternoon. Then, we construct the RSSI matrix, in which there are some missing values which correspond to unknown detected sensors. This matrix is used to obtain the partially known EDM matrix. We mention that the used technology and the number of sensor nodes explored for experimental verification relates to the availability of such equipment in our laboratory. Thus, we do not consider the optimal conditions determined before. The aim is to validate the effectiveness of our method.
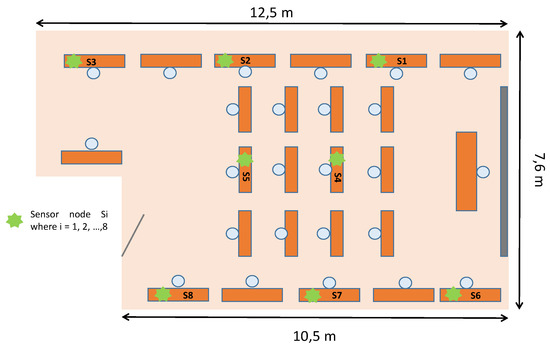
Figure 7.
Used configuration for real experimentations.
When applying our localization algorithm (Adam is used to estimate the complete EDM matrix) to localize each sensor node, we obtain a mean localization error which is 1.5 m. This error reaches 3.8 m when using the classic trilateration. In Figure 8, we present the CDF corresponding to the classic trilateration (without MC i.e., without matrix completion) and the CDF corresponding to our algorithm (with MC, i.e., with matrix completion).
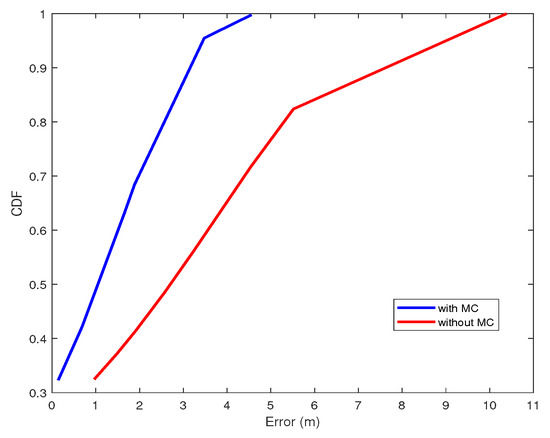
Figure 8.
CDFs for real measurements.
6. Conclusions
In this paper, we aim to improve the localization accuracy of the trilateration technique based on pairwise distances between sensor nodes. For this, we explore the problem of missing data in sensor network localization. Technically, we formulate the information distance from RSSI measurements using a propagation model. We obtain a squared Euclidean distance matrix with several unknown entries. Then, based on the matrix completion process, the complete EDM is efficiently generated by exploring only the available distances. For this, Gradient descent based advanced methods, some of which use an adaptative learning rate, are introduced. To perform trilateration, all pairwise distances between the node to localize and different sensor nodes are explored. To validate the merits of the proposed framework, an extensive set of simulations was carried out in noiseless and noisy environments using a real propagation model. Simulation results suggest that the proposed Gradient descent variants based matrix completion reliably estimate the complete EDM exploring partial known information. Trilateration combined with matrix completion outperforms the traditional localization system. Our simulation results indicate that trilateration combined with Adam which is used to solve the matrix completion problem outperforms the other combinations. This approach does not require a high computational complexity. Real experiments have been done in order to support simulation results and show that our approach outperforms the classic trilateration.
Since there are pairwise distances that are better estimated than others, we are interested in using weighted distances when applying trilateration in future work. The accorded weight increases when the distance is well estimated. New localization system improvements in terms of complexity can be provided using machine learning methods, since these aim to shift the prediction complexity to an offline phase.
Author Contributions
W.N. and R.Z. conceived the presented idea and developed the closed-form of each algorithm. Simulations and results presentation were conducted by W.N., R.Z., I.A. and M.T. verified the analytical methods and discussed the results contributed to the final manuscript. All authors provided critical feedback and helped the research, analysis and manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Atzori, L.; Iera, A.; Morabito, G. The internet of things: A survey. Comput. Netw. 2010, 54, 2787–2805. [Google Scholar] [CrossRef]
- Hennebert, C.; Denis, B.; Le Gall, F.; Copigneaux, B.; Clari, F.; Sottile, F.; Mauro, F.; Smadja, P.; Pascali, S.; Preuveneers, D.; et al. uBiquitous, secUre inTernet-of-things with Location and contEx-awaReness. BUTLER project D 2, 1–134. Available online: www.iot-butler.eu (accessed on 5 July 2018).
- Dil, B.; Dulman, S.; Havinga, P. Range-based localization in mobile sensor networks. In Proceedings of the European Workshop on Wireless Sensor Networks, Zurich, Switzerland, 13–15 February 2006; pp. 164–179. [Google Scholar]
- Singh, S.P.; Sharma, S.C. Range free localization techniques in wireless sensor networks: A review. Procedia Comput. Sci. 2015, 57, 7–16. [Google Scholar] [CrossRef]
- Awad, F.; Al-Sadi, A.; Alsmady, A. Distributed and adaptive location identification system for mobile devices. EURASIP J. Adv. Signal Process. 2018, 2018, 61. [Google Scholar] [CrossRef]
- Kaplan, E.; Hegarty, C. Understanding GPS: Principles and Applications; Artech House: Norwood, MA, USA, 2005. [Google Scholar]
- Gu, Y.; Chen, M.; Ren, F.; Li, J. HED: Handling environmental dynamics in indoor WiFi fingerprint localization. In Proceedings of the IEEE Wireless Communications and Networking Conference (WCNC), Doha, Qatar, 3–6 April 2016; pp. 1–6. [Google Scholar]
- Sun, L.; Zheng, Z.W.; He, T.; Li, F. Multifloor Wi-Fi localization system with floor identification. Int. J. Distrib. Sens. Netw. 2015, 11, 131523. [Google Scholar] [CrossRef]
- Cheng, J.; Song, Z.; Ye, Q.; Du, H. MIL: A mobile indoor localization scheme based on matrix completion. In Proceedings of the IEEE International Conference on Communications (ICC), Kuala Lumpur, Malaysia, 23–27 May 2016; pp. 1–55. [Google Scholar]
- Yang, Z.; Liu, Y. Quality of trilateration: Confidence-based iterative localization. IEEE Trans. Parallel Distrib. Syst. 2010, 21, 631–640. [Google Scholar] [CrossRef]
- Norrdine, A. An algebraic solution to the multilateration problem. In Proceedings of the 15th International Conference on Indoor Positioning and Indoor Navigation, Sydney, Australia, 13–15 November 2012; p. 2012. [Google Scholar]
- Najib Yasmeen, N.A.; Daud, N.; Abd Aziz, A.; Razali, R. 3-Dimensional wireless sensor network localization: A review. AIP Conf. Proc. 2016, 080029. [Google Scholar] [CrossRef]
- Kumar, P.; Reddy, L.; Varma, S. Distance measurement and error estimation scheme for RSSI based localization in Wireless Sensor Networks. In Proceedings of the 5th IEEE Conference on Wireless Communication and Sensor Networks (WCSN), Allahabad, India, 15–19 December 2009; pp. 1–4. [Google Scholar]
- Nguyen, T.L.; Shin, Y. Matrix completion optimization for localization in wireless sensor networks for intelligent IoT. Sensors 2016, 16, 722. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, L.; Kim, S.; Shim, B. Localization in Internet of Things network: Matrix completion approach. In Proceedings of the Information Theory and Applications Workshop (ITA), San Diego, CA, USA, 31 January–2 February 2016; pp. 1–4. [Google Scholar]
- Nguyen, L.; Shim, B. Localization of Internet of Things network via Euclidean distance matrix completion. In Proceedings of the IEEE/CIC International Conference on Communications in China (ICCC), Chengdu, China, 27–29 July 2016; pp. 1–4. [Google Scholar]
- Zhu, Y.; Jiang, A.; Kwan, H.K. ADMM-Based Sensor Network Localization Using Low-Rank Approximation. IEEE Sens. J. 2018, 18, 8463–8471. [Google Scholar] [CrossRef]
- Alfakih, A.Y.; Khandani, A.; Wolkowicz, H. Solving Euclidean distance matrix completion problems via semidefinite programming. Comput. Optim. Appl. 1991, 12, 13–30. [Google Scholar] [CrossRef]
- Ferreira, R.; Xavier, J.; Costeira, J.P.; Barroso, V. Newton algorithms for Riemannian distance related problems on connected locally symmetric manifolds. IEEE J. Sel. Top. Signal Process. 2013, 7, 634–645. [Google Scholar] [CrossRef]
- Cai, J.-F.; Candès, E.J.; Shen, Z. A singular value thresholding algorithm for matrix completion. SIAM J. Optim. 2010, 20, 1956–1982. [Google Scholar] [CrossRef]
- Chen, M.; Ganesh, A.; Lin, Z.; Ma, Y.; Wright, J.; Wu, L. Fast convex optimization algorithms for exact recovery of a corrupted low-rank matrix. In Coordinated Science Laboratory Report no. UILU-ENG-09-2214; Coordinated Science Laboratory, University of Illinois at Urbana-Champaign: Champaign, IL, USA, 2009. [Google Scholar]
- Lin, Z.; Chen, M.; Ma, Y. The augmented lagrange multiplier method for exact recovery of corrupted low-rank matrices. arXiv 2010, arXiv:1009.5055. [Google Scholar]
- Liu, C.; Shan, H.; Wang, B. Wireless Sensor Network Localization via Matrix Completion Based on Bregman Divergence. Sensors 2018, 18, 2974. [Google Scholar] [CrossRef] [PubMed]
- Xiao, F.; Liu, W.; Li, Z.; Chen, L.; Wang, R. Noise-tolerant wireless sensor networks localization via multinorms regularized matrix completion. IEEE Trans. Veh. Technol. 2018, 67, 2409–2419. [Google Scholar] [CrossRef]
- Grant, M.; Boyd, S.; Ye, Y. CVX: Matlab Software for Disciplined Convex Programming; CVX Research, Inc.: Austin, TX, USA, 2008. [Google Scholar]
- Guo, X.; Chu, L.; Sun, X. Accurate localization of multiple sources using semidefinite programming based on incomplete range matrix. IEEE Sens. J. 2016, 16, 5319–5324. [Google Scholar] [CrossRef]
- Guo, X.; Chu, L.; Ansari, N. Joint localization of multiple sources from incomplete noisy Euclidean distance matrix in wireless networks. Comput. Commun. 2018, 122, 20–29. [Google Scholar] [CrossRef]
- Chen, J.; Mitra, U. Unimodality-Constrained Matrix Factorization for Non-Parametric Source Localization. IEEE Trans. Signal Process. 2019, 67. [Google Scholar] [CrossRef]
- Nguyen, L.T.; Kim, J.; Kim, S.; Shim, B. Localization of IoT Networks Via Low-Rank Matrix Completion. IEEE Trans. Commun. 2019. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, Y.; Lei, H. Localization from Incomplete Euclidean Distance Matrix: Performance Analysis for the SVD-MDS Approach. IEEE Trans. Signal Proces. 2019, 67. [Google Scholar] [CrossRef]
- Torgerson, W.S. Multidimensional scaling of similarity. Psychometrika 1965, 30, 379–393. [Google Scholar] [CrossRef]
- Tsai, M. Path-loss and shadowing (large-scale fading). Nat. Taiwan Univ. Oct. 2011, 20, 2011. [Google Scholar]
- Recht, B.; Fazel, M.; Parrilo, P.A. Guaranteed minimum-rank solutions of linear matrix equations via nuclear norm minimization. SIAM Rev. 2010, 52, 471–501. [Google Scholar] [CrossRef]
- Candès, E.J.; Recht, B. Exact matrix completion via convex optimization. Found. Comput. Math. 2009, 9, 717. [Google Scholar] [CrossRef]
- Duchi, J.; Hazan, E.; Singer, Y. Adaptive subgradient methods for online learning and stochastic optimization. J. Mach. Learn. Res. 2011, 12, 2121–2159. [Google Scholar]
- Sebastian, R. An overview of gradient descent optimization algorithms. arXiv 2016, arXiv:1609.04747. [Google Scholar]
- Sutskever, I.; Martens, J.; Dahl, G.; Hinton, G. On the importance of initialization and momentum in deep learning. In Proceedings of the International Conference on Machine Learning, Atlanta, GA, USA, 16–21 June 2013; pp. 1139–1147. [Google Scholar]
- Wang, Y.; Kim, S.-P.; Principe, J.C. Comparison of TDNN training algorithms in brain machine interfaces. In Proceedings of the IEEE International Joint Conference on Neural Networks (IJCNN’05), Montreal, QC, Canada, 31 July–4 August 2005; pp. 2459–2462. [Google Scholar]
- Hinton, G.; Srivastava, N.; Swersky, K. Neural networks for machine learning lecture 6a overview of mini-batch gradient descent. Cited On 2012, 14, 31. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Cheng, J.; Ye, Q.; Jiang, H.; Wang, D.; Wang, C. STCDG: An efficient data gathering algorithm based on matrix completion for wireless sensor networks. IEEE Trans. Wirel. Commun. 2013, 12, 850–861. [Google Scholar] [CrossRef]
- Xie, K.; Ning, X.; Wang, X.; Xie, D.; Cao, J.; Xie, G.; Wen, J. Recover corrupted data in sensor networks: A matrix completion solution. IEEE Trans. Mob. Comput. 2017, 16, 1434–1448. [Google Scholar] [CrossRef]
- Strassen, V. Gaussian elimination is not optimal. Numer. Math. 1969, 13, 354–356. [Google Scholar] [CrossRef]
- Benoit, A. Algorithmique I-Cours et Travaux Dirigés L3; Ecole Normale Supérieure de Lyon: Lyon, France, 2009. [Google Scholar]
- Iannazzo, B. On the Newton method for the matrix p th root. SIAM J. Matrix Anal. Appl. 2006, 28, 503–523. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).