Abstract
Curve fitting to unorganized data points is a very challenging problem that arises in a wide variety of scientific and engineering applications. Given a set of scattered and noisy data points, the goal is to construct a curve that corresponds to the best estimate of the unknown underlying relationship between two variables. Although many papers have addressed the problem, this remains very challenging. In this paper we propose to solve the curve fitting problem to noisy scattered data using a parallel hierarchical genetic algorithm and B-splines. We use a novel hierarchical structure to represent both the model structure and the model parameters. The best B-spline model is searched using bi-objective fitness function. As a result, our method determines the number and locations of the knots, and the B-spline coefficients simultaneously and automatically. In addition, to accelerate the estimation of B-spline parameters the algorithm is implemented with two levels of parallelism, taking advantages of the new hardware platforms. Finally, to validate our approach, we fitted curves from scattered noisy points and results were compared through numerical simulations with several methods, which are widely used in fitting tasks. Results show a better performance on the reference methods.
1. Introduction
Curve fitting deals with the problem of reconstructing an unknown function from a finite set of data points, which are commonly noisy measurements without a regular structure [1], i.e., scattered data. In this regard, the most common methods applied to this problem are interpolation and approximation. The first one uses a fitting function to reconstruct a function from the given data and the second one tries to follow the behavior of the data to reconstruct the curve. Typically, interpolation is applied to noise-free data points, while approximation is applied to noisy data points [2].
Among the variety of approximation methods used to tackle the curve fitting problem (from scattered data), B-spline curves is one of the most widely used methods to define a mathematical function that best describes the behavior of the data [2,3,4,5,6]. Thus, a B-spline curve is a continuous piecewise polynomial function defined by two sets of parameters, knots and coefficients, being knot placement and their optimal number an important issue to consider in the search of the best approximation [6]. This means that we have to place the knots as precisely as possible and determine the optimal number of knots. In this sense, the problem is considered as a hard continuous multimodal and multivariate nonlinear optimization problem with many local optima. Additionally, we need to calculate the B-spline coefficients separately by ordinary least squares. Due to the number of degrees of freedom of the B-spline, the dimension of the search space tends to be huge and to the best of our knowledge, there is not solving method that simultaneously deals with all degrees of freedom. Besides, the data is generally scattered and presents some noise, making the problem harder to solve, therefore, it is difficult to obtain an optimal solution, and it requires a high processing power.
Consequently, meta-heuristic methods, such as evolutionary algorithms and specifically genetic algorithms (GA) [7] have been used to efficiently solve the aforementioned optimization problem. The GAs have been applied successfully to find near-optimal or optimal solutions to problems with a difficult and huge search space. However, the computational cost to perform a solution by using GAs is high, due to their exhaustive evolution process, which mimics the natural evolution of a population of living organisms. This computational cost is still an open issue in GAs, few papers dealing partially with this issue have been proposed [8]. In such a paper, authors propose the design of new operators, parallel execution sequences and constraints to reach termination. Nevertheless, the way in which the population is structured and how the parallel process is synchronized are what really matters to improve the performance.
In this paper, we tackle both, the curve fitting problem to noisy scattered data and its performance by implementing a parallel hierarchical genetic algorithm (PHGA). For the curve fitting problem, we use a novel hierarchical structure to represent both the model structure (number and placement of knots) and the model parameters (B-spline coefficients). This hierarchical structure combines binary and real encoding. We searched for the best B-spline model using a bi-objective fitness function. As a result, our method determines the number of knots and their place simultaneously and automatically, as well as B-spline coefficients. In addition, our approach is able to find the optimal solutions with the fewest parameters within the B-spline basis functions, without the need for any subjective parameters such as smoothing factor or other initialization values, i.e., our method is fully automatic.
In order to improve the performance of the HGA (hierarchical genetic algorithm), the algorithm is implemented using a full parallel model, taking advantage of the capabilities of the new hardware platforms. This is one of the main contributions of this study. In this sense, our approach presents two levels of parallelism. First, the parallelism at the level of individuals to improve the processing speed and second the parallelism at level of subpopulations which improves the algorithm by avoiding premature convergence due that it preserves the genetic diversity, and thus allows the algorithm to find better solutions.
The rest of the paper is organized as follows: in Section 2 we present a brief review of the literature related to the problem addressed in this paper. Section 3 provides to the reader the methods and materials used in this paper. In Section 4 the proposed approach is formulated. Simulation results and comparisons with popular methods are discussed in Section 5. Finally, we present in Section 6, some concluding remarks and perspectives of this study.
2. Related Work
Scattered data fitting can be posed as an optimization problem and it has been used in many fields and applications, such as applied mathematics, computer science, geology, biology and engineering, to name a few. Particularly, ref [2] used a standard regularized least square framework when using the wavelet domain instead of the B-spline domain. In [9], a scattered approximation method using a kernel-based multivariate interpolation and approximation was introduced. This was based on the Hilbert spaces, which construct and characterize their native kernels. In [3], authors describe a fast algorithm for scattered data interpolation and approximation making use of a coarse-to-fine hierarchy of control lattices to generate a sequence of bicubic B-spline functions. In [4], a method for fitting scattered data on a 2D smooth manifold was presented. The method was based on a local bivariate Powell–Sabin interpolation scheme. It was based on a split of the macro-triangle into three sub-triangles and there was a cubic polynomial on each piece. On the other hand, other works have focused their efforts on determine the placement and quantity of knots used for curve approximation, [5] presented a method for calculating knots placement for a cubic spline curve applying a half-split method to subdivide the data into a set of piecewise lineal functions using a predefined threshold compared with an error band calculated with the second derivative. Ref [6] presented a heuristic knots placement for B-splines curves approximation, this approach was based on smoothing discrete curvature characteristics as a criterion to determine if knots were correctly placed.
Recently, several approaches based on meta-heuristics methods [10,11,12,13] have been applied successfully to optimize a bi-objective function, which is expressed in the form of the weighted sum of two objectives. Particularity, Shahvari et al. shows tabu search (TS)-based approaches to solving the batching and scheduling problems, which are combinatorial optimization problems that suit the TS methods [14,15]. Although, the nature of the curve fitting problem is different, these approaches are successful examples of the use of the bi-objective models. However, there are some approaches that have used the TS method for nonlinear and parametric optimization problems with little success [16]. On the other hand, ref [10] use a GA with a two-dimensional chromosome structure to solve the hazardous materials routing and scheduling problem. Although there are similarities between our algorithm and the Ardjmand algorithm, there are important differences. First, the algorithms are applied to solve intrinsically different problems. The Ardjmand’s method is applied to solve a routing and scheduling problem, while our method is applied to solve a multivariate nonlinear optimization problem. Second, in the Ardjmand method they applied a GA while in our method we applied a PHGA. Third, the structure implemented to search in the solution space is distinctly different. Ardjmand proposed a two-dimensional structure that represents a route in one dimension and different route costs in the second dimension for each specific individual, while we proposed a structure that has two levels of chromosomes of different types with a hierarchical relationship that is a characteristic of the HGA. In our case, this work is a continuation of that presented in [17], where a HGA was used to approximate noisy and scattered data instead of uniform data, which implies a new parameters setting of the HGA. Additionally, in this work we contribute to a parallel implementation in two levels of parallelization, over the population and the individual. With this new approach the algorithm shows a better performance over the state of art algorithms and a speed up up to 145 times over a sequential implementation presented in the previous work.
There are techniques and methods that are intrinsically parallel, and can be implemented by taking advantage of new technologies for data processing, such as graphics processing units (GPUs) and multiprocessor computers, as well as tools developed for this purpose. The parallelization of methods and techniques has been widely developed in different knowledge fields showing significant improvements in response times for computationally expensive problems (see [18,19,20]). This work is focused on hierarchical genetic algorithms and its implementation and application as a parallel architecture for curve fitting. In this regard, the implementation of metaheuristics for several problems has been addressed using GPUs and CPUs mainly using CUDA, OpenCL, OpenMP and MPI. Table 1 shows some works which have addressed classic problems such as the traveling salesman [21,22,23] and others more specialized like path planning [24], etc.; being OpenCL and CUDA the technologies more used.

Table 1.
Overview of parallel metaheuristic implementations.
3. Background
3.1. Curve Fitting with B-Spline Curves
Fitting curve is known as the process of finding the equation of the curve which may be most suitable for predicting unknown values. The curve fitting problem assumes that there is a relationship between n pairs of values in order to find the best curve that fits the existing data, estimating well enough to be used to predict new values adequately. The problem of curve fitting comprises two stages: choosing a family of curves and selecting the best fitting curve [33].
In this paper, we have used functions f that can be approximated on the interval by a B-spline curve. The B-spline curve is a piecewise polynomial function of k order joined at certain n locations called knots and into an interval . A B-spline function of k order on a given set of k knots can be written as a linear combination:
where are B-spline coefficients and are the basis function of k order obtained by means of the recursive formula Cox-de Boor
and
where is an element of the knot vector defined by:
with a set of m interior knots placed along the domain of x, such that .
If the order k for B-spline is defined beforehand, a B-spline function f can be defined completely by pairs , where and . Then, the challenge is to find de number of knots , and their coeficients . A more detailed discussion of B-splines can be found in [34,35].
3.2. Hierarchical Genetic Algorithms
Hierarchy refers to the presence of modules at multiple levels above the base layer of primitive modules. Thus, a hierarchical problem is a problem involving at least one composite module that contains another composite module [36].
A HGA is an extension of a genetic algorithm, except that in HGA the information of the problem uses a genetic structure of chromosomes divided into modules at multiple levels above the base layer of primitive modules. In [37], authors proposed a hierarchical chromosome structure splitting it in two types of genes: control and parametric genes. The genes are encoded using binary values, and parametric genes can use any representation, although they are generally encoded as real numbers. The purpose of control genes is to enable or disable parametric allowing us to have phenotypes with different lengths using the same chromosomal representation. The hierarchical structure makes possible to split a problem into separable sub-problems where each of them has a definite goal to achieve; thus, a HGA allows us to work simultaneously finding partial solutions to encompass various targets for a general objective, and this is how we can address large multi-objective problems efficiently [38].
4. B-Spline Curve Fitting Using PHGA
In this paper, we used a PHGA to determine the number and place of knots in an interval , and we also used it to determine the coefficients of B-spline simultaneously under the criterion of minimum fitness. Next, we present the main features of the PHGA used in this study.
4.1. Chromosome Encoding
The chromosome has a hierarchical structure with control and parametric genes. Here, control and parametric genes are encoded as a fixed length binary string and real numbers respectively, i.e., chromosomes combine binary and real encoding, which are represented by the following vector:
where b is a control bit for the enabling and disabling of interior knots from the and coefficients of the B-spline function represented in the chromosome by a real value r. Due to that, we had m interior knots, coefficients are needed. We establish a correspondence one-to-one between the interior knots and the first m coefficients. The hierarchical chromosome structure is graphically shown in Figure 1, in where we can see that each scattered point is pared to one binary gene, it means that each point x becomes an interior knot for the B-spline function.
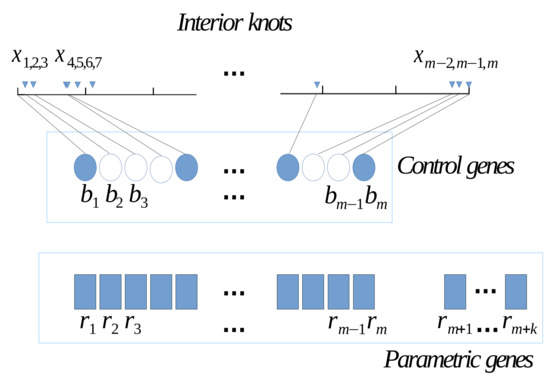
Figure 1.
Hierarchical chromosome structure.
4.2. Fitness Function
In order to evaluate the chromosome performance in the B-spline fitting problem, we use a bi-objective fitness function applying the Weighted Sum method [39] to the Akaike’s information criterion (AIC) and a penalization knot structure function (P). Then, the fitness function is given by:
where and are scale factors to normalize the objectives.
4.2.1. Akaike’s Information Criterion
The Akaike’s Information Criterion (AIC), proposed by [40], is a measure of the relative quality of statistical models for a given set of data; AIC deals with the trade-off of goodness and complexity of a model, that is to say, a likelihood function for the model fit and the number of estimated parameters for this model. Thus, the AIC value of the model is given by:
where the first term of the equation is the residual sum of squares used as a likelihood function between the fitted function and their reference values , moreover, p is the number of parameters used to estimate . In this paper the number of parameters consists of the number of interior knots m and the number of the B-spline coefficients , thus . Considering the number of parameters as a fitness criterion helps to reduce the number of interior knots and consequently avoid the overfitting problem.
4.2.2. Knot Structure Function
Due to the characteristics of the scattered data and the process of fitting a B-spline function using a PHGA, it was necessary to add a penalty function with the aim of promoting chromosomes with fewer knots and having a better distribution within an interval . From [41], we compute the penalty as:
where m is the size of the knots set , and is the number of values which satisfies , for , and .
4.3. Selection Scheme
Fitness proportional selection, also known as roulette wheel selection, was used for selecting individuals to reproduce offspring in the next generation. When using the roulette wheel selection method, the individuals are selected based on a probability determined for their fitness level, thus favoring exploitation of regions into the search space with high fitness level at the expense of other regions; therefore, this method tends to converge prematurely [42]. In order to prevent the premature convergence, we used the sigma scaling method, in which the standard deviation of the population fitness is used to scale the fitness scores according to:
were is the current fitness value calculated using Equation (6), and are the mean and standard deviation of current fitness values and c is a constant value to control the influence of standard deviation over the selection threshold. It is, Equation (9) serves to eliminate individuals with high and low fitness levels. To preserve the best individuals, we use Elitism, i.e., the n best individuals are selected to be copied without change to the new population.
4.4. Genetic Operators
4.4.1. Crossover Operator
Crossover is the process of taking two parent solutions and producing from them a child. The crossover operator is applied in the hope that it may create better offspring [43]. Since we have two types of genes, we implemented two crossover operators; for control genes uniform crossover was used and for parametric genes simulated binary crossover (SBX) was used. In uniform crossover each individual in the offspring is created recombining two parents, and each gene of a new individual is selected copying the corresponding gene from one of the parent according to a random value on a fixed probability. Using the SBX operator proposed in [44], two new individuals and are generated from two parents and applying:
where is the spread factor calculated by
where u is a random number between 0 and 1 and is a non-negative number that controls the distance between parents and new individuals generated. In Figure 2, we show the crossover process applied to control and parametric genes from two parents to obtain two offspring.
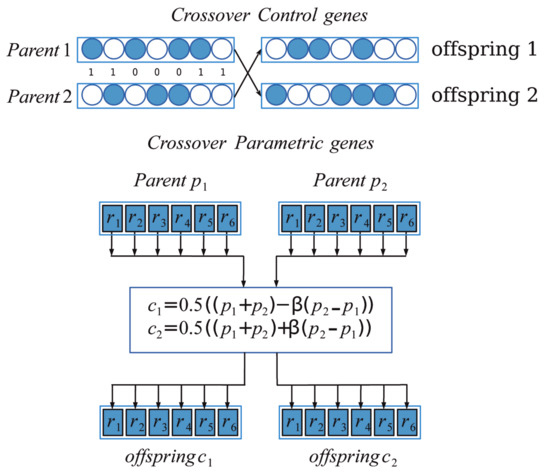
Figure 2.
Crossover operator. For control genes, the ones indicate which genes are interchanged according with a uniform probability.
4.4.2. Mutation Operator
The bit mutation method is used as mutation operator. In this method, each bit of the binary-valued chromosome is inverted or not depending on the mutation probability. On the other hand, for the real-valued chromosome each numeric value is changed also depending on the same mutation probability according to:
where is the maximum increment or decrement of the real value and is a function that generates a random value between 0 and 1.
4.5. Parallel Hierarchical Genetic Algorithm
In this paper we propose a PHGA based on a distributed model and a synchronous master-slave model; more detailed information about parallel models on genetic algorithms can be found in [8,45].
Basically, the structure of parallelization consists in dividing the global population into local subpopulations, each of which represents an island, and inside each island the level of parallelization is given by the quantity of individuals in the island and the operator that is applied to the population. Figure 3 shows graphically the iterative process that generates a new population into each island, where represents each individual in the island population and c represents the cores (threads or processors) used to perform the PHGA.
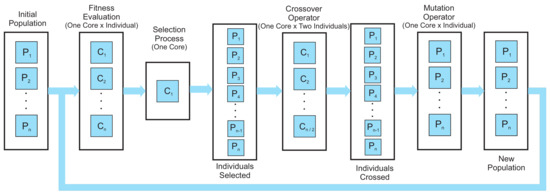
Figure 3.
Parallelization scheme.
The initial population is initialized randomly using a host device, and then the population is sent to a parallel device in charge of applying stochastic operators to find an adequate solution. The parallelization schema depends on the characteristics of each one of the processes involved in the PHGA. For the fitness function, one core is assigned to each individual in the population in order to calculate the fitness value for each individual; on the other hand, for the selection process only one core is required, because the sigma scaling is the same for each island and implementing it in parallel would reduce performance. The crossover operator takes two parents to produce two children, and thus a core is used for every two individuals of the population. Finally, the characteristics of the mutation operator allow us to implement parallelization of individual per core.
The inter-island communication occurs during the migration phase, which takes place after all of the processors have reached a certain number of iterations and have been synchronized; after migration, each processor resumes running the PHGA as before, until the next migration phase.
Migration Operator
The migration consists of a periodical exchange of individuals among subpopulations, i.e., a fixed proportion of each subpopulation is selected and sent to another subpopulation. At the same time, the same number of migrants are received from some other subpopulation and replace individuals selected according to some criteria [46]; after that, each island resumes running the PHGA until the next migration phase occurs. The migration operator in the island model involves some parameters to define, such as: migration topology, migration size, migration interval and migration algorithm, a more detailed discussion of this topic can be found in [47].
5. Simulation Results
5.1. Experimental Set
To evaluate the performance of our approach we compared the PHGA results with those obtained using the following methods: cubic smoothing spline (CSSPL), locally weighted scatterplot smoothing (LOWESS) and Fourier curve fitting (FCF). This evaluation considers six benchmark functions (see [2,48,49,50,51] for details), whose mathematical equations are shown in Table 2.

Table 2.
Test functions.
For each function several synthetic noisy data sets were created. Here, a data set consists of random values generated into a defined domain (see Table 2) using a random uniform distribution, which allows us to have unstructured data locations or scattered data. For building the data sets, the values were evaluated for each function f adding a zero-mean normal noise with a known in order to have a specific signal to noise ratio (SNR), defined as .
The number of values used for each function was 100 for each one of the 100 test sets generated for SNR = 3, SNR = 2 and SNR = 1 per function, resulting in 1800 tests to validate our approach. Since the domain of function 4 was defined over the interval , it was necessary to scale them to an interval in order to evaluate our approach under equal conditions.
Experiments over six functions were performed using PHGA, LOWESS, FCF, and CSSPL methods. Our approach, PHGA, was executed using 10 islands with a population of 200 individuals per island; each island evolved for 999 generations, and a migration process was performed each 200 epochs. The number of islands and epoch were selected taking into account the temporal and spatial complexity in our experiments as well as the point were PHGA achieved stability. In Table 3, the parameters used in the PHGA are shown.

Table 3.
Parameters of the genetic algorithm.
To implement LOWESS and FCF curve fitting we have relied on routine for LOWESS and FCF fitting, and routine for CSSPL fitting, both from the Curve Fitting Toolbox in MATLAB. For CSSPL, it was necessary to specify a smoothing parameter p, which was determined by:
where h is the average spacing between values, and d was determinated as the mean of the values that perform a fitting with the lowest error for each function, i.e., the data sets corresponding to each function were grouped with their three noise levels, then CSSPL was performed varying parameter d into a range, and finally the mean of the values d with the smallest error for each test set grouped by function was taken to perform CSSPL fitting for comparing with PHGA.
For the PHGA, each chromosome of the initial population consisted of m knots and its respective coefficients , which were placed and fixed randomly. In order to place the knots, a boolean random value was generated for each point and for true values knots were established at those points; then, its respective coefficient values were generated over the range to fulfill the structure of chromosome used (Section 3.1). The number and placement of the knots were selected randomly with a probability of 0.25 for all test sets; these and others parameters used for the genetic algorithm were determined experimentally and are shown in Table 3. As any approach based on genetic algorithms, these parameters depend on the application or problem, for this reason their value can change. In our case, such parameters are tuned in order to reach the best performance. Thus, if the parameters are modified, such performance can be altered.
5.2. Results
In the experimental phase we performed 18 tests by the method using six functions, one size of sample points and three levels of noise. Each experiment was executed using 100 different test sets and 999 epochs for the PHGA, then the best individual by island was selected agree with its fitness, to finally choose the best of the best. To evaluate and compare the results for each function, we created validation sets consisting of 200 values uniformly distributed into their respective domain (Table 2); then they were evaluated in their respective function and results were compared to the same set of values estimated by PHGA, CSSPL, FCF and LOWESS through a mean square error (MSE) given by:
where is the estimated function by PHGA, CSSPL, FCF and LOWESS, and the benchmark function . Table 4 shows the mean and standard error of the mean for MSE values obtained from each method for each test. As we can see in Table 4, in most of the cases, PHGA produced lower mean MSE values (marked in bold). This suggests that our method shows a considerable improvement over the CSSP, FCF and LOWESS methods, which is more appreciable in the box plots of the MSE values.

Table 4.
Mean of the computed mean square errors (MSEs) with estimated standard errors based on 100 test sets with 100 samples.
Box plots are an effective way to compare the distribution of our results, because we can see how is the data distributed into quartiles. For each function and SNR level we generated a box plot graph using the MSE values obtained from each test using PHGA, CSSPL, FCF and LOWESS approaches.
For the test with SNR = 3, showing in Figure 4, we can see that for function 1, the performance of PHGA was slightly better than CSSPL and FCF, since the distribution of the MSE obtained was similar and the median of the MSE for PHGA was lower. For function 2, PHGA was significantly better than the other methods due to the third quartile obtained with PHGA is slightly higher than the second quartile from CSSPL, which means that nearly of of error obtained with PHGA tests had a lower MSE values than the of error obtained using CSSPL, for FCF and LOWESS, PHGA improved considerably because of the upper adjacent value from PHGA errors was lower than the lower adjacent value from FCF and LOWESS. For function 3, we can see that the performance of PHGA and CSSPL was practically tied, and for FCF and LOWESS the third quartile from PHGA was lower than the first quartile from FCF and LOWESS. In the case of function 4, the third quartile from PHGA was lower than the median of CSSPL, for FCF and LOWES against PHGA, it last was considerably better. In function 5, visually there was no difference between PHGA and CSSPL but PHGA was slightly less dispersed. For function 6, PHGA shows better performance due to the third quartile from PHGA was lower than first quartile from CSSPL, and the performance of FCF and LOWESS was too high compared to the other alternatives.
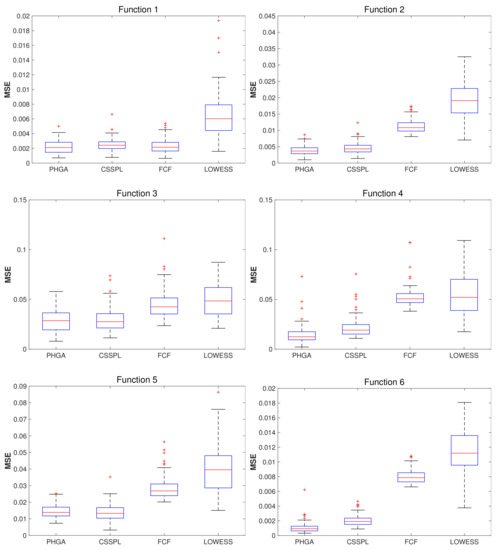
Figure 4.
Boxplots of the mean squared error (MSE) computed for each algorithm per function, using 100 test sets, 100 scattered points (x,y) and signal to noise ratio (SNR) = 3.
For the results obtained with SNR = 2, showing in Figure 5, we can see that function 1 shows better performance than the other methods covered in this work, the third quartile of PHGA boxplot was similar to mean of CSSPL and FCF methods, and third quartile of PHGA was lower then first quartile than LOWESS. For function 2, PHGA and CSSPL had similar performance and better than FCF and LOWESS, due to results of third quartile from PHGA and CSSPL were below of first quartile of FCF and LOWESS. In function 3, the four methods had similar performance, being CSSPL who had the best performance which was slightly better than PHGA and LOWESS, and FCF had the worst result. For function 4, PHGA had better performance and the others methods had similar performance. In function 5, the best performance was obtained for CSSPL slightly better than PHGA, in this case it is important to emphasize that the difference between PHGA and CSSPL was very small and PHGA had a smaller dispersion of the error. Finally for function 6, PHGA was far superior to the other methods.
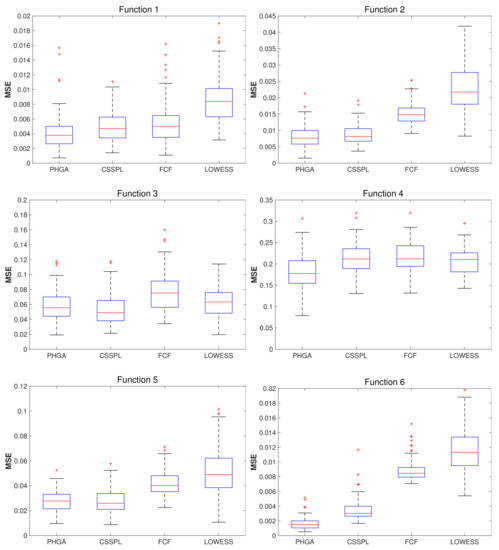
Figure 5.
Boxplots of MSE computed for each algorithm per function, using 100 test sets, 100 scattered points (x,y) and SNR = 2.
Figure 6 shows the results obtained with SNR = 1, where PHGA had a better performance in functions 1, 2, 4–6. In the case of function 3, LOWESS had the lowest error level compared with all the other methods, although PHGA did not have the best performance, it was very close to LOWESS and also PHGA had an error dispersion lower than LOWESS.
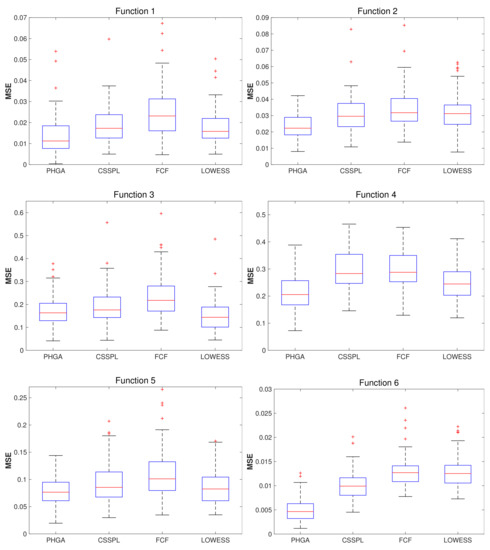
Figure 6.
Boxplots of MSE computed for each algorithm by function, using 100 test sets, 100 scatered points (x,y) and SNR = 1.
In order to visually compare the performances of PHGA, CSSPL, FCF and LOWESS approaches, we present in Figure 7, Figure 8 and Figure 9 some graphs of the best curves obtained with each one of the methods. In general, curves fitted with PHGA had a smoother appearance in contrast to curves adjusted by the others methods, this is because of the fitness function for the PHGA is a multi-objective function, looking for reducing the number of knots of the curve, placing them uniformly distributed in the domain of x and reducing the MSE.
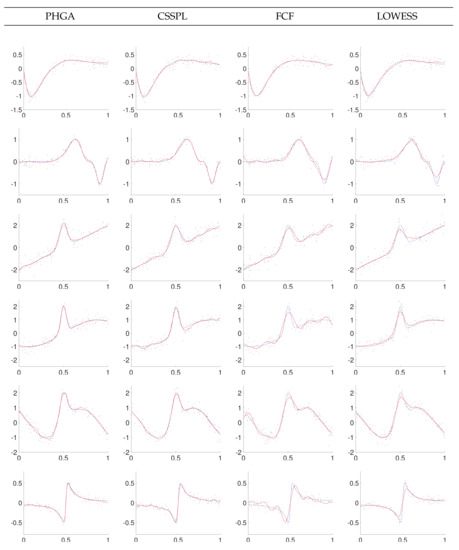
Figure 7.
Data and best fitting with SNR = 3 for parallel hierarchical genetic algorithm (PHGA), cubic smoothing spline (CSSPL), Fourier curve fitting (FCF) and locally weighted scatterplot smoothing (LOWESS) methods (solid line: estimated function; dashed line: real function).
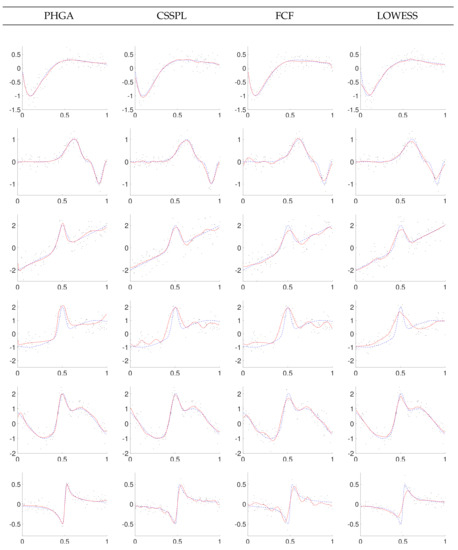
Figure 8.
Data and best fitting with SNR = 2 for PHGA, CSSPL, FCF and LOWESS methods (solid line: estimated function; dashed line: real function).
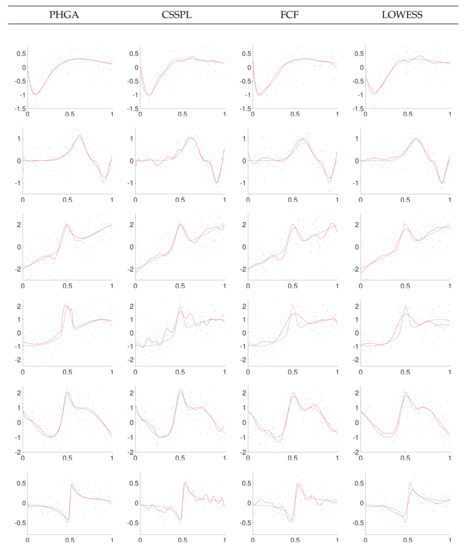
Figure 9.
Data and best fitting with SNR = 1 for PHGA, CSSPL, FCF and LOWESS methods (solid line: estimated function; dashed line: real function).
Based on the results showed in Figure 7, Figure 8 and Figure 9, it can be observed that the proposed PHGA shows a better visual performance that those obtained with the other methods. This is particularly visible in the experiments with higher noise i.e., experiments with SNR = 1. In this case, we can observe that curves fitted with CSSPL for the function 2, 4, and 6 present a remarkable over fitting. This is the main drawback of the CSSPL method due to the results are very sensitive to the smoothing parameter. For the proposed approach, it could be assumed that the success is due to the simultaneous global search performed over all degrees of freedom of the B-spline model, as well as, the ability of the GA to find optimal solutions despite of the high level of noise in the signal. On the other hand, we can see from standard errors of the mean that both algorithm presents nearly the same certainty in the estimate of the mean. About the FCF method, it shows oscillations for functions 4 and 6 in the three levels of noise due to the fact that it is based on sum of sine and cosine terms. In the case of LOWESS method, it produces smooth curves but in most of the experiments its MSE is upper to the other methods.
In order to evaluate the computational performance of our approach, two versions were implemented, sequential and parallel. The OpenCL framework was used for the parallel version due that it can be used over different platforms with multiple processors and for the sequential version C++ was chosen. Table 5 reports the average amount of time needed to run our approach using a single processor for sequential version, and eight, sixteen and thirty two processors for the parallel version. In such a table, the letter T is the time in seconds necessary to finish the execution of the genetic algorithm, and the letter S is the speed-up compared with the sequential version, under the same sense, different configurations of number of islands, subpopulation size and number of points to fit were set in the tests.

Table 5.
Average time execution in seconds and speed-up.
Figure 10, shows the average execution times for each configuration from Table 5. Here, it is clear that results with more than one processor seems linear. This is because we compare with a single processor. It is shown graphically in Figure 10, where the parallel version is significantly faster than sequential one obtaining a speed-up near of 20 for the less demanding test and a speedup of 145 for the more demanding test. Figure 11, shows the average execution times only from parallel version experiments, showing the difference of using different number of processors. In contrast with Figure 10, here we clearly observe that the response of the PHGA under different hardware configurations is not linear. Every test where tested in a computer with 44 intel Xeon CPU running at 2.10 GHz with 40 GB RAM.
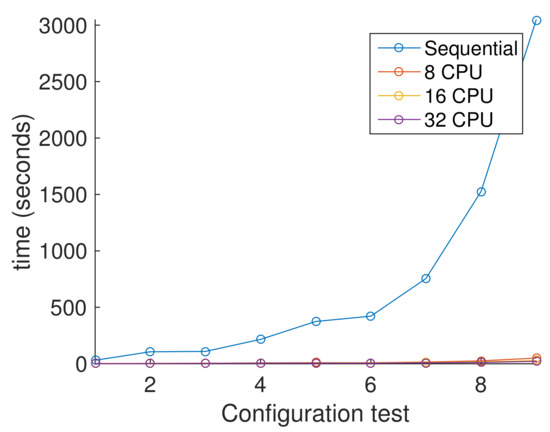
Figure 10.
Comparative performance between sequential version and parallel versions.
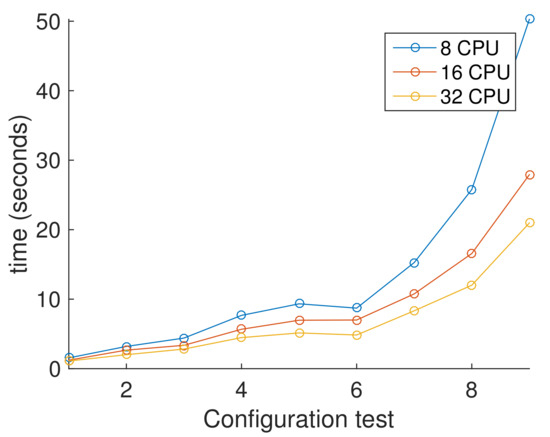
Figure 11.
Comparative performance between parallel versions using 8, 16 and 32 processors.
6. Conclusions
In this paper, we have proposed a parallel hierarchical genetic algorithm to approximate B-spline functions to scattered data placed randomly into an interval . The approach introduces a novel hierarchical gene structure for the chromosomal representation and a bi-objective fitness function based on a combination of the model selection criteria AIC and the knot structure function. As a result, our method determines the number and locations of the knots, and the B-spline coefficients simultaneously and automatically. The method does not require subjective parameters like smooth factor or any initialization value.
The proposed PHGA is implemented using a Full Parallel Model, with two levels of parallelism at level of the subpopulations and at level of the individuals, by dividing the population into islands and using a synchronous master-slave model inside each island respectively. This parallel schema is implemented, under an OpenCL framework, with the aim of reduce the time of processing, exploiting the characteristics of separability and modularity of hierarchical problems and island models. In our experiments we obtained a speed-up from 20 to 145, depending on the amount of data and the number of processors, which represents a significant reduction of execution time with respect to a sequential implementation.
To test our approach, we performed several simulations on six benchmark functions with three leves of SNRs, which were compared to solutions obtained using CSSPL, FCF and LOWESS methods. Simulation results show that the proposed approach presents better results than CSSPL, FCF and LOWESS method. Although in some cases numerically the results obtained for some function were not favorable, an important aspect to note is that, the difference is very small and the curves fitted using our approach look smoother than those obtained using the CSSPL, FNF and LOWESS method, which in some cases produce over fitted curves.
Finally, this paper has focused on smooth curve functions, but we are interested in extending our approach to un-smooth functions and surface fitting, as well as, experiment with other basis functions.
Author Contributions
Conceptualization, J.E.L.-R., C.H.G.-C. and H.R.-G.; funding acquisition, C.H.G.-C. and H.R.-G.; methodology, J.E.L.-R., J.G.A.-C. and C.H.G.-C.; project administration, M.d.J.E.-A., C.H.G.-C. and H.R.-G.; software, R.E.S.-Y., and J.E.L.-R.; supervision, C.H.G.-C. and H.R.-G.; validation, M.d.J.E.-A., J.E.L.-R. and C.H.G.-C.; writing—review and editing, J.E.L.-R., C.H.G.-C. and H.R.-G.; writing—original draft, and visualization, R.E.S.-Y., J.G.A.-C. and J.E.L.-R.
Funding
This research was funded by the CONACYT project FC2016-1961 “Neurociencia Computacional: de la teoría al desarrollo de sistemas neuromórficos” and the PRODEP project “Desarrollo de Técnicas para Mejorar el Desempeño Computacional de Algoritmos Bio-inspirados y su Aplicación en la Solución de Problemas de Optimización”.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Wendland, H. Scattered Data Approximation; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Johnson, M.J.; Shen, Z.; Xu, Y. Scattered data reconstruction by regularization in B-spline and associated wavelet spaces. J. Approx. Theory 2009, 159, 197–223. [Google Scholar] [CrossRef][Green Version]
- Lee, S.; Wolberg, G.; Shin, S.Y. Scattered Data Interpolation with Multilevel B-Splines. IEEE Trans. Vis. Comput. Graph. 1997, 3, 228–244. [Google Scholar] [CrossRef]
- Davydov, O.; Schumaker, L.L. Scattered Data Fitting on Surfaces Using Projected Powell-Sabin Splines. In Proceedings of the Mathematics of Surfaces XII: 12th IMA International Conference, Sheffield, UK, 4–6 September 2007; Martin, R., Sabin, M., Winkler, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2007; pp. 138–153. [Google Scholar]
- Tjahjowidodo, T.; Dung, V.; Han, M. A fast non-uniform knots placement method for B-spline fitting. In Proceedings of the 2015 IEEE International Conference on Advanced Intelligent Mechatronics (AIM), Busan, Korea, 7–11 July 2015; pp. 1490–1495. [Google Scholar]
- Li, W.; Xu, S.; Zhao, G.; Goh, L.P. A Heuristic Knot Placement Algorithm for B-Spline Curve Approximation. Comput.-Aided Des. Appl. 2004, 1, 727–732. [Google Scholar] [CrossRef]
- Holland, J.H. Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology, Control and Artificial Intelligence; The MIT Press: Cambridge, MA, USA, 1992. [Google Scholar]
- Luque, G.; Alba, E. Parallel Models for Genetic Algorithms. In Parallel Genetic Algorithms: Theory and Real World Applications; Springer: Berlin/Heidelberg, Germany, 2011; pp. 15–30. [Google Scholar]
- Iske, A. Scattered data approximation by positive definite kernel functions. Rend. Semin. Mat. Univ. Politec. Torino 2011, 69, 217–246. [Google Scholar]
- Ardjmand, E.; Young, W.A.; Weckman, G.R.; Bajgiran, O.S.; Aminipour, B.; Park, N. Applying genetic algorithm to a new bi-objective stochastic model for transportation, location, and allocation of hazardous materials. Expert Syst. Appl. 2016, 51, 49–58. [Google Scholar] [CrossRef]
- Shahvari, O.; Logendran, R. Hybrid flow shop batching and scheduling with a bi-criteria objective. Int. J. Prod. Econ. 2016, 179, 239–258. [Google Scholar] [CrossRef]
- Shahvari, O.; Logendran, R. An Enhanced tabu search algorithm to minimize a bi-criteria objective in batching and scheduling problems on unrelated-parallel machines with desired lower bounds on batch sizes. Comput. Oper. Res. 2017, 77, 154–176. [Google Scholar] [CrossRef]
- Shahvari, O.; Salmasib, N.; Logendranc, R.; Abbasid, B. An efficient tabu search algorithm for flexible flow shop sequence-dependent group scheduling problems. Int. J. Prod. Res. 2012, 50, 4237–4254. [Google Scholar] [CrossRef]
- Glover, F. Tabu search—Part I. ORSA J. Comput. 1989, 1, 190–206. [Google Scholar] [CrossRef]
- Piniganti, L. A Survey of Tabu Search in Combinatorial Optimization. Master’s Thesis, University of Nevada, Las Vegas, NV, USA, 2014. [Google Scholar]
- Glover, F. Tabu Search for nonlinear and parametric optimization (with links to genetic algorithms). Discret. Appl. Math. 1994, 49, 231–255. [Google Scholar] [CrossRef]
- Garcia-Capulin, C.H.; Cuevas, F.J.; Trejo-Caballero, G.; Rostro-Gonzalez, H. A hierarchical genetic algorithm approach for curve fitting with B-splines. Genet. Program. Evol. Mach. 2015, 16, 151–166. [Google Scholar] [CrossRef]
- Szwed, P.; Chmiel, W.; Kadłuczka, P. OpenCL Implementation of PSO Algorithm for the Quadratic Assignment Problem. In Artificial Intelligence and Soft Computing; Rutkowski, L., Korytkowski, M., Scherer, R., Tadeusiewicz, R., Zadeh, L.A., Zurada, J.M., Eds.; Springer International Publishing: Cham, Switzerlands, 2015; pp. 223–234. [Google Scholar]
- Yoshimura, M.; Izui, K. Hierarchical Parallel Processes of Genetic Algorithms for Design Optimization of Large-Scale Products. J. Mech. Des. 2004, 126, 217–224. [Google Scholar] [CrossRef]
- Lim, D.; Ong, Y.S.; Jin, Y.; Sendhoff, B.; Lee, B.S. Efficient Hierarchical Parallel Genetic Algorithms using Grid computing. Future Gener. Comput. Syst. 2007, 23, 658–670. [Google Scholar] [CrossRef]
- Plichta, A.; Gaciarz, T.; Baranowski, B.; Szominski, S. Implementation of the genetic algorithm by means of CUDA technology involved in travelling salesman problem. In Proceedings of the 28th European Conference on Modelling and Simulation (ECMS), Brescia, Italy, 27–30 May 2014. [Google Scholar]
- Bhardwaj, G.; Pandey, M. Parallel Implementation of Travelling Salesman Problem using Ant Colony Optimization. Int. J. Comput. Appl. Technol. Res. 2014, 3, 385–389. [Google Scholar] [CrossRef]
- Zhou, Y.; He, F.; Hou, N.; Qiu, Y. Parallel ant colony optimization on multi-core SIMD CPUs. Future Gener. Comput. Syst. 2018, 79, 473–487. [Google Scholar] [CrossRef]
- Cai, P.; Cai, Y.; Chandrasekaran, I.; Zheng, J. Parallel genetic algorithm based automatic path planning for crane lifting in complex environments. Autom. Constr. 2016, 62, 133–147. [Google Scholar] [CrossRef]
- Brookhouse, J.; Otero, F.E.B.; Kampouridis, M. Working with OpenCL to speed up a genetic programming financial forecasting algorithm: Initial results. In Proceedings of the Companion Publication of the 2014 Annual Conference on Genetic and Evolutionary Computation (GECCO Comp ’14), Vancouver, BC, Canada, 12–16 July 2014. [Google Scholar]
- Augusto, D.A.; Barbosa, H.J.C. Accelerated parallel genetic programming tree evaluation with OpenCL. J. Parallel Distrib. Comput. 2013, 73, 86–100. [Google Scholar] [CrossRef]
- Huang, C.S.; Huang, Y.C.; Lai, P.J. Modified genetic algorithms for solving fuzzy flow shop scheduling problems and their implementation with CUDA. Expert Syst. Appl. 2012, 39, 4999–5005. [Google Scholar] [CrossRef]
- Rocha, I.; Parente, E.; Melo, A. A hybrid shared/distributed memory parallel genetic algorithm for optimization of laminate composites. Compos. Struct. 2014, 107, 288–297. [Google Scholar] [CrossRef]
- Omkar, S.; Venkatesh, A.; Mudigere, M. MPI-based parallel synchronous vector evaluated particle swarm optimization for multi-objective design optimization of composite structures. Eng. Appl. Artif. Intell. 2012, 25, 1611–1627. [Google Scholar] [CrossRef]
- Walker, R.L. Search engine case study: Searching the web using genetic programming and MPI. Parallel Comput. 2001, 27, 71–89. [Google Scholar] [CrossRef]
- Imbernón, B.; Prades, J.; Giménez, D.; Cecilia, J.M.; Silla, F. Enhancing large-scale docking simulation on heterogeneous systems: An MPI vs. rCUDA study. Future Gener. Comput. Syst. 2018, 79, 26–37. [Google Scholar] [CrossRef]
- Li, D.; Li, K.; Liang, J.; Ouyang, A. A hybrid particle swarm optimization algorithm for load balancing of MDS on heterogeneous computing systems. Neurocomputing 2019, 330, 380–393. [Google Scholar] [CrossRef]
- Spanos, A. Curve Fitting, the Reliability of Inductive Inference, and the Error-Statistical Approach. Philos. Sci. 2007, 74, 1046–1066. [Google Scholar] [CrossRef]
- Boor, C.D. A Practical Guide to Splines; Applied Mathematical Sciences; Springer: New York, NY, USA, 2001. [Google Scholar]
- Piegl, L.; Tiller, W. The NURBS Book; Monographs in Visual Communication; Springer: Berlin/Heidelberg, Germany, 1997. [Google Scholar]
- Jong, E.D.D.; Watson, R.A.; Thierens, D. On the Complexity of Hierarchical Problem Solving. In Proceedings of the 7th Annual Conference on Genetic and Evolutionary Computation (GECCO ’05), Washington, DC, USA, 25–29 June 2005; ACM: New York, NY, USA, 2005; pp. 1201–1208. [Google Scholar]
- Man, K.F.; Tang, K.S.; Kwong, S. Genetic Algorithms: Concepts and Designs, 2nd ed.; Advanced Textbooks in Control and Signal Processing; Springer: London, UK, 1999. [Google Scholar]
- Jong, E.D.D.; Thierens, D.; Watson, R.A. Hierarchical Genetic Algorithms. In Proceedings of the Parallel Problem Solving from Nature—PPSN VIII: 8th International Conference, Birmingham, UK, 18–22 September 2004; Springer: Berlin/Heidelberg, Germany, 2004; pp. 232–241. [Google Scholar]
- Deb, K. Multi-Objective Optimization Using Evolutionary Algorithms; John Wiley & Sons, Inc.: New York, NY, USA, 2001. [Google Scholar]
- Akaike, H. A new look at the statistical model identification. IEEE Trans. Autom. Control 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Lee, T.C.M. Regression spline smoothing using the minimum description length principle. Stat. Probab. Lett. 2000, 48, 71–82. [Google Scholar] [CrossRef]
- Mitchell, M. An Introduction to Genetic Algorithms; A Bradford Book; MIT Press: Cambridge, MA, USA, 1998. [Google Scholar]
- Sivanandam, S.; Deepa, S. Introduction to Genetic Algorithms; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Deb, K.; Agrawal, R.B. Simulated Binary Crossover for Continuous Search Space. Complex Syst. 1995, 9, 115–148. [Google Scholar]
- Alba, E.; Troya, J.M. A Survey of Parallel Distributed Genetic Algorithms. Complex 1999, 4, 31–52. [Google Scholar] [CrossRef]
- Belding, T.C. The Distributed Genetic Algorithm Revisited. In Proceedings of the 6th International Conference on Genetic Algorithms; Morgan Kaufmann Publishers Inc.: San Francisco, CA, USA, 1995; pp. 114–121. [Google Scholar]
- Rucinski, M.; Izzo, D.; Biscani, F. On the impact of the migration topology on the Island Model. Parallel Computing. 2010, 36, 555–571. [Google Scholar] [CrossRef]
- Dimatteo, I.; Genovese, C.R.; Kass, R.E. Bayesian curve-fitting with free-knot splines. Biometrika 2001, 88, 1055–1071. [Google Scholar] [CrossRef]
- Denison, D.; Mallick, B.; Smith, A. Automatic Bayesian Curve Fitting. J. R. Stat. Soc. Ser. B (Stat. Methodol.) 1998, 60, 333–350. [Google Scholar] [CrossRef]
- Pittman, J. Adaptive Splines and Genetic Algorithms. J. Comput. Graph. Stat. 2002, 11, 615–638. [Google Scholar] [CrossRef]
- Gálvez, A.; Iglesias, A. Efficient particle swarm optimization approach for data fitting with free knot-splines. Comput.-Aided Des. 2011, 43, 1683–1692. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).