1. Introduction
Current research work aims to describe production steps independently of the process using the so-called process signature, which summarizes all interactions between material and process [
1,
2]. This new way of looking at and describing should enable the processing of materials in an even more targeted way, so that they can be optimally adapted to the respective requirements. The basic prerequisite for this is an exact understanding of the individual manufacturing processes. In this context, the cutting process with a defined cutting edge, as it occurs during turning and milling, is considered in this article. In order to understand chip formation and chip breakage, it is particularly important to determine the relationship between the loads acting on the material during machining and the changes remaining in the material afterwards.
The loads in terms of the strains can be quantified during the production process by means of speckle photography [
3,
4]. With this method, the surface to be measured is illuminated with a laser and the evaluation areas in the speckle images taken with the camera—before and during the occurrence of the deformation—are correlated with each other [
5,
6]. From the correlated image sections, local displacements can be calculated, whose theoretical resolutions are limited only by Heisenberg’s uncertainty relation [
7]. Due to the availability of compact diode lasers with a short-pulse length of less than 1 ns and pulse energies of more than 20 µJ, it is possible to integrate the measuring system into the machining area of machine tools and to investigate dynamic manufacturing processes with tool speeds of, for instance, more than v
c = 10
[
8].
However, the measuring of the remaining modifications (plastic deformations), which are ten times weaker in relation to the loads (elastic + plastic deformations), has been proven difficult so far, especially in processes with multiple stresses due to recurring loads and cyclic machining processes (e.g., milling). The modifications remaining in the material surface layer after the last tool intervention are usually inhomogeneous [
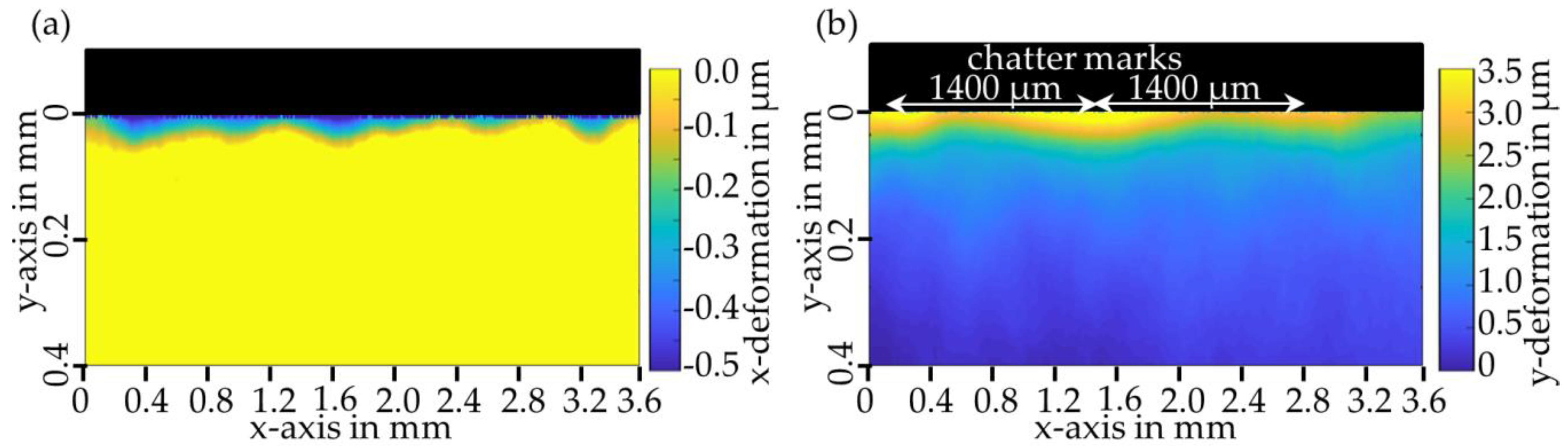
8]. In extreme cases, the periodic fluctuations of the modification also occur under continuous cutting conditions (as in the turning process) and correlate with undesired chatter marks on the surface, which can be seen in
Figure 1.
The properties of the chatter marks, such as periodicity and amplitude, are influenced by the resonance behavior of the complex manufacturing system [
9]. A causal trigger in the continuous process can be the disturbance of the system due to the effect of chip breakage or chip formation depending on the workpiece condition [
10]. The chip formation and chip breakage were investigated theoretically by means of finite element method (FEM) simulations, compared with high speed videos and discussed with the relationship to the process stability and the surface quality produced [
11].
When researching chip separation and chatter mark formation, mainly the resonance and vibration behavior of the machine tool and the workpiece are considered. Induced workpiece vibrations and dynamic strain states are difficult to determine so far, therefore these effects are currently not included in the investigations. In this respect, it is also not known how the remaining modifications in the form of periodic fluctuations of the strain [
8] are related to chip formation or chip breakage. However, it is probable that both the chip breakage and the penetration of the tool at the beginning of the chip formation generate a shock wave, which propagates through the material at the speed of sound. The open scientific questions therefore are:
Are dynamic processes in the workpiece stimulated during machining and is the lifetime of these shock waves long enough to cause feedback in processes with multiple loads (such as milling)?
Can the excited workpiece states be measured with the aid of speckle photography?
The aim of the paper is to investigate whether and how the external mechanical excitations of the workpiece affect internal mechanical properties such as deformation or strain, and to investigate these properties both theoretically and experimentally. For this purpose, after a short introduction to the theory of speckle photography (
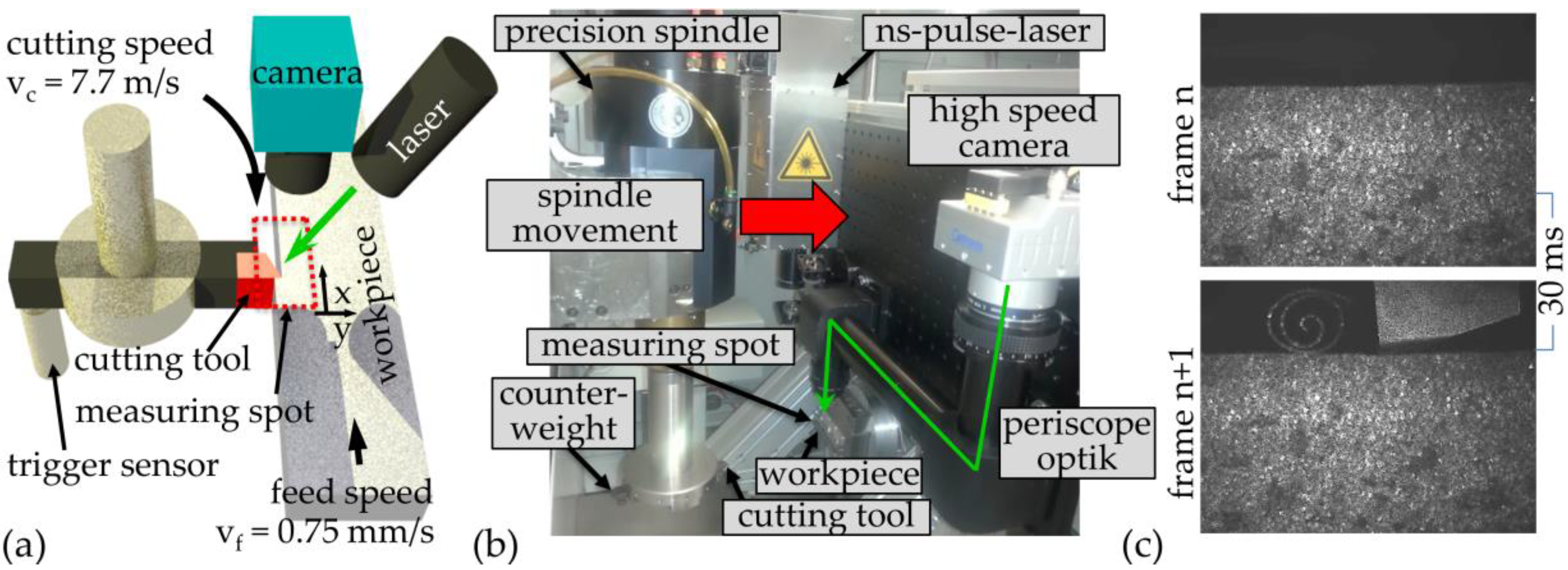
Section 2.1) and the presentation of the measurement setup (
Section 2.2), measurements are carried out in a running single-tooth circumferential milling process with a rotating tool (
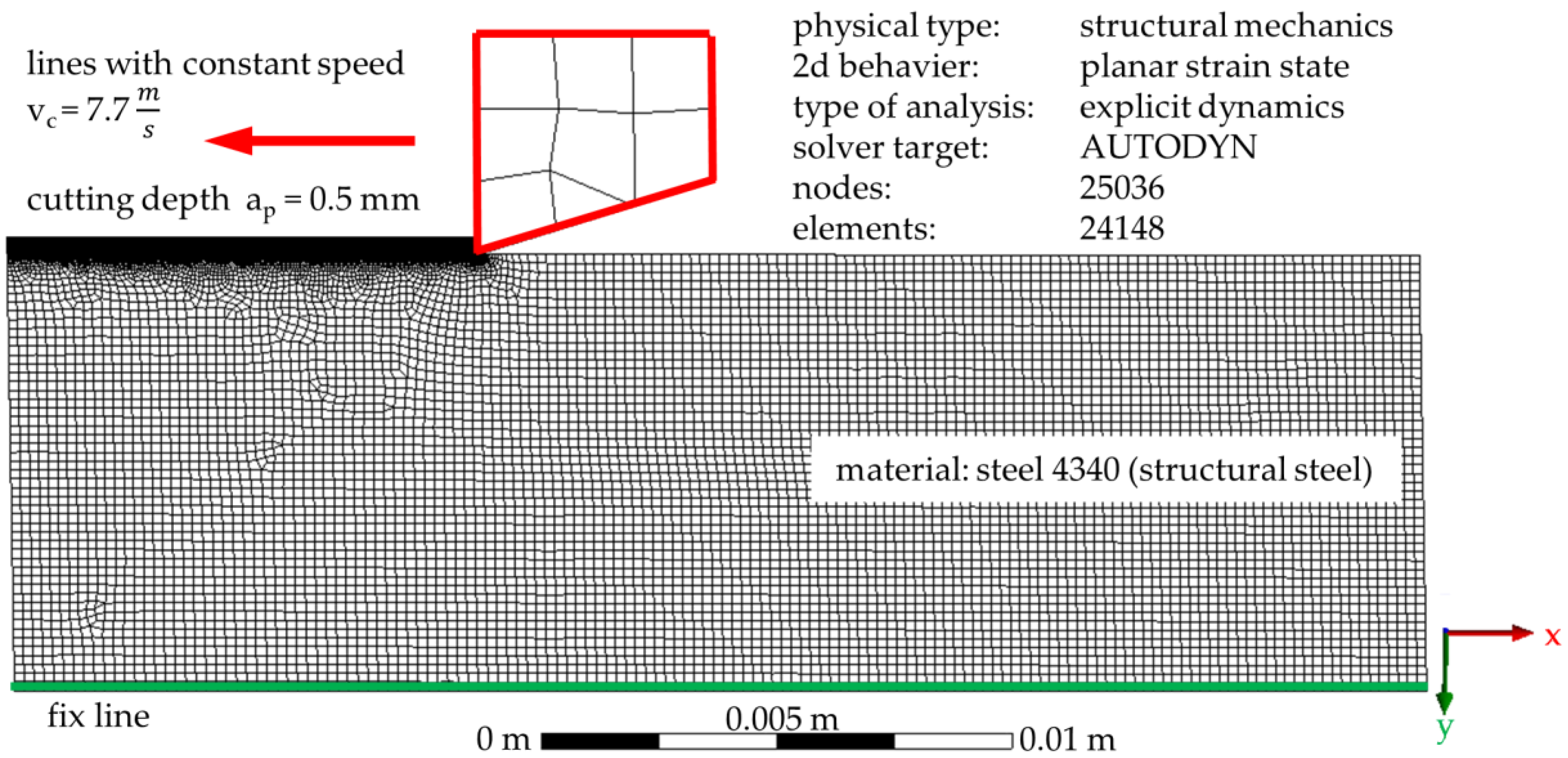
Section 3.1). These measurements are then compared with FEM simulations of a linear cutting process with constant cutting conditions and defined cutting edge (
Section 3.2). In order to enable a validation of the measuring method by the simulation results, the feed rate in the real milling process was selected in such a way that almost constant cutting conditions prevail here as well. The investigations of the resulting workpiece state due to multiple stresses are carried out in
Section 3.3. For this purpose, the workpiece condition is examined by means of speckle photography, at the time when the tool would interact with the workpiece a second time after the first intervention. For the first time, shock waves induced by the tool impact could be measured using speckle photography. A comparison with theoretical investigations of the chip rupture and the resulting induced formation of strain waves propagating through the workpiece take place in
Section 3.4. After a discussion of the results in
Section 4, a conclusion is finally drawn in
Section 5.
4. Discussion
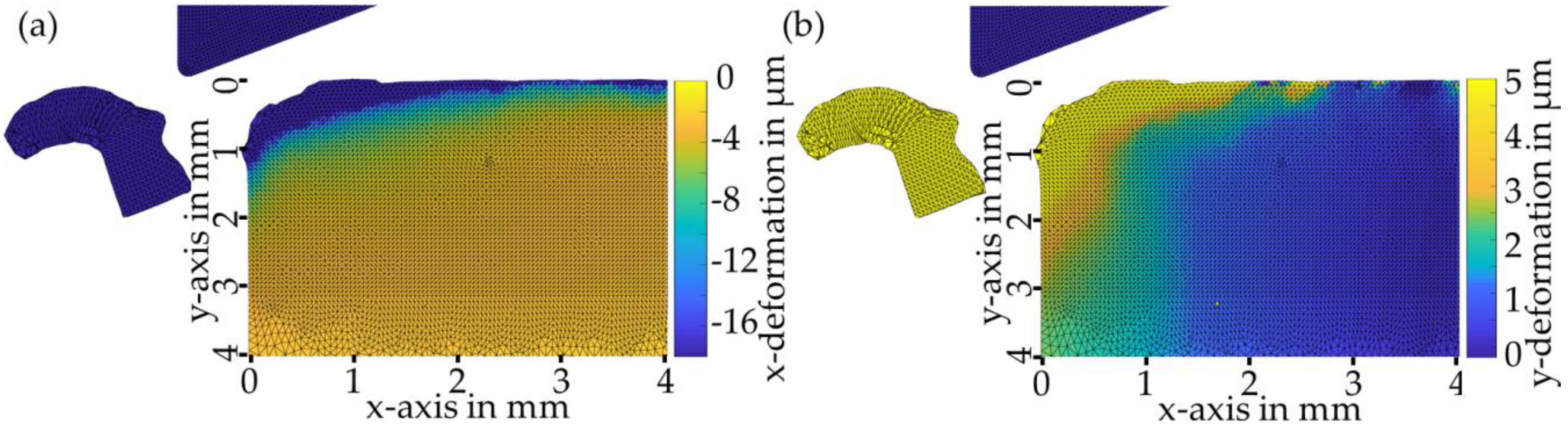
In a single-tooth milling process, dynamic loads and modifications in the form of deformations and strains were measured using speckle photography. The validation approach of the in-process measurements for the highly dynamic manufacturing process of single-tooth circumferential milling was based on FEM simulations. For this, similar cutting conditions were used in the simulation as in the real manufacturing and measuring processes. The measured loads in the form of deformations agree qualitatively with the simulated results. In particular, the displacements in the y-direction are quantitatively equivalent, with a penetration depth of about 3 mm and a maximum displacement of 2 µm. Hence, the applicability of speckle photography for in-process measurements during a milling process is validated.
In order to measure the influence of chip formation or chip separation on the internal strain state of the workpiece, it was originally intended to provide the trigger point with a slight time offset from cut to cut in this very dynamic milling process. Each individual measurement would thus take place at a different cutting depth and a slightly different rotation angle of the tool. Provided that the workpiece is homogeneous and the tool encounters the same initial state of the workpiece at each cut, the chip removal and its influence on the strain state of the workpiece could then be investigated with an extremely high time resolution. The smallest resolution (smallest meaningful trigger time offset) is defined by the jitter of the laser pulses, which amounts to 5 µs. At a cutting speed of vc = 7.7 , the trigger point could be shifted by this smallest unit to allow measurements of tool shifts of approx. 40 µm on the circular path.
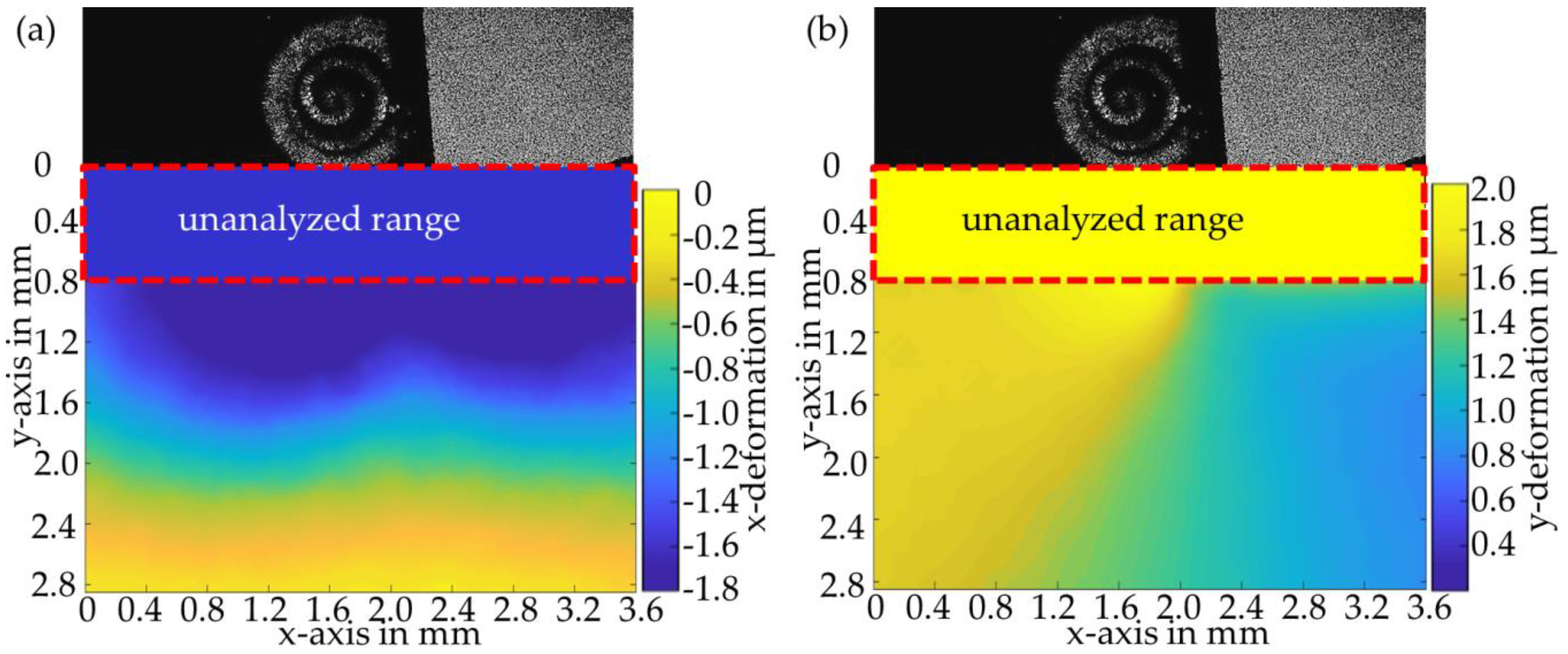
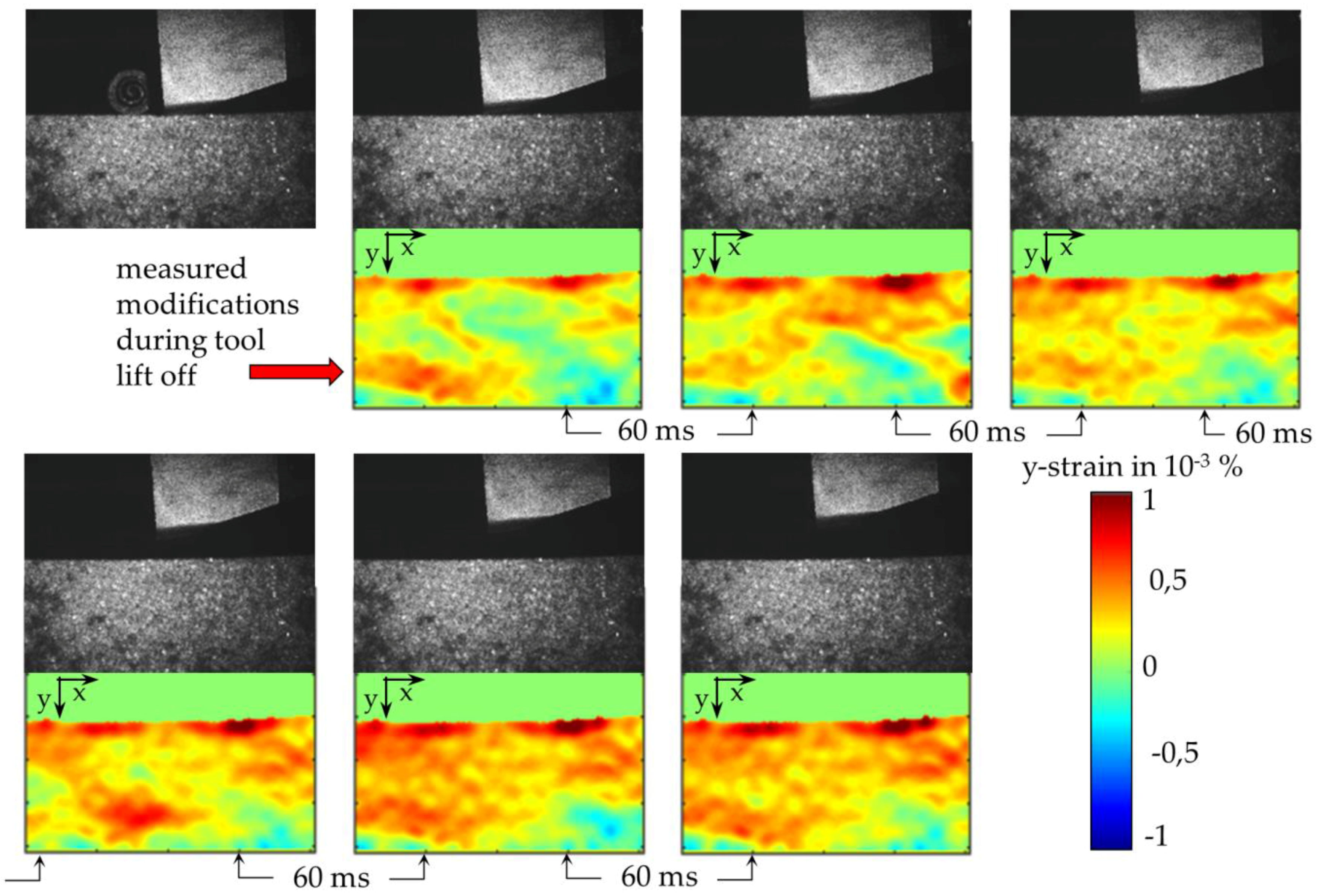
The results from
Figure 11 in
Section 3.3 illustrate why this approach does not work. In a subsequent cut, the tool never encounters the initial state of the workpiece, but rather a mechanically excited system with an inhomogeneous strain or residual stress state. In the periodic milling process shown, 60 ms elapse between tool intervention and the next intervention. The time required for the workpiece to reach a stable final state after excitation, however, is approx. 300 ms. Especially in the case of multiple loads with periodically recurring stresses, which occur more frequently than every 300 ms, it can be assumed that the process encounters an excited workpiece and that the previous load must therefore also be taken into account.
After a sufficient decay time, the measured modifications finally are one order of magnitude below the measured maximum loads.
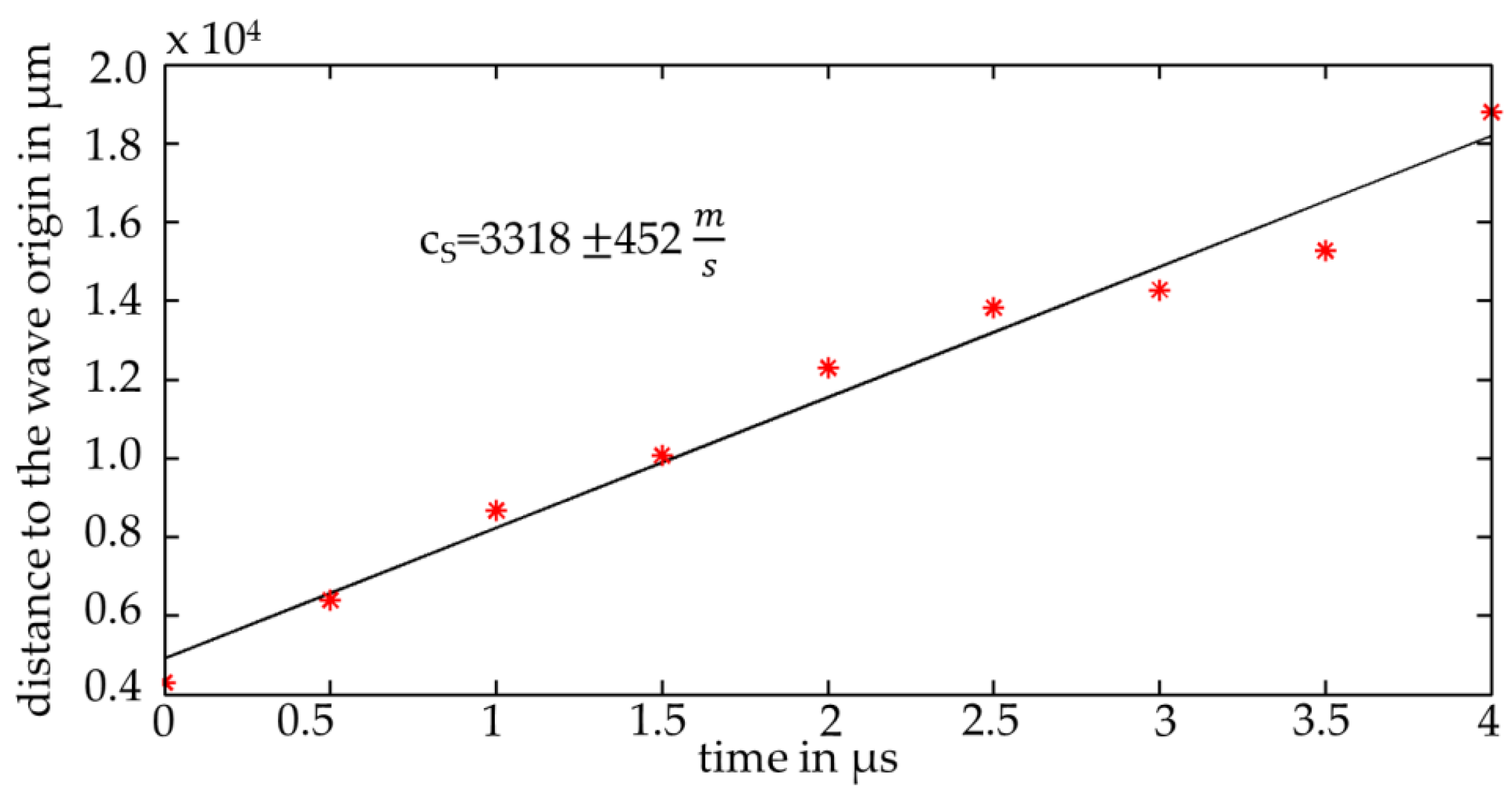
The chip formation and the chip breakage were theoretically investigated by means of a FEM simulation. It could be shown that strain waves propagate through the workpiece at approx. 3320 ± 452 , which are released from the workpiece side due to the tool exit. The propagation velocity of the simulated strain front corresponds within the uncertainty of the propagation velocity to the literature values for a sound wave in structural steel.
Furthermore, it is to be expected that the propagating strain front is reflected at the boundary surfaces and therefore passes through the workpiece several times before the wave vanishes due to the damping of the material.
This leads to the question, when do the oscillations excited by the impact theoretically come to a rest? According to Roderick and Truell [
16], the sound absorption coefficient for steel alloy (50CrMo4) is approx. 60 dB/1000 m at a sound frequency of less than 2 MHz. The sound wave with a propagation velocity of 3320
would require approximately 300 ms for the distance of 1000 m. According to the measurement results from
Figure 11, the remaining modification change after 300 ms has actually dropped to about one thousandth of the maximum (60 dB). Therefore, for low frequencies of the excitation pulse due to the tool intervention, the measured excitation duration basically corresponds to the literature values.
The formation of chatter marks (see
Figure 1) is explained in current research reports by chip formation and chip breakage, which stimulate the entire tool system and the workpiece to vibrate. The aspect that the tool encounters a workpiece that is usually excited periodically and in which the cutting forces and the dynamic strains already introduced are superimposed has not yet been considered. The results of this article show that although the dynamic excitation is smaller by a factor of 10 than the maximum occurring loads, these material dynamics should nevertheless be included in the research of chip removal. It is very probable that the current strain state influences the chip formation and in particular chip breakage. Therefore, it cannot be ruled out that the investigated dynamic expansion waves or shock waves, with their change in the residual stress state of the workpiece, have an influence on the formation of chatter marks.
Therefore, when investigating process dynamics, such as the formation of chatter marks, not only the vibration and resonance behavior of the machine tool or the workpiece should be considered in the future, but also the internal dynamic strain condition of the workpiece at the time the tool is engaged.
In order to display the dynamic deformation processes in the future with sufficient temporal resolution and also to be able to observe such things as chip breakage or the formation of chatter marks, at least three measurements should be taken in a minimum measuring field of 10 mm. At a sound velocity of 3330 an image acquisition rate of one million frames per second is required. A currently purchased camera system (Photron FASTCAM NOVA S12, Photron USA, Inc., San Diego, USA, 2019) is capable of this measurement frequency. Upcoming measurements during the single-tooth circumference milling process will be carried out with this system.
At the same time, it should be examined furthermore whether the measurement uncertainty and the resolution behavior of the system are sufficient to be able to make predictions about the residual stress states of the workpiece based on the determinations of the sound velocity components.
5. Conclusions
In machining processes such as single-tooth milling, dynamic vibrations of the manufacturing system usually occur. In contrast to these well-known effects, this paper examines the question of whether additional mechanically-induced dynamic loads in the workpiece are stimulated by the tool impact. For this purpose, the load during tool engagement is first measured by means of speckle photography and its applicability for in-process use is confirmed by comparison with theoretical predictions. Subsequently, it is shown both metrologically and simulatively that the tool impact induces "shock waves" during milling in the form of deformations and strains which propagate through the workpiece at the speed of sound. In the present case, the wave ebbs after many multiple reflections at the boundary surfaces, so that the resulting dynamic excitation decays after 300 ms. The cyclic multiple loads have a period duration of 60 ms, which is shorter than the sound decay time. Therefore, it can be assumed that the tool encounters an already excited initial state during machining. Especially in the description of chip formation, chip breakage, and the formation of chatter marks, the material-internal dynamic strain variations should therefore also be considered. Overall, the results illustrate the potential of speckle photography in combination with modern high-speed cameras and compact short-pulse lasers. Speckle photographic in-process measurements of dynamic deformations and strains can provide deeper insights into individual manufacturing processes. This enables the optimization of manufacturing processes (e.g., by specifically adapting the resonance behavior via the design of the workpiece geometry or the clamping device).