Cooperative Optimization of Electric Vehicles and Renewable Energy Resources in a Regional Multi-Microgrid System
Abstract
Featured Application
Abstract
1. Introduction
- An integration mechanism of RESs and EVs is illustrated, and a mathematical model of the V2G-integrated regional multi-microgrid system is established;
- The concept of EV’s ATSET is illustrated. Based on the ability of EV’s ATSET, a cooperative optimization method for economic dispatching and system capacity allocation is proposed;
- To fully exploiting the potential of the EV’s mobile energy storage ability, both the installation capacity of RESs and the number of EVCDIs are optimized in the cooperative optimization process.
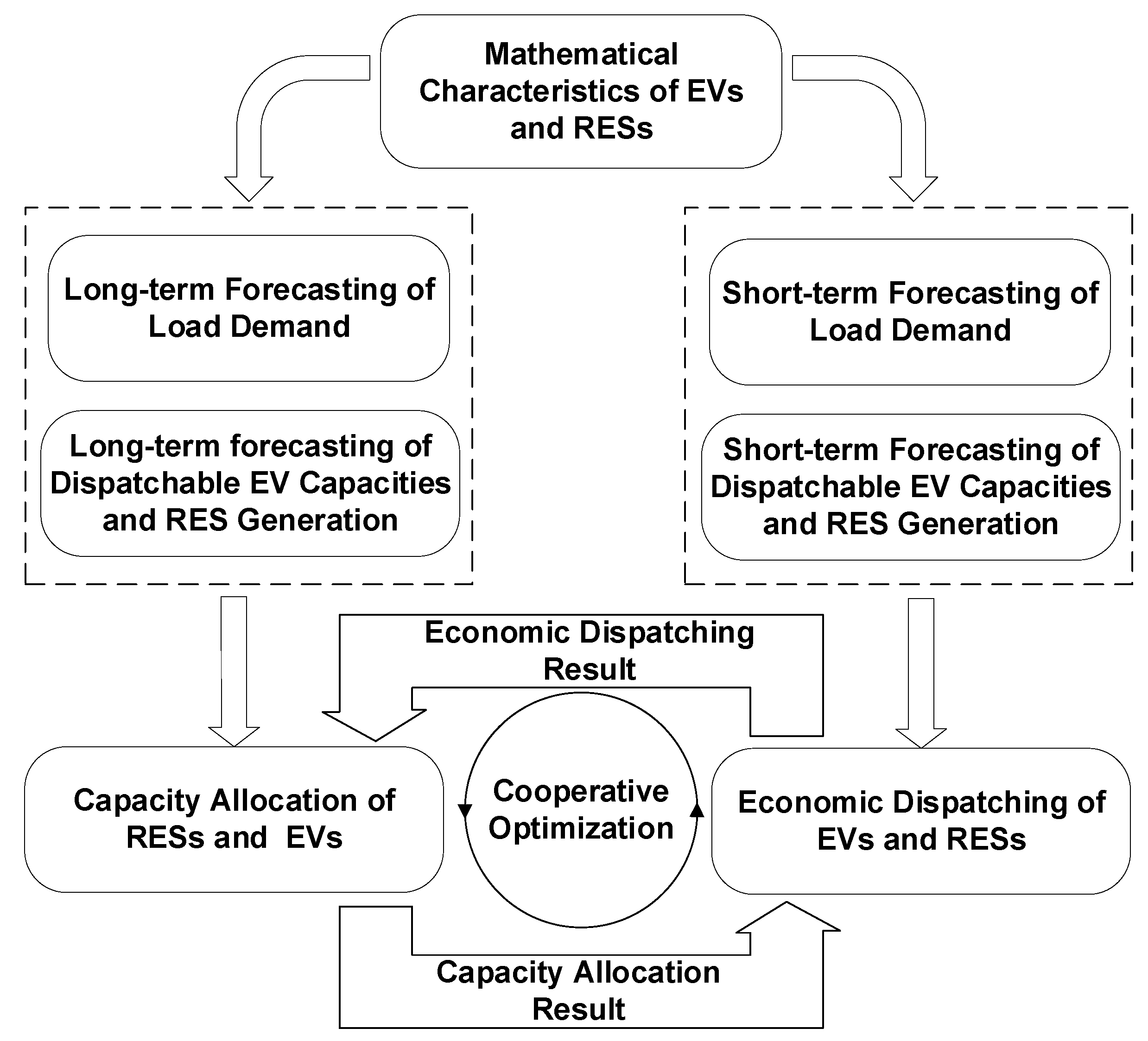
2. Concept of Cooperative Optimization
3. Mathematical Model
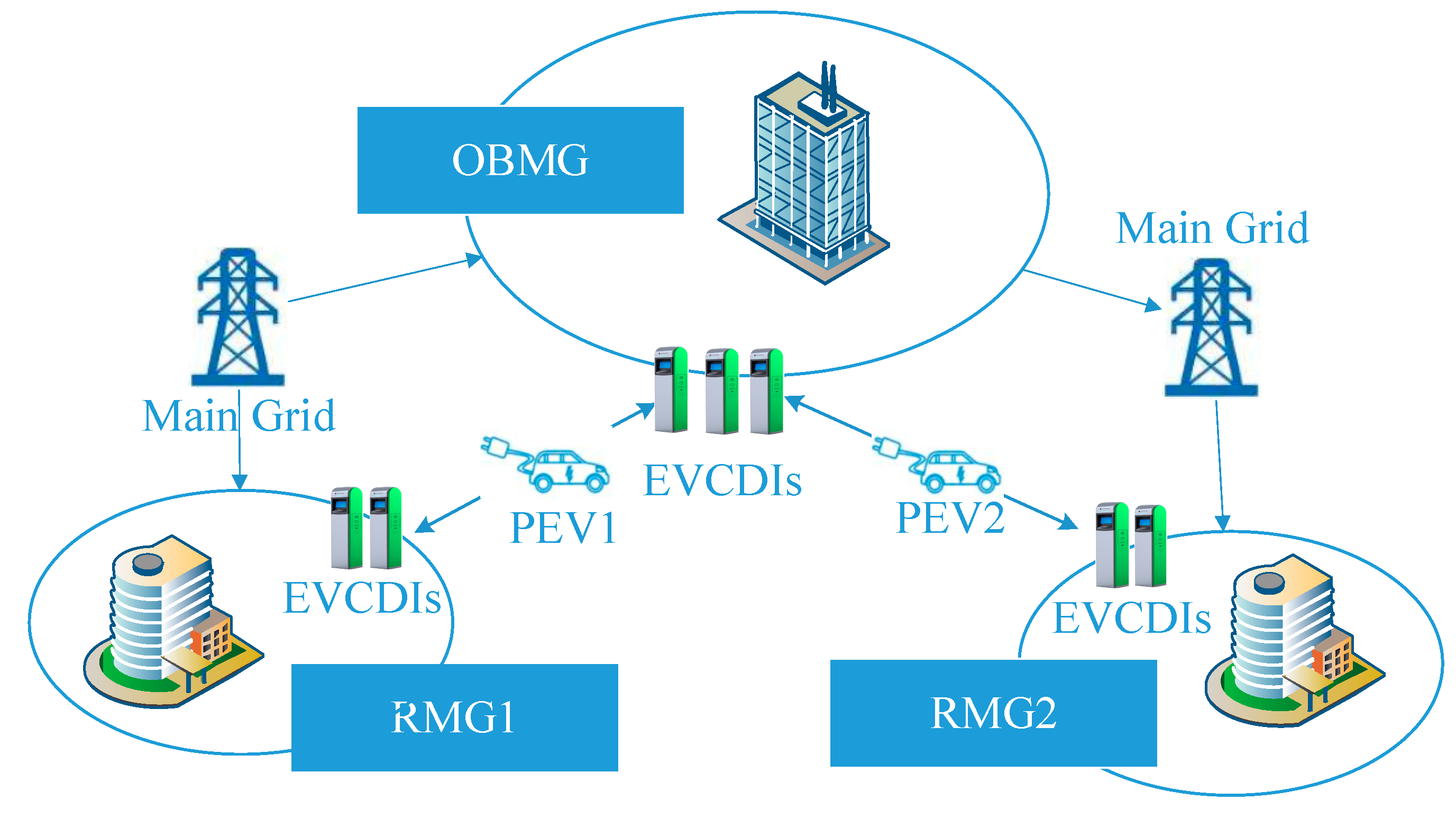
3.1. Structure of the Multi-Microgrid System
3.2. Renewable Energy Sources
3.3. Electric Vehicles
3.4. Operation Mechanism
4. Optimization Problem Formulation
4.1. Objective Function
4.2. Constraints
4.2.1. Balance of Power Supply and Demand
4.2.2. Capacity Constraint of EV Batteries
4.2.3. Power Limits
4.2.4. Installation Constraints
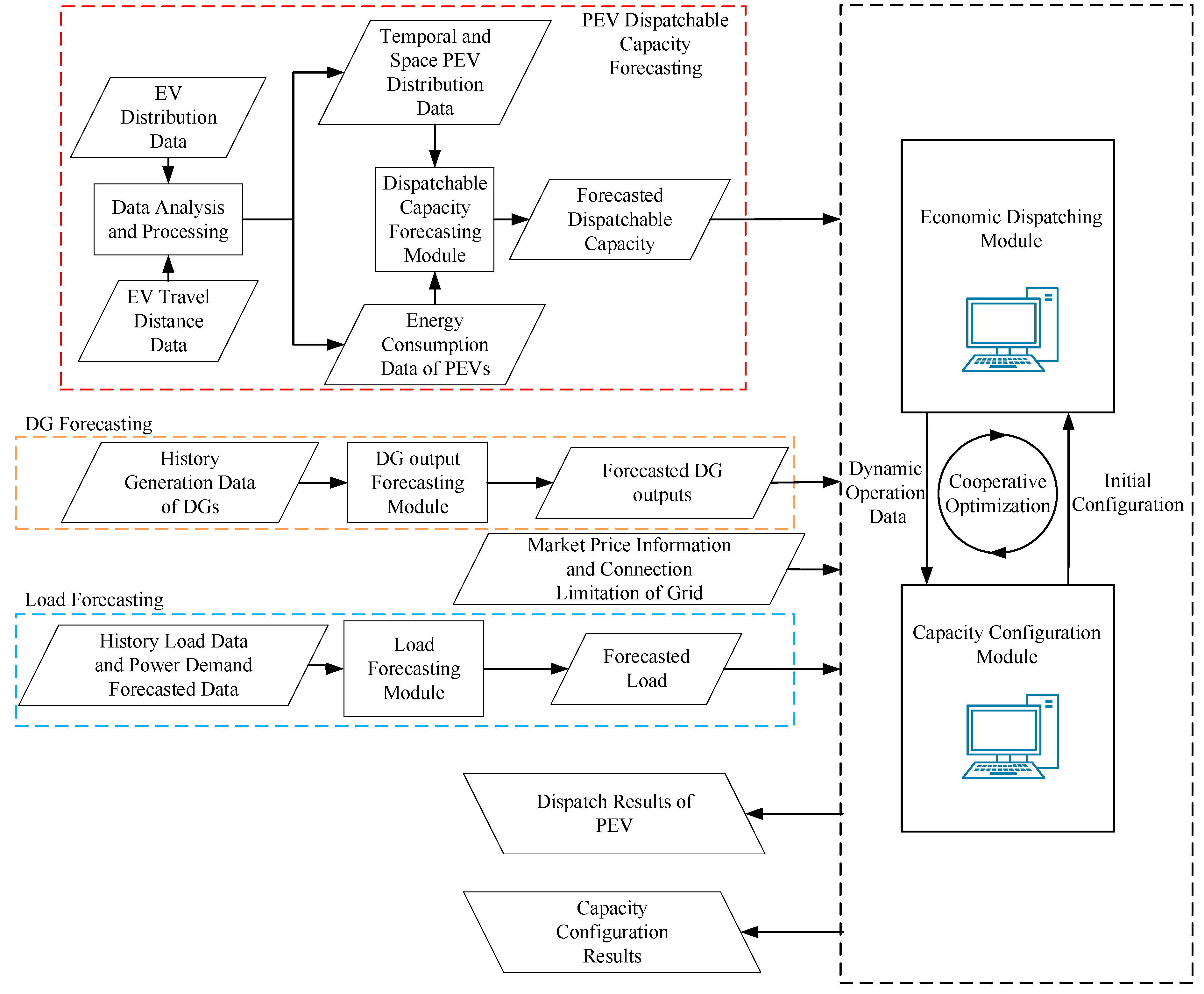
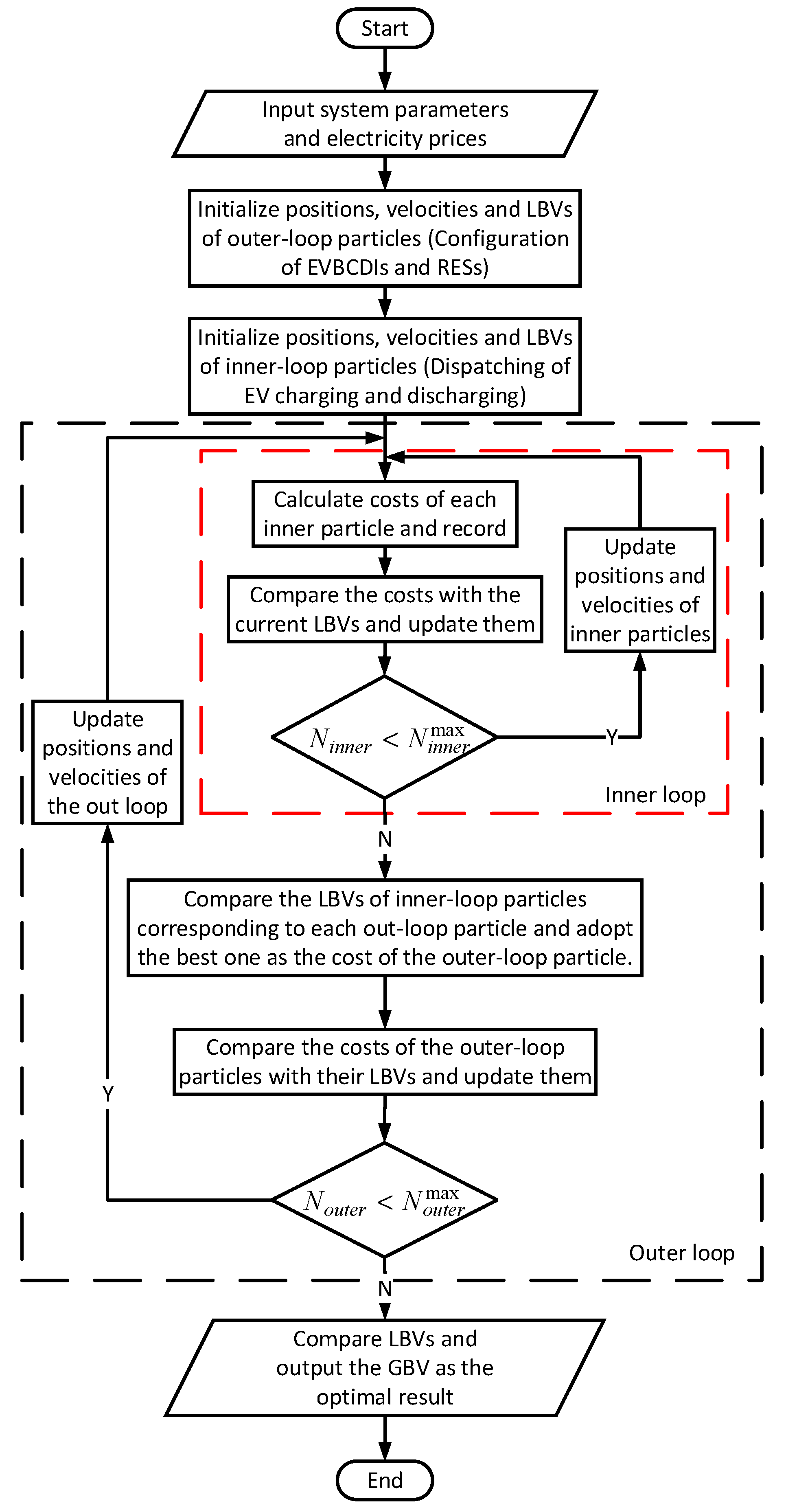
5. Two-Loop Optimization
5.1. Improved Particle Swarm Optimization
5.2. Two-Loop Optimization Process
6. Case Study and Discussion
6.1. Case Description
6.1.1. Case 1
6.1.2. Case 2
6.1.3. Case 3
6.1.4. Case 4
6.2. Simulation System Construction
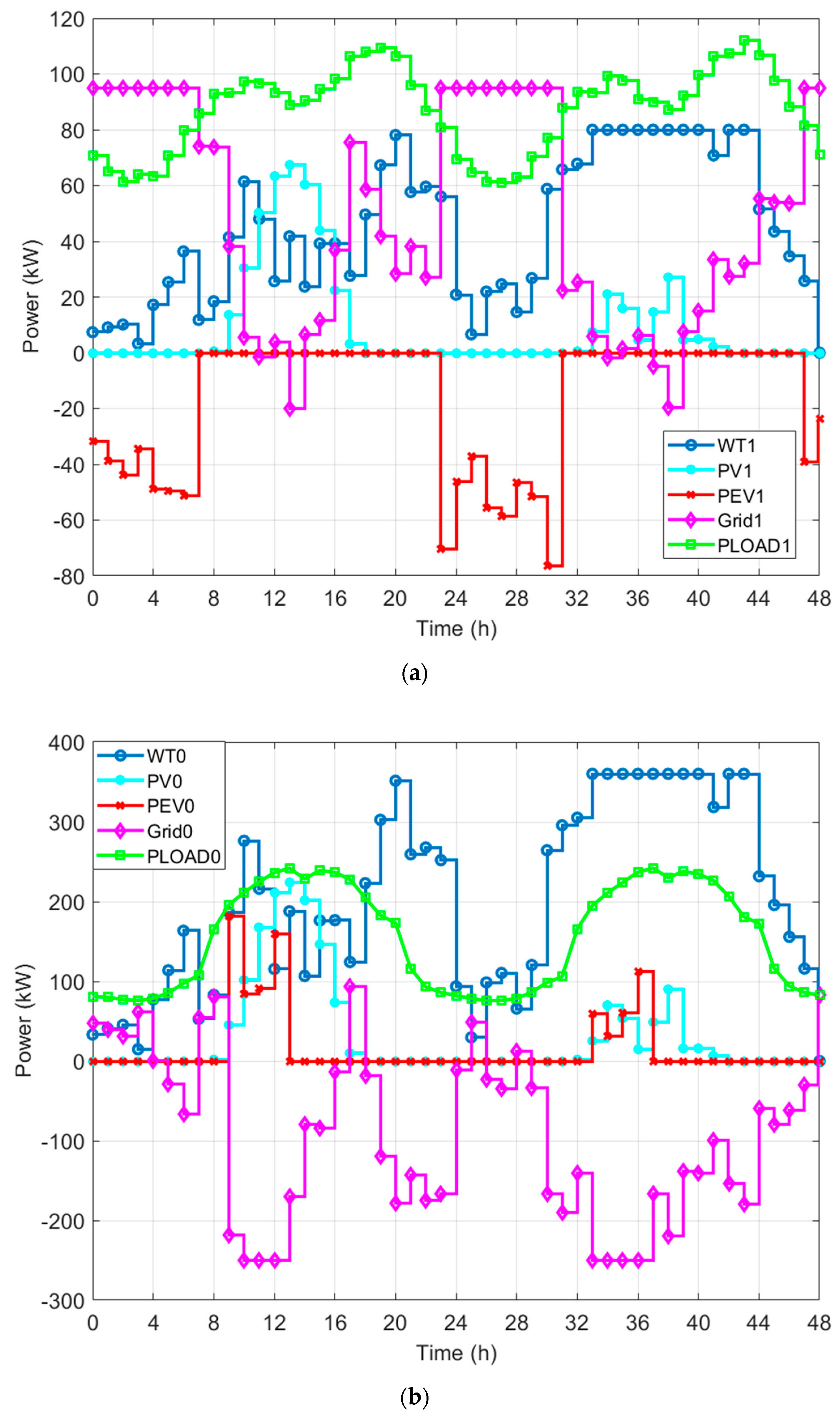
6.3. Simulation results
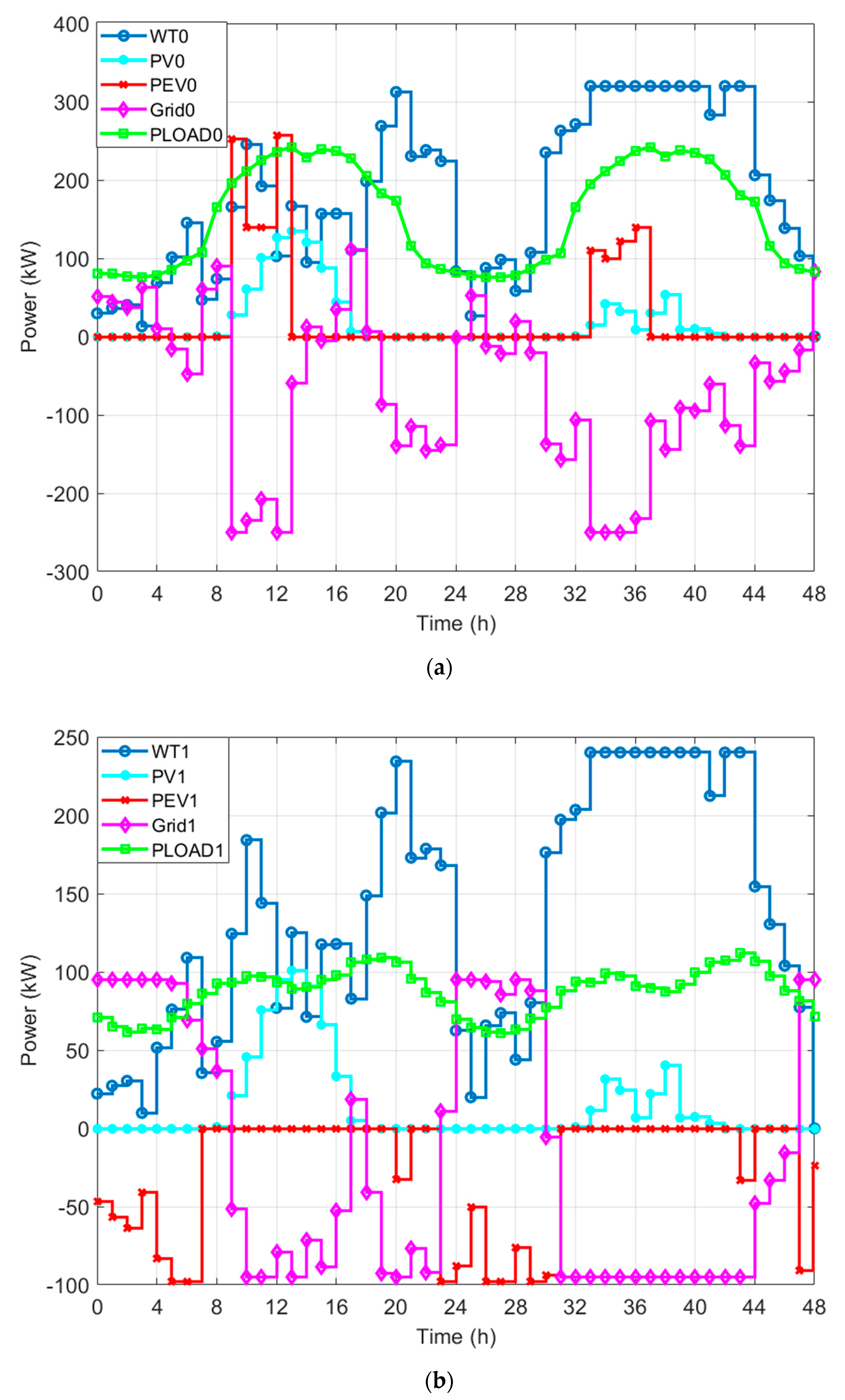
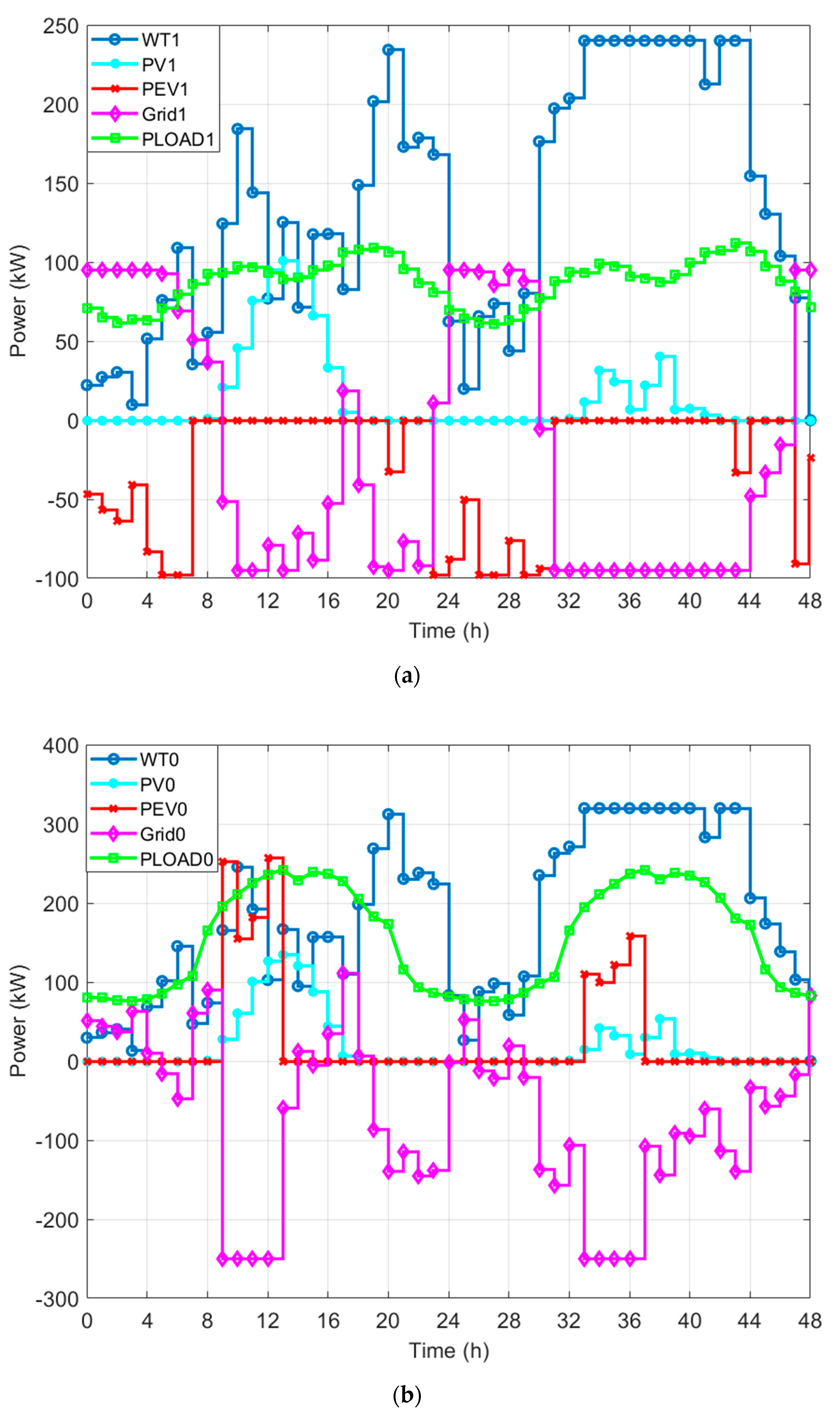
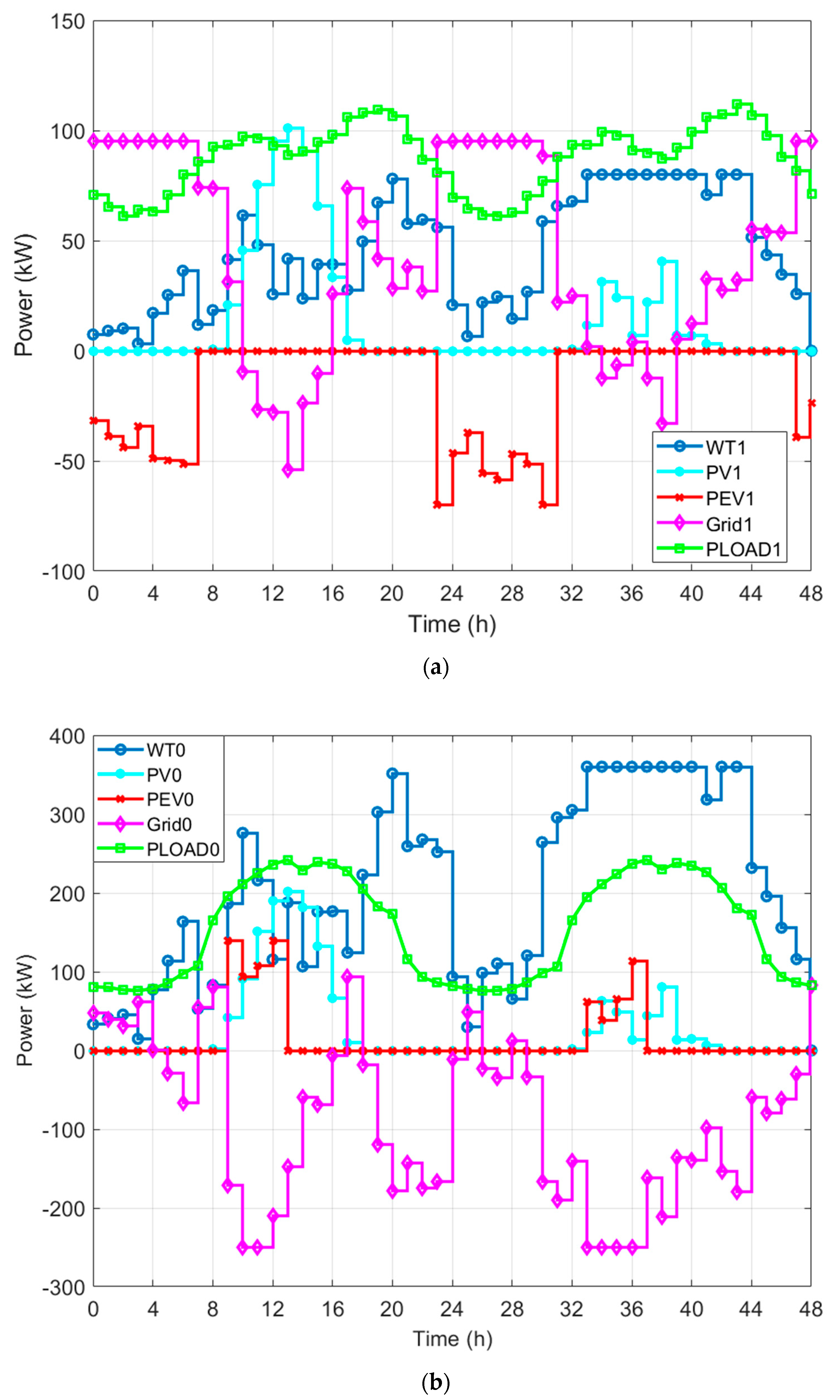
6.3.1. Case 1
6.3.2. Case 2
6.3.3. Case 3
6.3.4. Case 4
6.4. Comparison
- After optimization, the net exchanged energy between microgrids and the main grid decreases, which means that the microgrids becomes more independent from the main grid.
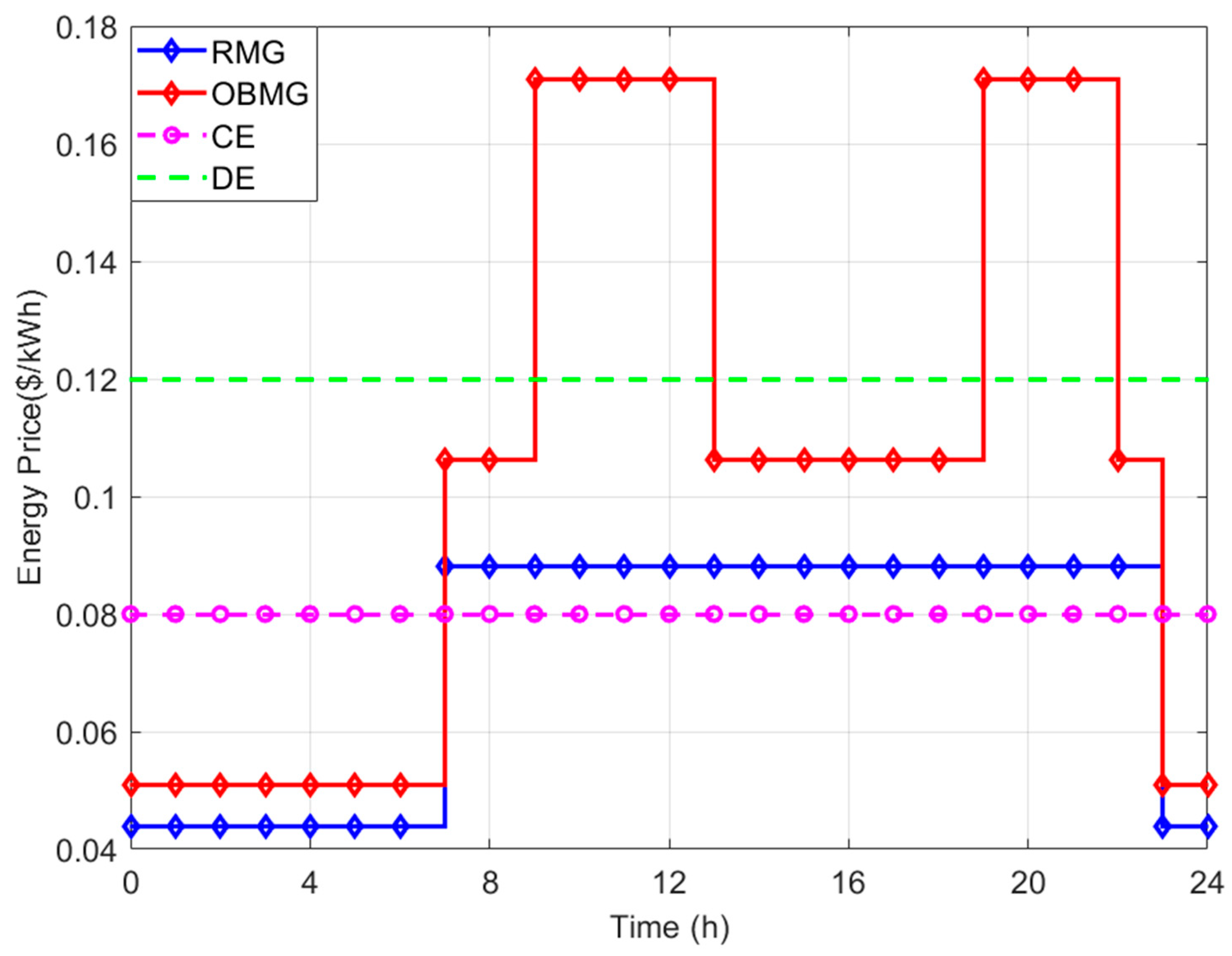
- Microgrids purchase energy from the main grid in load valley hours when electricity prices are low and sell energy to the main grid in load peak hours when prices are high, which contributes to the peak shaving of the main grid.
- In Cases 3 and 4, numbers of PVs in RMGs dramatically decrease, while number of PVs in OBMG is greatly increased. The reason is that for RMGs, the EV charging load is mainly distributed during night and the output of PVs at night is zero. Therefore, PV modules in RMGs are reduced to save installation costs.
- The total costs in Cases 2 and 3 are lower than that in Case 1. In Case 2, the numbers of EVBCDIs are optimized. Since redundant installation of EVBCDIs is cut down, the allocation is more proper and total cost is reduced. Similarly, in Case 3, the installation of RESs is optimized. The installation capacities of RESs are optimally configured according to the demand of the different kinds of microgrids, and the total cost is decreased compared to Case 1.
- In Case 4, economic dispatching and capacity allocation of RESs and EVs in the multi-microgrid system are optimized synergistically. Though the allocation cost of RESs is slightly increased, the dispatching cost of the system is significantly reduced because of the cooperative optimization of economic dispatching and capacity allocation for RESs and EVs. The total cost in Case 4 is the lowest of all four cases. The integration efficiency of RESs and EVs is improved, and more environmental benefits are achieved.
7. Conclusions
- By ATSET of EVs, energy can be transmitted through different microgrids, and economic dispatching of microgrids in the regional multi-microgrid system is cooperatively optimized. Optimized energy exchanging between regional multi-microgrid system and the main grid contributes to the peak shaving of the main grid.
- By optimizing both economic dispatching and capacity allocation of RESs and EVs, the total cost of the regional multi-microgrid system is dramatically reduced, and economic benefit is achieved. After a cooperative optimization, the independency of the microgrids’ operation is raised and integration efficiency of RESs and EVs is improved.
Author Contributions
Funding
Conflicts of Interest
References
- Wang, X.; Barnett, A. The evolving value of photovoltaic module efficiency. Appl. Sci. 2019, 9, 1227. [Google Scholar] [CrossRef]
- Mohammad, A.M.; Ahmad, S.Y.; Behnam, M.I.; Mousa, M.; Miadreza, S.; João, P.S.C. Stochastic network-constrained co-optimization of energy and reserve products in renewable energy integrated power and gas networks with energy storage system. J. Clean. Prod. 2019, 223, 747–758. [Google Scholar]
- Mei, F.; Wu, Q.; Shi, T.; Lu, J.; Pan, Y.; Zheng, J. An ultrashort-term net load forecasting model based on phase space reconstruction and deep neural network. Appl. Sci. 2019, 9, 1487. [Google Scholar] [CrossRef]
- Ross, M.; Hidalgo, R.; Abbey, C.; Joós, G. Energy storage system scheduling for an isolated microgrid. IET Renew. Power Gener. 2011, 5, 117–126. [Google Scholar] [CrossRef]
- Zhang, M.; Chen, J. The energy management and optimized operation of electric vehicles based on microgrid. IEEE Trans. Power Deliv. 2014, 29, 1427–1435. [Google Scholar] [CrossRef]
- Van Der Meer, D.; Mouli, G.R.C.; Mouli, G.M.E.; Elizondo, L.R.; Bauer, P. Energy management system with PV power forecast to optimally charge EVs at the workplace. IEEE Trans. Ind. Inform. 2018, 14, 311–320. [Google Scholar] [CrossRef]
- Meyer, D.; Wang, J. Integrating ultra-fast charging stations within the power grids of smart cities: A review. IET Smart Grid 2018, 1, 3–10. [Google Scholar] [CrossRef]
- Morais, H.; Sousa, T.; Vale, Z.; Faria, P. Evaluation of the electric vehicle impact in the power demand curve in a smart grid environment. Energy Convers. Manag. 2014, 82, 268–282. [Google Scholar] [CrossRef]
- Hu, J.; Morais, H.; Sousa, T.; Lind, M. Electric vehicle fleet management in smart grids: A review of services, optimization and control aspects. Renew. Sustain. Energy Rev. 2016, 56, 1207–1226. [Google Scholar] [CrossRef]
- Cerna, F.V.; Pourakbari-Kasmaei, M.; Contreras, J.; Gallego, L.A. Optimal selection of navigation modes of HEVs considering CO2 emissions reduction. IEEE Trans. Veh. Technol. 2019, 68, 2196–2206. [Google Scholar] [CrossRef]
- Parinaz, A.; Behnam, M.I.; Manijeh, A.; Mehdi, A.; Kazem, Z. Optimal scheduling of plug-in electric vehicles and renewable micro-grid in energy and reserve markets considering demand response program. Energies 2018, 186, 293–303. [Google Scholar]
- Zhang, H.; Hu, Z.; Xu, Z.; Song, Y. An integrated planning framework for different types of an integrated planning framework for different types of PEV charging facilities in urban area. IEEE Trans. Smart Grid 2014, 7, 2273–2284. [Google Scholar] [CrossRef]
- Ugirumurera, J.; Haas, Z. Optimal sizing of a completely green charging system for electric vehicles. IEEE Trans. Transp. Electrif. 2017, 3, 565–577. [Google Scholar] [CrossRef]
- Yang, H.; Pan, H.; Luo, F.; Qiu, J.; Deng, Y.; Lai, M.; Zhao, Y. Operational Planning of Electric Vehicles for Balancing Wind Power and Load Fluctuations in a Microgrid. IEEE Trans. Sustain. Energy 2017, 8, 592–604. [Google Scholar] [CrossRef]
- Lin, Y.; Dong, P.; Sun, X.; Liu, M. Two-level game algorithm for multi-microgrid in electricity market. IET Renew. Power Gener. 2017, 11, 1733–1740. [Google Scholar] [CrossRef]
- Aluisio, B.; Conserva, A.; Dicorato, M.; Forte, G.; Trovato, M. Optimal operation planning of V2G-equipped Microgrid in the presence of EV aggregator. Electr. Power Syst. Res. 2017, 152, 295–305. [Google Scholar] [CrossRef]
- Sideratos, G.; Hatziargyriou, N.D. An advanced statistical method for wind power forecasting. IEEE Trans. Power Syst. 2007, 22, 258–265. [Google Scholar] [CrossRef]
- Chen, C.; Duan, S.; Cai, T.; Liu, B. Online 24-h solar power forecasting based on weather type classification using artificial neural network. Sol. Energy 2011, 85, 2856–2870. [Google Scholar] [CrossRef]
- Chen, C.; Duan, S. Optimal integration of plug-in hybrid electric vehicles in microgrids. IEEE Trans. Ind. Inform. 2014, 10, 1917–1926. [Google Scholar] [CrossRef]
- Hu, J.; Si, C.; Lind, M.; Yu, R. Preventing distribution grid congestion by integrating indirect control in a hierarchical electric vehicles’ management system. IEEE Trans. Transp. Electrif. 2016, 2, 290–299. [Google Scholar] [CrossRef]
- Ortega-Vazquez, M. Optimal scheduling of electric vehicle charging and vehicle-to-grid services at household level including battery degradation and price uncertainty. IET Gener. Transm. Distrib. 2014, 8, 1007–1016. [Google Scholar] [CrossRef]
- Qian, K.; Zhou, C.; Yuan, Y. Analysis of the environmental benefits of distributed generation. In Proceedings of the 2008 IEEE Power and Energy Society General Meeting-Conversion and Delivery of Electrical Energy in the 21st Century, Pittsburgh, PA, USA, 20–24 July 2008; pp. 1–5. [Google Scholar]
- Coello Coello, C.A.; Pulido, G.T.; Lechuga, M.S. Handling multiple objectives with particle swarm optimization. IEEE Trans. Evol. Comput. 2004, 8, 256–279. [Google Scholar] [CrossRef]
- Saber, A.Y.; Venayagamoorthy, G.K. Plug-in vehicles and renewable energy sources for cost and emission reductions. IEEE Trans. Ind. Electron. 2011, 58, 1229–1238. [Google Scholar] [CrossRef]
- Chen, C.; Xiao, L.; Duan, S.; Chen, J. Cooperative optimization of electric vehicles in microgrids considering across-time-and-space energy transmission. IEEE Trans. Ind. Electron. 2019, 66, 1532–1542. [Google Scholar] [CrossRef]
- Ghosh, A.; Aggarwal, V. Control of charging of electric vehicles through menu-based pricing. IEEE Trans. Smart Grid 2018, 9, 5918–5929. [Google Scholar] [CrossRef]
| Case 1 | Case 2 | Case 3 | Case 4 | ||
|---|---|---|---|---|---|
| EVs | RMG1 | 10 | 14 | 10 | 14 |
| RMG2 | 10 | 15 | 10 | 12 | |
| WTs | RMG1 | 6 | 6 | 2 | 2 |
| RMG2 | 4 | 4 | 1 | 2 | |
| OBMG | 8 | 8 | 9 | 9 | |
| PVs | RMG1 | 9 | 9 | 9 | 6 |
| RMG2 | 6 | 6 | 0 | 0 | |
| OBMG | 12 | 12 | 18 | 20 | |
| Allocation cost of EVs ($) | 6570.0 | 9526.5 | 6570.0 | 8541.0 | |
| Allocation cost of RESs ($) | 88,640.9 | 88,640.9 | 70,174.1 | 72,020.8 | |
| Total cost of allocation ($) | 95,210.9 | 98,167.4 | 76,744.1 | 80,561.8 | |
| Case 1 | Case 2 | Case 3 | Case 4 | |
|---|---|---|---|---|
| Cost of RMG1 ($) | 67,872.8 | 67,491.1 | 55,053.9 | 56,012.3 |
| Cost of RMG2 ($) | 38,063.0 | 37,374.5 | 36,345.5 | 36,306.4 |
| Cost of OBMG ($) | 89,260.0 | 89,001.9 | 69,793.4 | 66,946.1 |
| Net Exchanged Energy (MWh) | 413.32 | 377.10 | 255.30 | 189.30 |
| Dispatching cost ($) | 97,028.4 | 95,700.1 | 84,448.7 | 78,703.0 |
| Total Cost ($) | 195,195.8 | 193,867.5 | 161,192.8 | 159,264.8 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, J.; Chen, C.; Duan, S. Cooperative Optimization of Electric Vehicles and Renewable Energy Resources in a Regional Multi-Microgrid System. Appl. Sci. 2019, 9, 2267. https://doi.org/10.3390/app9112267
Chen J, Chen C, Duan S. Cooperative Optimization of Electric Vehicles and Renewable Energy Resources in a Regional Multi-Microgrid System. Applied Sciences. 2019; 9(11):2267. https://doi.org/10.3390/app9112267
Chicago/Turabian StyleChen, Jin, Changsong Chen, and Shanxu Duan. 2019. "Cooperative Optimization of Electric Vehicles and Renewable Energy Resources in a Regional Multi-Microgrid System" Applied Sciences 9, no. 11: 2267. https://doi.org/10.3390/app9112267
APA StyleChen, J., Chen, C., & Duan, S. (2019). Cooperative Optimization of Electric Vehicles and Renewable Energy Resources in a Regional Multi-Microgrid System. Applied Sciences, 9(11), 2267. https://doi.org/10.3390/app9112267





