Study of Heat and Mass Transfer in Electroosmotic Flow of Third Order Fluid through Peristaltic Microchannels
Abstract
1. Introduction
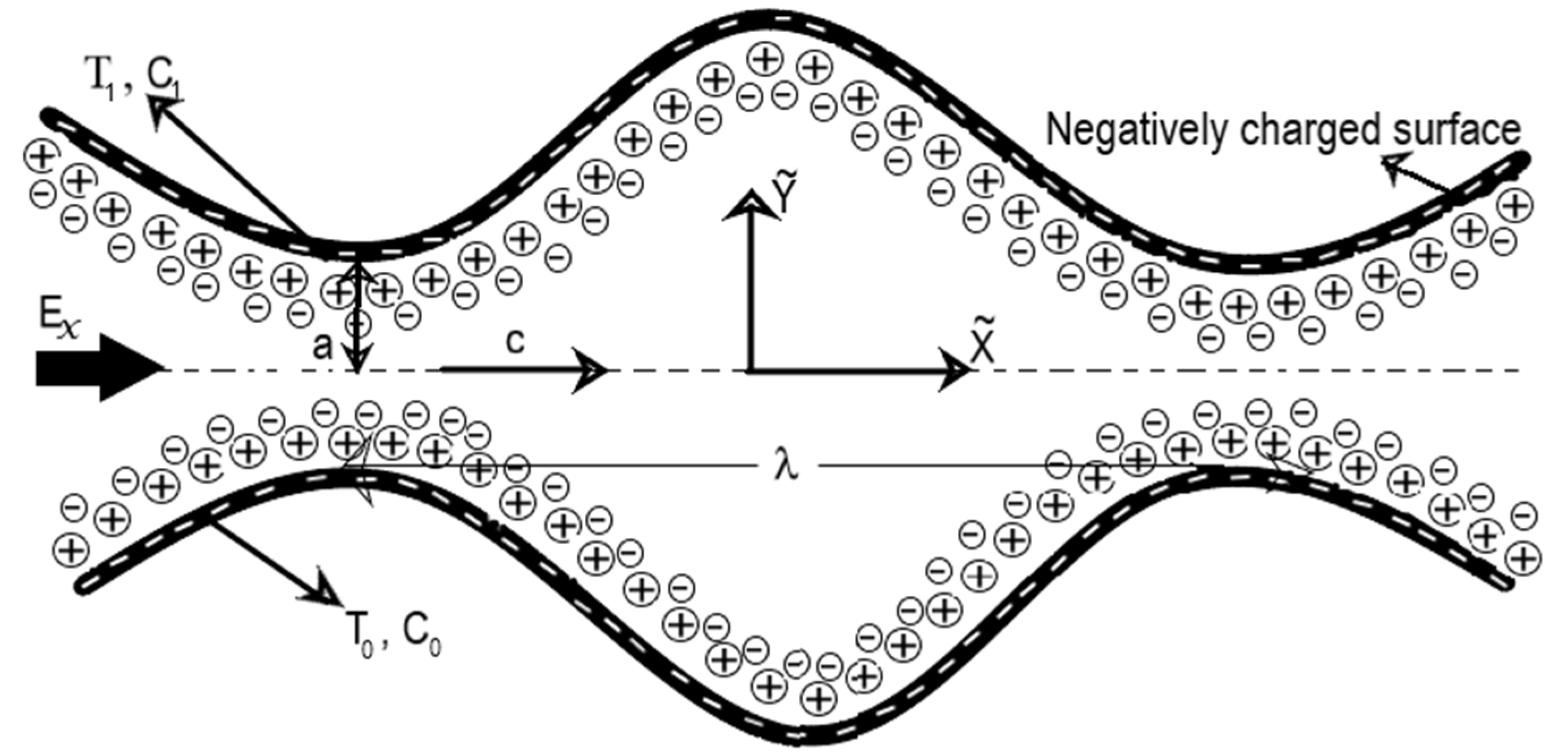
2. Mathematical Model
2.1. Flow Analysis
2.2. Governing Equations
2.3. Electrohydrodynamics (EHD)
2.4. Potential Distribution
2.5. Non-Dimensionlization, Lubrication Approach and Boundary Conditions
3. Solution Methodology
3.1. Series Solutions
3.2. Zero Order System
3.3. First Order System
4. Computational Discussion of Results
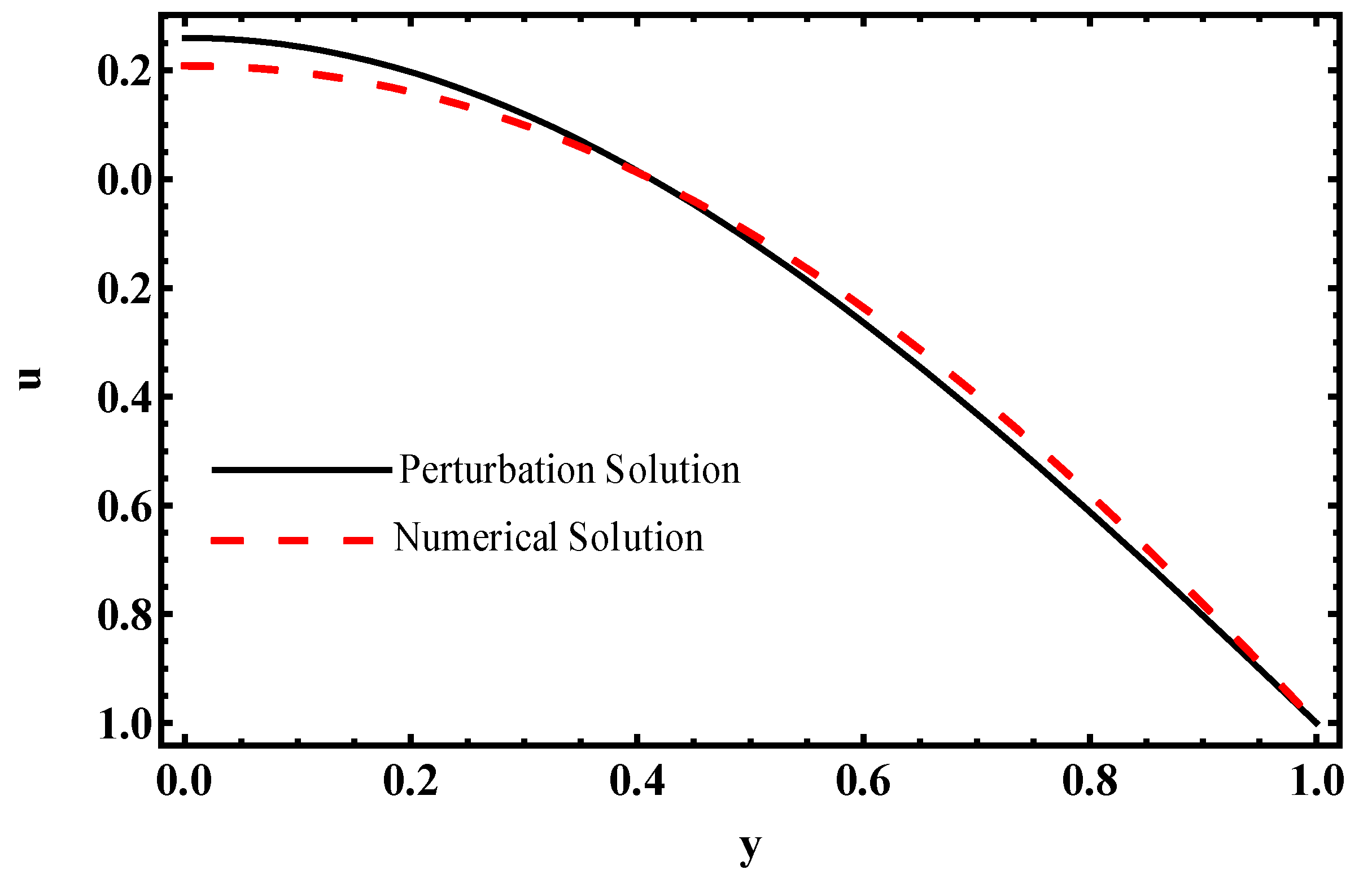
4.1. Comparative Analysis
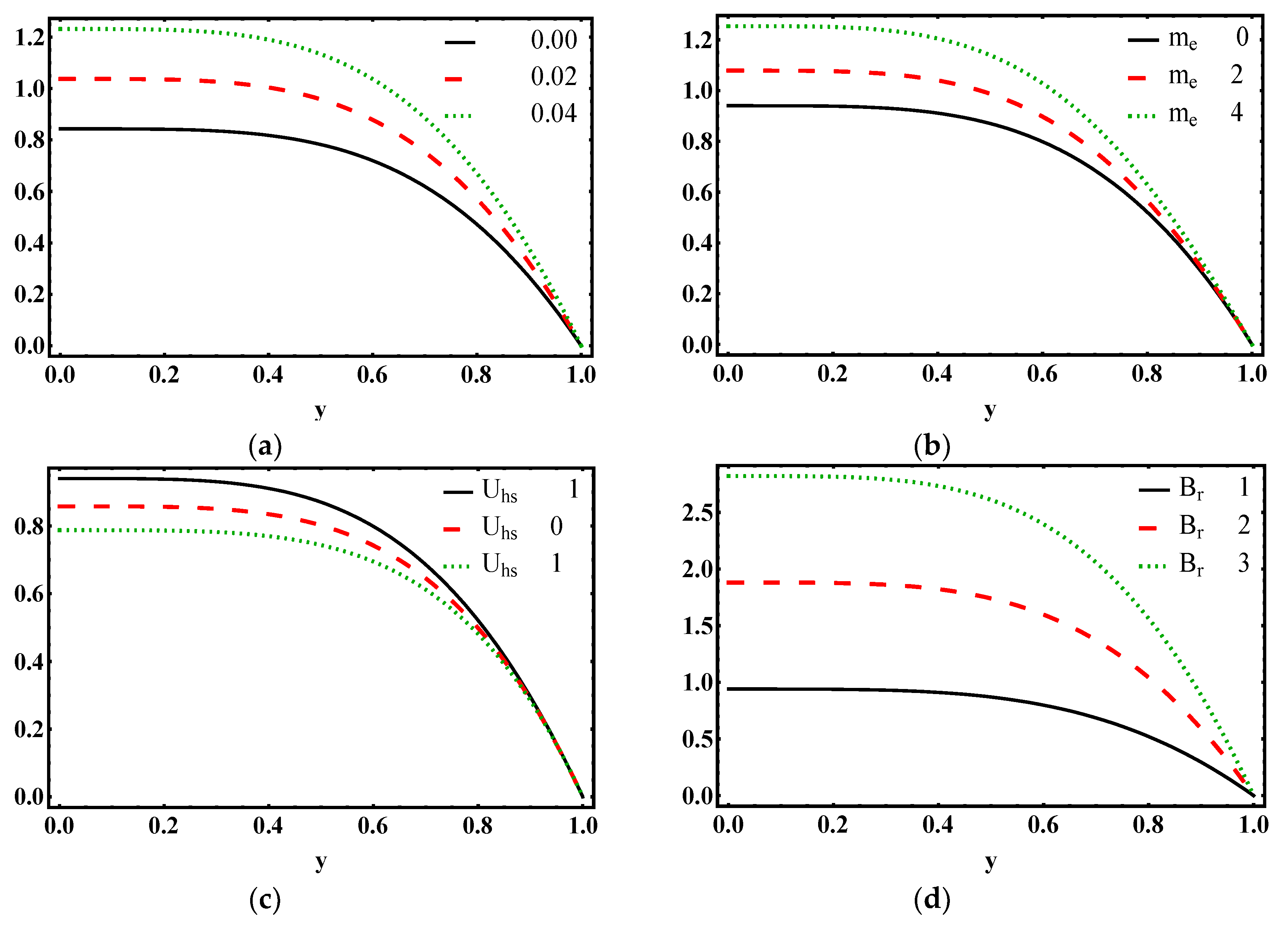
4.2. Flow Characteristics
4.3. Pumping Characteristics
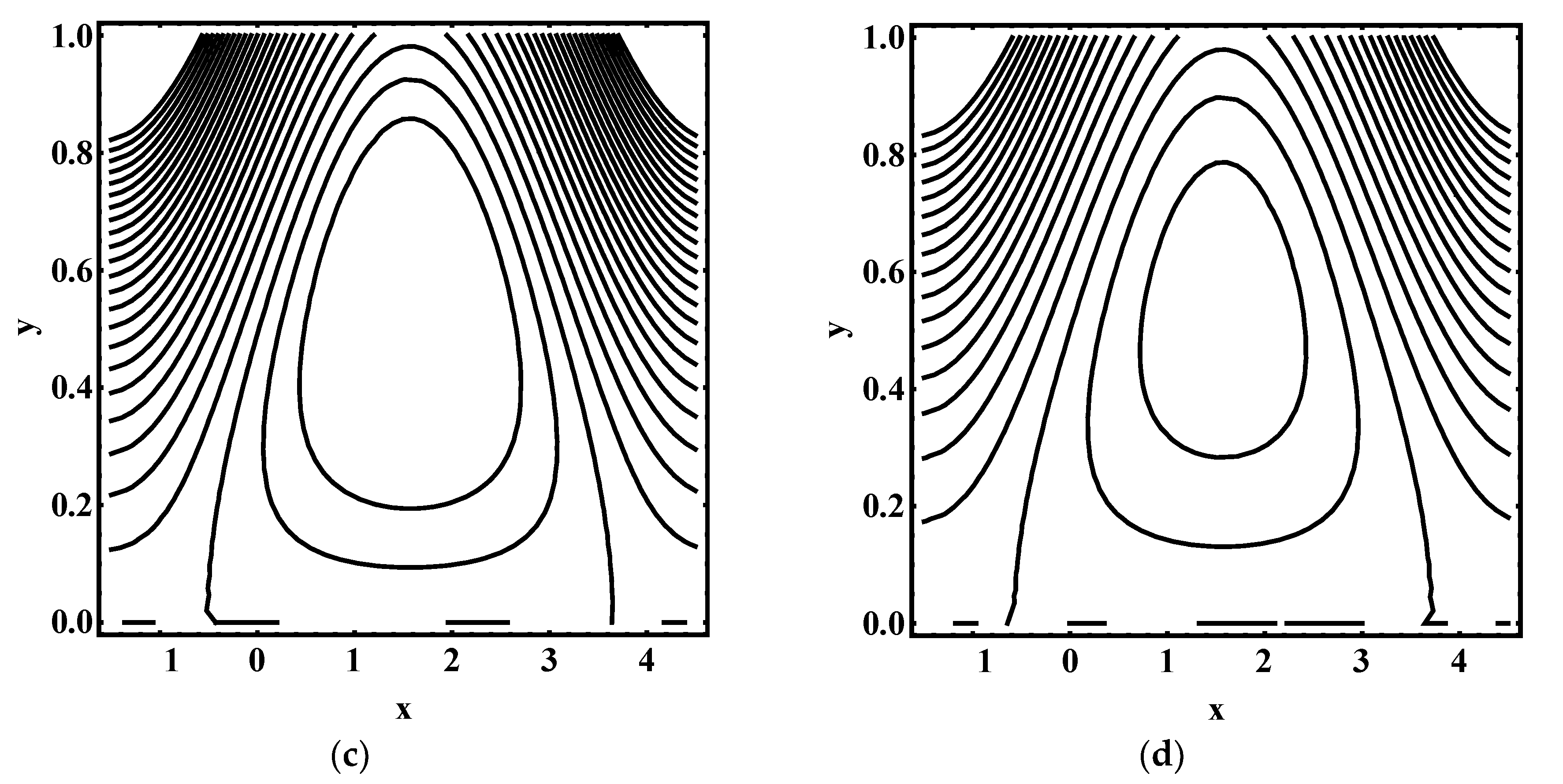
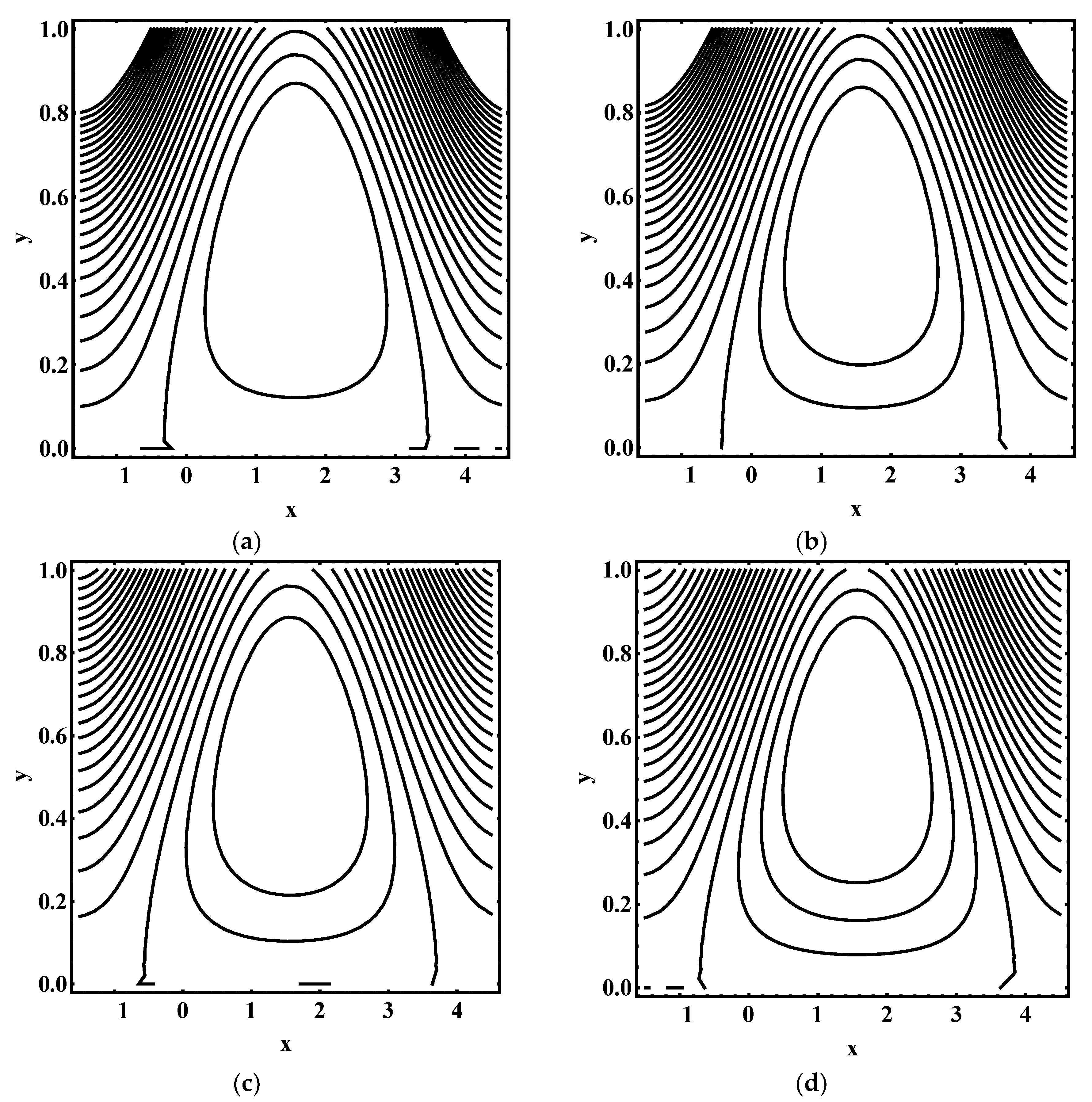
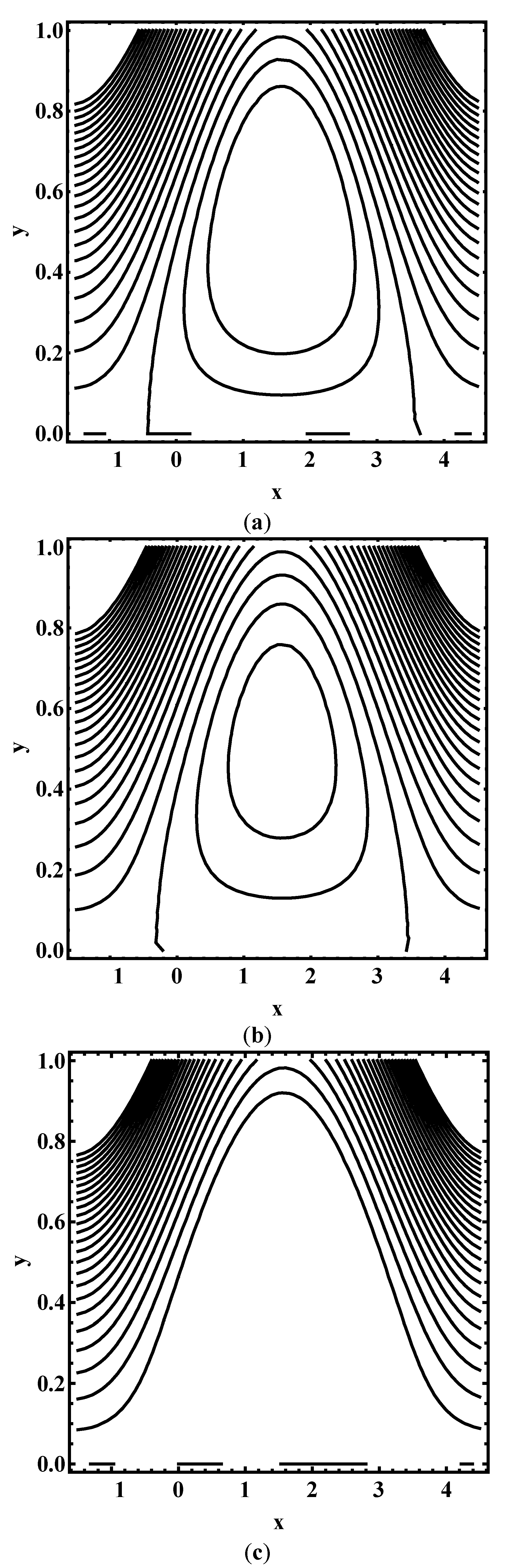
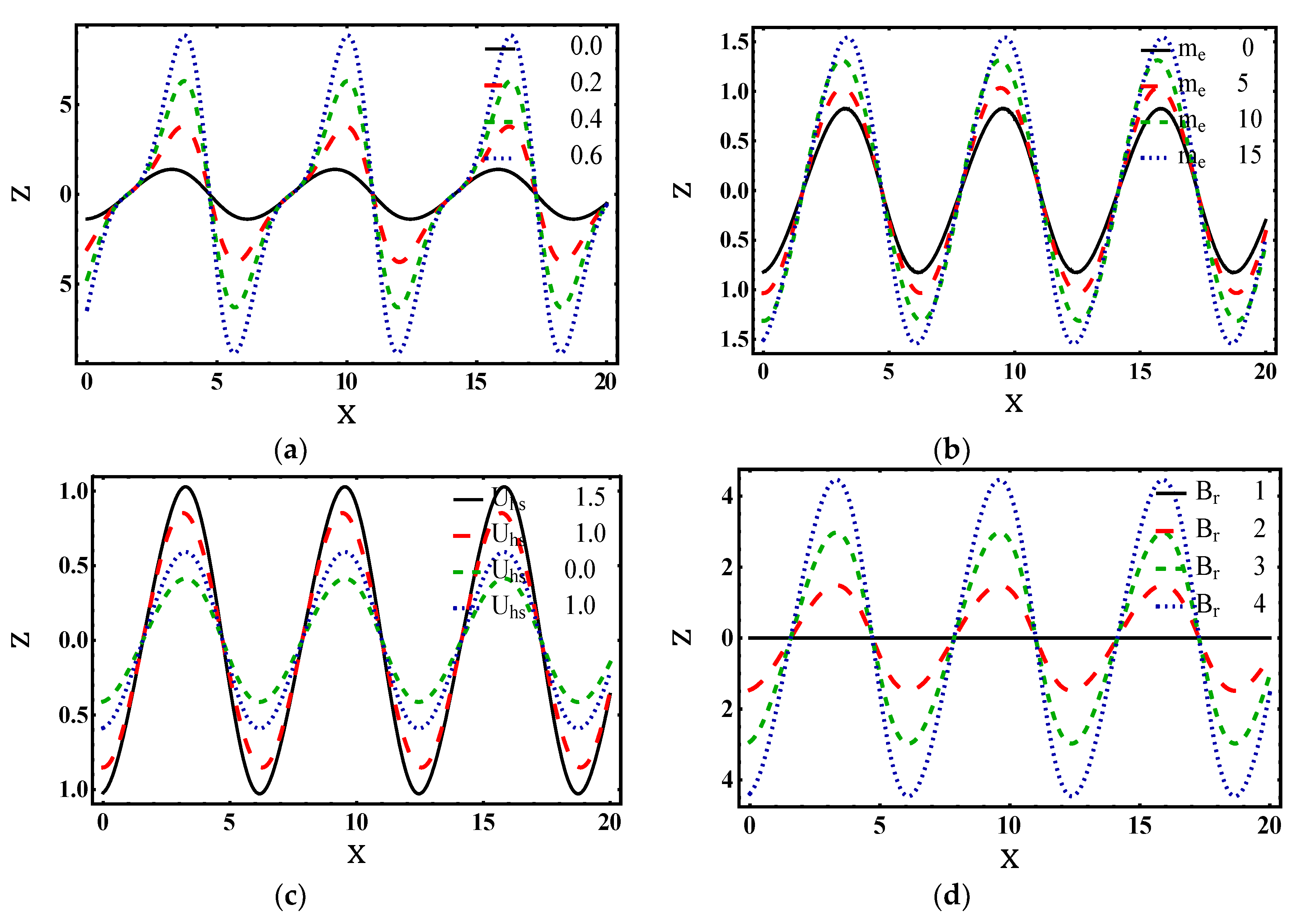
4.4. Trapping Characteristics
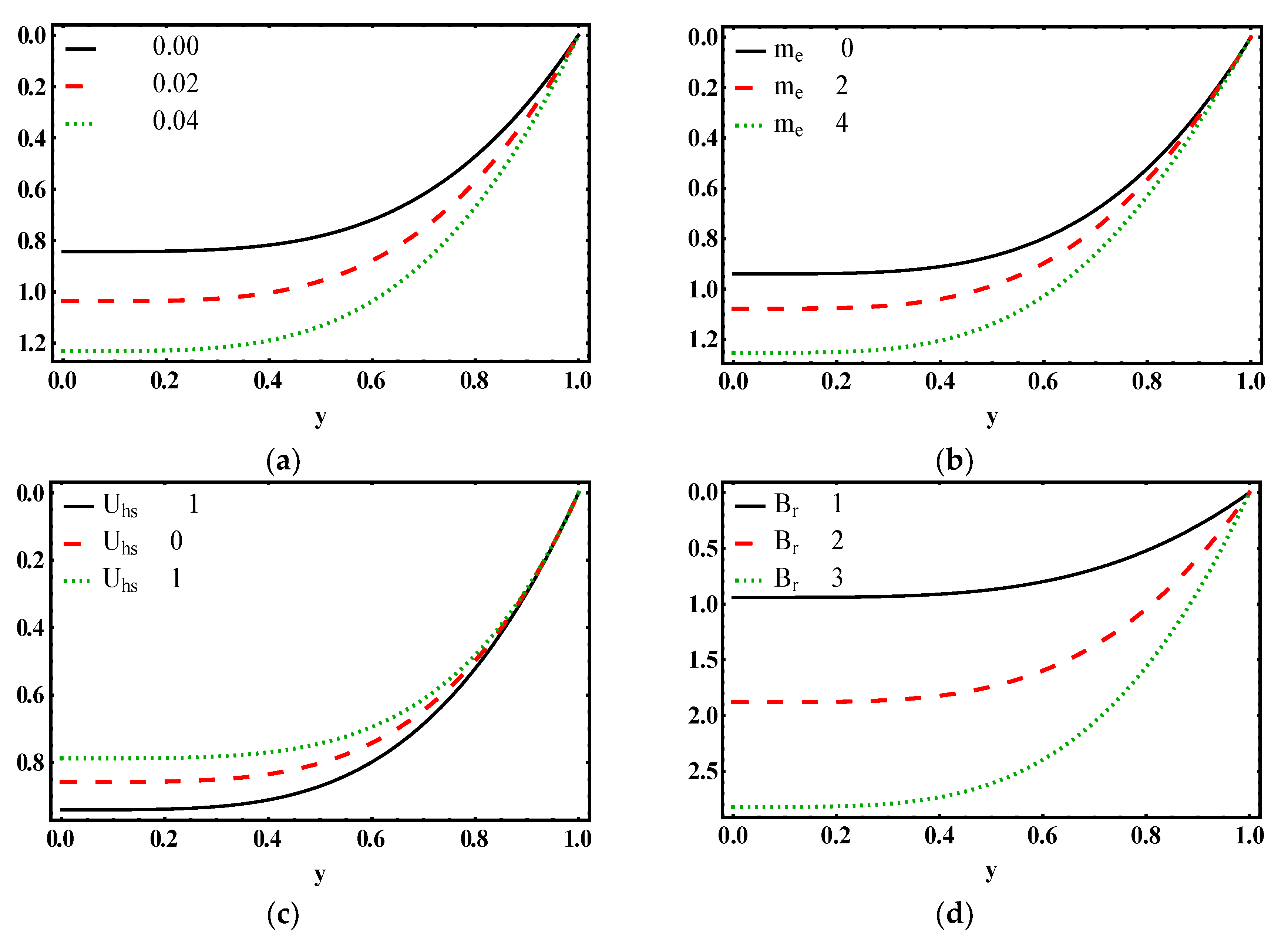
4.5. Temperature Characteristics
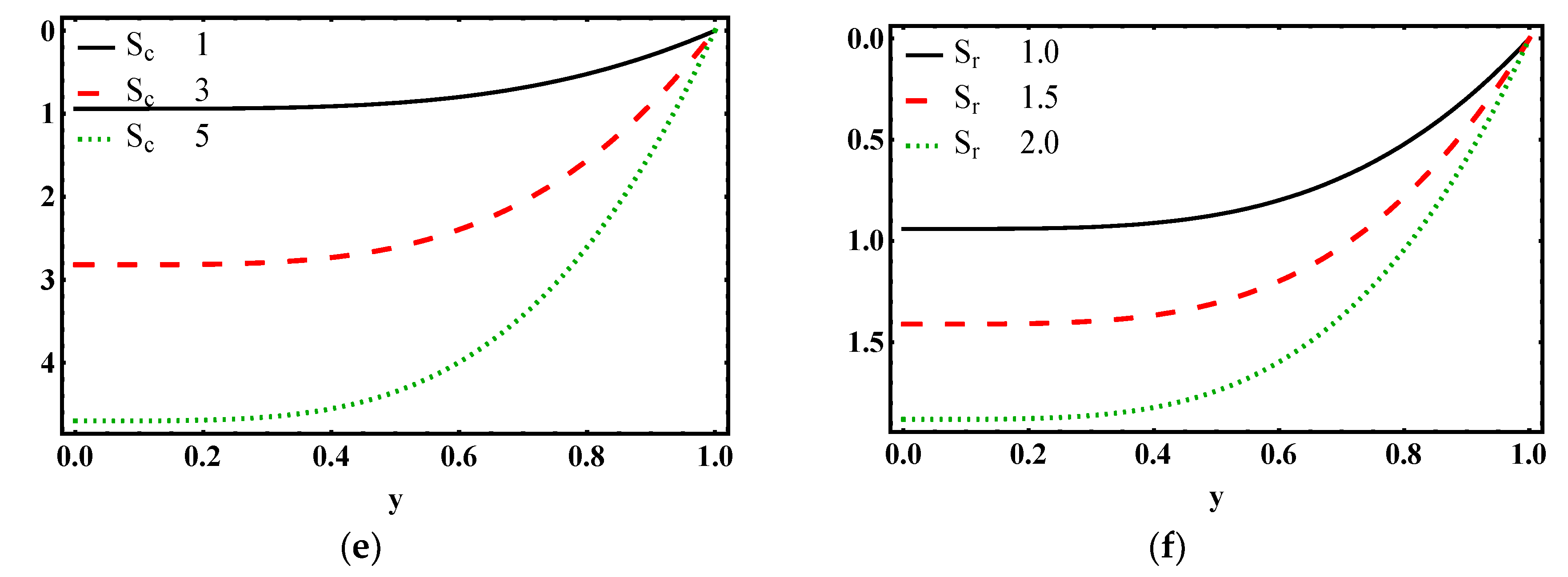
4.6. Concentration Characteristics
4.7. Heat Transfer Coefficient
4.8. Shear Stress Distribution
5. Concluding Remarks
- The axial velocity of third-grade fluid in the microchannel is enhanced due to an increase in electroosmotic parameter.
- For higher values of Schmidt or Soret number, concentration profile decreases.
- The magnitude of pressure rise decreases in the pumping region with the increase of electroosmotic parameter.
- Pressure gradient is more for EOF of third order fluid in comparison to peristaltically flowing fluid.
- Axial distribution of shear stress enhances for increasing values of maximum electroosmotic velocity.
- Volume of trapped bolus is strongly dependent upon the electroosmotic parameter whereas it is suppressed for Deborah number and maximum electroosmotic velocity.
- Temperature distribution in microchannel is crucial for electroosmotic parameter, Deborah number and Brinkman number.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| Symbols | Meaning | Dimensions |
| Channel’s half width | [L] | |
| Revilin Erickson tensor | [M/L] | |
| Wave amplitude | [L] | |
| Brinkman number | [-] | |
| Wave speed | [L/T] | |
| Dimensional concentration field | [N/] | |
| , | Concentration field at upper and lower wall | [N/] |
| Diffusivity of chemical species | [-] | |
| Mass diffusivity coefficient | [] | |
| Eckert number | [-] | |
| Axial electric field | [ML/A] | |
| Electron charge | [AT] | |
| Non-dimensional mean flow rate in moving frame | [-] | |
| Dimensional upper wall | [L] | |
| Non-dimensional upper wall | [-] | |
| Thermal conductivity | [ML/K] | |
| Ratio of thermal diffusion | [N/] | |
| Boltzmaan constant | [M/] | |
| Electroosmotic parameter | [-] | |
| Positive and negative ions | [AT] | |
| Bulk concentration | [AT] | |
| Dimensional pressure field | [ML/] | |
| Non-dimensional pressure field | [-] | |
| Peclet number | [-] | |
| Prandtl number | [-] | |
| Dimensional volume flow rate in fixed frame | [/T] | |
| Reynolds number | [-] | |
| Dimensional shear stress | [M/L] | |
| Non-dimensional shear stress | [-] | |
| Schmidt number | [-] | |
| Soret number | [-] | |
| Dimensional time | [T] | |
| Non-dimensional time | [-] | |
| Dimensional temperature field | [K] | |
| , | Temperature field at upper and lower wall | [K] |
| Mean temperature | [K] | |
| Dimensional velocity along direction | [L/T] | |
| Non-dimensional velocity along x direction | [-] | |
| Helmholtz–Smoluchowski velocity | [L/T] | |
| Dimensional velocity along direction | [L/T] | |
| Non-dimensional velocity along y direction | [-] | |
| Dimensional axial coordinate in fixed frame | [L] | |
| Non-dimensional axial coordinate in moving frame | [-] | |
| Dimensional transverse coordinate in fixed frame | [L] | |
| Non-dimensional transverse coordinate in moving frame | [-] | |
| heat transfer coefficient | [-] | |
| Valence of ions | [-] | |
| Peristaltic wave number | [-] | |
| , | Material constants | [-] |
| , | Material constants | [-] |
| Material coefficients | [-] | |
| Wavelength | [L] | |
| Material coefficients | [-] | |
| Debye length | [L] | |
| Dielectric permittivity | [-] | |
| Toatl charge density | [AT/] | |
| Density of fluid | [M/] | |
| Dimensional electric potential | [M] | |
| Non-dimensional electric potential | [-] | |
| Non-dimensional Deborah number | [-] | |
| Amplitude ratio | [-] | |
| Non-dimensional volume flow rate | [-] | |
| Non-dimensional temperature field | [-] | |
| Non-dimensional concentration field | [-] | |
| Dimensional stream function | [/T] | |
| Non-dmensional stream function | [-] |
Appendix A
References
- Huang, X.; Gordon, M.J.; Zare, R.N. Current-monitoring method for measuring the electroosmotic flow rate in capillary zone electrophoresis. Anal. Chem. 1998, 60, 1837–1838. [Google Scholar] [CrossRef]
- Gravesen, P.; Branebjerg, J.; Jensen, O.S. Microfluidics-a review. J. Micromech. Microeng. 1993, 3, 168. [Google Scholar] [CrossRef]
- Haswell, S.J. Development and operating characteristics of micro flow injection based on electroosmotic flow. Analyst 1997, 122, 1R–10R. [Google Scholar] [CrossRef]
- Patankar, N.A.; Hu, H.H. Numerical simulation of electroosmotic flow. Anal. Chem. 1998, 70, 1870–1881. [Google Scholar] [CrossRef] [PubMed]
- Kang, Y.; Yang, C.; Huang, X. Electroosmotic flow in a capillary annulus with high zeta potentials. J. Colloid Interface Sci. 2002, 253, 285–294. [Google Scholar] [CrossRef] [PubMed]
- Hayat, T.; Abbasi, F.M. Variable viscosity effects on the peristaltic motion of a third-order fluid. Int. J. Numer. Methods Fluids 2011, 67, 1500–1515. [Google Scholar] [CrossRef]
- Noreen, S. Mixed convection peristaltic flow of third order nanofluid with an induced magnetic field. PLoS ONE 2013, 8, e78770. [Google Scholar] [CrossRef]
- Noreen, S. Effects of joule heating and convective boundary conditions on magnetohydrodynamic peristaltic flow of couple-stress fluid. J. Heat Transf. 2016, 138, 094502. [Google Scholar] [CrossRef]
- Prakash, J.; Siva, E.P.; Balaji, N.; Kothandapani, M. Effect of peristaltic flow of a third-grade fluid in a tapered asymmetric channel. J. Phys. 2018, 1000, 012165. [Google Scholar] [CrossRef]
- Mallick, B.; Misra, J.C. Peristaltic flow of Eyring-Powell nanofluid under the action of an electromagnetic field. Eng. Sci. Technol. 2019, 22, 266–281. [Google Scholar] [CrossRef]
- Chakraborty, S. Augmentation of peristaltic microflows through electro-osmotic mechanisms. J. Phys. D Appl. Phys. 2006, 39, 5356. [Google Scholar] [CrossRef]
- Tang, G.H.; Li, X.F.; He, Y.L.; Tao, W.Q. Electroosmotic flow of non-Newtonian fluid in microchannels. J. Non-Newton. Fluid Mech. 2009, 157, 133–137. [Google Scholar] [CrossRef]
- Hadigol, M.; Nosrati, R.; Nourbakhsh, A.; Raisee, M. Numerical study of electroosmotic micromixing of non-Newtonian fluids. J. Non-Newton. Fluid Mech. 2011, 166, 965–971. [Google Scholar] [CrossRef]
- Yavari, H.; Sadeghi, A.; Saidi, M.H.; Chakraborty, S. Temperature rise in electroosmotic flow of typical non-Newtonian biofluids through rectangular microchannels. J. Heat Transf. 2014, 136, 031702. [Google Scholar] [CrossRef]
- Bandopadhyay, A.; Tripathi, D.; Chakraborty, S. Electroosmosis-modulated peristaltic transport in microfluidic channels. Phys. Fluids 2016, 28, 052002. [Google Scholar] [CrossRef]
- Jiang, Y.; Qi, H.; Xu, H.; Jiang, X. Transient electroosmotic slip flow of fractional Oldroyd-B fluids. Microfluid. Nanofluid. 2017, 21, 7. [Google Scholar] [CrossRef]
- Jhorar, R.; Tripathi, D.; Bhatti, M.M.; Ellahi, R. Electroosmosis modulated biomechanical transport through asymmetric microfluidics channel. Indian J. Phys. 2018, 92, 1229–1238. [Google Scholar] [CrossRef]
- Tripathi, D.; Yadav, A.; Bég, O.A.; Kumar, R. Study of microvascular non-Newtonian blood flow modulated by electroosmosis. Microvasc. Res. 2018, 117, 28–36. [Google Scholar] [CrossRef]
- Francesko, A.; Cardoso, V.F.; Lanceros-Méndez, S. Lab-on-a-chip technology and microfluidics. In Microfluidics for Pharmaceutical Applications; William Andrew: Norwich, UK, 2019; pp. 3–36. [Google Scholar]
- Jayavel, P.; Jhorar, R.; Tripathi, D.; Azese, M.N. Electroosmotic flow of pseudoplastic nanoliquids via peristaltic pumping. J. Braz. Soc. Mech. Sci. 2019, 41, 61. [Google Scholar] [CrossRef]
- Sadeghi, A.; Saidi, M.H.; Mozafari, A.A. Heat transfer due to electroosmotic flow of viscoelastic fluids in a slit microchannel. Int. J. Heat Mass Transf. 2011, 54, 4069–4077. [Google Scholar] [CrossRef]
- Babaie, A.; Saidi, M.H.; Sadeghi, A. Heat transfer characteristics of mixed electroosmotic and pressure driven flow of power-law fluids in a slit microchannel. Int. J. Therm. Sci. 2012, 53, 71–79. [Google Scholar] [CrossRef]
- Chen, C.H.; Hwang, Y.L.; Hwang, S.J. Non-Newtonian fluid flow and heat transfer in microchannels. Appl. Mech. Mater. 2013, 275, 462–465. [Google Scholar] [CrossRef]
- Sinha, A.; Shit, G.C. Electromagnetohydrodynamic flow of blood and heat transfer in a capillary with thermal radiation. J. Magn. Magn. Mater. 2015, 378, 143–151. [Google Scholar] [CrossRef]
- Shit, G.C.; Mondal, A.; Sinha, A.; Kundu, P.K. Electro-osmotically driven MHD flow and heat transfer in micro-channel. Physica A 2016, 449, 437–454. [Google Scholar] [CrossRef]
- Bhatti, M.M.; Zeeshan, A.; Ellahi, R.; Ijaz, N. Heat and mass transfer of two-phase flow with Electric double layer effects induced due to peristaltic propulsion in the presence of transverse magnetic field. J. Mol. Liq. 2017, 230, 237–246. [Google Scholar] [CrossRef]
- Reddy, K.V.; Makinde, O.D.; Reddy, M.G. Thermal analysis of MHD electro-osmotic peristaltic pumping of Casson fluid through a rotating asymmetric micro-channel. Indian J. Phys. 2018, 92, 1439–1448. [Google Scholar] [CrossRef]
- Yadav, A.; Bhushan, S.; Tripathi, D. Peristaltic pumping through porous medium in presence of electric double layer. EDP Sci. 2018, 192, 02043. [Google Scholar] [CrossRef][Green Version]
- Narla, V.K.; Tripathi, D.; Sekhar, G.R. Time-dependent analysis of electroosmotic fluid flow in a microchannel. J. Eng. Math. 2019, 114, 177–196. [Google Scholar] [CrossRef]
- Yang, C.; Jian, Y.; Xie, Z.; Li, F. Heat transfer characteristics of magnetohydrodynamic electroosmotic flow in a rectangular microchannel. Eur. J. Mech. B-Fluids 2019, 74, 180–190. [Google Scholar] [CrossRef]




| (a) | |||
| 0.0 | 0.2 | 0.4 | |
| 0.1 | −2.4917 | −3.0742 | −0.8223 |
| 0.2 | −2.3669 | −3.8790 | −2.2711 |
| 0.3 | −2.6497 | −4.5689 | −4.3309 |
| (b) | |||
| −1.0 | 0.0 | 1.0 | |
| 0.1 | −3.6869 | −1.1370 | 0.5727 |
| 0.2 | −3.7974 | −1.2903 | 0.4311 |
| 0.3 | −3.8395 | −1.4188 | 0.3188 |
| (c) | |||
| 2 | 4 | 6 | |
| 0.1 | −3.6869 | −10.778 | −6.3530 |
| 0.2 | −3.7974 | −8.7149 | −4.7301 |
| 0.3 | −3.8395 | −7.0505 | −3.6590 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Waheed, S.; Noreen, S.; Hussanan, A. Study of Heat and Mass Transfer in Electroosmotic Flow of Third Order Fluid through Peristaltic Microchannels. Appl. Sci. 2019, 9, 2164. https://doi.org/10.3390/app9102164
Waheed S, Noreen S, Hussanan A. Study of Heat and Mass Transfer in Electroosmotic Flow of Third Order Fluid through Peristaltic Microchannels. Applied Sciences. 2019; 9(10):2164. https://doi.org/10.3390/app9102164
Chicago/Turabian StyleWaheed, Sadia, Saima Noreen, and Abid Hussanan. 2019. "Study of Heat and Mass Transfer in Electroosmotic Flow of Third Order Fluid through Peristaltic Microchannels" Applied Sciences 9, no. 10: 2164. https://doi.org/10.3390/app9102164
APA StyleWaheed, S., Noreen, S., & Hussanan, A. (2019). Study of Heat and Mass Transfer in Electroosmotic Flow of Third Order Fluid through Peristaltic Microchannels. Applied Sciences, 9(10), 2164. https://doi.org/10.3390/app9102164




