Energy Concepts and Critical Plane for Fatigue Assessment of Ti-6Al-4V Notched Specimens
Abstract
1. Introduction
2. Theoretical Framework of Strain-Based Multiaxial Fatigue Criterion
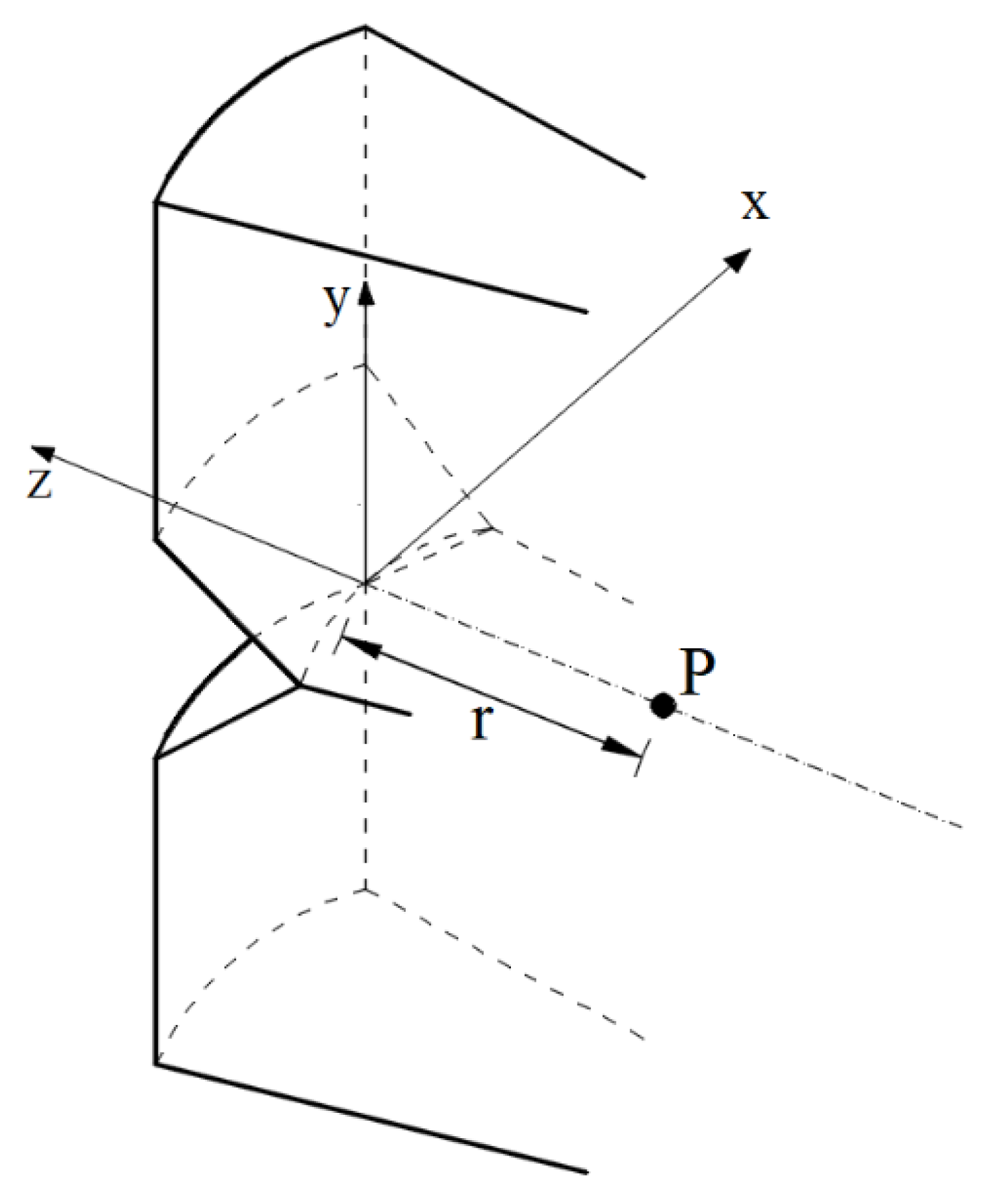
2.1. Step I: Verification Point Position
2.2. Step II: Critical Plane Orientation
2.3. Step III: Fatigue Life Assessment
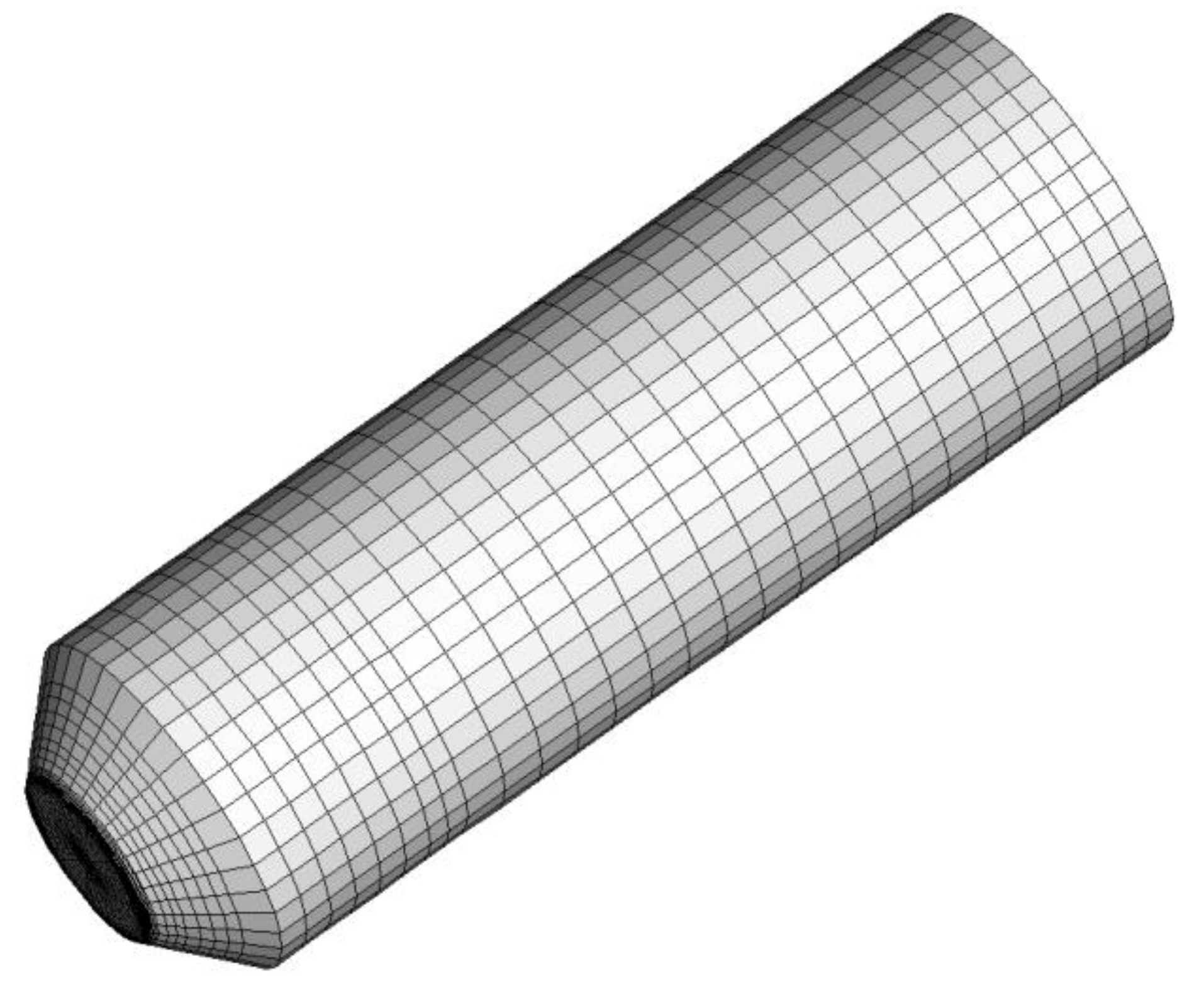
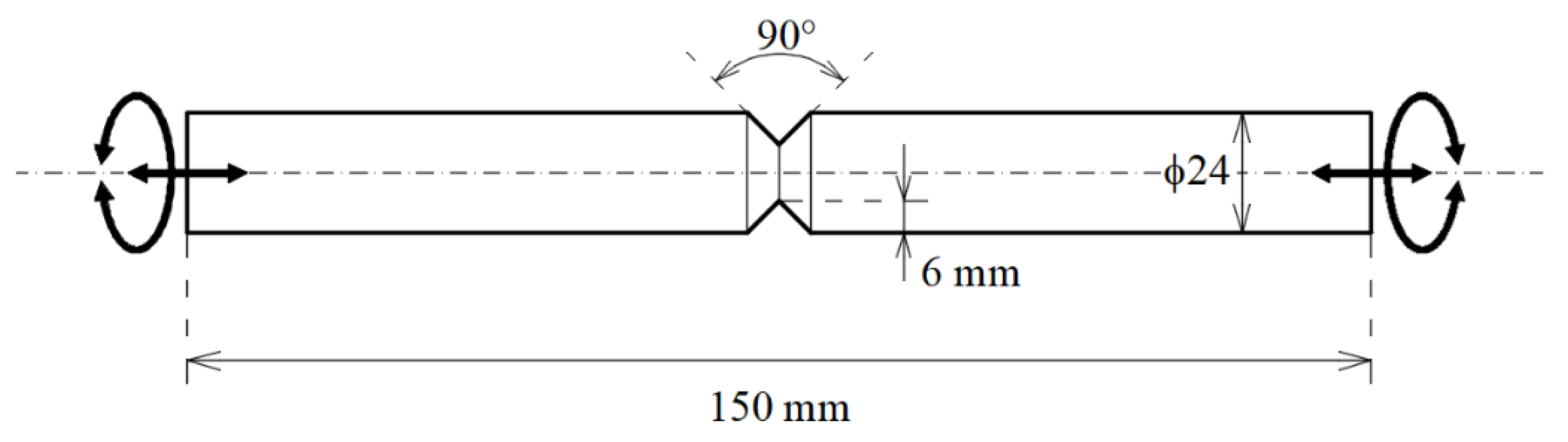
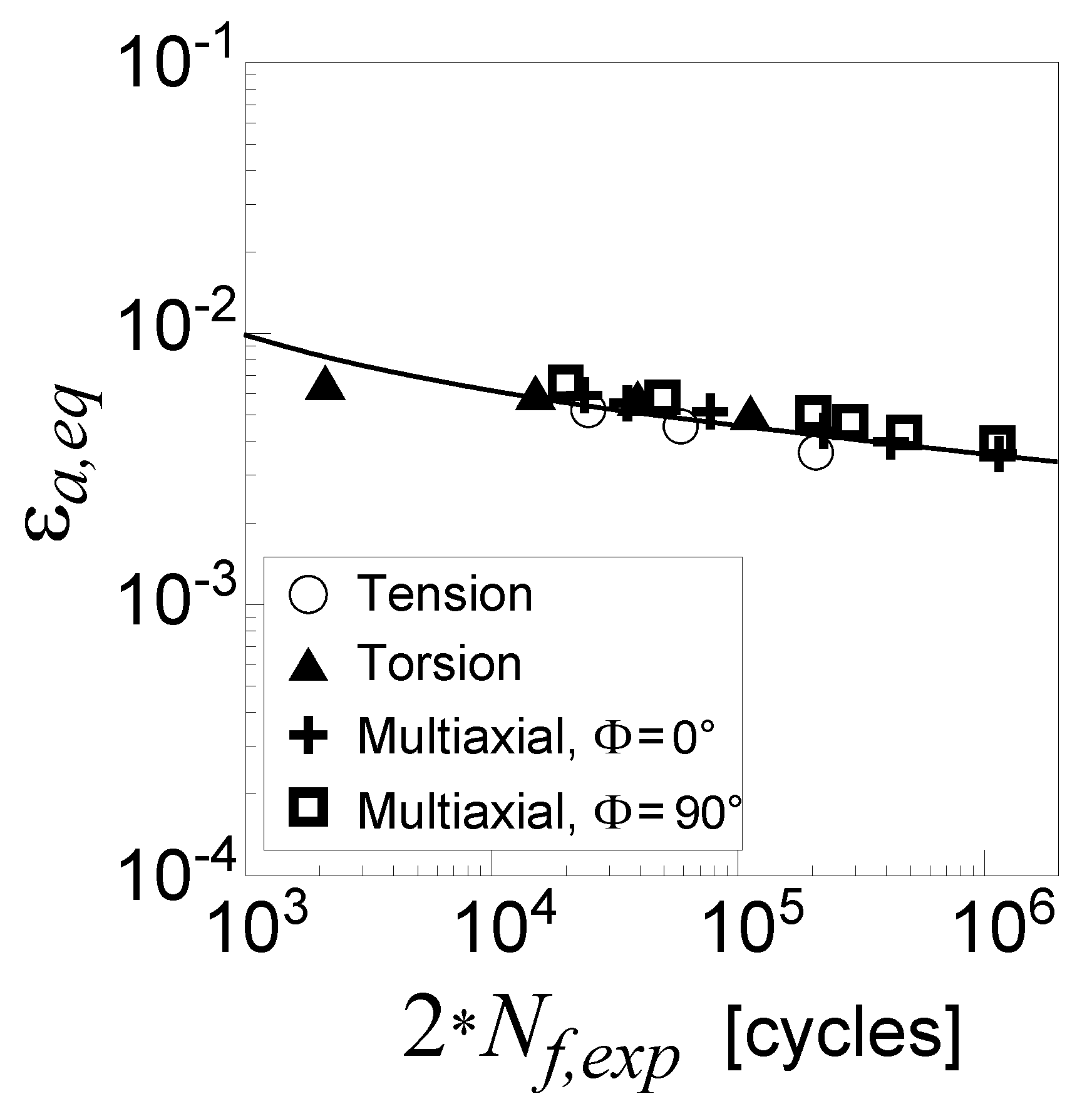
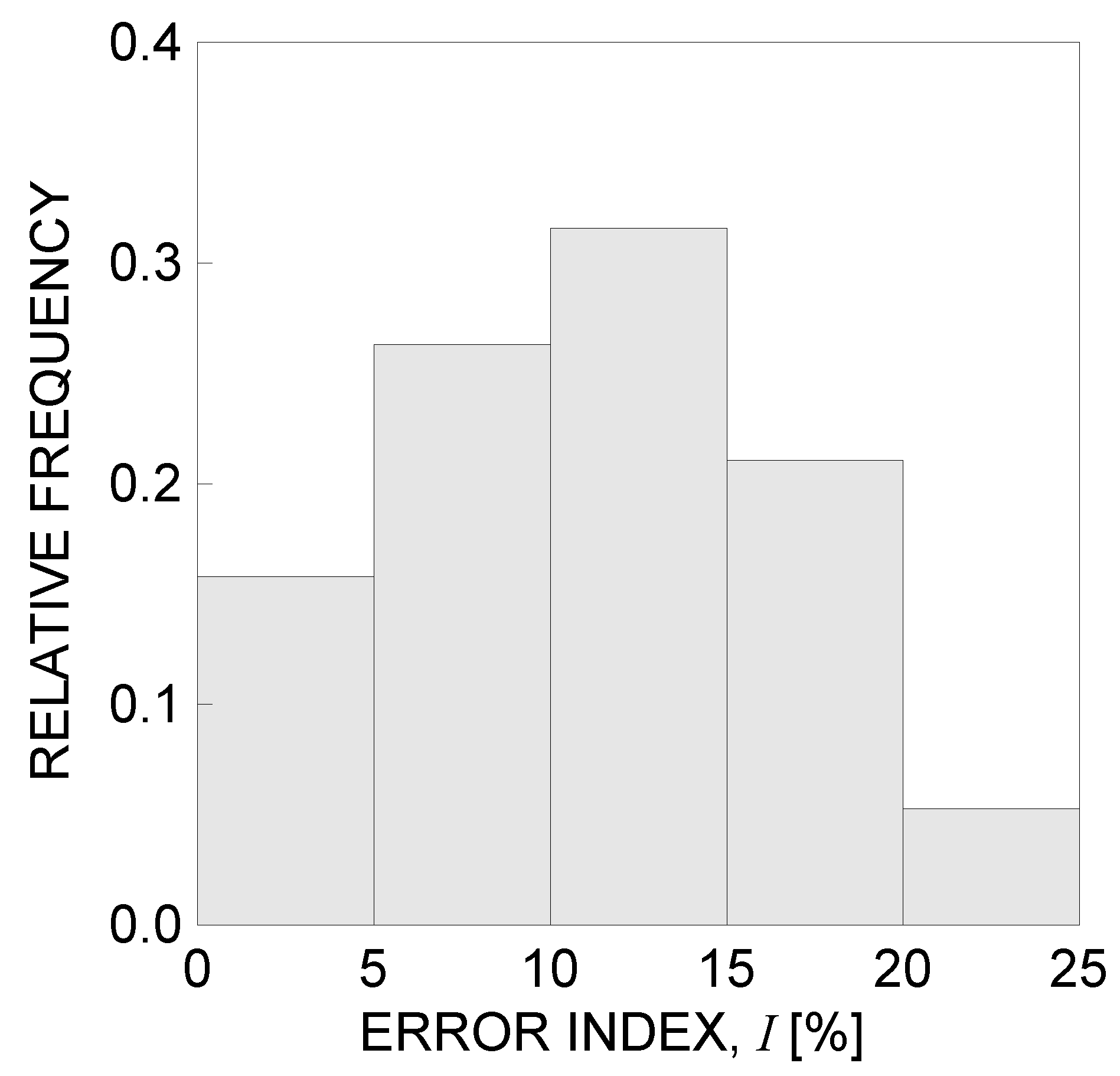
3. Criterion Validation
- V-notch with a depth of mm;
- Opening angle of ;
- Notch root radius of mm.
- Pure tension fatigue loading;
- Pure torsion fatigue loading;
- Combined in-phase () tension and torsion fatigue loading;
- Combined out-of-phase () tension and torsion fatigue loading.
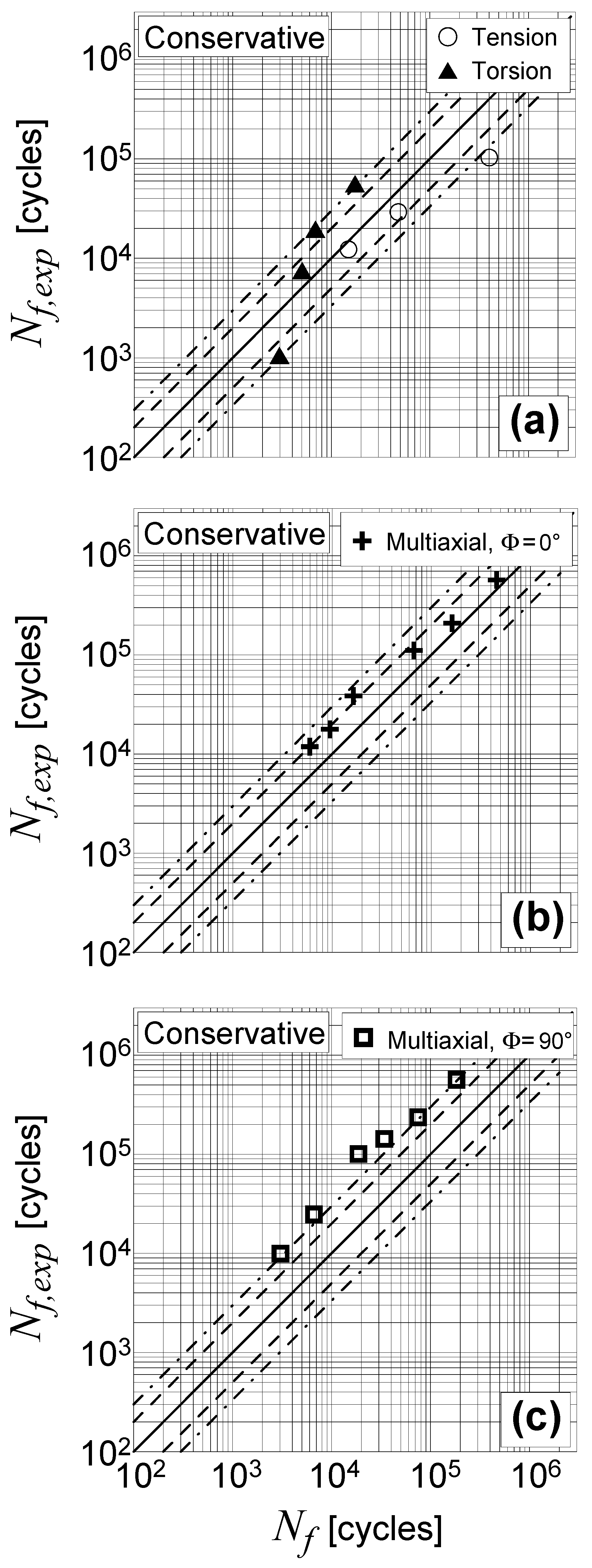
- (a)
- for pure tension fatigue loading ();
- (b)
- for pure torsion fatigue loading ();
- (c)
- for combined tension and torsion fatigue loading ().
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| principal strain directions | |
| averaged principal strain directions | |
| elastic modulus | |
| error index | |
| theoretical fatigue life | |
| experimental fatigue life | |
| verification point | |
| distance of the verification point from the notch tip | |
| mean control volume radius | |
| control volume radius related to Mode I | |
| control volume radius related to Mode III | |
| time | |
| perpendicular unit vector to the critical plane | |
| Manson–Coffin shear strain amplitude | |
| angle between the averaged direction and the normal to the critical plane | |
| notch stress intensity factor range under Mode I | |
| notch stress intensity factor range under Mode III | |
| high-cycle fatigue strength of smooth specimens under Mode I | |
| high-cycle Fatigue strength of smooth specimens under Mode III | |
| principal strains, with | |
| Manson–Coffin normal strain amplitude | |
| equivalent normal strain amplitude | |
| amplitude of the normal displacement vector component acting on the critical plane | |
| amplitude of the tangential displacement vector component acting on the critical plane | |
| biaxiality ratio | |
| elastic Poisson ratio | |
| effective Poisson ratio | |
| plastic Poisson ratio | |
| ultimate tensile strength | |
| yield strength | |
| phase angle between tension and torsion loading |
References
- Jasper, T.M. The value of the energy relation in the testing of ferrous metals at varying ranges of stress and at intermediate and high temperatures. Philos. Mag. Ser. 1923, 6, 609–627. [Google Scholar] [CrossRef]
- Macha, E.; Sonsino, C.M. Energy criteria of multiaxial fatigue failure. Fatigue Fract. Eng. Mater. Struct. 1999, 22, 1053–1070. [Google Scholar] [CrossRef]
- Garud, Y.S. A new approach to the evaluation of fatigue under multiaxial loadings. J. Eng. Mater. Technol. 1981, 103, 118–125. [Google Scholar] [CrossRef]
- Ellyin, F. Cyclic strain energy density as a criterion for multiaxial fatigue failure. In Biaxial and Multiaxial Fatigue; EGF, 3, Carpinteri, A., De Freitas, M., Spagnoli, A., Eds.; Mechanical Engineering: London, UK, 1989; pp. 571–583. [Google Scholar]
- Ellyin, F.; Golos, K.; Xia, Z. In-phase and out-of-phase multiaxial fatigue. J. Eng. Mater. Technol. 1991, 113, 112–118. [Google Scholar] [CrossRef]
- Ellyin, F.; Xia, Z. A general fatigue theory and its application to out-of-phase cyclic loading. J. Eng. Mater. Technol. 1993, 115, 411–416. [Google Scholar] [CrossRef]
- Molsky, K.; Glinka, G. A method of elastic-plastic stress and strain calculation at a notch root. Mater. Sci. Eng. 1981, 50, 93–100. [Google Scholar] [CrossRef]
- Glinka, G. Energy density approach to calculation of inelastic strain-stress near notches and cracks. Eng. Fract. Mech. 1985, 22, 485–508. [Google Scholar] [CrossRef]
- Moftakhar, A.; Buczynski, A.; Glinka, G. Calculation of elasto-plastic strains and stresses in notches under multiaxial loading. Int. J Fracture 1995, 70, 357–373. [Google Scholar] [CrossRef]
- Park, J.; Nelson, D. Evaluation of an energy-based approach and a critical plane approach for predicting constant amplitude multiaxial fatigue life. Int. J. Fatigue 2000, 22, 23–39. [Google Scholar] [CrossRef]
- Lazzarin, P.; Zambardi, R. A finite-volume-energy based approach to predict the static and fatigue behavior of components with sharp V-shaped notches. Int. J. Fract. 2001, 112, 275–298. [Google Scholar] [CrossRef]
- Lazzarin, P.; Berto, F. Some expressions for the strain energy in a finite volume surrounding the root of blunt V-notches. Int. J. Fract. 2005, 135, 161–185. [Google Scholar] [CrossRef]
- Atzori, B.; Berto, F.; Lazzarin, P.; Quaresimin, M. Multi-axial fatigue behaviour of a severely notched carbon steel. Int. J. Fatigue 2006, 28, 485–493. [Google Scholar] [CrossRef]
- Berto, F.; Lazzarin, P.; Tovo, R. Multiaxial fatigue strength of severely notched cast iron specimens. Int. J. Fatigue 2014, 67, 15–27. [Google Scholar] [CrossRef]
- Meneghetti, G.; Campagnolo, A.; Berto, F.; Atzori, B. Averaged strain energy density evaluated rapidly from the singular peak stresses by FEM: cracked components under mixed-mode (I+II) loading. Theor. Appl. Fract. Mech. 2015, 79, 113–124. [Google Scholar] [CrossRef]
- Ayatollahi, M.R.; Berto, F.; Campagnolo, A.; Gallo, P.; Tang, K. Review of local strain energy density theory for the fracture assessment of V-notches under mixed mode loading. Eng. Solid Mech. 2017, 5, 113–132. [Google Scholar] [CrossRef]
- Berto, F.; Ayatollahi, M.R.; Campagnolo, A. Fracture tests under mixed mode I + III loading: An assessment based on the local energy. Int. J. Damage Mech. 2017, 26, 881–894. [Google Scholar] [CrossRef]
- Torabi, A.R.; Berto, F.; Razavi, S.M.J. Ductile failure prediction of thin notched aluminum plates subjected to combined tension-shear loading. Theor. Appl. Fract. Mech. 2018, 97, 280–288. [Google Scholar] [CrossRef]
- Lazzarin, P.; Berto, F.; Atzori, B. A synthesis of data from steel spot welded joints of reduced thickness by means of local SED. Theor. Appl. Fract. Mech. 2013, 63–64, 32–39. [Google Scholar] [CrossRef]
- Chebat, F.; Peron, M.; Viespoli, L.M.; Welo, T.; Berto, F. Fatigue strength assessment of steel rollers: on the reliability of the strain energy density approach on real components. Appl. Sci. 2018, 8, 1015. [Google Scholar] [CrossRef]
- Viespoli, L.M.; Berto, F.; Somà, A. Fatigue life assessment for a welded detail: Advantages of a local energetic approach and experimental validation. Frattura ed Integrità Strutturale 2018, 12, 121–134. [Google Scholar] [CrossRef]
- Carpinteri, A.; Berto, F.; Campagnolo, A.; Fortese, G.; Ronchei, C.; Scorza, D.; Vantadori, S. Fatigue assessment of notched specimens by means of a critical plane-based criterion and energy concepts. Theor. Appl. Fract. Mech. 2016, 84, 57–63. [Google Scholar] [CrossRef]
- Carpinteri, A.; Fortese, G.; Ronchei, C.; Scorza, D.; Vantadori, S.; Berto, F. Joined application of a multiaxial critical plane criterion and a strain energy density criterion in low-cycle fatigue. Fract. Struct. Integr. 2017, 11, 66–70. [Google Scholar] [CrossRef]
- Vantadori, S.; Carpinteri, A.; Fortese, G.; Ronchei, C.; Scorza, D.; Zanichelli, A. Fatigue lifetime evaluation of notched components: implementation of the control volume concept in a strain-based LCF criterion. Theor. Appl. Fract. Mech. 2018, 97, 400–408. [Google Scholar] [CrossRef]
- Carpinteri, A.; Ronchei, C.; Spagnoli, A.; Vantadori, S. Lifetime estimation in the low/medium-cycle regime using the Carpinteri–Spagnoli multiaxial fatigue criterion. Theor. Appl. Fract. Mech. 2014, 73, 120–127. [Google Scholar] [CrossRef]
- Carpinteri, A.; Ronchei, C.; Scorza, D.; Vantadori, S. Fatigue life estimation for multiaxial low-cycle fatigue regime: The influence of the effective Poisson ratio value. Theor. Appl. Fract. Mech. 2015, 79, 77–83. [Google Scholar] [CrossRef]
- Berto, F.; Campagnolo, A.; Welo, T. Local strain energy density to assess the multiaxial fatigue strength of titanium alloys. Fract. Struct. Integr. 2016, 10, 69–79. [Google Scholar] [CrossRef]
- Attar, H.; Calin, M.; Zhang, L.C.; Scudino, S.; Eckert, J. Manufacture by selective laser melting and mechanical behavior of commercially pure titanium. Mater. Sci. Eng. A 2014, 593, 170–177. [Google Scholar] [CrossRef]
- Ehtemam Haghighi, S.; Lu, H.B.; Jian, G.Y.; Cao, G.H.; Habibi, D.; Zhang, L.C. Effect of α″ martensite on the microstructure and mechanical properties of beta-type Ti–Fe–Ta alloys. Mater. Des. 2015, 76, 47–54. [Google Scholar] [CrossRef]
- Liu, Y.J.; Li, S.J.; Wang, H.L.; Hou, W.T.; Hao, Y.L.; Yang, R.; Sercombe, T.B.; Zhang, C. Microstructure, defects and mechanical behavior of beta-type titanium porous structures manufactured by electron beam melting and selective laser melting. Acta Mater. 2016, 113, 56–67. [Google Scholar] [CrossRef]
- Liu, Y.J.; Wang, H.L.; Li, S.J.; Wang, S.G.; Wang, W.J.; Hou, W.T.; Hao, Y.L.; Yang, R.; Zhanga, L.C. Compressive and fatigue behavior of beta-type titanium porous structures fabricated by electron beam melting. Acta Mater. 2017, 126, 58–66. [Google Scholar] [CrossRef]
- Zhao, S.; Li, S.J.; Wang, S.G.; Hou, W.T.; Li, Y.; Zhang, L.C.; Hao, Y.L.; Yang, R.; Misra, R.D.K.; Murr, L.E. Compressive and fatigue behavior of functionally graded Ti-6Al-4V meshes fabricated by electron beam melting. Acta Mater. 2018, 150, 1–15. [Google Scholar] [CrossRef]
- Berto, F.; Campagnolo, A.; Lazzarin, P. Fatigue strength of severely notched specimens made of Ti–6Al–4V under multiaxial loading. Fatigue Fract. Eng. Mater. Struct. 2015, 38, 503–517. [Google Scholar] [CrossRef]
- Straus7, Theoretical Manual: Theoretical Background for Straus7 Finite Element Analysis Systems, G + D Computing. Sydney, 2004.
- Carpinteri, A.; Karolczuk, A.; Macha, E.; Vantadori, S. Expected position of the fatigue fracture plane by using the weighted mean principal Euler angles. Int. J. Fract. 2002, 115, 87–99. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ronchei, C.; Carpinteri, A.; Vantadori, S. Energy Concepts and Critical Plane for Fatigue Assessment of Ti-6Al-4V Notched Specimens. Appl. Sci. 2019, 9, 2163. https://doi.org/10.3390/app9102163
Ronchei C, Carpinteri A, Vantadori S. Energy Concepts and Critical Plane for Fatigue Assessment of Ti-6Al-4V Notched Specimens. Applied Sciences. 2019; 9(10):2163. https://doi.org/10.3390/app9102163
Chicago/Turabian StyleRonchei, Camilla, Andrea Carpinteri, and Sabrina Vantadori. 2019. "Energy Concepts and Critical Plane for Fatigue Assessment of Ti-6Al-4V Notched Specimens" Applied Sciences 9, no. 10: 2163. https://doi.org/10.3390/app9102163
APA StyleRonchei, C., Carpinteri, A., & Vantadori, S. (2019). Energy Concepts and Critical Plane for Fatigue Assessment of Ti-6Al-4V Notched Specimens. Applied Sciences, 9(10), 2163. https://doi.org/10.3390/app9102163






