Predicting the Aqueductal Cerebrospinal Fluid Pulse: A Statistical Approach
Abstract
1. Introduction
2. Materials and Methods
2.1. Subjects
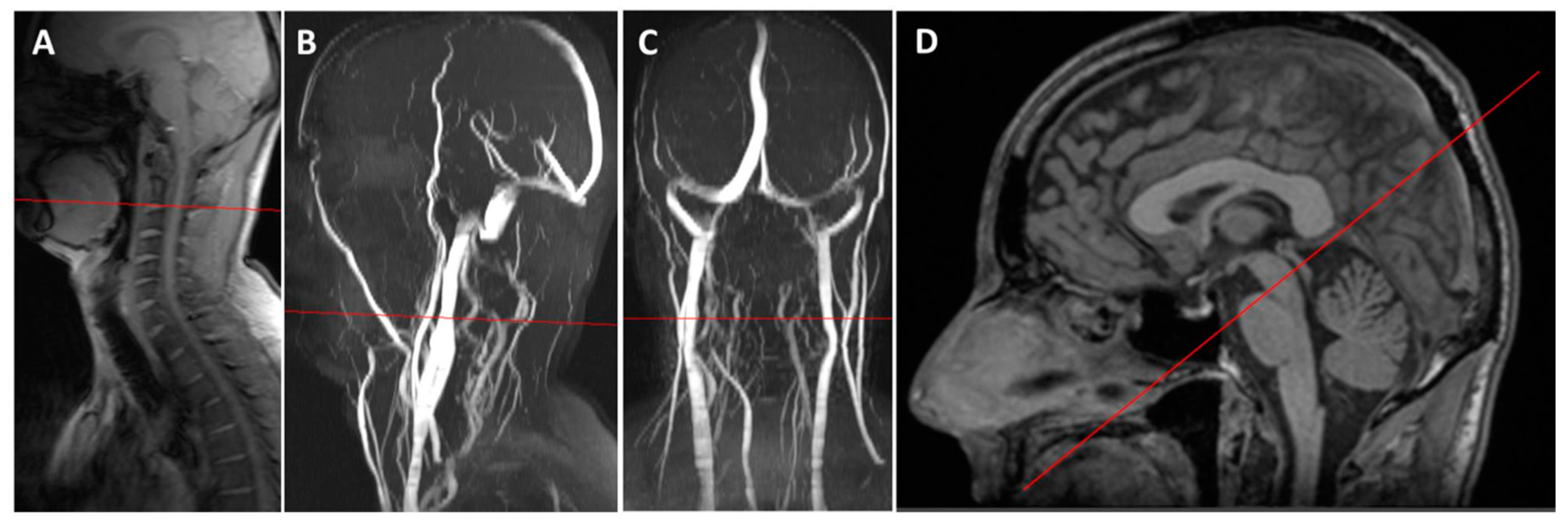
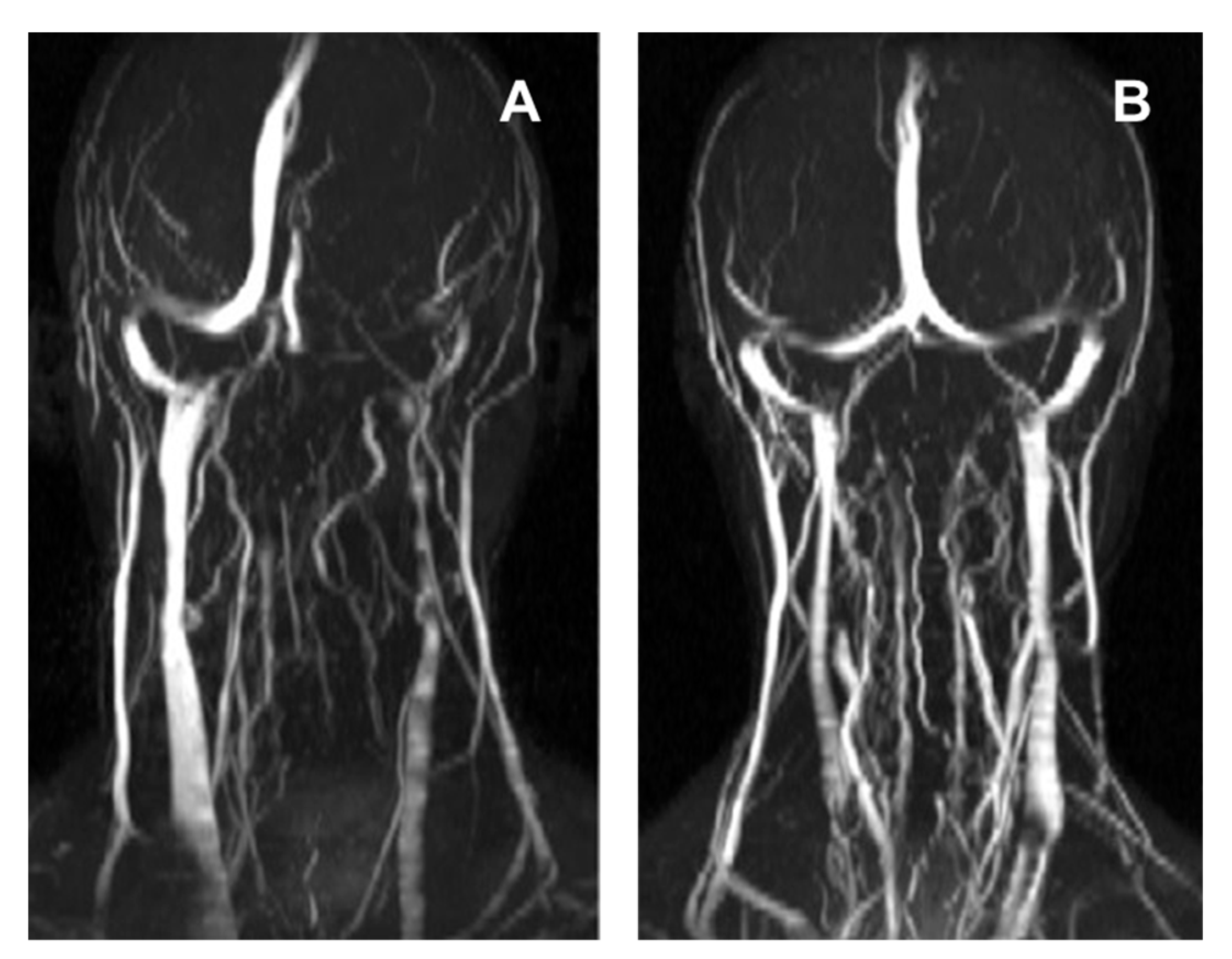
2.2. Magnetic Resonance Acquisition and Processing
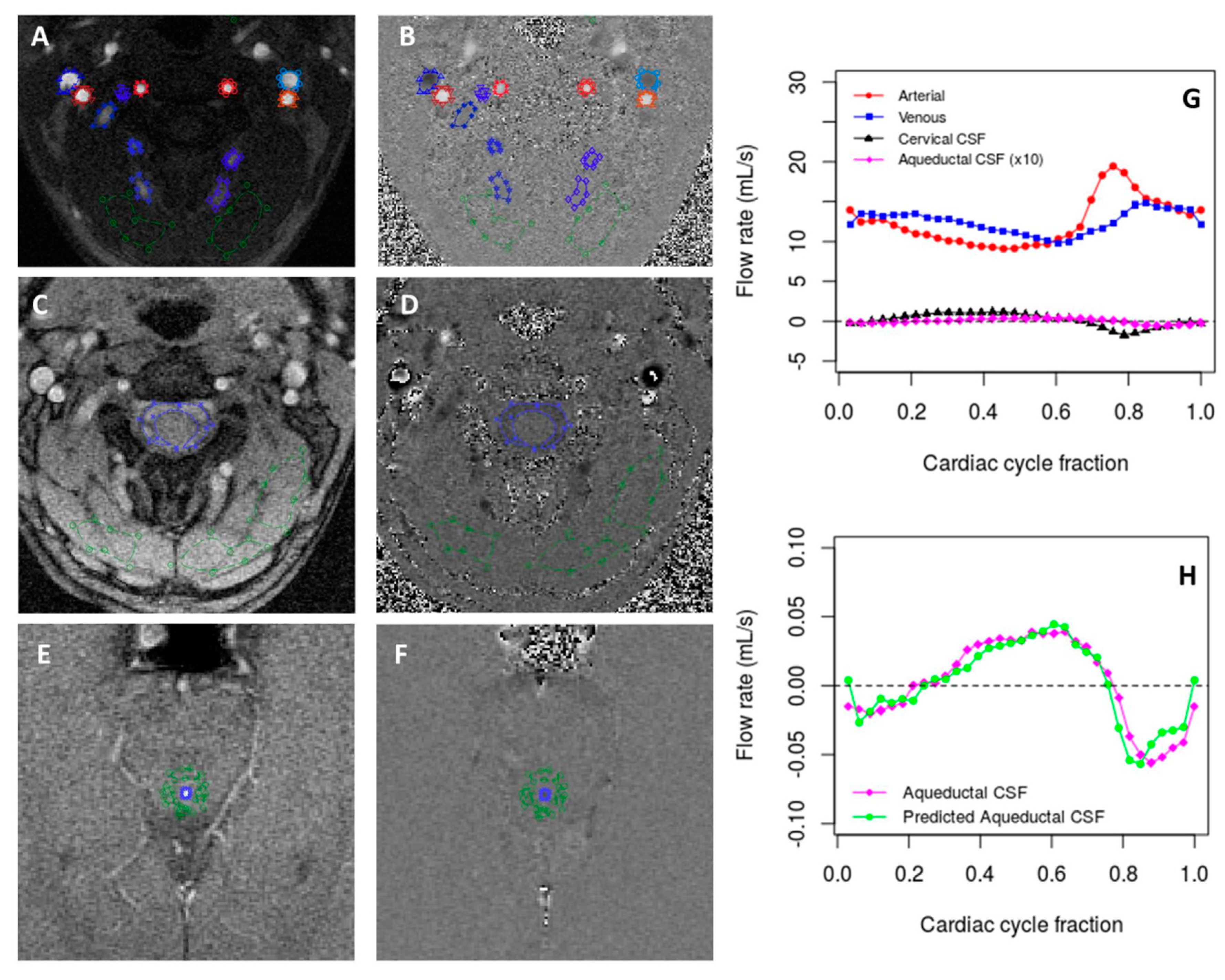
2.3. Flow Data Analysis
2.4. Statistical Analysis
3. Results
3.1. Demographic Results
3.2. Magnetic Resonance Imaging Results
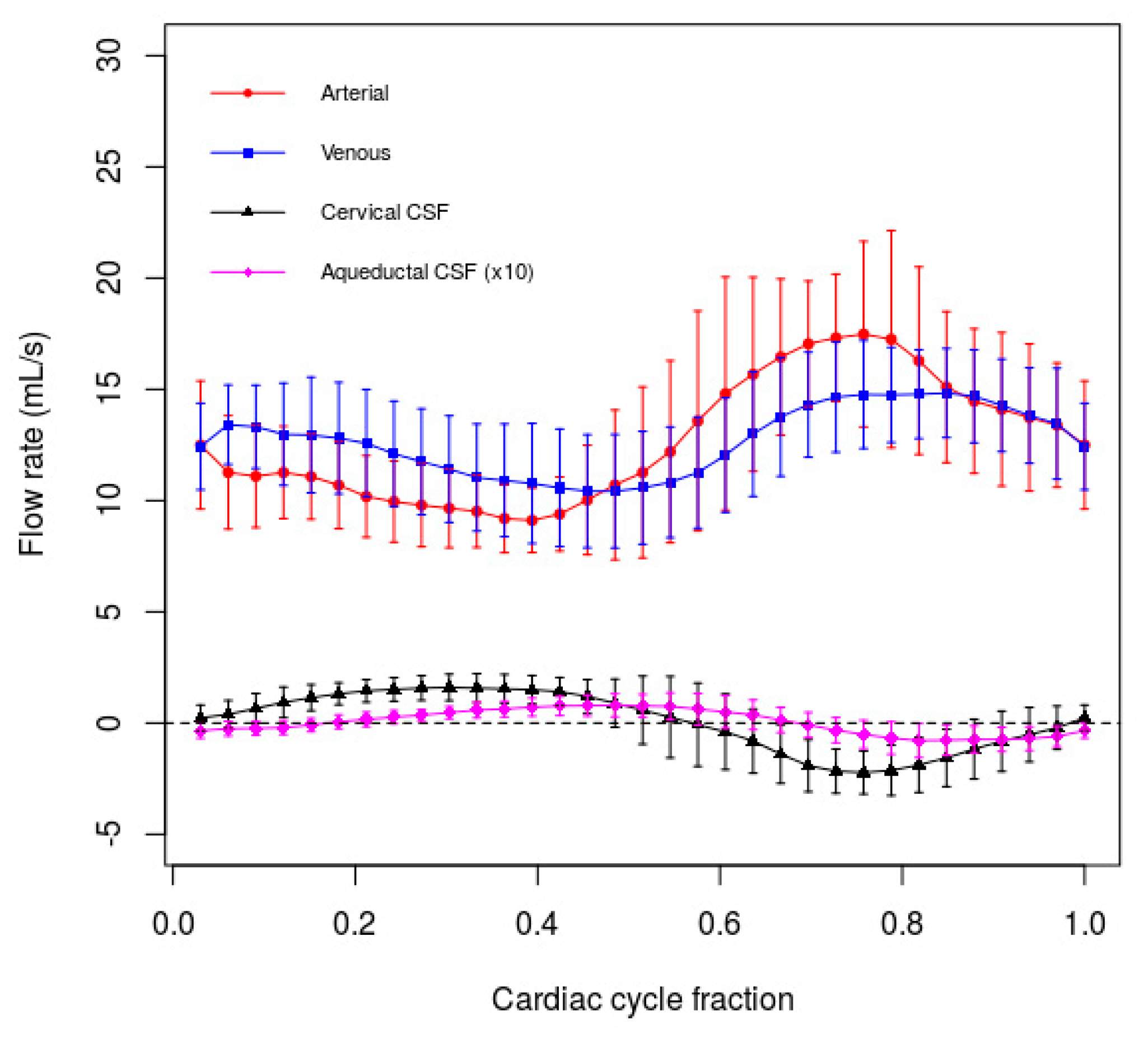
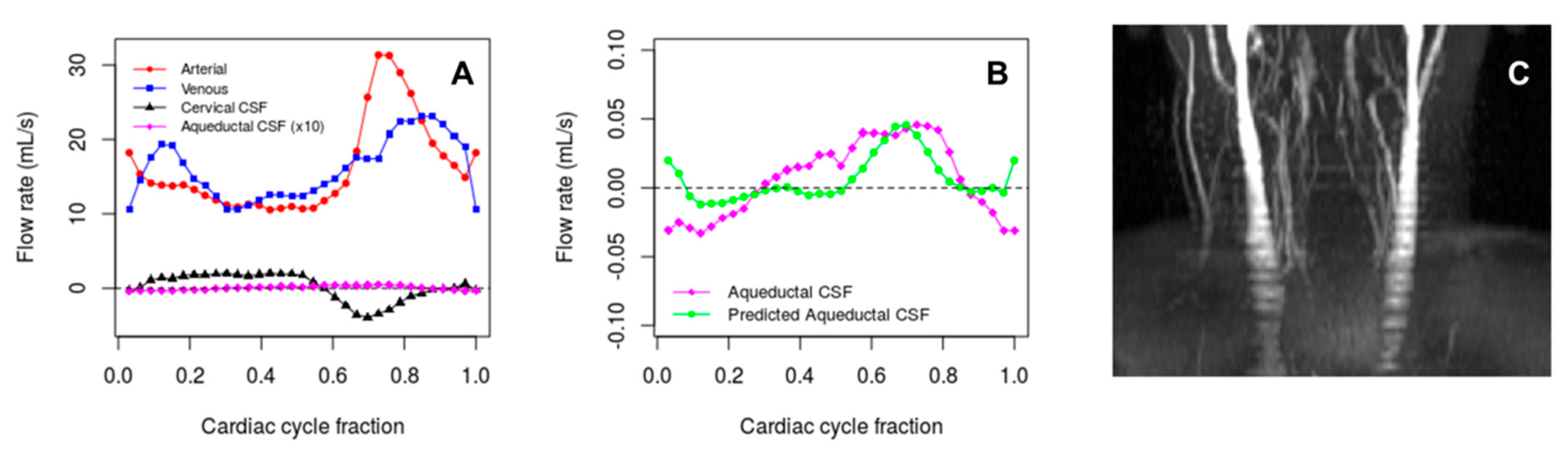
3.3. Data Analysis Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
References
- Zhu, D.C.; Xenos, M.; Linninger, A.A.; Penn, R.D. Dynamics of lateral ventricle and cerebrospinal fluid in normal and hydrocephalic brains. J. Magn. Reson. Med. 2006, 24, 756–770. [Google Scholar] [CrossRef] [PubMed]
- Hatt, A.; Cheng, S.; Tan, K.; Sinkus, R.; Bilston, L.E. MR Elastography Can Be Used to Measure Brain Stiffness Changes as a Result of Altered Cranial Venous Drainage During Jugular Compression. Am. J. Neuroradiol. 2015, 36, 1971–1977. [Google Scholar] [CrossRef] [PubMed]
- Zivadinov, R.; Magnano, C.; Galeotti, R.; Schirda, C.; Menegatti, E.; Weinstock-Guttman, B.; Marr, K.; Bartolomei, I.; Hagemeier, J.; Malagoni, A.M.; et al. Changes of cine cerebrospinal fluid dynamics in patients with multiple sclerosis treated with percutaneous transluminal angioplasty: A case-control study. J. Vasc. Interv. Radiol. 2013, 24, 829–838. [Google Scholar] [CrossRef] [PubMed]
- Magnano, C.; Schirda, C.; Weinstock-Guttman, B.; Wack, D.S.; Lindzen, E.; Hojnacki, D.; Bergsland, N.; Kennedy, C.; Belov, P.; Dwyer, M.G.; et al. Cine cerebrospinal fluid imaging in multiple sclerosis. J. Magn. Reson. Imaging 2012, 36, 825–834. [Google Scholar] [CrossRef] [PubMed]
- Zamboni, P.; Menegatti, E.; Weinstock-Guttman, B.; Schirda, C.; Cox, J.L.; Malagoni, A.M.; Hojnacki, D.; Kennedy, C.; Carl, E.; Dwyer, M.G.; et al. The severity of chronic cerebrospinal venous insufficiency in patients with multiple sclerosis is related to altered cerebrospinal fluid dynamics. Funct. Neurol. 2009, 24, 133–138. [Google Scholar]
- Gorucu, Y.; Albayram, S.; Balci, B.; Hasiloglu, Z.I.; Yenigul, K.; Yargic, F.; Keser, Z.; Kantarci, F.; Kiris, A. Cerebrospinal fluid flow dynamics in patients with multiple sclerosis: A phase contrast magnetic resonance study. Funct. Neurol. 2011, 26, 215–222. [Google Scholar]
- Oner, S.; Kahraman, A.S.; Ozcan, C.; Ozdemir, Z.M.; Unlu, S.; Kamisli, O.; Öner, Z. Cerebrospinal Fluid Dynamics in Patients with Multiple Sclerosis: The Role of Phase-Contrast MRI in the Differential Diagnosis of Active and Chronic Disease. Korean J. Radiol. 2018, 19, 72–78. [Google Scholar] [CrossRef] [PubMed]
- Luetmer, P.H.; Huston, J.; Friedman, J.A.; Dixon, G.R.; Petersen, R.C.; Jack, C.R.; McClelland, R.L.; Ebersold, M.J. Measurement of cerebrospinal fluid flow at the cerebral aqueduct by use of phase-contrast magnetic resonance imaging: Technique validation and utility in diagnosing idiopathic normal pressure hydrocephalus. Neurosurgery 2002, 50, 534–543. [Google Scholar]
- Gideon, P.; Stahlberg, F.; Thomsen, C.; Gjerris, F.; Sorensen, P.S.; Henriksen, O. Cerebrospinal fluid flow and production in patients with normal pressure hydrocephalus studied by MRI. Neuroradiology 1994, 36, 210–215. [Google Scholar] [CrossRef]
- Kim, D.S.; Choi, J.U.; Huh, R.; Yun, P.H.; Kim, D.I. Quantitative assessment of cerebrospinal fluid hydrodynamics using a phase-contrast cine MR image in hydrocephalus. Child’s Nerv. Syst. 1999, 15, 461–467. [Google Scholar] [CrossRef]
- Bradley, W.G.; Scalzo, D., Jr.; Queralt, J.; Nitz, W.N.; Atkinson, D.J.; Wong, P. Normal-pressure hydrocephalus: Evaluation with cerebrospinal fluid flow measurements at MR imaging. Radiology 1996, 198, 523–529. [Google Scholar] [CrossRef]
- Baledent, O.; Gondry-Jouet, C.; Meyer, M.E.; De Marco, G.; Le Gars, D.; Henry-Feugeas, M.C.; Idy-Peretti, I.M. Relationship between cerebrospinal fluid and blood dynamics in healthy volunteers and patients with communicating hydrocephalus. Investig. Radiol. 2004, 39, 45–55. [Google Scholar] [CrossRef]
- Hamilton, R.B.; Scalzo, F.; Baldwin, K.; Dorn, A.; Vespa, P.; Hu, X.; Bergsneider, M. Opposing CSF hydrodynamic trends found in the cerebral aqueduct and prepontine cistern following shunt treatment in patients with normal pressure hydrocephalus. Fluids Barriers CNS 2019, 16, 2. [Google Scholar] [CrossRef]
- Beggs, C.B.; Magnano, C.; Shepherd, S.J.; Belov, P.; Ramasamy, D.P.; Hagemeier, J.; Zivadinov, R. Dirty-Appearing White Matter in the Brain is Associated with Altered Cerebrospinal Fluid Pulsatility and Hypertension in Individuals without Neurologic Disease. J. Neuroimaging 2016, 26, 136–143. [Google Scholar] [CrossRef]
- Jolly, T.A.; Bateman, G.A.; Levi, C.R.; Parsons, M.W.; Michie, P.T.; Karayanidis, F. Early detection of microstructural white matter changes associated with arterial pulsatility. Front. Hum. Neurosci. 2013, 7, 782. [Google Scholar] [CrossRef]
- Beggs, C.B.; Magnano, C.; Shepherd, S.J.; Marr, K.; Valnarov, V.; Hojnacki, D.; Hojnacki, N.; Belov, P.; Grisafi, S.; Dwyer, M.G.; et al. Aqueductal cerebrospinal fluid pulsatility in healthy individuals is affected by impaired cerebral venous outflow. J. Magn. Reson. Imaging 2014, 40, 1215–1222. [Google Scholar] [CrossRef]
- Kitano, M.; Oldendorf, W.H.; Cassen, B. The Elasticity of the Cranial Blood Pool. J. Nucl. Med. 1964, 5, 613–625. [Google Scholar]
- Bilston, L.E. Brain tissue mechanical properties. In Biomechanics of the Brain; Miller, K., Ed.; Springer: New York, NY, USA, 2011; pp. 69–89. [Google Scholar]
- Ambarki, K.; Baledent, O.; Kongolo, G.; Bouzerar, R.; Fall, S.; Meyer, M.E. A new lumped-parameter model of cerebrospinal hydrodynamics during the cardiac cycle in healthy volunteers. IEEE Trans. Biomed. Eng. 2007, 54, 483–491. [Google Scholar] [CrossRef]
- Lagana, M.M.; Shepherd, S.J.; Cecconi, P.; Beggs, C.B. Intracranial volumetric changes govern cerebrospinal fluid flow in the Aqueduct of Sylvius in healthy adults. Biomed. Signal Process. Control 2017, 36, 84–92. [Google Scholar] [CrossRef]
- Alperin, N.J.; Lee, S.H.; Loth, F.; Raksin, P.B.; Lichtor, T. MR-Intracranial pressure (ICP): A method to measure intracranial elastance and pressure noninvasively by means of MR imaging: Baboon and human study. Radiology 2000, 217, 877–885. [Google Scholar] [CrossRef]
- Agarwal, N.; Contarino, C.; Limbucci, N.; Bertazzi, L.; Toro, E. Intracranial fluid dynamics changes in idiopathic intracranial hypertension: Pre and post therapy. Curr. Neurovasc. Res. 2018, 15, 164–172. [Google Scholar] [CrossRef]
- O’brien, J.T.; Paling, S.; Barber, R.; Williams, E.D.; Ballard, C.; McKeith, I.G.; Gholkar, A.; Crum, W.R.; Rossor, M.N.; Fox, N.C. Progressive brain atrophy on serial MRI in dementia with Lewy bodies, AD, and vascular dementia. Neurology 2001, 56, 1386–1388. [Google Scholar] [CrossRef]
- Vijayan, M.; Reddy, P.H. Stroke, vascular dementia, and Alzheimer’s disease: Molecular links. J. Alzheimer’s Dis. 2016, 54, 427–443. [Google Scholar] [CrossRef]
- Lagana, M.M.; Chaudhary, A.; Balagurunathan, D.; Utriainen, D.; Kokeny, P.; Feng, W.; Pietro, C.; David, H.; Haacke, M.E. Cerebrospinal fluid flow dynamics in multiple sclerosis patients through phase contrast magnetic resonance imaging. Curr. Neurovasc. Res. 2014, 11, 349–358. [Google Scholar] [CrossRef]
- Haacke, E.M.; Feng, W.; Utriainen, D.; Trifan, G.; Wu, Z.; Latif, Z.; Katkuri, Y.; Hewett, J.; Hubbard, D. Patients with multiple sclerosis with structural venous abnormalities on MR imaging exhibit an abnormal flow distribution of the internal jugular veins. J. Vasc. Interv. Radiol. 2012, 23, 60–68. [Google Scholar] [CrossRef]
- Bude, R.O.; Rubin, J.M. Relationship between the resistive index and vascular compliance and resistance. Radiology 1999, 211, 411–417. [Google Scholar] [CrossRef]
- Stoquart-ElSankari, S.; Baledent, O.; Gondry-Jouet, C.; Makki, M.; Godefroy, O.; Meyer, M.E. Aging effects on cerebral blood and cerebrospinal fluid flows. J. Cereb. Blood Flow Metab. 2007, 27, 1563–1572. [Google Scholar] [CrossRef]
- Bateman, G.A. Vascular compliance in normal pressure hydrocephalus. Am. J. Neuroradiol. 2000, 21, 1574–1585. [Google Scholar]
- Bateman, G.A.; Loiselle, A.M. Can MR measurement of intracranial hydrodynamics and compliance differentiate which patient with idiopathic normal pressure hydrocephalus will improve following shunt insertion? Acta Neurochir. 2007, 149, 455–462. [Google Scholar] [CrossRef]
- Johnson, J.W. A heuristic method for estimating the relative weight of predictor variables in multiple regression. Multivar. Behav. Res. 2000, 35, 1–19. [Google Scholar] [CrossRef]
- LeBreton, J.M.; Tonidandel, S. Multivariate relative importance: Extending relative weight analysis to multivariate criterion spaces. J. Appl. Psychol. 2008, 93, 329. [Google Scholar] [CrossRef]
- Holm, S. A simple sequentially rejective multiple test procedure. Scand. J. Stat. 1979, 6, 65–70. [Google Scholar]
- Tain, R.W.; Bagci, A.M.; Lam, B.L.; Sklar, E.M.; Ertl-Wagner, B.; Alperin, N. Determination of cranio-spinal canal compliance distribution by MRI: Methodology and early application in idiopathic intracranial hypertension. J. Magn. Reson. Imaging 2011, 34, 1397–1404. [Google Scholar] [CrossRef]
- Bateman, G.A. The reversibility of reduced cortical vein compliance in normal-pressure hydrocephalus following shunt insertion. Neuroradiology 2003, 45, 65–70. [Google Scholar] [CrossRef]
- Beggs, C.B. Cerebral venous outflow and cerebrospinal fluid dynamics. Veins Lymphat. 2014, 3, 1867. [Google Scholar] [CrossRef]
- Hakim, S.; Venegas, J.G.; Burton, J.D. The physics of the cranial cavity, hydrocephalus and normal pressure hydrocephalus: Mechanical interpretation and mathematical model. Surg. Neurol. 1976, 5, 187–210. [Google Scholar]
- El Sankari, S.; Czosnyka, M.; Lehmann, P.; Meyer, M.E.; Deramond, H.; Baledent, O. Cerebral Blood and CSF Flow Patterns in Patients Diagnosed for Cerebral Venous Thrombosis—An Observational Study. J. Clin. Imaging Sci. 2012, 2, 41. [Google Scholar] [CrossRef]
- Greitz, D.; Greitz, T. The pathogenesis and hemodynamics of hydrocephalus-Proposal for a new understanding. Int. J. Neuroradiol. 1997, 3, 367–375. [Google Scholar]
- Egnor, M.; Rosiello, A.; Zheng, L. A model of intracranial pulsations. Pediatr. Neurosurg. 2001, 35, 284–298. [Google Scholar] [CrossRef]
- Wagshul, M.E.; Eide, P.K.; Madsen, J.R. The pulsating brain: A review of experimental and clinical studies of intracranial pulsatility. Fluids Barriers CNS 2011, 8, 5. [Google Scholar] [CrossRef]
- Beggs, C.B. Venous hemodynamics in neurological disorders: An analytical review with hydrodynamic analysis. BMC Med. 2013, 11, 142. [Google Scholar] [CrossRef]
- Bateman, G.A.; Levi, C.R.; Schofield, P.; Wang, Y.; Lovett, E.C. The venous manifestations of pulse wave encephalopathy: Windkessel dysfunction in normal aging and senile dementia. Neuroradiology 2008, 50, 491–497. [Google Scholar] [CrossRef]
- Frydrychowski, A.F.; Winklewski, P.J.; Guminski, W. Influence of acute jugular vein compression on the cerebral blood flow velocity, pial artery pulsation and width of subarachnoid space in humans. PLoS ONE 2012, 7, e48245. [Google Scholar] [CrossRef] [PubMed]
- Shi, Y.; Thrippleton, M.J.; Marshall, I.; Wardlaw, J.M. Intracranial pulsatility in patients with cerebral small vessel disease: A systematic review. Clin. Sci. 2018, 132, 157–171. [Google Scholar] [CrossRef]
- Owler, B.K.; Pena, A.; Momjian, S.; Czosnyka, Z.; Czosnyka, M.; Harris, N.G.; Smielewski, P.; Fryer, T.; Donvan, T.; Carpenter, A.; et al. Changes in cerebral blood flow during cerebrospinal fluid pressure manipulation in patients with normal pressure hydrocephalus: A methodological study. J. Cereb. Blood Flow Metab. 2004, 24, 579–587. [Google Scholar] [CrossRef] [PubMed]
- Del Bigio, M.R. The ependyma: A protective barrier between brain and cerebrospinal fluid. Glia 1995, 14, 1–13. [Google Scholar] [CrossRef]
- Tullberg, M.; Jensen, C.; Ekholm, S.; Wikkelsø, C. Normal pressure hydrocephalus: Vascular white matter changes on MR images must not exclude patients from shunt surgery. Am. J. Neuroradiol. 2001, 22, 1665–1673. [Google Scholar]
- Moore, E.H. On the reciprocal of the general algebraic matrix, abstract. Bull. Am. Math. Soc. 1920, 26, 394–395. [Google Scholar]
| Subject | Age (Yrs) | Sex |
|---|---|---|
| 5002 | 31 | Female |
| 5004 | 28 | Female |
| 5005 | 38 | Male |
| 5006 | 32 | Male |
| 5007 | 37 | Female |
| 5010 | 36 | Male |
| 5011 | 30 | Female |
| 5012 | 60 | Female |
| 5015 | 22 | Female |
| 5016 | 28 | Female |
| 5031 | 21 | Female |
| 5033 | 45 | Male |
| 5035 | 23 | Female |
| Mean | 33.15 | na |
| SD | 10.61 | na |
| Signal | Mean Flow Rate (mL/s) Mean (SD) | Median Flow Rate (mL/s) Mean (SD) | Caudal Peak (mL/s) Mean (SD) | Cranial Peak (mL/s) Mean (SD) | Pulsatility Index Mean (SD) |
|---|---|---|---|---|---|
| Arterial flow rate | 12.34 (2.06) | 11.31 (2.01) | 8.36 (1.55) | 19.58 (4.51) | 0.91 (0.22) |
| Venous flow rate | −12.33 (2.02) | −12.26 (1.98) | −15.71 (2.86) | −8.89 (2.25) | 0.56 (0.23) |
| cCSF flow rate | 0.08 (0.10) | 0.59 (0.45) | −2.70 (1.05) | 1.72 (0.58) | 3.85 (129.86) |
| aCSF flow rate | 0.00 (>0.01) | 0.00 (0.01) | −0.10 (0.06) | 0.09 (0.05) | 31.28 (86.47) |
| Arterial Flow Rate Mean r Value (SD) | Venous Flow Rate Mean r Value (SD) | cCSF Flow Rate Mean r Value (SD) | aCSF Flow Rate Mean r Value (SD) | |
|---|---|---|---|---|
| Arterial flow rate | - | - | - | - |
| Venous flow rate | -0.601 (0.293) | - | - | - |
| cCSF flow rate | -0.837 (0.126) | 0.621 (0.178) | - | - |
| aCSF flow rate | -0.450 (0.406) | 0.763 (0.266) | 0.539 (0.384) | - |
| Arterial | Venous | cCSF | Model | Model | Model | Arterial | Venous | cCSF | ||
|---|---|---|---|---|---|---|---|---|---|---|
| Subject | Intercept | Coef. | Coef. | Coef. | p-value | MSE (mL/s)2 | Adj. r2 | RIW | RIW | RIW |
| 5002 | 0.1941 * | 0.0444 | 0.0596 | 0.0805 | <0.001 | 0.002 | 0.787 | 21.905 | 45.036 | 33.059 |
| 5004 | 0.2413 | −0.0006 * | 0.0204 | −0.0169 * | <0.001 | 0.002 | 0.656 | 31.312 | 57.687 | 11.001 |
| 5005 | 0.1716 | 0.0039 | 0.0179 | 0.0206 | <0.001 | <0.001 | 0.884 | 11.208 | 72.520 | 16.272 |
| 5006 | 0.5092 | −0.0150 | 0.0287 | −0.0178 | <0.001 | <0.001 | 0.894 | 33.611 | 51.167 | 15.221 |
| 5007 | 0.1438 * | 0.0090 * | 0.0247 | 0.0200 * | <0.001 | <0.001 | 0.876 | 6.841 | 84.902 | 8.257 |
| 5010 | −0.0944 * | 0.0150 | 0.0078 * | 0.0455 | <0.001 | 0.006 | 0.587 | 10.934 | 25.313 | 63.753 |
| 5011 | 0.1659 | 0.0050 | 0.0191 | −0.0031 * | <0.001 | <0.001 | 0.856 | 7.072 | 80.327 | 12.601 |
| 5012 | 0.2371 | −0.0129 | 0.0069 | −0.0272 | <0.001 | <0.001 | 0.847 | 39.786 | 44.572 | 15.642 |
| 5015 | 0.0868 | 0.0036 | 0.0094 | 0.0074 | <0.001 | <0.001 | 0.884 | 10.902 | 48.329 | 40.770 |
| 5016 | 0.4050 | −0.0034 * | 0.0340 | 0.0458 * | <0.001 | 0.001 | 0.947 | 21.941 | 43.624 | 34.435 |
| 5031 | 0.0436 * | −0.0004 * | 0.0018 * | −0.0111 | 0.004 | <0.001 | 0.295 | 21.353 | 8.460 | 70.187 |
| 5033 | 0.3757 | 0.0024 * | 0.0399 | 0.0353 | <0.001 | <0.001 | 0.956 | 24.352 | 50.036 | 25.612 |
| 5035 | −0.0446 * | 0.0065 | 0.0037 * | 0.0433 | <0.001 | <0.001 | 0.857 | 28.156 | 23.539 | 48.304 |
| Mean | 0.1873 | 0.0044 | 0.0211 | 0.0171 | <0.001 | 0.002 | 0.794 | 20.721 | 48.886 | 30.393 |
| Median | 0.1716 | 0.0036 | 0.0191 | 0.0200 | <0.001 | 0.001 | 0.857 | 21.905 | 48.329 | 25.612 |
| SD | 0.1728 | 0.0145 | 0.0165 | 0.0320 | <0.001 | 0.001 | 0.184 | 22.027 | 20.415 | 10.705 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Beggs, C.B.; Shepherd, S.J.; Cecconi, P.; Lagana, M.M. Predicting the Aqueductal Cerebrospinal Fluid Pulse: A Statistical Approach. Appl. Sci. 2019, 9, 2131. https://doi.org/10.3390/app9102131
Beggs CB, Shepherd SJ, Cecconi P, Lagana MM. Predicting the Aqueductal Cerebrospinal Fluid Pulse: A Statistical Approach. Applied Sciences. 2019; 9(10):2131. https://doi.org/10.3390/app9102131
Chicago/Turabian StyleBeggs, Clive B, Simon J Shepherd, Pietro Cecconi, and Maria Marcella Lagana. 2019. "Predicting the Aqueductal Cerebrospinal Fluid Pulse: A Statistical Approach" Applied Sciences 9, no. 10: 2131. https://doi.org/10.3390/app9102131
APA StyleBeggs, C. B., Shepherd, S. J., Cecconi, P., & Lagana, M. M. (2019). Predicting the Aqueductal Cerebrospinal Fluid Pulse: A Statistical Approach. Applied Sciences, 9(10), 2131. https://doi.org/10.3390/app9102131






