Modelling of Ion Transport in Electromembrane Systems: Impacts of Membrane Bulk and Surface Heterogeneity
Abstract
1. Introduction: Heterogeneity and Multiscale Nature of Ion Transport in Membrane Systems
2. Structure of Ion-Exchange Membranes
3. Irreversible Thermodynamics Approach
3.1. The Onsager Phenomenological Equations
3.2. The Kedem-Katchalsky Equations
3.3. The Nernst-Planck Equation
4. Modelling the Structure-Property Relationships
4.1. “Solution-Diffusion” Models
4.1.1. Teorell-Meyer-Sievers (TMS) Model
4.1.2. Multiphase Models
4.2. Modelling of Properties of Ion-Exchange (IEMs) Containing Nanoparticles
4.3. “Pore-flow” Models
5. Concentration Polarization in Electrodialysis (ED)
5.1. Current-Induced Concentration Gradients
5.2. 2D Modelling of Electrodialysis with Homogeneous Membranes
5.2.1. Governing Equations and General Boundary Conditions
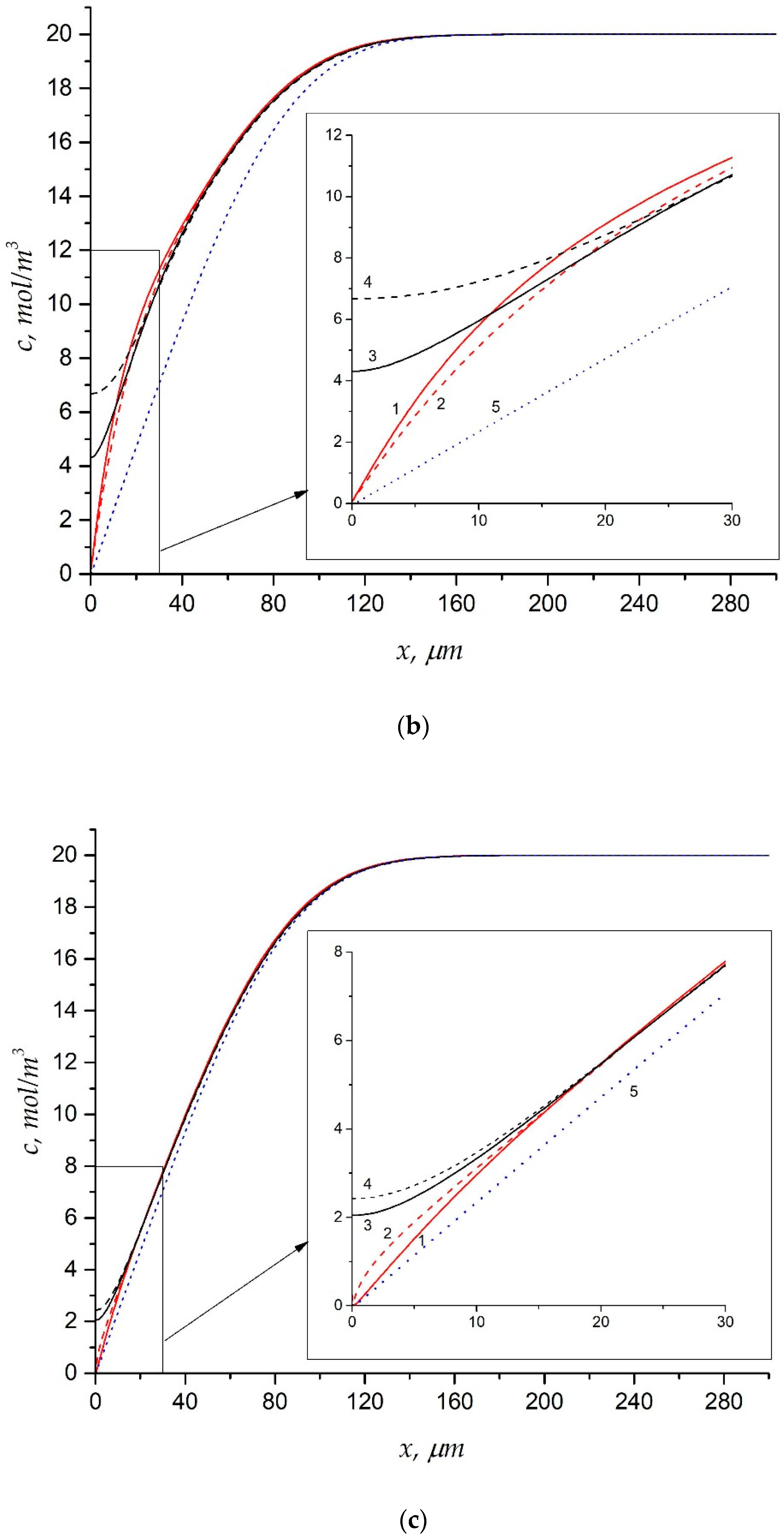
5.2.2. Concentration Distribution and Diffusion Layer Thickness
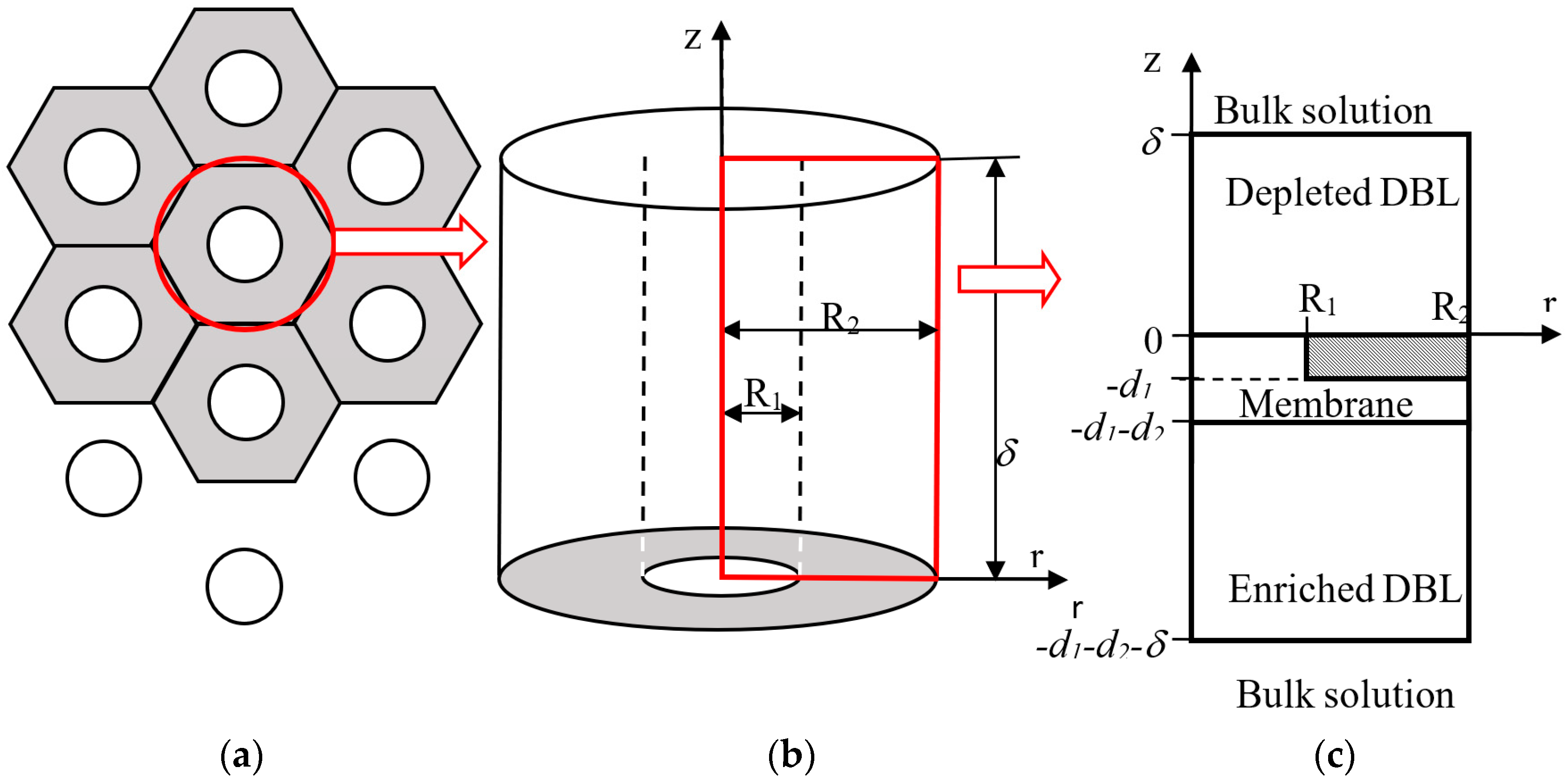
5.3. ED with Heterogeneous Membranes
Effect of Electrical Surface Heterogeneity on the Limiting Current Density and Diffusion Layer Thickness
6. Effect of Surface Heterogeneity on the Transient Behaviour of IEMs
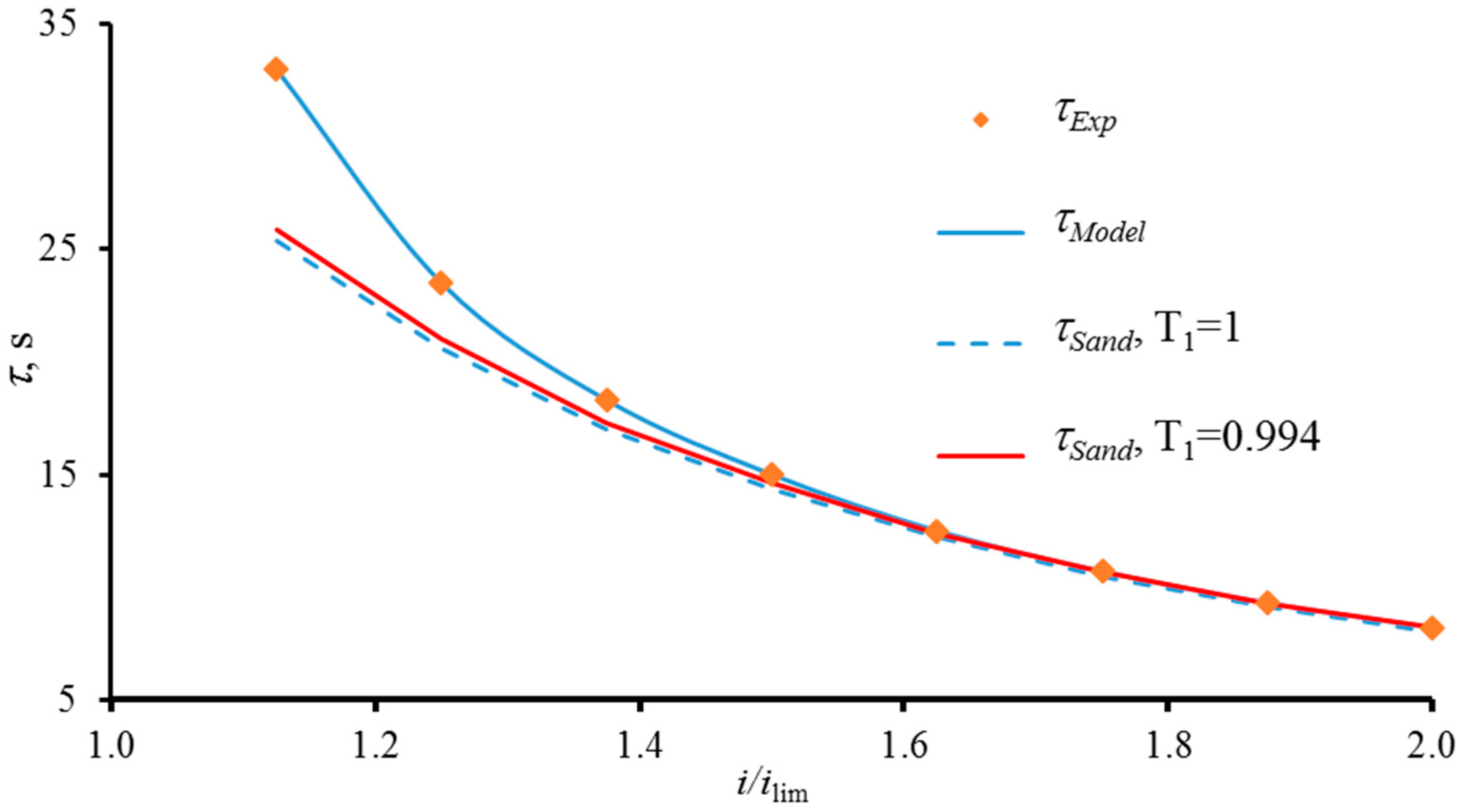
6.1. Modelling of Chronopotentiograms for Homogeneous Membranes. Effect of Finite-Length Diffusion Layer
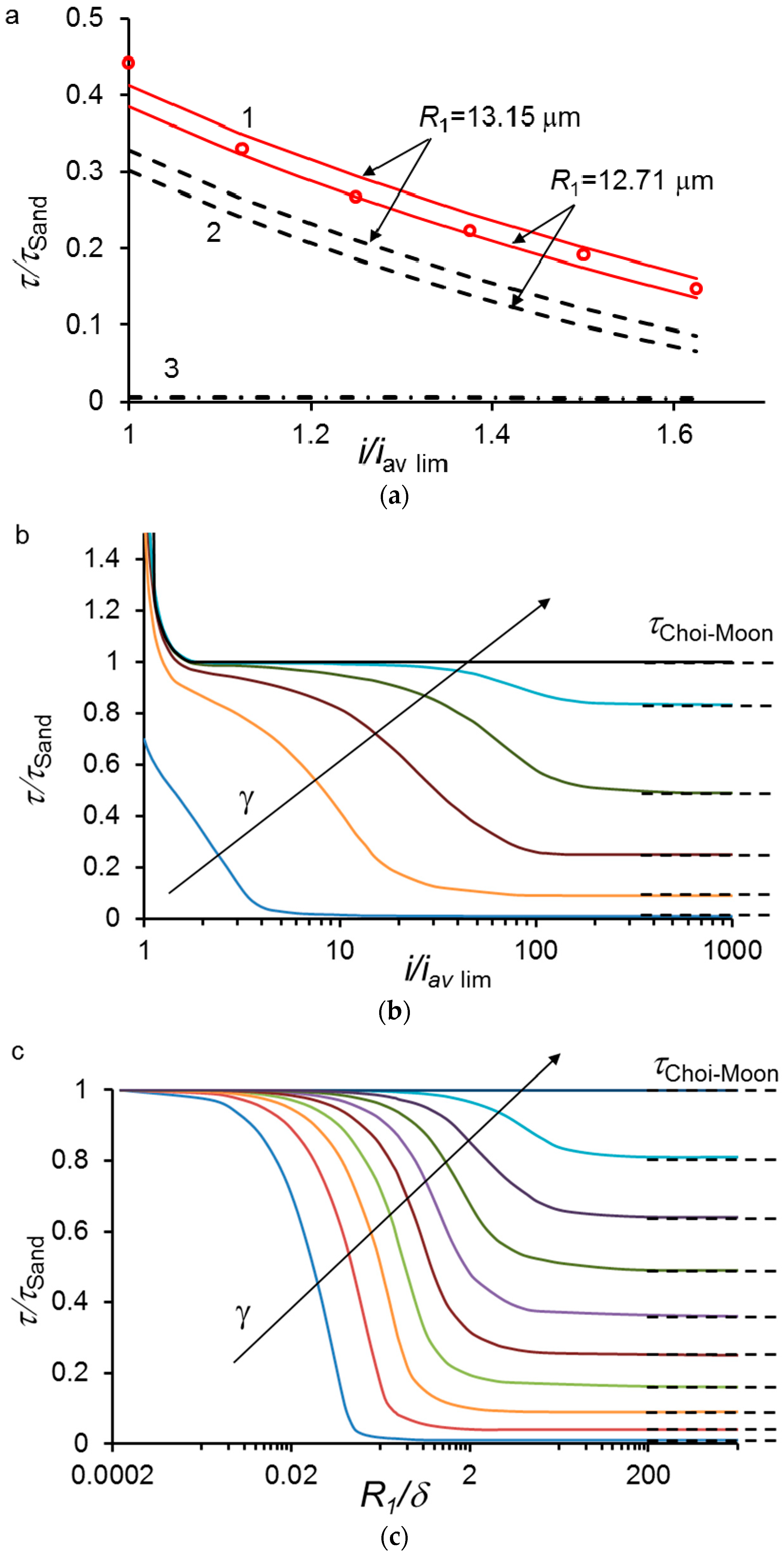
6.2. Impact of Surface Heterogeneity on the Transition Time of IEM
The Use of Electric Current Stream Function. Comparison with the Sand and Choi and Moon Theories
6.3. Phenomenon of Two Transition Times of Chronopotentiograms for Membranes with Heterogeneous Surface
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
List of Symbols
| Abbreviations | |
| AEM | anion-exchange membrane |
| CEM | cation-exchange membrane |
| DBL | diffusion boundary layer |
| DC | desalting compartment |
| DVB | divinylbenzene |
| ED | electrodialysis |
| EDL | electrical double layer |
| IEM | ion-exchange membrane |
| IEC | ion-exchange capacity |
| LEN | local electroneutrality (assumption) |
| NF | nanofiltration |
| PD | potential difference |
| PVC | polyvinylchloride |
| RO | reverse osmosis |
| TMS | (model of) Teorell-Meyer-Sievers |
| Symbols | |
| , | ion and electrolyte molar activity, respectively |
| , | electrolyte activities in the left- and right-hand side bathing solutions |
| b | the distance between two neighbouring fixed ions |
| ci | molar concentration of ion i |
| cs | molar concentration of salt |
| c | electrolyte concentration in the virtual solution |
| , | concentration of electrolyte, counterion in the solution bulk, respectively |
| d | membrane thickness |
| D | diffusion coefficient of electrolyte |
| Di | diffusion coefficient of ion i |
| E | potential difference |
| E | electric field strength |
| Emax | theoretical value of E for an ideal membrane not permeable for co-ions |
| fi | volume fraction of the gel (1) and intergel solution (2) phase |
| volume fraction of the nanoparticle’s EDL | |
| F | Faraday constant |
| Fj | thermodynamic force of j kind |
| i | current density |
| ilim | limiting current density |
| g | activity factor |
| h | intermembrane distance |
| ji | flux density of ion “i” |
| Ji | flux density of ion “i” |
| Jv | volume flux density |
| K | equilibrium constant |
| KD | Donnan equilibrium coefficient |
| KS | electrolyte partition coefficient |
| LD | thickness of the diffuse part of the EDL |
| Lp | hydraulic permeability coefficient |
| Lij | phenomenological conductance coefficient |
| m | virtual solution molality |
| Mw | water molar mass |
| n | number of molecules per fixed group |
| p | hydrostatic pressure |
| P | diffusion permeability |
| Pint | integral (or global) permeability |
| Q | ion-exchange capacity |
| r | pore radius |
| R | universal gas constant |
| Ra, Rc, Rcc | resistances of the AEM, CEM and the concentration compartment |
| R1 | radius of conductive area |
| Re | Reynolds number |
| Sh | Sherwood number |
| Sc | Schmidt number |
| t | time |
| t+app | apparent transport number of counter-ion |
| ti | transport number of ion “i” in solution or membrane |
| tw | water transport number |
| T | temperature |
| Ti | effective transport number of ion “i” in the membrane |
| V | velocity |
| average flow velocity | |
| flow velocity | |
| partial molar volume of species | |
| partial molar volume of an electrolyte | |
| partial molar volume of water | |
| x | normal to membrane coordinate |
| y | longitudinal coordinate |
| mean molar activity coefficient | |
| Y | dimensionless distances from the channel entrance |
| zi | charge number of ion i |
| Greek Symbols | |
| α | structural parameter |
| β | electro-osmotic permeability |
| β | structural parameter (similar to) |
| δ | Nernst’s diffusion layer thickness |
| (Donnan) electric potential difference between two phases | |
| γ | surface fraction of membrane conductive area |
| η | electric current scream function |
| ε, ε0 | relative dielectric permittivity, vacuum dielectric permittivity |
| ξ | parameter related to the linear charge density of the polyelectrolyte chain |
| κ | electric conductivity, S m−1 |
| λ | Debye length |
| λB | Bjerrum length |
| μl | electrochemical potential |
| ν | stoichiometric parameter |
| ν | kinematic viscosity |
| π | osmotic pressure |
| σ | Staverman’s reflection coefficient |
| τ | transition time |
| ϕ | electric potential |
| Indices | |
| over-bar means that the parameter refers to the membrane (gel) medium | |
| a | anion-exchange membrane |
| A | co-ion |
| c | cation-exchange membrane |
| cc | concentration compartment |
| D | Donnan |
| g | gel phase |
| i | ionic species |
| iso | isoconductance point |
| k | left-hand (I) and right-hand (II) interface |
| Lev | Leveque |
| lim | limiting |
| limloc | limiting local |
| limav | limiting average |
| m, mb | membrane |
| ms | membrane and bulk solution |
| N loc | Nernst local |
| N av | Nernst average |
| p | particle |
| pin | particle intergel |
| s | interstitial solution |
| sin | solution intergel |
| w | water |
| 1 | counterion |
| + | cations |
| − | anions |
References
- Ozin, G.A.; Arsenault, A.C. Nanochemistry: A Chemical Approach to Nanomaterials. In Nanochemistry: A Chemical Approach to Nanomaterials; Royal Society of Chemistry: London, UK, 2005; p. 876. ISBN 085404664X. [Google Scholar]
- Van Rijn, P.; Tutus, M.; Kathrein, C.; Zhu, L.; Wessling, M.; Schwaneberg, U.; Böker, A. Challenges and advances in the field of self-assembled membranes. Chem. Soc. Rev. 2013, 42, 6578–6592. [Google Scholar] [CrossRef] [PubMed]
- Timashev, S.F. Physical Chemistry of Membrane Processes; Ellis Horwood Ltd.: New York, NY, USA, 1991; ISBN 9780136629825. [Google Scholar]
- Nikonenko, V.V.; Yaroslavtsev, A.B.; Pourcelly, G. Ion Transfer in and Through Charged Membranes: Structure, Properties, and Theory. In Ionic Interactions in Natural and Synthetic Macromolecules; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2012; pp. 267–335. ISBN 9780470529270. [Google Scholar]
- Kreuer, K.D.; Paddison, S.J.; Spohr, E.; Schuster, M. Transport in proton conductors for fuel-cell applications: Simulations, elementary reactions, and phenomenology. Chem. Rev. 2004, 104, 4637–4678. [Google Scholar] [CrossRef] [PubMed]
- Strathmann, H. Ion-Exchange Membrane Separation Processes, 1st ed.; Elsevier: Amsterdam, The Netherlands, 2004; ISBN 9780444502360. [Google Scholar]
- Xu, T. Ion exchange membranes: State of their development and perspective. J. Membr. Sci. 2005, 263, 1–29. [Google Scholar] [CrossRef]
- Nagarale, R.K.; Gohil, G.S.; Shahi, V.K. Recent developments on ion-exchange membranes and electro-membrane processes. Adv. Colloid Interface Sci. 2006, 119, 97–130. [Google Scholar] [CrossRef] [PubMed]
- Mizutani, Y. Review Structure of ion Exchange Membranes. J. Membr. Sci. 1990, 49, 121–144. [Google Scholar] [CrossRef]
- Pismenskaya, N.D.; Nikonenko, V.V.; Melnik, N.A.; Shevtsova, K.A.; Belova, E.I.; Pourcelly, G.; Cot, D.; Dammak, L.; Larchet, C. Evolution with time of hydrophobicity and microrelief of a cation-exchange membrane surface and its impact on overlimiting mass transfer. J. Phys. Chem. B 2012, 116, 2145–2161. [Google Scholar] [CrossRef]
- Mareev, S.A.; Butylskii, D.Y.; Pismenskaya, N.D.; Larchet, C.; Dammak, L.; Nikonenko, V.V. Geometric heterogeneity of homogeneous ion-exchange Neosepta membranes. J. Membr. Sci. 2018, 563, 768–776. [Google Scholar] [CrossRef]
- Pismenskaia, N.; Sistat, P.; Huguet, P.; Nikonenko, V.; Pourcelly, G. Chronopotentiometry applied to the study of ion transfer through anion exchange membranes. J. Membr. Sci. 2004, 228, 65–76. [Google Scholar] [CrossRef]
- Svoboda, M.; Beneš, J.; Vobecká, L.; Slouka, Z. Swelling induced structural changes of a heterogeneous cation-exchange membrane analyzed by micro-computed tomography. J. Membr. Sci. 2017, 525, 195–201. [Google Scholar] [CrossRef]
- Vobecká, L.; Svoboda, M.; Beneš, J.; Belloň, T.T.; Slouka, Z.; Vobeckà, L.; Svoboda, M.; Beneš, J.; Belloň, T.T.; Slouka, Z.; et al. Heterogeneity of heterogeneous ion-exchange membranes investigated by chronopotentiometry and X-ray computed microtomography. J. Membr. Sci. 2018, 559, 127–137. [Google Scholar] [CrossRef]
- Volodina, E.; Pismenskaya, N.; Nikonenko, V.; Larchet, C.; Pourcelly, G. Ion transfer across ion-exchange membranes with homogeneous and heterogeneous surfaces. J. Colloid Interface Sci. 2005, 285, 247–258. [Google Scholar] [CrossRef] [PubMed]
- Vasil’eva, V.I.; Kranina, N.A.; Malykhin, M.D.; Akberova, E.M.; Zhiltsova, A.V. The surface inhomogeneity of ion-exchange membranes by SEM and AFM data. J. Surf. Investig. X-ray Synchrotron Neutron Tech. 2013, 7, 144–153. [Google Scholar] [CrossRef]
- Pourcelly, G. Electrodialysis: Ion Exchange. Encycl. Sep. Sci. 2000, 2665–2675. [Google Scholar] [CrossRef]
- Wódzki, R. ION EXCHANGE|Organic Membranes. Encycl. Sep. Sci. 2000, 1632–1639. [Google Scholar] [CrossRef]
- Wang, W.; Fu, R.; Liu, Z.; Wang, H. Low-resistance anti-fouling ion exchange membranes fouled by organic foulants in electrodialysis. Desalination 2017, 417, 1–8. [Google Scholar] [CrossRef]
- Sata, T. Studies on ion exchange membranes with permselectivity for specific ions in electrodialysis. J. Membr. Sci. 1994, 93, 117–135. [Google Scholar] [CrossRef]
- Saracco, G. Transport properties of monovalent-ion-permselective membranes. Chem. Eng. Sci. 1997, 52, 3019–3031. [Google Scholar] [CrossRef]
- Zhao, Y.; Tang, K.; Liu, H.; Van der Bruggen, B.; Sotto Díaz, A.; Shen, J.; Gao, C. An anion exchange membrane modified by alternate electro-deposition layers with enhanced monovalent selectivity. J. Membr. Sci. 2016, 520, 262–271. [Google Scholar] [CrossRef]
- Khan, M.I.; Zheng, C.; Mondal, A.N.; Hossain, M.M.; Wu, B.; Emmanuel, K.; Wu, L.; Xu, T. Preparation of anion exchange membranes from BPPO and dimethylethanolamine for electrodialysis. Desalination 2017, 402, 10–18. [Google Scholar] [CrossRef]
- Simons, R. Electric field effects on proton transfer between ionizable groups and water in ion exchange membranes. Electrochim. Acta 1984, 29, 151–158. [Google Scholar] [CrossRef]
- Simons, R. A mechanism for water flow in bipolar membranes. J. Membr. Sci. 1993, 82, 65–73. [Google Scholar] [CrossRef]
- Zabolotskii, V.I.; Shel ’deshov, N.V.; Gnusin, N.P. Dissociation of Water Molecules in Systems with Ion-exchange Membranes. Russ. Chem. Rev. 1988, 5713, 801–808. [Google Scholar] [CrossRef]
- Strathmann, H.; Krol, J.J.; Rapp, H.J.; Eigenberger, G. Limiting current density and water dissociation in bipolar membranes. J. Membr. Sci. 1997, 125, 123–142. [Google Scholar] [CrossRef]
- Scott, K. Sustainable and Green Electrochemical Science and Technology; John Wiley & Sons, Ltd.: Chichester, UK, 2017; ISBN 9781118698075. [Google Scholar]
- Mauritz, K.A.; Moore, R.B. State of understanding of Nafion. Chem. Rev. 2004, 104, 4535–4585. [Google Scholar] [CrossRef]
- Gebel, G. Structural evolution of water swollen perfluorosulfonated ionomers from dry membrane to solution. Polymer 2000, 41, 5829–5838. [Google Scholar] [CrossRef]
- Helfferich, F.G. Ion Exchange; Dover Publications: Mineola, NY, USA, 1995; ISBN 0486687848. [Google Scholar]
- Drozdov, A.D.; deClaville Christiansen, J. The effects of pH and ionic strength on equilibrium swelling of polyampholyte gels. Int. J. Solids Struct. 2017, 110–111, 192–208. [Google Scholar] [CrossRef]
- Kozmai, A.E.; Nikonenko, V.V.; Zyryanova, S.; Pismenskaya, N.D.; Dammak, L. A simple model for the response of an anion-exchange membrane to variation in concentration and pH of bathing solution. J. Membr. Sci. 2018, 567, 127–138. [Google Scholar] [CrossRef]
- Gierke, T.D.; Munn, G.E.; Wilson, F.C. The morphology in nafion perfluorinated membrane products, as determined by wide- and small-angle x-ray studies. J. Polym. Sci. Polym. Phys. 1981, 19, 1687–1704. [Google Scholar] [CrossRef]
- Rubatat, L.; Rollet, A.L.; Gebel, G.; Diat, O. Evidence of elongated polymeric aggregates in Nafion. Macromolecules 2002, 35, 4050–4055. [Google Scholar] [CrossRef]
- Kreuer, K.D. On the development of proton conducting polymer membranes for hydrogen and methanol fuel cells. J. Membr. Sci. 2001, 185, 29–39. [Google Scholar] [CrossRef]
- Berezina, N.P.; Kononenko, N.A.; Dyomina, O.A.; Gnusin, N.P. Characterization of ion-exchange membrane materials: Properties vs structure. Adv. Colloid Interface Sci. 2008, 139, 3–28. [Google Scholar] [CrossRef] [PubMed]
- Kononenko, N.A.; Fomenko, M.A.; Volfkovich, Y.M. Structure of perfluorinated membranes investigated by method of standard contact porosimetry. Adv. Colloid Interface Sci. 2015, 222, 425–435. [Google Scholar] [CrossRef] [PubMed]
- Kononenko, N.; Nikonenko, V.; Grande, D.; Larchet, C.; Dammak, L.; Fomenko, M.; Volfkovich, Y. Porous structure of ion exchange membranes investigated by various techniques. Adv. Colloid Interface Sci. 2017, 246, 196–216. [Google Scholar] [CrossRef] [PubMed]
- Divisek, J.; Eikerling, M.; Mazin, V.; Schmitz, H.; Stimming, U.; Volfkovich, Y.M. A Study of Capillary Porous Structure and Sorption Properties of Nafion Proton-Exchange Membranes Swollen in Water. J. Electrochem. Soc. 1998, 145, 2677. [Google Scholar] [CrossRef]
- Bryk, M.T.; Zabolotskii, V.I.; Atamanenko, I.D.; Dvorkina, G.A. Structural inhomogeneity of ion-exchange membranes in swelling state andmethods of its investigations. Sov. J. Water Chem. Technol. 1989, 11, 14. [Google Scholar]
- Berezina, N.P.; Shkirskaya, S.A.; Kolechko, M.V.; Popova, O.V.; Senchikhin, I.N.; Roldugin, V.I. Barrier effects of polyaniline layer in surface modified MF-4SK/Polyaniline membranes. Russ. J. Electrochem. 2011, 47, 995–1005. [Google Scholar] [CrossRef]
- Haubold, H.G.; Vad, T.; Jungbluth, H.; Hiller, P. Nano structure of NAFION: A SAXS study. Electrochim. Acta 2001, 46, 1559–1563. [Google Scholar] [CrossRef]
- Kornyshev, A.A.; Kuznetsov, A.M.; Spohr, E.; Ulstrup, J. Kinetics of proton transport in water. J. Phys. Chem. B 2003, 107, 3351–3366. [Google Scholar] [CrossRef]
- Paddison, S.J. Proton Conduction Mechanisms at Low Degrees of Hydration in Sulfonic Acid–Based Polymer Electrolyte Membranes. Annu. Rev. Mater. Res. 2003, 33, 289–319. [Google Scholar] [CrossRef]
- Larchet, C.; Nouri, S.; Auclair, B.; Dammak, L.; Nikonenko, V. Application of chronopotentiometry to determine the thickness of diffusion layer adjacent to an ion-exchange membrane under natural convection. Adv. Colloid Interface Sci. 2008, 139, 45–61. [Google Scholar] [CrossRef]
- Kamcev, J.; Paul, D.R.; Freeman, B.D. Ion activity coefficients in ion exchange polymers: Applicability of Manning’s counterion condensation theory. Macromolecules 2015, 48, 8011–8024. [Google Scholar] [CrossRef]
- Kamcev, J.; Galizia, M.; Benedetti, F.M.; Jang, E.S.; Paul, D.R.; Freeman, B.D.; Manning, G.S. Partitioning of mobile ions between ion exchange polymers and aqueous salt solutions: Importance of counter-ion condensation. Phys. Chem. Chem. Phys. 2016, 18, 6021–6031. [Google Scholar] [CrossRef]
- Kamcev, J.; Paul, D.R.; Freeman, B.D. Effect of fixed charge group concentration on equilibrium ion sorption in ion exchange membranes. J. Mater. Chem. A 2017, 5, 4638–4650. [Google Scholar] [CrossRef]
- Mumford, D. Selected Papers, 1st ed.; Springer: New York, NY, USA; Copenhagen, Denmark, 2004; ISBN 978-1-4419-1936-6. [Google Scholar]
- Manning, G.S. Limiting Laws and Counterion Condensation in Polyelectrolyte Solutions I. Colligative Properties. J. Chem. Phys. 1969, 51, 924–933. [Google Scholar] [CrossRef]
- Manning, G.S. The molecular theory of polyelectrolyte solutions with applications to the electrostatic properties of polynucleotides. Q. Rev. Biophys. 1978, 11, 179. [Google Scholar] [CrossRef] [PubMed]
- Muthukumar, M. Polymer Translocation, 1st ed.; CRC Press: Boca Raton, FL, USA, 2011; ISBN 9781420075175. [Google Scholar]
- Zabolotskii, V.V.; Nikonenko, V.V. Ion Transport in Membranes (in Russian); Nauka: Moscow, Russia, 1996; ISBN 5-02-001677-2. [Google Scholar]
- Lakshminarayanaiah, N. Transport Phenomena in Membranes; Acad. Press: New York, NY, USA, 1969; ISBN 9780124342507. [Google Scholar]
- Kontturi, K.; Murtomäki, L.; Manzanares, J.A. Ionic Transport Processes: In Electrochemistry and Membrane Science; Oxford University Press: Oxford, UK, 2008; ISBN 9780198719991. [Google Scholar]
- Tanaka, Y. Ion Exchange Membranes, Volume 12 2nd Edition. In Fundamentals and Applications; Elsevier Science: Amsterdam, The Netherlands, 2015; p. 522. ISBN 9780444633194. [Google Scholar]
- Yaroslavtsev, A.B.; Nikonenko, V.V.; Zabolotsky, V.I. Ion transfer in ion-exchange and membrane materials. Russ. Chem. Rev. 2003, 72, 393–421. [Google Scholar] [CrossRef]
- Weber, A.Z.; Newman, J. A combination model for macroscopic transport in polymer-electrolyte membranes. Top. Appl. Phys. 2009, 113, 157–198. [Google Scholar]
- Wang, C.Y. Fundamental models for fuel cell engineering. Chem. Rev. 2004, 104, 4727–4765. [Google Scholar] [CrossRef]
- Kondepudi, D.; Prigogine, I. Modern Thermodynamics: From Heat Engines to Dissipative Structures, 2nd ed.; John Wiley: Hoboken, NJ, USA, 2014; Volume 9781118371, ISBN 9781118698723. [Google Scholar]
- Spiegler, K.S. Transport processes in ionic membranes. Trans. Faraday Soc. 1958, 54, 1408–1428. [Google Scholar] [CrossRef]
- Zabolotsky, V.I.; Nikonenko, V.V. Effect of structural membrane inhomogeneity on transport properties. J. Membr. Sci. 1993, 79, 181–198. [Google Scholar] [CrossRef]
- Kedem, O.; Katchalsky, A. A physical interpretation of the phenomenological coefficients of membrane permeability. J. Gen. Physiol. 1961, 45, 143–179. [Google Scholar] [CrossRef] [PubMed]
- Narȩbska, A.; Koter, S.; Kujawski, W. Ions and water transport across charged nafion membranes. Irreversible thermodynamics approach. Desalination 1984, 51, 3–17. [Google Scholar] [CrossRef]
- Spiegler, K.S.; Kedem, O. Thermodynamics of hyperfiltration (reverse osmosis): Criteria for efficient membranes. Desalination 1966, 1, 311–326. [Google Scholar] [CrossRef]
- Auclair, B.; Nikonenko, V.; Larchet, C.; Métayer, M.; Dammak, L. Correlation between transport parameters of ion-exchange membranes. J. Membr. Sci. 2001, 195, 89–102. [Google Scholar] [CrossRef]
- Kedem, O.; Katchalsky, A. Permeability of composite membranes Part 1—Electric current, volume flow and flow of solute through membranes. Trans. Faraday Soc. 1963, 59, 1918–1930. [Google Scholar] [CrossRef]
- Meares, P. Coupling of ion and water fluxes in synthetic membranes. J. Membr. Sci. 1981, 8, 295–307. [Google Scholar] [CrossRef]
- Mason, E.A.; Lonsdale, H.K. Statistical-mechanical theory of membrane transport. J. Membr. Sci. 1990, 51, 1–81. [Google Scholar] [CrossRef]
- Koter, S.; Kujawski, W.; Koter, I. Importance of the cross-effects in the transport through ion-exchange membranes. J. Membr. Sci. 2007, 297, 226–235. [Google Scholar] [CrossRef]
- Kedem, O.; Perry, M. A simple procedure for estimating ion coupling from conventional transport coefficients. J. Membr. Sci. 1983, 14, 249–262. [Google Scholar] [CrossRef]
- Narȩbska, A.; Koter, S. Permselectivity of ion-exchange membranes in operating systems. Irreversible thermodynamics treatment. Electrochim. Acta 1993, 38, 815–819. [Google Scholar] [CrossRef]
- Gnusin, N.P.; Berezina, N.P.; Kononenko, N.A.; Dyomina, O.A. Transport structural parameters to characterize ion exchange membranes. J. Membr. Sci. 2004, 243, 301–310. [Google Scholar] [CrossRef]
- Larchet, C.; Auclair, B.; Nikonenko, V. Approximate evaluation of water transport number in ion-exchange membranes. Electrochim. Acta 2004, 49, 1711–1717. [Google Scholar] [CrossRef]
- Larchet, C.; Dammak, L.; Auclair, B.; Parchikov, S.; Nikonenko, V. A simplified procedure for ion-exchange membrane characterisation. New J. Chem. 2004, 28, 1260. [Google Scholar] [CrossRef]
- Paterson, R.; Gardner, C.R. Comparison of the transport properties of normal and expanded forms of a cation-exchange membrane by use of an irreversible thermodynamic approach. Part I. Membranes in the sodium form in 0·1 M-sodium chloride. J. Chem. Soc. A 1971, 2254–2261. [Google Scholar] [CrossRef]
- Robinson, R.A.; Stokes, R.H. Electrolyte Solutions, 2nd ed.; Butterworths: London, UK, 2002; ISBN 0-486-42225-9. [Google Scholar]
- Lebrun, L.; Da Silva, E.; Pourcelly, G.; Métayer, M. Elaboration and characterisation of ion-exchange films used in the fabrication of bipolar membranes. J. Membr. Sci. 2003, 227, 95–111. [Google Scholar] [CrossRef]
- Newman, J.S.; Thomas-Alyea, K.E. Electrochemical Systems; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2004; ISBN 3175723993. [Google Scholar]
- Zaltzman, B.; Rubinstein, I. Electro-osmotic slip and electroconvective instability. J. Fluid Mech. 2007, 579, 173–226. [Google Scholar] [CrossRef]
- Chu, K.T.; Bazant, M.Z. Electrochemical Thin Films at and above the Classical Limiting Current. SIAM J. Appl. Math. 2005, 65, 1485–1505. [Google Scholar] [CrossRef]
- Urtenov, M.A.K.; Kirillova, E.V.; Seidova, N.M.; Nikonenko, V.V. Decoupling of the Nernst-Planck and Poisson equations. Application to a membrane system at overlimiting currents. J. Phys. Chem. B 2007, 111, 14208–14222. [Google Scholar] [CrossRef]
- Kamcev, J.; Sujanani, R.; Jang, E.S.; Yan, N.; Moe, N.; Paul, D.R.; Freeman, B.D. Salt concentration dependence of ionic conductivity in ion exchange membranes. J. Membr. Sci. 2018, 547, 123–133. [Google Scholar] [CrossRef]
- Wijmans, J.G.; Baker, R.W. The solution-diffusion model: A review. J. Membr. Sci. 1995, 107, 1–21. [Google Scholar] [CrossRef]
- Baker, R.W. Membrane Technology and Applications, 3rd ed.; John Wiley and Sons Ltd.: Hoboken, NJ, USA, 2012; ISBN 9780470743720. [Google Scholar]
- Paul, D.R. Reformulation of the solution-diffusion theory of reverse osmosis. J. Membr. Sci. 2004, 241, 371–386. [Google Scholar] [CrossRef]
- Kamcev, J.; Paul, D.R.; Manning, G.S.; Freeman, B.D. Accounting for frame of reference and thermodynamic non-idealities when calculating salt diffusion coefficients in ion exchange membranes. J. Membr. Sci. 2017, 537, 396–406. [Google Scholar] [CrossRef]
- Kamcev, J.; Paul, D.R.; Manning, G.S.; Freeman, B.D. Predicting salt permeability coefficients in highly swollen, highly charged ion exchange membranes. ACS Appl. Mater. Interfaces 2017, 9, 4044–4056. [Google Scholar] [CrossRef] [PubMed]
- Yaroshchuk, A.E.; Dukhin, S.S. Phenomenological theory of reverse osmosis in macroscopically homogeneous membranes and its specification for the capillary space-charge model. J. Membr. Sci. 1993, 79, 133–158. [Google Scholar] [CrossRef]
- Choy, T.C. Effective Medium Theory: Principles and Applications; Oxford University Press: Oxford, UK, 2015; ISBN 0198518927. [Google Scholar]
- Kjelstrup, S.; Bedeaux, D. Non-Equilibrium Thermodynamics of Heterogeneous Systems; World Scientific Publishing Co. Pte. Ltd.: Singapore, 2008; ISBN 9789812779137. [Google Scholar]
- Galama, A.H.; Post, J.W.; Hamelers, H.V.M.; Nikonenko, V.V.; Biesheuvel, P.M. On the origin of the membrane potential arising across densely charged ion exchange membranes: How well does the Teorell-Meyer-Sievers theory work? J. Membr. Sci. Res. 2016, 2, 128–140. [Google Scholar] [CrossRef]
- Geise, G.M.; Paul, D.R.; Freeman, B.D. Fundamental water and salt transport properties of polymeric materials. Prog. Polym. Sci. 2014, 39, 1–42. [Google Scholar] [CrossRef]
- Bandini, S.; Bruni, L. Transport Phenomena in Nanofiltration Membranes. In Comprehensive Membrane Science and Engineering; Elsevier Science: Amsterdam, The Netherlands, 2010; pp. 1–21. ISBN 9780080932507. [Google Scholar]
- Jonsson, G.; Macedonio, F. Fundamentals in Reverse Osmosis. In Comprehensive Membrane Science and Engineering; Elsevier Science: Amsterdam, The Netherlands, 2010; Volume 2, pp. 1–22. ISBN 9780080932507. [Google Scholar]
- Caputo, M.; Cametti, C. Diffusion with memory in two cases of biological interest. J. Theor. Biol. 2008, 254, 697–703. [Google Scholar] [CrossRef]
- Tedesco, M.; Hamelers, H.V.M.; Biesheuvel, P.M. Nernst-Planck transport theory for (reverse) electrodialysis: II. Effect of water transport through ion-exchange membranes. J. Membr. Sci. 2017, 531, 172–182. [Google Scholar] [CrossRef]
- Ding, M.; Ghoufi, A.; Szymczyk, A. Molecular simulations of polyamide reverse osmosis membranes. Desalination 2014, 343, 48–53. [Google Scholar] [CrossRef]
- Ding, M.; Szymczyk, A.; Ghoufi, A. On the structure and rejection of ions by a polyamide membrane in pressure-driven molecular dynamics simulations. Desalination 2015, 368, 76–80. [Google Scholar] [CrossRef]
- Ding, M.; Szymczyk, A.; Goujon, F.; Soldera, A.; Ghoufi, A. Structure and dynamics of water confined in a polyamide reverse-osmosis membrane: A molecular-simulation study. J. Membr. Sci. 2014, 458, 236–244. [Google Scholar] [CrossRef]
- Ding, M.; Szymczyk, A.; Ghoufi, A. Hydration of a polyamide reverse-osmosis membrane. J. Membr. Sci. 2016, 501, 248–253. [Google Scholar] [CrossRef]
- Teorell, T. An Attempt to Formulate a Quantitative Theory of Membrane Permeability. Exp. Biol. Med. 1935, 33, 282–285. [Google Scholar] [CrossRef]
- Meyer, K.H.; Sievers, J.F. La perméabilité des membranes I. Théorie de la perméabilité ionique. Helv. Chim. Acta 1936, 19, 649–664. [Google Scholar] [CrossRef]
- Verbrugge, M.W.; Pintauro, P.N. Transport Models for Ion-Exchange Membranes; Springer: Boston, MA, USA, 1989; pp. 1–67. [Google Scholar]
- Miller, D.G. Application of Irreversible Thermodynamics to Electrolyte Solutions. I. Determination of Ionic Transport Coefficients lij for Isothermal Vector Transport Processes in Binary Electrolyte Systems. J. Phys. Chem. 1966, 70, 2639–2659. [Google Scholar] [CrossRef]
- Pitzer, K.S. Thermodynamic model for aqueous solutions of liquid-like density. Rev. Mineral. 1987, 81. [Google Scholar] [CrossRef]
- Wright, M.R. An Introduction to Aqueous Electrolyte Solutions; John Wiley: Hoboken, NJ, USA, 2007; ISBN 9780470842935. [Google Scholar]
- Manning, G.S. Polyelectrolytes. Annu. Rev. Phys. Chem. 1972, 23, 117–140. [Google Scholar] [CrossRef]
- Manning, G.S. Counterion binding in polyelectrolyte theory. Acc. Chem. Res. 1979, 12, 443–449. [Google Scholar] [CrossRef]
- Hiemenz, P.C.; Lodge, T.P. Polymer Chemistry, 2nd ed.; CRC Press: Boca Raton, Fl, USA, 2007; ISBN 1574447793. [Google Scholar]
- Tanaka, Y. Chapter 4 Theory of Teorell, Meyer and Sievers (TMS Theory). Membr. Sci. Technol. 2007, 12, 59–66. [Google Scholar] [CrossRef]
- Wang, X.-L.; Tsuru, T.; Nakao, S.-I.; Kimura, S. Electrolyte transport through nanofiltration membranes by the space-charge model and the comparison with Teorell-Meyer-Sievers model. J. Membr. Sci. 1995, 103, 117–133. [Google Scholar] [CrossRef]
- Filippov, A.N.; Starov, V.M.; Kononenko, N.A.; Berezina, N.P. Asymmetry of diffusion permeability of bi-layer membranes. Adv. Colloid Interface Sci. 2008, 139, 29–44. [Google Scholar] [CrossRef] [PubMed]
- Filippov, A.N.; Safronova, E.Y.; Yaroslavtsev, A.B. Theoretical and experimental investigation of diffusion permeability of hybrid MF-4SC membranes with silica nanoparticles. J. Membr. Sci. 2014, 471, 110–117. [Google Scholar] [CrossRef]
- Filippov, A.; Khanukaeva, D.; Afonin, D.; Skorikova, G.; Ivanov, E.; Vinokurov, V.; Lvov, Y. Transport Properties of Novel Hybrid Cation-Exchange Membranes on the Base of MF-4SC and Halloysite Nanotubes. J. Mater. Sci. Chem. Eng. 2015, 3, 58–65. [Google Scholar] [CrossRef]
- Filippov, A.; Afonin, D.; Kononenko, N.; Lvov, Y.; Vinokurov, V. New approach to characterization of hybrid nanocomposites. Colloids Surf. A Physicochem. Eng. Asp. 2017, 521, 251–259. [Google Scholar] [CrossRef]
- Fíla, V.; Bouzek, K. A mathematical model of multiple ion transport across an ion-selective membrane under current load conditions. J. Appl. Electrochem. 2003, 33, 675–684. [Google Scholar] [CrossRef]
- Fíla, V.; Bouzek, K. The effect of convection in the external diffusion layer on the results of a mathematical model of multiple ion transport across an ion-selective membrane. J. Appl. Electrochem. 2008, 38, 1241–1252. [Google Scholar] [CrossRef]
- Sokirko, A.V.; Manzanares, J.A.; Pellicer, J. The Permselectivity of Membrane Systems with an Inhomogeneous Distribution of Fixed Charge Groups. J. Colloid Interface Sci. 1994, 168, 32–39. [Google Scholar] [CrossRef]
- Moya, A.A.; Moleón, J.A. Study of the electrical properties of bi-layer ion-exchange membrane systems. J. Electroanal. Chem. 2010, 647, 53–59. [Google Scholar] [CrossRef]
- Balannec, B.; Ghoufi, A.; Szymczyk, A. Nanofiltration performance of conical and hourglass nanopores. J. Membr. Sci. 2018, 552, 336–340. [Google Scholar] [CrossRef]
- Dubinin, M.M. Surface and Porosity of Adsorbents. Russ. Chem. Rev. 1982, 51, 605–611. [Google Scholar] [CrossRef]
- Sélégny, E.; Boyd, G.; Gregor, H.P. Charged Gels and Membranes: Part I; Springer Science & Business Media: Berlin, Germany, 1976; ISBN 9401014647. [Google Scholar]
- Mafé, S.; Manzanares, J.A.; Ramirez, P. Modeling of surface vs. bulk ionic conductivity in fixed charge membranes. Phys. Chem. Chem. Phys. 2003, 5, 376–383. [Google Scholar] [CrossRef]
- Rojo, A.G.; Roman, H.E. Effective-medium approach for the conductivity of dispersed ionic conductors. Phys. Rev. B 1988, 37, 3696–3698. [Google Scholar] [CrossRef]
- Duan, H.L.; Karihaloo, B.L.; Wang, J.; Yi, X. Effective conductivities of heterogeneous media containing multiple inclusions with various spatial distributions. Phys. Rev. B 2006, 73, 174203. [Google Scholar] [CrossRef]
- Starov, V.M.; Zhdanov, V.G. Effective properties of suspensions/emulsions, porous and composite materials. Adv. Colloid Interface Sci. 2008, 137, 2–19. [Google Scholar] [CrossRef] [PubMed]
- Pal, R. Thermal conductivity of three-component composites of core-shell particles. Mater. Sci. Eng. A 2008, 498, 135–141. [Google Scholar] [CrossRef]
- Zhdanov, M. Generalized effective-medium theory of induced polarization. Geophysics 2008, 73, F197–F211. [Google Scholar] [CrossRef]
- Vasin, S.I.; Filippov, A.N.; Starov, V.M. Hydrodynamic permeability of membranes built up by particles covered by porous shells: Cell models. Adv. Colloid Interface Sci. 2008, 139, 83–96. [Google Scholar] [CrossRef]
- Maxwell, J.C. A Treatise on Electricity and Magnetism V2 (1873) (Clarendon Press Series); Clarendon: Oxford, UK, 1873; ISBN 978-0548642573. [Google Scholar]
- Mackie, J.S.; Meares, P. The Diffusion of Electrolytes in a Cation-Exchange Resin Membrane. I. Theoretical. Proc. R. Soc. A Math. Phys. Eng. Sci. 1955, 232, 498–509. [Google Scholar] [CrossRef]
- Wódzki, R.; Narebska, A. Composition and structure of cation permselective membranes II. Multilayer electrochemical model. Angew. Makromol. Chem. 1980, 88, 149–163. [Google Scholar] [CrossRef]
- Gnusin, N.P.; Zabolotsky, V.I.; Meshechkov, A.I. Development of the generalized conductance principle to the description of transfer phenomena in disperse systems under the acting of different forces. Russ. J. Phys. Chem. 1980, 54, 1518–1522. [Google Scholar]
- Hsu, W.Y.; Gierke, T.D.; Molnar, C.J. Morphological effects on the physical properties of polymer composites. Macromolecules 1983, 16, 1945–1947. [Google Scholar] [CrossRef]
- Belaid, N.; Ngom, B.; Dammak, L.; Larchet, C.; Auclair, B. Conductivité membranaire: Interprétation et exploitation selon le modèle à solution interstitielle hétérogène. Eur. Polym. J. 1999, 35, 879–897. [Google Scholar] [CrossRef]
- Elattar, A.; Elmidaoui, A.; Pismenskaia, N.; Gavach, C.; Pourcelly, G. Comparison of transport properties of monovalent anions through anion-exchange membranes. J. Membr. Sci. 1998, 143, 249–261. [Google Scholar] [CrossRef]
- Gohil, G.S.; Shahi, V.K.; Rangarajan, R. Comparative studies on electrochemical characterization of homogeneous and heterogeneous type of ion-exchange membranes. J. Membr. Sci. 2004, 240, 211–219. [Google Scholar] [CrossRef]
- Xu, T.W.; Li, Y.; Wu, L.; Yang, W.H. A simple evaluation of microstructure and transport parameters of ion-exchange membranes from conductivity measurements. Sep. Purif. Technol. 2008, 60, 73–80. [Google Scholar] [CrossRef]
- Sedkaoui, Y.; Szymczyk, A.; Lounici, H.; Arous, O. A new lateral method for characterizing the electrical conductivity of ion-exchange membranes. J. Membr. Sci. 2016, 507, 34–42. [Google Scholar] [CrossRef]
- Vyas, P.; Ray, P.; Adhikary, S.; Shah, B.; Rangarajan, R. Studies of the effect of variation of blend ratio on permselectivity and heterogeneity of ion-exchange membranes. J. Colloid Interface Sci. 2003, 257, 127–134. [Google Scholar] [CrossRef]
- Le, X.T.; Bui, T.H.; Viel, P.; Berthelot, T.; Palacin, S. On the structure-properties relationship of the AMV anion exchange membrane. J. Membr. Sci. 2009, 340, 133–140. [Google Scholar] [CrossRef]
- Le, X.T. Permselectivity and microstructure of anion exchange membranes. J. Colloid Interface Sci. 2008, 325, 215–222. [Google Scholar] [CrossRef]
- Berezina, N.; Gnusin, N.; Dyomina, O.; Timofeyev, S. Water electrotransport in membrane systems. Experiment and model description. J. Membr. Sci. 1994, 86, 207–229. [Google Scholar] [CrossRef]
- Tuan, L.X.; Buess-Herman, C. Study of water content and microheterogeneity of CMS cation exchange membrane. Chem. Phys. Lett. 2007, 434, 49–55. [Google Scholar] [CrossRef]
- Pismenskaya, N.D.; Nevakshenova, E.E.; Nikonenko, V.V. Using a Single Set of Structural and Kinetic Parameters of the Microheterogeneous Model to Describe the Sorption and Kinetic Properties of Ion-Exchange Membranes. Pet. Chem. 2018, 58, 465–473. [Google Scholar] [CrossRef]
- Zabolotskii, V.I.; Nikonenko, V.V.; Kostenko, O.N.; Elnikova, L.F. Analysis of ion-exchange membranes using microheterogeneous models. Russ. J. Phys. Chem. 1993, 67, 2423–2427. [Google Scholar]
- Tuan, L.X.; Mertens, D.; Buess-Herman, C. The two-phase model of structure microheterogeneity revisited by the study of the CMS cation exchange membrane. Desalination 2009, 240, 351–357. [Google Scholar] [CrossRef]
- Geise, G.M.; Falcon, L.P.; Freeman, B.D.; Paul, D.R. Sodium chloride sorption in sulfonated polymers for membrane applications. J. Membr. Sci. 2012, 423–424, 195–208. [Google Scholar] [CrossRef]
- Huguet, P.; Kiva, T.; Noguera, O.; Sistat, P.; Nikonenko, V. The crossed interdiffusion of sodium nitrate and sulfate through an anion exchange membrane, as studied by Raman spectroscopy. New J. Chem. 2005, 29, 955. [Google Scholar] [CrossRef]
- Zabolotsky, V.I.; Lebedev, K.A.; Nikonenko, V.V.; Shudrenko, A.A. Identification of a microheterogeneous model for a heterogeneous membrane. Russ. J. Electrochem. 1993, 29, 811–816. [Google Scholar]
- Karpenko-Jereb, L.V.; Berezina, N.P. Determination of structural, selective, electrokinetic and percolation characteristics of ion-exchange membranes from conductive data. Desalination 2009, 245, 587–596. [Google Scholar] [CrossRef]
- Lee, H.-J.; Hong, M.-K.; Han, S.-D.; Moon, S.-H. Influence of the heterogeneous structure on the electrochemical properties of anion exchange membranes. J. Membr. Sci. 2008, 320, 549–555. [Google Scholar] [CrossRef]
- Pismenskaya, N.D.; Belova, E.I.; Nikonenko, V.V.; Larchet, C. Electrical conductivity of cation-and anion-exchange membranes in ampholyte solutions. Russ. J. Electrochem. 2008, 44, 1285–1291. [Google Scholar] [CrossRef]
- Volfkovich, Y.; Filippov, A.; Bagotsky, V. Structural Properties of Porous Materials and Powders Used in Different Fields of Science and Technology; Springer: London, UK, 2014; ISBN 978-1-4471-6376-3. [Google Scholar]
- Chaabane, L.; Bulvestre, G.; Larchet, C.; Nikonenko, V.; Deslouis, C.; Takenouti, H. The influence of absorbed methanol on the swelling and conductivity properties of cation-exchange membranes: Evaluation of nanostructure parameters. J. Membr. Sci. 2008, 323, 167–175. [Google Scholar] [CrossRef]
- Choi, J.-H.H.; Kim, S.-H.H.; Moon, S.-H.H. Heterogeneity of ion-exchange membranes: The effects of membrane heterogeneity on transport properties. J. Colloid Interface Sci. 2001, 241, 120–126. [Google Scholar] [CrossRef] [PubMed]
- Tuan, L.X.; Verbanck, M.; Buess-Herman, C.; Hurwitz, H.D. Properties of CMV cation exchange membranes in sulfuric acid media. J. Membr. Sci. 2006, 284, 67–78. [Google Scholar] [CrossRef]
- Villaluenga, J.P.G.; Barragán, V.M.; Izquierdo-Gil, M.A.; Godino, M.P.; Seoane, B.; Ruiz-Bauzá, C. Comparative study of liquid uptake and permeation characteristics of sulfonated cation-exchange membranes in water and methanol. J. Membr. Sci. 2008, 323, 421–427. [Google Scholar] [CrossRef]
- Kumar, M.; Singh, S.; Shahi, V.K. Cross-Linked Poly(vinyl alcohol)−Poly(acrylonitrile-co-2-dimethylamino ethylmethacrylate) Based Anion-Exchange Membranes in Aqueous Media. J. Phys. Chem. B 2010, 114, 198–206. [Google Scholar] [CrossRef] [PubMed]
- Alberti, G.; Casciola, M. Solid state protonic conductors, present main applications and future prospects. Solid State Ionics 2001, 145, 3–16. [Google Scholar] [CrossRef]
- Adjemian, K.T.; Lee, S.J.; Srinivasan, S.; Benziger, J.; Bocarsly, A.B. Silicon Oxide Nafion Composite Membranes for Proton-Exchange Membrane Fuel Cell Operation at 80–140°C. J. Electrochem. Soc. 2002, 149, A256–A261. [Google Scholar] [CrossRef]
- Jalani, N.H.; Dunn, K.; Datta, R. Synthesis and characterization of Nafion®-MO2 (M = Zr, Si, Ti) nanocomposite membranes for higher temperature PEM fuel cells. Electrochim. Acta 2005, 51, 553–560. [Google Scholar] [CrossRef]
- Pereira, F.; Vallé, K.; Belleville, P.; Morin, A.; Lambert, S.; Sanchez, C. Advanced Mesostructured Hybrid Silica−Nafion Membranes for High-Performance PEM Fuel Cell. Chem. Mater. 2008, 20, 1710–1718. [Google Scholar] [CrossRef]
- Safronova, E.Y.; Volkov, V.I.; Yaroslavtsev, A.B. Ion mobility and conductivity of hybrid ion-exchange membranes incorporating inorganic nanoparticles. Solid State Ion. 2011, 188, 129–131. [Google Scholar] [CrossRef]
- Gerasimova, E.; Safronova, E.; Ukshe, A.; Dobrovolsky, Y.; Yaroslavtsev, A. Electrocatalytic and transport properties of hybrid Nafion® membranes doped with silica and cesium acid salt of phosphotungstic acid in hydrogen fuel cells. Chem. Eng. J. 2016, 305, 121–128. [Google Scholar] [CrossRef]
- Niepceron, F.; Lafitte, B.; Galiano, H.; Bigarré, J.; Nicol, E.; Tassin, J.-F. Composite fuel cell membranes based on an inert polymer matrix and proton-conducting hybrid silica particles. J. Membr. Sci. 2009, 338, 100–110. [Google Scholar] [CrossRef]
- Yaroslavtsev, A.B. Correlation between the properties of hybrid ion-exchange membranes and the nature and dimensions of dopant particles. Nanotechnol. Russ. 2012, 7, 437–451. [Google Scholar] [CrossRef]
- Safronova, E.Y.; Prikhno, I.A.; Yurkov, G.Y.; Yaroslavtsev, A.B. Nanocomposite membrane materials based on nafion and cesium acid salt of phosphotungstic heteropolyacid. Chem. Eng. Trans. 2015, 43, 679–684. [Google Scholar] [CrossRef]
- Golubenko, D.V.; Pourcelly, G.; Yaroslavtsev, A.B. Permselectivity and ion-conductivity of grafted cation-exchange membranes based on UV-oxidized polymethylpenten and sulfonated polystyrene. Sep. Purif. Technol. 2018, 207, 329–335. [Google Scholar] [CrossRef]
- Ng, L.Y.; Mohammad, A.W.; Leo, C.P.; Hilal, N. Polymeric membranes incorporated with metal/metal oxide nanoparticles: A comprehensive review. Desalination 2013, 308, 15–33. [Google Scholar] [CrossRef]
- Martynov, G.A.; Starov, V.M.; Churaev, N.V. Theory of Membrane Separation of Solutions. 1. Formulation of the Problem and Solution of Transport-Equations. Colloid J. USSR 1980, 42, 402. [Google Scholar]
- Porozhnyy, M.; Huguet, P.; Cretin, M.; Safronova, E.; Nikonenko, V. Mathematical modeling of transport properties of proton-exchange membranes containing immobilized nanoparticles. Int. J. Hydrogen Energy 2016, 41, 15605–15614. [Google Scholar] [CrossRef]
- Novikova, S.A.; Safronova, E.Y.; Lysova, A.A.; Yaroslavtsev, A.B. Influence of incorporated nanoparticles on the ionic conductivity of MF-4SC membrane. Mendeleev Commun. 2010, 20, 156–157. [Google Scholar] [CrossRef]
- Parvizian, F.; Hosseini, S.M.; Hamidi, A.R.; Madaeni, S.S.; Moghadassi, A.R. Electrochemical characterization of mixed matrix nanocomposite ion exchange membrane modified by ZnO nanoparticles at different electrolyte conditions “pH/concentration”. J. Taiwan Inst. Chem. Eng. 2014, 45, 2878–2887. [Google Scholar] [CrossRef]
- Morrison, F.A.; Osterle, J.F. Electrokinetic Energy Conversion in Ultrafine Capillaries. J. Chem. Phys. 1965, 43, 2111–2115. [Google Scholar] [CrossRef]
- Levine, S.; Marriott, J.; Neale, G.; Epstein, N. Theory of electrokinetic flow in fine cylindrical capillaries at high zeta-potentials. J. Colloid Interface Sci. 1975, 52, 136–149. [Google Scholar] [CrossRef]
- Koter, S. Transport of simple electrolyte solutions through ion-exchange membranes—The capillary model. J. Membr. Sci. 2002, 206, 201–215. [Google Scholar] [CrossRef]
- García-Morales, V.; Cervera, J.; Manzanares, J.A. Pore entrance effects on the electrical potential distribution in charged porous membranes and ion channels. J. Electroanal. Chem. 2007, 599, 203–208. [Google Scholar] [CrossRef]
- Sparreboom, W.; van den Berg, A.; Eijkel, J.C.T. Principles and applications of nanofluidic transport. Nat. Nanotechnol. 2009, 4, 713–720. [Google Scholar] [CrossRef] [PubMed]
- Bazant, M.Z.; Squires, T.M. Induced-charge electrokinetic phenomena. Curr. Opin. Colloid Interface Sci. 2010, 15, 203–213. [Google Scholar] [CrossRef]
- Guzmán-Garcia, A.G.; Pintauro, P.N.; Verbrugge, M.W.; Hill, R.F. Development of a space-charge transport model for ion-exchange membranes. AIChE J. 1990, 36, 1061–1074. [Google Scholar] [CrossRef]
- Lefebvre, X.; Palmeri, J. Nanofiltration theory: Good Co-Ion exclusion approximation for single salts. J. Phys. Chem. B 2005, 109, 5525–5540. [Google Scholar] [CrossRef]
- Yaroshchuk, A.; Boiko, Y.; Makovetskiy, A. Ion-Rejection, Electrokinetic and Electrochemical Properties of a Nanoporous Track-Etched Membrane and Their Interpretation by Means of Space Charge Model. Langmuir 2009, 25, 9605–9614. [Google Scholar] [CrossRef]
- Szymczyk, A.; Zhu, H.; Balannec, B. Ion Rejection Properties of Nanopores with Bipolar Fixed Charge Distributions. J. Phys. Chem. B 2010, 114, 10143–10150. [Google Scholar] [CrossRef]
- Hou, X.; Guo, W.; Jiang, L. Biomimetic smart nanopores and nanochannels. Chem. Soc. Rev. 2011, 40, 2385. [Google Scholar] [CrossRef] [PubMed]
- Peters, P.B.; van Roij, R.; Bazant, M.Z.; Biesheuvel, P.M. Analysis of electrolyte transport through charged nanopores. Phys. Rev. E 2016, 93, 053108. [Google Scholar] [CrossRef] [PubMed]
- Moya, A.A.A.; Nikonenko, V.V.V. A Comparative Theoretical Study of Potential Distribution and Conductivity in Cation- and Anion-Exchange Nanoporous Membranes Filled with Ternary Electrolytes. Electrochim. Acta 2015, 180, 929–938. [Google Scholar] [CrossRef]
- Ryzhkov, I.I.; Lebedev, D.V.; Solodovnichenko, V.S.; Shiverskiy, A.V.; Simunin, M.M. Induced-Charge Enhancement of the Diffusion Potential in Membranes with Polarizable Nanopores. Phys. Rev. Lett. 2017, 119, 226001. [Google Scholar] [CrossRef] [PubMed]
- Catalano, J.; Hamelers, H.V.M.; Bentien, A.; Biesheuvel, P.M. Revisiting Morrison and Osterle 1965: The efficiency of membrane-based electrokinetic energy conversion. J. Phys. Condens. Matter 2016, 28, 324001. [Google Scholar] [CrossRef] [PubMed]
- Szymczyk, A.; Zhu, H.; Balannec, B. Pressure-Driven Ionic Transport through Nanochannels with Inhomogenous Charge Distributions. Langmuir 2010, 26, 1214–1220. [Google Scholar] [CrossRef]
- Zhu, H.; Szymczyk, A.; Balannec, B. On the salt rejection properties of nanofiltration polyamide membranes formed by interfacial polymerization. J. Membr. Sci. 2011, 379, 215–223. [Google Scholar] [CrossRef]
- de Jong, J.; Lammertink, R.G.H.; Wessling, M. Membranes and microfluidics: A review. Lab Chip 2006, 6, 1125. [Google Scholar] [CrossRef]
- Laser, D.J.; Santiago, J.G. A review of micropumps. J. Micromech. Microeng. 2004, 14, R35–R64. [Google Scholar] [CrossRef]
- Zangle, T.A.; Mani, A.; Santiago, J.G. Theory and experiments of concentration polarization and ion focusing at microchannel and nanochannel interfaces. Chem. Soc. Rev. 2010, 39, 1014. [Google Scholar] [CrossRef]
- Deng, D.; Dydek, E.V.; Han, J.H.; Schlumpberger, S.; Mani, A.; Zaltzman, B.; Bazant, M.Z. Overlimiting current and shock electrodialysis in porous media. Langmuir 2013, 29, 16167–16177. [Google Scholar] [CrossRef] [PubMed]
- Alizadeh, S.; Mani, A. Multiscale Model for Electrokinetic Transport in Networks of Pores, Part I: Model Derivation. Langmuir 2017, 33, 6205–6219. [Google Scholar] [CrossRef] [PubMed]
- Dickhout, J.M.; Moreno, J.; Biesheuvel, P.M.; Boels, L.; Lammertink, R.G.H.; de Vos, W.M. Produced water treatment by membranes: A review from a colloidal perspective. J. Colloid Interface Sci. 2017, 487, 523–534. [Google Scholar] [CrossRef] [PubMed]
- Eikerling, M.; Kornyshev, A.A. Proton transfer in a single pore of a polymer electrolyte membrane. J. Electroanal. Chem. 2001, 502, 1–14. [Google Scholar] [CrossRef]
- Mansouri, A.; Scheuerman, C.; Bhattacharjee, S.; Kwok, D.Y.; Kostiuk, L.W. Transient streaming potential in a finite length microchannel. J. Colloid Interface Sci. 2005, 292, 567–580. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Pintauro, P.N. Multicomponent space-charge transport model for ion-exchange membranes. AIChE J. 2000, 46, 1177–1190. [Google Scholar] [CrossRef]
- Höltzel, A.; Tallarek, U. Ionic conductance of nanopores in microscale analysis systems: Where microfluidics meets nanofluidics. J. Sep. Sci. 2007, 30, 1398–1419. [Google Scholar] [CrossRef] [PubMed]
- Schoch, R.B.; Han, J.; Renaud, P. Transport phenomena in nanofluidics. Rev. Mod. Phys. 2008, 80, 839–883. [Google Scholar] [CrossRef]
- Bazant, M.Z.; Kilic, M.S.; Storey, B.D.; Ajdari, A. Towards an understanding of induced-charge electrokinetics at large applied voltages in concentrated solutions. Adv. Colloid Interface Sci. 2009, 152, 48–88. [Google Scholar] [CrossRef]
- Cwirko, E.H.; Carbonell, R.G. Interpretation of transport coefficients in Nafion using a parallel pore model. J. Membr. Sci. 1992, 67, 227–247. [Google Scholar] [CrossRef]
- Szymczyk, A.; Fievet, P.; Aoubiza, B.; Simon, C.; Pagetti, J. An application of the space charge model to the electrolyte conductivity inside a charged microporous membrane. J. Membr. Sci. 1999, 161, 275–285. [Google Scholar] [CrossRef]
- Luo, T.; Abdu, S.; Wessling, M. Selectivity of ion exchange membranes: A review. J. Membr. Sci. 2018, 555, 429–454. [Google Scholar] [CrossRef]
- Manzanares, J.; Kontturi, K. Diffusion and migration. In Encyclopedia of Electrochemistry. V. 2. Interfacial Kinetics and Mass Transport; Bard, A., Stratmann, M., Calvo, E.J., Eds.; VCH-Wiley: Weinheim, Germany, 2003; pp. 81–121. ISBN 9783527302505. [Google Scholar]
- Hwang, S.-T.; Kammermeyer, K. Membranes in Separation; Wiley: New York, NY, USA, 1975; ISBN 978-0898748017. [Google Scholar]
- Peers, A.M. Membrane phenomena. Discuss. Faraday Soc. 1956, 21, 124. [Google Scholar] [CrossRef]
- Balster, J.; Yildirim, M.H.; Stamatialis, D.F.; Ibanez, R.; Lammertink, R.G.H.; Jordan, V.; Wessling, M. Morphology and microtopology of cation-exchange polymers and the origin of the overlimiting current. J. Phys. Chem. B 2007, 111, 2152–2165. [Google Scholar] [CrossRef] [PubMed]
- Nikonenko, V.V.; Kovalenko, A.V.; Urtenov, M.K.; Pismenskaya, N.D.; Han, J.; Sistat, P.; Pourcelly, G. Desalination at overlimiting currents: State-of-the-art and perspectives. Desalination 2014, 342, 85–106. [Google Scholar] [CrossRef]
- Urtenov, M.K.; Uzdenova, A.M.; Kovalenko, A.V.; Nikonenko, V.V.; Pismenskaya, N.D.; Vasil’eva, V.I.; Sistat, P.; Pourcelly, G. Basic mathematical model of overlimiting transfer enhanced by electroconvection in flow-through electrodialysis membrane cells. J. Membr. Sci. 2013, 447, 190–202. [Google Scholar] [CrossRef]
- Pismenskaya, N.D.; Pokhidnia, E.V.; Pourcelly, G.; Nikonenko, V.V. Can the electrochemical performance of heterogeneous ion-exchange membranes be better than that of homogeneous membranes? J. Membr. Sci. 2018, 566, 54–68. [Google Scholar] [CrossRef]
- Rubinstein, I.; Zaltzman, B. Electro-osmotically induced convection at a permselective membrane. Phys. Rev. E 2000, 62, 2238–2251. [Google Scholar] [CrossRef]
- Nikonenko, V.V.; Vasil’eva, V.I.; Akberova, E.M.; Uzdenova, A.M.; Urtenov, M.K.; Kovalenko, A.V.; Pismenskaya, N.P.; Mareev, S.A.; Pourcelly, G. Competition between diffusion and electroconvection at an ion-selective surface in intensive current regimes. Adv. Colloid Interface Sci. 2016, 235, 233–246. [Google Scholar] [CrossRef]
- Nikonenko, V.V.; Mareev, S.A.; Pis’menskaya, N.D.; Uzdenova, A.M.; Kovalenko, A.V.; Urtenov, M.K.; Pourcelly, G. Effect of electroconvection and its use in intensifying the mass transfer in electrodialysis (Review). Russ. J. Electrochem. 2017, 53, 1122–1144. [Google Scholar] [CrossRef]
- Rubinstein, I.; Zaltzman, B. Equilibrium Electroconvective Instability. Phys. Rev. Lett. 2015, 114, 114502. [Google Scholar] [CrossRef] [PubMed]
- Pismenskaya, N.D.; Nikonenko, V.V.; Belova, E.I.; Lopatkova, G.Y.; Sistat, P.; Pourcelly, G.; Larshe, K. Coupled convection of solution near the surface of ion-exchange membranes in intensive current regimes. Russ. J. Electrochem. 2007, 43, 307–327. [Google Scholar] [CrossRef]
- Kim, S.J.; Wang, Y.C.; Lee, J.H.; Jang, H.; Han, J. Concentration polarization and nonlinear electrokinetic flow near a nanofluidic channel. Phys. Rev. Lett. 2007, 99, 1–4. [Google Scholar] [CrossRef] [PubMed]
- Kwak, R.; Guan, G.; Peng, W.K.; Han, J. Microscale electrodialysis: Concentration profiling and vortex visualization. Desalination 2013, 308, 138–146. [Google Scholar] [CrossRef]
- Rubinstein, S.M.; Manukyan, G.; Staicu, A.; Rubinstein, I.; Zaltzman, B.; Lammertink, R.G.H.H.; Mugele, F.; Wessling, M. Direct observation of a nonequilibrium electro-osmotic instability. Phys. Rev. Lett. 2008, 101, 236101. [Google Scholar] [CrossRef] [PubMed]
- Yossifon, G.; Chang, H.C. Selection of nonequilibrium overlimiting currents: Universal depletion layer formation dynamics and vortex instability. Phys. Rev. Lett. 2008, 101, 254501. [Google Scholar] [CrossRef] [PubMed]
- Zabolotskiy, V.I.I.; But, A.Y.; Vasil’eva, V.I.; Akberova, E.M.M.; Melnikov, S.S.S.; Vasil, V.I.; Akberova, E.M.M.; Melnikov, S.S.S. Ion transport and electrochemical stability of strongly basic anion-exchange membranes under high current electrodialysis conditions. J. Membr. Sci. 2017, 526, 60–72. [Google Scholar] [CrossRef]
- Shaposhnik, V.A.; Vasil’eva, V.I.; Grigorchuk, O.V. Diffusion boundary layers during electrodialysis. Russ. J. Electrochem. 2006, 42, 1202–1207. [Google Scholar] [CrossRef]
- Vasil’eva, V.I.; Zhil’tsova, A.V.; Malykhin, M.D.; Zabolotskii, V.I.; Lebedev, K.A.; Chermit, R.K.; Sharafan, M.V. Effect of the chemical nature of the ionogenic groups of ion-exchange membranes on the size of the electroconvective instability region in high-current modes. Russ. J. Electrochem. 2014, 50, 120–128. [Google Scholar] [CrossRef]
- de Valença, J.C.; Kurniawan, A.; Wagterveld, R.M.; Wood, J.A.; Lammertink, R.G.H. Influence of Rayleigh-Bénard convection on electrokinetic instability in overlimiting current conditions. Phys. Rev. Fluids 2017, 2, 033701. [Google Scholar] [CrossRef]
- Jo, M.; Wagterveld, R.M.; Karatay, E.; Wood, A.; Lammertink, R.G.H.; de Valença, J.; Jõgi, M.; Wagterveld, R.M.; Karatay, E.; Wood, J.A.; et al. Con fi ned Electroconvective Vortices at Structured Ion Exchange Membranes. Langmuir 2018, 34, 2455–2463. [Google Scholar] [CrossRef]
- Kwak, R.; Pham, V.S.; Lim, K.M.; Han, J. Shear flow of an electrically charged fluid by ion concentration polarization: Scaling laws for electroconvective vortices. Phys. Rev. Lett. 2013, 110, 1–5. [Google Scholar] [CrossRef]
- Chang, H.-C.; Yossifon, G.; Demekhin, E.A. Nanoscale Electrokinetics and Microvortices: How Microhydrodynamics Affects Nanofluidic Ion Flux. Annu. Rev. Fluid Mech. 2012, 44, 401–426. [Google Scholar] [CrossRef]
- Mishchuk, N.А. Concentration polarization of interface and non-linear electrokinetic phenomena. Adv. Colloid Interface Sci. 2010, 160, 16–39. [Google Scholar] [CrossRef] [PubMed]
- Davidson, S.M.; Wessling, M.; Mani, A. On the Dynamical Regimes of Pattern-Accelerated Electroconvection. Sci. Rep. 2016, 6, 22505. [Google Scholar] [CrossRef]
- Andersen, M.B.; Van Soestbergen, M.; Mani, A.; Bruus, H.; Biesheuvel, P.M.; Bazant, M.Z. Current-induced membrane discharge. Phys. Rev. Lett. 2012, 109, 1–5. [Google Scholar] [CrossRef]
- Dukhin, S.S. Electrokinetic phenomena of the second kind and their applications. Adv. Colloid Interface Sci. 1991, 35, 173–196. [Google Scholar] [CrossRef]
- Mishchuk, N.; Gonzalez-Caballero, F.; Takhistov, P. Electroosmosis of the second kind and current through curved interface. Colloids Surf. A Physicochem. Eng. Asp. 2001, 181, 131–144. [Google Scholar] [CrossRef]
- Squires, T.M.; Bazant, M.Z. Induced-charge electro-osmosis. J. Fluid Mech. 2004, 509, 217–252. [Google Scholar] [CrossRef]
- Leinweber, F.C.; Tallarek, U. Concentration polarization-based nonlinear electrokinetics in porous media: Induced-charge electroosmosis. J. Phys. Chem. B 2005, 109, 21481–21485. [Google Scholar] [CrossRef]
- Rubinstein, I.; Shtilman, L. Voltage against current curves of cation exchange membranes. J. Chem. Soc. Faraday Trans. 2 1979, 75, 231–246. [Google Scholar] [CrossRef]
- Forgacs, C.; Ishibashi, N.; Leibovitz, J.; Sinkovic, J.; Spiegler, K.S. Polarization at ion-exchange membranes in electrodialysis. Desalination 1972, 10, 181–214. [Google Scholar] [CrossRef]
- Davis, T.A.; Grebenyuk, V.; Grebenyuk, O. Membrane Technology in Chemical Industry; Nunes, S., Peinemann, K., Eds.; Wiley-VCH: Weinheim, Germany, 2001; ISBN 978-3-527-31316-7. [Google Scholar]
- Mishchuk, N.A.; Heldal, T.; Volden, T.; Auerswald, J.; Knapp, H. Micropump based on electroosmosis of the second kind. Electrophoresis 2009, 30, 3499–3506. [Google Scholar] [CrossRef] [PubMed]
- Ajdari, A. Pumping liquids using asymmetric electrode arrays. Phys. Rev. E 2000, 61, R45–R48. [Google Scholar] [CrossRef]
- Kim, D.; Posner, J.D.; Santiago, J.G. High flow rate per power electroosmotic pumping using low ion density solvents. Sens. Actuators A Phys. 2008, 141, 201–212. [Google Scholar] [CrossRef]
- Volgin, V.M.; Davydov, A.D. Calculation of limiting current density of metal electrodeposition on vertical plane electrode under conditions of natural convection. Electrochim. Acta 2004, 49, 365–372. [Google Scholar] [CrossRef]
- Trau, M.; Saville, D.A.; Aksay, I.A. Field-Induced Layering of Colloidal Crystals. Science 1996, 272, 706–709. [Google Scholar] [CrossRef]
- Sonin, A.A.; Probstein, R.F. A hydrodynamic theory of desalination by electrodialysis. Desalination 1968, 5, 293–329. [Google Scholar] [CrossRef]
- Gnusin, N.P.; Zabolotsky, V.I.; Nikonenko, V.V.; Urtenov, M.K. Convective-diffusion model of the electrodialytic desalination. Limiting current and diffusion layer. Sov. Electrochem. 1986, 22, 273. [Google Scholar]
- Zabolotskii, V.I.; Gnusin, N.P.; Nikonenko, V.V.; Urtenov, K.M. Convective diffusion model of the process of electrodialysis desalination: Distribution of concentration and current density. Elektrokhimiya 1985, 3, 296–302. [Google Scholar]
- Tedesco, M.; Hamelers, H.V.M.; Biesheuvel, P.M. Nernst-Planck transport theory for (reverse) electrodialysis: I. Effect of co-ion transport through the membranes channel. J. Membr. Sci. 2016, 510, 370–381. [Google Scholar] [CrossRef]
- Shaposhnik, V.A.; Kuzminykh, V.A.; Grigorchuk, O.V.; Vasil’eva, V.I. Analytical model of laminar flow electrodialysis with ion-exchange membranes. J. Membr. Sci. 1997, 133, 27–37. [Google Scholar] [CrossRef]
- Shaposhnik, V.A.; Grigorchuk, O.V.; Korzhov, E.N.; Vasil’eva, V.I.; Klimov, V.Y. The effect of ion-conducting spacers on mass transfer—Numerical analysis and concentration field visualization by means of laser interferometry. J. Membr. Sci. 1998, 139, 85–96. [Google Scholar] [CrossRef]
- Solan, A.; Winograd, Y.; Katz, U. An analytical model for mass transfer in an electrodialysis cell with spacer of finite mesh. Desalination 1971, 9, 89–95. [Google Scholar] [CrossRef]
- Winograd, Y.; Solan, A.; Toren, M. Mass transfer in narrow channels in the presence of turbulence promoters. Desalination 1973, 13, 171–186. [Google Scholar] [CrossRef]
- Kim, Y.; Walker, W.S.; Lawler, D.F. Electrodialysis with spacers: Effects of variation and correlation of boundary layer thickness. Desalination 2011, 274, 54–63. [Google Scholar] [CrossRef]
- Sano, Y.; Bai, X.; Amagai, S.; Nakayama, A. Effect of a porous spacer on the limiting current density in an electro-dialysis desalination. Desalination 2018, 444, 151–161. [Google Scholar] [CrossRef]
- Balster, J.; Pünt, I.; Stamatialis, D.F.; Wessling, M. Multi-layer spacer geometries with improved mass transport. J. Membr. Sci. 2006, 282, 351–361. [Google Scholar] [CrossRef]
- Balster, J.; Stamatialis, D.F.; Wessling, M. Membrane with integrated spacer. J. Membr. Sci. 2010, 360, 185–189. [Google Scholar] [CrossRef]
- Pawlowski, S.; Sistat, P.; Crespo, J.G.; Velizarov, S. Mass transfer in reverse electrodialysis: Flow entrance effects and diffusion boundary layer thickness. J. Membr. Sci. 2014, 471, 72–83. [Google Scholar] [CrossRef]
- Pawlowski, S.; Rijnaarts, T.; Saakes, M.; Nijmeijer, K.; Crespo, J.G.; Velizarov, S. Improved fluid mixing and power density in reverse electrodialysis stacks with chevron-profiled membranes. J. Membr. Sci. 2017, 531, 111–121. [Google Scholar] [CrossRef]
- Pawlowski, S.; Nayak, N.; Meireles, M.; Portugal, C.A.M.; Velizarov, S.; Crespo, J.G. CFD modelling of flow patterns, tortuosity and residence time distribution in monolithic porous columns reconstructed from X-ray tomography data. Chem. Eng. J. 2018, 350, 757–766. [Google Scholar] [CrossRef]
- Tado, K.; Sakai, F.; Sano, Y.; Nakayama, A. An analysis on ion transport process in electrodialysis desalination. Desalination 2016, 378, 60–66. [Google Scholar] [CrossRef]
- Tanaka, Y. A computer simulation of feed and bleed ion exchange membrane electrodialysis for desalination of saline water. Desalination 2010, 254, 99–107. [Google Scholar] [CrossRef]
- Campione, A.; Gurreri, L.; Ciofalo, M.; Micale, G.; Tamburini, A.; Cipollina, A. Electrodialysis for water desalination: A critical assessment of recent developments on process fundamentals, models and applications. Desalination 2018, 434, 121–160. [Google Scholar] [CrossRef]
- Zabolotskii, V.I.; Shel’deshov, N.V.; Orel, I.V.; Lebedev, K.A. Determining the ion transference numbers through a membrane by its hydrodynamic isolation. Russ. J. Electrochem. 1997, 33, 1066–1071. [Google Scholar]
- Lebedev, K.A.; Zabolotskii, V.I.; Nikonenko, V.V. Selectivity of Ion-Exchange Membranes. Theoretical Basis for Procedures Used to Determine Migrational Transport Numbers. Sov. Electrochem. 1987, 23, 555–559. [Google Scholar]
- Lévêque, A. Les lois de la transmission de chaleur par convection. Ann. Mines 1928, 13, 201–299. [Google Scholar]
- Geankoplis, C. Transport Processes and Separation Process Principles: (Includes Unit Operations), 4th ed.; Prentice Hall Professional Technical Reference: Upper Saddle River, NJ, USA, 2003; ISBN 013101367X. [Google Scholar]
- Mareev, S.A.A.; Butylskii, D.Y.; Pismenskaya, N.D.D.; Nikonenko, V.V.V. Chronopotentiometry of ion-exchange membranes in the overlimiting current range. Transition time for a finite-length diffusion layer: Modeling and experiment. J. Membr. Sci. 2016, 500, 171–179. [Google Scholar] [CrossRef]
- Belova, E.I.; Lopatkova, G.Y.; Pismenskaya, N.D.; Nikonenko, V.V.; Larchet, C.; Pourcelly, G. Effect of anion-exchange membrane surface properties on mechanisms of overlimiting mass transfer. J. Phys. Chem. B 2006, 110, 13458–13469. [Google Scholar] [CrossRef]
- Conway, B.E.; Bockris, J.O.; Yeager, E.; Khan, S.U.M.; White, R.E. (Eds.) Comprehensive Treatise of Electrochemistry; Springer: Boston, MA, USA, 1983; Volume 7, ISBN 978-1-4613-3586-3. [Google Scholar]
- Zabolotsky, V.I.I.; Novak, L.; Kovalenko, A.V.V.; Nikonenko, V.V.; Urtenov, M.H.H.; Lebedev, K.A.A.; But, A.Y.Y. Electroconvection in systems with heterogeneous ion-exchange membranes. Pet. Chem. 2017, 57, 779–789. [Google Scholar] [CrossRef]
- Sharafan, M.V.; Zabolotskii, V.I.; Bugakov, V.V. Electric mass transport through homogeneous and surface-modified heterogeneous ion-exchange membranes at a rotating membrane disk. Russ. J. Electrochem. 2009, 45, 1162–1169. [Google Scholar] [CrossRef]
- Rubinstein, I.; Zaltzman, B.; Pundik, T. Ion-exchange funneling in thin-film coating modification of heterogeneous electrodialysis membranes. Phys. Rev. E 2002, 65, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Rubinstein, I. Electroconvection at an electrically inhomogeneous permselective interface. Phys. Fluids A Fluid Dyn. 1991, 3, 2301–2309. [Google Scholar] [CrossRef]
- Mishchuk, N.A. Polarization of systems with complex geometry. Curr. Opin. Colloid Interface Sci. 2013, 18, 137–148. [Google Scholar] [CrossRef]
- Pham, V.S.; Li, Z.; Lim, K.M.; White, J.K.; Han, J. Direct numerical simulation of electroconvective instability and hysteretic current-voltage response of a permselective membrane. Phys. Rev. E 2012, 86, 1–11. [Google Scholar] [CrossRef] [PubMed]
- MacDonald, D.D. Transient Techniques in Electrochemistry; Springer: New York, NY, USA, 1977; ISBN 978-1-4613-4147-5. [Google Scholar]
- Nikonenko, V.V.; Pismenskaya, N.D.; Belova, E.I.; Sistat, P.; Huguet, P.; Pourcelly, G.; Larchet, C. Intensive current transfer in membrane systems: Modelling, mechanisms and application in electrodialysis. Adv. Colloid Interface Sci. 2010, 160, 101–123. [Google Scholar] [CrossRef] [PubMed]
- Dukhin, S.S.; Mishchuk, N.A. Unlimited increase in the current through an ionite granule. Kolloidn. Zhurnal 1987, 49, 1197. [Google Scholar]
- Gueshi, T.; Tokuda, K.; Matsuda, H. Voltammetry at partially covered electrodes: Part I. Chronopotentiometry and chronoamperometry at model electrodes. J. Electroanal. Chem. Interfacial Electrochem. 1978, 89, 247–260. [Google Scholar] [CrossRef]
- Krol, J.J.; Wessling, M.; Strathmann, H. Chronopotentiometry and overlimiting ion transport through monopolar ion exchange membranes. J. Membr. Sci. 1999, 162, 155–164. [Google Scholar] [CrossRef]
- Martí-Calatayud, M.C.C.; Buzzi, D.C.C.; García-Gabaldón, M.; Bernardes, A.M.M.; Tenório, J.A.S.; Pérez-Herranz, V. Ion transport through homogeneous and heterogeneous ion-exchange membranes in single salt and multicomponent electrolyte solutions. J. Membr. Sci. 2014, 466, 45–57. [Google Scholar] [CrossRef]
- Sand, H.J.S., III. On the Concentration at the Electrodes in a Solution, with special reference to the Liberation of Hydrogen by Electrolysis of a Mixture of Copper Sulphate and Sulphuric Acid. Philos. Mag. Ser. 1901, 1, 45–79. [Google Scholar] [CrossRef]
- Lerche, D.; Wolf, H. Quantitative Characterisation of current-induced diffusion layers at cation-exchange membranes. I. investigations of temporal and local behaviour of concentration profile at constant current density. Bioelectrochem. Bioenerg. 1975, 2, 293–302. [Google Scholar] [CrossRef]
- Warburg, E. Ueber das Verhalten sogenannter unpolarisirbarer Elektroden gegen Wechselstrom. Ann. Phys. 1899, 303, 493–499. [Google Scholar] [CrossRef]
- Zholkovskij, E.K.; Vorotyntsev, M.A.; Staude, E. Electrokinetic Instability of Solution in a Plane-Parallel Electrochemical Cell. J. Colloid Interface Sci. 1996, 181, 28–33. [Google Scholar] [CrossRef]
- Franceschetti, D.R.; Macdonald, J.R.; Carolina, N.; Buck, R.P. Interpretation of Finite-Length-Warburg-Type Impedances in Supported and Unsupported Electrochemical Cells with Kinetically Reversible Electrodes. J. Electrochem. Soc. 1991, 138, 1368. [Google Scholar] [CrossRef]
- Sistat, P.; Pourcelly, G. Chronopotentiometric response of an ion-exchange membrane in the underlimiting current-range. Transport phenomena within the diffusion layers. J. Membr. Sci. 1997, 123, 121–131. [Google Scholar] [CrossRef]
- Van Soestbergen, M.; Biesheuvel, P.M.; Bazant, M.Z. Diffuse-charge effects on the transient response of electrochemical cells. Phys. Rev. E 2010, 81, 1–13. [Google Scholar] [CrossRef]
- Choi, J.-H.; Moon, S.-H. Pore size characterization of cation-exchange membranes by chronopotentiometry using homologous amine ions. J. Membr. Sci. 2001, 191, 225–236. [Google Scholar] [CrossRef]
- Amatore, C.; Savéant, J.M.; Tessier, D. Charge transfer at partially blocked surfaces: A model for the case of microscopic active and inactive sites. J. Electroanal. Chem. Interfacial Electrochem. 1983, 147, 39–51. [Google Scholar] [CrossRef]
- Ward, K.R.; Lawrence, N.S.; Hartshorne, R.S.; Compton, R.G. The theory of cyclic voltammetry of electrochemically heterogeneous surfaces: Comparison of different models for surface geometry and applications to highly ordered pyrolytic graphite. Phys. Chem. Chem. Phys. 2012, 14, 7264. [Google Scholar] [CrossRef] [PubMed]
- Zabolotskii, V.I.; Bugakov, V.V.; Sharafan, M.V.; Chermit, R.K. Transfer of electrolyte ions and water dissociation in anion-exchange membranes under intense current conditions. Russ. J. Electrochem. 2012, 48, 650–659. [Google Scholar] [CrossRef]
- Baltrūnas, G.; Valiūnas, R.; Popkirov, G. Identification of electrode surface blocking by means of thin-layer cell: 1. The model. Electrochim. Acta 2007, 52, 7091–7096. [Google Scholar] [CrossRef]
- Bard, A.J.; Faulkner, L.R. Electrochemical Methods: Fundamentals and Applications, 2nd ed.; John Wiley & Sons, Inc.: New York, NY, USA, 2001; ISBN 9781118312803. [Google Scholar]
- Szunerits, S.; Thouin, L. Microelectrode Arrays. In Handbook of Electrochemistry; Zoski, C., Ed.; Elsevier: Amsterdam, The Netherlands, 2007; ISBN 978-0-444-51958-0. [Google Scholar]
- Amatore, C.; Pebay, C.; Sella, C.; Thouin, L. Mass Transport at Microband Electrodes: Transient, Quasi-Steady-State, and Convective Regimes. ChemPhysChem 2012, 13, 1562–1568. [Google Scholar] [CrossRef]
- Ma, X.; Zhang, H.; Xing, F. A three-dimensional model for negative half cell of the vanadium redox flow battery. Electrochim. Acta 2011, 58, 238–246. [Google Scholar] [CrossRef]
- Probstein, R.F. Physicochemical Hydrodynamics: An Introduction; John Wiley & Sons, Inc.: New York, NY, USA, 2005; ISBN 9780471010111. [Google Scholar]
- Green, Y.; Yossifon, G. Effects of three-dimensional geometric field focusing on concentration polarization in a heterogeneous permselective system. Phys. Rev. E 2014, 89, 013024. [Google Scholar] [CrossRef]
- Green, Y.; Yossifon, G. Time-dependent ion transport in heterogeneous permselective systems. Phys. Rev. E 2015, 91, 063001. [Google Scholar] [CrossRef] [PubMed]
- Mareev, S.A.; Nichka, V.S.; Butylskii, D.Y.; Urtenov, M.K.; Pismenskaya, N.D.; Apel, P.Y.; Nikonenko, V.V. Chronopotentiometric Response of an Electrically Heterogeneous Permselective Surface: 3D Modeling of Transition Time and Experiment. J. Phys. Chem. C 2016, 120, 13113–13119. [Google Scholar] [CrossRef]
- Peyret, R.; Taylor, T. Computational Methods for Fluid Flow; Springer: New York, NY, USA, 1983; ISBN 978-3-642-85952-6. [Google Scholar]
- Lamb, H. Hydrodynamics, 6th ed.; Cambridge University Press: Cambridge, MA, USA; Dover Publications: New York, NY, USA, 1932; ISBN 0486602567. [Google Scholar]
- Taylor, G.I.; Sharman, C.F. A Mechanical Method for Solving Problems of Flow in Compressible Fluids. Proc. R. Soc. A Math. Phys. Eng. Sci. 1928, 121, 194–217. [Google Scholar] [CrossRef]
- Pattanayak, D.N.; Williams, R.A.; Poksheva, J.G. Generalized stream function representation for current flow in semiconducting media. Appl. Phys. Lett. 1982, 41, 459–461. [Google Scholar] [CrossRef]
- Khapaev, M.M.; Kupriyanov, M.Y.; Goldobin, E.; Siegel, M. Current distribution simulation for superconducting multi-layered structures. Supercond. Sci. Technol. 2002, 16, 24–27. [Google Scholar] [CrossRef]
- Bandelier, B.; Daveau, C.; Ashtiani, P.H.; Raïs, A.; Rioux-Damidau, F. Use of stream functions for the computation of currents in thin circuits determination of the impedances. IEEE Trans. Magn. 2000, 36, 760–764. [Google Scholar] [CrossRef]
- Bobachev, A.A.; Modin, I.N.; Pervago, E.V.; Shevnin, V.A. Stream-function used for current-lines’ construction in 2-dimensional DC modeling. In Proceedings of the 5th EEGS-ES Meeting, Budapest, Hungary, 5–9 September 1999; pp. 1–4. [Google Scholar]
- Peeren, G.N. Stream function approach for determining optimal surface currents. J. Comput. Phys. 2003, 191, 305–321. [Google Scholar] [CrossRef]
- Pismensky, A.V.; Urtenov, M.K.; Nikonenko, V.V.; Sistat, P.; Pismenskaya, N.D.; Kovalenko, A.V. Model and experimental studies of gravitational convection in an electromembrane cell. Russ. J. Electrochem. 2012, 48, 756–766. [Google Scholar] [CrossRef]
- Rubinstein, I.; Maletzki, F. Electroconvection at an electrically inhomogeneous permselective membrane surface. J. Chem. Soc. Faraday Trans. 1991, 87, 2079–2087. [Google Scholar] [CrossRef]
- Butylskii, D.Y.; Mareev, S.A.; Pismenskaya, N.D.; Apel, P.Y.; Polezhaeva, O.A.; Nikonenko, V.V. Phenomenon of two transition times in chronopotentiometry of electrically inhomogeneous ion exchange membranes. Electrochim. Acta 2018, 273, 289–299. [Google Scholar] [CrossRef]

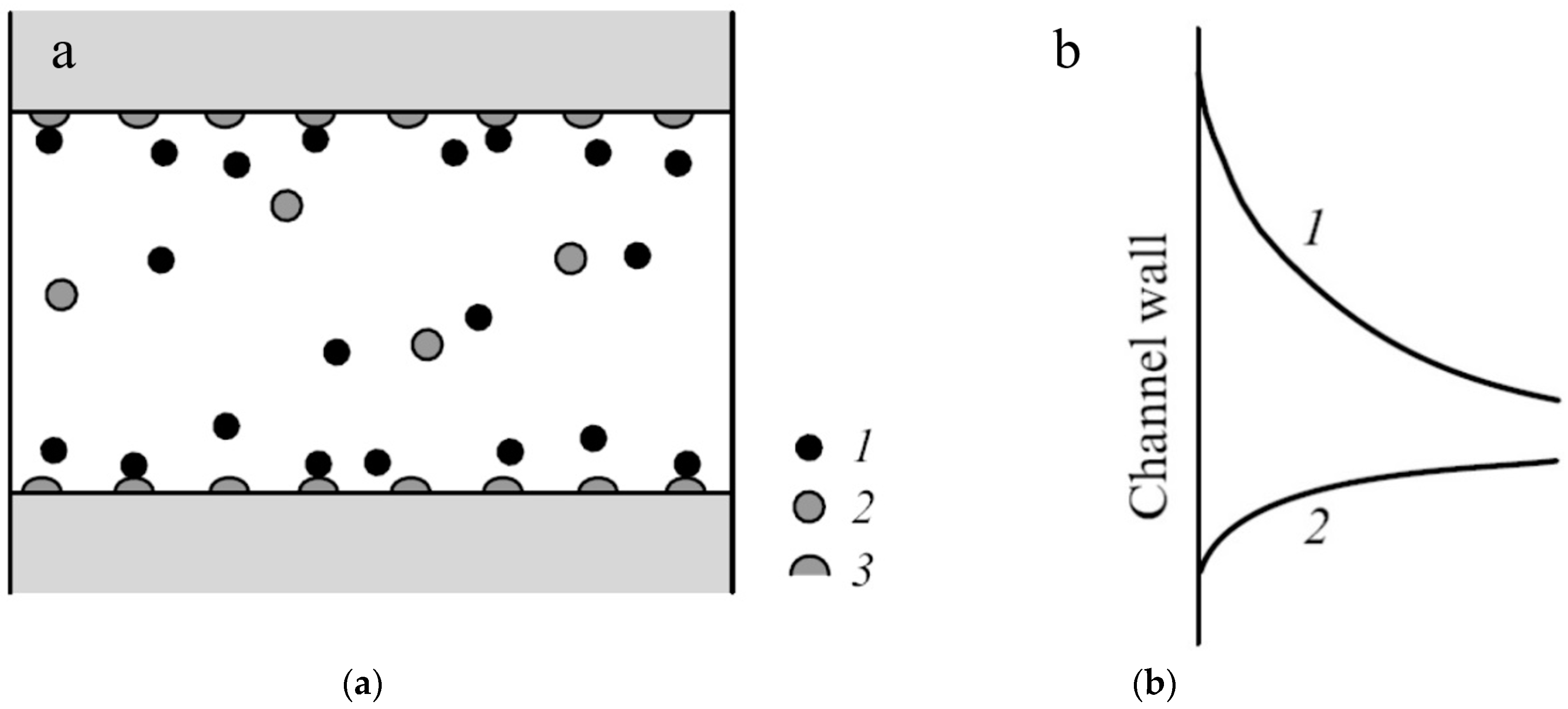

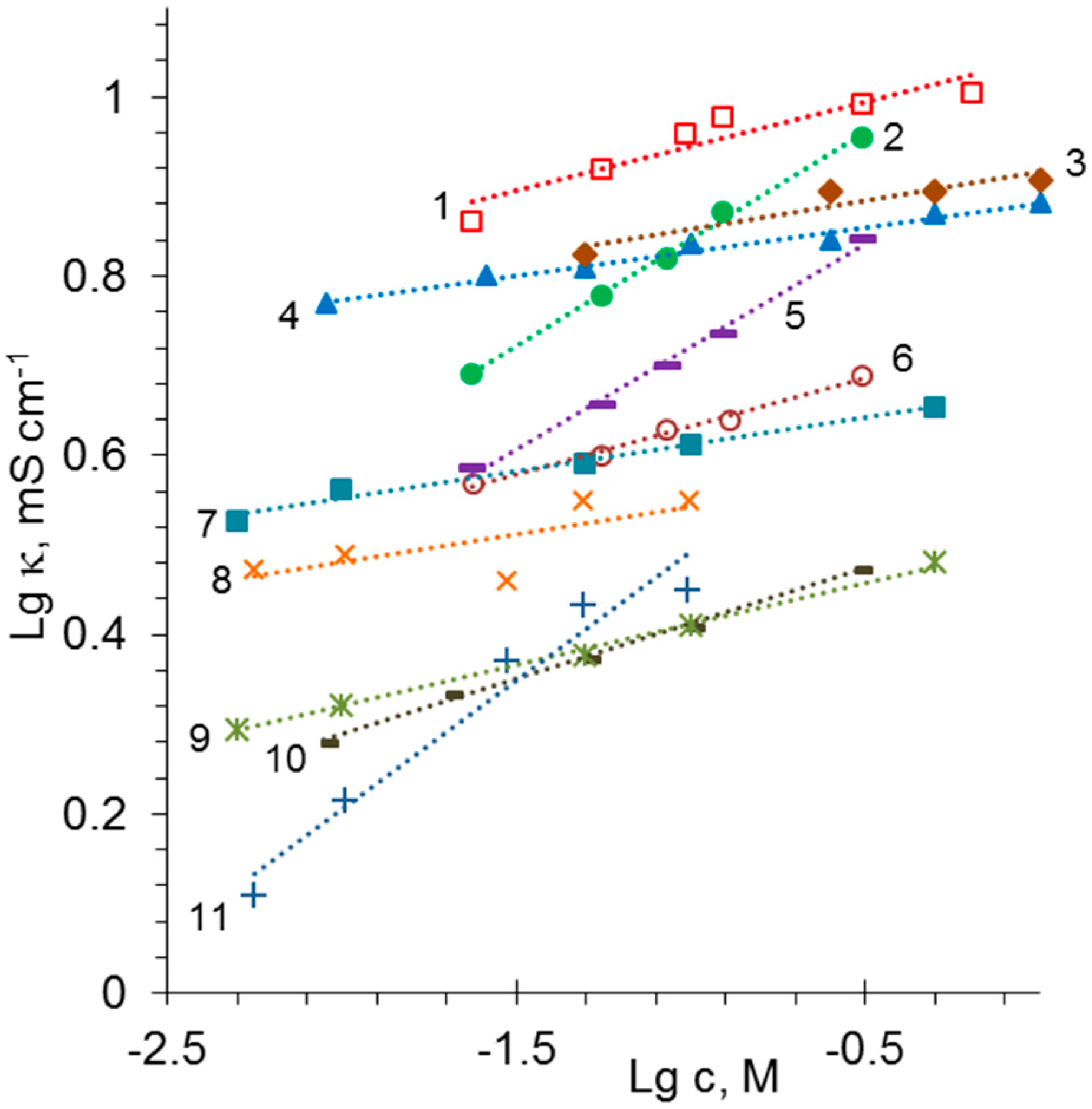
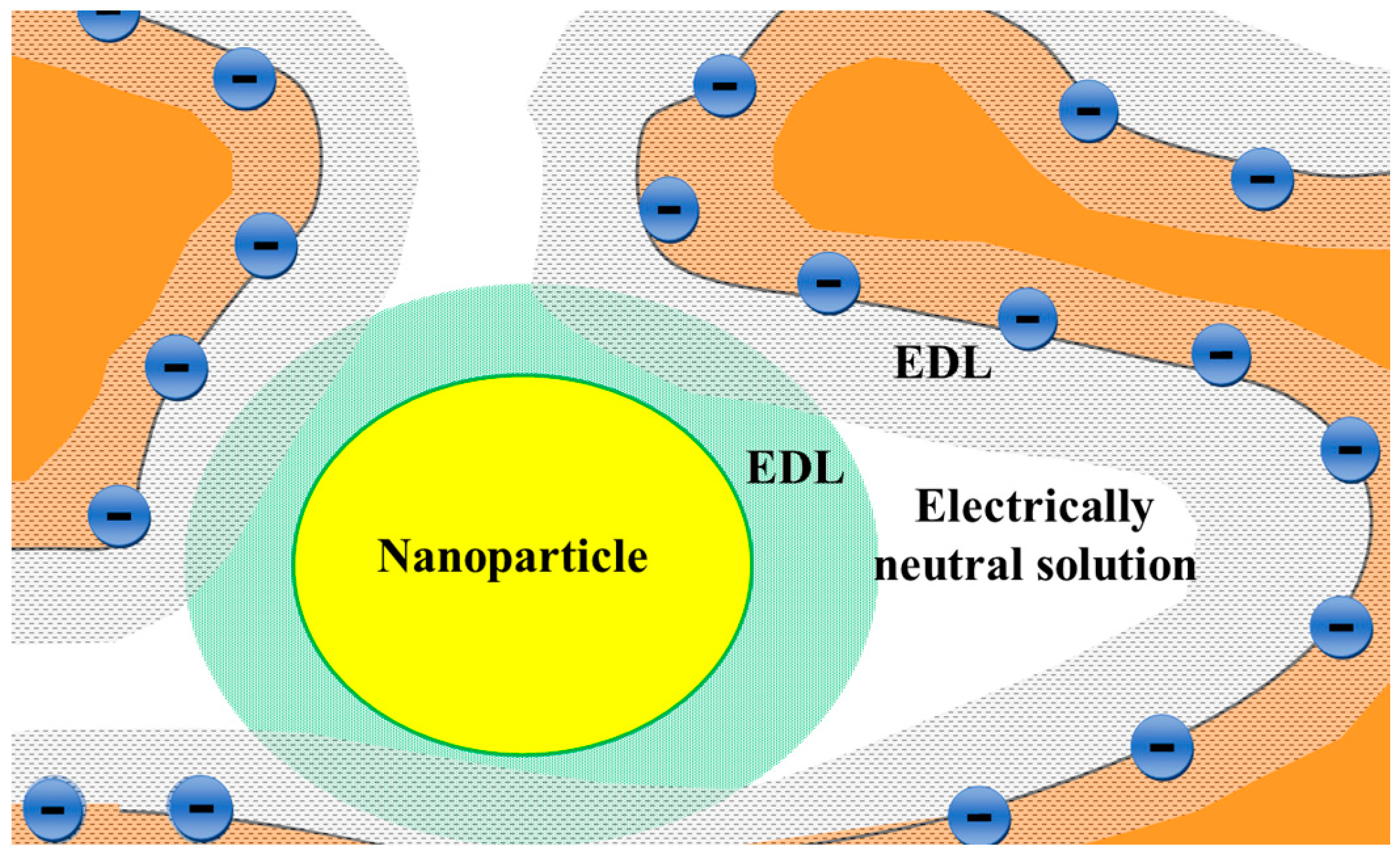
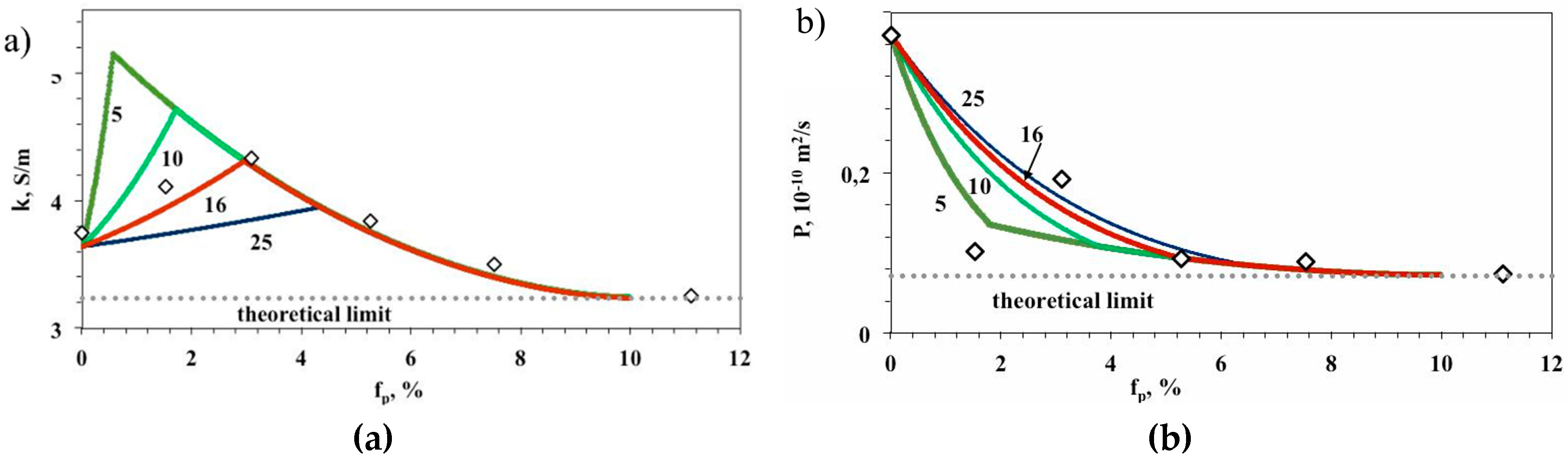


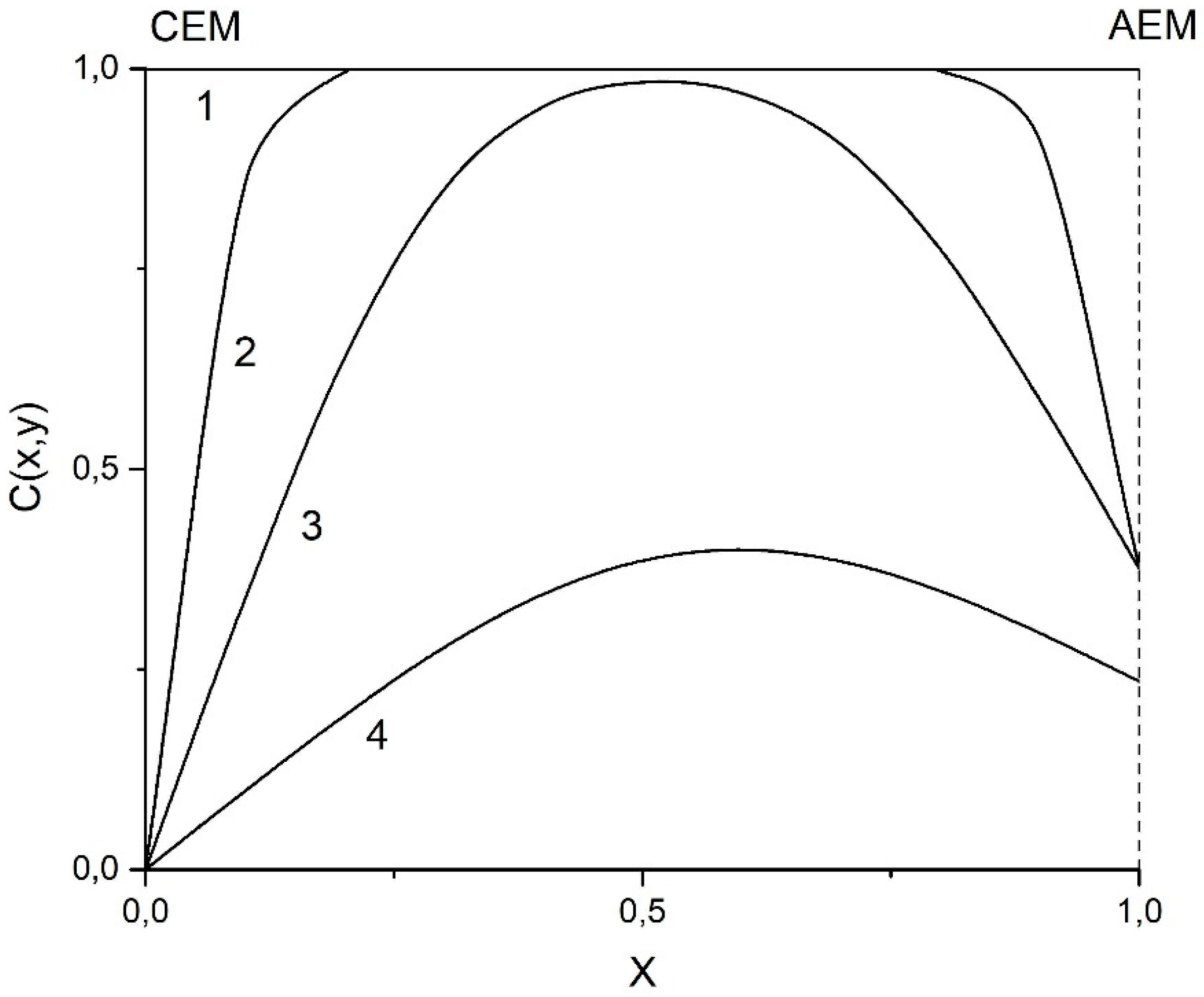
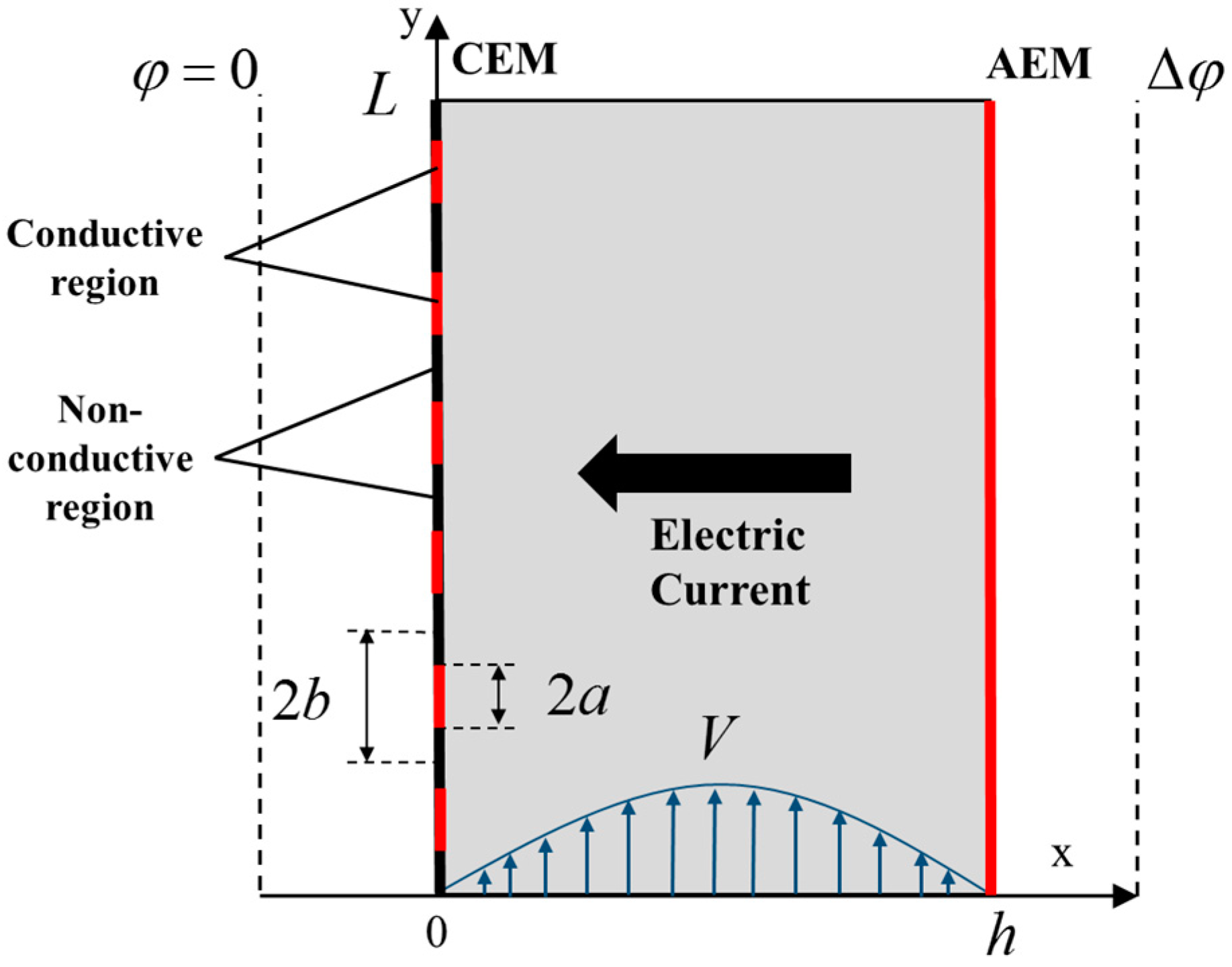

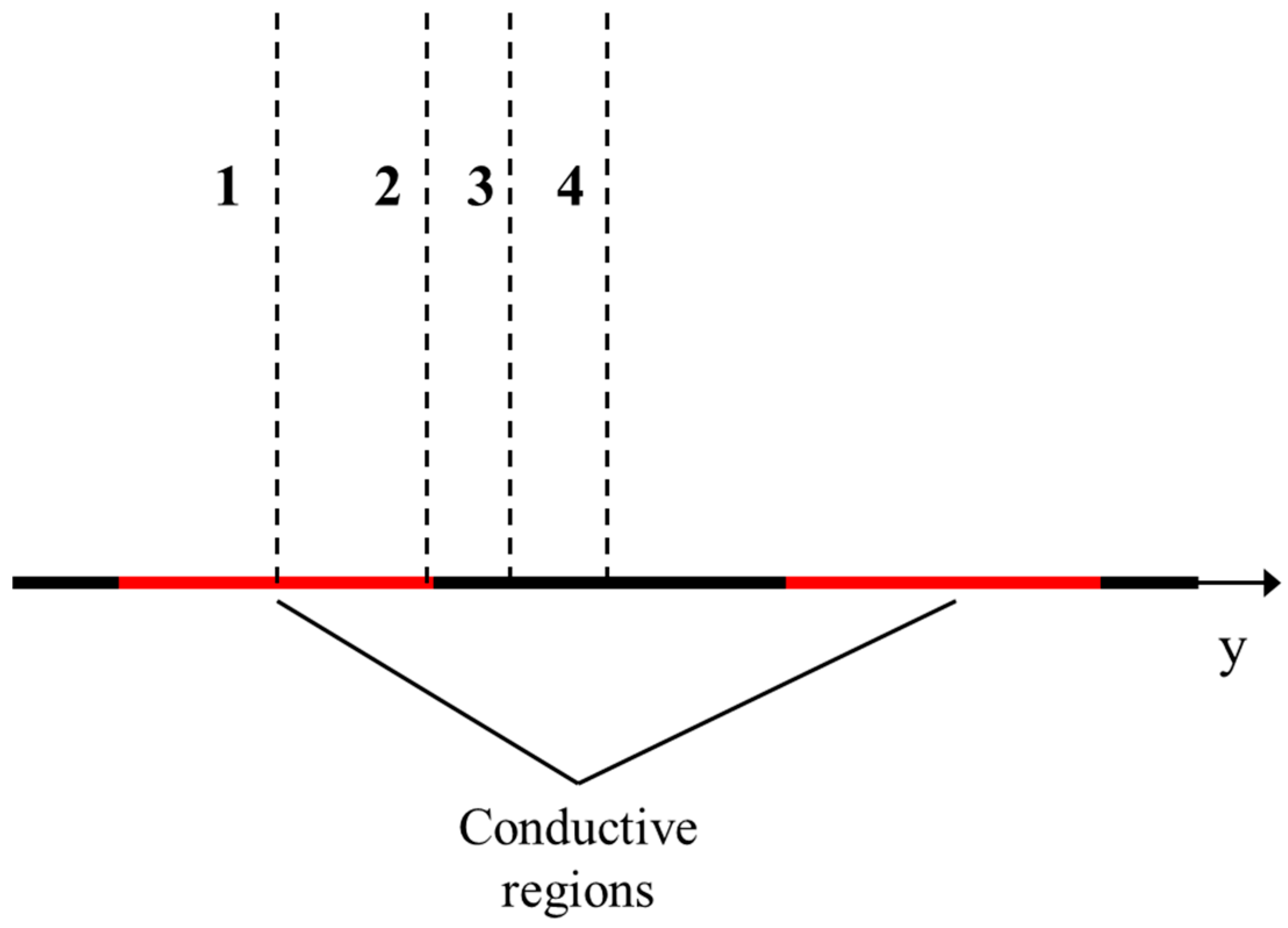
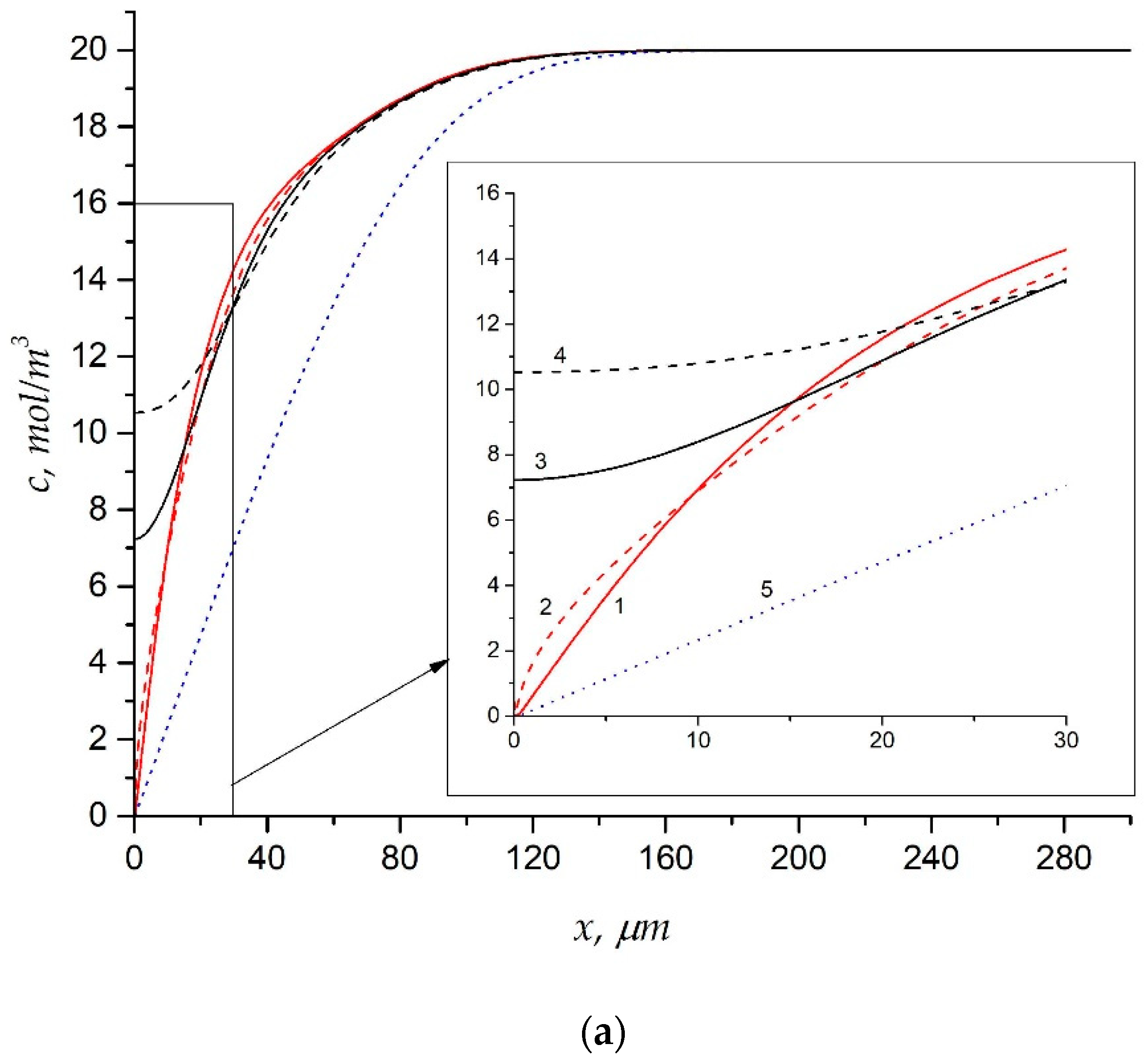

| Membrane | Type, Manufacturer | IEC, meq/g | Water Content, g/gdry mbr or % When in g/gwet mbr | Conductivity of Gel Phase, κg, mS cm−1 | Apparent Volume Fraction of Inter-Gel Solution, f2 app |
|---|---|---|---|---|---|
| AMX, anion-exchange | Homogeneous, Neosepta Astom (Japan) | 1.30 ± 0.05 [144] | 0.10–0.14 [144] | 3.72 * (KCl) [141] 2.19 ± 0.02 (KCl) [144] 3.2 (NaCl) [154] | 0.11 * (KCl) [141] 0.099 (KCl) [144] 0.06 (NaCl) [154] |
| CMX, cation-exchange | Idem | 1.65 [153] | 0.275 [153] | 8.79 * (KCl) [141] 6.72 (NaCl) [153] | 0.10 * (KCl) [141] 0.06 (NaCl) [153] |
| CMS, cation-exchange | Idem | 2.2 [146] | 22–30% [146] | 2.7 (NaCl) [146] | 0.13 (NaCl) [146] |
| AMV anion-exchange | Homogeneous, Selemion Asahi Glass (Japan) | 1.85 ± 0.04 [144] | 0.14–0.18 [144] | 3.80 ± 0.01 (KCl) [144] 3.50 (NaCl) [153] | 0.06 (KCl) [144] 0.07 in NaCl [153] |
| Nafion 125, cation-exchange, perfluorinated | Homogeneous, DuPont™ | 0.81 [153] | 0.129 [153] | 6.70 (NaCl) [153] | 0.07 (NaCl) [153] |
| MF-4SK, cation-exchange, perfluorinated | Homogeneous, Plastpolymer (Russia) | 0.86 [153] | 0.156 [153] | 6.40 (NaCl) [153] | 0.05 (NaCl) [153] |
| MA-41, anion-exchange | Heterogeneous Shchekinoazot (Russia) | 1.25 [155] | 0.29 [155] | 3.99 * (KCl) [141] | 0.24 * (KCl) [141] |
| MK-40, cation-exchange | Idem | 2.53 [153] | 0.503 [153] | 5.64 * (KCl) [141] 5.27 [153] | 0.25 * (KCl) [141] 0.18 [153] |
| LNA in NaCl | Heterogeneous, Lin’an (China) | 1.63 [154] | 49–55% [154] | 2.2 (NaCl) [154] | 0.28 (NaCl) [154] |
| γ | δtot, μm | |
|---|---|---|
| 0.1 | 54 | 128 |
| 0.2 | 72 | 134 |
| 0.5 | 86 | 136 |
| 1 | 85 | 139 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nikonenko, V.; Nebavsky, A.; Mareev, S.; Kovalenko, A.; Urtenov, M.; Pourcelly, G. Modelling of Ion Transport in Electromembrane Systems: Impacts of Membrane Bulk and Surface Heterogeneity. Appl. Sci. 2019, 9, 25. https://doi.org/10.3390/app9010025
Nikonenko V, Nebavsky A, Mareev S, Kovalenko A, Urtenov M, Pourcelly G. Modelling of Ion Transport in Electromembrane Systems: Impacts of Membrane Bulk and Surface Heterogeneity. Applied Sciences. 2019; 9(1):25. https://doi.org/10.3390/app9010025
Chicago/Turabian StyleNikonenko, Victor, Andrey Nebavsky, Semyon Mareev, Anna Kovalenko, Mahamet Urtenov, and Gerald Pourcelly. 2019. "Modelling of Ion Transport in Electromembrane Systems: Impacts of Membrane Bulk and Surface Heterogeneity" Applied Sciences 9, no. 1: 25. https://doi.org/10.3390/app9010025
APA StyleNikonenko, V., Nebavsky, A., Mareev, S., Kovalenko, A., Urtenov, M., & Pourcelly, G. (2019). Modelling of Ion Transport in Electromembrane Systems: Impacts of Membrane Bulk and Surface Heterogeneity. Applied Sciences, 9(1), 25. https://doi.org/10.3390/app9010025









