1. Introduction
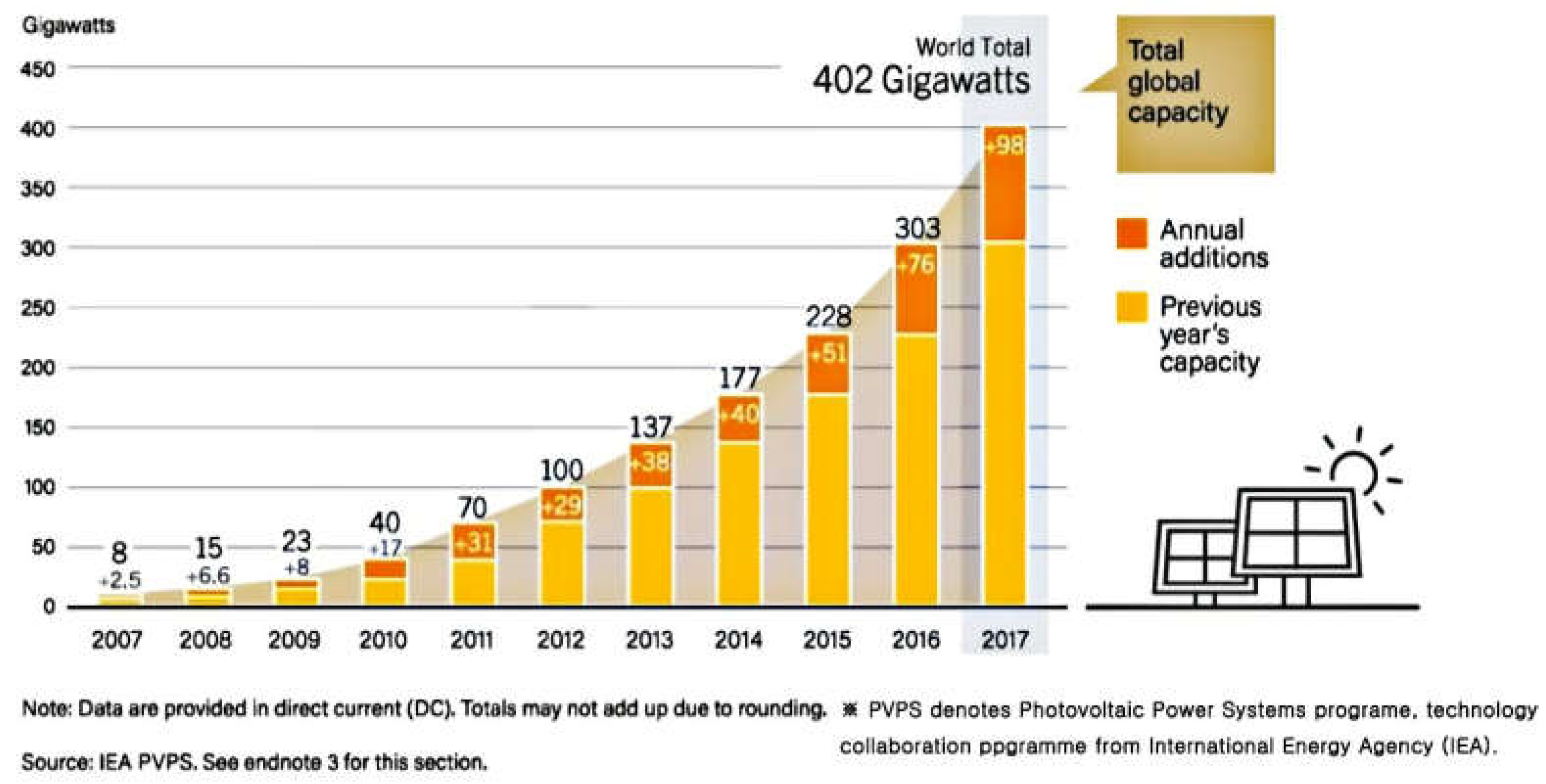
With photovoltaic (PV) systems becoming a mature and environmentally-friendly technology over the past few years, several countries have begun to invest aggressively in PV energy resources. For example, China has increased its PV budget by 30.7% of that of 2017. In addition to developed countries such as China, developing ones such as the Marshall Islands, Rwanda, and the Solomon Islands are also increasingly investing in renewable energy [
1], thereby leading to increased PV generation over the past decade [
2].
Figure 1 [
1] depicts the increasing trend of PV power generation, which implies that PV systems are expected to spread globally.
However, PV generation depends on weather conditions such as temperature, relative humidity, precipitation, and solar radiation. In other words, the PV output fluctuates frequently because of weather factors. With more PV systems integrating with grids, such fluctuating PV generation can severely impact the stability, reliability, quality, and system operation of power systems while also reducing economic benefits. Therefore, the accurate forecasting of PV generation becomes very important for grid operations involving distributed energy resources. As mentioned in [
3], several studies have focused on the prediction of solar power generation and solar radiation in this context. Among the 15,700 solar irradiation and power prediction articles appearing in a Google Scholar search, 6340 were published in 2016.
However, there are still problems in accurately forecasting solar power generation because of inaccurate predictions arising due to missing data, where “missing data” refers to completely absent data objects/series or imperfect data, i.e., partial data [
4]. In this context, it has been reported [
5] that when the missing data ratio in the total data is less than 1%, the impact is negligible. Further, missing rates between 1% and 5% correspond to manageable or flexible sample data. On the other hand, missing data rates >5% of the total data require suitable solutions [
5]. Further, missing data rates of >15% significantly adversely affect the prediction model [
6,
7]. Thus far, PV power generation prediction studies have reported poor performances on rainy days relative to sunny days [
8,
9,
10]. This implies that the existence of many missing precipitation data values significantly deteriorates the prediction accuracy. Hence, methods to address the missing data need to be urgently studied.
Several studies on missing data imputation have been conducted in multiple contexts. In [
5,
6,
7,
11,
12], missing data imputation algorithms based on statistical methods and machine learning approaches such as the
k-nearest neighbors (KNN) method have been proposed. Other studies [
13,
14,
15,
16] have proposed missing data imputation methods for solar irradiation. In [
13], the authors proposed three missing data imputations that can replace missing data for solar radiation: inverse-distance weighting (IDW), multiple linear regression (MLR), and multivariate imputation by chain equations (MICE). Among these, MICE affords outputs closest to the original solar radiation values when the missing values are replaced. In [
14], the authors estimated the temperature and relative humidity for solar irradiance prediction using the Fourier series and support vector machines (SVMs), while in [
15], the authors examined several missing weather data imputation methods ranging from simple ones such as mean imputation to complicated ones such as the multilayer perceptron and Markov chain Monte Carlo approaches. In [
16], the authors devised two missing imputation methods using atmospheric temperature and relative humidity: the decision matrix and the regression correlation of weather data. The first method affords a minimum correlation coefficient value of 0.95, RMSE of 87.6 W/
, NRMSE of 8.29%, and an index of agreement of 0.97 for irradiation. Here, NRMSE is the value obtained by dividing the RMSE value by the difference between the maximum and the minimum values of measured irradiation data. On the other hand, the second method yields higher error than the first method. In addition to research on solar radiation, several research works have focused on meteorological factors [
17,
18,
19,
20]. In [
17], the authors demonstrated the drawbacks of the IDW method and proposed three other methods: the coefficient correlation weighing method (CCWM), the artificial neural network estimation method (ANNEM), and the kriging estimation method (KEM), which outperformed conventional methods. Meanwhile, another study [
18] has suggested the fixed functional set genetic algorithm method (FFSGAM), which utilizes genetic algorithms and nonlinear optimization methods to estimate the missing data. When compared with IDW, the FFSGAM yields greater prediction accuracy. Here, we note that only six rain-gauging stations in Korea are able to estimate missing data; thus, missing data imputation becomes extremely important in this context. The method proposed in [
19] is similar to that in [
17] in that both are based on hybrid models. The former approach utilizes an artificial neural network (ANN) and a regression tree (RT) and affords better prediction accuracy than the ANN or RT models alone. Meanwhile, in [
20], the authors demonstrated 17 deterministic missing data imputations for missing precipitation data and concluded that the most suitable method is multiple linear regression weighted by the square of the missing data ratio.
Several studies have demonstrated improved prediction performance via application of these methods to classification or prediction models [
21,
22]. In [
21], the authors demonstrated a neural network model of breast cancer diagnosis with the use of three statistical methods and three missing data machine learning methods. In [
22], the authors demonstrated that the conventional road traffic congestion prediction performance can be improved via application of a missing data imputation method based on machine learning techniques.
However, very few studies have applied missing weather data imputation to PV generation forecasts. Although in [
23], the authors developed a PV forecasting model using missing data imputation methods, they only considered missing PV power data imputation, and not missing weather data imputation. Missing data imputation forms a significant data preprocessing issue in predicting solar power generation because precipitation data are generally inaccurate. For example, as per the Korea Meteorological Administration, the approximate missing data rate was 16% in 2015 and 2016 and 19% in 2017. In particular, it is difficult to estimate how rainfall must be considered because a large amount of precipitation data is missing. However, very few researches have focused on how solar power generation forecasts change when the missing-point replacement method is applied.
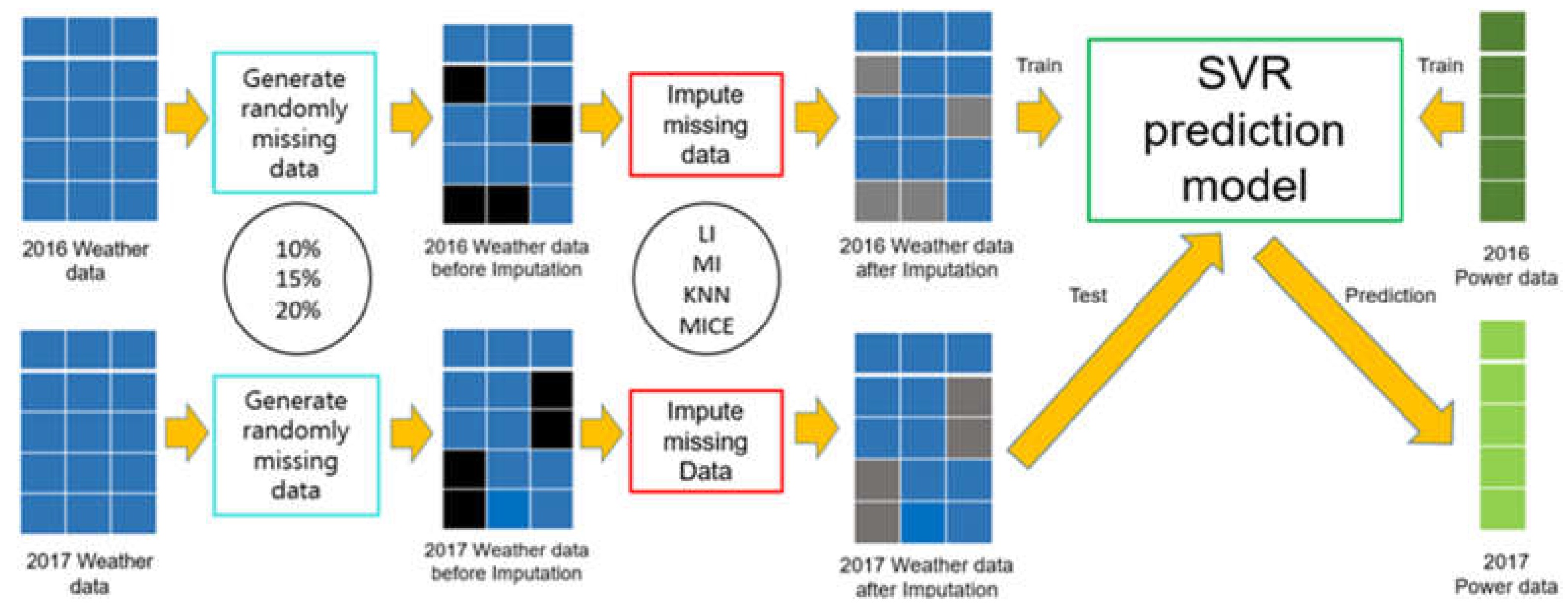
Against this backdrop, here, we generate randomly missing data in the weather data of the period of 2016–2017 with three missing data ratios, corresponding to the missing completely at random (MCAR) process [
24]. Next, we replace the missing data with suitable values by using four different approaches, linear interpolation (LI), mode imputation (MI),
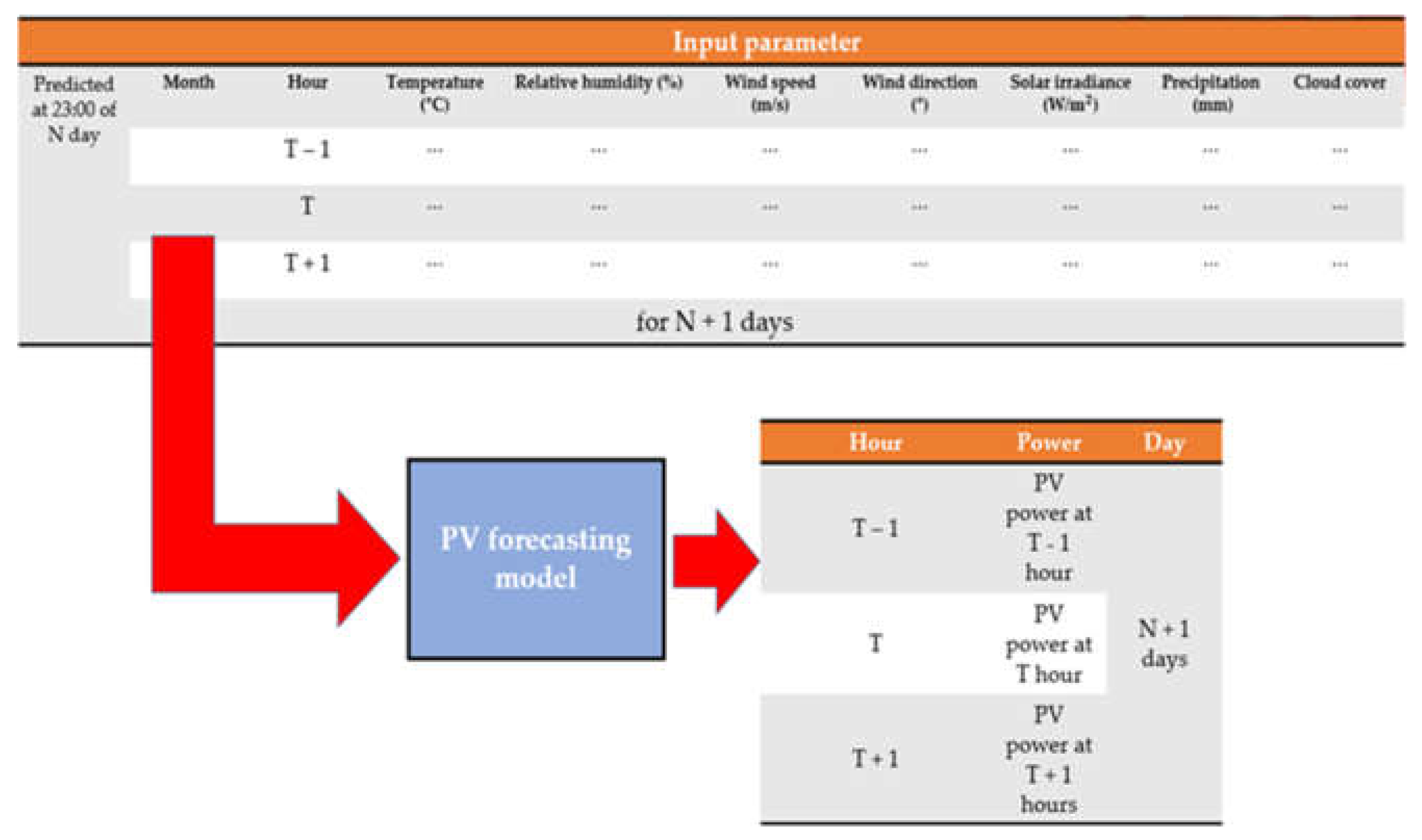
k-nearest neighbors (KNN), and multivariate imputation by chain equations (MICE). Thirdly, for four cases that utilize the missing data imputation methods and one that does not do so, we construct forecasting models using the SVR method with the solar power generation data for 2016. Finally, we predict solar PV generation for 2017 with the forecasting model and missing value-corrected weather data of 2017. Further, we calculate and compare the forecast errors for a specific period in 2017, and we examine the accuracy resulting from the application of the missing data imputation methods.
The rest of the paper is organized as follows:
Section 2 describes the meteorological and historical PV power generation data used in predicting solar power generation along with the four missing data imputation methods.
Section 3 describes the error evaluation performance of the missing data imputation methods applied to the model. In
Section 4, we calculate the error of the missing data imputation for each method and present the results. Finally,
Section 5 concludes the paper.
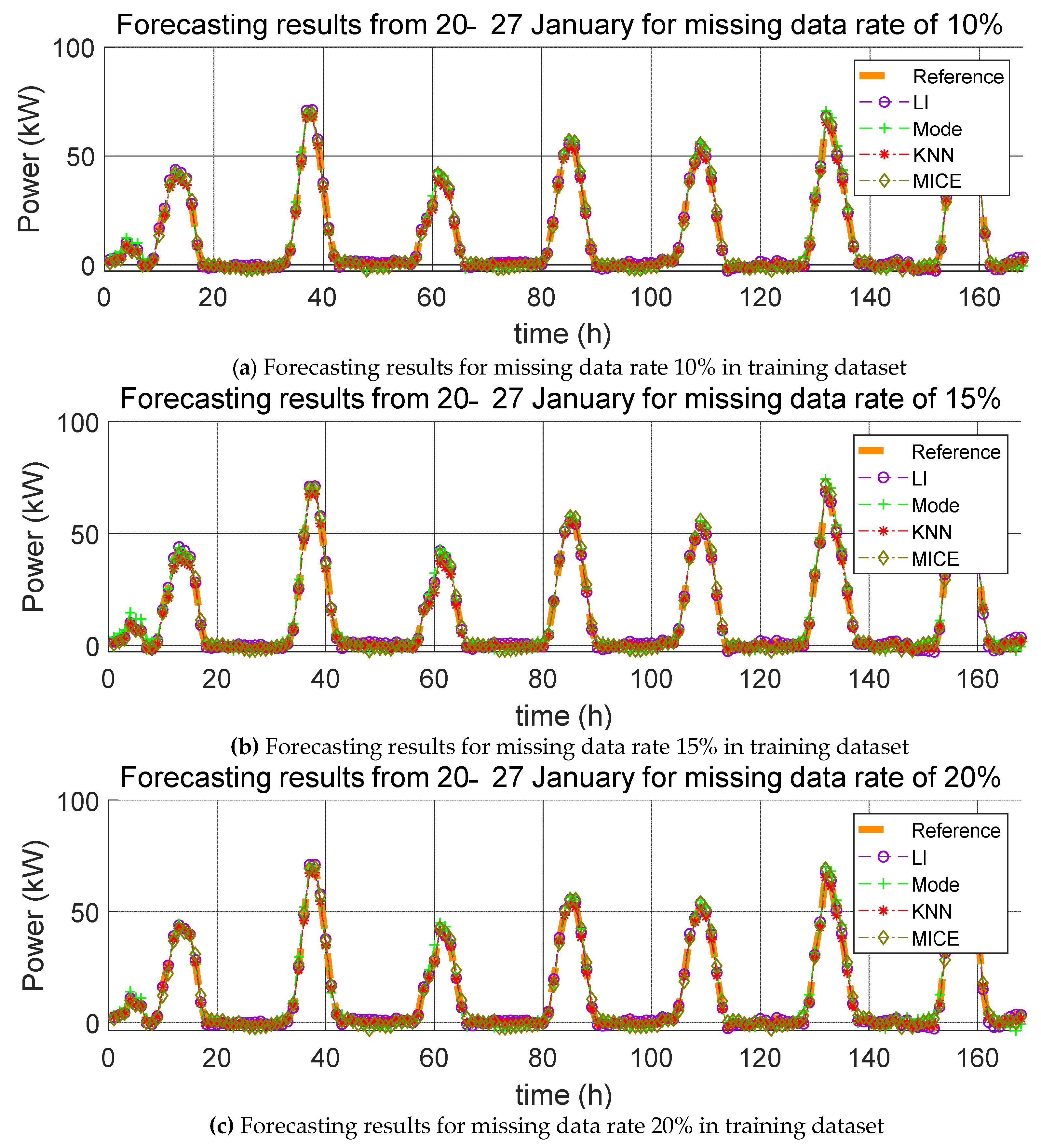
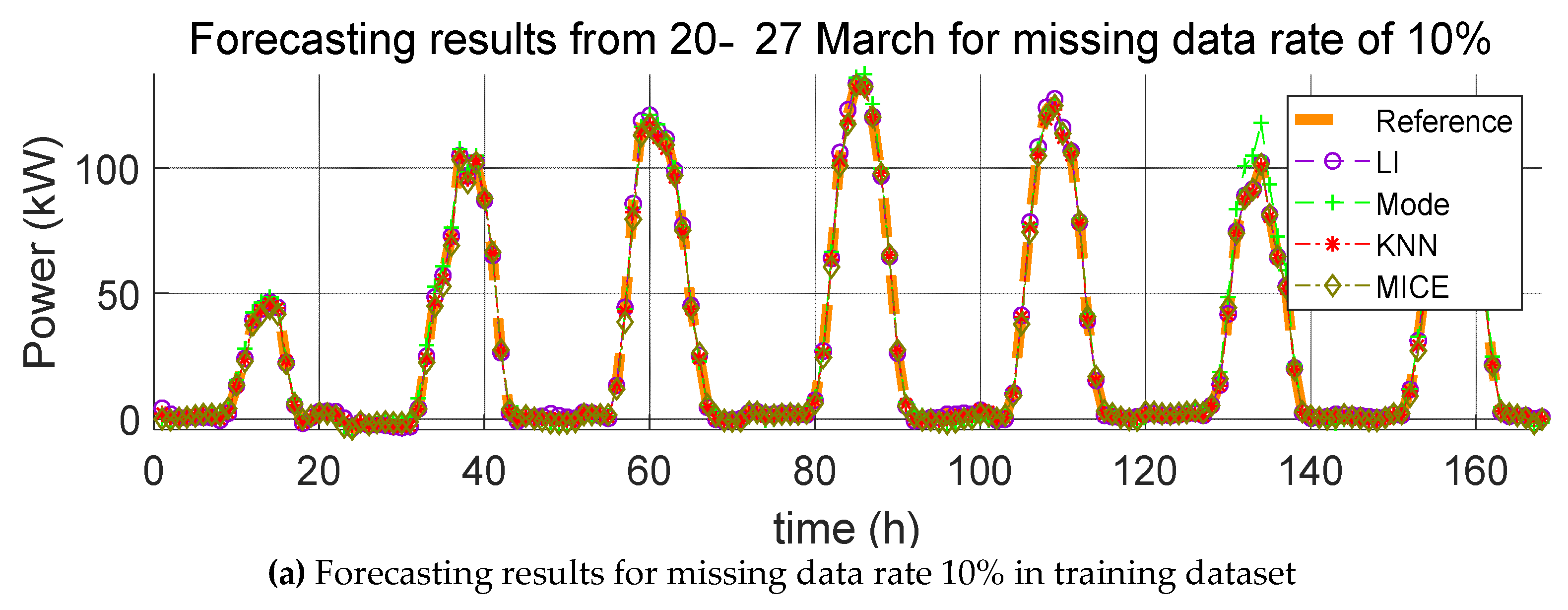
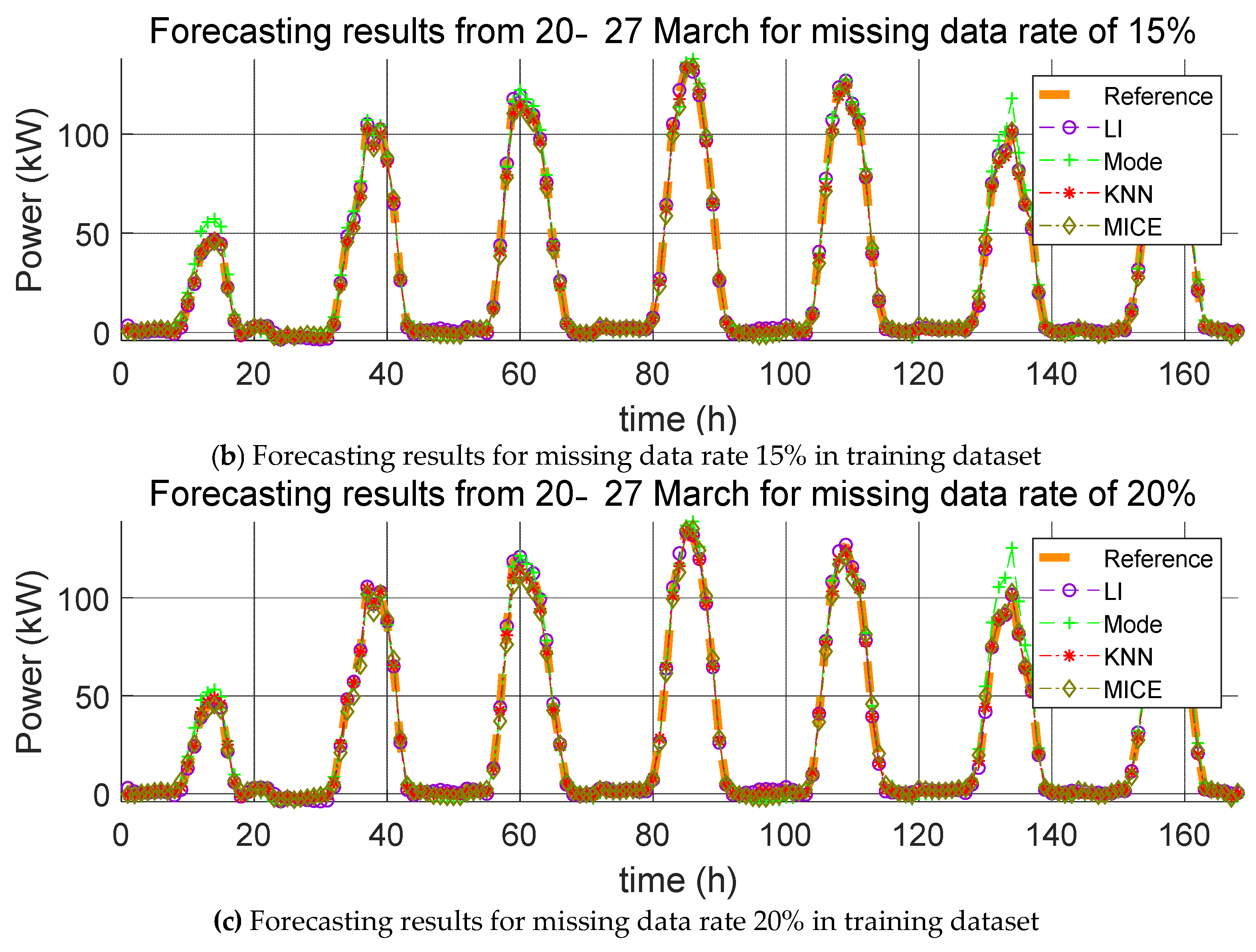
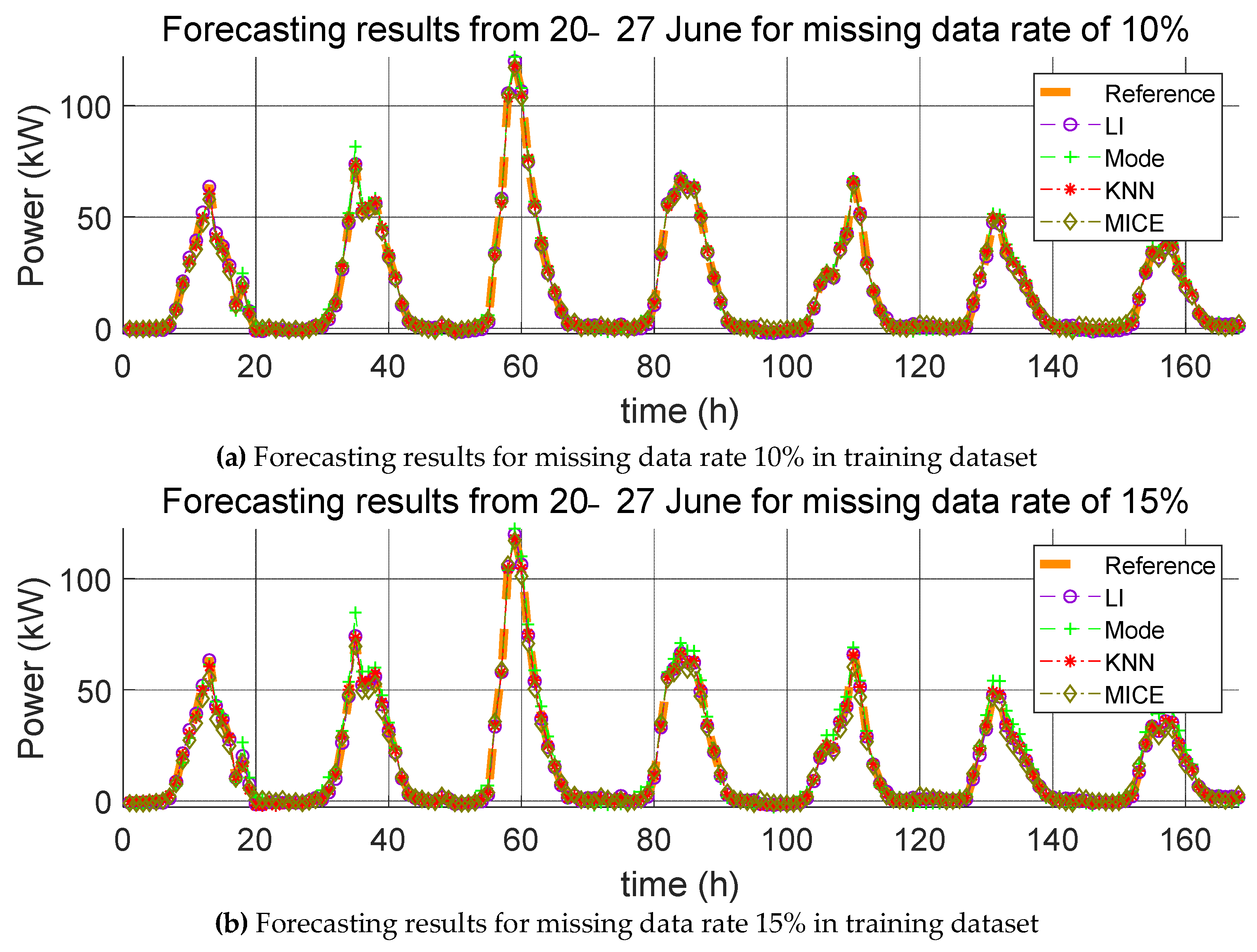
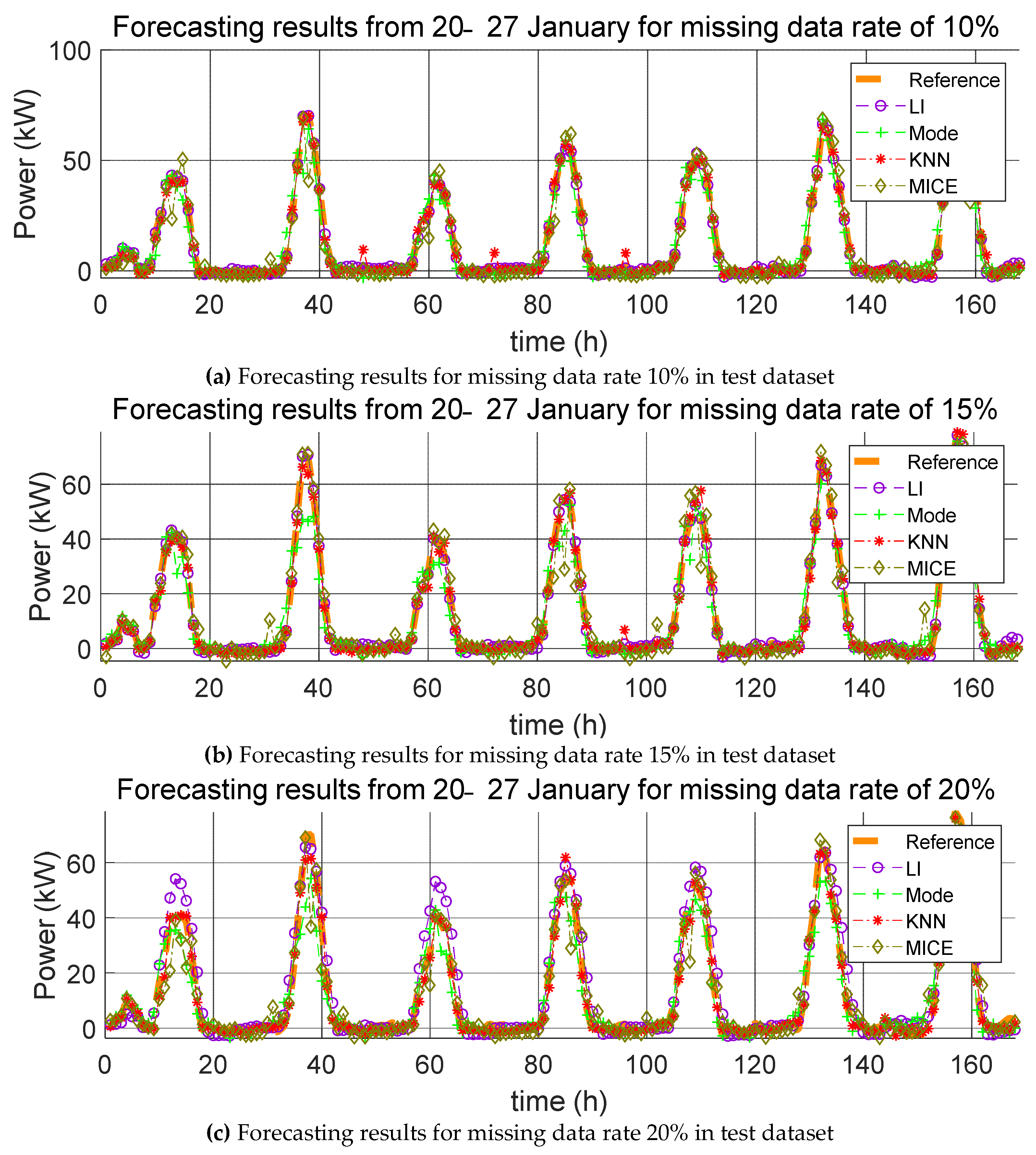
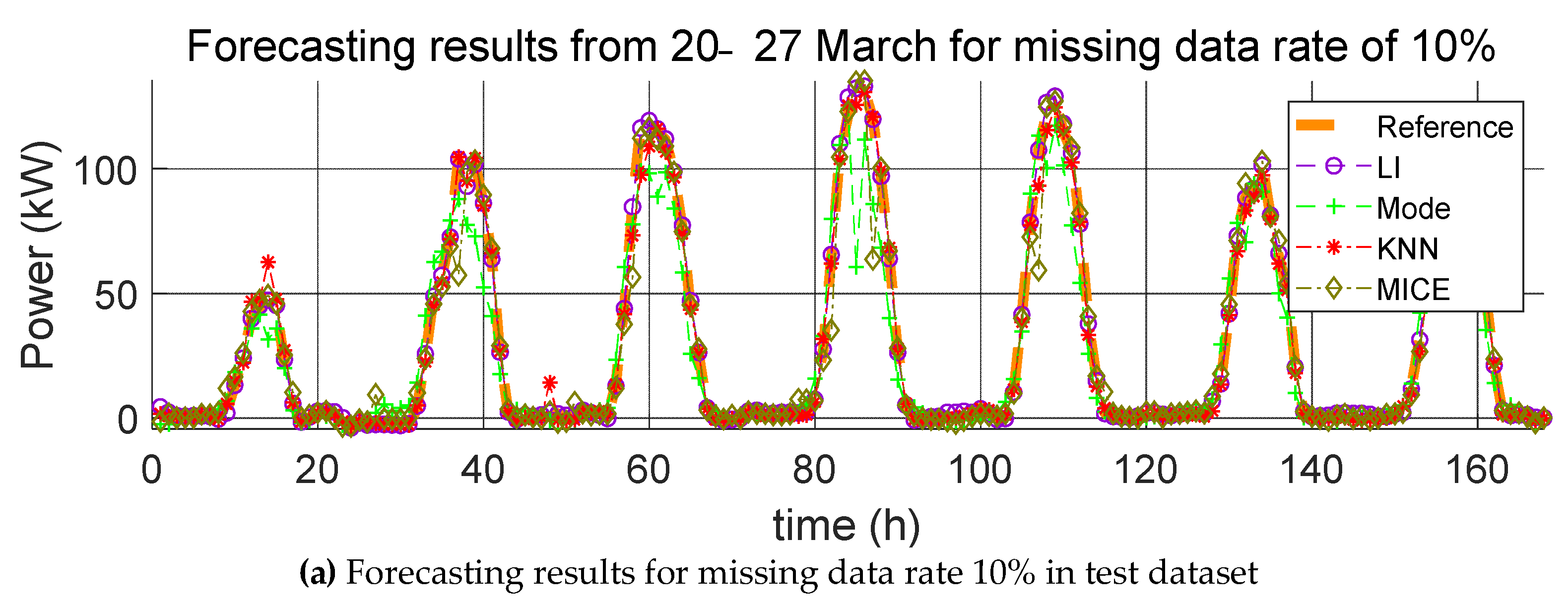
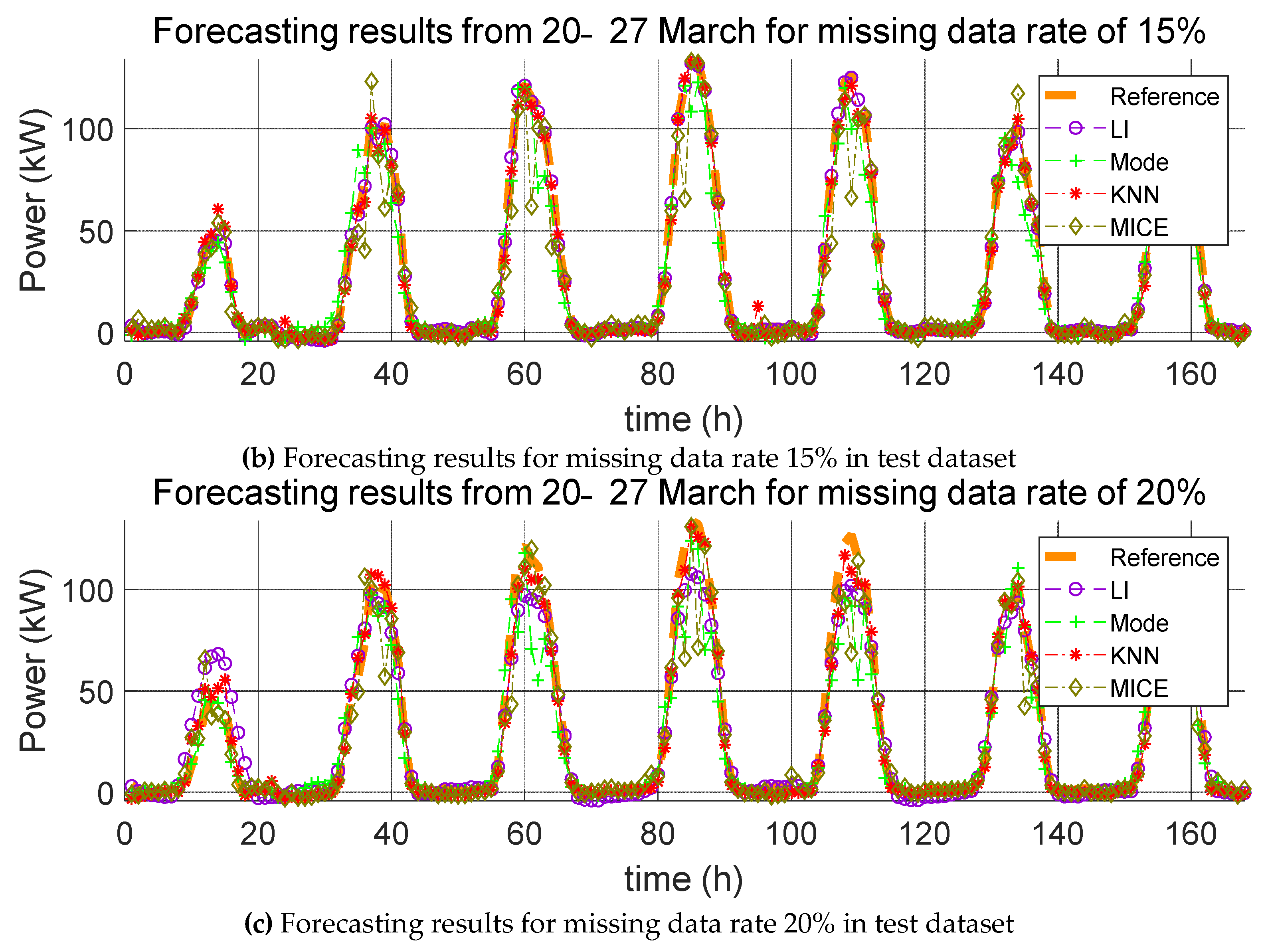
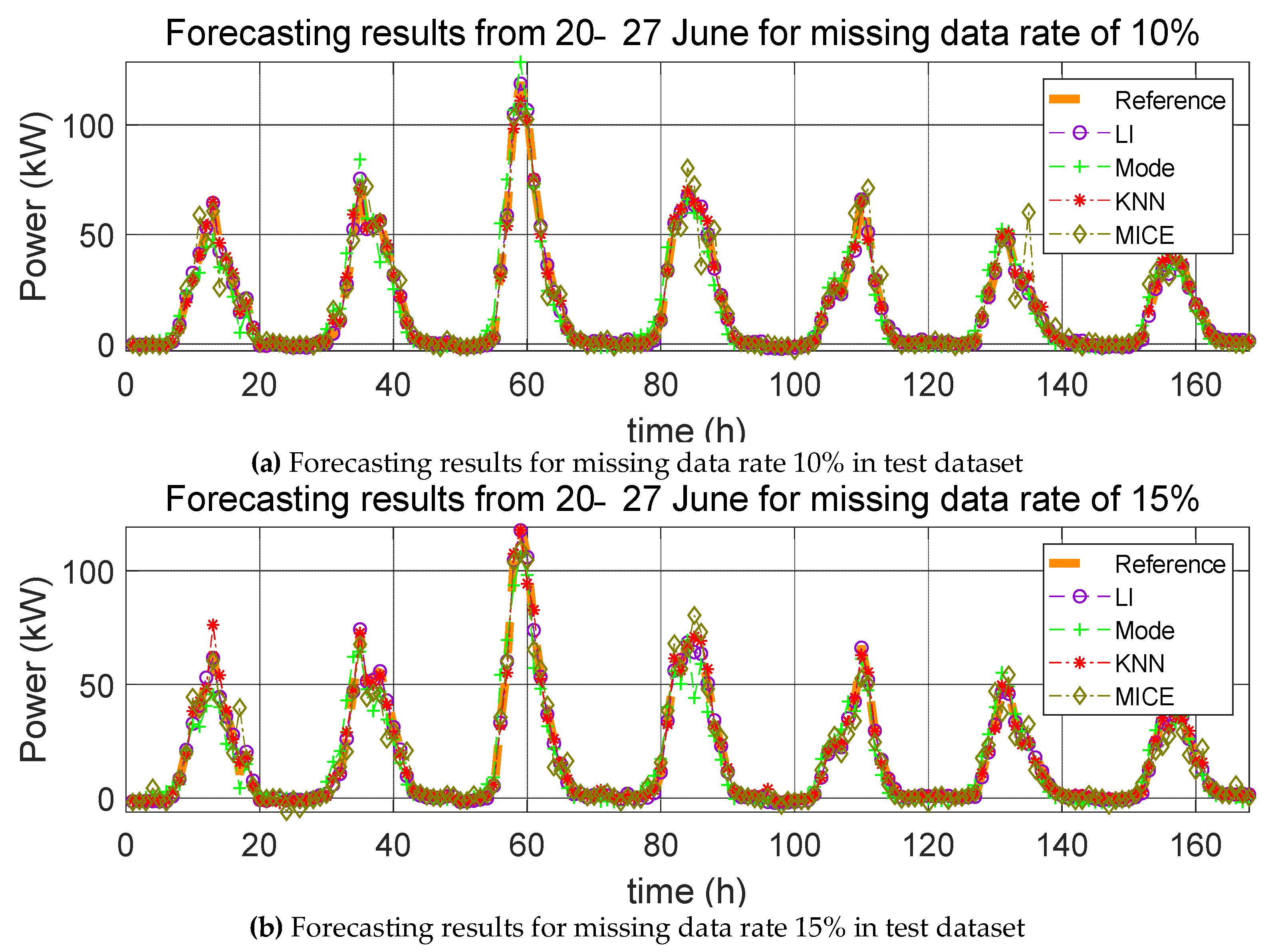
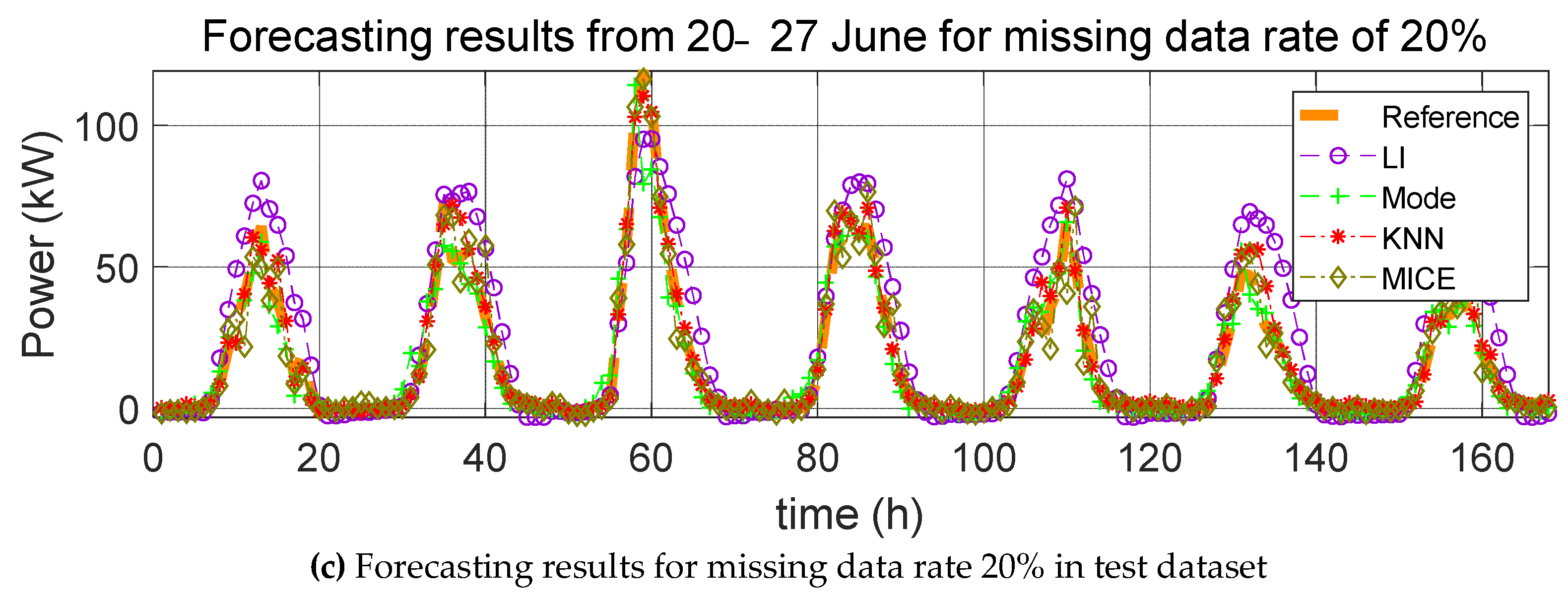
3. Impact Evaluation of Missing Data Imputation on PV Forecasting
In order to verify the effect of missing data imputation on PV forecasting, we used four error indices, root mean square error (RMSE), mean relative error (MRE), root mean square deviation (RMSD), and mean relative deviation (MRD), defined, respectively, as follows:
RMSE and MRE are performance errors of prediction models used in previous studies. RMSD and MRD are indicators that quantify the effect of the selected missing data imputation method on the PV power prediction model. Here,
denotes the predicted PV power data without using missing data imputation. In other words,
is the output predicted by the model trained with the initial weather data. We set
as the predicted value and not the actual value in order to identify only the effect of missing data imputation. These indices are very different from the error metrics used in previous forecasting studies [
8,
9,
10,
23]. If
is set as the actual output, the prediction error can be changed according to the forecast model and not the imputation method. Further, in the above equations,
denotes the predicted value obtained with the application of missing data imputation,
the PV power capacity, N the number of forecast PV power outputs, and
the actual PV power. In this study,
= 196 kW
p. The RMSE and MRE can be calculated from these values. According to [
9], RMSE indicates the average size of the error. A larger error corresponds to a larger weight being added to RMSE. The special importance of RMSE is that it indicates that the occurrence of a sudden large error is more problematic than multiple small errors occurring multiple times. Further, we use the MRE instead of the MAPE because a small real value can cause a large error. For example, in the case of the PV model, there is almost no solar power generation at 06:00, and the MAPE value is only measured for actual solar power generation. We therefore choose the error index of MRE.