Surface-Wave Extraction Based on Morphological Diversity of Seismic Events
Abstract
Featured Application
Abstract
1. Introduction
2. Conventional Method: Extracting Surface Waves in the f-v Domain
3. New Method: Sparse Representations of Wavefields Based on MCA
3.1. Frequency-Domain High-Resolution LRT
3.2. Time-Domain High-Resolution HRT
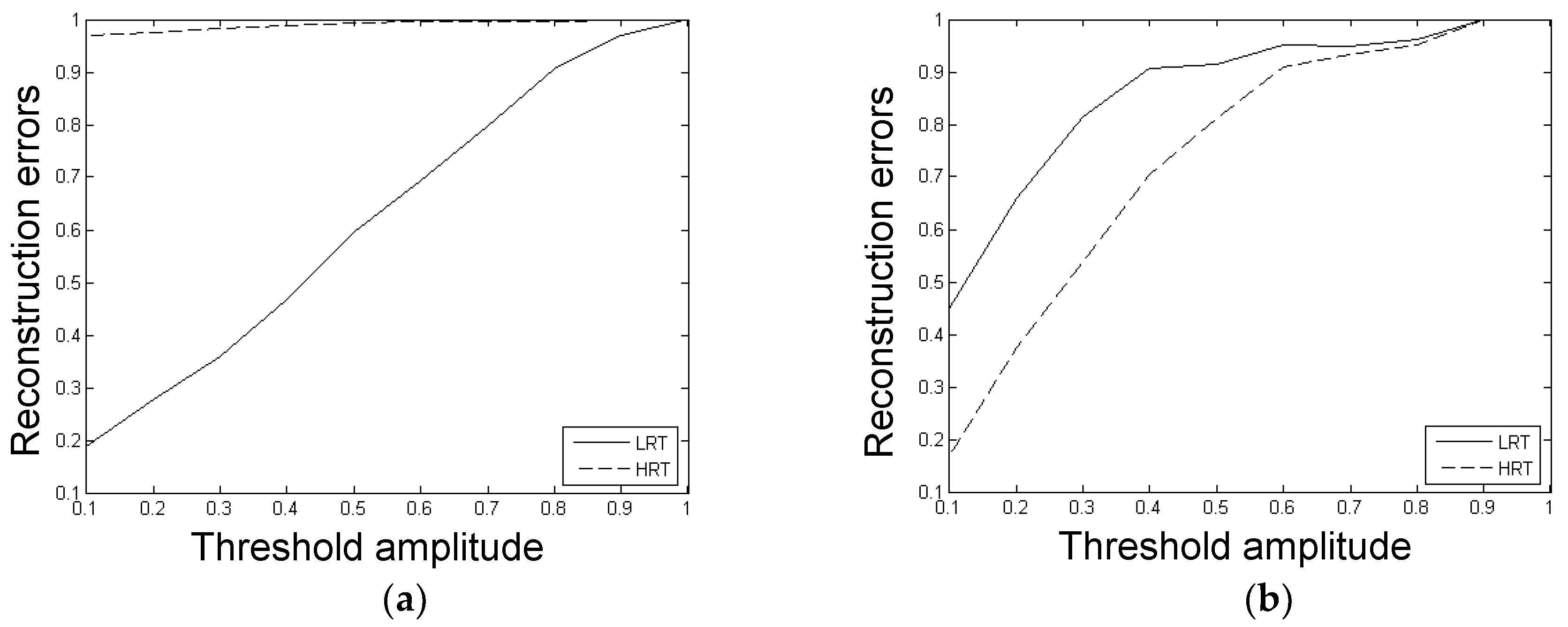
3.3. Performance of Sparse Representations Using LRT and HRT
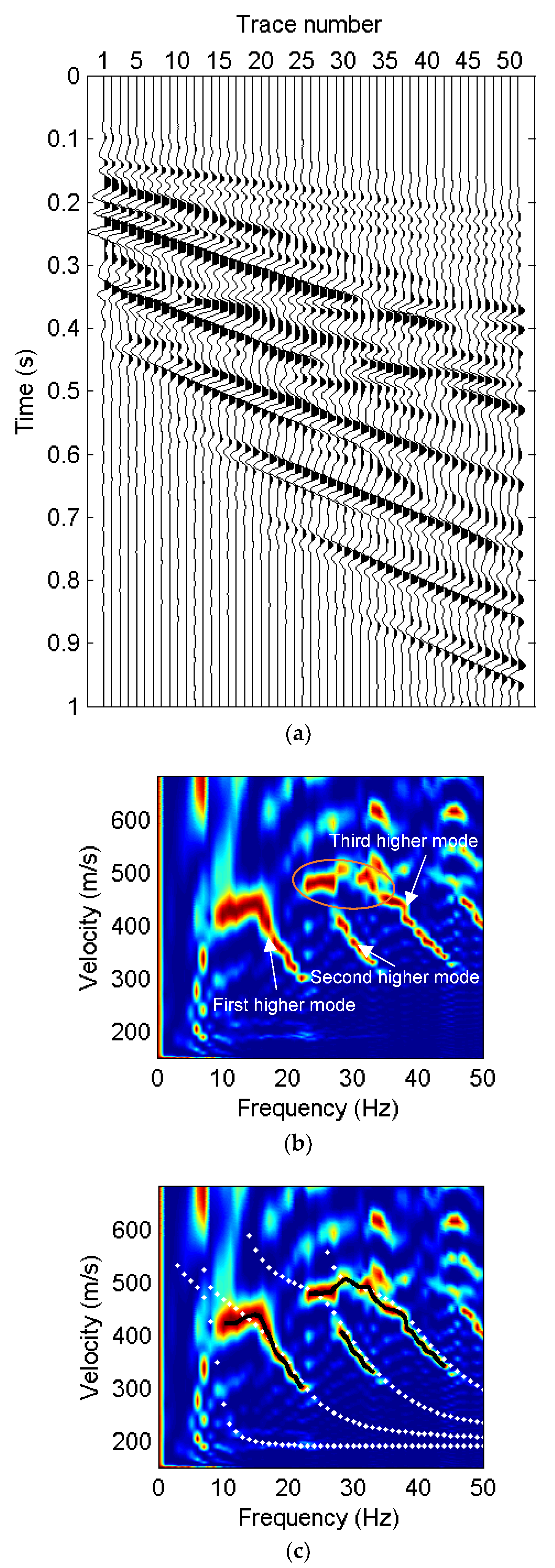
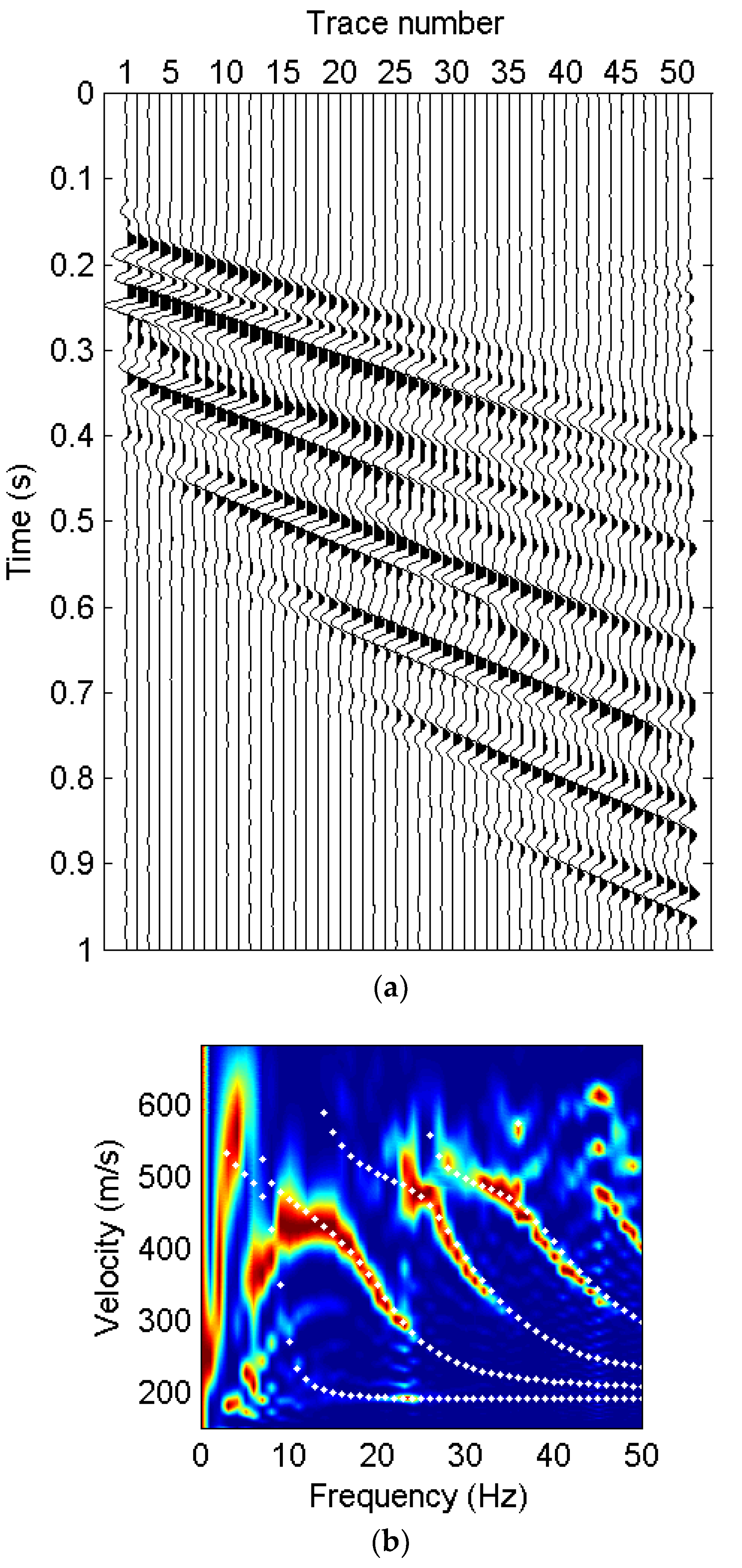
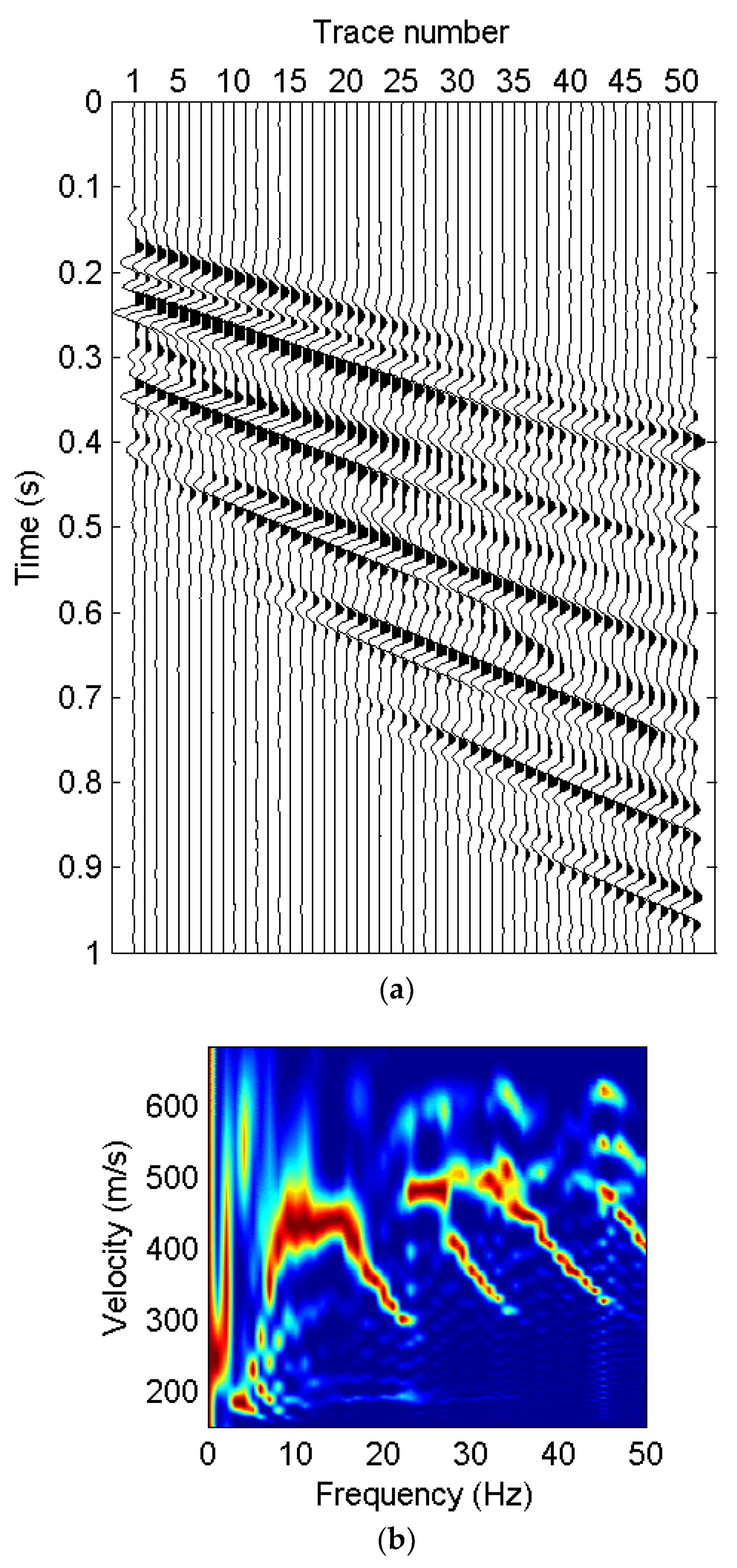
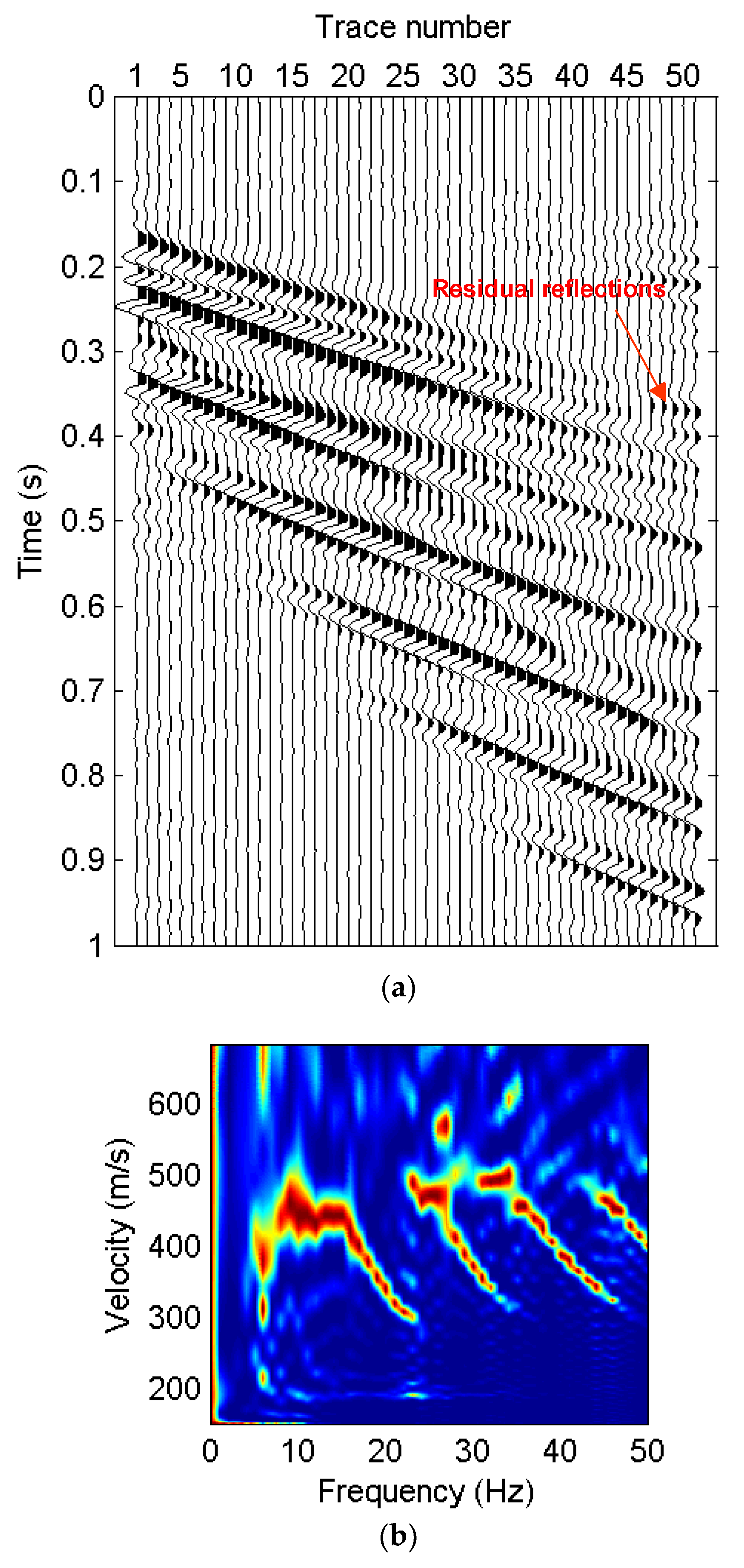
4. Examples
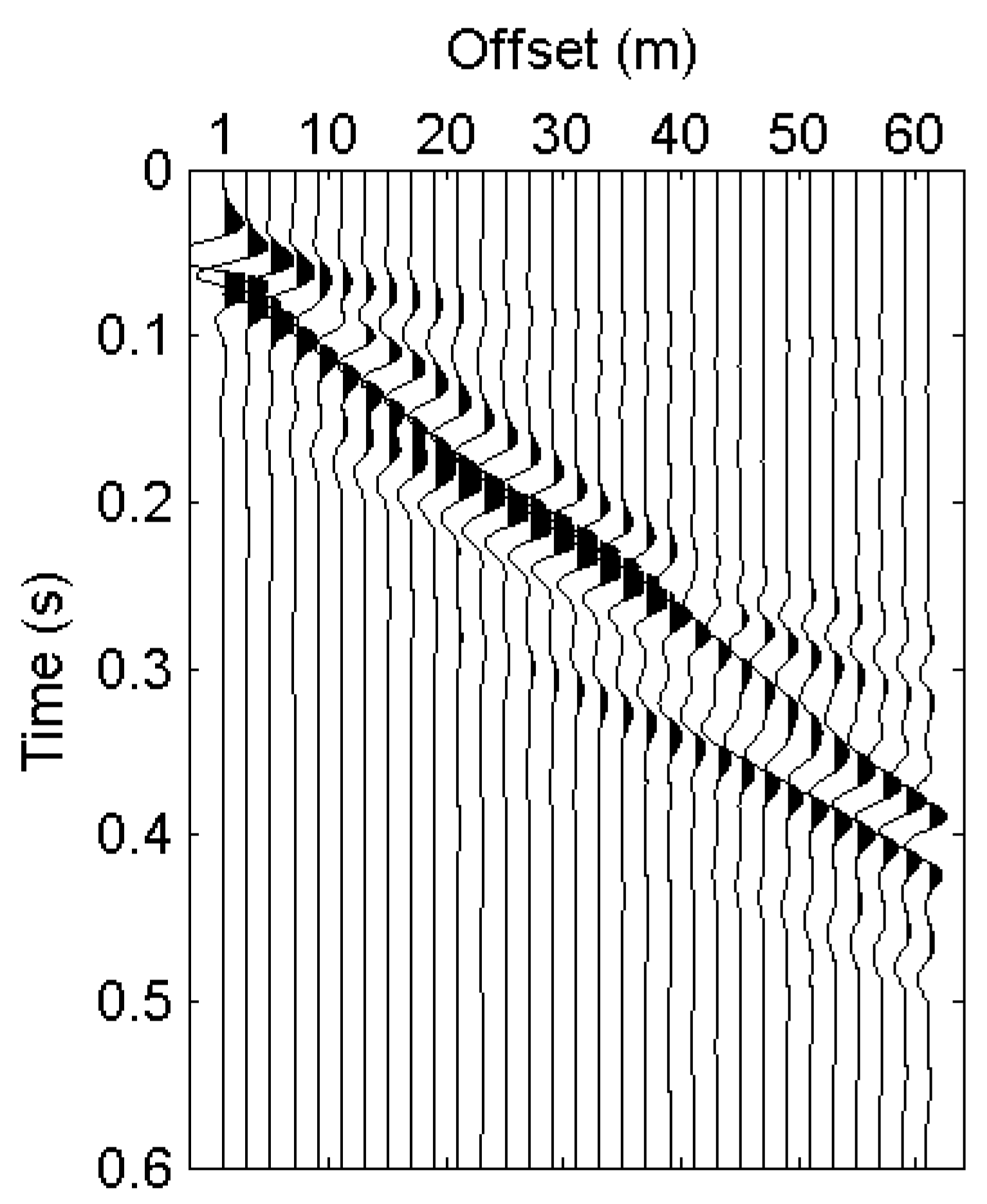
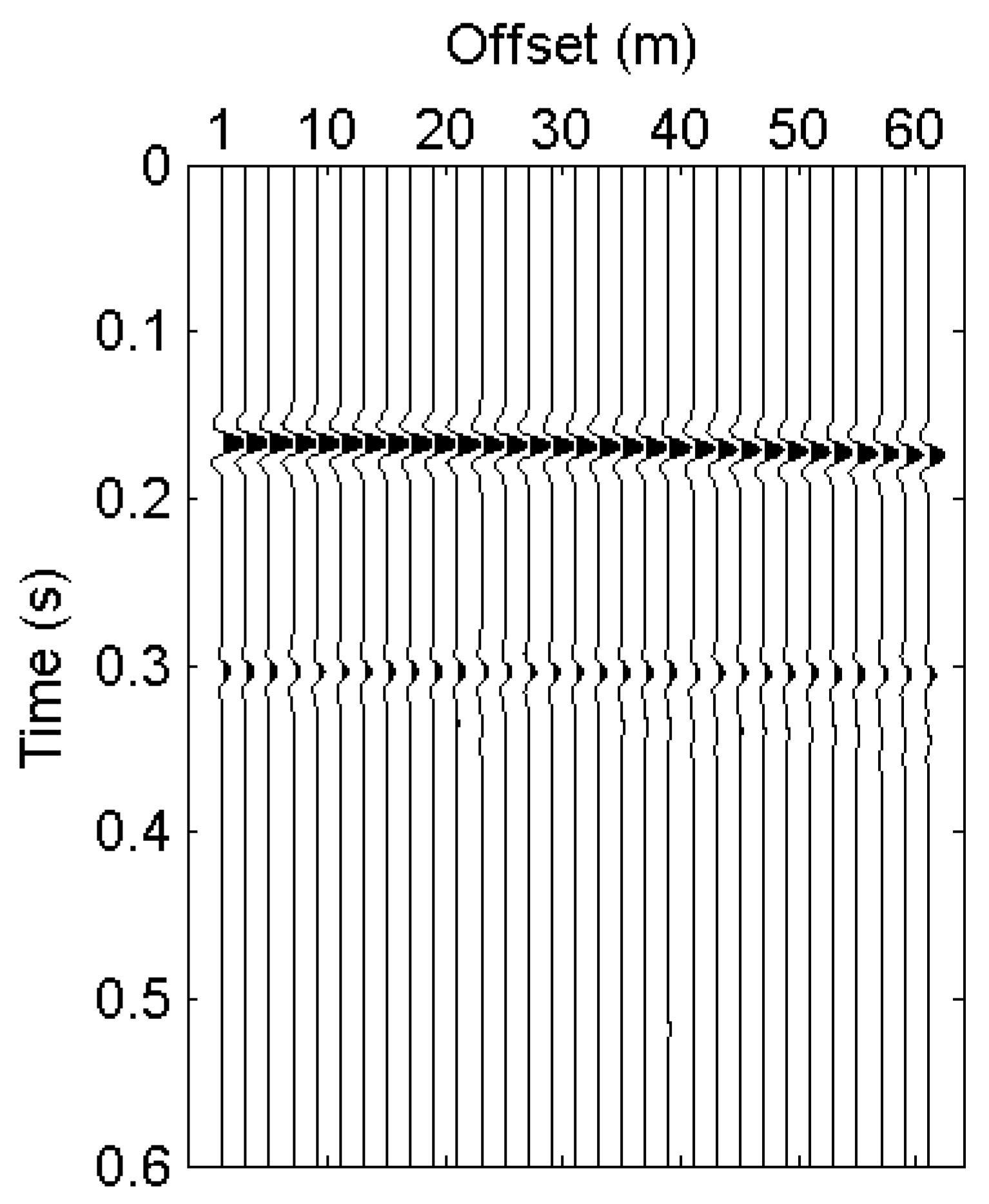
4.1. Synthetic Examples
4.1.1. Distortion of Surface-Wave Dispersive Energy Caused by Reflections
4.1.2. Recovery of the Surface-Wave Dispersive Energy
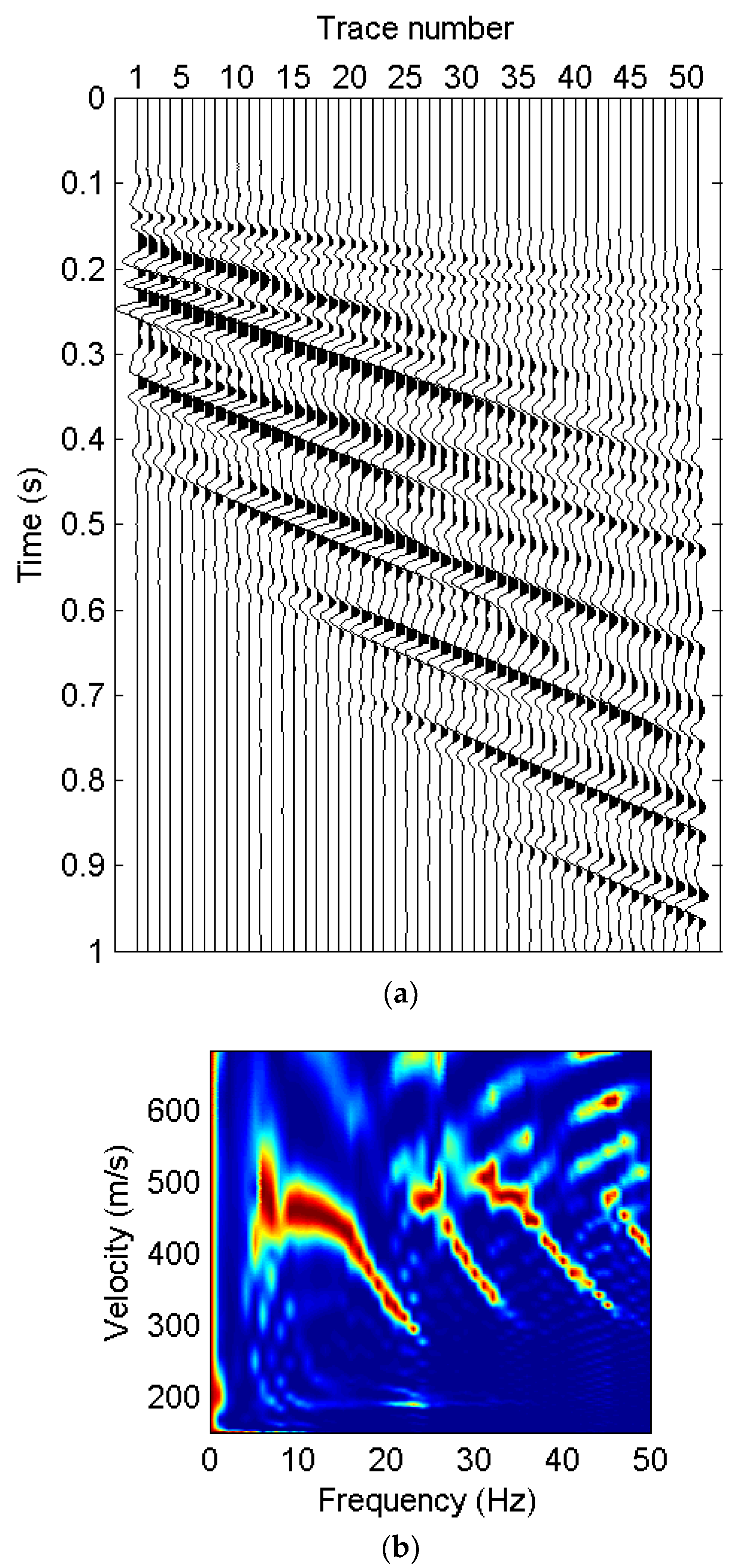
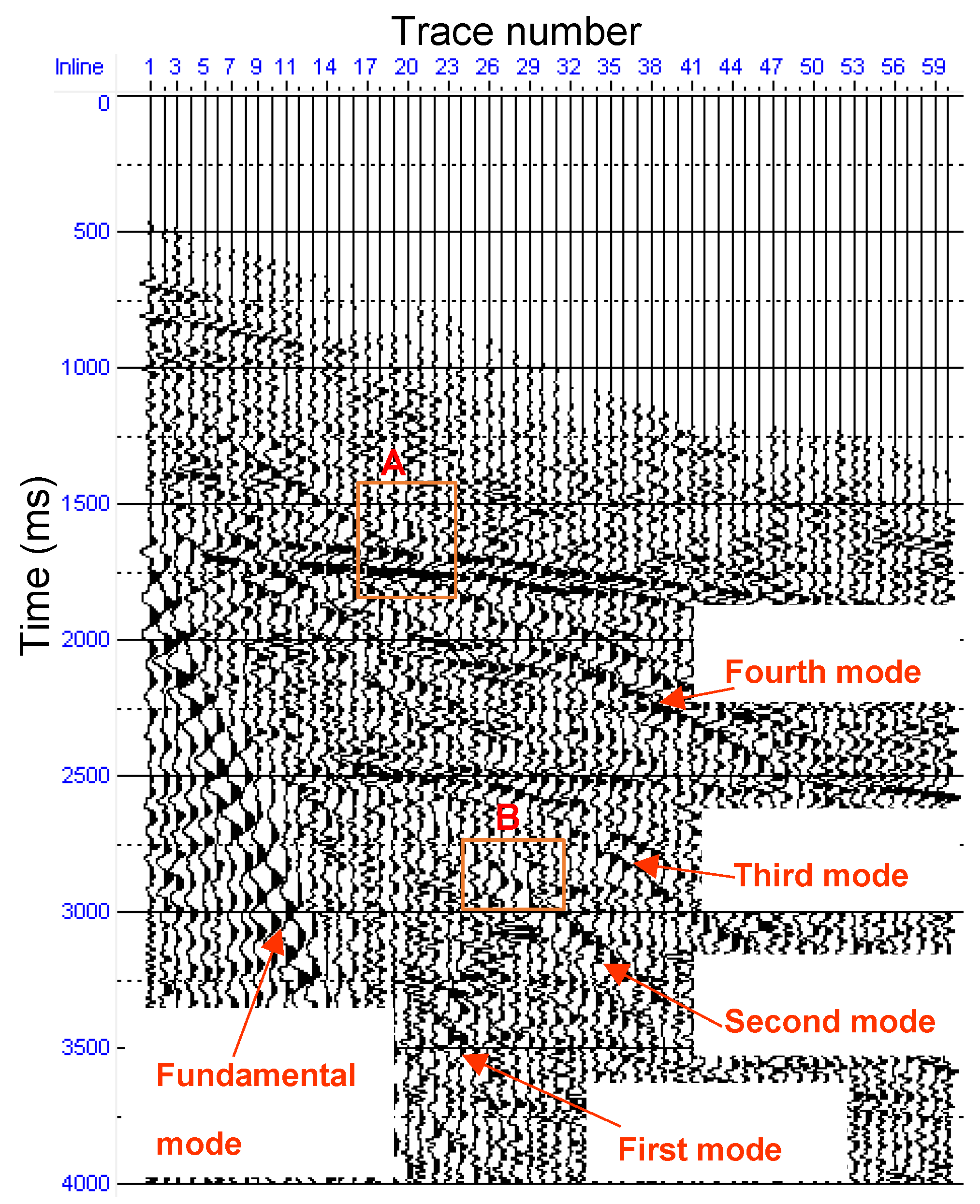
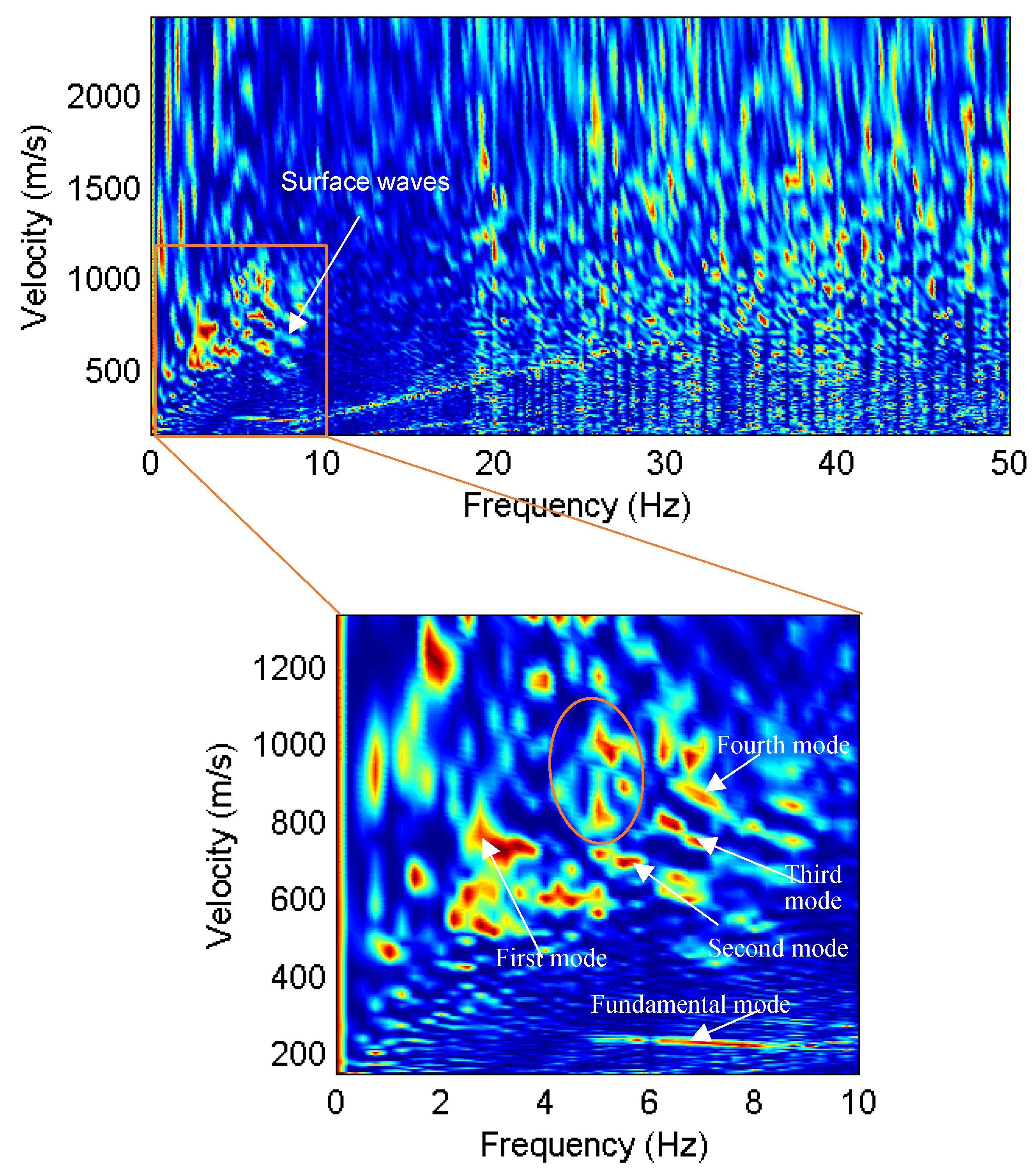
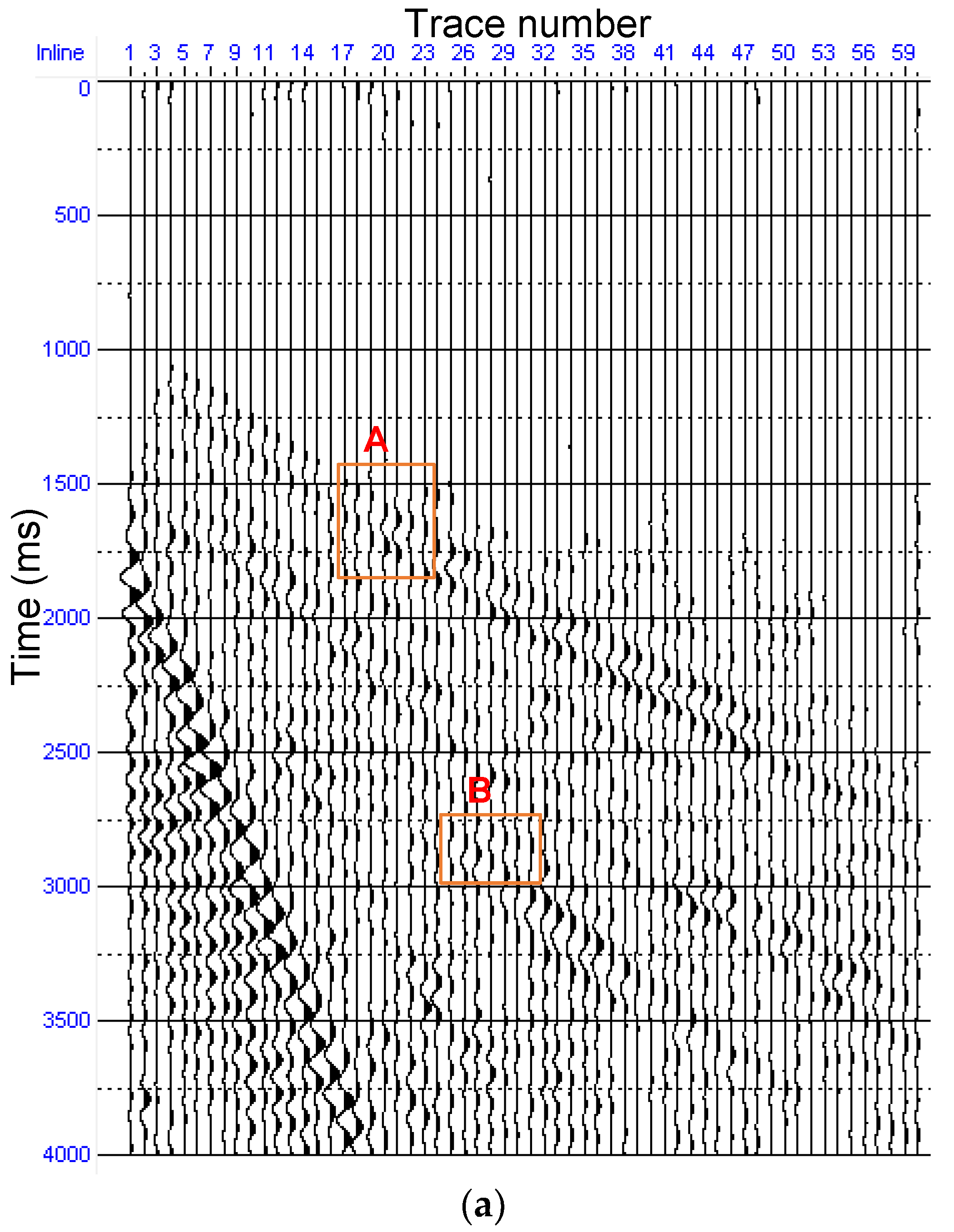
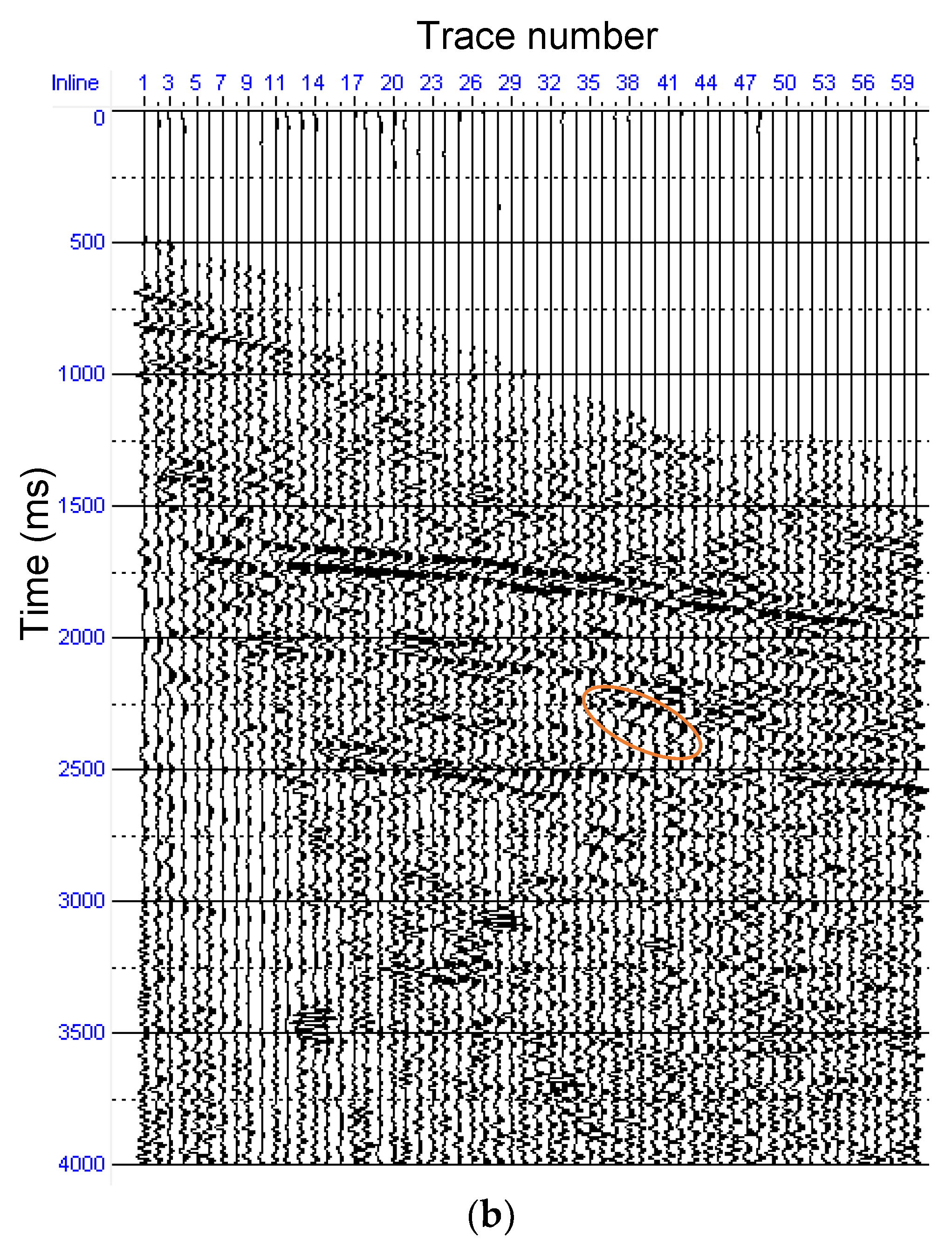
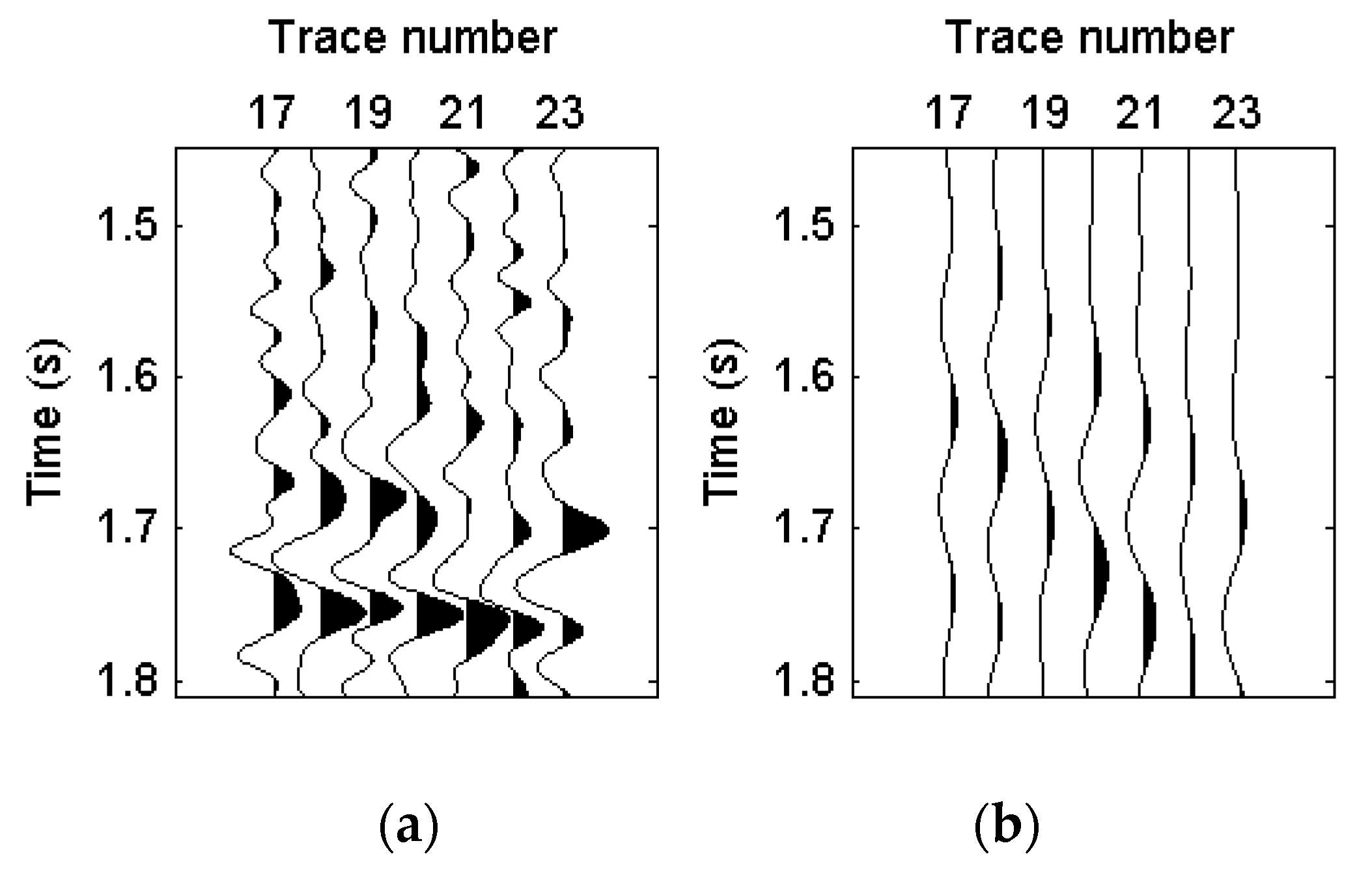
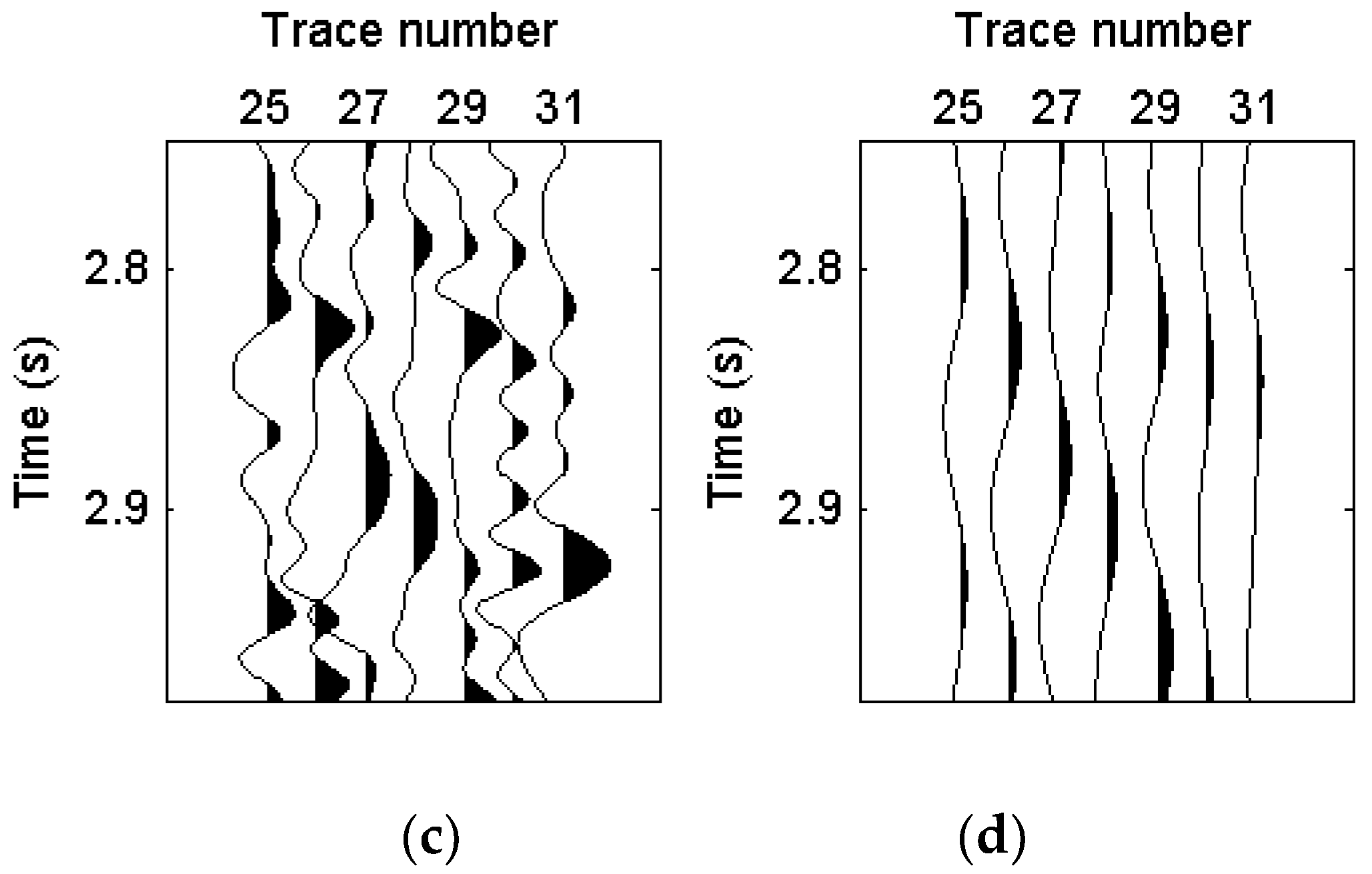
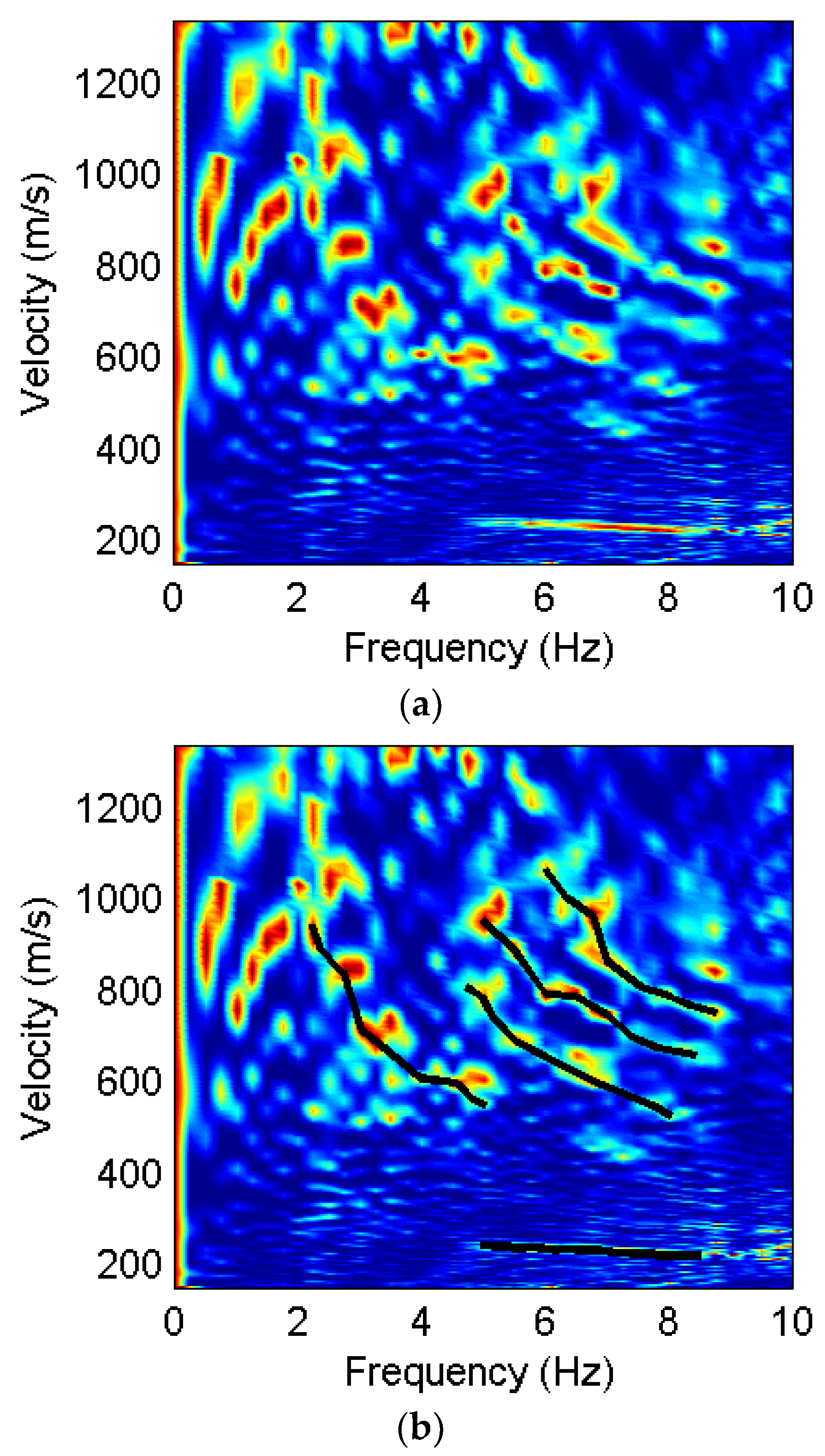
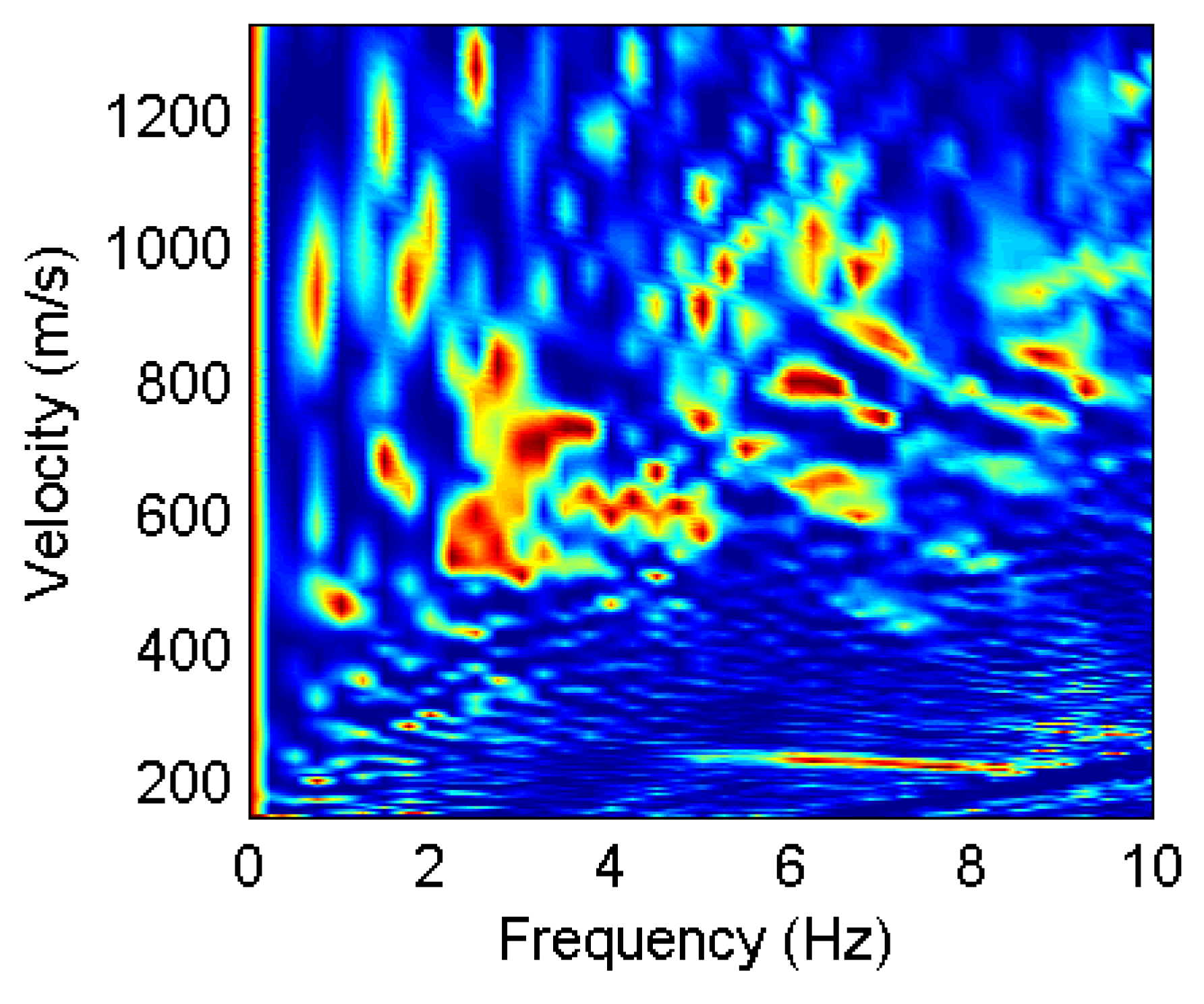
4.2. Field Example
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Eker, A.M.; Akgün, H.; Koçkar, M.K. Local Site Characterization and Seismic Zonation Study by Utilizing Active and Passive Surface Wave Methods: A Case Study for the Northern Side of Ankara, Turkey. Eng. Geol. 2012, 151, 64–81. [Google Scholar] [CrossRef]
- Kästle, E.D.; El-Sharkawy, A.; Boschi, L.; Meier, T.; Rosenberg, C.; Bellahsen, N.; Cristiano, L.; Weidle, C. Surface Wave Tomography of the Alps Using Ambient-Noise and Earthquake Phase Velocity Measurements. J. Geophys. Res. Solid Earth 2018, 123, 1770–1792. [Google Scholar] [CrossRef]
- Yang, C.Y.; Wang, Y.; Lu, J. Application of Rayleigh Waves on PS-Wave Static Corrections. J. Geophys. Eng. 2012, 9, 90–97. [Google Scholar] [CrossRef]
- Muyzert, E. Scholte Wave Velocity Inversion for a near Surface S-Velocity Model and PS-Statics. In Proceedings of the 70th Annual International Meeting, SEG, Expanded Abstracts, Calgary, AB, Canada, 6–11 August 2000; pp. 1197–1200. [Google Scholar] [CrossRef]
- Song, X.H.; Gu, H.M.; Liu, J.P.; Zhang, X.Q. Estimation of Shallow Subsurface Shear-Wave Velocity by Inverting Fundamental and Higher-Mode Rayleigh Waves. Soil Dyn. Earthq. Eng. 2007, 27, 599–607. [Google Scholar] [CrossRef]
- Xia, J.H.; Miller, R.D.; Park, C.B.; Tian, G. Inversion of High Frequency Surface Waves with Fundamental and Higher Modes. J. Appl. Geophys. 2003, 52, 45–57. [Google Scholar] [CrossRef]
- Poggi, V.; Fäh, D. Estimating Rayleigh Wave Particle Motion from Three-Component Array Analysis of Ambient Vibrations. Geophys. J. Int. 2010, 180, 251–267. [Google Scholar] [CrossRef]
- Kimman, W.P.; Campman, X.; Trampert, J. Characteristics of Seismic Noise: Fundamental and Higher Mode Energy Observed in the Northeast of the Netherlands. Bull. Seismol. Soc. Am. 2012, 102, 1388–1399. [Google Scholar] [CrossRef]
- Savage, M.K.; Lin, F.C.; Townend, J. Ambient Noise Cross-Correlation Observations of Fundamental and Higher-Mode Rayleigh Wave Propagation Governed by Basement Resonance. Geophys. Res. Lett. 2013, 40, 3556–3561. [Google Scholar] [CrossRef]
- Luo, Y.H.; Xia, J.H.; Miller, R.D.; Xu, Y.X.; Liu, J.P.; Liu, Q.S. Rayleigh-Wave Dispersive Energy Imaging Using a High-Resolution Linear Radon Transform. Pure Appl. Geophys. 2008, 165, 903–922. [Google Scholar] [CrossRef]
- Xia, J.H.; Xu, Y.X.; Luo, Y.H.; Miller, R.D.; Cakir, R.; Zeng, C. Advantages of Using Multichannel Analysis of Love Waves (Malw) to Estimate near-Surface Shear-Wave Velocity. Surv. Geophys. 2012, 33, 841–860. [Google Scholar] [CrossRef]
- Zhang, S.X.; Chan, L.S. Possible Effects of Misidentified Mode Number on Rayleigh Wave Inversion. J. Appl. Geophys. 2003, 53, 17–29. [Google Scholar] [CrossRef]
- Liu, Z.; Chen, Y.; Ma, J. Ground Roll Attenuation by Synchrosqueezed Curvelet Transform. J. Appl. Geophys. 2018, 151, 246–262. [Google Scholar] [CrossRef]
- Naghizadeh, M.; Sacchi, M. Ground-Roll Attenuation Using Curvelet Downscaling. Geophysics 2018, 83, V185–V195. [Google Scholar] [CrossRef]
- Hosseini, S.A.; Javaherian, A.; Hassani, H.; Torabi, S.; Sadri, M. Adaptive Attenuation of Aliased Ground Roll Using the Shearlet Transform. J. Appl. Geophys. 2015, 112, 190–205. [Google Scholar] [CrossRef]
- Lu, J.; Yun, W.; Yang, C.Y. Instantaneous Polarization Filtering Focused on Suppression of Surface Waves. Appl. Geophys. 2010, 7, 88–97. [Google Scholar] [CrossRef]
- Lu, J.; Wang, Y.; Chen, J.Y. Noise Attenuation Based on Wave Vector Characteristics. Appl. Sci. 2018, 8, 672. [Google Scholar] [CrossRef]
- Trad, D.; Sacchi, M.D.; Ulrych, T.J. A Hybrid Linear-Hyperbolic Radon Transform. J. Seism. Explor. 2001, 9, 303–318. [Google Scholar]
- Hu, Y.; Wang, L.M.; Cheng, F.; Luo, Y.H.; Shen, C.; Mi, B.B. Ground-Roll Noise Extraction and Suppression Using High-Resolution Linear Radon Transform. J. Appl. Geophys. 2016, 128, 8–17. [Google Scholar] [CrossRef]
- Luo, Y.H.; Xia, J.H.; Miller, R.D.; Xu, Y.; Liu, J.P.; Liu, Q.S. Rayleigh-Wave Mode Separation by High-Resolution Linear Radon Transform. Geophys. J. Int. 2009, 179, 254–264. [Google Scholar] [CrossRef]
- Ibrahim, A.; Sacchi, M.D. Simultaneous Source Separation Using a Robust Radon Transform. Geophysics 2014, 79, V1–V11. [Google Scholar] [CrossRef]
- Trad, D.; Ulrych, T.J.; Sacchi, M.D. Latest Views of the Sparse Radon Transform. Geophysics 2003, 68, 386–399. [Google Scholar] [CrossRef]
- Starck, J.L.; Elad, M.; Donoho, D.L. Redundant Multiscale Transforms and Their Application for Morphological Component Separation. Adv. Imaging Electron Phys. 2004, 132, 287–348. [Google Scholar] [CrossRef]
- Starck, J.L.; Elad, M.; Donoho, D.L. Image Decomposition Via the Combination of Sparse Representations and a Variational Approach. IEEE Trans. Image Process. 2005, 14, 1570–1582. [Google Scholar] [CrossRef] [PubMed]
- Wang, W.; Gao, J.H.; Chen, W.C.; Xu, J. Data Adaptive Ground-Roll Attenuation Via Sparsity Promotion. J. Appl. Geophys. 2012, 83, 19–28. [Google Scholar] [CrossRef]
- Jiang, X.X.; Zheng, F.; Jia, H.Q.; Lin, J.; Yang, H.Y. Time-Domain Hyperbolic Radon Transform for Separation of P-P and P-Sv Wavefields. Stud. Geophys. Geod. 2016, 60, 91–111. [Google Scholar] [CrossRef]
- Gholami, A.; Aghamiry, H.S. Iteratively Re-Weighted and Refined Least Squares Algorithm for Robust Inversion of Geophysical Data. Geophys. Prospect. 2017, 65, 201–215. [Google Scholar] [CrossRef]
- Trad, D.; Ulrych, T.J.; Sacchi, M.D. Accurate Interpolation with High-Resolution Time-Variant Radon Transforms. Geophysics 2002, 67, 25–26. [Google Scholar] [CrossRef]
- Sabbione, J.I.; Sacchi, M.D. Restricted Model Domain Time Radon Transforms. Geophysics 2016, 81, A17–A21. [Google Scholar] [CrossRef]
- Sabbione, J.I.; Velis, D.R.; Sacchi, M.D. Microseismic Data Denoising Via an Apex-Shifted Hyperbolic Radon Transform. In Proceedings of the 83rd Annual International Meeting, SEG, Expanded Abstracts, Houston, TX, USA, 22–27 September 2013; pp. 2155–2161. [Google Scholar] [CrossRef]
- Xu, Y.X.; Xia, J.H.; Miller, R.D. Numerical Investigation of Implementation of Air-Earth Boundary by Acoustic-Elastic Boundary Approach. Geophysics 2007, 72, SM147–SM153. [Google Scholar] [CrossRef]
- Sun, J.Z.; Chen, X.; Tian, X.F. Engineering Infrastructure Nondestructive Testing with Rayleigh Waves: Case Studies in Transportation and Archaeology. J. Geophys. Eng. 2007, 4, 268. [Google Scholar] [CrossRef]
- Gong, X.B.; Yu, C.X.; Wang, Z.H. Separation of Prestack Seismic Diffractions Using an Improved Sparse Apex-Shifted Hyperbolic Radon Transform. Explor. Geophys. 2016, 48, 476–484. [Google Scholar] [CrossRef]
| Thickness (m) | Vp (m/s) | Vs (m/s) | Density (kg/m3) |
|---|---|---|---|
| 10 | 800 | 200 | 2000 |
| - | 1200 | 400 | 2000 |
| Thickness (m) | Vp (m/s) | Vs (m/s) | Density (kg/m3) |
|---|---|---|---|
| 100 | 1200 | 400 | 2000 |
| 150 | 2200 | 1320 | 2250 |
| - | 3300 | 2045 | 2400 |
| Thickness (m) | Vp (m/s) | Vs (m/s) | Density (kg/m3) |
|---|---|---|---|
| 10 | 800 | 200 | 2000 |
| 90 | 1200 | 600 | 2000 |
| Thickness (m) | Vp (m/s) | Vs (m/s) | Density (kg/m3) |
|---|---|---|---|
| 10 | 800 | 200 | 2000 |
| 90 | 1200 | 600 | 2000 |
| 600 | 2200 | 1320 | 2250 |
| - | 3300 | 2045 | 2400 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qiu, X.; Wang, C.; Lu, J.; Wang, Y. Surface-Wave Extraction Based on Morphological Diversity of Seismic Events. Appl. Sci. 2019, 9, 17. https://doi.org/10.3390/app9010017
Qiu X, Wang C, Lu J, Wang Y. Surface-Wave Extraction Based on Morphological Diversity of Seismic Events. Applied Sciences. 2019; 9(1):17. https://doi.org/10.3390/app9010017
Chicago/Turabian StyleQiu, Xinming, Chao Wang, Jun Lu, and Yun Wang. 2019. "Surface-Wave Extraction Based on Morphological Diversity of Seismic Events" Applied Sciences 9, no. 1: 17. https://doi.org/10.3390/app9010017
APA StyleQiu, X., Wang, C., Lu, J., & Wang, Y. (2019). Surface-Wave Extraction Based on Morphological Diversity of Seismic Events. Applied Sciences, 9(1), 17. https://doi.org/10.3390/app9010017






