1. Introduction
Harmony is a central part of music and an important consideration for music information retrieval systems. Generative statistical models for chord sequences are widely used for tasks such as automatic chord estimation [
1], chord prediction [
2,
3] melody harmonization [
4,
5,
6,
7], music analysis [
8], and classification [
9,
10]. Representations of pitch space such as the Tonnetz have provided a basis for reasoning about triadic transformations using mathematical group theory [
11,
12,
13].
Harmony and chord sequences play a fundamental role in the understanding of electronic dance music, particularly classically tonal sub-genres of trance coming under different labels such as uplifting trance, epic trance, progressive trance, and euphoric trance. Relying mainly on simple major and minor triadic forms, the chord sequences within trance music repeat on several levels, and a pivotal issue for trance generation is therefore the generation of idiomatic chord loops.
For chord sequence generation, somewhat surprisingly, a trained statistical generative model does not imply a method for direct generation of sequences: this must be implemented as a meta-procedure which involves certain design choices on the space of sequences desired. Single random samples from a model are likely to fall within the mean of the overall sequence distribution, and if only a limited number of sequences is to be presented, it is better to perform some optimization and focus on a subset of high probability sequences. This implies that the model is not overfit to a training corpus, otherwise high probability sequences may be excessively “normative” or contain excessive copying of corpus sequences. The approach taken here is to deliberately underfit the corpus, by using a low-order statistical model. In this way, surprising sequences can be generated, and the pattern and diatonicity functionality of the plug-in can be used to restrict the sequences manually if desired.
In recent years, many tools have emerged that integrate the process of chord sequence exploration into Digital Audio Workstations (DAWs). They allow a composer to explore chord progressions by selecting from compatible chords substitutions, and some can suggest single chord continuations. These tools typically contain a catalogue of template sequences from which to start an exploration session. Absent from the panorama are generative tools that work with coherent chord sequences: those where important intra-sequence repetition is explicitly defined and manipulated. As discussed in this Introduction, this is a difficult goal to achieve due to weaknesses in the generative capacity of standard statistical models.
The pervasive type of statistical model class for music is the
n-gram model [
14,
15]. An
n-gram model defines the probability of the next event in a sequence based on the proximal history of
events. Training and inference from such models is computationally efficient and they perform well in music where local dependencies are the dominant carrier of information. The problem with
n-gram models is that they cannot cope efficiently with long range dependencies, because capturing these requires an exponentially increasing amount of training data in the distance between dependent events. This has led some researchers to consider the more powerful model class of
context free grammars [
16,
17,
18,
19] which can encode arbitrarily distant dependencies, but severe training and inference complexities come with their additional generative capacity.
Somewhat surprisingly, neither
n-gram nor context-free grammars can deal explicitly with the phenomenon of repetition, for example, neither can express the language of all sequences of the form
where
W is an arbitrary sequence. These forms are ubiquitous in music and especially in repetition-oriented music such as electronic dance music loops. Conklin [
20] provided a partial solution to this problem, by overlaying a structural pattern on an underlying
n-gram model. Patterns are learned by extracting information from a single template piece, or they can be designed by a composer, as developed in this paper.
The theory behind the plug-in combines machine learning of statistical models, and sampling from the models for generation. A novel aspect of the method is in the guided sampling using a specified chord sequence pattern which contains both variables and locked chords. The theory was initially designed for trance loop generation [
20], and is here extended with a diatonicity component. A voicing algorithm is integrated to generate a multi-voice musical texture which realises the underlying symbolic chord representation. The plug-in is implemented in the JUCE framework [
21], to ensure cross-host and cross-platform compatibility and to simplify user interface development. We currently support Audio Unit and VST plug-in hosts on macOS and VST plug-in hosts on Microsoft Windows.
2. Methods
This section presents the theory behind the chord generation plug-in. The chord and pattern language is defined. Then, the statistical model used for chord sequence generation is presented, along with a description of the method for training from a corpus. A method for controlling the diatonicity of generated sequences is introduced, and a method for rendering chords into MIDI events is described.
2.1. Chords
The chord generation plug-in works with a purely symbolic and diatonic representation of chords, not one based on pitch class numbers, thus is able to distinguish between enharmonic chords. The set of chords
considered is all diatonic roots (diatonic pitch class plus at most one sharp or flat), crossed with triad quality:
where
is a set of triad qualities (major and minor, in this initial version of the plug-in).
2.2. Semiotic Patterns
A
pattern is a sequence of variables
. Variables may be repeated in the pattern and can be instantiated by specific chords. A
substitution is an injective mapping from the set of variables occurring in the pattern to
(a mapping is
injective if no chord is mapped onto by two distinct variables). A pattern can be viewed as a graph with sequence indices as nodes, and with edges between nodes indexing the same variable. This can be translated into a convenient linear representation, as shown at the bottom of
Table 1, where the variables are represented as different geometric shapes. A pattern is instantiated by any chord sequence that complies with the specified equality relations encoded by equivalent shapes. For example, the pattern in
Table 1 is instantiated by any eight-chord sequence with the first and last three chords retrogrades of one another, separated by two other distinct chords.
The
language defined by a pattern
is the set of all chord sequences instantiating the pattern for any possible substitution. The plug-in interface presents to the user a pattern manipulation facility, and generated sequences that are in
. As described in
Section 3.2, this is done by sampling from the statistical model, triggered by any operation that affects a variable in the working pattern.
2.3. Statistical Model
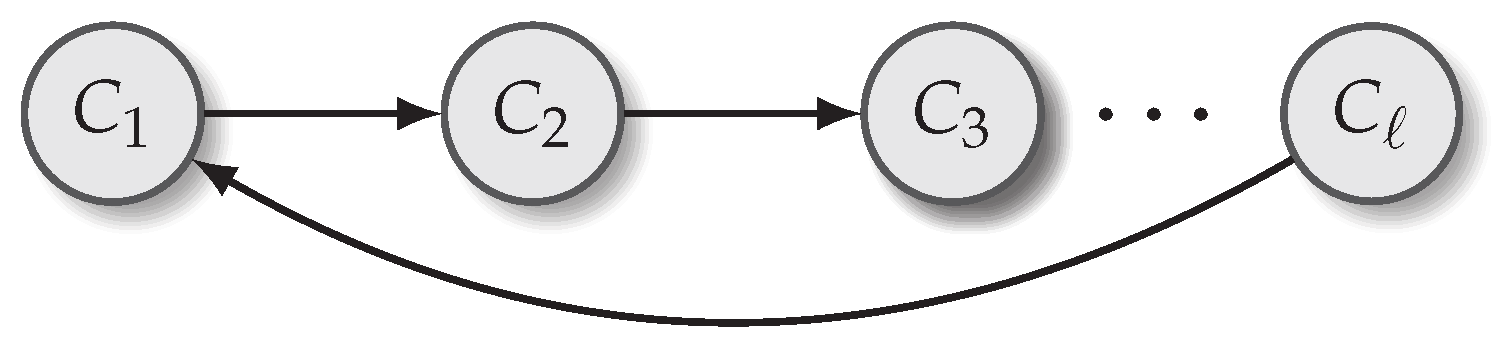
The core of the statistical model is a cyclic first-order model that factors the full joint probability of the chord sequence using a first-order Markov assumption. The probability of a chord sequence
is defined as:
where the introduction of
above ensures that the model is cyclic: that the first chord in the sequence depends on the last. As shown in
Figure 1, this can be depicted by a graphical model. The
are random variables each ranging over all possible chord types
, and edges show statistical dependencies.
2.4. Training the Model
A small corpus of anthem loops transcribed from Uplifting Trance pieces [
22] was used to train the statistical model. During model training, since the sequences represent loops, for every corpus sequence, its first chord was concatenated to the sequence before training.
To deal with sparse data and achieve a transposition invariant model, relational features of chords were used (see
Table 1). Each chord was assigned the derived attributes
and
, which represent the chord root movement (in diatonic intervals) and chord quality movement (major to minor, minor to minor, etc.), respectively. These can be linked together into a new attribute
, which has pairs as values. Since a value for
uniquely determines the next chord, it is possible to create a transition matrix over all possible chord bigrams
:
where
v is the value of the attribute
for the chord bigram
,
is the count of
v in the corpus, and
N is the number of chords in the corpus where the attribute is defined. Basic add-one smoothing was performed to ensure that no transitions have zero probability.
Training a first-order statistical model therefore comprises three steps: transforming all pieces in the training corpus by computing the attribute
for every chord; then, for all
v in the range of the attribute
, estimating the probability
as
, where
is the number of chords in the corpus having the value
v, and
N is the number of chords in the corpus; and, finally, a transition matrix over all concrete events can be compiled according to Equation (
3).
2.5. Sampling from a Model
Generating chord sequences given a pattern is done by sampling from the trained statistical model, retaining high probability sequences. A conceptually simple sampling method is known as
iterative random walk [
20]. For a single random walk, chords are progressively added to a sequence, maintaining variable substitutions previously made in the sequence and following the transition matrix probabilities. This procedure can be iterated many times to generate a rough picture of the sequence distribution.
For a creative chord generation method, it is very important that the model employed does not overfit the training data. The model must generalize away from the concrete corpus to a much wider population of unseen sequences to generate inspiring and even surprising new sequences. To determine the fit of the model to the trance corpus,
Figure 2 shows the distribution of 100,000 sampled sequences instantiating an eight-chord cyclic pattern (denoted
), and the location of the 150 training sequences as determined by a leave-one-out procedure. On the
x-axis is the per-event information content defined as
for a sequence
. The density of sampled sequences follows a typical shape for an
n-gram model. It can be seen that the model does not overfit the corpus, and that the corpus sequences generally are slightly towards the left tail of the sequence distribution. This result ensures that sampling from the model will not simply reproduce corpus sequences or their close variants.
2.6. Diatonicity
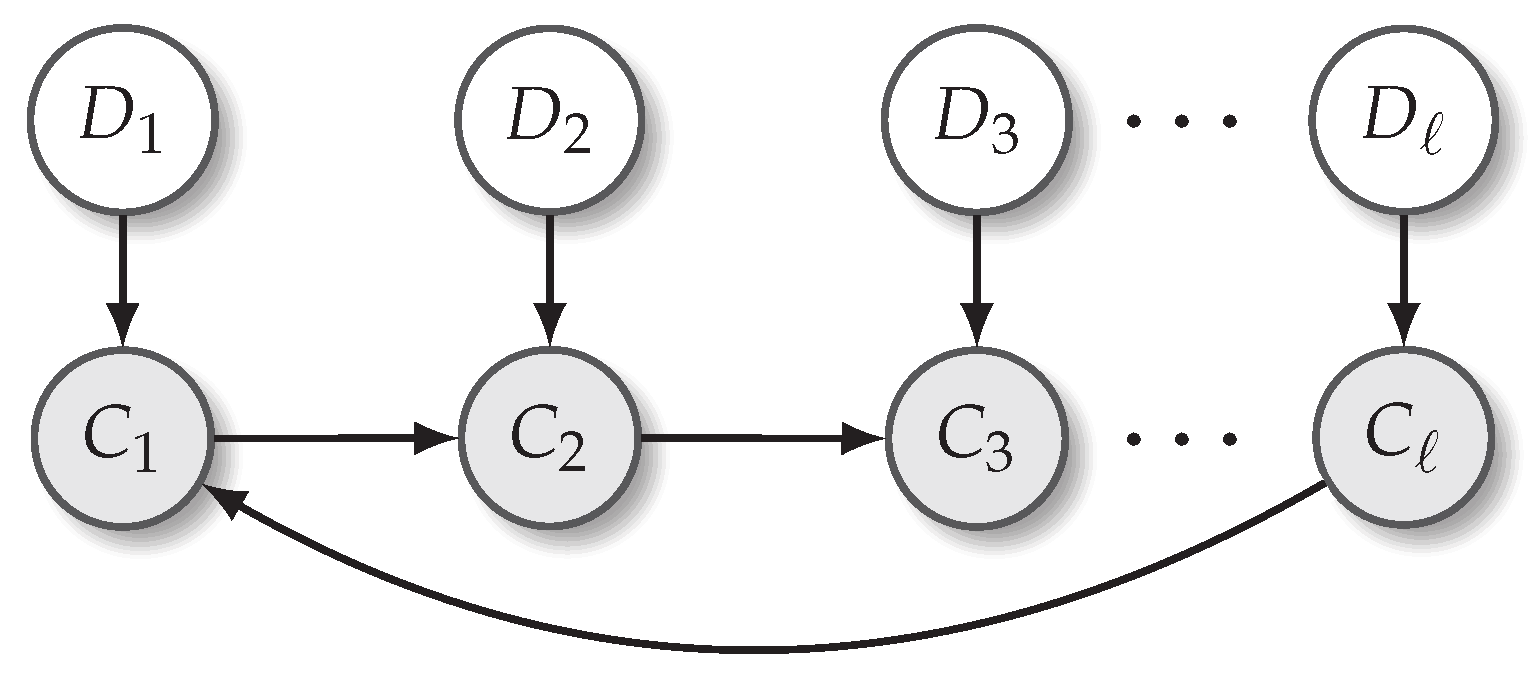
The statistical model described above is based on root and triad quality movements and captures local statistics but does not enforce global key consistency. In some settings, it may be desirable to restrict chords to a particular key, generate more adventurous sequences that do not follow a key, or in general something in between.
Consider the set of chords
compatible with a specified key, e.g. for A major (ionian mode):
Different sets
are defined for all seven modes formed above all diatonic roots (Equation (
1)). To control the overall diatonicity of a chord sequence in a given key, the sequence can be viewed as progressing jointly with a sequence
sampled from Bernoulli variables
indicating whether the respective chord
is diatonic in the given key, so
if
is in
. The joint probability can be factored as:
with
Figure 3 depicting this as a graphical model.
For the plug-in we assume the are i.i.d., i.e. that they have the same probability distribution. This allows the diatonicity of a chord sequence to be expressed simply by one global parameter . Therefore, will give a fully diatonic sequence, implies and a fully non-diatonic sequence will be generated.
The right-hand term of Equation (
4) can be expressed in terms of the basic model in Equation (
2) according to the following derivation
Given that the
are i.i.d., this derivation implies conveniently that, once
and
have been specified, they can be efficiently “compiled” into the basic transition matrix (Equation (
3)) by substituting Equation (
5) into Equation (
4) and precomputing
for both
and
and for all possible chord bigrams
.
2.7. Voicing
To render the generated chords into MIDI note structures, a voicing algorithm is used to generate smooth note transitions. Given a specified number of voices, for every position, all compact triads for all inversions are considered. The pitch height of the voicing is determined by an adjustable parameter, and the range is fixed to one octave. The L1 distance defines the distance between two successive pitch vectors [
23] and a dynamic programming algorithm is used to recover the sequence of voicings with minimum overall distance.
3. Results
The methods described above were applied to generate cyclic chord sequences which satisfy given semiotic patterns and diatonicity settings. First, the effect of the important diatonicity methods are illustrated using a suite of generated sequences. The details of the DAW plug-in are then discussed. Finally, some feedback on the plug-in received by a small user focus group is presented.
3.1. Diatonicity
As mentioned earlier, an important extension to the basic chord generation model (
Table 2) was the addition of the ability to specify a key and control overall diatonicity within that key (
Section 2.6). This was done by incorporating a diatonicity parameter
.
Table 2 illustrates a range of sampled sequences generated by the method. An eight-chord cyclic pattern was used (the same pattern used in
Table 1), with the variable ◇ locked to the chord
. The key is set to A major. Each sequence in
Table 2 represents the highest probability generation within 1000 iterations of random walk. Chords not in the set
for A major are boxed.
As expected, when ranging from
to
, an increasing number of diatonic chords appear in the sequences. Even non-diatonic sequences still have reasonable local transitions because the model is based on chord root and quality movement learned from the corpus, and, according to Equation (
4), chords are filtered and normalized according to the diatonicity value at a particular position.
It can be seen that the locking of the variable ◇ in a sense “pulls” even completely non-diatonic sequences reasonably back to the home key after divergence to distant chords. For example, the first sequence even touches on but eventually returns to the home key through the resolving chord . As discussed below, this locking facility is important for creative exploration of chord sequences.
3.2. The Plug-In
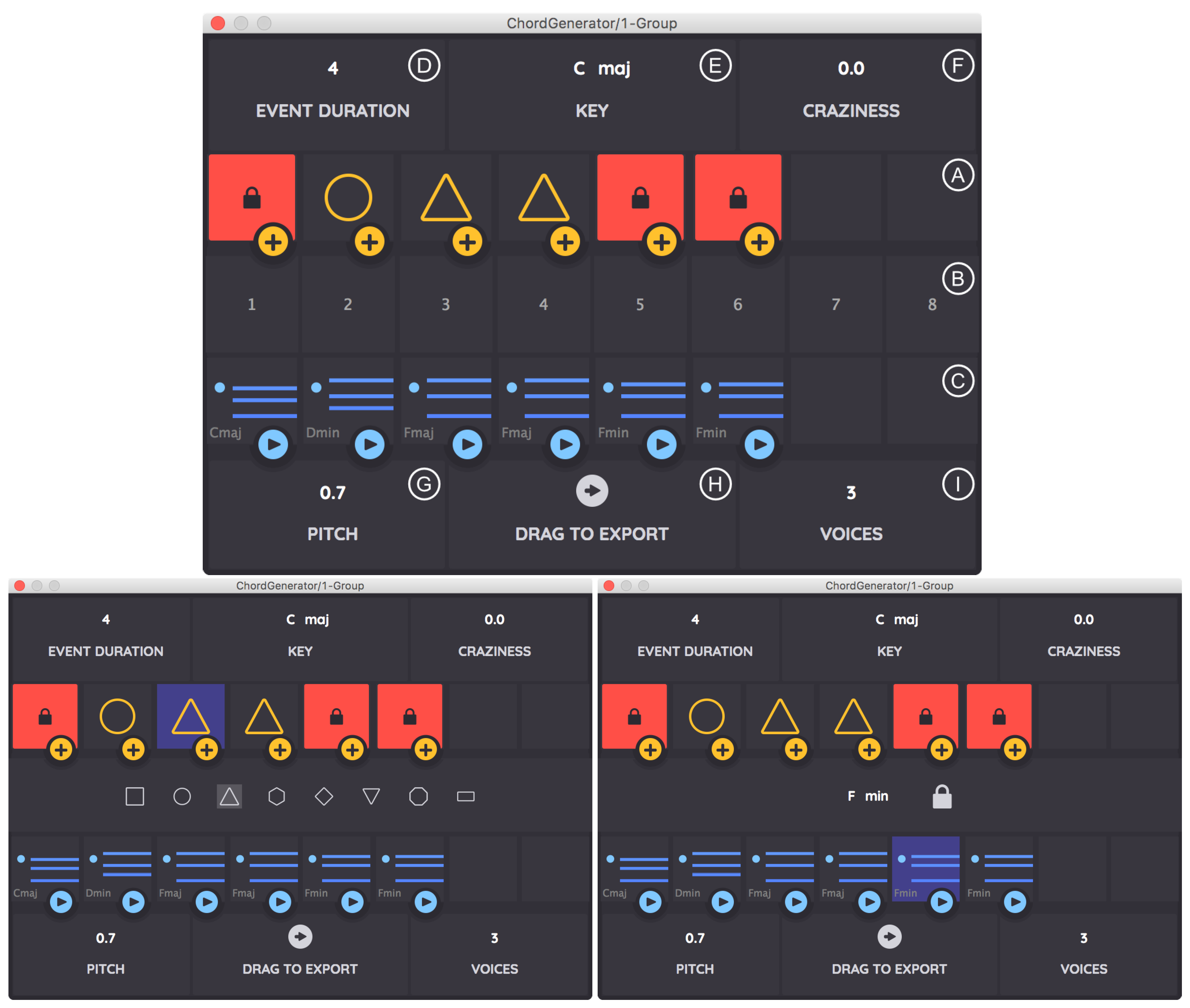
The plug-in has several components as shown in
Figure 4 (left: Ⓐ–Ⓘ), the principal parts being at the top the
workspace Ⓐ containing pattern variables and at the bottom the
factory Ⓒ: a generated chord sequence aligning with the variables. The
construction zone Ⓑ can be in different states, as shown in
Figure 4: displaying the mainline sequence in the factory and offering selection from a set of eight variant sequences instantiating the pattern (
Figure 4: left), selection of a variable for a particular position (upper right), and changing, locking, and unlocking of the chord at a particular position (lower right). The sequence displayed in the factory is therefore either a mainline sequence or one of the eight variants.
A user may manipulate parameters including: the key for generation Ⓔ, the diatonicity Ⓕ, and the chord duration Ⓓ in beats. The voicing register can be specified Ⓖ as can the number of voices in the generated sequence Ⓘ. A generated sequence can be exported to the host DAW Ⓗ.
Sequences instantiating the current pattern are generated by sampling from the statistical model. Whenever a new variable is introduced into the pattern, a new mainline chord for this variable is generated by using the most likely chord given the context (chords before and/or after the current slot). The eight variants are selected from the highest probability sequences encountered during multiple random walks on the model (Equation (
4) and
Figure 3). Each random walk is required to respect the the current variable substitution.
A key feature of the plug-in is the ability to lock and unlock individual positions while leaving others free to be generated by the statistical model. Chord slots can be locked to the displayed chord or manually set to a selected chord. The lock operation saves the existing variable at a position, and internally creates a new hidden variable which is sampled as described above. The unlock operation restores the original variable at that position, and, if it is now the only occurrence of that variable in the pattern, new mainline and variant sequences are generated by sampling, as described above.
3.3. User Feedback
To explore the usability of the plug-in, we handed out the development prototype to twelve users and asked them for their opinions. User 1 is a radio commercial producer without formal music education. User 2 is an electronic/experimental musician, singer, and digital/visual artist; although she has some music education, she primarily writes music “by ear”. User 3, similar to User 2, comes from the field of experimental music and digital art. User 4 is a researcher working in the field of Music Technology, and he is also a trained musician. User 5 is a professional producer working mainly in the field of film scoring, and he has studied music at a renowned institution. User 6 is a sound technician and musician without music education. User 7 describes himself as a hobby musician who likes to use generative music tools. Users 8–12 are semi-professional producers. Users 1–5 and 8–11 use macOS, Users 6, 7, and 12 use Microsoft Windows. The users tested the VST version of the plug-in in Ableton Live, Steinberg Cubase, Apple Logic Pro X, Tracktion Waveform, and FL Studio.
The primary benefits of the plug-in, and underlying theory, highlighted by these test users include the support of routine processes in music production or generation and its creative potential. For users such as User 1, generative approaches could substantially accelerate routine workflows such as laying out a basic harmonic pattern which is subsequently used as an inspiration for jingles. User 4 was impressed by how we solved the pattern definition workflow and how easy it is to get an audible result. While User 4 felt that some technical/UI-related limitations excluded the generation of advanced rhythmic patterns, User 5 immediately recognized the potential of the software to generate multi-level polyrhythmic patterns — something he routinely does in his work by means of manual MIDI editing, which could be streamlined with the plug-in. Users 2 and 3, working in experimental music and digital art, would not use the plug-in in their music-making routine but might use it to overcome writer’s block and get new inspiration. User 7 appreciated the simplicity of the user interface and the quality of the generated chord sequences, and was particularly impressed by the possibility to jump between chord sequence variants. Users 8–12 pointed out that they really liked that the I2C8 plug-in does one thing well instead of trying to be too general, and they praised the intuitive design of the user interface, which enabled them to use it without reading the manual beforehand.
Critical feedback related to technical constraints of the plug-in in the context of a DAW, e.g. most parameters are not editable if the plug-in is in playback mode (User 4). Users 2 and 3 commented that it could be complicated to set up the plug-in; however, that is mostly due to the way MIDI plug-ins are handled in host DAWs. User 6, on the other hand, had no problems with using the software but felt that its functionality was limited and would prefer a product that more explicitly incorporates music theory. User 9 proposed including a generative engine for chord durations and MIDI velocities as well. User 10 missed the functionality to synchronize the generated chord sequences over several instances of the plug-in to easily generate arrangements with more than one harmony track. User 11 found the diatonicity function quite unique and would like to see an extension to more complex chords (containing sevenths and ninths). User 12 suggested that we include more complex rhythmic patterns and a feature for automatic arpeggiation of generated chord sequences.
4. Discussion and Conclusions
This paper has presented the theory and implementation of a plug-in for dedicated chord sequence generation. Based originally on a statistical model for trance sequence generation [
20], the theory has been delivered in a plug-in which also provides important extensions such as diatonicity control, chord locking, and voicing.
The method implemented by the plug-in clearly separates it from other tools that are already on the market. Most of these tools could be described as being chord recommendation engines or chord sequence builders, whereas we generate a set of full chord sequences that satisfy a given structural pattern. Intelligent assistant functionalities are a new market segment which did not exist until recently. They have become a necessity as in recent years more and more people have started making music, yet many have little to no knowledge of the basics of music and little interest in studying these basics. Equally, the pressure on experienced producers to deliver creative output to the industry has risen dramatically.
This trend has led to the emergence of tools that provide semi-automation and assistance on various levels in the music production chain. The majority of the available solutions offers a rather limited set of musical capabilities. Such possibilities may seem impressive to a newcomer in music production. However, since the same rule sets are followed perpetually, the creative output soon becomes levelled and monotonous. Therefore, such technologies are not useful to advanced producers.
At present, there is a vacuum for tools for semi-pro and pro users that deliver high-quality chord generation output, yet are simple and fun to use. This is a new market which in particular caters to electronic music producers. It is the fastest-growing segment within the complete market. It has seen a continuous rise over the past years thanks to the popularity of the genre. A steady influx of young people are experimenting with electronic music production. It is accompanied by an explosion in blogs, forums, etc. communicating about how to create those beats. Through the effective promotion of several DJs in electronic music, one can be attracted by the opportunity to reach superstar status. Electronic music festivals have taken the world by storm in recent years, a fact which amplifies the prevalence of all types of electronic genres.
For future work, we view the extension of the voicing algorithm as highest priority: extending this with bass- and melody-specific statistical models giving explicit rather than implicit control of these lines. Combined with the ability to open multiple plug-in instances, the user can isolate and independently explore each line. This will allow a user to progress from chord sequence generation through to the generation of a full musical texture.
Author Contributions
Conceptualization, D.C., M.G., and S.O.; Methodology, D.C. and M.G.; S.O. software, M.G.; Validation, M.G. and D.C.; Formal Analysis, D.C.; Writing—Original Draft Preparation, D.C., M.G., and S.O.; Writing—Review and Editing, D.C.; Project Supervision and Administration, S.O.; and Funding Acquisition, D.C. and S.O.
Funding
This research was supported by the project I2C8 (Inspiring to Create) which is funded by the European Union’s Horizon 2020 Research and Innovation programme under grant agreement number 754401.
Acknowledgments
Thanks to Kerstin Neubarth for valuable discussions on the research and the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| DAW | Digital Audio Workstation |
| VST | Virtual Studio Technology |
| EDM | Electronic Dance Music |
| UI | user interface |
| JUCE | Jules’ Utility Class Extensions |
References
- McVicar, M.; Santos-Rodriguez, R.; Ni, Y.; De Bie, T. Automatic chord estimation from audio: a review of the state of the art. IEEE/ACM Trans. Audio Speech Lang. Process. 2014, 22, 556–575. [Google Scholar] [CrossRef]
- Scholz, R.; Vincent, E.; Bimbot, F. Robust modeling of musical chord sequences using probabilistic n-grams. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP 2009), Taipei, Taiwan, 19–24 April 2009; pp. 53–56. [Google Scholar]
- Di Giorgi, B.; Dixon, S.; Zanoni, M.; Sarti, A. A data-driven model of tonal chord sequence complexity. IEEE/ACM Transactions on Audio, Speech Lang. Process. 2017, 25, 2237–2250. [Google Scholar] [CrossRef]
- Simon, I.; Morris, D.; Basu, S. MySong: Automatic accompaniment generation for vocal melodies. In Proceedings of the SIGCHI Conference on Human Factors in Computing Systems (CHI 2008), Florence, Italy, 5–10 April 2008; pp. 725–734. [Google Scholar]
- Huang, C.Z.A.; Duvenaud, D.; Gajos, K.Z. ChordRipple: Recommending chords to help novice composers go beyond the ordinary. In Proceedings of the 21st International Conference on Intelligent User Interfaces, Sonoma, CA, USA, 7–10 March 2016; ACM: New York, NY, USA, 2016; pp. 241–250. [Google Scholar]
- Papadopoulos, A.; Roy, P.; Pachet, F. Assisted lead sheet composition using FlowComposer. In Principles and Practice of Constraint Programming; Rueher, M., Ed.; Springer International Publishing: Cham, Switzerland, 2016; pp. 769–785. [Google Scholar]
- Raczyński, S.A.; Fukayama, S.; Vincent, E. Melody harmonization with interpolated probabilistic models. J. New Music Res. 2013, 42, 223–235. [Google Scholar] [CrossRef]
- Pardo, B.; Birmingham, W.P. Algorithms for chordal analysis. Comput. Music J. 2002, 26, 27–49. [Google Scholar] [CrossRef]
- Pérez-Sancho, C.; Rizo, D.; Iñesta, J.M.; Pérez-Sancho, C.; Rizo, D.; Iñesta, J.M. Genre classification using chords and stochastic language models. Connect. Sci. 2009, 20, 145–159. [Google Scholar] [CrossRef]
- Hedges, T.; Roy, P.; Pachet, F. Predicting the composer and style of jazz chord progressions. J. New Music Res. 2014, 43, 276–290. [Google Scholar] [CrossRef]
- Cohn, R. Audacious Euphony Chromaticism and the Consonant Triad’s Second Nature; Oxford University Press: New York, NY, USA, 2012. [Google Scholar]
- Lewin, D. Generalized Musical Intervals and Transformations; Yale University Press: New Haven, CT, USA, 1987. [Google Scholar]
- Hook, J. Uniform triadic transformations. J. Music Theory 2002, 46, 57–126. [Google Scholar] [CrossRef]
- Conklin, D.; Witten, I. Multiple viewpoint systems for music prediction. J. New Music Res. 1995, 24, 51–73. [Google Scholar] [CrossRef]
- Rohrmeier, M.; Pearce, M. Musical syntax I: Theoretical perspectives. In Springer Handbook of Systematic Musicology; Bader, R., Ed.; Springer: Berlin/Heidelberg, Germany, 2018; pp. 473–486. [Google Scholar]
- Gilbert, E.; Conklin, D. A probabilistic context-free grammar for melodic reduction. In Proceedings of the IJCAI 2007: International Workshop on Artificial Intelligence and Music, Hyderabad, India, 6–12 January 2007; pp. 83–94. [Google Scholar]
- Rohrmeier, M. Towards a generative syntax of tonal harmony. J. Math. Music 2011, 5, 35–53. [Google Scholar] [CrossRef]
- Abdallah, S.; Gold, N.; Marsden, A. Analysing symbolic music with probabilistic grammars. In Computational Music Analysis; Meredith, D., Ed.; Springer: Basel, Switzerland, 2016; pp. 157–189. [Google Scholar]
- Tsushima, H.; Nakamura, E.; Itoyama, K.; Yoshii, K. Generative statistical models with self-emergent grammar of chord sequences. J. New Music Res. 2018, 47, 1–23. [Google Scholar] [CrossRef]
- Conklin, D. Chord sequence generation with semiotic patterns. J. Math. Music 2016, 10, 92–106. [Google Scholar] [CrossRef]
- ROLI Ltd. The JUCE Library. Available online: https://juce.com/ (accessed on 16 June 2018).
- UTALC. Uplifting Trance Anthem Loop Corpus. Available online: http://www.lacl.fr/~lbigo/utalc (accessed on 16 June 2018).
- Tymoczko, D. Scale theory, serial theory and voice leading. Music Anal. 2008, 27, 1–49. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).